Abstract
Microsatellites (short tandem polynucleotide repeats) are found throughout eukaryotic genomes at frequencies many orders of magnitude higher than the frequencies predicted to occur by chance. Most of these microsatellites appear to have evolved in a generally neutral manner. In contrast, microsatellites are generally absent from bacterial genomes except in locations where they provide adaptive functional variability, and these appear to have evolved under selection. We demonstrate a mutational bias towards deletion (repeat contraction) in a native chromosomal microsatellite of the bacterium Mycoplasma gallisepticum, through the collection and analysis of independent mutations in the absence of natural selection. Using this and similar existing data from two other bacterial species and four eukaryotic species, we find strong evidence that deletion biases resulting in repeat contraction are common in bacteria, while eukaryotic microsatellites generally experience unbiased mutation or a bias towards insertion (repeat expansion). This difference in mutational bias suggests that eukaryotic microsatellites should generally expand wherever selection does not exclude them, whereas bacterial microsatellites should be driven to extinction by mutational pressure wherever they are not maintained by selection. This is consistent with observed bacterial and eukaryotic microsatellite distributions. Hence, mutational biases that differ between eukaryotes and bacteria can account for many of the observed differences in microsatellite DNA content and distribution found in these two groups of organisms.
Microsatellites are defined as tandem repetitive DNA sequences with repeat motif lengths of six base pairs or less. These sequences are found in great excess throughout the genomes of all studied eukaryotes (Hancock 1995; Cox and Mirkin 1997). Tandem repeats experience replication slippage, a unique mutational process that leads to insertions and deletions of one or a few repeat units. These mutations occur at rates orders of magnitude above background base-pair and insertion/deletion (indel) mutation rates (Levinson and Gutman 1987; Schlotterer and Tautz 1992). It has been argued that, among microsatellite repeats alone, replication slippage generates more genetic change in eukaryotes each generation than do all base substitution mutations (Bell 1996).
Eukaryotic microsatellites appear to evolve in a generally neutral manner. They are most commonly found in positions where they are least likely to have functional effects (Metzgar et al. 2000), and they generally yield allelic distributions consistent with neutrality (Schlotterer and Pemberton 1994). Modeling studies have shown that adaptively neutral replication slippage is enough to explain the extreme excess of tandem repeats in eukaryotic genomes, given that the insertions generated by replication slippage are at least as common as deletions (Bell and Jurka 1997; Kruglyak et al. 1998). Approximate mutational symmetry (equal rates of insertion and deletion) or asymmetry in favor of repeat expansion has been found in both yeast (Henderson and Petes 1992; Strand et al. 1994) and higher eukaryotes (Fig. 1; Amos et al. 1996; Ellegren 2000; Jones et al. 1999; Kayser et al. 2000; Primmer et al. 1996; Rubinsztein et al. 1999; Xu et al. 2000).
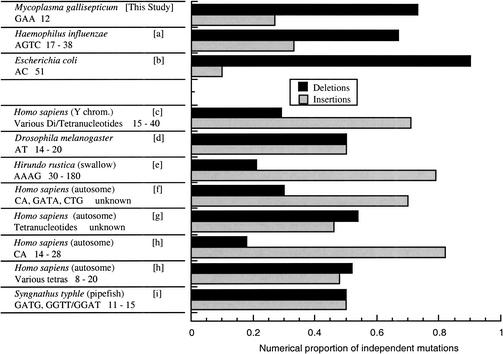
Figure 1.
Bacterial tandem repeats are biased towards deletion, while eukaryotic repeats are unbiased or biased towards insertion. Organism identifications (species names) are shown on the first line, followed by the source reference in brackets. Repeat types (motif sequences) are shown on the second line below the species names, followed by the lengths of the repeats (number of motifs). Data sources are as follows: a) De Bolle et al. 2000; b) Morel et al. 1998; c) Kayser et al. 2000; d) Harr and Schlotterer 2000; e) Primmer et al. 1996; f) Rubinsztein Amos and Cooper, 1999; g) Xu et al. 2000; h) Ellegren 2000; i) Jones et al. 1999.
It was recently shown that certain types of eukaryotic microsatellites experience a length-dependent increase in either the magnitude or the rate of deletions relative to the magnitude or rate of insertions (Wierdl et al. 1997; Ellegren 2000; Harr and Schlotterer 2000; Xu et al. 2000). Above a certain critical length, repeat expansion at these loci is limited by an increasing tendency to contract, such that once a microsatellite reaches a certain length, the average change in length due to mutation is negative.
It has been clearly shown that replication slippage also occurs in bacteria (Levinson and Gutman 1987; Morel et al. 1998; Metzgar et al. 2001). Despite this fact, microsatellites do not generally occur in bacterial genomes at higher frequencies than would be predicted assuming chance association of nucleotides (Field and Wills 1998; Field et al. 1999). The only exceptions to this absence are functional repeats (contingency loci), which are located in or near antigenic determinant genes and genes for other pathogenicity factors in bacterial pathogens (Moxon et al. 1994). These repeats provide functional hypermutability to these genes, allowing the pathogens carrying them to rapidly and adaptively switch antigenic phenotypes between generations, and as such are quite obviously under selection in the presence of host immune responses (Moxon et al. 1994).
How do bacteria avoid the genome-wide accumulation and expansion of tandem repeats that is both predicted by theory and also clearly apparent in eukaryotes? Two potential mechanisms are selection and mutational biases. Purifying selection might be acting against individual cells carrying mutations at any repetitive locus, or directional selection for decreased genome size might favor individuals with short microsatellites in general. These selective mechanisms would come at a considerable cost, because the repetitive sites at which such selection would have to act are very numerous and mutate at high rates (Metzgar et al. 2001). Selection acting on all of the repeats in a bacterial genome would generate a very high mutational load (loss of many individuals to selection) and would have to act against very small incremental increases in genome size or repetitivity, many of which would be expected to have minimal phenotypic effects.
The recurrent detriments associated with direct selection acting against individuals with expanded repeats could, over many generations, favor lineages in which fewer expansions occurred or in which expansions were outnumbered by contractions (lineages with mutational biases). Recurrent selection acting differentially on the products of mutational mechanisms can generate selective pressure on the mechanisms themselves, so long as the genes regulating these mutational mechanisms remain linked to the directly selected genes on which they act, through the process of second-order selection (Weber 1996; Metzgar and Wills 2000). Second-order selection can act effectively in asexual organisms such as bacteria because asexuality allows long-term maintenance of linkage between the directly selected products of mutation and the mutational mechanisms that are responsible for their existence. In clonal lineages under selection for decreased microsatellite length or variability, second-order selection would be expected to favor (respectively) deletion biases or low mutation rates. Since microsatellites are known to have high rates of replication slippage in both bacteria and eukaryotes, we hypothesize here that bacterial genomes are protected from tandem repeat expansion by the action of strong, pervasive deletion biases in their microsatellite mutation spectra.
We have collected and sequenced 44 independent mutations occurring in a native trinucleotide-repeat contingency locus of Mycoplasma gallisepticum, an avian-parasitic bacterium, and compared rates of insertion and deletion (see Methods). The contingency repeat analyzed here lies upstream of an antigenic determinant gene (a pMGA hemagglutinin). When the repeat is 12 trinucleotide units long the gene is on, but the gene is turned off when replication slippage changes this length. One of us (L.L.) had previously replaced the affected pMGA gene with a lacZ reporter, allowing visual identification of mutants (Liu et al. 2000). These mutants arose in separate laboratory cultures, which both insured their independence and minimized the potential effects of natural selection on the distribution of observed mutations. Mutants were collected after minimal culture time to minimize selective competition. However, the mutation rate of Mycoplasmas is high enough that multiple mutants did undoubtedly arise in some cultures. We therefore performed competition experiments to control for strong selective benefits correlated with deletion mutations occurring in the locus under study.
The results were congruent with previously existing data from the bacteria Haemophilus influenzae and Escherichia coli, showing that a strong bias towards deletion does exist across a broad spectrum of tandem repeats in several widely diverged bacterial species. This bias appears to result from biases in mutation, as opposed to selection.
RESULTS AND DISCUSSION
The number and type of mutations seen in the M. gallisepticum trinucleotide repeat locus are shown in Table 1. Length mutations in the microsatellite accounted for 100% of the independent mutants collected in this study. Of 44 mutants, we found 12 insertions and 32 deletions—approximately a three to one bias towards deletion (Table 1 and Fig. 1).
Table 1.
The Mutational Spectra of Microsatellite Repeats in Bacteria
| Organism | Repeat motif | Repeat length | N | Source | Number of mutations, by change in repeat number | Average change in allele length (in repeats) | Sign test p-value (insertions vs. deletions) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| deletions | insertions | |||||||||||
| −>2 | −2 | −1 | +1 | +2 | +>2 | |||||||
| H. influenzae | AGTC | 17 | 19 | (a) | 1a | 3 | 11 | 3 | 1 | 0 | −.89 | |
| H. influenzae | AGTC | 23 | 14 | (a) | 0 | 0 | 9 | 4 | 1 | 0 | −.29 | |
| H. influenzae | AGTC | 32 | 22 | (a) | 0 | 1 | 12 | 9 | 0 | 0 | −.23 | |
| H. influenzae | AGTC | 38 | 8 | (a) | 1a | 0 | 4 | 2 | 1 | 0 | −.63 | |
| (total from above) | AGTC | 17–38 | 63 | (a) | 2a | 4 | 36 | 18 | 3 | 0 | −0.44 | p < .02 |
| E. coli | AC | 51 | 21 | (b) | 5 | 4 | 10 | 1 | 0 | 1 | −2.9 | p < .001 |
| M. gallisepticum | GAA | 12 | 44 | this work | 2 | 14 | 16 | 7 | 5 | 0 | −0.80 | p < .005 |
N is the number of independent mutants analyzed. Repeat length refers to the number of repeats in the microsatellite before mutations have occurred. Length changes are shown in numbers of repeat motifs (a change of −2 in the AC repeat means that the sequence ACAC was deleted). For calculation of average change in length, these were conservatively counted as a loss of 4 repeats (since a loss of three repeats would not be seen in this system). Sign tests were not performed independently for each length of the H. influenzae microsatellite because of the small sample number. Data sources are as follows: (a) De Bolle et al. 2000; (b) Morel et al. 1998.
The actual magnitude of these mutations was not reported.
The competition experiments showed that the growth rates of different mutants were highly variable, but the observed variation was not correlated to microsatellite length (Table 2). A competition between a random single-repeat insertion mutant and a single-repeat deletion mutant showed a 10-fold fitness advantage of the insertion mutant, whereas a similar competition between double-repeat insertion and deletion mutants showed an eight-fold advantage of the deletion mutant. These results suggest that growth-rate differences between mutants derive from mutations unrelated to the length of the microsatellite analyzed here, and support earlier work demonstrating general variability in Mycoplasma growth rates (Dybvig et al. 1989).
Table 2.
Growth Rate of Mutants Does Not Appear to Be Controlled by the Direction of the Analyzed Microsatellite Mutations
| Competition | Microsatellite length | Initial mixture | Time in competition | Final mixture | Relative growth |
|---|---|---|---|---|---|
| 1 | 11 (single deletion) | 1 | 4 days | 2 | 1 |
| 13 (single insertion) | 2.5 | 48a | 9.6 | ||
| 2 | 10 (double deletion) | 1 | 1 day | 16 | 8 |
| 14 (double insertion) | 1 | 2 | 1 |
Competition experiments between mutants with different microsatellite lengths. Initial mixture ratios were determined by plating separate pre-competition cultures at a 10−6 dilution on plates and counting colonies. Final mixture ratios were determined by plating the mixes after the stated “time in competition” and sequencing the microsatellite locus from random colonies.
Includes several colonies that carried microsatellites longer than 13 repeats (these are most likely derived through mutation from the clone with 13 repeats). These included 14 repeats (4), 15 repeats (3), and 16 repeats (2).
Together, the results of our experiments support the hypothesis that the microsatellite analyzed here experiences a mutational bias towards deletion.
Two other studies, in addition to the data we present here, also support the general hypothesis that deletions dominate the spectrum of length mutations in bacterial repetitive DNA.
A strong deletion bias (2:1, as shown in Table 1 and Fig. 1) was detected by De Bolle and coworkers in Haemophilus influenzae during a study of phase variation driven by a contingency locus in this bacterial pathogen, and this bias was observed for repeats of varying length (De Bolle et al. 2000). The authors of that study noted that the functional repeats of H. influenzae must be maintained against this deletion bias by selection favoring their hypervariability (and therefore their length). As in our work, mutants were collected in the absence of the strong selective pressure that would be expected to affect the length of these repeats in natural environments. Mutational length changes in the microsatellite accounted for 100% of the observed loss-of-color mutants.
Another piece of evidence for a general bacterial deletion bias was found in a study (Morel et al. 1998) designed to test the effects of a variety of mutator phenotypes on microsatellite mutational dynamics in E. coli. The authors of that study placed a lacZ reporter under the mutational control of a human dinucleotide microsatellite. This construct was then inserted into the chromosome of a wild-type E. coli and assayed for relative rates of insertion and deletion mutations. The authors found an extreme bias towards deletions (approximately 10 to 1, as shown in Table 1) in this organism, a pattern that they report also held true for repeats of various lengths other than those for which the data were specifically enumerated. Unlike M. gallisepticum and H. influenzae, E. coli is not an obligate pathogen and does not maintain contingency repeats. E. coli exhibits a deficiency of almost all microsatellite types (Field and Wills 1998).
The data from E. coli provide critical support for our hypothesis. Of the three bacteria studied, E. coli is the only one in which the microsatellite is not part of a natural contingency locus. Since contingency loci are the only significantly long microsatellites found (to date) in bacteria, they provide the only opportunities to study the mutational dynamics of natural microsatellites. However, their mutation rates are functionally important and as such they might be controlled by specific targeted mutational systems. The high mutation rate and strong deletion bias shown by a long, artificial, unselected microsatellite in E. coli, an organism with no contingency loci and hence no reason to support any related mutational mechanisms, demonstrate that the hypermutability and strong deletion biases seen in contingency loci are not confined to functional repeats, nor are they confined to organisms which carry functional repeats.
This evidence aside, it seems unlikely that deletion biases would be a part of specialized mutational systems targeted to contingency loci. Selection, if acting specifically on the mutational spectra of contingency loci, would be expected to counteract deletion biases because contingency repeats must stay long to retain their adaptive hypermutability. With this in mind, it is interesting to note that the strongest deletion bias found in the data presented here comes from E. coli, the only model organism in this study which does not maintain contingency loci.
Our data showing a deletion bias in M. gallisepticum extend the demonstration of a general deletion bias to both another group of bacteria and to a trinucleotide repeat type. They also provide evidence that the bias is not inherent to the mismatch repair (MMR) system, since Mycoplasmas do not appear to have the genes for this system (Himmelreich et al. 1996). All of the bacterial repeats analyzed here show strong numerical deletion biases, while none of the eukaryotic repeats that have been studied show such a bias (Fig. 1). Taking into account the magnitude of each mutation, the bacterial microsatellites analyzed here also show consistently negative average changes in microsatellite length (Table 1).
Many other studies have collected insertion and deletion rate data from bacteria, but these studies were done in ways that prevent unbiased comparisons of these rates. Some studies in which insertion and deletion rates were enumerated involved serial selection, making it impossible to differentiate mutational and selective effects. Others assayed off-to-on mutations in nontriplet contingency repeats, preventing identification of insertion and deletion events of equal size. Some were done using repeats that are carried on multiple-copy plasmids, and in these systems plasmid segregation dynamics make it difficult to identify independent and unselected mutants. In addition, there is no reason to assume that replication slippage has the same effects on episomal microsatellites and on microsatellites that are part of a chromosome. These studies, however, do reveal a bias towards deletions; in E. coli, one study demonstrated that long, plasmid-carried dinucleotide microsatellites show approximately the same 10:1 deletion bias that is shown by similar microsatellites inserted into the chromosome (Levinson and Gutman 1987). Identical plasmid-carried microsatellites in Saccharomyces cerevisiae show no such bias (Henderson and Petes 1992). A recent study also demonstrated highly significant deletion biases in short, plasmid-borne di- and tetranucleotide microsatellites in both mutL+ and mutL− E. coli (Eckert and Yan 2000).
The three sets of data presented here, all of which support a strong general bias towards deletion in bacterial tandem repeats, are the only ones identifiable in the current literature which allow unbiased comparisons of unselected insertion and deletion mutation rates in bacterial microsatellites. These data show that mutational deletion biases in bacteria extend across a variety of repeats (di-, tri-, and tetranucleotides) and across a divergent sample of species from the bacterial domain, including those that utilize and maintain functional repeats (H. influenzae and M. gallisepticum) and those that do not (E. coli). These data sets can be compared with statistically similar data sets from eukaryotes that show no consistent deletion bias, and in fact sometimes yield a significant bias towards insertion (Fig. 1). These data sets had been collected specifically for the purposes of comparing insertion and deletion rates, and the justifications for using these data sets for this purpose are clearly stated in the original manuscripts. While eukaryotic repeats experience a length-dependent mutational bias, tending toward expansion when short and contraction when long (Wierdl et al. 1997; Ellegren 2000; Harr and Schlotterer 2000; Xu et al. 2000), the bias toward contraction in bacterial microsatellites appears to be length-independent (see Table 1, especially data from H. influenzae). This evidence strongly supports the hypothesis that genome evolution in bacteria is mutationally driven toward microsatellite contraction and hence minimization of genomic microsatellite content, and explains why bacterial microsatellites occur only in locations where they are maintained by positive selection. Eukaryotic microsatellites, in contrast, have expanded to great excess wherever selection does not exclude them. This is the predictable result of unbiased (or insertion-biased) replication slippage acting in the absence of selection.
In addition to repetitive DNA content and genome size, many other genomic characteristics that differ between groups of organisms may also result from differences in mutational mechanisms. Further investigation will reveal how much the character of genomes depends on direct selection acting on mutant alleles at many different loci, and how much depends on indirect second-order selection favoring organisms that have a high probability of producing particular types of mutations.
METHODS
Collection of Independent Mutants
The mutation rate of the color-marked contingency microsatellite in M. gallisepticum was sufficiently high that by the time a blue colony (derived from a lacZ+ cell) was large enough to collect, it inevitably contained lacZ− (white) cells. To collect independent mutants, a single lacZ+ colony was resuspended and spread on a plate containing X-gal. Growth conditions and blue/white analysis were as described previously (Liu et al. 2000). Blue colonies were then picked from this plate, such that each was derived from a blue cell. These colonies were then independently resuspended and replated on X-gal plates (one plate each), and single white colonies were picked at random from the resulting plates (one mutant colony per plate).
PCR and Sequencing
Independent mutants were picked and grown in liquid media. Aliquots of this liquid culture were frozen in 10% glycerol at −80°C. Five μL of liquid culture was transferred to a microfuge tube containing 300 μL of 10% wt/vol 100 mesh chelex beads (Sigma). The tube was vortexed for 10 sec, followed by boiling for 10 min, vortexing for 10 sec, then spinning down the beads for 3 min at 12,000g in a microfuge. PCR was performed to amplify the repetitive segment as described previously (Liu et al. 2000). The products were cleaned using a Concert PCR purification kit (GibcoBRL) and sequenced using standard ABI Big Dye protocols (Applied Biosystems) at the UCSD Cancer Center DNA Sequencing Core Facility.
Statistical Analysis of Deletion Bias Significance
We performed one-tailed sign tests (Zar 1984) to assess the significance of the deletion bias in each study, comparing the number of deletions of all lengths to the number of insertions. p-values are shown in Table 1.
Competition Experiments
We performed two competition experiments to test for growth-rate differences between clones carrying microsatellites of different lengths. Liquid cultures of mutants bearing single-repeat and double-repeat insertion and deletion mutations were grown, then diluted and plated to titer. Dilution cultures were started using mixtures of the single-repeat insertion and deletion mutants (experiment 1) and the double-repeat insertion and deletion mutants (experiment 2). These mixtures were grown to high density (“time in competition” in Table 2) and plated. Random colonies were selected and sequenced to determine the ratio of insertion and deletion mutants present after competition. The multiplicative difference between the initial and final population ratios was used as a measure of growth rate differences between the clones. Results are shown in Table 2.
Acknowledgments
D.M. was supported by a NASA NSCORT Exobiology Fellowship. L.L. was supported by NIH grant AI41113. This work was personally supported by C. Wills and K. Dybvig.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Footnotes
E-MAIL dmetzgar@hermes.scripps.edu; FAX (858) 784-8990.
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.198602.
REFERENCES
- Amos W, Sawcer SJ, Feakes RW, Rubinsztein DC. Microsatellites show mutational bias and heterozygote instability. Nat Genet. 1996;13:390–391. doi: 10.1038/ng0896-390. [DOI] [PubMed] [Google Scholar]
- Bell GI. Evolution of simple sequence repeats. Comput Chem. 1996;20:41–48. doi: 10.1016/s0097-8485(96)80006-4. [DOI] [PubMed] [Google Scholar]
- Bell GI, Jurka J. The length distribution of perfect dimer repetitive DNA is consistent with its evolution by an unbiased single-step mutation process. J Mol Evol. 1997;44:414–421. doi: 10.1007/pl00006161. [DOI] [PubMed] [Google Scholar]
- Cox R, Mirkin SM. Characteristic enrichment of DNA repeats in different genomes. Proc Natl Acad Sci. 1997;94:5237–5242. doi: 10.1073/pnas.94.10.5237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Bolle X, Bayliss CD, Field D, van de Ven T, Saunders NJ, Hood DW, Moxon ER. The length of a tetranucleotide repeat tract in Haemophilus influenzae determines the phase variation rate of a gene with homology to type III DNA methyltransferases. Mol Microbiol. 2000;35:211–222. doi: 10.1046/j.1365-2958.2000.01701.x. [DOI] [PubMed] [Google Scholar]
- Dybvig K, Simecka JW, Watson HL, Cassell GH. High frequency variation in Mycoplasma pulmonis colony size. J Bacteriol. 1989;171:5165–5168. doi: 10.1128/jb.171.9.5165-5168.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckert KA, Yan G. Mutational analyses of dinucleotide and tetranucleotide microsatellites in Escherichia coli: Influence of sequence on expansion mutagenesis. Nucleic Acids Res. 2000;28:2831–2838. doi: 10.1093/nar/28.14.2831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellegren H. Heterogeneous mutation processes in human microsatellite DNA sequences. Nat Genet. 2000;24:400–402. doi: 10.1038/74249. [DOI] [PubMed] [Google Scholar]
- Field D, Hood D, Moxon R. Contribution of genomics to bacterial pathogenesis. Curr Opin Gen Dev. 1999;9:700–703. doi: 10.1016/s0959-437x(99)00021-0. [DOI] [PubMed] [Google Scholar]
- Field D, Wills C. Abundant microsatellite polymorphism in Saccharomyces cerevisiae, and the different distributions of microsatellites in eight prokaryotes and S. cerevisiae, result from strong mutation pressures and a variety of selective forces. Proc Natl Acad Sci. 1998;95:1647–1652. doi: 10.1073/pnas.95.4.1647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hancock JM. The contribution of slippage-like processes to genome evolution. J Mol Evol. 1995;41:1038–1047. doi: 10.1007/BF00173185. [DOI] [PubMed] [Google Scholar]
- Harr B, Schlotterer C. Long microsatellite alleles in Drosophila melanogaster have a downward mutation bias and short persistence times, which cause their genome-wide underrepresentation. Genetics. 2000;155:1213–1220. doi: 10.1093/genetics/155.3.1213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henderson ST, Petes TD. Instability of simple sequence DNA in Saccharomyces cerevisiae. Mol Cell Biol. 1992;12:2749–2757. doi: 10.1128/mcb.12.6.2749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Himmelreich R, Hilbert H, Plagens H, Pirkl E, Li BC, Herrmann R. Complete sequence analysis of the genome of the bacterium Mycoplasma pneumoniae. Nucleic Acids Res. 1996;24:4420–4449. doi: 10.1093/nar/24.22.4420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones AG, Rosenqvist G, Berglund A, Avise JC. Clustered microsatellite mutations in the pipefish Syngnathus typhle. Genetics. 1999;152:1057–1063. doi: 10.1093/genetics/152.3.1057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kayser M, Roewer L, Hedman M, Henke L, Henke J, Braver S, Krueger C, Krawczac M, Nagy M, Dobosz T, et al. Characteristics and frequency of germline mutations at microsatellite loci from the human Y chromosome, as revealed by direct observation in father/son pairs. Am J Hum Genet. 2000;66:1580–1588. doi: 10.1086/302905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruglyak S, Durrett RT, Schug MD, Aquadro CF. Equilibrium distributions of microsatellite repeat length resulting from a balance between slippage events and point mutations. Proc Natl Acad Sci. 1998;95:10774–10778. doi: 10.1073/pnas.95.18.10774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levinson G, Gutman GA. Slipped-strand mispairing: A major mechanism for DNA sequence evolution. Mol Biol Evol. 1987;4:203–221. doi: 10.1093/oxfordjournals.molbev.a040442. [DOI] [PubMed] [Google Scholar]
- Liu L, Dybvig K, Panangala VS, van Santen VL, French CT. GAA trinucleotide repeat region regulates M9/pMGA gene expression in Mycoplasma gallisepticum. Infect Immun. 2000;68:871–876. doi: 10.1128/iai.68.2.871-876.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metzgar D, Bytof J, Wills C. Selection against frameshift mutations limits microsatellite expansion in coding DNA. Genome Res. 2000;10:72–80. [PMC free article] [PubMed] [Google Scholar]
- Metzgar D, Thomas E, Davis C, Field D, Wills C. The microsatellites of Escherichia coli: An analysis of the variability and distribution of short repetitive DNAs in a nonpathogenic prokaryote. Mol Microbiol. 2001;39:183–190. doi: 10.1046/j.1365-2958.2001.02245.x. [DOI] [PubMed] [Google Scholar]
- Metzgar D, Wills C. Evidence for the adaptive evolution of mutation rates. Cell. 2000;101:581–584. doi: 10.1016/s0092-8674(00)80869-7. [DOI] [PubMed] [Google Scholar]
- Morel P, Reverdy C, Michel B, Ehrlich SD, Cassuto E. The role of SOS and flap processing in microsatellite instability in Escherichia coli. Proc Natl Acad Sci. 1998;95:10003–10008. doi: 10.1073/pnas.95.17.10003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moxon ER, Rainey PB, Nowak MA, Lenski RE. Adaptive evolution of highly mutable loci in pathogenic bacteria. Curr Biol. 1994;4:24–33. doi: 10.1016/s0960-9822(00)00005-1. [DOI] [PubMed] [Google Scholar]
- Primmer CR, Ellegren H, Saino N, Moller AP. Directional evolution in germline microsatellite mutations. Nat Genet. 1996;13:391–393. doi: 10.1038/ng0896-391. [DOI] [PubMed] [Google Scholar]
- Rubinsztein DC, Amos B, Cooper G. Microsatellite and trinucleotide-repeat evolution: Evidence for mutational bias and different rates of evolution in different lineages. Phil Trans R Soc Lond B. 1999;354:1095–1099. doi: 10.1098/rstb.1999.0465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlotterer C, Pemberton J. The use of microsatellites for genetic analysis of natural populations. In: Schierwater B, Streit B, Wagner GP, DeSalle R, editors. Molecular ecology and evolution: Approaches and applications. Basel, Switzerland: Birkhauser Verlag; 1994. pp. 203–214. [Google Scholar]
- Schlotterer C, Tautz D. Slippage synthesis of simple sequence DNA. Nucleic Acids Res. 1992;20:211–215. doi: 10.1093/nar/20.2.211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strand M, Prolla T, Liskay R, Petes T. Destabilization of tracts of simple repetitive DNA in yeast by mutations affecting DNA mismatch repair. Nature. 1994;365:274–276. doi: 10.1038/365274a0. [DOI] [PubMed] [Google Scholar]
- Weber M. Evolutionary plasticity in prokaryotes: A panglossian view. Biol Phil. 1996;11:67–88. [Google Scholar]
- Wierdl M, Dominska M, Petes TD. Microsatellite instability in yeast: Dependence on the length of the microsatellite. Genetics. 1997;146:769–779. doi: 10.1093/genetics/146.3.769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu X, Peng M, Fang Z, Xu X. The direction of microsatellite mutations is dependent upon allele length. Nat Genet. 2000;24:396–399. doi: 10.1038/74238. [DOI] [PubMed] [Google Scholar]
- Zar J H. The sign test (22.6) In: Kurtz B, editor. Biostatistical Analysis. Englewood Cliffs, New Jersey: Prentice-Hall, Inc.; 1984. pp. 386–387. [Google Scholar]