Neural network analysis of lymphoma microarray data: prognosis and diagnosis near-perfect

Abstract

Background

Microarray chips are being rapidly deployed as a major tool in genomic research. To date most of the analysis of the enormous amount of information provided on these chips has relied on clustering techniques and other standard statistical procedures. These methods, particularly with regard to cancer patient prognosis, have generally been inadequate in providing the reduced gene subsets required for perfect classification.

Results

Networks trained on microarray data from DLBCL lymphoma patients have, for the first time, been able to predict the long-term survival of individual patients with 100% accuracy. Other networks were able to distinguish DLBCL lymphoma donors from other donors, including donors with other lymphomas, with 99% accuracy. Differentiating the trained network can narrow the gene profile to less than three dozen genes for each classification.

Conclusions

Here we show that artificial neural networks are a superior tool for digesting microarray data both with regard to making distinctions based on the data and with regard to providing very specific reference as to which genes were most important in making the correct distinction in each case.

Background

Alizadeh et al. [1] did a large scale, long-term study of diffuse large B-cell lymphoma (DLBCL), using microarray data chips. By doing cluster analysis on this data, they were able to diagnose 96 donors with an accuracy of 93% for this specific lymphoma; they were not able to predict which individual patients would survive to the end of the long-term study. The International Prognostic Index for this disease was incorrect for 30% of these patients.

Cluster analysis, together with other statistical methods for identifying and correlating minimal gene lists with outcome, have become established as the primary tools for the analysis of microarray data in cancer studies. We wished to test a different approach, ANN.

These two approaches to the analysis of microarray data differ substantially in their mode of operation. In the first examination of the data, clustering, as applied in numerous recent cancer studies, is an unsupervised mapping of the input data examples based on the overall pairwise similarity of those examples to each other (here, similarity with respect to the expression levels of thousands of genes); the method is unsupervised in that no information of the desired outcome is provided. Subsequent analysis of the clusters in these studies generally attempts to reduce the gene set to the subset of genes that are most informative for the problem at hand. This step is a supervised step since there is an explicit effort to find correlations in the pattern of gene expression that match the classification one is attempting to make among the input examples (see Discussion for specific examples). The input for this supervised step is the product of an unsupervised step. As this subselection is not routinely subjected to independent test using input examples originally withheld from the subselection process, it is generally not possible to judge how specifically the subselection choices relate to this specific set of examples as opposed to the general population of potential examples. To the extent that the gene set employed is much larger than the gene set that really determines the classification, it is possible that much of the clustering result will be based on irrelevant similarities.

On the other hand, backpropagation neural networks are a supervised learning method that has an excellent reputation for classification problems. During the training phase, the ANN are supplied with both the input data and the answer and are specifically tasked to make the classification of interest, given a training set of examples from all classes. That is, the ANN are constantly checking to see if they have gotten the 'correct' answer, the answer being the actual classification not just the overall similarity of inputs.

Networks accomplish this by continually adjusting their internal weighted connections to reduce the observed error in matching input to output. When the network has achieved a solution that correctly identifies all training examples, the weights are fixed; it is then tested on input examples that were not part of the training set to see if the solution is a general one. It is only in this independent test that the quality of the network is judged.

Investigators are not limited to a single network. It is feasible to train a series of networks using, say, 90% of the examples for training and holding back 10% for testing. A different 10 % can be tested in a second network and so on. In this way, with the training of ten networks, each input can be found in a test set one time and can, therefore, be independently evaluated. The data presented below, with the exception of a few cases, are the output of ten slightly different trained networks, operating in test mode, which collectively evaluate the entire donor pool. This 'round-robin' procedure was employed, in duplicate, in every trial described throughout this work. The fact that one ends up with 10 networks is not an impediment to analysis since any future examples could be submitted to all 10 networks for evaluation, with a majority poll deciding the classification. That is, six networks in agreement on a particular input datum would determine the classification of that input. These networks are, of course, likely to be very similar in that their training sets differ only slightly.

A second major advantage of backpropagation networks follows from the first. Not only are neural networks trained to the specific question, rather than a loose derivative of that question, and tested for generality, but they can also be asked for a quantitative assessment of how they got the correct answer. Numerical partial differentiation of the network with respect to a given test input example [2,3] allows one to see the network's evaluation of the relative impact of each gene in arriving at the correct answer for this particular input. Cluster analysis, including the statistical correlations, has no corresponding highly focused sight for targeting specific similarities as opposed to non-specific similarities. To the extent that this is true, neural networks should be able to identify relatively small gene subsets which will significantly outperform the initial gene sets in classification and which will also significantly outperform the gene subsets suggested by cluster analysis.

Results

Determining patient prognosis from microarray data

Cluster analysis [1,4] had shown that the 4026 gene expression panels for 40 DLBCL patients contained some information relevant to the question of prognosis but these authors did not make an attempt to provide survival predictions for individual patients.

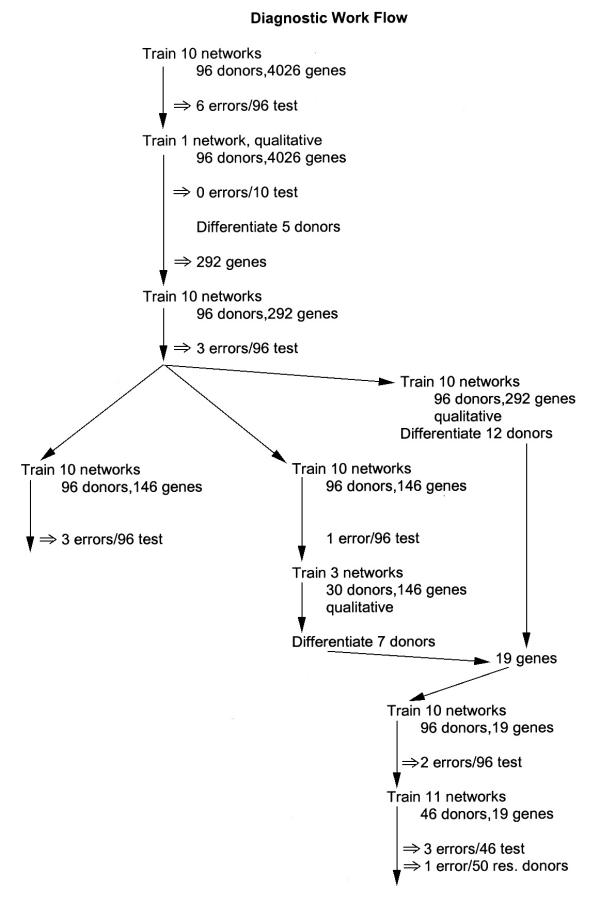
We wished to see if the neural network strategy, of train, test, differentiate, retrain on the reduced gene set, and retest, could produce any useful result with respect to prognosis on an individual basis. The approach would be: [1] use the entire gene set without preprocessing to train a network, testing to confirm that it had at least a good fit to the problem and, [2] use the network's definition of the problem, by differentiating the network, to focus on those genes most essential to the classification. These genes would then form the basis for training new networks with hopefully improved performance. Over 130 networks were trained for this study. Figure 1 shows a work flow schematic for this study. Table 1 provides a summary overview of the data, including data not shown.

Figure 1.

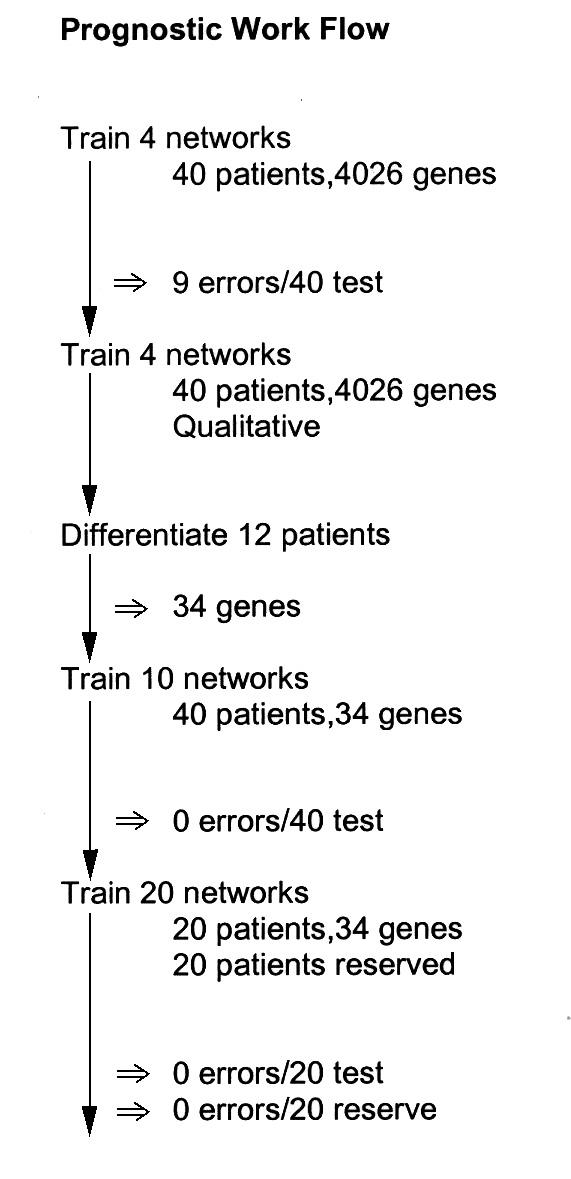
Flow schematic for the prognostic studies. This diagram shows the work path of the networks developed for optimizing patient prognosis.

Table 1.

Summary of all data with web site designators

Network	# Networks	Trn/Tst		# Genes	# Correct	False Positive	Shown/NS
P1	4	30/10		4026	31/40	8	NS
P2D	4	30/10		4026	31/40	5	NS
P3	10	36/4		34	39/40	0	NS
P4	10	36/4		34	40/40	0	Table 2
P5	20	19/1		34	20/20	0	NS
		/20		34	20/20	0	NS
P5	2	20/20		34	39/40	1	Comment
D1	10	9–86/10		4026	90/96	2	NS
D2D	1	86/10		4026	10/10	0	NS
D3	10	9–86/10	1–90/6	292	93/96	1	NS
D4	10	9–86/10	1–90/6	292	93/96	1	NS
D5	10	9–86/10	1–90/6	146 odd	93/96	1	NS
D6	10	9–86/10	1–90/6	146 even	95/96	1	Table 4
D7	10	9–86/10	1–90/6	146 even	95/96	1	NS
D8D	10	9–86/10	1–90/6	292	94/96	1	NS
D9D	3	86/10		146 even	95/96	1	NS
D10	10	9–86/10	1–90/6	19	94/96	1	Table 5
D11	11	9–42/4	2–41/5	19	43/46	1	NS
		/50		19	49/50	0	NS

P1 indicates prognosis data first reference. D2D indicates diagnostic data used for differentiation, second diagnostic reference.

Initially a network was trained to accept microarray data on the complete panel of 4026 genes from 40 patients. This network had 12078 input neurons with a semi-quantitative assessment of each gene, 100 middle-layer neurons, and a single output neuron. The networks were originally designed with 3 input bits per datum: one for sign,'-' = 1, and 2 for quantitative degree of signal with 00 being 0 to 0.5, 01 being >0.5 to 1.0, 10 being >1.0 to 2.0, and 11 being >2.0. Thus '011' would indicate a particular gene whose expression, relative to control, was increased at a magnitude >2. The training set included 30 donors, with 10 additional donors being held back as test data. The network was trained by processing 12 iterations of the complete training set. The test set, drawn from a mixture of survivors and non-survivors, was then run. The entire process was then repeated with a different choice of test data each time. In this round-robin fashion, all donors serve as test data for one of the networks, and each training set is necessarily slightly different. A round robin series of 4 networks was generated. Data underlying Figure 5 of the earlier report http://llmpp.nih.gov/lymphoma/data.shtml were used for training. The networks were asked to predict, based on the 4026 gene set, which of 40 DLBCL patients would survive to the end of the study (longest point = 10.8 yrs). Networks initially varied with from 1 to 3 errors on 10 test patients each, for a total of 31 of 40 patients correctly predicted (data not shown).¹ However, a trained neural network can be numerically differentiated [2,3] to show the relative dependence of the output (classification) on each active input neuron within an input vector. Briefly stated, the differentiation process involves slightly perturbing the activation (down from 1.0 to 0.85) of each active input neuron, one at a time, to note the specific change in the output value. In that there is one gene for each active node, the largest change in the output points to the most influential gene. We then trained qualitative networks, with 2 bits per gene, on the 4026 gene set in order to differentiate them ('1 0' for expression greater than, or equal to, the control, '0 1' for less than the control). The networks had 67 middle layer neurons. This coding has the effect that there is an active neuron for each gene in the set regardless of expression level and the total number of active input neurons is constant from input to input. By taking the top 25% of genes in each of 12 differentiations and requiring agreement of at least 4 of 12 patients in choosing each gene, we obtained a set of 34 genes. (These cutoff criteria are necessarily arbitrary and are only justified by subsequent proof that they produced gene subsets having the desired information.) A round-robin series of 10 networks, with 4 test donors each, produced a single error (DLCL0018) in survival predictions when trained on these 34 genes (data not shown)¹. The second round-robin training with the same gene set produced no errors, correctly evaluating all 40 patients in a series of 10 test sets (Table 2).

Table 2.

Test results of ten networks trained on 34 genes to predict survival among 40 patients

DC	NC	DC	NC
1.000000	0.956252	0.000000	0.189422
1.000000	0.958524	1.000000	0.983387
0.000000	0.030129	1.000000	0.966530
0.000000	0.051647	1.000000	0.972530
0.000000	0.015859	1.000000	0.986147
1.000000	0.960534	0.000000	0.025629
1.000000	0.959209	1.000000	0.934555
1.000000	0.988239	0.000000	0.153694
1.000000	0.883620	0.000000	0.058486
1.000000	0.983992	1.000000	0.985480
1.000000	0.828421	1.000000	0.949153
1.000000	0.527326	1.000000	0.956245
0.000000	0.046066	0.000000	0.147404
0.000000	0.025371	0.000000	0.025772
1.000000	0.987961	1.000000	0.782100
0.000000	0.145338	1.000000	0.977907
0.000000	0.130954	0.000000	0.223562
0.000000	0.148107	0.000000	0.039306
0.000000	0.020277	1.000000	0.982544
1.000000	0.956488	0.000000	0.025932

DC indicates the actual donor class, with 0.0 being negative. NC gives the network evaluation. The NC cutoff throughout this work is: ≥ 0.50 is taken as 1 and <0.50 is taken as 0. * marks the errors

For a second study, we took 20 patients and held them in reserve to model information from a "follow-up" study. Twenty networks were trained, on the 34 gene set, using the remaining 20 patients; each had 19 patients in the training set and 1 in the test set. Collectively, these networks made no errors in the prognosis of 20 patients. The data for the 20 reserve patients were then tested on all 20 trained networks to emulate follow-up data. Out of 400 individual scores, there were 5 errors distributed over 2 patients. A poll of the 20 networks, therefore, produced no errors by a majority, correctly classifying all 20 members of the follow-up group.(data not shown)

The 34 genes are given in Table 3. In 5 of 12 cases, the gene chosen as most influential in determining the correct prognosis was 18593, a tyrosine kinase receptor gene. While this gene set may not be the absolute best possible, it clearly does contain sufficient information for error-free predictions on these patients. The identification of this gene set will hopefully lead eventually to a better understanding of the interaction of these genes in this disease as a result of future studies.

Table 3.

34 genes identified in prognostic series

14706	Unknown Hs. 180836	17856	Interferon alpha/beta receptor-2
21367	Unknown Hs. 134746	21653	Unknown Hs. 1510936
13601	Similar to high mobility group	15656	Unknown
20397	FBP1 = FUSE binding protein 1	14393	Unknown Hs. 29205
17901	*pre-pro-orphanin	16631	Adenosine kinase
13097	Unknown	13318	Unknown Hs. 122428
14560	Unknown Hs. 32533	18330	Topoisomerase II beta
13867	Unknown	14983	Unknown
15664	Unknown	17721	Id1 = Inhibitor of DNA binding 1
20490	Unknown Hs. 122407	16850	pM5 protein = homology to collagenase
13650	Unknown	20481	Unknown Hs. 37629
18252	myosin-IC	17398	receptor r-1BB ligand
16886	JAW1	14772	Unknown
18593	Receptor protein-tyrosine kinase	19280	BENE
20759	Unknown Hs. 33053	21603	Unknown Hs. 33431
17802	thymosin beta-4	19258	tre-2
17887	A-raf = c-raf-1 kinase	21091	Unknown Hs. 199250

Diagnosing lymphoma from microarray data

The diagnosis of DLBCL lymphoma by biopsy is not trivial. Even with gene expression data, clustering techniques produced a misreading of 7 out of 96 donors [1], a result unimproved in their hands by further analysis of reduced gene panels. We wished to see if back propagation neural networks could do better using the same data set. Figure 2 shows a work flow schematic for this study. This testing over the whole donor set with 4026 genes produced 6 errors in diagnosis (data not shown).

Figure 2.

Flow schematic for the diagnostic studies. This diagram shows the work path of the networks developed for optimizing patient diagnosis.

Thus, in the first round, ANN merely match cluster analysis. In preparation for differentiation, a network was trained with the same donor sets as the first network above, but coded qualitatively. This network correctly classified the 10 members of the test set (data not shown). The 5 positive donors from the test set were each used, in turn, to differentiate the network. In these cases, the first criterion for selection was broad: the gene had to contribute at least 10% as much as the gene making the maximum contribution to the correct classification; the second criterion was that 3 or more of the donors had to agree on the selection. This produced a subset of 292 genes. The number of genes referenced by a given donor under identical criteria ranged from 45 to 1448. Only 38% of the genes overlapped the 670 gene subset identified by cluster analysis. It was of interest to see if these genes were sufficient for correct classification of the donors. Ten different networks were trained with the 292 gene subset. Three (OCI Ly1 and DLBCL0009 and tonsil) errors were produced over 96 donors in 2 separate series (data not shown).

At this point, the neural networks were doing a much-improved diagnosis; it remained to be seen if the gene set could be further refined. The set of 292 genes was then treated in two different ways: [1] it was arbitrarily split into even and odd halves, with each half being used to train ten new networks. [2] it was used whole to train ten qualitative networks for further differentiation.

Twenty different networks were then trained using a 146 gene (odd or even numbered) subset of the 292 gene set in 2 series of 10. The odd set again produced 3 errors (data not shown). In the even set, a single error was made over 96 donors in ten different test sets, identifying the 'tonsil' inlier in the earlier cluster analysis [1] as positive (Table 4). Ten additional networks were trained on the even set with the same result (data not shown).

Table 4.

Test results of ten neural networks, trained on 146 genes to diagnose 96 donors for DLBCL lymphoma

DC	NC	DC	NC	DC	NC
1.0000	0.9714	1.0000	0.9877	1.0000	0.9881
1.0000	0.9744	1.0000	0.9889	1.0000	0.9877
1.0000	0.9645	1.0000	0.9754	1.0000	0.9877
1.0000	0.9778	1.0000	0.9847	1.0000	0.9876
1.0000	0.9784	1.0000	0.9715	1.0000	0.9862
0.0000	0.0202	0.0000	0.0183	0.0000	0.0138
0.0000	0.0222	0.0000	0.0186	0.0000	0.0145
0.0000	0.9698*	0.0000	0.0176	0.0000	0.0153
0.0000	0.3162	0.0000	0.0182	0.0000	0.0140
0.0000	0.0170	0.0000	0.0205	0.0000	0.0155
1.0000	0.9820	1.0000	0.9870	1.0000	0.9849
1.0000	0.9817	1.0000	0.9849	1.0000	0.9839
1.0000	0.9821	1.0000	0.9790	1.0000	0.9858
1.0000	0.9803	1.0000	0.9859	1.0000	0.9849
1.0000	0.9611	1.0000	0.9811	1.0000	0.9841
0.0000	0.0127	0.0000	0.0276	0.0000	0.0217
0.0000	0.0415	0.0000	0.0435	0.0000	0.0221
0.0000	0.0109	0.0000	0.2255	0.0000	0.0213
0.0000	0.0115	0.0000	0.1417	0.0000	0.0216
0.0000	0.0115	0.0000	0.1463	0.0000	0.0218
1.0000	0.9857	1.0000	0.9703	1.0000	0.9953
1.0000	0.9850	1.0000	0.9765	1.0000	0.9953
1.0000	0.9877	1.0000	0.9752	1.0000	0.9953
1.0000	0.9436	1.0000	0.9742	1.0000	0.9644
1.0000	0.9861	1.0000	0.9760	1.0000	0.9950
0.0000	0.0149	0.0000	0.2234	1.0000	0.9817
0.0000	0.0169	0.0000	0.1811	0.0000	0.0005
0.0000	0.0166	0.0000	0.0336	0.0000	0.0005
0.0000	0.0153	0.0000	0.0177	0.0000	0.0006
0.0000	0.0149	0.0000	0.0152	0.0000	0.0005
				0.0000	0.0005
				0.0000	0.0177
				0.0000	0.0180
				0.0000	0.0177
				0.0000	0.0184
				0.0000	0.0218

1.0 indicates positive for DLBCL. DC indicates the actual donor class, with 0.0 being negative. NC gives the network evaluation. The NC cutoff throughout this work is: ≥ 0.50 is taken as 1 and <0.50 is taken as 0. * marks the errors

The differentiation of the networks from the 292 gene set pointed to 8 genes. Given the high accuracy of the even 146 gene set, we also trained networks on this set for differentiation. These pointed to 11 additional genes. In these cases, only genes in the top 20% in influence chosen in common by at least 25% of the differentiated examples were considered. Networks trained on these 19 genes produced 2 errors over 96 donors in 10 test sets (Table 5). The 19 genes, using the designation from the initial report, are given in Table 6.

Table 5.

Test results of ten networks trained on 19 genes to diagnose 96 donors

DC	NC	DC	NC	DC	NC
1.000000	0.980997	1.000000	0.951646	1.000000	0.994965
1.000000	0.980266	1.000000	0.949929	1.000000	0.993213
1.000000	0.980299	1.000000	0.954199	1.000000	0.985740
1.000000	0.981223	1.000000	0.953238	1.000000	0.994986
1.000000	0.981232	1.000000	0.672729	1.000000	0.994926
0.000000	0.013813	0.000000	0.013613	0.000000	0.014911
0.000000	0.013742	0.000000	0.062331	0.000000	0.009041
0.000000	0.014832	0.000000	0.014121	0.000000	0.009042
0.000000	0.027310	0.000000	0.013801	0.000000	0.009257
0.000000	0.013980	0.000000	0.014666	0.000000	0.418724
1.000000	0.943310	1.000000	0.961199	1.000000	0.986271
1.000000	0.958110	1.000000	0.976879	1.000000	0.985485
1.000000	0.958936	1.000000	0.960848	1.000000	0.985739
1.000000	0.958939	1.000000	0.978911	1.000000	0.985737
1.000000	0.949335	1.000000	0.977826	1.000000	0.985630
0.000000	0.011627	0.000000	0.017476	0.000000	0.058905
0.000000	0.011927	0.000000	0.031951	0.000000	0.020912
0.000000	0.051333	0.000000	0.016654	0.000000	0.020145
0.000000	0.011654	0.000000	0.018255	0.000000	0.019559
0.000000	0.011726	0.000000	0.016824	0.000000	0.019841
1.000000	0.057607*	1.000000	0.936583	1.000000	0.988447
1.000000	0.980012	1.000000	0.936982	1.000000	0.986334
1.000000	0.979991	1.000000	0.936143	1.000000	0.987346
1.000000	0.964250	1.000000	0.936898	1.000000	0.978961
1.000000	0.979686	1.000000	0.731036	1.000000	0.987996
0.000000	0.015370	0.000000	0.026660	1.000000	0.643879
0.000000	0.020867	0.000000	0.028480	0.000000	0.293788
0.000000	0.015957	0.000000	0.027146	0.000000	0.046603
0.000000	0.015354	0.000000	0.027307	0.000000	0.017312
0.000000	0.015939	0.000000	0.047564	0.000000	0.030104
				0.000000	0.860242*
				0.000000	0.020264
				0.000000	0.020140
				0.000000	0.021367
				0.000000	0.021137
				0.000000	0.020277

DC indicates the actual donor class, with 0.0 being negative. NC gives the network evaluation. The NC cutoff throughout this work is: ≥ 0.50 is taken as 1 and <0.50 is taken as 0. * marks the errors

Table 6.

19 genes identified in diagnostic series

19307	Unknown
17250	phospholipaseC
21021	Unknown Hs. 75859
14811	Unknown
16722	CDC-like kinase
12977	similar to retinoblastoma binding protein
18547	CD55
17204	C-rel NF-kB
13828	6-pyruvoyl-tetrahydropterin
17839	tyrosine kinase receptor
21501	cGMP specific binding protein
19337	IP-10
16442	CD14
16877	Thy1
16152	Fc epsilon receptor
19391	osteonectin
19379	cyclin D2
16866	gap junction protein beta1
19376	NK killer cell protein 4

We also wished to test this gene set in the context of a follow-up study. For this purpose, we set aside 50 donors as "follow-up" data, using the remaining 46 donors in the usual training/testing round robin. Eleven networks were trained, 9 with 42 training vectors and 4 test vectors and 2 with 41 training vectors and 5 test vectors. Collectively, these produced 3 errors over 46 donors or 93% correct. The follow-up donors were then tested on the 11 networks. A poll of these networks showed a majority vote for 1 error or 98% correct.

Discussion

The rather remarkable conclusion of this analysis is that there is sufficient information in a single gene expression time point of less than 5 dozen genes to provide perfect prognosis (out to ten years) and near-perfect diagnosis for this set of donors. Furthermore, neural networks, through a strategy of train and differentiate, bring that information to the fore by progressively focusing on the genes within the larger set which are most responsible for the correct classifications, providing at once a reduction in the noise level and specific donor profiles. This focus on the specific classification problem led to a set of 34 genes for prognosis and a second set of 19 genes for diagnosis. These sets are mutually exclusive. The gene subsets suggested by cluster analysis [1] are not supersets of these sets; the 670 gene set of the initial report captured only 7 of the 19 gene set used for diagnosis and the 148 gene staging set captured only 2 of the 34 gene set used for prognosis. The 234 gene subset proposed by Hastie, et al. [4] for prognosis contains 6 of the 34 gene set. There was no overlap with the 13 gene set identified by Shipp, et al [5] to correlate with their cured/fatal classes for this disease. At first, it might seem surprising that the gene subsets identified here do not appear to be subsets of those identified earlier by Alizadeh et al. But this surprise is based on a naive intuition. The fact is that we do not know the level of information redundancy that exists in these large arrays. Apropos of this point, Alon et al. [6] discarded the 1500 genes indicated by cluster analysis as most discriminatory in their study of colon cancer and, upon reclustering, found their diagnosis unimpaired. Likewise, it may be that while the top 10% of relevant genes might be sufficient for perfect classification, so might the next 10%. These sets by definition are mutually exclusive. By extension, it is not difficult to believe that some other large gene set might be able to get 75% of the classifications correct with little or no overlap with those genes in the top 10%.

We have been careful to avoid any claim that the gene sets extracted in this procedure are the "best" gene sets. Only in one, highly qualified sense can they be said to be best; that is in classifying this data set there are no other gene sets which offer a statistically significant improvement in classification accuracy. That is not to say that there may not be other sets which could do as well. Nor is there any implication that these genes are seminal in the etiology of this disease. They may not be necessary but they are sufficient to do this classification. They may not be sufficient to the classification of a much larger patient set. Forty patients are unlikely to be fully representative of the general patient population with this disease. It should be noted, however, that the same caveats apply to the analysis of these data by any other method.

There have been a number of additional studies of cancer using microarray data for either prognostic or diagnostic purposes. The following listing includes a brief discussion of 7 of these studies:

(1) Shipp et al.[5] did a study of 58 DLBCL patients and 19 follicular lymphoma patients. They first sought to classify DLBCL and FL patients. They clustered 6817 genes. Using their own weighted combination of informative gene markers, they picked out 30 genes whose expression levels would be used to do a 2-way classification. They correctly classified 71/77 patients for a diagnostic accuracy of 92%. They then attempted to develop high risk and low risk groups with respect to 5 year prognosis. They used several different methods for associating particular gene clusters with survival outcome: Kaplan Meier analysis, Support Vector Machine, and K-nearest neighbor analysis. They selected 13 genes as most informative and achieved the best result with SVM modeling. They did not explicitly state how many patients initially sorted into the high risk/low risk groups but other data suggest 17 and 41 respectively. The only way in which these survival probability plots can be compared to the patient by patient predictions presented above is to associate low risk with survival and high risk with non-survival (Please note:this equation was not made by any of the authors, with the exception of [3] below, discussing risk groups). If one makes this association, their best result is 14/58 errors for a 5 yr. survival accuracy of 76%.

(2) Rosenwald et al. [7] did what they termed a follow-up study on the original Alizadeh et al. study of DLBCL patients. However, it was not really a follow-up study because a different chip was used for the microarray data. The Alizadeh study identified 2 groups based on an analysis of weighting the gene cluster groups: germinal center B cell-like tumors which correlated with low risk and activated B cell-like tumors which correlated with high risk. If these groups were made survivors and non-survivors, the prognosis accuracy would have been 75%. In the follow-up, the authors found it necessary to introduce a third group, consisting of patients who did not fit either of the previous 2 categories. Although lacking the associated gene profile, this third group had a survival pattern much like the activated B cell-like group. The authors used Cox proportional hazards modeling to assign groups on the basis of the expression of 100 genes. The 5 yr. survival for the low risk group was 60%, 35% for the activated B cell-like group, and 39% for the 3rd group. An improved result was obtained using 16 genes drawn from 4 signature gene groupings plus a score for BMP6 expression. Kaplan Meier estimates of survival were determined for 4 quartiles for which the 5 yr. survival rate was 73%,71%,34%,15%. If these 4 are collapsed into 2 categories of survivor and non-survivor, it would produce 62/240 errors for a prognosis accuracy of 74%.

(3) van't Veer et al. [8] did a study of 78 patients with breast cancer. Starting with 5000 signature genes, they narrowed down the gene pool to 231 genes by examining the correlation coefficient of each gene with the prognostic outcome. They then rank ordered these genes and added them 5 at a time to a one-man-out test of their 77 patients for predicted outcome. This was repeated until an optimum outcome classification was reached. This occurred at 70 genes. A patient by patient classification based on the weighting of these 70 genes was able to produce a survival classification with 13/78 errors for an accuracy of 83%.

(4) Beer et al. [9] used clustering and Cox hazard analysis to generate a list of 50 genes to be used in Kaplan Meier 5 yr. projections of survival. They had 86 patients with lung cancer in the study. With 22 patients originally assigned to the low risk group and 19 to the high risk group, the corresponding 5 yr. survival rates were 83% and 40%. If treated as survival categories this would produce 12/41 errors for a prognosis classification accuracy of 71%. Although these authors had complete 5 yr. survival data on 41 of the patients in the study, they at no point attempted to analyze this group specifically for direct comparison with predictions.

(5) Khan et al.[10] used linear neural networks to analyze microarray data from patients with small round blue-cell tumors. They wished to classify the 4 subcategories of this tumor. Principle Component Analysis was used to reduce 2308 genes to 10 components. Neural networks were trained using 2/3 of a 63 patient pool to train and 1/3 to test in a fully cross-validated fashion. The groups were shuffled 1250 times to produce 3750 networks. These networks correctly classified all 63 patients in a 4-way classification. The networks were analyzed for the most influential inputs to produce a list of 96 genes. New networks were calibrated with just these 96 genes; these again correctly classified the 63 patients and also correctly classified the 25 patients who had been withheld from the whole process.

(6) Dehanasekaran et al. [11] did a study of 60 prostate biopsy samples, 24 non-tumorous,14 tumor in situ, 20 metastatic tumor. Cluster analysis of microarray data from nearly 10,000 genes misplaced 2 samples out of 26 for a diagnostic accuracy of 92%. The authors did not state why they limited the clustering result to 26 samples when they had 60. Although they performed additional analyses, they did not involve using the array data for either diagnosis or prognosis.

(7) Golub et al. [12] wished to be able to distinguish acute myeloid leukemia (AML) from acute lymphoblastic leukemia (ALL). Starting with the expression of 6817 genes from 38 patients, they did a 2-class clustering. They then did a neighbor analysis to identify 1100 genes occurring above chance levels which related to the AML/ALL distinction. They choose an informative subset of 50 genes to weight for class assignment of the patients. They were able to correctly classify 29/34 patients for a diagnostic accuracy of 85%. They next attempted to use self-organizing-maps (SOM) for 2 classes in place of the initial clustering. This produced only 4/38 errors for 89% diagnostic accuracy. Drawing a 20 gene predictor from these SOM classes, they again produced 4/38 errors, maintaining a 89% accuracy. These authors also attempted to use array data to predict clinical outcome on 15 AML patients but without success.

The identification of specific genes associated with a particular biological characteristic such as malignant phenotype would be useful in many settings, [1] Precise classification and staging of tumors is critical for the selection of the appropriate therapy. At present, classification is accomplished by morphologic, immunohistochemical, and limited biological analyses. Neural net analysis in the form of specific donor profiles could provide a fine structure analysis of tumors characterizing them by a precise weighting of the genes, which they express differentially. At present, only subsets of patients with a given type of tumor respond to therapy. Networks trained to distinguish responders from non-responders would allow a comparison of tumor-expressed genes in responders and non-responders to find those genes most predictive of response. Recently we have used neural networks on the data of Perou et al. [12] for classifying breast tumors as hormonally responsive or non-responsive. Networks that gave a perfect classification with 496 genes pointed to a subset of 12 genes. Retraining on these 12 genes produced no error in classifying 62 tissue samples from their study (unpublished data). We have also analyzed the data of Dhanasekaran, et al [11]. Here the original set of 9984 genes was reduced to 34 genes. Retraining on these 34 genes gave no errors in a 3-way (normal, early tumor, metastatic disease) classification of 53 patients (unpublished data). Given the significant impairment in the quality of life for many patients undergoing chemotherapy and/or radiation therapy, such prospective information would be extremely beneficial. [3] T cell and antibody-mediated immunotherapy may be efficacious approaches for limiting tumor growth in cancer patients. At present there is a paucity of known tumor rejection antigens that can be targeted. Neural net analysis may identify a panel of tumor-encoded genes shared by many patients with the same type of cancer and thereby provide a repertoire of potentially novel tumor rejection antigens. [4] For many patients with autoimmune disease the target antigen(s) is unknown. Enhanced identification of cell-type specific markers of the target organ through neural net profiling could identify potential target antigens as candidate molecules for testing and tolerance induction.

Conclusions

We believe neural networks will be an ideal tool to assimilate the vast amount of information contained in microarrays. The artificial networks presented here were not selected from a large number of attempts. The networks described here are the first or second attempts with the data and format stated; the longest training session lasted less than 5 minutes. Indeed, the trained neural network may, in the form of its weight matrix, have the best possible "understanding" of the very broad statement being made in the microarray, a view that is accessible with the differentiation of the network. In this study, that viewpoint suggested a small subset of genes, which proved sufficient to give a near-perfect classification in each of two problems. This approach should be suitable for any microarray study and, indeed, other global studies such as 2-D gels and mass-spec data which contain sufficient information for training.

Methods

The data from microarray experiments are stored in spreadsheet form, representing the positive or negative level of expression, relative to some control state, of 1000's of genes for two or more experimental conditions. A short software program is sufficient to translate these data directly into a binary representation suitable as input vectors for a neural network. The neural network software used throughout this study was NeuralWorks Professional II Plus v.5.3.Neural networks were trained on the corresponding data sets, with a fraction of the data, typically 10%, withheld for testing purposes. All open fields in the data array were set to zero. The trained networks were then asked to classify new test data as to donor type. Since the gene expression levels are read directly from the spreadsheet, their order and names are provided by the spreadsheet. Given the large amount of input data, these networks generally converge to a low error level very quickly during training, often in a few minutes or less. Subsequently additional networks were trained with a simplified input that contained only qualitative information in the form of a plus or minus sign to characterize the expression of each gene in the panel. This reduced the input size to 2 bits per gene, 01 for below the control and 10 for above, or equal to, the control. The output neuron was trained to output 1.0 for a positive donor and 0.0 for a negative donor in the diagnostic networks; for the prognostic networks 1.0 indicated a non-survivor and 0.0 a survivor. The 4026 gene panel network was provided, respectively, 100 or 67 middle-layer neurons for the 3 bit or 2 bit per gene inputs. With a very large number of input neurons it is possible to overload the middle-layer neurons, effectively always operating them at one extreme limit or the other; this can have the undesirable effect of reducing their sigmoid transfer function to a step function, with the loss of the network's non-linearity. This is clearly indicated if multiple output values are found to be exactly identical. Networks were trained to an error level below 0.05 after which they were tested with previously unseen data. A possible disadvantage of neural networks, especially with a large input space and a relatively small sample number, is overtraining. In overtraining, a network can learn the specifics of each training example as opposed to finding a global solution for the entire training set. This behavior is characterized by a degradation in test scores as training sessions are extended. Although we saw no evidence of this in this study, we did look to see how much additional training would be necessary to degrade the test results in the case of the initial diagnosis networks with 4026 genes. It was not until we doubled the training iterations dictated by the 0.05 output error cutoff that we saw some increased test error. At double the normal training interval, 8 networks were unchanged, but 2 networks showed an increased error of 1. This is suggestive, but not proof, of the onset of overtraining. The networks trained on the reduced 34 or 19 gene sets had 6 or 4 middle-layer neurons.

To differentiate a trained network with respect to specific inputs, a network was trained on the 4026 gene panel with 2 bits per gene. The 5 positive donors from the test set were each differentiated, using software that we designed for that purpose [2]. The selected genes were then compared among the 5 sets, with genes occurring in 3 or more instances being included in the final subset. This requirement generated a subset of 292 genes from the original 4026 genes. Networks were trained on this 292 gene subset and on two 146 gene subsets, representing every other gene from the 292 set. All were coded with 3 bits per gene and employed networks with 25 or 12 middle-layer neurons, respectively. Other networks were trained on the 292 gene set and the 146 'even' set, coded with 2 bits per gene for subsequent differentiation.

The differentiation of the large panel networks trained for prognosis arbitrarily employed more selective criteria (see text) for subset determination with the result that a single differentiation reduced the gene set from 4026 genes to 34 genes. Subsequent networks demonstrated that this was a highly effective selection.

All networks in this study were three-layer back propagation networks trained with a learning coefficient of 0.3 and a momentum coefficient of 0.4 using the generalized delta learning rule and the standard sigmoidal transfer function. The cutoff, in all cases, between positive and negative scoring was taken to be 0.05 RMS error at the output neuron No network required more than 4 minutes training time on a PC at 650 Mh; in the majority of cases, the network was fully trained in less than a minute. Training and testing a 10 network round-robin series could generally be done in less than 20 minutes. Training was deliberately kept to a minimum to avoid over-training. The networks represented here were in each case the first or second attempt result for the given problem. There was no "data trolling."

Note

¹All data not shown can be found at the site http://research.umbc.edu/~moneill/GBMS