Abstract
To elucidate the regulation of kinetochore microtubules (kMTs) by kinetochore proteins in Saccharomyces cerevisiae, we need tools to characterize and compare stochastic kMT dynamics. Here we show that autoregressive moving average (ARMA) models, combined with a statistical framework for testing the significance of differences between ARMA model parameters, provide a sensitive method for identifying the subtle changes in kMT dynamics associated with kinetochore protein mutations. Applying ARMA analysis to G1 kMT dynamics, we found that 1), kMT dynamics in the kinetochore protein mutants okp1-5 and kip3Δ are different from those in wild-type, demonstrating the regulation of kMTs by kinetochore proteins; 2), the kinase Ipl1p regulates kMT dynamics also in G1; and 3), the mutant dam1-1 exhibits three different phenotypes, indicating the central role of Dam1p in maintaining the attachment of kMTs and regulating their dynamics. We also confirmed that kMT dynamics vary with temperature, and are most likely differentially regulated at 37°C. Therefore, when elucidating the role of a protein in kMT regulation using a temperature-sensitive mutant, dynamics in the mutant at its nonpermissive temperature must be compared to those in wild-type at the same temperature, not to those in the mutant at its permissive temperature.
INTRODUCTION
One of the most intriguing processes in cell biology is the symmetric segregation of replicated chromosomes from mother to daughter cells during mitosis. To achieve this, cells assemble specialized machinery known as the mitotic spindle, which is composed of microtubules (MTs) that emanate from two oppositely located spindle poles. MTs grow and shrink and switch between growth and shrinkage in an apparently stochastic process referred to as dynamic instability (1). Dynamic instability is thought to promote the capture of chromatids by MTs (2,3), which, after proper bipolar attachment (4), pull sister chromatids apart into the two daughter cells.
MT-chromosome attachment takes place at the centromere (CEN), where a protein complex known as the kinetochore assembles and acts as the interface between centromeric DNA and kinetochore MTs (kMTs). In addition to establishing a physical linkage between chromosomes and MTs, it seems likely that kinetochore proteins are involved in regulating the dynamics of attached MTs. However, very little is known about the specific functions of kinetochore proteins in terms of how they may control kMT dynamics, what chemical or mechanical signals they may process, and in what hierarchy they may transmit these signals to kMTs.
To establish the roles of kinetochore proteins in kMT regulation, we chose a quantitative genetics approach, using the budding yeast Saccharomyces cerevisiae as a model system. Our strategy relies on the quantitative comparison of kMT dynamics in wild-type (WT) and in strains carrying kinetochore protein mutations, to eventually consolidate this data pool into a mechanistic model of the kinetochore and its regulation of kMT dynamics.
In addition to its powerful genetics, S. cerevisiae offers several advantages for studying kinetochore function. 1), Each sister chromatid is attached to only one kMT (5), whose minus-end is fixed at the spindle pole body (SPB) (6). Thus, the motion of a chromatid is the direct result of assembly and disassembly at the plus end of one kMT, and will be altered when kinetochore proteins are mutated if the latter indeed regulate kMT dynamics. 2), The motion of a single chromatid can be visualized by a TetO/TetR-based fluorescent tag proximal to the CEN (7,8). By fusing a second fluorescent tag to the SPB-specific protein Spc42p, the dynamics of the kMT connecting the tagged CEN to the SPB can be obtained from the temporal variation of the distance between the two tags (9). 3), The S. cerevisiae kinetochore is composed of a relatively small number of proteins (∼70), many of whose properties are known from biochemical and biophysical assays (10,11). These proteins can be genetically deleted or mutated to deduce their role in regulating kMT dynamics. 4), Unlike chromosomes in higher organisms, S. cerevisiae chromosomes remain attached to the SPB via kMTs in G1. This provides us with an even simpler model system to study, in which no forces are exerted on, or signals transmitted to, the kinetochore or its associated MT due to cohesion between sister chromatids.
However, the comparison of S. cerevisiae kMT dynamics between different conditions is not straightforward. Not only are the observed kMT length series intrinsically stochastic due to the random switching of MTs between assembly and disassembly (1), but they also suffer from extrinsic stochasticity due to undersampling. As discussed in Dorn et al. (9), the S. cerevisiae spindle requires three-dimensional imaging, currently limiting temporal sampling to 1 frame/s. However, the average time spent in either the growth phase or the shrinkage phase is observed to be ∼1.5 s (9). Thus, our sampling rate is at the limits of, if not even slower than, the necessary sampling rate. Undersampling increases the disconnect between consecutively observed kMT states, increasing the apparent randomness, i.e., introducing extrinsic stochasticity, in kMT behavior.
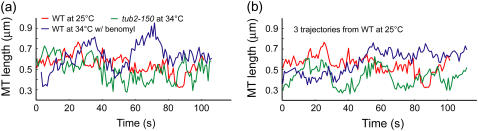
Since in a stochastic system the state at time t defines the set of possible states and not the exact state at time t + 1, kMT length series cannot be compared time point by time point. Rather, they must be compared indirectly via a set of parameters, referred to as descriptors throughout this article, which capture the characteristics of these length series. But changes in kMT behavior associated with protein mutations, even if lethal, are often qualitatively comparable in magnitude to the intrinsic heterogeneity and cell-to-cell variation of WT kMT dynamics (Fig. 1). Consequently, very sensitive descriptors of kMT dynamics must be devised to capture the details of kMT states and the transitions between them.
FIGURE 1.
Very sensitive analysis tools are needed to characterize kMT dynamics. MT length series from (a) three different conditions and (b) the same condition are shown. The randomness in these series and the weakness of the effects of mutations on the dynamics render the distinction of meaningful phenotypes difficult.
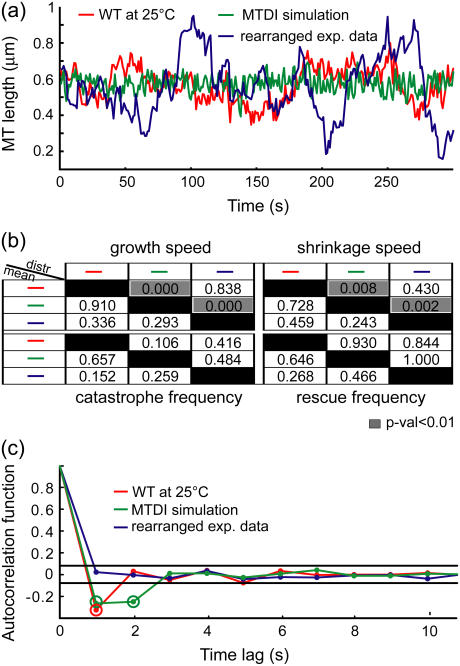
Generally, MT dynamics have been analyzed within the framework of the original MT dynamic instability model (1): They are characterized by the average growth and shrinkage speeds, and the average time spent in growth (equal to the inverse of catastrophe frequency) and in shrinkage (equal to the inverse of rescue frequency) (12,13). More advanced schemes have considered not only the averages of these descriptors but also their distributions (9,14–16). However, even by including speed and frequency heterogeneity, differences between the three evidently dissimilar MT length series shown in Fig. 2 a are not detected. The mean speeds and frequencies in the three cases are the same (Fig. 2 b, below diagonal), and the speed and frequency distributions cannot distinguish between the experimental MT length series and their randomly rearranged counterparts (Fig. 2 b, above diagonal). In contrast, the autocorrelation function of the corresponding MT plus-end velocity series reveals a difference between the three cases (Fig. 2 c). This implies that the growth and shrinkage speeds and times are not a complete set of descriptors of kMT dynamics, and that the autocorrelation function extracts information about kMT dynamics that these traditionally employed descriptors do not capture.
FIGURE 2.
Growth and shrinkage speeds and rescue and catastrophe frequencies do not characterize kMT dynamics completely. (a) kMT length trajectories from WT at 25°C, from a Monte Carlo simulation of MT dynamics, and from a random rearrangement of the sequence of experimental MT velocities in WT at 25°C. (b) Discrimination matrices showing p-values for comparing the means (using Student's t-test, below diagonal) and distributions (using Kolmogorov-Smirnov test, above diagonal) of the traditional MT dynamics descriptors of the three trajectories. p-Values <0.01 (highlighted in gray) indicate statistically significant differences. Although these trajectories are visually different, the traditional descriptors fail to detect most of the differences. (c) Autocorrelation functions of the plus-end velocities derived from these three trajectories detect differences between them. The two horizontal lines indicate the 99% confidence range for significant correlation values (highlighted by a second circle).
The autocorrelation function and other functions derived from it, such as the partial autocorrelation function and the spectral density, have been used previously to characterize MT behavior (16–18). However, such nonparametric time series analysis tools are not appropriate to characterize and compare S. cerevisiae kMT dynamics. Changes in dynamics caused by mutations are very subtle and difficult to detect in a qualitative comparison of autocorrelation, partial autocorrelation, and spectral density plots (Supplementary Material, Fig. S1). Rather, a quantitative comparison of parameters describing the autocorrelation and partial autocorrelation functions and spectral densities is needed. Such parameters can be descriptive, such as the width of spectral densities and the decay constant of autocorrelation functions, or can be the set of adjustable parameters in generic functions fitted to autocorrelation and spectral density plots. In either case, the parameter uncertainties and covariances that are needed for the quantitative comparison of parameters are not readily available. Therefore, it is very difficult to quantitatively compare in a rigorous manner the information extracted by nonparametric time series analysis tools.
To capture the details of kMT states, the transitions between them and the time-correlation in kMT behavior, and to allow the quantitative comparison of kMT dynamics by statistical testing procedures, we propose the characterization of kMT plus-end velocity series with parameters of autoregressive moving average (ARMA) models (19). ARMA models are time series analysis tools that reveal the dependence of a stochastic variable on its history and on an associated white noise process that renders the variable's behavior stochastic. They provide a platform for the analysis of kMT behavior that is independent of any assumptions regarding the physical basis of the observed dynamics. Indeed, ARMA models were proposed as a possible method for the characterization of MT dynamics (16). However, the methodology was not practically implemented and its applicability to the dynamics of interest, advantages, and disadvantages were not thoroughly investigated. ARMA models were also utilized for the analysis of cell motility (20). However, in that study the fitting was restricted to an ARMA(1,1) model, based on a priori knowledge about the dynamics.
ARMA models are primarily utilized to predict future values of a time series (19). In contrast, our goal is to employ ARMA model parameters for the comparison of time series to distinguish between mutants based on their kMT dynamics. To achieve this, we have expanded the ARMA model fitting framework with statistical tools that test the significance of differences between ARMA model parameters, taking into account their uncertainties and interdependencies. Due to their ability to capture local details, ARMA model parameters are ideal for the quantitative comparison of stochastic time series with subtle differences between them. To the best of our knowledge, this is the first time that ARMA model parameters are employed for the rigorous statistical comparison and classification of stochastic behavior resulting from normal and mutated molecular systems in living cells.
In this article, we demonstrate the performance of the ARMA analysis framework by classifying phenotypes of kMT dynamics in S. cerevisiae in the G1 phase of the cell cycle. We show ARMA model profiles of kMT dynamics in WT and in mutants of kinetochore proteins, motors and MT-associated proteins. Based on these data, we have discovered that 1), the linker kinetochore protein Okp1p affects kMT assembly and disassembly rates; 2), Dam1p—part of the DASH complex that forms rings around kMTs (21,22)—is critical for proper kMT attachment and regulation; and 3), the kinase Ipl1p that is essential for achieving bipolar attachment (23,24) regulates kMT dynamics also in G1. Furthermore, the motor Kip3p, located at the kinetochore, affects kMT dynamics, whereas the motor Kar3p, located at the SPB, does not. Finally, we confirm that kMT dynamics vary with temperature, and that they are most likely differentially regulated at 37°C.
MATERIALS AND METHODS
Image acquisition and analysis
Single kMT trajectories in the budding yeast S. cerevisiae in G1 were acquired as described in Dorn et al. (9) and Rines et al. (25). In brief, tandem copies of the Tet operator (TetO) were placed next to the CEN of Chromosome IV (7,8). A single, diffraction-limited tag of the CEN was then obtained by fusing the corresponding repressor with GFP (TetR-GFP). The SPB, on the other hand, was tagged with GFP fused to the protein Spc42p. The motion of the two tags was tracked in 3D using a DeltaVision optical sectioning microscope. Every second, 16–18 z-slices were taken at a lateral spatial sampling of 48 or 66 nm and an axial sampling of 200 or 250 nm. Photobleaching and phototoxicity limited the total observation time in each experiment to 100–200 s (25).
These movies were then analyzed automatically, as described in Dorn et al. (9), and Thomann et al. (26,27). The analysis determined the positions of the CEN and SPB tags at all observation time points. Moreover, the uncertainties in the extracted positions were calculated from the image noise using error propagation methods (9). From these positions and uncertainties, the SPB-CEN distance and its uncertainty were calculated at each time point. In the case of chromosome attachment, the SPB-CEN distance was approximately equal to the length of the corresponding kMT, and its variation over time reflected kMT dynamics (9).
ARMA ANALYSIS OF MT DYNAMICS
Introduction to ARMA models
An ARMA model relates the value of an observed variable to its values at previous time points (the autoregressive (AR) component of the model) as well as to the present and past values of a white noise (WN) variable (the moving average (MA) component). An ARMA(p,q) process is defined as
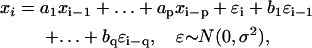 |
(1) |
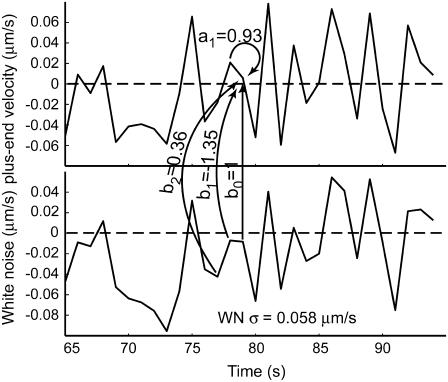
where xi (i = 1,2,…,n) is the series being analyzed, ɛi (i = 1,2,…,n) the WN series (assumed to be normally distributed with mean zero and variance σ2), p the AR order, {a1,…,ap} the AR coefficients, q the MA order, and {b1,…,bq} the MA coefficients. An ARMA(1,2) model is depicted in Fig. 3. Throughout the article, {a1,…,ap,b1,…,bq} are collectively referred to as ARMA coefficients, whereas {a1,…,ap,b1,…,bq,σ2}, used for time series characterization, are referred to as ARMA descriptors.
FIGURE 3.
Illustration of an ARMA(1,2) model. The MT plus-end velocity at time t is the sum of 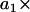 (velocity at time t − 1), WN at time t,
(velocity at time t − 1), WN at time t, 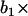 (WN at time t − 1) and
(WN at time t − 1) and 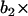 (WN at time t − 2).
(WN at time t − 2).
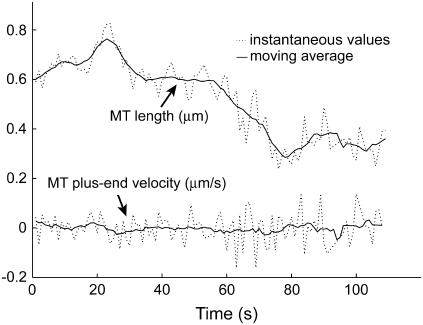
Time series to be described by ARMA models must be nonperiodic and stationary with zero mean (19). MT length trajectories are indeed nonperiodic, but not stationary (Fig. 4). Hence, Eq. 1 cannot be applied to them. Therefore, we analyzed the instantaneous MT plus-end velocity series, defined as 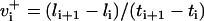 (l = MT length, t = time, and i = time point). Calculating v+ is equivalent to taking the first difference of MT length trajectories, removing linear trends, and rendering the series stationary with zero mean (Fig. 4). Note that we do not treat growth and shrinkage separately; instead, the plus-end velocity is positive when an MT grows and negative when it shrinks.
(l = MT length, t = time, and i = time point). Calculating v+ is equivalent to taking the first difference of MT length trajectories, removing linear trends, and rendering the series stationary with zero mean (Fig. 4). Note that we do not treat growth and shrinkage separately; instead, the plus-end velocity is positive when an MT grows and negative when it shrinks.
FIGURE 4.
MT length trajectories are not stationary, as indicated for an experimental kMT length series over 110 s. The moving average of the series over seven time points indicates linear trends, i.e., nonstationarity, in the series. In contrast, the moving average of the differenced series, the instantaneous MT plus end velocity, does not vary with time (≈0 at all times).
Eq. 1 is guaranteed to have a unique solution (19) if and only if the polynomial
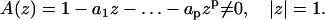 |
(2) |
This implies that two trajectories are equivalent if they are described by the same ARMA model, which satisfies the above condition. Without loss of generality, we impose two more conditions on Eq. 1 for mathematical and computational convenience: the causality condition, A(z) ≠ 0 for all |z| ≤ 1; and the invertibility condition, B(z) = 1−b1z−…−bpzp ≠ 0 for all |z| ≤ 1 (19).
Estimation of ARMA descriptors
Requirements
The characterization of time series with an ARMA model involves estimating the AR order p, the MA order q, the corresponding coefficients {a1,…,ap,b1,…,bq} and the WN variance σ2. To apply ARMA analysis to MT plus-end velocity series, the estimation algorithm must have the following properties:
It must be able to handle series with missing observations, since kMT plus-end velocity series suffer from the occasional absence of data. This happens when tag detection and tracking fail, mainly due to low signal/noise ratio.
It should account for the uncertainty of observations due to measurement noise, as reported by our image analysis software (9,26,27). Observations with lower uncertainty should have a larger contribution to the estimation of descriptors than those with higher uncertainty.
It should be able to combine data from several movies to accumulate a large enough data set that is representative of the dynamics under a certain condition. As will be shown below, unambiguous descriptor estimation requires series of 1500–2000 time points. However, due to photobleaching and phototoxicity, experimental kMT trajectories are limited to lengths of 100–200 time points. Even without photobleaching, the duration of the specific phase of the S. cerevisiae cell cycle of interest might be too short to accumulate the required number of time points. For example, the G1 phase in S. cerevisiae lasts ∼20 min (1200 s) in the mother (28), which is shorter than the required trajectory length. Thus, trajectories from several movies must be appropriately combined to achieve the required number of observations.
Besides the estimation of descriptor values, the framework must also propagate the uncertainty in kMT plus-end velocity series to predict the uncertainty in and interdependency between the estimated descriptors. This information is required for the comparison of ARMA descriptors by statistical hypothesis testing.
A critical aspect of the fitting is determining the orders p and q of the ARMA model. As model order gets larger, a model becomes more flexible and thus fits the data better. However, at the same time, the interdependency between ARMA coefficients increases and their reliability decreases (19). Thus, an optimal balance between improved fitting and decreased reliability with increasing p and q must be achieved.
Algorithm
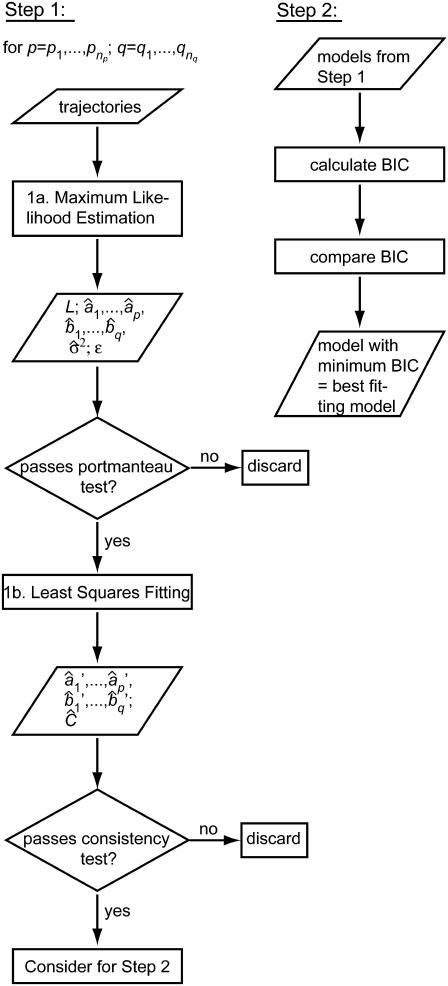
In view of the above requirements, the estimation of ARMA descriptors is achieved via a two-step procedure (Fig. 5):
FIGURE 5.
Flowchart of the ARMA model fitting algorithm. See text for details.
1. For a range of AR orders 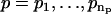 and MA orders
and MA orders 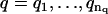 , the best fitting values of {a1,…,ap,b1,…,bq,σ2} and the uncertainties in {a1,…,ap,b1,…,bq} are determined in two steps:
, the best fitting values of {a1,…,ap,b1,…,bq,σ2} and the uncertainties in {a1,…,ap,b1,…,bq} are determined in two steps:
1a. Maximum likelihood estimation (MLE): Jones (29) has proposed an algorithm that fits ARMA models to series with missing observations and that determines the contribution of a data point to the estimation based on its uncertainty. Using a state-space representation of ARMA models, the algorithm uses Kalman recursion to predict the velocities at the observed time points. The likelihood, L, of a model is then calculated as
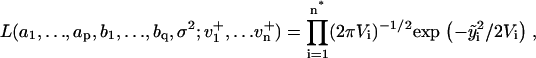 |
(3) |
where i is the time point, n the total number of time points, 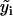 the difference between the predicted and observed velocity values at time point i, and Vi the sum of the prediction variance and measurement error variance at time point i. The asterisk above n indicates that only time points that have actual observations are included in the product in Eq. 2. The best set of ARMA descriptors
the difference between the predicted and observed velocity values at time point i, and Vi the sum of the prediction variance and measurement error variance at time point i. The asterisk above n indicates that only time points that have actual observations are included in the product in Eq. 2. The best set of ARMA descriptors 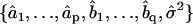 is the one maximizing the likelihood L.
is the one maximizing the likelihood L.
We have extended the algorithm by Jones to concatenate several time series in the estimation of one set of descriptors, assuming that kMT plus-end velocity series from different movies correspond to different segments of one series with an infinite number of missing observations between them. This allows the construction of one likelihood from as many series as necessary:
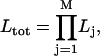 |
(4) |
where j is the time series number, M the total number of concatenated series, and Lj the likelihood calculated by fitting series j (Eq. 3). The maximization of Ltot then yields descriptor estimates for kMT dynamics under one experimental condition.
The goodness of fit of a model determined by MLE must be determined by checking the “whiteness” of the WN series ({ɛ1,…,ɛn} in Eq. 1). If the model represents the time series appropriately, {ɛ1,…,ɛn} will be uncorrelated, since all correlation between time points is explicitly captured by the ARMA coefficients. We test the degree of correlation in the WN series using the Ljung-Box portmanteau test (19). Only models that pass the portmanteau test are considered in steps 1b and 2.
1b. Least squares (LS): MLE yields estimates of model coefficients, but not their uncertainties and interdependencies. To obtain this information for the subsequent statistical comparison of ARMA descriptors, model fitting is reformulated as an LS problem, where the observed plus-end velocity values are regressed onto previous velocity values and the WN series estimated in step 1a. LS delivers another estimate of the ARMA coefficients 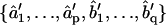 and their variance-covariance matrix Ĉ (30). Consistency between MLE and LS is ensured by testing the similarity between the ARMA coefficients they yield (see coefficient comparison test below). Only models that pass this consistency test are considered in step 2.
and their variance-covariance matrix Ĉ (30). Consistency between MLE and LS is ensured by testing the similarity between the ARMA coefficients they yield (see coefficient comparison test below). Only models that pass this consistency test are considered in step 2.
2. Among the valid models obtained from step 1, the best fitting model is the one minimizing the Bayesian Information Criterion (BIC) (31). For an ARMA(p,q) model, the BIC is given by
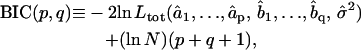 |
(5) |
where N is the total number of fitted time points contained in the concatenated series. The first term in the BIC decreases with increasing model order, whereas the second term penalizes higher model orders. Therefore, the model that minimizes the BIC offers the best fit to the data with only the necessary number of parameters. The BIC has been shown to be a consistent order-selection criterion whose minimization guarantees convergence to the correct model order as a series gets longer (31).
Properties of algorithm
Descriptor estimation requires 1500–2000 time points
The characterization of stochastic time series requires sufficient data to represent all possible states of the system and all possible transitions between states. If a time series is too short, only a subset of its possible states will be sampled and descriptor estimation will be biased.
Since low-order ARMA models seem to be needed for characterizing kMT plus-end velocity series (see Results and Discussion), we determined the number of data points required for the fitting of low-order ARMA models. Based on simulated ARMA trajectories, we found that the algorithm requires trajectories that are 1500–2000 time points long to estimate ARMA descriptors within 5–10% of their true values (Supplementary Material, Fig. S2, a and b). Descriptors derived from shorter trajectories were often far from their true values, and suffered from large uncertainties and high variability. In agreement with simulation results, the fitting of ARMA models to experimental kMT plus-end velocity series also requires 1500–2000 time points (Fig. S2 c). Thus, the integration of measurements from 15–25 experiments is necessary to accommodate for the implicit heterogeneity of kMT dynamics in single-cell observations.
Estimation is robust with up to 30% of observations missing
Missing observations in a trajectory not only reduce the effective number of available time points, but also lead to suboptimal Kalman recursion in the MLE step (step 1a above). Nevertheless, the fitting of simulated ARMA trajectories shows that, for trajectories with ∼2000 time points, low-order ARMA descriptors are insensitive to the deletion of up to 20–30% of the data points (supplementary material, Fig. S3). Experimental trajectories analyzed in this study have 7–22% of the observations missing. Therefore we expect that their ARMA descriptors are estimated robustly.
Comparison of ARMA descriptors
Comparison of models of equal order
The ARMA descriptors of a time series are the orders p and q, the coefficients {a1,…,ap,b1,…,bq}, and the WN variance σ2. For simplicity, we initially assume that the two ARMA models to be compared have the same order. In this case, one must compare the ARMA coefficients and the WN variances of the two models:
-
Comparison of ARMA coefficients. Due to the interdependency between the estimated ARMA coefficients describing kMT dynamics (as represented by the large off-diagonal values of the variance-covariance matrices shown in supplementaryTable S1), a comparison of the coefficients independently of each other is misleading and will give erroneous results. Instead, the ARMA coefficients in each model must be treated as one entity, and a group comparison that uses the full variance-covariance matrices must be performed. For example, a coefficient-by-coefficient comparison of WT at 34 and 37°C (see Table S1) that does not take into account the interdependencies between coefficients will lead to the conclusion that their coefficients are statistically indistinguishable. However, a proper group test of the coefficients, as described below, will show that they are different. The following statistical test is used for comparing the ARMA coefficients in two models of order p and q fitted to trajectories of total lengths n1 and n2.
Let ξ1 and ξ2, of length p + q, be the two coefficient sets to be compared.
Let C1 and C2, of size (p + q) × (p + q), be their variance-covariance matrices.
Define the null hypothesis, H0: ξ = ξ1 − ξ2 = 0, i.e., the coefficients are equal.
Define the alternative hypothesis, HA: ξ ≠ 0, i.e., the coefficients are different.
Calculate the test statistic value, given by T0 = ξTC−1ξ/(p + q), where C = C1 + C2. Under H0, the test statistic, T, is Fisher-distributed with degrees of freedom p + q and n = min(n1,n2) (30).
Calculate the p-value = p(T ≥ T0) assuming that H0 is true.
Reject H0 if the p-value is <10−3. If H0 is rejected, the ARMA coefficients of the two models are considered to be different.
-
Comparison of WN variances.
Let
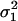 and
and 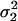 be the two WN variances to be compared.
be the two WN variances to be compared.Define the null hypothesis, H0:
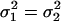 , i.e., the WN variances are equal.
, i.e., the WN variances are equal.Define the alternative hypothesis, HA:
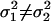 , i.e., the WN variances are different.
, i.e., the WN variances are different.Calculate the test statistic value, given by
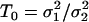 . Under H0, the test statistic, T, is Fisher-distributed with degrees of freedom n1 and n2, where n1 and n2 are the lengths of the two fitted series.
. Under H0, the test statistic, T, is Fisher-distributed with degrees of freedom n1 and n2, where n1 and n2 are the lengths of the two fitted series.Calculate the p-value = p(T ≥ T0) assuming that H0 is true.
Reject H0 if the p-value is <10−10. If H0 is rejected, the WN variances of the two models are considered to be different.
Comparison of models of different orders
The uncertainty in the estimated coefficient values and the interdependency between them renders obsolete the simple notion that two models with different orders are necessarily different. As an illustrative example, suppose we want to compare model A, of order (1,2), with model B, of order (2,2). By definition, model A can be rewritten as an ARMA(2,2) model with a2 = 0. Suppose that a2 in model B is small and not significantly different from zero. In this case, the difference in the orders of models A and B is meaningless and one cannot conclude that the two models are different simply because they have different orders. On the contrary, one should perform a group test on the sets of coefficients after rewriting model A as an ARMA(2,2) with a2 = 0.
Given this indirect but intimate coupling between model orders and coefficients, model differences cannot be inferred from differences in their orders. Instead, we first compensate for order mismatch by padding the coefficient sets with zeros and modifying their variance-covariance matrices accordingly (see Appendix for an illustration of order mismatch compensation), and then compare the new coefficient sets using the coefficient comparison test described above. If the coefficients of the two models are found to be significantly different, then the orders are also significantly different. Otherwise, the differences in model order are meaningless.
Of course, the WN variances of the two models are also compared using the test described above.
p-Value thresholds
The thresholds 10−3 and 10−10, below which p-values indicate statistically significant differences between ARMA coefficients and WN variances, respectively, were determined with a bootstrapping-like method, where we analyzed the variability in kMT dynamics between cells of the same strain. Each of the three largest experimental data sets available was divided into two random, mutually exclusive subsets, and their best fitting ARMA descriptors were compared. The test was repeated 1000 times for each time series, with different subsets in each case. In 90% of the cases, the ARMA coefficients and WN variance comparison p-values were found to be >10−3 and 10−10, respectively. In other words, the probability of obtaining an ARMA coefficient comparison p-value <10−3 or a WN variance comparison p-value <10−10 when the dynamics are in reality equivalent is 10%. Thus, to conclude with 90% confidence that two conditions or strains exhibit different kMT dynamics, their ARMA coefficient comparison p-value should be <10−3, their WN variance comparison p-value should be <10−10, or both.
RESULTS AND DISCUSSION
We analyzed the dynamics of G1 chromosomes and kMTs in S. cerevisiae in various strains and under several experimental conditions. Plus-end velocity series were fitted with ARMA models of orders p,q = 0,…,3 and all but one phenotype of dam1-1 (which was best described by an ARMA(1,0) ≡ AR(1) model) were characterized best by ARMA(1,2) models. The estimated descriptors and their variance-covariance matrices are provided in Table S1.
Interpretation of ARMA descriptors and their variations
ARMA descriptors have no direct link to the molecular mechanisms underlying kMT dynamics, and their interpretation is not straightforward. To get insight into the meaning of ARMA descriptors, we generated MT plus-end velocity series via Monte Carlo simulations using the MT dynamic instability model proposed by Odde and Buettner (16). Based on experimental evidence, this model assumes that the time an MT spends in the growth phase or the shrinkage phase is Γ-distributed. It is useful for investigating the meaning of ARMA descriptors because variations in the width of phase-time distributions alter the coupling between MT states. In particular, a narrower distribution (i.e., smaller standard deviation) leads to more regularity in the switching and, hence, longer-range coupling, whereas a wider distribution leads to less regularity and hence less persistent coupling. For our simulations, we have extended the model of Odde and Buettner (16) such that the growth and shrinkage speeds do not assume a single value each, but are also Γ-distributed. The Γ-distribution has been chosen because it is always positive and it is very close to a normal distribution when the standard deviation is small. This extension of the model is consistent with our observation that both growth and shrinkage speeds assume a range of values, even within one growth or shrinkage phase (9).
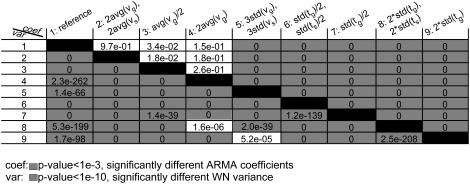
We performed nine simulations (parameters shown in Table 1), and the generated MT length trajectories were sampled at 1-s intervals. This rendered the analyzed trajectories aliased like our experimental data. The orders of the ARMA models that best describe the generated plus-end velocity series are shown in Table 1. The p-values for comparing the ARMA descriptors of the nine trajectories are shown in Fig. 6. In the following, we present our main observations:
ARMA orders indicate the persistence of coupling between kMT states (Table 1): Simulations 1–5 use the same parameters for the growth and shrinkage time distributions, and hence are described by ARMA models of the same order. Simulations 6 and 7, on the other hand, used narrower phase-time distributions, leading to more persistent correlation. The resulting plus-end velocity series required higher-order ARMA models. Similarly, simulations 8 and 9 used wider phase-time distributions, leading to less persistent correlation and lower-order ARMA models. Although in these simulations more persistent coupling was induced by more regularity in the switching, higher-order ARMA models do not necessarily mean more periodicity in the data. For instance, more persistent coupling might be the result of an increase in the average phase time.
WN variance reflects the range of observed plus-end velocities: Variations in average growth and shrinkage speeds alone do not change the coupling between kMT states. Hence, they did not affect ARMA orders or coefficients (Table 1, and Fig. 6, first four rows and columns, above diagonal). However, they affected the WN variance, which increased or decreased depending on whether the average speeds increased or decreased, respectively (Fig. 6, first four rows and columns, below diagonal).
ARMA coefficients represent the type of coupling between time points: In simulation 5, the widths of the growth and shrinkage speed distributions were larger than those in simulation 1. This led to increased heterogeneity in the simulated MT plus-end velocities, which changed the nature of the coupling between successive MT states. Therefore, simulations 1 and 5 required models of the same order but different coefficients. Similarly, the phase time distributions of simulations 6–9 differed among each other and from simulation 1. Changing the time distribution altered the coupling between kMT states, a change that resulted in variations in the ARMA coefficients (Fig. 6, above diagonal). Interestingly, the ARMA coefficients of simulations 6 and 7 were different from each other, even though both of their plus-end velocity series required models of the same ARMA order. The same holds for simulations 8 and 9. These examples highlight the ability of ARMA coefficients to detect differences in coupling, even when correlation persists to the same extent in two series. These are the subtle differences that might be not noticeable in a qualitative comparison of autocorrelation and partial autocorrelation functions and spectral densities of time series.
TABLE 1.
Model parameters used in generating synthetic kMT plus-end velocity series and the ARMA orders needed for their fitting
| Sim no. | Parameter changed | vg (μ/min) | vs (μm/min) | tg (s) | ts (s) | ARMA order |
|---|---|---|---|---|---|---|
| 1 | 4 ± 0.3 | 4 ± 0.3 | 0.8 ± 0.26 | 0.8 ± 0.26 | (1,2) | |
| 2 | avg(vg), avg(vs) | 8 ± 0.3 | 8 ± 0.3 | 0.8 ± 0.26 | 0.8 ± 0.26 | (1,2) |
| 3 | avg(vg) | 2 ± 0.3 | 4 ± 0.3 | 0.8 ± 0.26 | 0.8 ± 0.26 | (1,2) |
| 4 | avg(vg) | 8 ± 0.3 | 4 ± 0.3 | 0.8 ± 0.26 | 0.8 ± 0.26 | (1,2) |
| 5 | std(vg), std(vs) | 4 ± 0.9 | 4 ± 0.9 | 0.8 ± 0.26 | 0.8 ± 0.26 | (1,2) |
| 6 | std(tg), std(ts) | 4 ± 0.3 | 4 ± 0.3 | 0.8 ± 0.13 | 0.8 ± 0.13 | (2,2) |
| 7 | std(tg) | 4 ± 0.3 | 4 ± 0.3 | 0.8 ± 0.13 | 0.8 ± 0.26 | (2,2) |
| 8 | std(tg), std(ts) | 4 ± 0.3 | 4 ± 0.3 | 0.8 ± 0.52 | 0.8 ± 0.52 | (1,0) |
| 9 | std(tg) | 4 ± 0.3 | 4 ± 0.3 | 0.8 ± 0.52 | 0.8 ± 0.26 | (1,0) |
FIGURE 6.
ARMA descriptors distinguish between dynamics simulated with different model parameters. The discrimination matrix shows p-values for the comparison of ARMA coefficients (above diagonal) and WN variance (below diagonal). Coefficient comparison p-values <10−3 and variance comparison p-values <10−10 (highlighted in gray) indicate statistically significant differences. p-Values of 0 indicate p-values <10−324.
Note that, in the case of undersampled data, changes in the WN variance must be interpreted with caution when the corresponding ARMA coefficients also change. For example, the WN variance varied between simulation 1 and simulations 6–9 (Fig. 6, below diagonal), although the growth and shrinkage speeds were the same in the simulations. This is a consequence of undersampling, which alters the observed velocity values. Sampling the trajectories generated in simulations 8 and 9 every 0.1 s instead of every 1 s, for instance, yielded trajectories that were not undersampled and whose WN variances were found to be indistinguishable (p ˙≈ 10−3). However, the same trajectories, when undersampled, had significantly different WN variances (p ˙≈ 10−208, Fig. 6).
In summary, the order of an ARMA model describing a kMT velocity series indicates the persistence of coupling between plus-end velocities over time, the ARMA coefficients represent the type of coupling between kMT velocity states at different time points, and the WN variance is proportional to the range of observed plus-end velocities.
ARMA descriptors provide a more complete characterization of kMT dynamics than do growth and shrinkage speeds and times
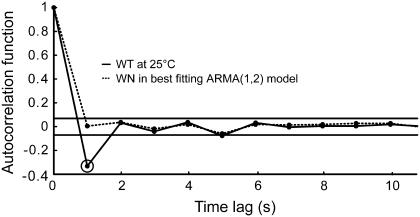
By definition, the white noise term in an ARMA model (ɛ in Eq. 1) is completely uncorrelated. If a series is well described by an ARMA model of a certain order, the resulting ɛ series should be completely uncorrelated. On the other hand, if an ARMA model is not suitable, then some residual correlation from the original trajectory will be observed in the autocorrelation function of the ɛ term. Therefore, the ability of ARMA models to describe S. cerevisiae kMT dynamics is reflected in the “whiteness” of the ɛ series in the estimated models. Testing for the “whiteness” of the ɛ term is an integral part of our algorithm (step 1a in the model fitting process), and the models chosen to describe kMT dynamics under all conditions considered satisfy this criterion. Fig. 7 demonstrates the goodness of fit of an ARMA(1,2) model to kMT plus-end velocity series in WT at 25°C: Although the velocity has a significant correlation at lag 1 s, the ɛ series is completely uncorrelated.
FIGURE 7.
The fit of plus-end velocities with the appropriate ARMA model extracts all correlation between data points. The significant autocorrelation in the plus-end velocities in WT at 25°C at time lag 1 s (highlighted by a second circle) is absent from the WN series of the best fitting ARMA(1,2) model. The two horizontal lines indicate the 99% confidence range for significant correlation values.
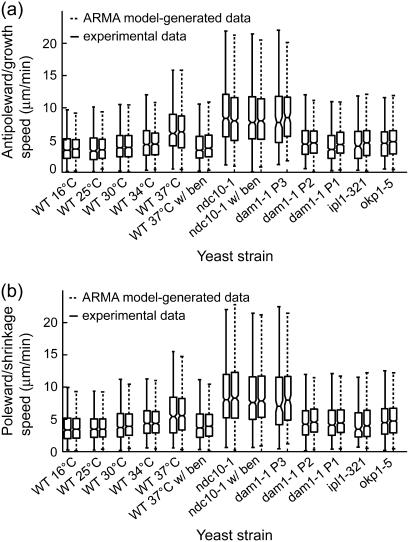
The uniqueness of ARMA model solutions under the condition expressed in Eq. 2 implies that the ARMA descriptors of kMT dynamics should allow us to generate synthetic dynamics that are equivalent, at the level of observation, to the experimentally observed dynamics. To test this, we used the ARMA descriptors of the strains and conditions analyzed in this article (Table S1) to generate synthetic plus-end velocity series. These series were found to have the same autocorrelation, partial autocorrelation, and spectral density as the original experimental series (Fig. S1). Furthermore, time integration of the synthetic velocity series yields synthetic kMT length trajectories that should be equivalent to the experimentally observed kMT length series. To test this equivalence, we assigned each synthetic length an observational error that was randomly generated in agreement with experimental observational error distributions (9), and determined the growth and shrinkage speeds and switching frequencies of both the experimental kMT length trajectories and the ARMA-generated trajectories via the algorithm described in Dorn et al. (9). Both the speed distributions (Fig. 8) and frequency distributions (data not shown) of the synthetic trajectories were found to match those of the corresponding experimental data. These findings illustrate that ARMA analysis not only supplies us with a very detailed description of kMT dynamics, but also with a unique way of using these descriptors to generate trajectories that mimic experimental data.
FIGURE 8.
ARMA descriptors implicitly contain the dynamic information captured by growth and shrinkage speeds. Box and whisker plots of (a) growth and (b) shrinkage speed distributions from experimental data and corresponding ARMA-generated trajectories (see text for details) show that the experimental and ARMA-generated distributions are equivalent. Box lines indicate the 25th percentile, median, and 75th percentile of a distribution, whereas whiskers show its extent. Boxes whose notches do not overlap represent distributions whose medians differ at the 5% significance level.
In contrast, MT growth and shrinkage speed and time distributions do not provide us with a rule of how to reproduce experimental data. As illustrated in the introduction, whether a kMT transitions to a state based on its current state (original WT at 25°C data, which has a significant correlation at lag 1 s, Fig. 2 c) or independently of it (rearranged data, which has no significant correlation, Fig. 2 c), the resulting speed and frequency distributions are the same (Fig. 2 b). This means that there are multiple scenarios of kMT behavior that could result in the same speed and frequency distributions. Therefore, the description of kMT dynamics by only the growth and shrinkage speeds and times (even when their distributions are taken into account and not only their averages) is incomplete. Additional descriptors are needed, such as the probability of transitioning to a slow growth-speed state versus the probability of transitioning to a fast growth-speed state after a state of fast shrinkage speed, or, since speeds vary even within one state (9), the probability of transitioning from a fast growth state to a slow growth state. Without these additional descriptors, kMT dynamics in two mutants might have the same growth and shrinkage speed and time distributions, and thus appear to be the same, even though they are different. This conclusion does not purport that dynamic instability is an inappropriate model of S. cerevisiae kMT dynamics—it simply means that, within the context of dynamic instability models, the average and distributions of growth and shrinkage speeds and rescue and catastrophe frequencies are not sufficient, and additional parameters are needed to obtain a complete characterization of kMT dynamics.
An alternative approach for the analysis of MT dynamics that requires the estimation of only a small number of parameters is diffusion analysis (9), or diffusion-with-drift analysis (32,33). In this model, an MT end is assumed to undergo a one-dimensional, possibly confined, random walk with drift. Thus there are at most three parameters to be estimated for a full characterization of kMT dynamics in the context of this model (diffusion constant, drift coefficient, and confinement radius). However, diffusion-with-drift models are only asymptotically equivalent to dynamic instability models (32). They do not capture the details of MT behavior at a short timescale (32), which is precisely the scale at which changes in kMT dynamics due to kinetochore and MT-associated protein mutations occur (9). Therefore, diffusion analysis is inappropriate for our task.
In summary, ARMA analysis provides us with a succinct, yet very detailed, description of kMT dynamics. It captures the coupling between kMT velocity states over time, i.e., how kMTs transition from one state to the next—information that is not captured by the traditionally employed average growth and shrinkage speeds and times, and only partly captured when their distributions are also calculated. Furthermore, ARMA descriptors implicitly include these growth and shrinkage speed and time distributions, and thus they define a more complete set of descriptors of kMT dynamics.
ARMA descriptors reveal that G1 kMT dynamics are regulated by kinetochore proteins
In this study, we utilized comparative ARMA analysis to test our hypothesis that kinetochore proteins are involved in the regulation of kMT dynamics. Such a role would be revealed by differences in the ARMA descriptors of kMT dynamics between mutant S. cerevisiae strains and WT. We have focused on the G1 kMT-kinetochore system because of its relative simplicity: although G1 S. cerevisiae chromosomes are attached to kMTs (9), no forces due to cohesion between sister chromatids are exerted on kinetochores or their associated MTs since DNA has not been replicated yet. In contrast to cohesion forces, other forces that are present in G1, such as viscous drag, are not kinetochore-specific. They are not expected to influence kinetochore protein activity or play a direct role in the regulation of kMT dynamics. Therefore, for the purpose of elucidating the regulation of kMT dynamics by kinetochore proteins, they can be neglected. Consequently, G1 provides a simpler system to test comparative ARMA analysis and establish it as a suitable framework for future screens of kinetochore proteins at various stages of the cell cycle.
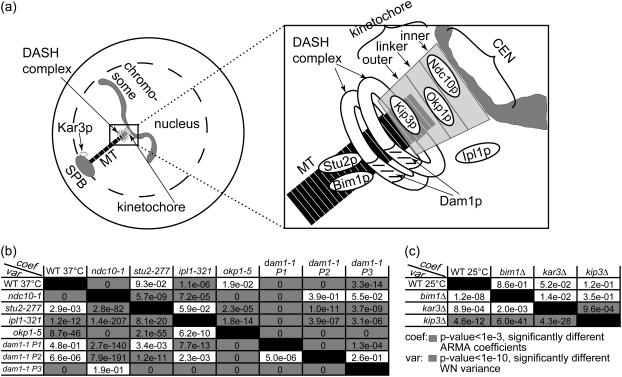
We analyzed chromosome motion, and thus kMT dynamics in the case of attachment, in mutants of the core kinetochore protein Ndc10p, the linker kinetochore protein Okp1p, and the outer kinetochore motor Kip3p. Furthermore, we analyzed chromosome motion resulting from mutating the kMT-binding protein Dam1p—part of the DASH complex that forms rings around kMTs (21,22)—and motion in a mutant of the chromosomal passenger protein Ipl1p. Finally, we also analyzed kMT dynamics in mutants of the MT-associated proteins Bim1p and Stu2p, and of the minus-end directed motor Kar3p that is located at the SPB. A schematic indicating the approximate locations of these proteins is shown in Fig. 9 a.
FIGURE 9.
ARMA descriptors detect differences between kMT dynamics in mutants of kinetochore and other MT-binding proteins in G1. (a) Schematic of an S. cerevisiae G1 cell (for graphical simplicity, only one chromosome is depicted) with a zoom-in on the region of kMT-chromosome attachment, showing the approximate locations of the investigated proteins. (b) Discrimination matrix showing p-values for the comparison of kMT dynamics in WT at 37°C and various temperature-sensitive mutants at their nonpermissive temperature of 37°C. (c) Discrimination matrix showing p-values for the comparison of kMT dynamics in WT and strains carrying deletions of nonessential proteins at 25°C. Coefficient comparison p-values <10−3 and variance comparison p-values <10−10 (highlighted in gray) indicate statistically significant differences. p-Values of 0 indicate p-values <10−324.
Control experiments
We analyzed CEN tag motion in WT and in the mutant ndc10-1, both at 37°C (the nonpermissive temperature of ndc10-1), with and without 40 μg/ml of the drug benomyl that is known to affect MT dynamics (9,34). In WT, chromosomes are attached to kMTs and their motion is driven by kMT dynamics. Thus, the addition of benomyl alters CEN tag motion (9). Accordingly, ARMA descriptors of WT with and without benomyl were significantly different: p ≈ 10−16 for the ARMA coefficient comparison test, and p ≈ 10−24 for the WN variance comparison test. On the other hand, the mutant ndc10-1 fails to form a kinetochore at 37°C and its chromosomes do not get attached to MTs (35,36). Thus, CEN tag motion in ndc10-1 is independent of kMT dynamics, and the addition of benomyl should have no effect on it (9). This was found to be indeed the case: p = 0.38 for the ARMA coefficient comparison test, and p = 0.37 for the WN variance comparison test. Furthermore, chromosome motion in ndc10-1 was observed to be different from that in WT (Fig. 9 b). These examples illustrate the ability of ARMA models to properly detect differences in kMT dynamics, and to indicate the lack thereof when a system perturbation does not affect the observed motion.
Comparative analysis of mutants
The p-values for comparing kMT-dynamics in the S. cerevisiae strains studied are shown in Fig. 9, b and c. The following is a summary of our major findings:
The linker kinetochore protein Okp1p regulates kMT assembly and disassembly rates.
Okp1p is part of the COMA linker complex in the kinetochore (23). It localizes to centromeres in G1 (37). The okp1-5 mutant at 37°C suffers from reduced transient sister separation in metaphase (11). Using ARMA descriptors, we detected a difference between kMT dynamics in okp1-5 and those in WT, where the WN variance in okp1-5 was much smaller than that in WT, although the ARMA coefficients stayed the same. This indicates that Okp1p plays a role in regulating kMT assembly and disassembly rates in G1, but not the coupling between kMT states from one time point to another. The reduced assembly and disassembly rates of kMTs in okp1-5 might account for the reduced transient sister separation observed in metaphase.
Dam1p is required for proper kMT attachment and regulation.
Dam1p is part of the DASH complex that forms rings around kMTs, mediating the attachment of MTs to kinetochores (21,22). Mutations in DASH subunits prevent proper bipolar attachment and destabilize the spindle in metaphase (38). Interestingly, we found three classes of chromosome dynamics in this mutant at 37°C. Some cells had ARMA descriptors that were statistically indistinguishable from those in ndc10-1, indicating that their chromosomes were detached (Fig. 9 b, dam1-1 P3). Other dam1-1 cells had WN variances similar to the WN variance of WT, indicating that their chromosomes were attached (dam1-1 P1 and P2 in Fig. 10), but their ARMA coefficients were different from those of WT and from each other.
FIGURE 10.
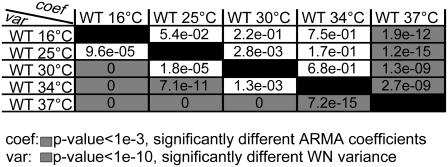
The regulation of kMT dynamics at 37°C is different from that at lower temperatures. Shown are the p-values for comparing the ARMA descriptors of kMT dynamics in WT at several temperatures. Coefficient comparison p-values <10−3 and variance comparison p-values <10−10 (highlighted in gray) indicate statistically significant differences. p-Values of 0 indicate p-values <10−324. Between 16 and 34°C, only the WN variances are different. At 37°C, however, the ARMA coefficients are also different.
The fact that we see both attached and detached phenotypes for this mutant shows the central role of the DASH complex in mediating the linkage between kMTs and the kinetochore. Mutations in Dam1p induce a profound instability in the kinetochore-kMT attachment, and any further perturbation can induce a complete loss of the kMT-kinetochore link. Moreover, the attached case exhibits two modes of kMT dynamics, a behavior hitherto not observed for any other mutation. This reflects the direct or indirect involvement of the DASH complex in the regulation of kMT dynamics by the kinetochore.
Ipl1p regulates kMT dynamics in G1.
Ipl1p (S. cerevisiae homolog of Aurora kinases) is a key regulator in the mitotic spindle. In metaphase, it induces kMTs of sister chromatids with syntelic attachment to depolymerize and detach, giving the sister chromatids the chance to reattach properly to two SPBs (23,24). Once bipolar attachment is achieved, tension is thought to downregulate Ipl1p, stabilizing kMTs (23,24). Our analysis indicates a role for Ipl1p in regulating kMT dynamics in G1 as well: although ipl1-321 at 37°C required an ARMA model of the same order as WT, its ARMA coefficients and WN variance were significantly different from those of WT. They were also significantly different from those of ndc10-1. In fact, the WN variance of ipl1-321 was even smaller than that of WT which was much smaller than that of ndc10-1 (Table S1). Therefore, chromosomes in ipl1-321 were attached to MTs, but regulated differently from WT. The change in ARMA coefficients when Ipl1p is mutated implies that Ipl1p plays a role in regulating the transitions of kMTs between states.
The outer kinetochore motor Kip3p regulates kMT dynamics.
Kip3p is a kinesin-8 that localizes to kinetochores and its deletion has been observed to alter kMT dynamics in G1 (39). Our analysis reveals that Kip3p indeed plays a role in regulating kMT assembly and disassembly rates in G1, since the WN variance of kip3Δ is significantly different from that of WT (at 25°C). In particular, the WN variance of WT is larger than that of kip3Δ (Table S1), implying that Kip3p promotes assembly and/or disassembly rates when present. On the other hand, the ARMA coefficients of kip3Δ and WT are the same, indicating that Kip3p does not influence the coupling between kMT states over time.
The minus-end directed motor Kar3p has no effect on kMT dynamics in G1.
Kar3p is a minus-end-directed motor that localizes mostly to the SPB in S. cerevisiae (39). Since it destabilizes MT minus-ends in vitro (40), the question arises whether it also destabilizes kMT minus-ends in vivo. Our analysis shows that deleting it does not alter kMT dynamics. This implies that Kar3p plays no role in G1 spindle dynamics, and provides further evidence that there is no kMT flux in S. cerevisiae. Consequently, chromosome motion observed in our experiments results from assembly and disassembly at the plus-ends of kMTs only.
The MT-binding proteins Stu2p and Bim1p do not regulate kMT dynamics in G1.
Stu2p is a microtubule associated protein, without which cells produce fewer and less dynamic cytoplasmic MTs in G1, and less dynamic kMTs in metaphase (41). Stu2-10 cells arrest in metaphase, and, if allowed to proceed to anaphase, have unusually short spindles (42). A recent study of chromosome capture by MTs after DNA replication suggests that Stu2p increases MT rescue to prevent chromosomes from falling off of MTs (43). Surprisingly, we did not see any differences in kMT dynamics between stu2-277 and WT in G1, although Stu2p seems to be in the nucleus in G1 (data not shown). This could suggest either that Stu2p does not influence kMT dynamics in G1 or that the mutation in stu2-277 does not affect the interaction between Stu2p and kMTs.
Bim1p, the S. cerevisiae homolog of EB1, is another MT-binding protein that has been observed to promote the dynamicity of cytoplasmic MTs (44), a property that is needed for proper spindle orientation (45). EB1 in higher organisms has also been found to play a role in spindle formation (46). However, although Bim1p is found in the nucleus in G1 (data not shown), we do not see any change in kMT dynamics when Bim1p is deleted, indicating that Bim1p does not play a role in kMT regulation in G1.
ARMA descriptors reveal differential regulation of kMT dynamics in WT at 37°C
To reveal protein function, it is common practice in genetics to compare the phenotypes of temperature-sensitive mutants at their permissive and nonpermissive temperatures. This practice assumes that temperature changes have no effect on the observed phenotype. For the design of future screens, we have tested whether this assumption holds for the profiling of protein mutations based on kMT dynamics.
We analyzed kMT dynamics in WT in the temperature range 16–37°C. Upon varying the temperature, MT polymer dynamics were expected to change due to thermodynamic equilibrium shifts between polymerization and depolymerization (47). Between 16 and 34°C, only the WN variance increased (Fig. 10), although the ARMA coefficients remained the same, indicating that in this range only the polymerization and/or depolymerization rates increased with temperature. However, at 37°C, both WN variance and ARMA coefficients were different from those at lower temperatures (Fig. 10). This change in ARMA coefficients indicates that changes in kMT dynamics at 37°C are not only due to thermodynamic equilibrium shifts due to rising temperature, but that, most likely, new regulatory pathways, such as the heat shock pathways (48), get activated.
In conclusion, kMT dynamics in a mutant at its nonpermissive temperature must be compared to those in WT at the same temperature, and not to those in the mutant at its permissive temperature. This point is particularly important if the nonpermissive temperature is 37°C, where our data show that new regulatory pathways might get activated. This critical principle of experimental design with temperature-sensitive mutants has been followed in all comparisons in Fig. 9.
CONCLUSION
This study establishes ARMA models as a new, rigorous method for the characterization and comparison of MT dynamics. We have developed an algorithm that combines noisy, incomplete experimental measurements and estimates ARMA descriptors including their variance-covariance matrices. To compare stochastic time series, we have also developed a statistical scheme that compares ARMA model parameters quantitatively, taking into account their uncertainties and interdependencies.
We have demonstrated that ARMA models extract the time correlation between kMT states, and implicitly include the information contained in the traditionally used but incomplete growth and shrinkage speeds and rescue and catastrophe frequencies. Thus, ARMA descriptors provide a more complete set of descriptors of kMT dynamics. This makes them ideally suited for the comparison of experimental kMT dynamics under different conditions, and for the comparison of experimental and simulated kMT dynamics for the sake of calibrating mechanistic models of the kinetochore and its regulation of kMT dynamics.
Applying ARMA analysis to kMT dynamics in various S. cerevisiae strains in the G1 phase of the cell cycle, we have shown that the kinetochore does play a role in regulating kMT behavior. In particular, we have shown that the linker kinetochore protein Okp1p and the outer kinetochore motor Kip3p affect kMT assembly and disassembly rates. The key spindle regulator Ipl1p also regulates kMT dynamics in G1. Furthermore, the MT-binding protein Dam1p is required for the proper attachment and regulation of kMTs to kinetochores, and its mutation makes the system labile, exhibiting multiple phenotypes, some associated with chromosome detachment and others with differentially regulated kMT dynamics. Finally, a crucial find in our analysis is that kMT dynamics at 37°C are differentially regulated from dynamics at lower temperatures, implying that the effects of mutations must be deduced from comparing a mutant to WT at the same temperature. This finding is especially relevant to temperature-sensitive mutants, where it implies that kMT dynamics in the mutant at its nonpermissive temperature must be compared to dynamics in WT at that temperature, and not to dynamics in the mutant at its permissive temperature.
ARMA models are potentially of general utility in cell biology, beyond MT characterization. They offer low-dimensional descriptor spaces for the characterization of intrinsically and extrinsically stochastic data that are often the readouts of time-dependent biological processes. Our augmentation of ARMA analysis with statistical tools for descriptor comparison provides a powerful new approach for the identification of cellular phenotypes based on dynamic molecular processes with a strong stochastic component.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Acknowledgments
The authors thank the Danuser and Sorger group members and Dr. Vitaly Klyachko for helpful discussions and critical readings of the manuscript.
This work was supported in part by National Institutes of Health grant R01 GM68956 to P.K.S. and G.D. K.J. is a Paul Sigler/Agouron Fellow of the Helen Hay Whitney Foundation. J.F.D. is a fellow of the Roche Research Foundation.
APPENDIX A: COMPENSATION OF ORDER MISMATCH FOR THE COMPARISON OF ARMA COEFFICIENTS
Comparing the coefficients of two models that have different AR and MA orders requires first a modification of the coefficient vectors and their variance-covariance matrices to eliminate order mismatch. If one model is an ARMA(p1,q1) and the other is an ARMA(p2,q2), then both models should be represented as ARMA(p12,q12), where 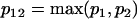 and
and 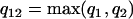 .
.
The conversion procedure is illustrated in the following example, where an ARMA(1,3) model is compared to an ARMA(3,2) model. In this case, both should be represented as ARMA(3,3) models.
Modification of coefficient vectors
An ARMA(p,q) model is equivalent to an ARMA(p′,q′) model (p′ ≥ p and q′ ≥ q) if 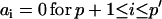 and
and 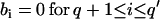 in the ARMA(p′,q′) model. Thus, the coefficient vectors of the two models,
in the ARMA(p′,q′) model. Thus, the coefficient vectors of the two models, 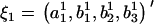 and
and 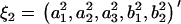 , are rewritten as
, are rewritten as 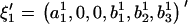 and
and 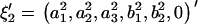 .
.
Modification of variance-covariance matrices
A fit with an ARMA(p,q) model is equivalent to a fit with an ARMA(p′,q′) model (p′ ≥ p and q′ ≥ q) with the constraints 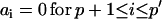 and
and 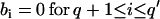 . Thus, in principle,
. Thus, in principle, 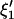 can be obtained by fitting data with an ARMA(3,3) model and imposing the constraints
can be obtained by fitting data with an ARMA(3,3) model and imposing the constraints 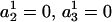 . Similarly,
. Similarly, 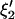 can be obtained by fitting data with an ARMA(3,3) model and imposing the constraint
can be obtained by fitting data with an ARMA(3,3) model and imposing the constraint 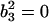 .
.
The variance-covariance matrix, C′, of parameters obtained in a constrained minimization is related to the variance-covariance matrix, C, of the same parameters but estimated in an unconstrained minimization through the equation
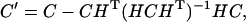 |
(A1) |
where H is the matrix of constraints (30). In our example, C for each model is the variance-covariance matrix obtained when fitting the data corresponding to that model with an ARMA(3,3) process. Note that, in general, we already have C, since each data set is fitted by a series of models during the descriptor estimation stage, and the common ARMA model, e.g., ARMA(3,3) in this case, is usually one of those already tested.
Equation A1 also requires the matrix of constraints, H. When representing an ARMA(p,q) model as an ARMA(p′,q′) model, H is given by
 |
In our example, the constraint matrices are given by
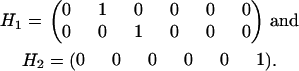 |
Using C1, C2 and H1, H2 in Eq. A1, the variance-covariance matrices corresponding to 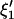 and
and 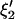 are given by
are given by
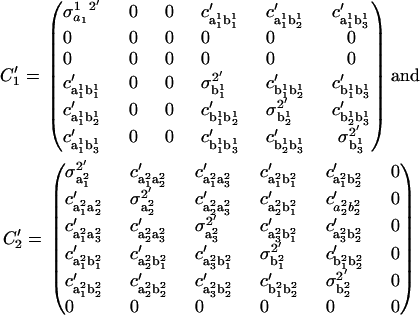 |
The variances 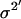 and the covariances
and the covariances 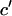 are functions of the variances and covariances from the unconstrained ARMA(3,3) fitting, as determined by Eq. A1. As expected, the constrained coefficients have zero variance and zero covariance with all other coefficients.
are functions of the variances and covariances from the unconstrained ARMA(3,3) fitting, as determined by Eq. A1. As expected, the constrained coefficients have zero variance and zero covariance with all other coefficients.
References
- 1.Mitchison, T., and M. Kirschner. 1984. Dynamic instability of microtubule growth. Nature. 312:237–242. [DOI] [PubMed] [Google Scholar]
- 2.Holy, T. E., and S. Leibler. 1994. Dynamic instability of microtubules as an efficient way to search in-space. Proc. Natl. Acad. Sci. USA. 91:5682–5685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kirschner, M., and T. Mitchison. 1986. Beyond self-assembly: from microtubules to morphogenesis. Cell. 45:329–342. [DOI] [PubMed] [Google Scholar]
- 4.Alberts, B., A. Johnson, J. Lewis, M. Raff, K. Roberts, and P. Walter. 2002. Molecular Biology of the Cell. Garland Science, New York.
- 5.O'Toole, E. T., M. Winey, and J. R. McIntosh. 1999. High-voltage electron tomography of spindle pole bodies and early mitotic spindles in the yeast Saccharomyces cerevisiae. Mol. Biol. Cell. 10:2017–2031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Maddox, P. S., K. S. Bloom, and E. D. Salmon. 2000. The polarity and dynamics of microtubule assembly in the budding yeast Saccharomyces cerevisiae. Nat. Cell Biol. 2:36–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Robinett, C. C., A. Straight, G. Li, C. Willhelm, G. Sudlow, A. Murray, and A. S. Belmont. 1996. In vivo localization of DNA sequences and visualization of large-scale chromatin organization using lac operator/repressor recognition. J. Cell Biol. 135:1685–1700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Straight, A. F., A. S. Belmont, C. C. Robinett, and A. W. Murray. 1996. Gfp tagging of budding yeast chromosomes reveals that protein-protein interactions can mediate sister chromatid cohesion. Curr. Biol. 6:1599–1608. [DOI] [PubMed] [Google Scholar]
- 9.Dorn, J. F., K. Jaqaman, D. R. Rines, G. S. Jelson, P. K. Sorger, and G. Danuser. 2005. Interphase kinetochore microtubule dynamics in yeast analyzed by high-resolution microscopy. Biophys. J. 89:2835–2854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Cheeseman, I. M., D. G. Drubin, and G. Barnes. 2002. Simple centromere, complex kinetochore: Linking spindle microtubules and centromeric DNA in budding yeast. J. Cell Biol. 157:199–203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.De Wulf, P., A. D. McAinsh, and P. K. Sorger. 2003. Hierarchical assembly of the budding yeast kinetochore from multiple subcomplexes. Genes Dev. 17:2902–2921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Walker, R. A., E. T. Obrien, N. K. Pryer, M. F. Soboeiro, W. A. Voter, H. P. Erickson, and E. D. Salmon. 1988. Dynamic instability of individual microtubules analyzed by video light-microscopy: rate constants and transition frequencies. J. Cell Biol. 107:1437–1448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Shaw, S. L., E. Yeh, P. Maddox, E. D. Salmon, and K. Bloom. 1997. Astral microtubule dynamics in yeast: a microtubule-based searching mechanism for spindle orientation and nuclear migration into the bud. J. Cell Biol. 139:985–994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gildersleeve, R. F., A. R. Cross, K. E. Cullen, A. P. Fagen, and R. C. Williams. 1992. Microtubules grow and shorten at intrinsically variable rates. J. Biol. Chem. 267:7995–8006. [PubMed] [Google Scholar]
- 15.Howell, B., D. J. Odde, and L. Cassimeris. 1997. Kinase and phosphatase inhibitors cause rapid alterations in microtubule dynamic instability in living cells. Cell Motil. Cytoskeleton. 38:201–214. [DOI] [PubMed] [Google Scholar]
- 16.Odde, D. J., and H. M. Buettner. 1995. Time series characterization of simulated microtubule dynamics in the nerve growth cone. Ann. Biomed. Eng. 23:268–286. [DOI] [PubMed] [Google Scholar]
- 17.Odde, D. J., H. M. Buettner, and L. Cassimeris. 1996. Spectral analysis of microtubule assembly dynamics. AIChE J. 42:1434–1442. [Google Scholar]
- 18.Odde, D. J., and H. M. Buettner. 1998. Autocorrelation function and power spectrum of two-state random processes used in neurite guidance. Biophys. J. 75:1189–1196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Brockwell, P. J., and R. A. Davis. 2002. Introduction to Time Series and Forecasting. Springer-Verlag, New York.
- 20.Dunn, G. A., and A. F. Brown. 1989. A unified approach to analysing cell motility. J. Cell Sci. Suppl. 8:81–102. [DOI] [PubMed] [Google Scholar]
- 21.Miranda, J. L., P. D. Wulf, P. K. Sorger, and S. C. Harrison. 2005. The yeast dash complex forms closed rings on microtubules. Nat. Struct. Mol. Biol. 12:138–143. [DOI] [PubMed] [Google Scholar]
- 22.Westermann, S., A. Avila-Sakar, H. W. Wang, H. Niederstrasser, J. Wong, D. G. Drubin, E. Nogales, and G. Barnes. 2005. Formation of a dynamic kinetochore-microtubule interface through assembly of the dam1 ring complex. Mol. Cell. 17:277–290. [DOI] [PubMed] [Google Scholar]
- 23.McAinsh, A. D., J. D. Tytell, and P. K. Sorger. 2003. Structure, function, and regulation of budding yeast kinetochores. Annu. Rev. Cell Dev. Biol. 19:519–539. [DOI] [PubMed] [Google Scholar]
- 24.Dewar, H., K. Tanaka, K. Nasmyth, and T. U. Tanaka. 2004. Tension between two kinetochores suffices for their bi-orientation on the mitotic spindle. Nature. 428:93–97. [DOI] [PubMed] [Google Scholar]
- 25.Rines, D. R., X. W. He, and P. K. Sorger. 2002. Quantitative microscopy of green fluorescent protein-labeled yeast. In Guide to Yeast Genetics and Molecular Biology. C. Guthrie and G. R. Fink, editors. Academic Press, San Diego. 16–34. [DOI] [PubMed]
- 26.Thomann, D., D. R. Rines, P. K. Sorger, and G. Danuser. 2002. Automatic fluorescent tag detection in 3D with super-resolution: application to the analysis of chromosome movement. J. Microsc. 208:49–64. [DOI] [PubMed] [Google Scholar]
- 27.Thomann, D., J. Dorn, P. K. Sorger, and G. Danuser. 2003. Automatic fluorescent tag localization. II. Improvement in super-resolution by relative tracking. J. Microsc. 211:230–248. [DOI] [PubMed] [Google Scholar]
- 28.Brewer, B. J., E. Chlebowiczsledziewska, and W. L. Fangman. 1984. Cell-cycle phases in the unequal mother/daughter cell cycles of Saccharomyces cerevisiae. Mol. Cell. Biol. 4:2529–2531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Jones, R. H. 1980. Maximum likelihood fitting of ARMA models to time series with missing observations. Technometrics. 22:389–395. [Google Scholar]
- 30.Koch, K.-R. 1988. Parameter estimation and hypothesis testing in linear models. Springer-Verlag, Berlin.
- 31.Hannan, E. J. 1980. The estimation of the order of an ARMA process. Ann. Stat. 8:1071–1081. [Google Scholar]
- 32.Maly, I. V. 2002. Diffusion approximation of the stochastic process of microtubule assembly. Bull. Math. Biol. 64:213–238. [DOI] [PubMed] [Google Scholar]
- 33.Vorobjev, I. A., V. I. Rodionov, I. V. Maly, and G. G. Borisy. 1999. Contribution of plus and minus end pathways to microtubule turnover. J. Cell Sci. 112:2277–2289. [DOI] [PubMed] [Google Scholar]
- 34.Gupta, K., J. Bishop, A. Peck, J. Brown, L. Wilson, and D. Panda. 2004. Antimitotic antifungal compound benomyl inhibits brain microtubule polymerization and dynamics and cancer cell proliferation at mitosis, by binding to a novel site in tubulin. Biochemistry. 43:6645–6655. [DOI] [PubMed] [Google Scholar]
- 35.Hyman, A. A., and P. K. Sorger. 1995. Structure and function of kinetochores in budding yeast. Annu. Rev. Cell Dev. Biol. 11:471–495. [DOI] [PubMed] [Google Scholar]
- 36.Goh, P. Y., and J. V. Kilmartin. 1993. Ndc10: a gene involved in chromosome segregation in Saccharomyces cerevisiae. J. Cell Biol. 121:503–512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ortiz, J., O. Stemmann, S. Rank, and J. Lechner. 1999. A putative protein complex consisting of Ctf19, Mcm21 and Okp1 represents a missing link in the budding yeast kinetochore. Genes Dev. 13:1140–1155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Janke, C., J. Ortiz, T. U. Tanaka, J. Lechner, and E. Schiebel. 2002. Four new subunits of the dam1-duo1 complex reveal novel functions in sister kinetochore biorientation. EMBO J. 21:181–193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Tytell, J. D., and P. K. Sorger. 2006. Analysis of kinesin motor function at budding yeast kinetochores. J. Cell Biol. 172:861–874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Endow, S., S. Kang, L. Satterwhite, M. Rose, V. Skeen, and E. Salmon. 1994. Yeast Kar3 is a minus-end microtubule motor protein that destabilizes microtubules preferentially at the minus ends. EMBO J. 13:2708–2713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kosco, K. A., C. G. Pearson, P. S. Maddox, P. J. J. Wang, I. R. Adams, E. D. Salmon, K. Bloom, and T. C. Huffaker. 2001. Control of microtubule dynamics by Stu2p is essential for spindle orientation and metaphase chromosome alignment in yeast. Mol. Biol. Cell. 12:2870–2880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Severin, F., B. Habermann, T. Huffaker, and T. Hyman. 2001. Stu2 promotes mitotic spindle elongation in anaphase. J. Cell Biol. 153:435–442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Tanaka, K., N. Mukae, H. Dewar, M. van Breugel, E. K. James, A. R. Prescott, C. Antony, and T. U. Tanaka. 2005. Molecular mechanisms of kinetochore capture by spindle microtubules. Nature. 434:987–994. [DOI] [PubMed] [Google Scholar]
- 44.Tirnauer, J. S., E. O'Toole, L. Berrueta, B. E. Bierer, and D. Pellman. 1999. Yeast Bim1p promotes the G1-specific dynamics of microtubules. J. Cell Biol. 145:993–1007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Hwang, E., J. Kusch, Y. Barral, and T. C. Huffaker. 2003. Spindle orientation in Saccharomyces cerevisiae depends on the transport of microtubule ends along polarized actin cables. J. Cell Biol. 161:483–488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Rogers, S. L., G. C. Rogers, D. J. Sharp, and R. D. Vale. 2002. Drosophila EB1 is important for proper assembly, dynamics, and positioning of the mitotic spindle. J. Cell Biol. 158:873–884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Sept, D., H. J. Limbach, H. Bolterauer, and J. A. Tuszynski. 1999. A chemical kinetics model for microtubule oscillations. J. Theor. Biol. 197:77–88. [DOI] [PubMed] [Google Scholar]
- 48.Craig, E. A., and K. Jacobsen. 1984. Mutations of the heat inducible 70-kilodalton genes of yeast confer temperature sensitive growth. Cell. 38:841–849. [DOI] [PubMed] [Google Scholar]