Abstract
Most evolutionary game theory models solve for equilibrium levels of some behaviour on the restrictive assumptions that players choose their actions simultaneously, and that a player cannot change its action after observing that of its opponent. An alternative framework is provided by sequential or ‘Stackelberg’ games in which one player commits to a ‘first move’ and the other has an opportunity to observe this move before choosing its response. Recent interest in the economic literature has focused on Stackelberg games which exhibit ‘endogenous timing’, i.e. games in which a leader and a follower arise spontaneously as a consequence of each player attempting to maximize its reward. Here, we provide the first demonstration of endogenous timing in an evolutionary context using a simple model of resource competition (the ‘tug-of-war’ model). We show that whenever two related individuals compete for a share of communal resources, both do best to adopt distinct roles in a sequential game rather than engage in simultaneous competition. Somewhat counterintuitively, the stable solution is for the weaker individual to act as leader and commit to a first move, because this arrangement leads to a lower total effort invested in competition. Endogenous timing offers a new explanation for the spontaneous emergence of leaders and followers in social groups, and highlights the benefits of commitment in social interaction.
Keywords: game theory, evolutionarily stable strategies, negotiation, social conflict, cooperation
1. Introduction
Game theory has proved to be a remarkably successful tool for understanding the evolution of social behaviour (Maynard Smith 1982; Dugatkin & Reeve 2000). One major class of model involves two players who can choose from a continuous set of actions. Most models of this type assume that each player makes its choice before it has observed the action of the other, and that neither player can alter its action after it has observed that of its opponent. For this reason such models are sometimes referred to as ‘simultaneous’ or ‘sealed-bid’ models (Schwagermeyer et al. 2002; McNamara et al. 2003). The usefulness of sealed-bid models for understanding the evolution of behaviour has recently been called into question on empirical grounds because the assumption that players do not respond on a behavioural time-scale is at odds with evidence from many species that animals do, in fact, respond dynamically to changes in each other's behaviour (Reeve & Gamboa 1987; Wright & Cuthill 1990; Markman et al. 1995; Clutton-Brock et al. 1999; Sanz et al. 2000); and on theoretical grounds because incorporating such responses in evolutionary models can render the sealed-bid equilibrium unstable. Specifically, McNamara et al. (1999) showed that the sealed-bid equilibrium to the classic biparental care game of Houston & Davies (1985) is unstable if parents can adjust their level of effort after observing that of their partner.
Negotiation models assume that a resolution is reached through a cost-free phase of back and forth responses between the two players. That is, one player offers a bid x, to which the other responds with y, leading the first player to reply with z, and so on until the series settles down to an equilibrium (McNamara et al. 1999; Taylor & Day 2004). In some cases, however, it may be in the interest of the first player to stick with its move x rather than countering with z and entering into a series of exchanges. This might be because changing one's move is costly, or because repeated rounds of negotiation ultimately lead to a less profitable outcome. In this case, the interaction takes the form of a sequential or Stackelberg game: one player ‘moves’ first, and this move is observed by the other player before deciding on its reply (von Stackelberg 1934). The game then ends. In many sequential games, the role of first mover is preferable to that of second mover, leading to a coordination problem or ‘Stackelberg war’ over who gets to move first (Schelling 1960). Recently, however, economic theorists have focused on games in which both players prefer to adopt sequential roles rather than engage in simultaneous competition, and there is no conflict over who moves first. Such games are said to exhibit endogenous timing (ET) or ‘endogenous leadership’ because the roles of first and second mover emerge spontaneously as a consequence of each player attempting to maximize its rewards, rather than being assigned exogenously (Albaek 1990; Hamilton & Slutsky 1990; Amir & Grilo 1999; van Damme & Hurkens 1999, 2004).
In a biological context, ET may have implications for a wide range of coordination problems, i.e. problems that require players to coordinate their actions to gain a reward or avoid a penalty (Bednekoff 1997, 2001; Clutton-Brock et al. 1999; Rands et al. 2003). For example, in some social foraging situations, one member of a pair consistently chooses when to forage, and the other member follows this timing. Dynamic models suggest that the roles of leader and follower can emerge spontaneously as a result of animals following simple rules of thumb (Rands et al. 2003). ET equilibria, in which both players agree on who should move first, provide an alternative explanation for the spontaneous emergence of leadership roles. Furthermore, ET has implications for evolutionary models that incorporate real-time behavioural responses. Where a sequential equilibrium yields higher fitness than either sealed-bid or negotiated solutions, selection will favour leadership and commitment in one party and responsiveness in the other. Models that exhibit ET, therefore, highlight the potential benefits of commitment in behavioural interactions, adding to the growing recognition of commitment as a potential force moulding the evolution of social behaviour (Nesse 2001). ET equilibria incorporate the concept of responsiveness and represent an alternative stable endpoint to that of negotiation models which will apply where repeated sequences of bid exchange are infeasible or unprofitable.
Here, we provide the first demonstration of ET in an evolutionary game. Specifically, we compare the relative profitability of simultaneous and sequential moves in a simple model of resource competition, and determine the conditions for which both individuals will prefer to adopt distinct roles of leader and follower rather than engage in sealed-bid conflict. The model serves a heuristic purpose in understanding the mechanisms that can generate ET in a simple two-player game, but the principles involved could find wider application in topics such as the evolution of cooperation and parental care.
2. The model
Our model is based on the tug-of-war model of Reeve et al. (1998), originally developed to analyse reproductive conflicts among cooperative breeders. More generally, however, the model embodies the principle of the tragedy of the commons (Hardin 1968) in a two-player game. Each player can invest in selfish acts to increase their personal share of a communal resource, but only at the expense of depleting the total amount of resource to be shared. In other words, selfishness results in a bigger slice of a smaller pie. The cost to the total resource reflects the time and/or energy expended on selfish behaviour, which could otherwise be used in cooperative or peaceful endeavours. For example, cooperative breeders might engage in aggression or infanticide to increase their share of reproduction on the nest, but these behaviours are likely to reduce the overall productivity of the nest (Nonacs & Reeve 1995; Reeve et al. 1998; Langer et al. 2004). Individuals competing over a shared food resource may waste time and energy in conflict while the resource becomes depleted (Giraldeau & Caraco 2000).
To model this type of competition, let x and y denote the effort expended on selfish behaviour by player 1 and player 2, respectively. The direct fitness payoffs accruing to each individual as a function of their own selfish effort and that of their partner are modelled by the following functions
| 2.1a |
| 2.1b |
and the inclusive fitnesses of the two players are
| 2.1c |
| 2.1d |
where r is the coefficient of relatedness between the two players and the parameter b scales the relative competitiveness or ‘strength’ of player 2 relative to player 1. Strength in this context means that a stronger player obtains a larger fraction of the resource for a given level of effort. Values of b<1 imply that player 1 is stronger than player 2; b>1 implies that player 1 is weaker than player 2. Note that these expressions assume that the cost of selfishness is purely in terms of a decline in the communal resource value, and that there are no personal costs. Incorporating an element of personal costs does not alter the conclusions we derive from the analysis that follows, unless such costs constitute a major component of the total cost of selfish acts (unpublished simulations). While personal costs are permitted, therefore, the model is aimed at cases where costs are predominantly communal in nature.
Given the above fitness expressions, what are the evolutionarily stable strategy (ESS) levels of selfish effort for the two individuals? The solution depends on the assumptions we make about the information available to the two players when deciding on their best action. In particular, the solution depends on whether the players choose their actions independently, or whether one individual is allowed to observe the other's action before choosing its response.
(a) Solution 1: simultaneous equilibrium
First, we consider a sealed-bid game in which each player produces a fixed effort without knowing the effort of the other individual, and there is no opportunity for the players to respond to each other's effort on a behavioural time-scale (Reeve et al. 1998). For any given fixed effort by player 1 there will exist some best-fixed effort for player 2 to invest. This ‘best effort’ for player 2 will depend on relatedness and relative strength, the two pieces of information that are common knowledge to both players. Over evolutionary time, we expect the players' efforts to converge on an equilibrium at which each produces its best effort given the effort of the other. This is the Nash equilibrium {x*, y*} at which neither player can gain by altering its level of effort.
We solve for the best effort of player 1 for any fixed effort of its partner by taking the partial derivative of its fitness expression with respect to x, setting equal to zero and solving for x. Player 2's best effort for any fixed effort of player 1 is found by the same method. At the ESS, each player produces its best effort. Thus, to solve for the ESS combination of efforts, we solve the simultaneous equations ∂W1(x, y)/∂x=0, ∂W2(x, y)/∂y=0 for x and y, respectively. This yields the following solution
| 2.2a |
| 2.2b |
This matches the solution obtained by Reeve et al. (1998).
(b) Solution 2: sequential equilibrium
Here, we assume that there is an asymmetry in the information each player has about the other's strategy. Specifically, we assume that player 1 chooses its level of selfish effort first, and player 2 observes this effort level before choosing its response. Accordingly, we will refer to player 1 in this game as the ‘first mover’, and player 2 as the ‘second mover’. The key feature of the Stackelberg game is that the second mover has advance information about the first mover's action before it decides on its response. While it is perhaps easiest to think of the two moves as taking place in chronological sequence, this need not be the case. For example, a game in which one player reliably informed the other of its intentions before both acted simultaneously would be sequential rather than simultaneous in nature.
The first mover (player 1) should take into account the fact that the second mover (player 2) will observe its chosen effort level before responding. Let denote the best response of player 2 after it has observed player 1's effort level x. We can then find the first mover's best effort (which we label in the Stackelberg game) as that which maximizes
and the second mover's best effort, , as that which maximizes
The sequential solution is obtained by backwards induction, starting with the second mover. To obtain an expression for , we differentiate W2(x, y) with respect to y, set equal to zero and solve for y. We then substitute this expression for in place of y in W1 and maximize with respect to x to yield .
Using this method we obtain the following expression for
The analytical expressions for the sequential game are somewhat unwieldy, but can be written as
| 2.3a |
| 2.3b |
Since negative effort is not permitted, we require a separate expression for the effort of the first mover in the region where our expression for falls to zero, which occurs when the strength of the second mover falls below a threshold . In this region, the first mover's stable effort is found by solving for x, which yields two roots
| 2.3c |
and
| 2.3d |
Solution (2.3c) represents an unstable equilibrium, since if the first mover puts in zero effort the second mover will be selected to cheat and increase its own selfish effort from zero. Solution (2.3d) is stable and represents the minimum effort that the first mover must maintain in order to keep the second mover's best response pinned back at zero. It may also be noted that any solution with has , so that formula (2.3d) gives the maximum possible first mover effort at the sequential equilibrium.
In summary, then, the ESS solution for the sequential case is given by
3. Results
(a) Levels of effort
We plot our results as a function of a new variable, relative strength, defined as
so that θ<0 implies that player 1 is stronger than player 2, θ>0 implies that player 1 is weaker than player 2 and θ=0 implies that the two players are of identical strength.
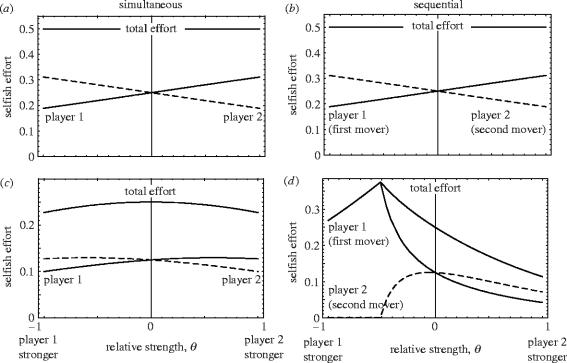
Figure 1a,b illustrates that among unrelated individuals the solutions to the simultaneous and sequential forms of the game are identical regardless of the relative strength of the two players. When the players are related, however, the solutions of the two types of game diverge. Figure 1c shows the ESS efforts of the first and second mover in the sealed-bid game for a given value of relatedness, while figure 1d plots the effort levels in the sequential game for the same relatedness value. In the sealed-bid game (figure 1c), the effort of the weaker individual is always higher than that of the stronger individual, and the maximum total effort occurs where the players are of equal strength (i.e. ∂(x*+y*)/∂θ=0 at θ=0). In the sequential game, by contrast, the efforts of the two players depend critically on whether the first mover is weaker or stronger than the second mover. When the first mover is much stronger than the second mover, the first mover is able to keep the second mover squeezed out of profitable selfish effort by maintaining a relatively high level of selfish effort itself. In this region, the best response of the second mover is zero and the first mover is able to completely monopolize group productivity. As the second mover's relative strength increases further, however, its best effort rises from zero, and the first mover's relative strength falls, until the best effort of the second mover surpasses that of the first mover as it becomes the stronger party (i.e. θ>0).
Figure 1.
Equilibrium levels of effort in simultaneous and sequential versions of the tug-of-war as a function of relative strength, for two values of relatedness, (a) and (b) r=0; (c) and (d) r=0.5. When the two players are unrelated, the solutions to the simultaneous and sequential forms of the game are identical. Among related individuals, by contrast, the two types of model produce very different outcomes.
(b) Do players prefer to act sequentially?
Now that we have expressions for the ESS effort of the two players in the simultaneous and the sequential games, we can ask when the players will prefer to play one type of game over the other. To highlight that the key difference between the two types of game is one of information rather than of temporal order, we adopt a signalling interpretation of the sequential equilibrium in the following discussion. Specifically, we equate the role of first mover with that of a signaller who transmits information about its intended effort to the other player, and the role of second mover with that of a receiver who can attend to or ignore this signal before choosing its own level of effort.
Consider two players for whom r is greater than 0. Assume that the default form of the game is for both players to submit simultaneous sealed bids {x*, y*}. Would a mutation that caused its bearer to signal unilaterally its level of selfish effort be favoured by natural selection? Suppose the first mover signals its level of selfish effort to be (for the sake of argument we assume that this signal is reliable and honest). The second mover has the option to ignore the signal and continue as before to invest y*, or to attend to the signal and invest at the second mover ESS level . Let the inclusive fitness payoff to the first mover in the case where the second mover attends to its signal be written as , and its payoff in the case where the second mover ignores its signal be written as . Similarly, let the inclusive fitness of the second mover when it either attends or does not attend to the first mover's signal be written as and , respectively. We can represent these payoffs in table 1.
Table 1.
Pay offs to a signaller (first mover) and a receiver (second mover) in a tug-of-war game.
| player 2 | |||
|---|---|---|---|
| attend | ignore | ||
| player 1 | signalling | , | , |
| not signalling | — | W1(x*, y*), W2(x*, y*) | |
The transition from a simultaneous to a sequential game requires (i) that player 1 favours signalling over not signalling and (ii) player 2 favours attending to the signal rather than ignoring it. Considering the latter condition first, player 2 will favour attending to the signal if
| 3.1 |
Since is by definition the best reply to in the sequential game, inequality (3.1) must always hold. That is, if player 1 is allowed to inform player 2 of its level of competitive effort, and this information is considered by player 2 to be reliable, it will always pay player 2 to attend to this information and adjust its selfish effort accordingly.
Since it pays player 2 to attend to player 1's signal, the only condition required for the spontaneous transition from a simultaneous to a sequential game is that the role of first mover is profitable for player 1. Define and to be the relative inclusive fitness payoff to player 1 and player 2, respectively, of adopting the roles of first mover and second mover in a sequential game versus engaging in simultaneous competition. Then the condition for player 1 to favour moving first is
| 3.2 |
To explore the sign of inequality (3.2), we plot (and , defined as ) as a function of relative strength in figure 2, for two representative values of relatedness. The results indicate that for all θ≠0. That is, an individual will favour moving first in a sequential game regardless of whether it is stronger or weaker than its opponent. We conclude that in a tug-of-war over communal resources at least one of the players will favour making a unilateral first move, thereby breaking the informational symmetry of the simultaneous game.
Figure 2.
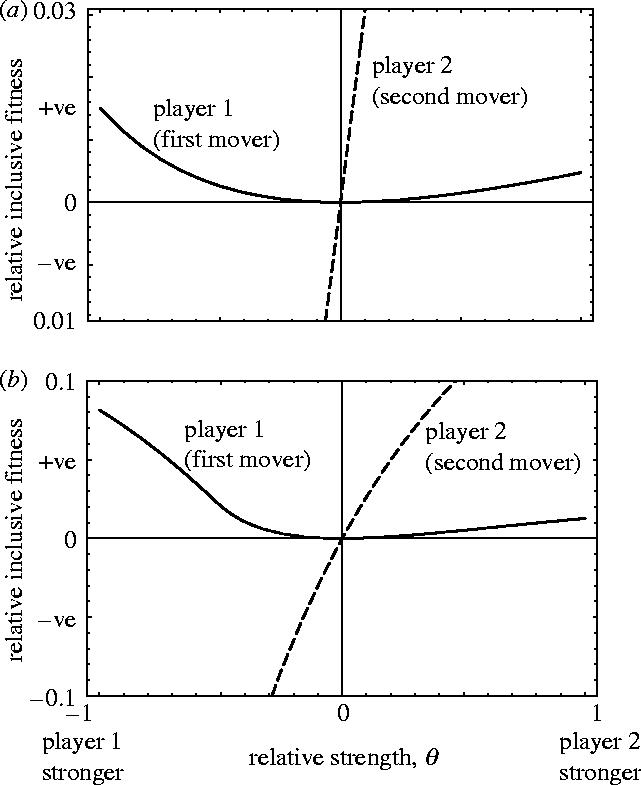
Relative inclusive fitness payoff of acting sequentially versus simultaneously as a function of relative strength, for two values of relatedness, (a) r=0.1; (b) r=0.5. Positive values of the relative inclusive fitness payoff indicate that a player prefers to play sequentially rather than simultaneously; negative values indicate the opposite. The role of first mover in a sequential game is more profitable than engaging in simultaneous competition regardless of whether stronger or weaker than one's opponent. The role of second mover, by contrast, is profitable only when stronger than the other player.
(c) Is there conflict over which individual will move first?
A second key result evident from figure 2 is that the sign of is the same as the sign of θ. That is, while the role of first mover is profitable regardless of relative strength, the role of second mover is profitable only when one is stronger than one's opponent. A stronger individual has the option of playing first or second, and both these options yield a higher payoff than engaging in sealed-bid competition. The question therefore arises as to which of these two options a stronger individual will prefer? To answer this question we need to compare the inclusive fitness payoff to a stronger individual of moving first versus second in a sequential game.
Figure 3 shows the profitability to a stronger individual of the two roles, first and second mover, respectively, as a function of the disparity in strength between the two individuals. The results show that a stronger individual will prefer the role of second mover to that of first mover. Now, since a weaker individual prefers the role of first mover over second mover, there is no conflict between the two players over which role they will adopt. The stable outcome is for the players to engage in sequential rather than simultaneous competition, and for the weaker player to signal its level of effort to the stronger player. The model exhibits ET, or a ‘natural Stackelberg solution’ (Albaek 1990).
Figure 3.
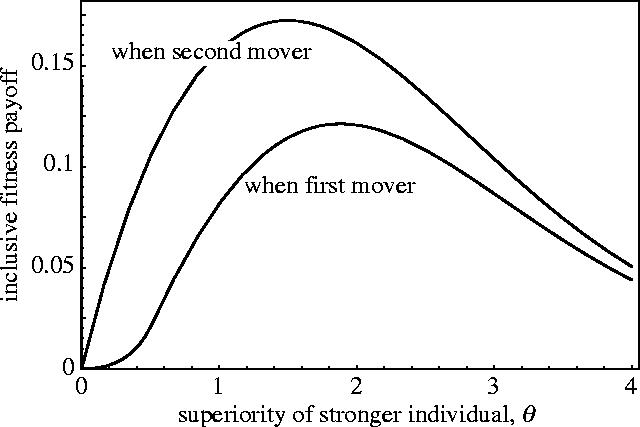
Relative inclusive fitness payoff to a stronger player of moving first versus second in a sequential game. Other parameter: r=0.5.
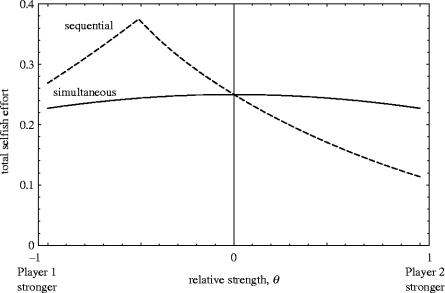
Figure 4 helps to understand why this arrangement is profitable for both weaker and stronger individuals. Where the stronger player moves first (θ<0), total selfish effort in a sequential game is higher than in a simultaneous game. By contrast, where the weaker player moves first (θ>0), total effort is lower in the sequential game. The crossover point occurs at θ=0, regardless of the value of relatedness. Thus, a sequential arrangement in which the weakest moves first produces a more collusive, efficient outcome than a simultaneous arrangement, and both weaker and stronger individuals benefit from adopting their respective roles of first and second mover.
Figure 4.
Total selfish effort in the two types of game, as a function of relative strength. The sequential arrangement, in which the stronger player moves second, leads to lower total effort invested in competition. Other parameter: r=0.5.
Moreover, any simultaneous tug-of-war is inherently unstable to invasion by a mutation in either player for moving first, and either route leads to the ESS outcome in which the weaker individual is the first mover. To see this, assume the default state is for two players to submit sealed bids in a simultaneous tug-of-war. Any mutation that caused its bearer to make a unilateral first move when weaker than its opponent could invade the simultaneous game and lead directly to the sequential ESS arrangement. On the other hand, a mutation that caused the stronger individual to move first could also invade the simultaneous equilibrium. Since this would benefit the stronger but not the weaker player, however, there would be counterselection on the weaker individual to pre-empt the action of the stronger individual by moving one step earlier. Once the weaker individual acts before the stronger, we have arrived at the sequential ESS arrangement by which neither player benefits from further changes in the order of play.
4. Discussion
We have shown that ET is a property of the tragedy of the commons (or tug-of-war) played among relatives. Where two related individuals of differing strength compete for a share of communal resources, both prefer to adopt roles in a sequential game rather than engage in simultaneous, sealed-bid competition, and both agree that the weaker individual should act as leader and the stronger as follower. This arrangement leads to a lower total selfish effort invested in competition than either a simultaneous game or a sequential game in which the roles of leader and follower are reversed.
The result that the weaker individual becomes the endogenous leader of the tug-of-war game seems somewhat counterintuitive, in part perhaps because of an unconscious and erroneous equation of ‘leadership’ with ‘strength’. The result arises, however, because relatedness ensures that the payoffs of the two players are correlated, so both have an interest in minimizing total conflict rather than simply maximizing their selfish share. Total conflict is minimized when the weaker individual moves first, because this effectively ‘evens up’ the contest. That is, the great fitness boost to the weaker player of moving first more than compensates for the direct fitness cost to the stronger player of moving second. In an interesting parallel, several economic models of duopoly competition predict that firms that are less cost-efficient, or have a higher variance in cost, will emerge as the endogenous leaders (Albaek 1990; Amir & Grilo 1999; van Damme & Hurkens 2004; but see van Damme & Hurkens 1999 for a counterexample). In these cases, stronger firms benefit from acting as follower, because this affords them reduced uncertainty about their opponent's costs and actions. These models suggest other potential mechanisms leading to ET among unrelated individuals, which remain unexplored in a biological context.
To our knowledge, the possibility of ET has not previously been considered in evolutionary game theory. To assess the applicability of our analysis to biological systems, it is worth reviewing some of the key assumptions of the model. These are as follows: (i) two related individuals of differing competitive ability engage in a pairwise contest; (ii) selfish acts increase personal success in competition at a cost to the total amount of resource to be shared, or the probability of obtaining the resource; (iii) the two individuals can assess who is stronger and who is weaker before engaging in a contest; and (iv) individuals can reliably assess the level of competitiveness of the action of their opponent.
The above assumptions will hold reasonably well for a number of diverse competitive scenarios, four of which are described here. As mentioned in §2, the tug-of-war model was originally developed to study reproductive conflict in cooperative breeders. In co-foundress associations of primitively social insects, such as Polistes paper wasps and allodapine bees (Reeve & Nonacs 1992, 1997; Field et al. 1998; Langer et al. 2004), and plural breeding groups of birds such as acorn woodpeckers (Koenig et al. 1995), rival breeders may engage in selfish activity such as aggression, oophagy and egg-destruction to increase their personal share of reproduction, at a likely cost to the total productivity of the nest or group. Similarly, chicks begging in a nest face competition from a related opponent for a share of parental resources, but elevated levels of begging will often entail both personal and shared costs (Parker 1985; Godfray & Parker 1992; Kilner 2001). In the context of mating competition, males of the American toad Bufo americanus return to their natal ponds in spring and compete to attract females via loud vocalizations (Waldman et al. 1992). Neighbouring males may often be kin, and effort expended on vocalizing is likely to carry personal and shared predation costs. As a final specific example, the tug-of-war model could be applied to conflicts over food between juvenile Atlantic salmon (Salmo Jalmar), where individuals preferentially associate with kin and compete for access to resource-rich territories (Griffiths & Armstrong 2002). In all these cases, individuals can probably assess whether they are larger or stronger than their opponent (through physical interactions, e.g. visual or auditory assessment), and also evaluate the competitive action of their opponent (e.g. the level of aggression, begging, or calling).
If the natural Stackelberg solution holds in these types of scenario, we would predict the smaller or weaker of the two that should initiate competitive acts. Thus, in the example of co-breeders sharing a nest or breeding territory we would expect a weaker individual to initiate attempts to monopolize reproduction, e.g. by infanticide, egg-destruction or aggressive dominance testing, and in the case of chicks competing for parental resources it should be the smaller or weaker chick that begs first upon presentation of a stimulus. Our model may also offer an explanation for otherwise puzzling observations of smaller individuals attacking first in some species (Enquist & Jakobsson 1986; Moretz 2003; the so called ‘Napoleon complex’; Just & Morris 2003). The model makes two further testable predictions: that weaker individuals should expend less effort in competition (in absolute terms) than stronger individuals, and that total effort expended in selfish competition should be lower the greater the disparity in strength between the competitors. By contrast, if the simultaneous solution holds we would predict that (i) neither player should consistently initiate competitive behaviours; (ii) weaker individuals should invest more in competition; and (iii) there should be little or no correlation between total effort expended on competition and the disparity in strength of the individuals. Data from a diverse range of competitive systems might be used to test these predictions.
If other two-player games can be shown to possess ET, then we may gain important new insights into how animals avoid coordination failures in other contexts. For example, animals in a group will often face a tradeoff between scanning for predators and feeding (Bednekoff 1997, 2001). How then, to coordinate vigilance behaviour? Assuming that we can view repeated vigilance or foraging bouts as independent one-shot games, ET would lead to the spontaneous emergence of leaders and followers in each round, solving the general coordination problem. This last point, however, draws attention to the limitation of our approach, namely, that we consider only a one-shot game in which animals must make a single decision. By contrast, both dynamic models of social coordination (e.g. Rands et al. 2003) and the process of negotiation (McNamara et al. 1999) deal with repeated sequences of interaction. Can we generalize our results to the problem of repeated interactions? Does ET in a one-shot model imply the same in a dynamic setting?
If the sequential game analysed here were to be repeated a finite number of times, with each game independent of the other, then the principle of backward induction dictates that the players should invest the same ESS efforts in each round. This is because the ESS solution holds for the last round of the game, and, therefore, players in the penultimate round can have no effect on the outcome of the last round. Similarly, players in the third-to-last round can have no effect on the outcome of the penultimate round and so on. Thus, in a finitely repeated tug-of-war both players do best in each round to adopt distinct roles in which the weakest moves first.
The difficulty with this argument is that in an iterated interaction the leader in one round becomes the follower in the next, so any division between rounds must be considered arbitrary. Consider a numerical example. For parameters r=0.5, b=1.5, the ESS effort levels in the sequential game are and . If player 1 were given an opportunity to move again after player 2's response, making it the de facto follower for its next move, it should increase its effort to x=0.13. This illustrates, incidentally, that any signal of intent in a one-shot interaction will be considered unreliable without some other guarantee of its credibility (such as a cost of cheating; see also McNamara & Houston 2002). Player 1's second move of x=0.13 would be met with y=0.11 by player 2, and so on in a series of exchanges that converge toward a different equilibrium from the one-shot Stackelberg solution. This new equilibrium is in fact the simultaneous solution to the game, not the ‘negotiated’ equilibrium (sensu McNamara et al. 1999). The distinction is important. Iterating the sequential solution back and forth assumes that the players make each bid as if it will be their last; i.e. they do not take future interactions into account when deciding on their response. This assumption might apply where iterated interactions occur too infrequently for natural selection to favour anything other than such ‘myopic’ strategies. Negotiation models, by contrast, assume that players make their bids as if they anticipate that the exchange will continue indefinitely until an equilibrium is reached. This assumption is likely to hold where iterated interactions occur consistently and frequently enough to favour strategies that are optimal over the duration of the repeated interaction. Unfortunately, it is not possible to compare the payoffs of the stable Stackelberg equilibrium with that of a negotiated equilibrium in the tug-of-war model, because we cannot solve for the ESS rules for responding in the current game using the analytical methods of McNamara et al. (1999). This is because these methods are limited to models in which fitness functions are quadratic, which is not the case for the tug-of-war model (see equations (2.1a) and (2.1b)). We can postulate, however, that where changing bids are sufficiently costly, both players will prefer the sequential equilibrium to that reached by negotiation or through sealed bids. In this case, the first mover's action is credible or ‘self-enforcing’ (Nesse 2001), because it has no incentive to deviate from its initial bid.
To summarize, the stable sequential and negotiated equilibria represent ends of a continuum of expectation animals have about their opportunity to change their bids in future, or, equivalently, their level of commitment to a particular action. Where changing one's bid is costly, animals may prefer to adopt distinct roles of leader and follower rather than engage in a series of negotiated exchanges. In games with ET, these roles emerge spontaneously as a consequence of the payoff structure of the game, solving the problem of which individual should act as first mover and avoiding the coordination failure that leads to a less profitable simultaneous equilibrium. The first mover has an incentive both to inform the second mover of its effort, and to stick with its effort level after the second mover has responded. A full theory of how animals should respond to each other in nature needs to incorporate this potential for self-enforcing commitment as well as negotiation.
Acknowledgments
Thanks to R. Johnstone, S. Dall, S. Rands and two anonymous referees for helpful comments. M.A.C. was supported by a Royal Society University Research Fellowship. S.F.S. thanks the Department of Neurobiology and Behavior and Laboratory of Ornithology at Cornell University for support.
References
- Albaek S. Stackelberg leadership as a natural solution under cost uncertainty. J. Ind. Econ. 1990;38:335–347. [Google Scholar]
- Amir R, Grilo I. Stackelberg versus Cournot equilibrium. Games Econ. Behav. 1999;26:1–21. 10.1006/game.1998.0650 [Google Scholar]
- Bednekoff P.A. Mutualism among safe, selfish sentinels: a dynamic game. Am. Nat. 1997;150:373–392. doi: 10.1086/286070. 10.1086/286070 [DOI] [PubMed] [Google Scholar]
- Bednekoff P.A. Coordination of safe, selfish sentinels based on mutual benefits. Ann. Zool. Fenn. 2001;38:5–14. [Google Scholar]
- Clutton-Brock T.H, O'Riain M.J, Brotherton P.N.M, Gaynor D, Kansky R, Griffin A.S, Manser M. Selfish sentinels in cooperative mammals. Science. 1999;284:1640–1644. doi: 10.1126/science.284.5420.1640. 10.1126/science.284.5420.1640 [DOI] [PubMed] [Google Scholar]
- Dugatkin L.A, Reeve H.K, editors. Game theory and animal behavior. Oxford University Press; Oxford, UK: 2000. [Google Scholar]
- Enquist M, Jakobsson S. Assessment of fighting ability in the cichlid fish Nannacara anomala. Ethology. 1986;72:143–153. [Google Scholar]
- Field J, Solis C.R, Queller D.C, Strassmann J.E. Social and genetic structure of paper wasp cofoundress associations: comparison with models of reproductive skew. Am. Nat. 1998;151:545–563. doi: 10.1086/286140. 10.1086/286140 [DOI] [PubMed] [Google Scholar]
- Giraldeau L.-A, Caraco T. Princeton University Press; Princeton, NJ: 2000. Social foraging theory. [Google Scholar]
- Godfray H.J.C, Parker G.A. Sibling competition, parent–offspring conflict, and clutch size. Anim. Behav. 1992;43:473–490. [Google Scholar]
- Griffiths S.W, Armstrong J.D. Kin-biased territory overlap and food sharing among Atlantic salmon juveniles. J. Anim. Ecol. 2002;71:480–486. 10.1046/j.1365-2656.2002.00614.x [Google Scholar]
- Hamilton J.H, Slutsky S.M. Endogenous timing in duopoly games: Stackelberg or Cournot equilibria. Games Econ. Behav. 1990;2:29–46. 10.1016/0899-8256(90)90012-J [Google Scholar]
- Hardin G. The tragedy of the commons. Science. 1968;162:1243–1248. [PubMed] [Google Scholar]
- Houston A.I, Davies N.B. The evolution of cooperation and life history in the dunnock Prunella modularis. In: Sibly R.M, Smith R.H, editors. Behavioural ecology: ecological consequences of adaptive behaviour. Blackwell Scientific Publications; Oxford, UK: 1985. pp. 471–487. [Google Scholar]
- Just W, Morris M.W. The Napoleon complex: why smaller males pick fights. Evol. Ecol. 2003;17:509–522. 10.1023/B:EVEC.0000005629.54152.83 [Google Scholar]
- Kilner R.M. A growth cost of begging in captive canary chicks. Proc. Natl Acad. Sci. USA. 2001;98:11 394–11 398. doi: 10.1073/pnas.191221798. 10.1073/pnas.191221798 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koenig W.D, Mumme R.L, Stanback M.T, Pitelka F.A. Patterns and consequences of egg destruction among joint nesting acorn woodpeckers. Anim. Behav. 1995;50:607–621. 10.1016/0003-3472(95)80123-5 [Google Scholar]
- Langer P, Hogendoorn K, Keller L. Tug-of-war over reproduction in a social bee. Nature. 2004;428:844–847. doi: 10.1038/nature02431. 10.1038/nature02431 [DOI] [PubMed] [Google Scholar]
- Markman S, YomTov Y, Wright J. Male parental care in the orange-tufted sunbird: behavioural adjustments in provisioning and nest guarding effort. Anim. Behav. 1995;50:655–669. 10.1016/0003-3472(95)80127-8 [Google Scholar]
- Maynard Smith J. Cambridge University Press; Cambridge: 1982. Evolution and the theory of games. [Google Scholar]
- McNamara J.M, Houston A.I. Credible threats and promises. Phil. Trans. R. Soc. B. 2002;357:1607–1616. doi: 10.1098/rstb.2002.1069. 10.1098/rstb.2002.1069 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McNamara J.M, Gasson C.E, Houston A.I. Incorporating rules for responding into evolutionary games. Nature. 1999;401:368–371. doi: 10.1038/43869. 10.1038/43872 [DOI] [PubMed] [Google Scholar]
- McNamara J.M, Houston A.I, Barta Z, Osorno J.-L. Should young ever be better off with one parent than two? Behav. Ecol. 2003;14:301–310. 10.1093/beheco/14.3.301 [Google Scholar]
- Moretz J.A. Aggression and RHP in the northern swordtail fish, Xiphophorus cortezi: the relationship between size and contest dynamics in male–male competition. Ethology. 2003;109:995–1008. 10.1046/j.0179-1613.2003.00938.x [Google Scholar]
- Nesse R.M. Natural selection and the capacity for subjective commitment. In: Nesse R.M, editor. Evolution and the capacity for commitment. Russell Sage Foundation; New York: 2001. pp. 1–44. [Google Scholar]
- Nonacs P, Reeve H.K. The ecology of cooperation in wasps: causes and consequences of alternative reproductive decisions. Ecology. 1995;76:953–967. [Google Scholar]
- Parker G.A. Models of parent–offspring conflict V. Effects of the behaviour of two parents. Anim. Behav. 1985;33:519–533. [Google Scholar]
- Rands S.A, Cowlishaw G, Pettifor R.A, Rowcliffe J.M, Johnstone R.A. Spontaneous emergence of leaders and followers in foraging pairs. Nature. 2003;423:432–434. doi: 10.1038/nature01630. 10.1038/nature01630 [DOI] [PubMed] [Google Scholar]
- Reeve H.K, Gamboa G.J. Queen regulation of worker foraging in paper wasps: a social feedback control system. Behaviour. 1987;102:147–167. [Google Scholar]
- Reeve H.K, Nonacs P. Social contracts in wasp societies. Nature. 1992;359:823–825. 10.1038/359823a0 [Google Scholar]
- Reeve H.K, Nonacs P. Within-group aggression and the value of group members: theory and a field test with social wasps. Behav. Ecol. 1997;8:75–82. [Google Scholar]
- Reeve H.K, Emlen S.T, Keller L. Reproductive sharing in animal societies: reproductive incentives or incomplete control by dominant breeders? Behav. Ecol. 1998;9:267–278. [Google Scholar]
- Sanz J.J, Kranenbarg S, Tinbergen J.M. Differential response by males and females to manipulation of partner contribution in the great tit. Parus major. J. Anim. Ecol. 2000;69:74–84. 10.1046/j.1365-2656.2000.00373.x [Google Scholar]
- Schelling T.C. Harvard University Press; Cambridge, MA: 1960. The strategy of conflict. [Google Scholar]
- Schwagermeyer P.L, Mock D.W, Parker G.A. Biparental care in house sparrows: negotiation or sealed bid? Behav. Ecol. 2002;13:713–721. 10.1093/beheco/13.5.713 [Google Scholar]
- Taylor P.D, Day T. Stability in negotiation games and the emergence of cooperation. Proc. R. Soc. B. 2004;271:669–674. doi: 10.1098/rspb.2003.2636. 10.1098/rspb.2003.2636 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Damme E, Hurkens S. Endogenous Stackelberg leadership. Games Econ. Behav. 1999;28:105–129. 10.1006/game.1998.0687 [Google Scholar]
- van Damme E, Hurkens S. Endogenous price leadership. Games Econ. Behav. 2004;47:404–420. 10.1016/j.geb.2004.01.003 [Google Scholar]
- von Stackelberg H. Springer; Berlin: 1934. Marktform und Gleichgewicht. [Google Scholar]
- Waldman B, Rice J.E, Honeycutt R.L. Kin recognition and incest avoidance in toads. Am. Zool. 1992;32:18–30. [Google Scholar]
- Wright J, Cuthill I. Biparental care: short term manipulation of partner contribution and brood size in the starling Sternus vulgaris. Behav. Ecol. 1990;1:116–124. [Google Scholar]