Mitosis, stature and evolution of plant mating systems: low-Φ and high-Φ plants

Abstract

There is a long-recognized association in plants between small stature and selfing, and large stature and outcrossing. Inbreeding depression is central to several hypotheses for this association, but differences in the evolutionary dynamics of inbreeding depression associated with differences in stature are rarely considered. Here, we propose and test the Φ model of plant mating system evolution, which assumes that the per-generation mutation rate of a plant is a function of the number of mitoses (Φ) that occur from zygote to gamete, and predicts fundamental differences between low-Φ (small-statured) and high-Φ (large-statured) plants in the outcomes of the joint evolution of outcrossing rate and inbreeding depression. Using a large dataset of published population genetic studies of angiosperms and conifers, we compute fitted values of inbreeding depression and deleterious mutation rates for small- and large-statured plants. Consistent with our Φ model, we find that populations of small-statured plants exhibit a range of mating systems, significantly lower mutation rates, and intermediate inbreeding depression, while large-statured plants exhibit very high mutation rates and the maximum inbreeding depression of unity. These results indicate that (i) inbred progeny typically observed in large-statured plant populations are completely lost prior to maturity in nearly all populations; (ii) evolutionary shifts from outcrossing to selfing are generally not possible in large-statured species, rather, large-statured species are more likely to evolve mating systems that avoid selfing such as self-incompatibility and dioecy; (iii) destabilization of the mating system—high selfing rate with high-inbreeding depression—might be a common occurrence in large-statured species; and (iv) large-statured species in fragmented populations might be at higher risk of extinction than previously thought. Our results help to unify and simplify a large and diverse field of research, and serve to emphasize the importance that developmental and genetic constraints play in the evolution of plant mating systems.

1. Introduction

The great majority of flowing plants are hermaphroditic, and it has been long recognized that, across species, the rate of self-fertilization (‘selfing rate’) within plant populations seems to correlate negatively with size of the adult plant, measured either in height or breadth (Stebbins 1950, 1957; Schemske & Lande 1985; Barrett et al. 1996). However, the specific causal mechanisms underlying this relationship are not understood. There are many possible advantages to selfing that could in theory benefit plants irrespective of stature, including an automatic genetic transmission advantage (Fisher 1941), reproductive assurance (Darwin 1876; Stebbins 1950; Schoen et al. 1996; Morgan et al. 1997), and more efficient use of resources (Holsinger et al. 1984; Uyenoyama et al. 1993; Sakai 1995; Zhang 2000). Selfing may also mitigate constraints on time to reproduction specifically associated with annual plants, which by necessity are small-statured (Guerrant 1989; Aarssen 2000).

The primary disadvantage to selfing is the presence of inbreeding depression, defined as a lifetime relative reduction in mean fitness of selfed progeny ${\overline{\omega }}_{\text{i}}$ as compared to outcrossed progeny ${\overline{\omega }}_{\text{o}}$ and calculated as $\delta =1-{\overline{\omega }}_{\text{i}}/{\overline{\omega }}_{\text{o}}$ (Charlesworth & Charlesworth 1987; Husband & Schemske 1996). On average, small-statured plants appear to have lower inbreeding depression in early fitness components than large-statured plants (Husband & Schemske 1996; Lynch & Walsh 1998). If this difference extends over the lifetime of the plant, then small-statured plants have a weaker overall barrier to the evolution of self-fertilization than large-statured plants, and this difference may be responsible for the selective maintenance of outcrossing in large-statured species. However, the magnitude of lifetime inbreeding depression in nature is generally unknown in large-statured species due to the time and effort required to estimate it directly in controlled fitness studies in the field. Moreover, the biological mechanisms responsible for these apparent stature-based differences in inbreeding depression are unclear, and a better understanding of these differences is fundamental to plant reproductive biology.

Here, we describe and test a general model, which we call the Φ model (pronounced ‘$\text{f}\overline{\text{i}}$’ and serving as a symbol for mitotic cell division), which proposes a mechanism for the evolution of inbreeding depression in small and large plants. As in other models of inbreeding depression (e.g. Lande & Schemske 1985; Charlesworth & Charlesworth 1987; Lande et al. 1994), the Φ model assumes that inbreeding depression is caused by recurrent recessive deleterious mutation. However, our model assumes that the rate of deleterious mutation is a positive function of Φ, the number of mitoses that occur during plant development and growth from zygote to gamete production. The association between the letter Φ and mitosis is reflected in its symbolic resemblance to a dividing cell. There is a minimum error rate during DNA replication due to necessary biophysical and chemical constraints within the cell (Maki 2002; Kunkel 2004), which results in a minimum deleterious mutation rate per mitotic cell division. Because plants do not segregate a separate germ line, mutations occurring during mitotic growth may become fixed in plant meristems and become incorporated into gametes (Klekowski 1988), resulting in an increase in lifetime deleterious mutation rate with an increase in Φ. Other positive correlates of Φ include plant stature, woodiness, generation time, and lifetime inbreeding depression.

It is possible that low-Φ plants have a high-inbreeding depression if they have an unusually large rate of mutation per somatic cell division, or if they have a predominantly outcrossing mating system which would allow the accumulation of recessive deleterious mutations, the effects of which would be exposed in selfed progeny (Lande & Schemske 1985). However, our assumption of a minimum (per somatic cell division) rate of mutation prevents sufficiently large-statured plants from exhibiting inbreeding depression less than one even if they are substantially selfed.

This novel distinction we propose between low-Φ and high-Φ plants is based on threshold behaviour of theoretical population genetic models for the evolution of inbreeding depression (Lande et al. 1994). For mutation to recessive deleterious alleles, at any given mutation rate and selfing rate, there is an equilibrium number of recessive deleterious alleles per plant and an equilibrium degree of inbreeding depression associated with the effects of these alleles; both the number of deleterious alleles and the degree of inbreeding depression increase with an increase in the mutation rate or a decrease in the selfing rate. When inbreeding depression approaches δ≅1, the efficiency of selection against deleterious alleles drops and the number of deleterious alleles maintained within the population may increase beyond that required to produce δ=1. The theoretical mechanism by which the efficiency of selection drops is the phenomenon of ‘selective interference’, in which mutations at many loci combine to eliminate variation in fitness among selfed individuals and thus collectively interfere with selection against any single mutation (Lande et al. 1994). Under these conditions, until the selfing rate increases beyond a threshold sufficient to decrease the equilibrium number of deleterious alleles to a level allowing for δ<1, no selfed progeny will survive to reproductive maturity in a finite population. We can then define high-Φ plants as those with sufficiently high mutation rates to reach this threshold of zero survival of selfed progeny despite high selfing rates. Thus, for high-Φ plants in a finite population, selfed fitness variation is zero and no selfed progeny survive to reproductive maturity.

The threshold nature of this model predicts a sharp distinction between species of low-Φ and high-Φ plants, with intermediate examples being rare. Testing of this model requires knowledge of lifetime inbreeding depression in nature, which can be measured using neutral genetic markers to jointly estimate progeny selfing rate S and adult inbreeding coefficient F in the same population (Ritland 1990).

There is now a large enough body of published research in which the required population genetic information is known that we can test the Φ model of plant mating system evolution. We collected studies from all species published in which selfing rate and adult inbreeding coefficient have been estimated within the same population, coded each species as either low-Φ if small-statured, or high-Φ if large-statured, fit standard mutation–selection equilibrium models to each group, and estimated inbreeding depression and minimum mutation rate U in the two groups from these models. The questions we ask are: (i) is inbreeding depression less than 1 in the low-Φ group and 1 in the high-Φ group? (ii) What are the corresponding minimum genomic mutation rates in the low-Φ and high-Φ groups? (iii) Are these differences statistically significant?

2. Methods

(a) Criteria for population genetic datasets

Values of adult inbreeding coefficient F and progeny selfing rate S were gathered from studies of populations of small- and large-statured hermaphroditic plants (see electronic supplementary material). Small-statured plants were herbaceous and often annuals, while large-statured plants had generation lengths >10 yr and were trees or shrubs. Only those studies were included which provided estimates of F and S derived from genetic markers sampled within the same natural population and which estimate S>0. Where multiple values were available from the same population (e.g. S from different years), one was chosen at random. Because our interest was in overall differences between small- and large-statured plants, we placed no further restrictions on taxonomy, distribution or conservation status of species. Cultivated populations such as crops or forestry plots were excluded. S was typically computed from the multi-locus outcrossing rate t_m=1−S. The total dataset comprised 28 taxonomic families, 82 species and 221 populations, each treated separately in the statistical computations.

In any meta-analysis, the analysis of interest could be performed (i) on each published study separately, and then the results of all analyses summarized, or (ii) on the pooled data from all studies, with confidence intervals arising from within the single larger analysis, as was done for the present study. The former method is not possible here because many of the reported inbreeding coefficients F are negative and hence their observed values cannot be used to estimate mutation rate. The main advantage of the second approach in our study is that random errors in the estimates of adult inbreeding coefficient, which contribute to both negative and positive values, are averaged out across studies, so that all observed values of the response variable can be utilized in the estimates.

(b) Model fits and assumptions

We fit several population genetic models (Lande & Schemske 1985; Charlesworth & Charlesworth 1987; Charlesworth et al. 1991) to the relationship between multi-locus selfing rate and adult inbreeding coefficient. These models assume an equilibrium relationship among mutation, selfing, and selection. Random recessive or partially dominant mutations cause a reduction in fitness of selfed progeny. Mutations are eliminated each generation by viability selection in progeny produced by selfing (all mutations) and random outcrossing (only partially dominant mutations). For the multi-locus model, which allows for the possibility of selective interference (Lande et al. 1994), inbreeding depression could be reduced only with selfing rates above a threshold rate S_t.

We used a Gauss–Newton algorithm to obtain least-squares estimates of model parameters U, δ and S_t with the δ constrained ≤1. Models were fitted separately to the small- and large-statured datasets. We also estimated all parameters separately for large-statured species with height ≤20 m, and height >20 m, but found no significant difference between the two, and these estimates are not reported; our assignment of height class to each population of large-statured species is included in the electronic supplementary material. To assess the impact of measurement error in the explanatory variable (selfing rate S), we created simulated datasets in which the genetic model was assumed true, and a normally distributed error term was added to both explanatory and response variables. We then quantified any bias in the estimates of the model parameters as it related to error in measurement of the explanatory variable.

Many of the reported adult inbreeding coefficients were negative, as is expected from both random and systematic error in the estimation methods the authors used (Ritland 1986). Because our models assume that the inbreeding coefficient cannot be negative, we repeated our analyses allowing the entire curve to be vertically offset according to the mean inbreeding coefficient at S=0. Parameters estimated from these offset curves are reported only where analyses of simulated data showed that the offset introduced no bias. For visual clarity, only non-offset curves are shown in the figures.

We obtained confidence intervals on all estimated parameters from 1000 bootstraps of the dataset. We also confirmed significant differences between small- and large-statured plants in their parameter estimates using randomization tests, in which each dataset was bootstrapped without replacement from the full dataset, and the parameters were estimated from those bootstrapped datasets. We report probabilities as frequencies out of 1000 randomizations in which the parameter difference in the bootstrapped datasets was equal to or greater than that observed in the actual data (one-tailed).

All model fits, statistical tests and simulations were performed using the data analysis language R (R Development Core Team 2004).

(c) Single-locus models

In the absence of inbreeding depression, all selfed progeny produced at rate S become adults, and the expectation for the adult inbreeding coefficient is F=S/(2−S) (Wright 1921 and line of ×s in figure 1). This may be considered a null model for the relationship between F and S. The addition of a constant reduction in fitness of inbred progeny δ gives

$$F=\frac{S(1-\delta )}{2-S(1+\delta )},$$ 2.1

which is modified from equation (3) of Ritland (1990); this model is called here the constant-δ model.

Figure 1.

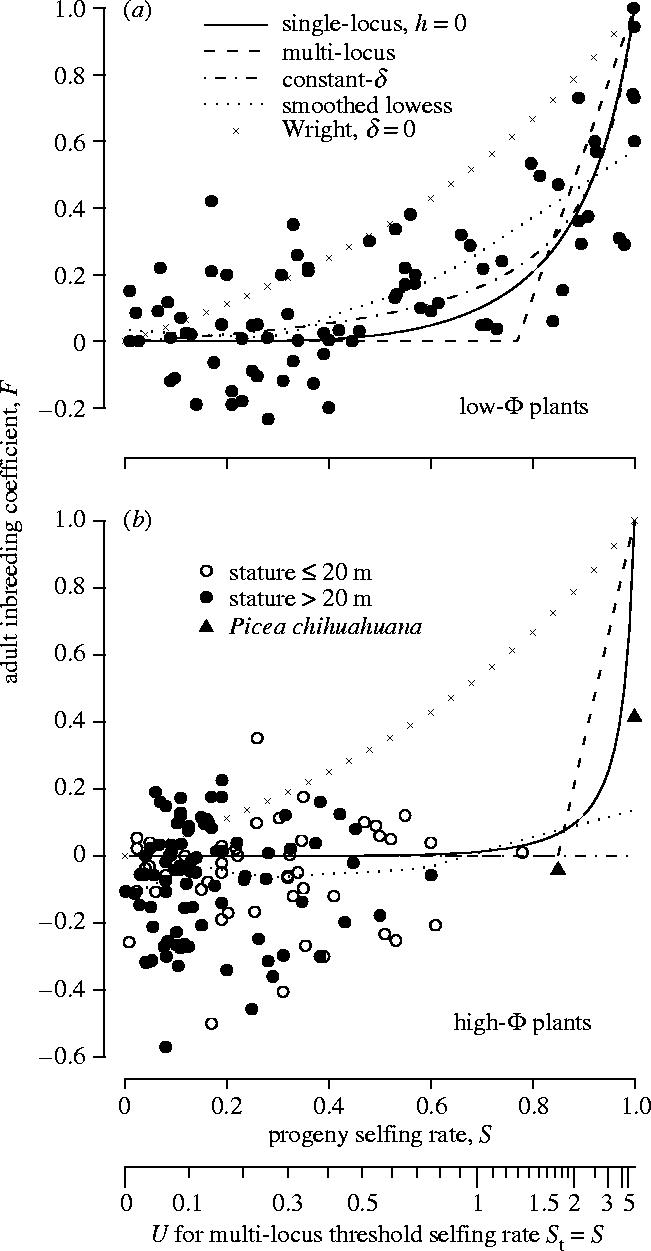
Fits of the single-locus, multi-locus and constant-δ models to population genetic estimates of adult inbreeding coefficient F versus progeny selfing rate S for (a) small-statured, low-Φ and (b) large-statured, high-Φ plants, as described in table 2. Fits are shown using the same line types in both panels. The Wright model (with inbreeding depression δ=0) and a locally smoothed lowers curve are provided for reference. Plots of the single-locus model with dominance coefficient h=0.02 were similar to those for h=0 and have been omitted for clarity. Populations of high-Φ plants with height ≤20 m are indicated with open circles, while those with height >20 m are indicated with closed circles. Populations of Picea chihuahuana (height >20 m) mentioned in the text are indicated with closed triangles.

We considered a single-locus model in which δ is not fixed, but evolves in response to S and the mutation rate U to lethal mutations (s=1) that are either completely recessive (h=0) or slightly dominant (0<h≪1). The contribution to δ of mutation at a single diploid locus i is δ_i≈μ/S (Lande & Schemske 1985), where μ is the per-locus mutation rate. Accumulating these effects multiplicatively across a genome containing L such loci gives $\delta =1-\text{exp}\left(-{\sum }_L{\delta }_i\right)$ (Crow 1970); non-multiplicative fitness functions are unlikely to change our main results (Charlesworth et al. 1991). The summation for δ is equivalent to μL/S and substitution of U gives $\delta =1-\text{exp}(-U/S)$. Further substitution provides

$$F=\frac{S\text{exp}\left(-\frac{U}{S}\right)}{2-S\left[2-\text{exp}\left(-\frac{U}{S}\right)\right]}.$$ 2.2

The deviation of this model from Wright's null model increases with increasing U. This model is called here the single-locus multiplicative model with h=0.

For slightly dominant lethal alleles (s=1, 0<h≪1), a single-locus approximation for δ_i which may be derived from equations in Ohta & Cockerham (1974) and Charlesworth & Charlesworth (1987) is δ_i≈μA/B, where $A=1+S-h(2+3S)$, $B=S+h(2-S)$. Proceeding as above gives

$$F=\frac{S\text{exp}\left(-\frac{UA}{2B}\right)}{2-S\left[2-\text{exp}\left(-\frac{UA}{2B}\right)\right]}.$$ 2.3

As values of h=0.02 are examined in this paper, this model is called here the single-locus multiplicative model with h=0.02.

(d) Multi-locus model

Multi-locus models follow the frequency of deleterious mutations simultaneously at many loci, and do not have analytical solutions (Charlesworth et al. 1991; Lande et al. 1994; Schultz & Willis 1995). However, if the dominance coefficient of mutations is low, the relationship between selfing rate and adult inbreeding coefficient is a simple discontinuous function, with F=0 for low values of the selfing rate, and F>0 for selfing rate above an abrupt threshold S_t that is dependent on the mutation rate (Lande et al. 1994). This function can be easily modelled, and because our main interest is the threshold selfing rate, we simplify the model by assuming that for S above S_t the slope is constant and the line intersects the point (1, 1)

$$F=\{\begin{array}{ll}\frac{S-S_{\text{t}}}{1-S_{\text{t}}}\hfill & \text{if}F>0,\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$ 2.4

The value of U that results in a threshold selfing rate equivalent to the estimated S_t is then found via bisection search of the mutation rate parameter space of the multi-locus model. U was determined as the midpoint of the interval of candidate mutation rates when interval size dropped below 10⁻⁶. The C-language program used to determine U from S_t is available from the corresponding author.

3. Results

The assembled datasets included population genetic estimates from 84 populations of small-statured plants and 137 populations of large-statured plants, representing 22 and 60 species, respectively (table 1, electronic supplementary material).

Table 1.

Mean adult inbreeding coefficient F and progeny selfing rate S for all populations included in the datasets. (All means are significantly different from 0 at p<0.0001 and from 1 at p<0.000 01, except for F of high-Φ plants ≤20 m, which differs from 0 at p=0.067. The complete datasets are given in the electronic supplementary material.)

dataset	n pops.	n spp.	F±s.e.m.	S±s.e.m.
small-statured low-Φ	84	22	0.165±0.028	0.465±0.033
large-statured high-Φ	137	62	−0.059±0.014	0.216±0.015
height ≤20 m	50	39	−0.041±0.022	0.303±0.024
height >20 m	87	23	−0.078±0.018	0.166±0.018

Model fits are presented in table 2 and figure 1. Small- and large-statured plant species differed significantly in constant-δ and in U estimated from either a recessive or slightly dominant mutation model. While the estimated constant-δ was less than 1 for the small-statured species, it was equal to 1 for the large-statured, indicating complete mortality of selfed progeny regardless of the selfing rate. The genomic mutation rates estimated for the large-statured species were approximately 80% greater than for the small-statured species. The difference between the two groups in threshold selfing rate S_t and corresponding U estimated from the multi-locus model was not significant but was consistent with the foregoing differences.

Table 2.

Fits for each model. (Constant-δ: equation (2.1); single-locus multiplicative, h=0: equation (2.2); single-locus multiplicative, h=0.02: equation (2.3); multi-locus: equation (2.4). Parameter estimates include their confidence intervals, and are δ, fitness reduction of inbred progeny; U, per-generation genomic mutation rate; S_t, threshold selfing rate. The p values are for a bootstrap comparison of the low-Φ and high-Φ parameter estimates, while offset indicates whether or not a non-biasing offset was used to improve model fit. For further details see the text.)

model	parameter	low-Φ	high-Φ	p	offset?
constant-δ	δ	0.83 [0.74, 0.93]	1 [1, 1]	<0.001	no
single-locus, h=0	U	1.63 [0.63, 4.0]	3.14 [0.99, 4.7]	0.007	yes
single-locus, h=0.02	U	1.82 [0.84, 4.3]	3.48 [1.5, 5.3]	0.007	yes
multi-locus	St	0.77 [0.48, 0.84]	0.85 [0.61, 0.85]	0.2	no
	U, h=0	1.3 [0.52, 1.7]	1.7 [0.78, 1.7]
	U, h=0.02	1.5 [0.66, 1.9]	2.0 [0.94, 2.0]

The estimates of threshold selfing rate were complicated by the fact that the residual least squares in the model fit was minimized for the large-statured species at S=0.85, above which the residual least squares stayed constant. Hence for these species S_t is presented conservatively as 0.85, although the least-squares estimates are in reality the set S_t ≥0.85. In the small-statured species, the S_t reported is the unique value found.

Measurement error in reported multi-locus selfing rate had a small downward effect on these parameter estimates. For example, for a true U=1 in the single-locus h=0 model, if the standard deviation of the measurement error term was increased from 0–0.02 to 0.05–0.1, the estimate of U decreased from 1.0–0.99 to 0.93–0.82. Hence if there is a small measurement error in the reported selfing rate, then our reported parameter fits will likely be biased slightly downward by an amount approximately equal to the measurement error term.

4. Discussion

The sharp contrast between small- and large-statured plants in estimated population genetic parameters and fitness of selfed and outcrossed progeny (figure 1a,b; table 2) supports the utility of the Φ model in explaining the genetic and developmental mechanisms responsible for the correlation between plant stature and mating system. In the remainder of this discussion we will use small-statured and low-Φ, and large-statured and high-Φ, interchangeably.

While our results appear to indicate that high-Φ plants generally correspond to those commonly referred to as trees or shrubs, and low-Φ plants to herbs, these designations are not quantitative and the disproportionate rarity of genetic studies of intermediate-statured species makes a precise cutoff metric premature. More genetic research is needed in intermediate populations, with accompanying studies of cell size, anatomy, and meristem organization, to understand more precisely the developmental boundary between low- and high-Φ.

(a) Comparisons to previous research

Mutation rate estimates for low-Φ plants were similar to, or somewhat higher than, estimates for individual species of low-Φ plants produced by a variety of methods (Klekowski 1998; Schultz et al. 1999; Willis 1999). In contrast, mutation rate estimates for high-Φ plants were significantly larger than low-Φ estimates for the constant-δ and single-locus models; multi-locus model estimates were also higher, but not significantly so (see table 2). These results are in accord with estimates of rates of chlorophyll deficiency mutations that are 10× to 20× higher in some large-statured species (Klekowski & Godfrey 1989; Klekowski 1998).

Our findings also confirm theoretical predictions indicating that traits particular to high-Φ plants can have profound effects on the evolutionary dynamics of inbreeding depression. Morgan (2001) found that theoretical life histories incorporating long lifetimes with recurrent somatic mutation can create a ‘selective sieve’ that favours the disproportionate accumulation of highly recessive deleterious alleles. This favours the development of a threshold in high-Φ plants, as we found here. In similar theoretical models, Lande et al. (1994) found that the combination of increased mutation rates and highly recessive deleterious alleles could lead to inbreeding depression that is resistant to selection across a wide range of selfing rates. Finally, recurrent somatic mutation expected during growth of long-lived plants (Klekowski 1988; Corradini et al. 2002) was found by Morgan (2001) to increase inbreeding depression and decrease population mean fitness. Taken together, these previous findings are in accord with our results and are consistent with the generalization that the mating system of plants can be profoundly influenced by internal developmental and genetic constraints inherent in their overall stature. Specifically, selfed progeny of high-Φ plants do indeed have very low or essentially zero mean fitness under natural conditions.

(b) Alternative explanations for the data

The small- and large-statured datasets clearly differ in the density of datapoints for which S>0.4, with the large-statured dataset relatively depauperate of data points above this selfing rate (figure 1). The datasets were constructed from a comprehensive search of the literature, so this difference presumably reflects a true difference in the range of selfing rate estimates, a difference that has also been observed in other studies (Barrett et al. 1996). Nonetheless, this may be interpreted as a possible cause for the differences in model fits and parameter estimates between datasets. However, when values of F are compared between datasets using subsets of datapoints where (say) S<0.4 and S≥0.4, differences consistent with the overall trends are still apparent (table 3). Mean F where S<0.4 is approximately 0 in both datasets. Mean F increases to 0.30 in the small-statured dataset where S≥0.4 but remains approximately 0 for large-statured plants (table 3).

Table 3.

Mean adult inbreeding coefficient F for subranges of each dataset, and a comparison of mean F within each subrange across datasets using Welch's t′ for unequal variances (Zar 1999).

	S<0.4		S≥0.4
dataset	n	F±s.e.m.	n	F±s.e.m.
small-statured low-Φ	42	0.029±0.024	42	0.302±0.041
large-statured high-Φ	118	−0.067±0.016	19	−0.012±0.038
Welch's t′	$t_{79}^{\prime }=3.38$, p=0.001		$t_{53}^{\prime }=5.61$, p<0.000 01

Another possibility is that many of the populations of large-statured plants are in fact not at equilibrium, perhaps as a result of recent anthropogenic activity. If we assume this, a past equilibrium that included selfing would still be reflected in higher values of adult F, and none of the large-statured plant populations, save a single population of Picea chihuahuana, approach the maximum values of F observed in the dataset for small-statured plants (figure 1).

Finally, our method strictly treats each population within a stature set as an equivalent replicate of the estimated parameters. In reality, populations might vary in their mutation rates within these sets. This assumption, however, is likely to have little effect on our conclusions. First, the possibility of variation within stature group was explored in our subclassification of the high-Φ dataset by overall height. In this analysis, no significant difference was found among the subsets in any parameter. This result is consistent with either (i) the absence of substantial variation among high-Φ species, or (ii) the presence of variation, but mutation rates nevertheless remained high and above the threshold for reduction of inbreeding depression. Second, our method does allow for stochastic variation among populations. If populations do vary in mutation parameters, then our analysis treats this as stochastic variation, and our estimated parameters should be interpreted as fitted means.

(c) Implications of the Φ model for mating system evolution

One of the most common evolutionary transitions in plants is the shift from a predominantly outcrossing mating system to selfing (Stebbins 1950; Baker 1955). The Φ model, supported by our present results, predicts that this transition can occur only in small-statured plants. In our analysed populations of low-Φ plants, mating systems span the spectrum of selfing rates and levels of inbreeding, and for the majority of species, data are consistent with an intermediate inbreeding depression that can evolve in response to the selfing rate in accordance with population genetic theory (figure 1a). Conversely, the intermediate inbreeding depression observed in low-Φ plants can select either for selfing or outcrossing depending on the location of the fitness thresholds for these mating systems. Our model explains this evolutionary lability as allowed by a lower rate of somatic mutation to deleterious recessive alleles in species of smaller stature, with the evolutionary optimum determined jointly by the mutation rate and the efficiency of purging by the mating system.

In sharp contrast, in populations of high-Φ plants, the overall data indicate no relationship between F and S, and an inbreeding depression essentially fixed at 1 regardless of observed selfing rates ranging from 0 to over 0.8. This means that selfing can have no net advantage over a very wide range of selfing rates in high-Φ plants, regardless of any ecological or other genetic benefits that might in theory favour selfing. Thus we would expect to find that selfed progeny, whether produced naturally or by hand pollination, would disappear from natural populations of high-Φ plants due to viability selection before reaching adulthood. This expectation is consistent with previous empirical studies in trees, for which long-term direct estimates of inbreeding depression approach 1 (Hardner & Potts 1997; Sorensen 1999), and for which estimates of inbreeding coefficients decrease from positive to 0 across increasingly mature life stages (e.g. Hufford & Hamrick 2003). Taken together, these results imply that selfing is not an adaptive part of the mating system for nearly all populations of high-Φ plants. Our model explains this as the presence of somatic mutation rates to recessive alleles high enough to cause selective interference that prevents these alleles from being purged from natural populations (Lande et al. 1994).

These results do not imply that high-Φ plants cannot evolve changes in the mating system. On the contrary, the strong selection against selfed offspring observed here implies that an increase in selfing rate in large-statured plants can strongly destabilize the mating system, and select for new morphologies that reduce the rate of self-pollination and/or self-fertilization. For example, loss of a self-incompatibility system in a high-Φ plant can lead to precipitous reductions in fitness in marginal habitats or in portions of the range in which limited availability of pollen or pollinators causes an increase in self-fertilization. In such a population, male sterility mutations can be strongly selected, leading to the evolution of gynodioecy and perhaps eventually dioecy (Miller & Venable 2000; Rankin et al. 2002; Schultz 2002). Our results imply that the alternative scenario for the population, namely that a high-selfing rate purges deleterious mutations and leads to a permanent shift in the mating system toward selfing, is simply not possible within high-Φ plants. This is again due to selective interference caused by the high mutation rate, which prevents purging under natural conditions.

We did observe a few examples from nature of moderately inbred adults in natural populations of high-Φ plants. These appear to be populations with a history of fragmentation and genetic isolation. In these populations, rates of selfing or biparental inbreeding might increase as a result of smaller effective sizes or changes in pollinator species or density. If the population survives higher inbreeding rates long enough to generate recombinant offspring lacking mutations, it might then evolve a permanently higher rate of selfing. The genetic and environmental conditions under which this can occur are unclear. In our dataset, just one of two relict populations of the conifer P. chihuahuana with high S (Ledig et al. 1997, closed triangles in figure 1b) has unusually high F in adults. The extreme homozygosity of Pinus resinosa has been hypothesized to be due to a similar process occurred in fragmented forests formed during past glaciations (Walter & Epperson 2001); however there is insufficient population genetic data for this species to be included in our analysis.

These examples are clearly rare, as is predicted by our model and the very low or zero fitted fitness of selfed individuals indicated in the high-Φ dataset as a whole. Our results agree with the conclusion that, in high-Φ plants generally, selfed progeny are ‘an incidental and largely unavoidable consequence of adaptations for outcrossing in plants that have more than one flower at anthesis at the same time’ (Lloyd 1992, in reference to geitonogamy).

Overall, these findings indicate the need for caution in interpreting differences in estimates of S among populations of high-Φ plants in terms of mating strategies, e.g. facultative selfing. Such differences in fact cannot indicate mating system variation in the absence of correlated variation in inbreeding status in reproductively mature adults. The term ‘mixed progeny production’ is thus more appropriate for these species than ‘mixed mating system’. Surveys of plant ‘mating systems’ based purely on the mating status of juveniles may not be informative of the true mating status of adults in the population, and may lead to misleading conclusions on the ecological and evolutionary status of a plant mating system.

In summary, our distinction between high- and low-Φ plants is of fundamental theoretical and practical significance. We predict that the evolution of self-fertilization by increments, from low to high values with concomitant decreases in inbreeding depression (Lande & Schemske 1985; Uyenoyama et al. 1993), is usually impossible in high-Φ plants, regardless of the genetic, ecological or energetic advantages that selfing might bring. Selfing can thus evolve by natural selection in high-Φ plants only under extraordinary circumstances, such as the sudden appearance of a high rate of inbreeding simultaneously in a large number of plants in a large population with low probability of extinction. Because of the rarity of these circumstances, we predict that selfing in high-Φ plants is almost always maladaptive, and if high enough may provoke extreme evolutionary responses such as a male-sterility dimorphism. Our Φ model suggests that abundant empirical data demonstrating the production of selfed seedlings and juveniles in many high-Φ species via both open pollination (e.g. Murawski & Hamrick 1992; Barrett et al. 1996) and hand self-pollination (e.g. Bullock 1985; Kärkkäinen et al. 1996) provides no evidence for the adaptive production of selfed progeny, because these individuals will not survive to contribute genetically to the next generation under natural conditions.