Skip to main content
PMC home page
Proceedings of the Royal Society B: Biological Sciences logoLink to Proceedings of the Royal Society B: Biological Sciences
. 2005 Jun 21;272(1570):1379–1384. doi: 10.1098/rspb.2005.3093

Higher-level mechanisms detect facial symmetry

Gillian Rhodes 1,*, Marianne Peters 1, Kieran Lee 1, M Concetta Morrone 2,3, David Burr 2,4
PMCID: PMC1560337  PMID: 16006321

Abstract

The role of symmetry detection in early visual processing and the sensitivity of biological visual systems to symmetry across a wide range of organisms suggest that symmetry can be detected by low-level visual mechanisms. However, computational and functional considerations suggest that higher-level mechanisms may also play a role in facial symmetry detection. We tested this hypothesis by examining whether symmetry detection is better for faces than comparable patterns, which share low-level properties with faces. Symmetry detection was better for upright faces than for inverted faces (experiment 1) and contrast-reversed faces (experiment 2), implicating high-level mechanisms in facial symmetry detection. In addition, facial symmetry detection was sensitive to spatial scale, unlike low-level symmetry detection mechanisms (experiment 3), and showed greater sensitivity to a 45° deviation from vertical than is found for other aspects of face perception (experiment 4). These results implicate specialized, higher-level mechanisms in the detection of facial symmetry. This specialization may reflect perceptual learning resulting from extensive experience detecting symmetry in faces or evolutionary selection pressures associated with the important role of facial symmetry in mate choice and ‘mind-reading’ or both.

Keywords: visual perception, symmetry detection, face perception

1. Introduction

Bilateral symmetry is highly salient to humans and other animals (Corballis & Beale 1976; Lehrer et al. 1994; Baylis & Driver 1995; Møller & Swaddle 1997; Wagemans 1997). It facilitates early visual processes, such as figure–ground segmentation (Rock 1983) and the perception of surface orientation (Saunders & Knill 2001), and it can be detected pre-attentively (Driver et al. 1992; Wolfe & Friedman-Hill 1992). The role of symmetry detection in early visual processing and the sensitivity of many biological visual systems to symmetry suggest that symmetry can be detected by low-level visual mechanisms. These mechanisms operate on simple image properties, independent of object identity. Consistent with this view, a low-level, biologically plausible model of symmetry detection performs well on natural images (Scognomilio et al. 2003; see also Wagemans 1997; Dakin & Herbert 1998).

All forms of symmetry perception do not, however, use the same mechanisms (Gurd et al. 2002). Neuropsychological dissociations indicate that different mechanisms underlie the implicit use of symmetry in figure/ground segmentation and explicit judgements of figural symmetry (Driver et al. 1992; Marshall & Halligan 1994). Different mechanisms also appear to be used for detecting symmetry in radial frequency-generated shapes, which resemble human head outlines, and in the dot patterns commonly used to study symmetry perception (Wilson & Wilkinson 2002). Furthermore, symmetry detection is not restricted to low-level visual processing, contributing to high-level processes of object recognition (e.g. with symmetric image features signalling symmetric objects; Biederman 1987) and face perception (Rhodes et al. 1998; Simmons et al. 2004). These observations suggest that higher-level coding mechanisms, which respond to abstract properties of objects, may also play a role in symmetry detection (see also Wilson & Wilkinson 2002).

Here, we consider whether specialized, higher-level mechanisms contribute to the detection of symmetry in human faces. Both computational and functional considerations suggest that they might. People are highly sensitive to individual differences in facial symmetry (Rhodes et al. 1998; Simmons et al. 2004), which are at least as subtle as the structural differences that mediate recognition and other aspects of face perception, for which specialized, high-level computational and neural mechanisms are used (Campbell et al. 1990; Vecera & Johnson 1995; Farah 1996; Haxby et al. 2000; Kanwisher 2000; Ricciardelli et al. 2000). Therefore, computational considerations suggest that specialized, higher-level mechanisms may contribute to facial symmetry detection.

Functional considerations also suggest a role for specialized, higher-level mechanisms, because facial symmetry information is used in at least two biologically important domains—mate choice and ‘mind-reading’. In mate choice, humans are very sensitive to facial asymmetries (Møller & Swaddle 1997; Rhodes et al. 1998; Simmons et al. 2004). They find symmetric faces attractive (Rhodes et al. 1998, 1999; Mealey et al. 1999; Perrett et al. 1999; Rhodes & Zebrowitz 2002; Little & Jones 2003), and they interpret symmetry as a sign of important aspects of mate quality, such as health and intelligence (Rhodes et al. 2001b; Rhodes & Zebrowitz 2002; Zebrowitz & Rhodes 2004). To the extent that symmetry is a valid signal of mate quality, a preference for facial symmetry may be an adaptation for finding high-quality mates (Møller & Swaddle 1997; Thornhill & Gangestad 1999; Fink & Penton-Voak 2002; Little & Jones 2003), in which case specialized mechanisms may have evolved (Williams 1966). In mind-reading, facial symmetry can signal the intentional states and attentional focus of others. For example, a symmetric face and eyes indicate that we are the focus of another's attention and deviations from symmetry, resulting from deviated gaze or head turn, can indicate the direction of attention (Wilson et al. 2000). Functionally, the importance of facial symmetry detection in mate choice and mind-reading may have created selection pressure for the evolution of specialized, higher-level mechanisms for detecting facial symmetry.

In the present experiments, we investigate whether specialized, higher-level mechanisms contribute to facial symmetry detection. The use of such mechanisms in other aspects of face perception is characterized by superior performance on faces than other patterns, which share low-level properties but do not fully engage these mechanisms. In particular, performance is better on faces than either inverted (upside down) faces (Yin 1969; Moscovitch et al. 1997; Murray et al. 2000; Rossion & Gauthier 2002; Rhodes et al. 2004) or contrast-reversed faces (Galper 1970; Kemp et al. 1990; Lewis & Johnston 1997; George et al. 1999; Hole et al. 1999; Ricciardelli et al. 2000). Therefore, if specialized, higher-level mechanisms contribute to the perception of facial symmetry, then symmetry detection should be better for faces than inverted or contrast-reversed faces. Alternatively, if facial symmetry is detected by generic, low-level mechanisms (e.g. Dakin & Herbert 1998; Scognomilio et al. 2003), then there should be no advantage for normal, upright faces.

We compared symmetry detection for normal, upright faces and inverted faces in experiment 1, and contrast-reversed faces in experiment 2. Inverted and contrast-reversed faces both share low-level properties with normal faces, but are not fully processed as faces by the visual system (George et al. 1999; Rossion & Gauthier 2002; Rhodes et al. 2004). In experiment 3, we compared symmetry detection for normal and bandpass filtered faces containing either low (1.4 cycles per face), middle (10 cycles per face) or high (60 cycles per face) spatial frequencies. Low-level symmetry detection mechanisms show little effect of spatial scale (Dakin & Hess 1997; Dakin & Herbert 1998; Rainville & Kingdom 2002). Therefore, any sensitivity to spatial scale would implicate higher-level mechanisms. In experiment 4, we examined the sensitivity of symmetry detection in faces and non-faces to a deviation from the vertical. Given the well-known advantage for detecting vertical symmetry over other forms of bilateral symmetry (e.g. Palmer & Hemenway 1978; Wenderoth 1994), we expected that tilt would impair performance in both cases. Greater impairment for faces than non-faces would further implicate higher-level mechanisms.

2. Experiment 1

We compared symmetry detection for briefly presented upright and inverted faces, using a 2-alternative forced choice procedure in which a normal face and a perfectly symmetric version of that face were presented sequentially. Both faces were presented either upright or inverted. If specialized, higher-level mechanisms contribute to facial symmetry detection, then performance should be better for upright than inverted faces.

(a) Method

(i) Participants

Participants were 48 (24 male) University of Western Australia undergraduates.

(ii) Stimuli

Normal and perfectly symmetric versions of 26 faces (13 male) were taken from Rhodes et al. (1998; experiment 2). All had neutral expressions with head and eyes directed straight ahead. The perfectly symmetric versions were made by blending the forward and mirror images of a face. The normal versions were also blends, which were made by blending low and high symmetry morphs of the face. Because both the normal and perfectly symmetric versions were blends, cues associated with blending (e.g. amount of blur) could not be used to discriminate between the normal and symmetric versions. In addition, cues from the hair could not be used to discriminate between versions, because the normal and perfectly symmetric versions of each face had the same, perfectly symmetric hairstyle (achieved by pasting the symmetric hairstyle from the perfectly symmetric image on to its corresponding normal image). The faces were displayed in oval masks that hid most of the hair. The images measured approximately 10.5×14.5 cm on the computer screen. A normal and symmetric pair is shown in figure 1.

Figure 1.

Figure 1

Open in a new tab

Normal (left) and perfectly symmetric (right) versions of a face. Note that both versions have the perfectly symmetric hairstyle.

(iii) Procedure

In each trial, participants saw the following sequence: a mask (jumbled face) for 500 ms, a face for 200 ms, the mask for 500 ms, a second face for 200 s and, finally, the mask for 500 ms. The two faces were the normal and perfectly symmetric versions of the same face. In each trial, participants had to indicate which of the two faces was symmetric. In half of the trials, the symmetric version was shown first and, in the other half, the normal version was shown first. Half the trials were presented upright, and half inverted (counterbalanced with order of the normal and symmetric versions). Each pair of faces was shown once in each orientation and once in each order condition, giving a total of 104 (26×2×2) trials. Each participant viewed the trials in a different random order.

(b) Results and discussion

A three-way ANOVA was carried out on the percentage of correct scores, with gender of participant as a between-participants factor, and gender of face and orientation as repeated-measures factors. There was a significant main effect of orientation, F(1,46)=12.02, p<0.002, with more accurate performance on upright (M=73.1%, s.e.m.=1.3%) than inverted faces (M=68.7%, s.e.m.=1.2%; figure 2). There were no other significant effects. The results implicate specialized, higher-level mechanisms in facial symmetry detection.

Figure 2.

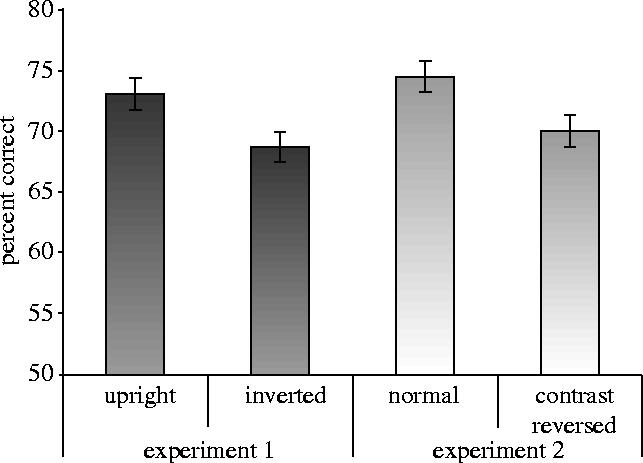
Figure 2

Open in a new tab

Mean percentage correct for symmetry detection in upright and inverted faces (experiment 1) and normal and contrast-reversed faces (experiment 2) with s.e.m. bars shown.

3. Experiment 2

This experiment was identical to experiment 1, except that inverted faces were replaced by contrast-reversed faces. Better performance for normal than contrast-reversed faces would implicate specialized, higher-level mechanisms in facial symmetry detection.

(a) Method

(i) Participants

Participants were 48 (24 male) new University of Western Australia undergraduates.

(ii) Stimuli

Contrast-reversed versions of the faces used in experiment 1 were made in Adobe Photoshop.

(iii) Procedure

The procedure was identical to that of experiment 1, except that contrast-reversed faces replaced inverted faces.

(b) Results and discussion

A three-way ANOVA was carried out on the percentage of correct scores, with gender of participant as a between-participants factor, and gender of face and face type (normal, contrast-reversed) as repeated-measures factors. There was a significant main effect of face type, F(1,46)=10.00, p<0.003, with better performance on normal (M=74.5%, s.e.m.=1.2%) than contrast-reversed faces (M=70.1%, s.e.m.=1.2%; figure 2). This advantage for normal faces again implicates higher-level, specialized mechanisms in facial symmetry detection. There was a significant main effect of gender of face, F(1,46)=6.39, p<0.02, with better performance on male (M=73.7%, s.e.m.=1.1%) than female faces (M=70.9%, s.e.m.=1.3%), but this did not interact with face type, F<1. The advantage for male faces may reflect greater asymmetry in male than female faces (Simmons et al. 2004). There were no other significant effects.

4. Experiment 3

Here, we examined the sensitivity of facial symmetry detection to spatial scale. In addition to normal faces, we showed low, medium and high bandpass filtered faces, made using three separate bandpass filters of 1.4 octave width at half-height, with peak frequencies at 1.4, 10 and 60 cycles per face. Sensitivity to spatial scale would rule out purely low-level mechanisms, which are insensitive to spatial scale (Dakin & Hess 1997; Dakin & Herbert 1998; Rainville & Kingdom 2002).

(a) Method

(i) Participants

Participants were 48 (24 male) new University of Western Australia undergraduates.

(ii) Stimuli

Low, medium and high bandpass filtered versions were made for each of the faces used in experiment 1 (figure 3a). Each face image was padded to an image of 696×696 pixels with the mean luminance value and filtered with

G(w)=e–ln(w/p)2)/σ2,

where w is the norm of the (wx, wy) spatial frequency vector, p is the peak spatial frequency and σ is the band of the filter. The function G(w) corresponds to a parabola on log–log coordinate with peak spatial frequency equal to p. Three filters were used with p equal to 134, 20 and 3 cycles per picture corresponding on average to 60, 10 and 1.4 cycles per face. (The average face length was equal to 350 pixels.) σ was equal to 1.2, generating a filter of 1.4 octave width at half-height. The filters had very little overlap in spatial frequencies. After filtering, the images were transformed back and cut to the original size. The relative contrast between the output images at various scales was unaffected by the filtering procedure.

Figure 3.

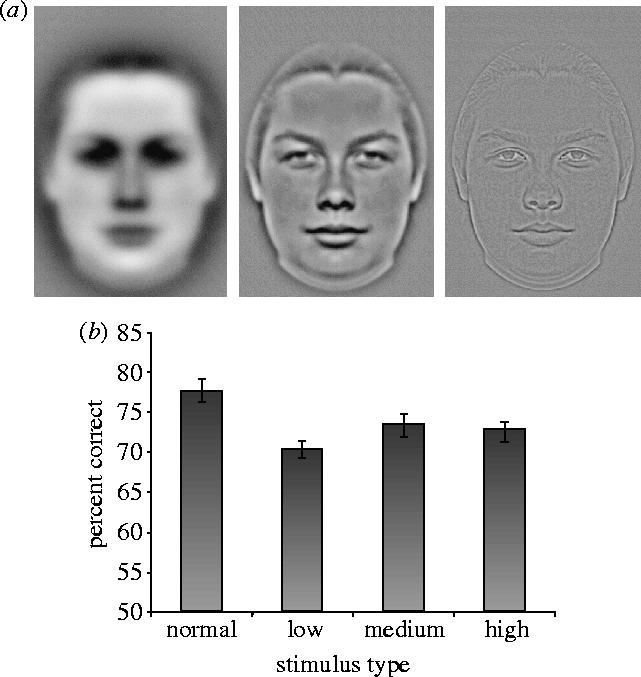
Figure 3

Open in a new tab

(a) Example of perfectly symmetric low-, medium- and high-pass filtered faces used in experiment 3. (b) Mean percentage correct for symmetry detection in normal, low-, medium- and high-pass filtered faces (experiment 3) with s.e.m. bars shown.

(iii) Procedure

The procedure was the same as for experiment 1, except that there were four image types—normal-, low-, medium- and high-pass filtered faces.

(b) Results and discussion

A three-way ANOVA was carried out on the percentage of correct scores, with gender of participant as a between-participants factor, and gender of face and spatial frequency components (normal, low, medium and high) as repeated-measures factors. There was a significant main effect of spatial frequency composition, F(3,46)=10.75, p<0.0001 (figure 3b). Performance was significantly better for normal faces (M=77.7%, s.e.m. =1.4%) than for any of the filtered faces (M=69.9%, s.e.m.=1.5%, low; M=73.2%, s.e.m.=1.5%, medium; M=72.5%, s.e.m.=1.2%, high), all t's>3.23, p's<0.002, indicating that all frequencies contributed to symmetry perception. However, performance was worst on the low-pass faces, which differed significantly from the medium-pass faces, t(138)=2.34, p<0.03. This sensitivity to spatial scale contrasts with findings for low-level symmetry detection mechanisms, further implicating higher-level mechanisms. As in experiment 2, there was a significant effect of face gender, F(1,46)=23.94, p<0.0001, with better performance on male (M=75.5%, s.d.=14.2%) than female faces (M=71.1%, s.d.=13.8%). There were no other significant effects.

5. Experiment 4

We examined the sensitivity of symmetry detection for faces and non-faces to a 45° deviation from vertical. The non-faces were created by inverting, contrast-reversing and low-pass filtering faces to produce images that do not look like faces. These ‘non-faces’ were well matched to faces on many low-level properties, but contained only low spatial frequency information. For both faces and non-faces, we expected tilt to reduce performance. The question of interest was whether tilt would differentially impair symmetry detection in faces and non-faces, thus implicating different mechanisms.

(a) Method

(i) Participants

Participants were 36 (18 male) new University of Western Australia undergraduates.

(ii) Stimuli

The normal faces were the same as in the previous experiments. The non-faces were created by inverting and contrast reversing the low bandpass filtered faces from experiment 3.

(iii) Procedure

The procedure was the same as for experiment 1, except that both types of image (face and non-face) were shown at 45 and 0°.

(b) Results and discussion

A four-way ANOVA was conducted on the percentage of correct scores, with gender of participant as a between-subjects factor, and gender of face, image type (face, non-face) and orientation (0°, 45°) as repeated-measures factors. There was a significant effect of orientation, as expected, F(1,34)=33.67, p<0.0001, with better performance on upright (M=75.0, s.e.m.=1.0) than tilted images (M=68.6, s.e.m.=1.1). There was a marginal effect of image type, F(1,34)=3.08, p<0.09, which interacted with orientation, F(1,34)=5.25, p<0.03. Performance was significantly better for faces (M=77.7, s.e.m.=1.2) than non-faces (M=72.3, s.e.m.=1.7) at 0°, t(34)=3.63, p<0.0009, but not at 45° (M=68.8, s.e.m.=1.4, faces; M=68.3, s.e.m.=1.6, non-faces), t<1. Most importantly, the effect of misorientation was larger for faces than non-faces (figure 4). A one-way repeated-measures ANOVA on difference scores (0−45°) confirmed that the upright advantage was significantly greater for faces (M=8.8, s.e.m.=1.7) than non-faces (M=4.0, s.e.m.=1.3), F(1,35)=5.41, p<0.03, indicating that detection of symmetry in faces is more sensitive to tilt than detection of symmetry in other comparable patterns.

Figure 4.

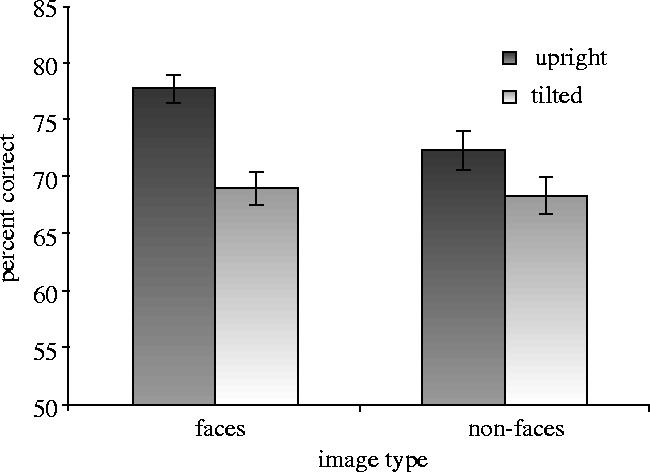
Figure 4

Open in a new tab

Mean percentage correct for symmetry detection in upright and 45° tilted faces and non-faces (experiment 4) with s.e.m. bars shown.

There was a significant main effect of gender of face, F(1,34)=25.18 (M=69.3, s.e.m.=1.0, female; M=74.3, s.e.m.=1.1, male), as found in experiments 2 and 3. However, in this case, it interacted with image type, F(1,34)=15.94, p<0.0003, and the advantage for male images was restricted to non-faces. There were no other significant effects.

6. General discussion

Symmetry detection was better for faces than either inverted or contrast-reversed faces, which are well-matched to faces on low-level properties. These results implicate higher-level mechanisms in the detection of facial symmetry and rule out purely low-level mechanisms (although these could contribute as well). The sensitivity of facial symmetry detection to spatial scale corroborates this conclusion, because low-level symmetry detection mechanisms are insensitive to changes in spatial scale (Dakin & Hess 1997; Dakin & Herbert 1998; Rainville & Kingdom 2002).

Facial symmetry detection was impaired by spatial frequency filtering. In contrast to face recognition (Nasanen 1999), middle spatial frequencies (8–16 cycles per face) were not the most useful. Therefore, different higher-level mechanisms may contribute to facial symmetry detection and face recognition. The advantage for facial symmetry detection was also narrowly tuned to vertical, disappearing with a 45° tilt. In contrast, other face-coding mechanisms continue to be engaged by misoriented faces up to 90° (Moscovitch et al. 1997; Murray et al. 2000; Sturzel & Spillman 2000; McKone et al. 2001), again suggesting distinct mechanisms for detecting facial symmetry and other aspects of face perception.

Our results cannot be explained either by generic symmetry detection mechanisms or by generic face processing mechanisms. They suggest that the higher-level mechanisms used to detect facial symmetry are jointly specialized for faces and symmetry detection. Such specialization could result from perceptual learning (Fahle & Poggio 2002), whereby generic symmetry detection mechanisms become tuned by extensive experience with faces. This experience might reflect the importance of facial symmetry in mate choice and mind-reading. This perceptual expertise account seems plausible given the rather small symmetry detection advantage we observed for faces (around four points).

Several lines of evidence are also consistent with a contribution from evolved mechanisms. First, young infants are sensitive to facial symmetry, suggesting a predisposition to attend to symmetry in faces (Rhodes et al. 2002). Second, facial symmetry is attractive across cultures (Rhodes et al. 2001a). Third, facial symmetry may provide valid cues to mate quality (Thornhill & Møller 1997; Rhodes & Zebrowitz 2002; but see Rhodes et al. 2001b).

Little & Jones (2003) have reported a preference for facial symmetry in upright but not inverted faces, which they interpret as an adaptation for mate choice. Alternatively, their results could reflect the greater difficulty of detecting symmetry in inverted faces, which are rarely seen. Symmetry preferences may also depend on relevant experience (Enquist & Arak 1994; Johnstone 1994; Jansson et al. 2002). Future research is needed to determine precisely how symmetry detection and preferences are related.

To conclude, our results show that despite the widespread sensitivity of biological visual systems to symmetry, the contribution of symmetry detection to low-level visual analysis and the effectiveness of low-level models of symmetry detection, symmetry detection is not always mediated by low-level mechanisms. Instead, higher-level mechanisms contribute to the detection of bilateral symmetry in human faces. Future research is needed to understand the computational and neural specializations underlying these mechanisms.

Acknowledgments

This work was supported by the Australian Research Council. We thank Rebecca Glauert for assistance with stimulus construction.

References

  1. Baylis G.C, Driver J. Obligatory edge assignment in vision: the role of figure and part segmentation in symmetry detection. J. Exp. Psychol. Hum. Percept. Perform. 1995;21:1323–1342. [Google Scholar]
  2. Biederman I. Recognition-by-components: a theory of human image understanding. Psychol. Rev. 1987;94:115–147. doi: 10.1037/0033-295X.94.2.115. [DOI] [PubMed] [Google Scholar]
  3. Campbell R, Heywood C.A, Cowey A, Regard M, Landis T. Sensitivity to eye gaze in prosopagnosic patients and monkeys with superior temporal sulcus ablation. Neuropsychologia. 1990;28:1123–1142. doi: 10.1016/0028-3932(90)90050-x. [DOI] [PubMed] [Google Scholar]
  4. Corballis M.C, Beale I.L. Erlbaum; Hillsdale, NJ: 1976. The psychology of left and right. [Google Scholar]
  5. Dakin S.C, Herbert A.M. The spatial region of integration for visual symmetry detection. Proc. R. Soc. B. 1998;265:659–664. doi: 10.1098/rspb.1998.0344. 10.1098/rspb.1998.0344 [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Dakin S.C, Hess R.F. The spatial mechanisms mediating symmetry perception. Vision Res. 1997;37:2915–2930. doi: 10.1016/s0042-6989(97)00031-x. [DOI] [PubMed] [Google Scholar]
  7. Driver J, Bayliss C.G, Rafal R.D. Preserved figure-ground segregation and symmetry perception in visual neglect. Nature. 1992;360:73–75. doi: 10.1038/360073a0. [DOI] [PubMed] [Google Scholar]
  8. Enquist M, Arak A. Symmetry, beauty and evolution. Nature. 1994;372:169–172. doi: 10.1038/372169a0. [DOI] [PubMed] [Google Scholar]
  9. Fahle M, Poggio T. MIT Press; Cambridge, MA: 2002. Perceptual learning. [Google Scholar]
  10. Farah M.J. Is face recognition ‘special’? Evidence from neuropsychology. Behav. Brain Res. 1996;76:181–189. doi: 10.1016/0166-4328(95)00198-0. [DOI] [PubMed] [Google Scholar]
  11. Fink B, Penton-Voak I. Evolutionary psychology of facial attractiveness. Curr. Dir. Psychol. Sci. 2002;11:154–158. [Google Scholar]
  12. Galper R.E. Recognition of faces in photographic negative. Psychon. Sci. 1970;19:207–208. [Google Scholar]
  13. George N, Dolan R.J, Fink G.R, Baylis G.C, Russell C, Driver J. Contrast polarity and face recognition in the human fusiform gyrus. Nat. Neurosci. 1999;2:574–580. doi: 10.1038/9230. [DOI] [PubMed] [Google Scholar]
  14. Gurd J.M, Fink G.R, Marshall J.C. Tacit symmetry detection and explicit symmetry processing. Behav. Brain Sci. 2002;25:409. [Google Scholar]
  15. Haxby J.V, Hoffman E.A, Gobbini M.I. The distributed human neural system for face perception. Trends Cogn. Sci. 2000;4:223–233. doi: 10.1016/s1364-6613(00)01482-0. [DOI] [PubMed] [Google Scholar]
  16. Hole G.J, George P.A, Dunsmore V. Evidence for holistic processing of faces viewed as photographic negatives. Perception. 1999;28:341–359. doi: 10.1068/p2622. [DOI] [PubMed] [Google Scholar]
  17. Jansson L, Forkman B, Enquist M. Experimental evidence of receiver bias for symmetry. Anim. Behav. 2002;63:617–621. [Google Scholar]
  18. Johnstone R.A. Female preferences for symmetrical males as a by-product of selection for mate recognition. Nature. 1994;372:172–175. doi: 10.1038/372172a0. [DOI] [PubMed] [Google Scholar]
  19. Kanwisher N. Domain specificity in face perception. Nat. Neurosci. 2000;3:759–763. doi: 10.1038/77664. [DOI] [PubMed] [Google Scholar]
  20. Kemp R, McManus C, Pigott T. Sensitivity to the displacement of facial features in negative and inverted images. Perception. 1990;19:531–543. doi: 10.1068/p190531. [DOI] [PubMed] [Google Scholar]
  21. Lehrer M, Horridge G.A, Zhang S.W, Gadgagkar R. Shape vision in bees: innate preference for flower-like patterns. Phil. Trans. R. Soc. B. 1994;347:123–137. [Google Scholar]
  22. Lewis M.B, Johnston R.A. The Thatcher illusion as a test of configural disruption. Perception. 1997;26:225–227. doi: 10.1068/p260225. [DOI] [PubMed] [Google Scholar]
  23. Little A.C, Jones B.C. Evidence against perceptual bias views for symmetry preferences in human faces. Proc. R. Soc. B. 2003;270:1759–1763. doi: 10.1098/rspb.2003.2445. 10.1098/rspb.2003.2445 [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Marshall J.C, Halligan P.W. The Yin and the Yang of visuo-spatial neglect: a case study. Neuropsychologia. 1994;32:1037–1057. doi: 10.1016/0028-3932(94)90151-1. [DOI] [PubMed] [Google Scholar]
  25. McKone E, Martini P, Nakayama K. Categorical perception of face identity in noise isolates configural processing. J. Exp. Psychol. Hum. Percept. Perform. 2001;27:573–599. doi: 10.1037//0096-1523.27.3.573. [DOI] [PubMed] [Google Scholar]
  26. Mealy L, Bridgestock R, Townsend G. Symmetry and perceived facial attractiveness. J. Pers. Soc. Psychol. 1999;76:151–158. doi: 10.1037//0022-3514.76.1.151. [DOI] [PubMed] [Google Scholar]
  27. Møller A.P, Swaddle J.P. Oxford University Press; Oxford: 1997. Asymmetry, developmental stability and evolution. [Google Scholar]
  28. Moscovitch M, Winocur G, Behrmann M. What is special about face recognition? Nineteen experiments on a person with visual object agnosia and dyslexia but normal face recognition. J. Cogn. Neurosci. 1997;9:555–604. doi: 10.1162/jocn.1997.9.5.555. [DOI] [PubMed] [Google Scholar]
  29. Murray J.E, Yong E, Rhodes G. Revisiting the perception of upside-down faces. Psychol. Sci. 2000;11:498–502. doi: 10.1111/1467-9280.00294. [DOI] [PubMed] [Google Scholar]
  30. Nasanen R. Spatial frequency bandwidth used in the recognition of facial images. Vision Res. 1999;39:3824–3833. doi: 10.1016/s0042-6989(99)00096-6. [DOI] [PubMed] [Google Scholar]
  31. Palmer S.E, Hemenway K. Orientation and symmetry: effects of multiple, rotational and near symmetries. J. Exp. Psychol. Hum. Percept. Perform. 1978;4:691–702. doi: 10.1037//0096-1523.4.4.691. [DOI] [PubMed] [Google Scholar]
  32. Perrett D.I, Burt D.M, Penton-Voak I.S, Lee K.L, Rowland D.A, Edwards R. Symmetry and human facial attractiveness. Evol. Hum. Behav. 1999;20:295–307. [Google Scholar]
  33. Rainville S.J.M, Kingdom F.A.A. Scale invariance is driven by stimulus density. Vision Res. 2002;42:351–367. doi: 10.1016/s0042-6989(01)00290-5. [DOI] [PubMed] [Google Scholar]
  34. Rhodes G, Zebrowitz L.A. Ablex; Westport, CT: 2002. Facial attractiveness: evolutionary, cognitive and social perspectives. [Google Scholar]
  35. Rhodes G, Proffitt F, Grady J.M, Sumich A. Facial symmetry and the perception of beauty. Psychon. Bull. Rev. 1998;5:659–669. [Google Scholar]
  36. Rhodes G, Roberts J, Simmons L. Reflections on symmetry and attractiveness. Psychol. Evol. Gend. 1999;1:279–295. [Google Scholar]
  37. Rhodes G, Yoshikawa S, Clark A, Lee K, McKay R, Akamatsu S. Attractiveness of facial averageness and symmetry in non-Western populations: in search of biologically based standards of beauty. Perception. 2001a;30:611–625. doi: 10.1068/p3123. [DOI] [PubMed] [Google Scholar]
  38. Rhodes G, Zebrowitz L.A, Clark A, Kalick S.M, Hightower A, McKay R. Do facial averageness and symmetry signal health? Evol. Hum. Behav. 2001b;22:31–46. doi: 10.1016/s1090-5138(00)00060-x. [DOI] [PubMed] [Google Scholar]
  39. Rhodes G, Geddes K, Jeffery L, Dziurawiec S, Clark A. Are average and symmetric faces attractive to infants? Discrimination and looking preferences. Perception. 2002;31:315–322. doi: 10.1068/p3129. [DOI] [PubMed] [Google Scholar]
  40. Rhodes G, Jeffery L, Watson T, Jaquet E, Winkler C, Clifford C.W.G. Orientation-contingent face aftereffects and implications for face coding mechanisms. Curr. Biol. 2004;14:2119–2123. doi: 10.1016/j.cub.2004.11.053. [DOI] [PubMed] [Google Scholar]
  41. Ricciardelli P, Baylis G, Driver J. The positive and negative of human expertise in gaze perception. Cognition. 2000;77:B1–B14. doi: 10.1016/s0010-0277(00)00092-5. [DOI] [PubMed] [Google Scholar]
  42. Rock I. MIT Press; Cambridge, MA: 1983. The logic of perception. [Google Scholar]
  43. Rossion B, Gauthier I. How does the brain process upright and inverted faces? Behav. Cogn. Neurosci. Rev. 2002;1:63–75. doi: 10.1177/1534582302001001004. [DOI] [PubMed] [Google Scholar]
  44. Saunders J.A, Knill D.C. Perception of 3D surface orientation from skew symmetry. Vision Res. 2001;41:3163–3183. doi: 10.1016/s0042-6989(01)00187-0. [DOI] [PubMed] [Google Scholar]
  45. Scognamillo R, Rhodes G, Morrone C, Burr D. A feature based model of symmetry detection. Proc. R. Soc. B. 2003;270:1727–1733. doi: 10.1098/rspb.2003.2434. 10.1098/rspb.2003.2434 [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Simmons L.W, Rhodes G, Peters M, Koehler N. Are human preferences for facial symmetry focused on signals of developmental instability? Behav. Ecol. 2004;15:864–871. [Google Scholar]
  47. Sturzel F, Spillman L. Thatcher illusion: dependence on angle of rotation. Perception. 2000;29:937–942. doi: 10.1068/p2888. [DOI] [PubMed] [Google Scholar]
  48. Thornhill R, Gangestad S.W. Facial attractiveness. Trends Cogn. Sci. 1999;3:452–460. doi: 10.1016/s1364-6613(99)01403-5. [DOI] [PubMed] [Google Scholar]
  49. Thornhill R, Møller A.P. Developmental stability, disease and medicine. Biol. Rev. 1997;72:497–548. doi: 10.1017/s0006323197005082. [DOI] [PubMed] [Google Scholar]
  50. Vecera S.P, Johnson M.H. Gaze detection and the cortical processing of faces: evidence from infants and adults. Vis. Cogn. 1995;2:59–87. [Google Scholar]
  51. Wagemans J. Characteristics and models of human symmetry detection. Trends Cogn. Sci. 1997;1:9–32. doi: 10.1016/S1364-6613(97)01105-4. [DOI] [PubMed] [Google Scholar]
  52. Wenderoth P. The salience of vertical symmetry. Perception. 1994;23:221–236. doi: 10.1068/p230221. [DOI] [PubMed] [Google Scholar]
  53. Williams G.C. Princeton University Press; Princeton, NJ: 1966. Adaptation and natural selection: a critique of some current evolutionary thought. [Google Scholar]
  54. Wilson H.R, Wilkinson F. Symmetry perception: a novel approach for biological shapes. Vision Res. 2002;42:589–597. doi: 10.1016/s0042-6989(01)00299-1. [DOI] [PubMed] [Google Scholar]
  55. Wilson H.R, Wilkinson F, Lin L.-M, Castillo M. Perception of head orientation. Vision Res. 2000;40:459–472. doi: 10.1016/s0042-6989(99)00195-9. [DOI] [PubMed] [Google Scholar]
  56. Wolfe J.M, Friedman-Hill S.R. On the role of symmetry in visual search. Psychol. Sci. 1992;3:194–198. [Google Scholar]
  57. Yin R.K. Looking at upside-down faces. J. Exp. Psychol. 1969;81:141–145. [Google Scholar]
  58. Zebrowitz L.A, Rhodes G. Sensitivity to ‘bad genes’ and the anomalous face overgeneralization effect: cue validity, cue utilization, and accuracy in judging intelligence and health. J. Nonverbal Behav. 2004;28:167–185. [Google Scholar]

Articles from Proceedings of the Royal Society B: Biological Sciences are provided here courtesy of The Royal Society

RESOURCES