A Molecular Dynamics Study and Free Energy Analysis of Complexes between the Mlc1p Protein and Two IQ Motif Peptides

Abstract

The Mlc1p protein from the budding yeast Saccharomyces cerevisiae is a Calmodulin-like protein, which interacts with IQ-motif peptides located at the yeast's myosin neck. In this study, we report a molecular dynamics study of the Mlc1p-IQ2 protein-peptide complex, starting with its crystal structure, and investigate its dynamics in an aqueous solution. The results are compared with those obtained by a previous study, where we followed the solution structure of the Mlc1p-IQ4 protein-peptide complex by molecular dynamics simulations. After the simulations, we performed an interaction free-energy analysis using the molecular mechanics Poisson-Boltzmann surface area approach. Based on the dynamics of the Mlc1p-IQ protein-peptide complexes, the structure of the light-chain-binding domain of myosin V from the yeast S. cerevisiae is discussed.

INTRODUCTION

Calmodulin (CaM) is a ubiquitous, multifaceted, intercellular, Ca⁺²-binding protein. It regulates more than 100 different target proteins, and plays an important regulatory role in a wide variety of functions such as growth, proliferation, movement, apoptosis, fertilization, muscle contraction, and vesicular fusion (for review see (1–3)). The primary structure of CaM and CaM-like proteins (for example, the Troponin C and the myosin light chains) is highly conserved in all cell types. These proteins are built of three structural domains: the N-lobe, the C-lobe, and an elongated, mostly helical, interdomain that connects the two lobes to form a dumbbell-like shape. Each lobe contains two EF-hand motifs of helix-loop-helix, responsible for binding of Ca⁺². Crystallographic data have shown that the fully Ca⁺²-bound CaM (Holo-CaM) may adopt either an extended (4,5) or a compact conformation (6). The Ca⁺²-free (Apo-CaM) structure solved by nuclear magnetic resonance (NMR) (7) shows a considerable flexibility of the protein, as its interdomain bends, bringing the lobes of the protein into a close contact. The distinct difference between the Apo- and Holo- structures of the protein is attributed to the shape of the interdomain. At the crystal structures it may comprise elongated or curved shapes, whereas at the Ca⁺²-free solution states it tends to be mostly bent.

The CaM and CaM-like proteins form complexes with a large number of CaM-binding proteins. The structures of these protein-peptide complexes were investigated by means of NMR (8) and protein crystallography studies (9–17). These studies revealed that, upon binding of the peptides, the interdomain of Holo-CaM adopts a bent conformation accompanied by partial unwinding. The bending of the interdomain brings the two lobes of the protein into a close proximity. Thus, the flexibility of the interdomain region is critical for the ability of CaM to interact with target peptides. Various aspects of the interaction of CaM with its targets, such as recognition and activation, are reviewed by Vetter and Leclerc (18).

The flexibility of CaM and its fundamental role in Ca⁺²-signaling processes made it an attractive subject for computational studies. Early molecular dynamics (MD) simulations of Holo-CaM confirmed the flexibility of the interdomain (19–21). Due to the limited computational resources available at that time, these simulations were carried out over subnanosecond timescales and included relatively few, if any, water molecules. During the last decade, MD simulations of Apo- and Holo-CaM were carried out under more realistic conditions, addressing issues concerning the relative positions of its N- and C-lobes and the flexibility of its interdomain (22–30).

CaM-binding proteins do not share a strong sequence homology. Nonetheless, many of them often possess a region that is characterized by a basic helix consisting ∼25 amino acids. This helix, known as the IQ motif, confers to the consensus sequence IQXXXRGXXXXR, but the sequence rather loosely adheres to this consensus. The isoleucine in the first position is frequently replaced by another branched-chain amino acid such as leucine or valine (or, rarely, a methionine). The arginines in both the sixth and the terminal positions are sometimes replaced by lysine or histidine, and the seventh-position glycine is poorly conserved. Despite the lack of strict conservation, there is no doubt that this sequence is a recognizable protein motif that binds CaM and CaM-related proteins. IQ motifs are widely distributed among different kinds of proteins, including myosins, sodium and calcium channels, EF-hand-containing phosphatases, the IQ-GAP protein, spindle pole and centrosomal proteins, plant cyclic nucleotide-regulated channels, transient receptor proteins, ethylene-inducible proteins, and a variety of other proteins. IQ motifs were first identified as Apo-CaM binding sites; however, it is now clear that the binding of IQ motifs shows different levels of Ca⁺²-dependency. These motifs occur in some proteins which exhibit Ca⁺²-dependent CaM interaction, as well as in those that promote Ca⁺²-independent retention of CaM (31–34).

The protein Mlc1p is a CaM-like protein from the budding yeast Saccharomyces cerevisiae, associated with the yeast's mechano-chemical myosin system. Its counterparts, the IQ peptides, are derived from the Myo2p protein. The latter is a class V myosin, which localizes to the bud tip during bud formation, and to the bud neck during cytokinesis (35,36). The Myo2p protein is involved in processes such as vesicle movement (37–39), polarized growth (40), and mitotic spindle orientation (41,42). Structurally, the Myo2p is a homodimer. Each monomer is composed of an N-terminal head motor domain, an extended neck domain that serves as a lever arm, and a C-terminal globular domain (43–45). The neck domain bears a sequence of six IQ motifs (designated IQ1–IQ6) that are responsible for binding of light chain proteins to the myosin. The IQ motifs of the Myo2p protein are the binding sites for CaM and CaM-related light chain proteins, such as the Mlc1p protein.

A useful approach for calculation of free energies, called molecular mechanics Poisson-Boltzmann surface area (MM-PBSA), was developed by Srinivasan and co-workers in 1998 (46). The MM-PBSA strategy has been used for estimation of free energies of different RNA (46), DNA (47,48) and protein conformations (49), binding affinities of protein complexes and mutational analysis on them (50–54), binding affinities of small compound-protein complexes (55,56), interaction energies of RNA-protein (57), RNA and metal ions (58), and RNA-ligand complexes (59). The calculation approach is based on applying of a continuum model to solute configurations derived from an MD simulation in explicit solvent. For each selected solute configuration, a molecular mechanics energy term is determined. Free energies of solvation are estimated by applying Poisson-Boltzmann (PB) calculations for the electrostatic contribution and a surface-area-dependent term for the nonelectrostatic contribution to solvation. Solute entropic contributions are estimated from a normal mode analysis. To get a statistically meaningful value of the interaction free energy of a complex, calculations are commonly carried out on several snapshots extracted from an MD trajectory with explicit solvent.

In a previous study (60), we used MD simulations to model the x-ray structure of the Mlc1p-IQ4 protein-peptide complex outside its crystal lattice, in an aqueous environment. Upon release of crystal constraints, a major conformational rearrangement of the complex was observed in solution. The Mlc1p protein had lost its dumbbell-like extended shape and was transformed into a collapsed form, which tightly engulfed the IQ4 peptide. To evaluate the generality of the newly gained Mlc1p-IQ4 complex structure, we examined the dynamics of a related protein-peptide complex. The latter, composed of the same Mlc1p protein but with the IQ2 peptide, was also resolved by x-ray crystallography (61). The MD simulation results of the Mlc1p-IQ2 protein-peptide complex, and their comparison to the previous MD simulations of the Mlc1p-IQ4 protein-peptide complex, are presented throughout this article.

Comparison of the two Mlc1p-IQ complexes reveals a higher similarity in their simulated configurations than that presented by their crystal structure states. Clear progression toward a relatively common compact shape is observed as the configurations of the two protein-peptide complexes evolve through their MD trajectories. The fact that, at the end of the simulations, the two complexes relax and obtain stable configurations, enables us to perform a comprehensive interaction energy analysis. For the interaction free energy calculations, we applied the MM-PBSA methodology, and found that in both cases the major contribution to the stabilization of the protein-peptide complexes is attributed to the molecular mechanics component of the interaction energy and the nonpolar component of the solvation energy. Thus, intracomplex van der Waals (VdW), electrostatic, and nonspecific hydrophobic interactions are responsible for keeping the protein and the peptide in a close contact. Nevertheless, when the electrostatic interactions of the solute with the solvent are taken into account, it appears that the total solvation energy is in favor of the unbound state of the protein-peptide complexes. Furthermore, our simulations allow the reassessment of the already proposed model structure of the light-chain-binding domain (LCBD) of myosin V (62). We suggest a dynamic model, incorporating the ability of the Mlc1p protein and the IQ peptides to flex and curve. It appears that the solution structure of the LCBD is under internal strain, which may be crucial for the myosin's mechano-chemical function in the cell. Overall, we use the structural, dynamical, and energetic analysis of the Mlc1p-IQ complexes to improve our understanding regarding the interactions of the Mlc1p protein with IQ peptides, the Apo-CaM interactions with target peptides, and the structure of the LCBD of myosin V.

MATERIALS AND METHODS

MD simulations

The MD simulations were performed using the GROMACS 3.2.1 package of programs (63–65), with the GROMOS96 43a1 force field (66). The simulations' conditions for both Mlc1p-IQ protein-peptide complexes were the same. The detailed simulations' procedures for the Mlc1p-IQ2 structure are described below, whereas those of the Mlc1p-IQ4 structure are described in a previous publication (60). The crystal structure of the Mlc1p protein bound to an IQ2 peptide of the Myo2p protein (PDB file No. 1M45), determined by x-ray crystallography at 1.65 Å (61), was downloaded from the Protein Data Bank (67). Four missing residues (D-50, S-51, R-54, and D-55) were added to the structure using the PROFIX program, which is incorporated in the JACKAL molecular modeling package (68). The protein-peptide complex was embedded in a box containing the single-point-charge water model (69), which extended to at least 12 Å between the protein-peptide structure and the edge of the box. Assuming normal charge states of ionizable groups corresponding to pH 7, the net charge of the Mlc1p-IQ2 structure is −7e. Hence, 35 sodium and 28 chloride ions were added to the simulation box at random positions, to neutralize the system at a physiological salt concentration of ∼100 mM. Before the dynamics simulation, internal constraints were relaxed by energy minimization. After the minimization, an MD equilibration run was performed under position restraints for 40 ps. Then, an unrestrained MD run was initiated. The first 100-ps of the run were treated as a further equilibration simulation, and the remainder 12 ns were saved and used for the analysis. During the MD run, the LINCS algorithm (70) was used to constrain the lengths of all bonds; the waters were restrained using the SETTLE algorithm (71). The time step for the simulation was 2 fs. The simulation was run under NPT conditions, using Berendsen's coupling algorithm for keeping the temperature and the pressure constant (72) (P = 1 bar; τ_P = 0.5 ps; τ_T = 0.1 ps; T = 300 K). Van der Waals (VdW) forces were treated using a cutoff of 12 Å. Long-range electrostatic forces were treated using the particle-mesh Ewald method (73). The coordinates were saved every 1-ps.

Visual presentations

All protein figures were created using the Visual Molecular Dynamics computer program (74).

Interhelical angles

The angle between each successive pair of helices was calculated as previously described (60).

Dihedral angle calculation

The position of the protein's lobes toward each other can be expressed by measuring the dihedral angle between the planes defined by the two lobes and the interdomain. Each plane was defined by the straight section of the interdomain and a selected representative residue located at each lobe. The C-α atoms of residues N-47, L-58, and V-69 defined one plane, while the C-α atoms of residues L-58, V-69, and E-129 defined the other. The calculation of the dihedral angles was performed for the last snapshot of the simulations at t = 12 ns using a standard GROMACS utility.

The electrostatic potential around the peptides

The electrostatic potential around the IQ peptides was calculated for the extracted structures of the peptides as derived from the Mlc1p-IQ protein-peptide simulations. The coordinates of 21 snapshot structures, extracted every 100 ps from t = 10 until t = 12 ns, were used for the electrostatic potentials calculations. The electrostatic potential surface around each peptide was calculated by solving the nonlinear Poisson-Boltzmann (PB) equation through the use of the adaptive Poisson-Boltzmann solver (APBS) software package (75) with a grid spacing of 0.5 Å.

The protein-peptide interaction free energies

The general strategy used for calculating the protein-peptide interaction free energy is based on the molecular mechanics Poisson-Boltzmann surface area method. This method was successfully employed by numerous studies (46–59), and involves calculating energies for snapshot configurations taken from the MD trajectories of the Mlc1p-IQ complexes. The configurations of the protein-peptide complexes, the protein, and the peptides were obtained from the MD simulations of the Mlc1p-IQ2 and the Mlc1p-IQ4 structures. The coordinates of 21 snapshot structures, extracted at 100-ps intervals during the last two nanoseconds of the simulations, where both complexes appeared to gain a stable configuration, were used for the calculations. The calculations performed for each of these snapshots with their average values are presented; these were intended for estimation of the protein-peptide energy interaction.

The changes in the Gibbs free energy of interaction were calculated from the atomic structures of the protein and the peptide undergoing the interaction to form the protein-peptide complex. Thus, the free energy of interaction was defined as

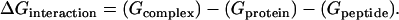(1)

The calculations of the free energy of each molecule were carried out according to

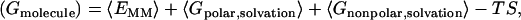(2)

where the free energy was decomposed into molecular mechanics (〈E_MM〉), polar solvation (〈G_{polar,solvation}〉), nonpolar solvation (〈G_{nonpolar,solvation}〉), and entropy (TS) contributions. The angle-brackets denote an average over a set of snapshots along an MD trajectory. Each term on the right side of the equation was calculated as detailed below.

Molecular mechanics calculations

The molecular mechanics contribution to the interaction free energy was calculated according to

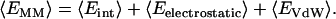(3)

The value (〈E_int〉) includes bond, angle, and torsional angle energies, while (〈E_{electrostatic}〉) and (〈E_VdW〉) denote the intramolecular electrostatic and VdW energies. The value (〈E_{electrostatic}〉) was calculated using the APBS software package (75). The value (〈E_VdW〉) was calculated using a standard GROMACS utility.

Polar solvation calculations

The electrostatic contribution to the solvation energy, (〈G_{polar,solvation}〉), was determined by using a continuum electrostatic with the Poisson-Boltzmann (PB) approach (76). We used the APBS software package (75), with a grid spacing of 0.5 Å and solution of 100 mM NaCl, for the numerical solution of the nonlinear PB equation. The term (〈G_{polar,solvation}〉) refers to the energy associated with the transfer of the solute from a continuum medium with a low dielectric constant (ɛ = 4) to a continuum medium with the dielectric constant of water (ɛ = 78.4).

Crucial to the application of PB models, and a source of many scientific disputes, is the so-called macromolecule dielectric constant, ɛ. It is generally accepted that, in a continuous electrostatics approach, the dielectric constant of the solute is a scaling factor that represents all the contributions that are not treated explicitly, rather than a true dielectric constant (77,78). Different protein-associated dielectric constants are frequently used in the literature, and we chose to perform the calculation with a dielectric constant of 4 as commonly employed (76,79–81). To make sure that the conclusions derived from our calculations are not dependent upon the choice of the value used, we repeated the calculation for representative snapshots with a lower (ɛ = 2) and a higher (ɛ = 8) dielectric constant. Comparison between the results indicated that, although the value of the calculated (〈G_{polar,solvation}〉) varies with ɛ, its trend is independent from the dielectric constant used.

Nonpolar solvation calculations

The nonpolar contribution to the solvation free energy, (〈G_{nonpolar,solvation}〉), was determined by using the solvent-accessible surface area (SASA). The SASA was calculated by a standard GROMACS utility, which implements the double cube lattice method (82) with a probe radius of 1.4 Å. The nonpolar solvation energy was described as G_{nonpolar,solvation}= γ × (SASA) + β. The constants γ and β are 2.2 kJ mol⁻¹ nm⁻² and 3.84 kJ mol⁻¹, respectively. These values of γ and β are in accord with the MM-PBSA approach (53,55–57,59).

Entropy calculations

Entropy changes upon binding of the peptide were calculated by use of normal mode analysis. The conformations of the protein, the peptide, and the protein-peptide complex were extracted from the last frame of each of the trajectories as performed in Chong et al. (53). The structures were subjected to rigorous energy minimization, until the maximal force operating on an atom was <10⁻⁶ kJ mol⁻¹ nm⁻¹. Normal mode analysis (83–85) was performed by calculating and diagonalizing the mass-weighted Hessian matrix. The frequency of the normal mode was then used to calculate the vibration entropy (86) as given by

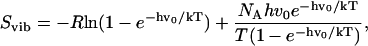(4)

where S_vib is the vibrational entropy, h is Planck's constant, v₀ is the frequency of the normal mode, k is the Boltzmann constant, T is the absolute temperature, and N_A is Avogadro's number. All calculations were performed with the GROMACS program (63–65), compiled with double precision.

RESULTS AND DISCUSSION

This study presents a comparative MD study of structures of a CaM-like protein (Mlc1p) in a complex with two IQ peptides (IQ2 and IQ4), carried out under realistic conditions of constant temperature and pressure and in a presence of a physiological salt concentration. A more detailed analysis of the dynamics and the trajectory of the Mlc1p-IQ4 protein-peptide complex can be found elsewhere (60). The current article yields significant findings regarding the structure, dynamics, and energetics of the Mlc1p-IQ complexes. Additionally, a reassessment of the model structure of the LCBD of myosin V from the yeast Saccharomyces cerevisiae is discussed.

Comparison between the crystallographic and simulated structures

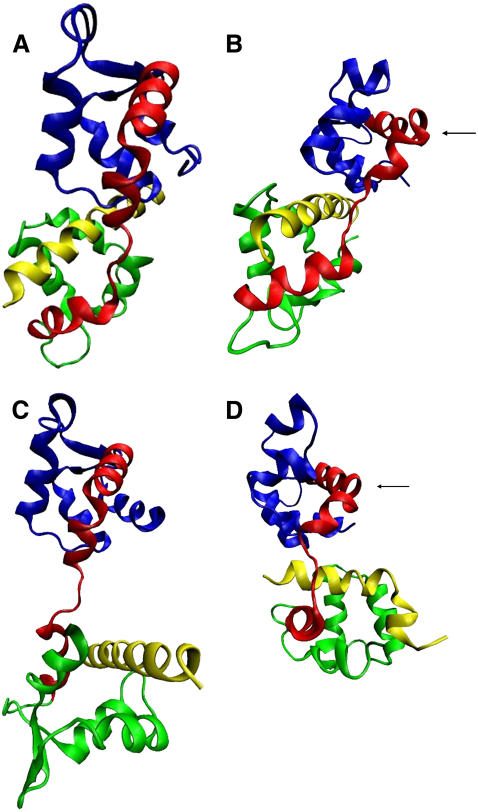
The crystallographic structures and those obtained by the simulations of the Mlc1p protein with the IQ2 and IQ4 peptides are presented in Fig. 1. The N-lobe, the interdomain, the C-lobe, and the IQ peptides are colored in blue, red, green, and yellow, respectively. At the crystalline structure of the Mlc1p-IQ2 complex (Fig. 1 A), the Mlc1p protein is found at a compact state as evident by its curved interdomain. In this configuration, the C-lobe of the protein engulfs the IQ2 peptide, which interacts also with the N-lobe and the interdomain of the protein. Overall, the configurations of the Mlc1p protein and the IQ2 peptide barely change throughout the 12-ns long simulation, and hence their final simulated state structures (Fig. 1 B) resemble the crystalline ones. Thus, the simulated structure of the Mlc1p-IQ2 complex exhibits only some minor conformational deformations compared to its crystalline structure. These deformations consist of appearance of a new kink located at helix D of the protein's interdomain (Fig. 1 B, see arrow), a consequent rotation of the N-lobe, and minor changes of the interhelical angles observed mainly at its C-lobe, as elaborated below.

FIGURE 1.

Cartoon diagrams of the crystal and the simulated structures of the Mlc1p protein when it binds the IQ2 peptide (PDB 1M45), and the IQ4 peptide (PDB 1M46). The N-lobe (residues 1–59), the interdomain (residues 60–92), the C-lobe (residues (93–148), and the IQ peptides are shown in blue, red, green, and yellow, respectively. Both crystal structures, and both simulated solution structures, are presented with the same orientation, where the N-lobes are structurally aligned. (A) The crystal structure of the Mlc1p-IQ2 complex; (B) the simulated structure of the Mlc1p-IQ2 complex after 12-ns simulation; (C) the crystal structure of the Mlc1p-IQ4 complex; and (D) the simulated structure of the Mlc1p-IQ4 complex after 12-ns simulation. The black arrows in frames B and D mark the kink of helix D.

Unlike the Mlc1p-IQ2 complex, the Mlc1p-IQ4 complex experiences a complicated deformation process in the course of its MD simulations. The simulated solution structure of the Mlc1p-IQ4 complex (Fig. 1 D) greatly deviates from its crystalline configuration (Fig. 1 C). At its crystalline structure, the Mlc1p protein confers to an elongated dumbbell-like configuration, while the IQ4 peptide is mainly bound to the C-lobe of the Mlc1p protein. When the complex is simulated in solution, the straight extended shape of the Mlc1p protein is lost, as its interdomain refolds. The C-lobe of the protein reshapes in a manner that engulfs the IQ4 peptide, while the latter curves, making close contacts with the protein. The presence of these large-scale domain motions of the protein could be inferred from experimental data regarding structures of CaM with bound peptides (8–17). Nevertheless, our MD study provided detailed explanations about their nature, namely that they involve structural refolding occurring on the nanosecond timescale (60).

At the crystal state of the Mlc1p-IQ2 complex, the protein assumes a compact state; while at the crystal state of the Mlc1p-IQ4 complex, the Mlc1p confers to an extended configuration. These distinctive states can be attributed either to complex-specific interactions, to the different crystallization conditions of each complex (61,87), or to a combination of both. A close examination of the crystal and simulated structures of both protein-peptide complexes (Fig. 1) reveals that, after the simulations, the protein's structures are more similar than in their crystalline states. The calculated backbone atoms RMSD between the Mlc1p proteins found at the Mlc1p-IQ2 and the Mlc1p-IQ4 crystal structures (Fig. 1, A and C), is as large as 1.296 nm. However, this value drops to 0.959 nm when calculated between the solution structures of the protein after 12-ns simulations (Fig. 1, B and D). A value of 0.959 nm may still seem to be quite high, but it should be noted that, due to the shape of the protein, any attempt to align two of its structures is expected to result in a relatively high RMSD. Therefore, the decline of the RMSD from 1.296 nm to 0.959 nm is structurally notable, as seen in Fig. 1. On the top of the RMSD calculation, other structural indicators (such as length of the interdomain, distance between the lobes center-of-mass and gyration radius) were calculated for the crystal and the simulated structures of the protein (data not shown). All these point out that the solution configurations of the Mlc1p protein are more similar than its crystalline ones. Additionally, it should be mentioned that the simulated structures of the protein acquire special conformational features not present in either of the crystals. Besides exhibiting a common compact form of the simulated protein, during the simulations a new kink appears at both of its structures (Fig. 1, B and D, see arrow). This kink is missing from the crystal structures of neither of the Mlc1p-IQ complexes.

Though both simulated structures are characterized by an overall similarity, there is still a difference between them, as the C-lobe of the protein points toward opposite directions. The position of the C-lobe of the Mlc1p protein in respect to its N-lobe may be expressed by calculation of the dihedral angle between the planes defined by the two lobes and the interdomain. We found that, at the end of the simulations, the dihedral angle at the Mlc1p-IQ2 simulated structure is 128.54°, while the dihedral angle at the Mlc1p-IQ4 simulated structure is significantly smaller, 72.1°. The difference represents the different binding modes and orientations of the IQ peptides toward the protein, since various Mlc1p-binding partners may affect and dictate its structure. The Mlc1p protein is considerably flexible, enabling it to wrap around the IQ peptides in different ways. Its tolerance and adaptivity toward different IQ peptides make it an appropriate candidate to bind a variety of target helical peptides. Evidently, this unique property enables it to bind six IQ peptides of the LCBD of myosin V, each distinguished by a unique sequence.

The dynamics of the protein-peptide complexes

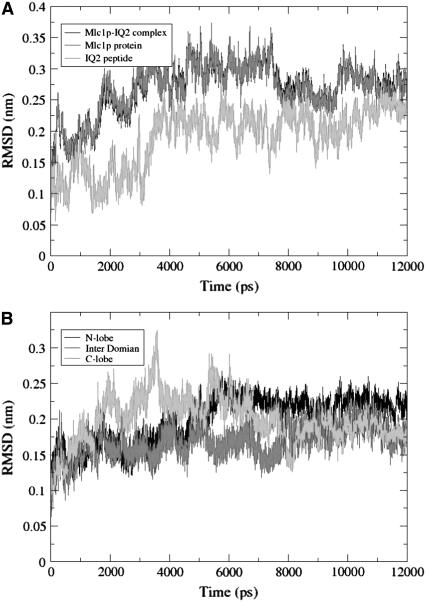
A quantitative expression of the conformational change is given by the RMSD of the backbone atoms of the protein-peptide complexes. Fig. 2 A depicts the RMSD values as calculated for the whole Mlc1p-IQ2 complex (black), and its components: the Mlc1p protein (dark gray), and the IQ2 peptide (light gray). The RMSD of the protein-peptide complex exhibits some structural fluctuations that can be fully attributed to the Mlc1p protein. It increases until ∼0.35 nm, stays around this value for ∼4 ns, decreases for a short while, and then stabilizes at ∼0.28 nm. The RMSD track of the IQ2 peptide, which contributes little to the RMSD of the complex, exhibits a different pattern. It appears to explore the configurational space until ∼3.2 ns, and then increases to a value of ∼0.23 nm. From this time point until the end of the simulation, the RMSD of the IQ2 peptide is relatively stable.

FIGURE 2.

(A) The RMSD of the backbone atoms of the Mlc1p-IQ2 complex (black), the Mlc1p protein (dark gray), and the IQ2 peptide (light gray) as a function of the simulation time. (B) The RMSD of the backbone atoms of the different domains of the Mlc1p protein as a function of the simulation time. The domains of the protein are defined as follows: residues 1–59 for the N-lobe (black), 60–92 for the interdomain (dark gray), and 93–148 for the C-lobe (light gray).

The fluctuations of the Mlc1p protein can be resolved into a contribution of its structural domains. Accordingly, the RMSD of its N-lobe (black), interdomain (dark gray), and C-lobe (light gray) are presented in Fig. 2 B. The RMSD of the N-lobe exhibits a sharp increase at ∼5 ns, and then stabilizes at a value of ∼0.24 nm. The RMSD of the interdomain, which is the flexible domain of the Mlc1p protein, hardly changes. The stability of the interdomain throughout the simulation time is not surprising since its structure is already bent and curved at the Mlc1p-IQ2 protein-peptide crystalline structure. Apparently, the C-lobe is much more flexible than the other structural domains, exhibiting the largest variations in its RMSD value. Inspection of the Mlc1p-IQ2 structure reveals that most of its eight α-helices retain their structures and the angles between them, except the angles found at the C-lobe. The angle between its G and H helices increases from ∼100° at the beginning of the simulation to ∼115° at the end of it. The angle between its E and F helices changes from ∼110° to ∼123° during the timeframe of 2.7 until 5.5 ns, but settles back at its original value. The fluctuations of the RMSD of the C-lobe are due to these interhelical motions.

As opposed to the relatively minor oscillations of the backbone atoms RMSD of the Mlc1p-IQ2 complex, whose maximal values fluctuate up to ∼0.35 nm, examination of the RMSDs of the Mlc1p-IQ4 simulation reveals a different scenario (60). The Mlc1p-IQ4 structure experiences a compaction event, in which the RMSD of the complex and the protein almost doubles (from ∼0.4 to ∼0.75 nm). The RMSD of the peptide increases with a short delay after that of the complex and the protein. Clearly, the simulated solution structure of the Mlc1p-IQ4 complex is distinctively different from its crystalline structure.

Structural evolution of the simulated Mlc1p protein at the protein-peptide complexes

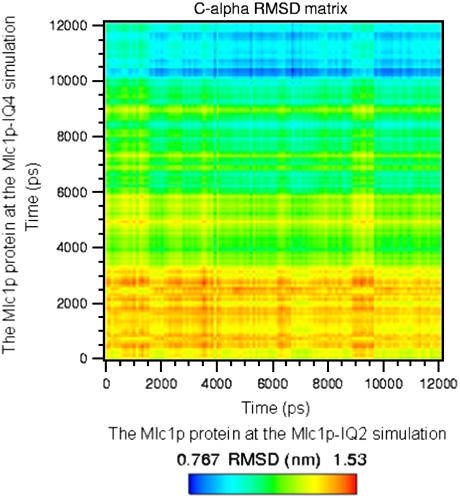
A dynamic comparison of the trajectories of the Mlc1p protein in both simulations is shown in Fig. 3. The RMSD of the C-α atoms of the Mlc1p protein obtained from the Mlc1p-IQ4 simulation's trajectory is presented in relation to the C-α atoms of the Mlc1p protein obtained from the Mlc1p-IQ2 simulation's trajectory. The two-dimensional matrix representation exemplifies the time evolution of the protein's configurations as a function of the simulations time. A color code is used for visualizing how the two structures of the Mlc1p protein, in the Mlc1p-IQ protein-peptide complexes, approach a common compact shape during the simulations. The pattern of the colors exhibits progressive yet reversible changes, indicating that both structures are fluctuating, and the similarity between them varies. The mutual evolution of the conformational changes, as shown in Fig. 3, suggests that the convergence and settling of the Mlc1p protein's structures toward relatively similar compact configurations can be divided into three phases: a relaxation phase (from the beginning of the simulation until ∼3.2 ns), a progression phase (from ∼3.2 until ∼10 ns), and a quiescent phase (from ∼10 ns until the end of the simulations).

FIGURE 3.

Matrix representation of mutual C-α atoms' RMSD of the Mlc1p protein obtained upon comparison of the two simulations. The RMSD values of the Mlc1p protein for the Mlc1p-IQ4 simulation's trajectory were calculated in relation to those of the Mlc1p protein obtained from the Mlc1p-IQ2 simulation's trajectory and vice versa. The values are given by color codes; blue and red represent high and low similarity, respectively.

The relaxation phase is represented by the yellow-reddish color at the bottom of the figure, stretching over its full width and extending up to ∼3.2 ns mark of the ordinate. At this phase, the Mlc1p protein at the Mlc1p-IQ4 complex responds to the absence of the packing forces present at the crystal lattice. Hence, the structures sampled by the protein from both simulations are still remarkably different, each remaining close to its crystal form. At the progression phase, the Mlc1p protein at the Mlc1p-IQ4 simulation undergoes a major conformational change (60), rendering it more similar to that of the Mlc1p-IQ2 simulation. This newly gained configuration is stabilized by hydrophobic interactions, where minor rearrangements of the side chains contribute to a relatively slow progression stabilizing process. The refolded conformation of the Mlc1p protein obtained from the Mlc1p-IQ4 simulation becomes more similar to the structure of the Mlc1p protein obtained from the Mlc1p-IQ2 simulation. This tendency increases along the ordinate as seen by the shift from the yellow-greenish to the green-bluish colors. Finally, at the quiescent phase, the new structure of the Mlc1p protein obtained from the Mlc1p-IQ4 simulation is already stabilized. The higher degree of similarity between the protein's structures, as reflected by the smaller RMSD values one with respect to the other, is observed at this phase (represented by the bluish hue). Evidently, as the simulations progress, the structures of the proteins become more similar in a time-dependent manner. Thus, the final MD-derived solution structures of the protein are more similar than its crystal structure states. Furthermore, these final MD-derived solution structures of the protein resemble also compact configurations of the CaM protein presented at crystal structures of Holo-CaM with target peptides (9–16).

It is of interest to point out that the structures of the protein at both simulations do not co-evolve in parallel. The structure derived from the Mlc1p-IQ2 simulation experiences limited changes, whereas that derived from the Mlc1p-IQ4 simulation assumes a significant modification. Thus, the Mlc1p′ structures evolve at different rates toward a more similar configuration.

Carrying out the same analysis only for the interdomain of the Mlc1p protein (data not shown) reveals a pattern resembling that of the whole protein. The structure of the interdomain of the Mlc1p protein, obtained from the Mlc1p-IQ2 simulation, is almost invariable, while that obtained from the Mlc1p-IQ4 simulation evolves with time. A high degree of similarity is obtained after ∼10 ns, as observed for the whole protein.

The root mean-square fluctuation (RMSF) of the Mlc1p protein at the protein-peptide complexes

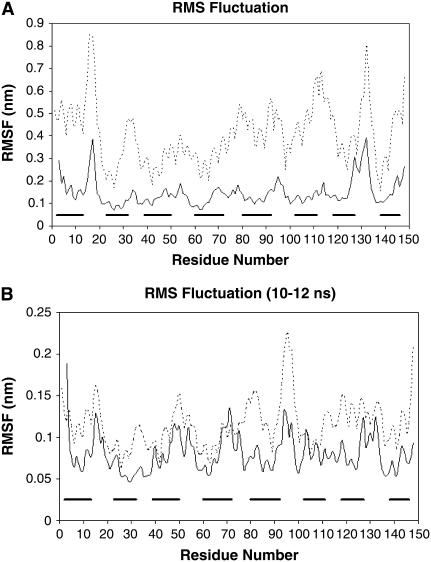
To further analyze the trajectories of the Mlc1p protein at both simulations, we computed the standard deviation from the RMSD for each of its residues, i.e., their root mean-square fluctuations (RMSF). Fig. 4 A presents the RMSF of the Mlc1p protein at the Mlc1p-IQ2 structure simulation (solid line), and at the Mlc1p-IQ4 structure simulation (dashed line). Residues of the Mlc1p protein, that comprise α-helices at the crystalline configurations of the Mlc1p-IQ protein-peptide complexes, are shown as bold horizontal bars parallel to the abscissa. The RMSF curves reveal the different behavior of the protein at both simulations, characterizing the mobility of each of its residues during the MD runs.

FIGURE 4.

The root mean-square fluctuation (RMSF) as a function of the residue number of the Mlc1p protein. The RMSF was calculated for the backbone atoms of the Mlc1p protein for each residue at both simulations. The solid line represents the RMSF of the Mlc1p protein at the simulation of the Mlc1p-IQ2 structure, while the dashed line represents the RMSF of the Mlc1p protein at the simulation of the Mlc1p-IQ4 structure. The bold horizontal bars, drawn in parallel to the abscissa, represent the α-helices that the Mlc1p protein comprises. The RMSF of both MD trajectories is presented for the entire simulations time (A), and for the timeframe t = 10 ns until t = 12 ns (B).

In general, the structural sections of the protein, namely its eight α-helices, are more rigid and confined and tend to be less flexible than its other sections (e.g., residues 39–50). Correspondingly, the protein's unstructured sections show an increased motility. Thus, at both simulations, the RMSF data indicate large fluctuations of segments belonging to loops that connect secondary structure elements (e.g., residues 14–20 and 128–137), as well as of residues located at the edges of the α-helical sections (e.g., residues 90–92, and 123–125). While these features are common to both complexes, the Mlc1p protein exhibits a different mobility when it binds the IQ2 or the IQ4 peptides as the absolute values of the RMSF differ. The RMSF curve of the Mlc1p protein at the Mlc1p-IQ4 simulation consistently reveals a higher extent of motion than that of the protein at the Mlc1p-IQ2 simulation. Despite these different degrees of motion, the RMSF of some sections of the protein is correlated (for example, the RMSF of the N-lobe of the protein, between both simulations, is correlated, with R² = 0.69). However, other sections of the protein do not exhibit such correlation. The variation in the correlations between the structural domains of the protein implies that the main differences regarding the dynamics of the protein at both simulations are located at its interdomain and C-lobe.

It can be argued that the relatively high RMSF of the protein at the Mlc1p-IQ4 simulation is due to its structural modification process, by which it refolds, and that process is still going on. However, detailed structural and energy analysis presented in our previous publication (60) suggests that its major conformational change had been completed in the course of the simulation. To observe the behavior of the Mlc1p protein at the stable period at both simulations, we repeated the RMSF analysis during the timeframe 10–12 ns (Fig. 4 B). The RMSF curves reveal a pattern similar to that calculated for the entire simulations time, although the extent of the fluctuations is smaller. Nevertheless, the RMSF curves resemble each other more than those obtained for the entire simulations' time. This indicates as well that the Mlc1p protein at the Mlc1p-IQ4 simulation had already experienced its structural modification and may not significantly evolve at the discussed timeframe. We wish to note that, even at this timeframe, we found that the RMSF of the protein derived from the Mlc1p-IQ4 simulation is still higher than that obtained by the protein from the Mlc1p-IQ2 simulation. This is in accord with the observation that more contacts are involved in the Mlc1p-IQ2 interaction than in the Mlc1p-IQ4 interaction (see Fig. 6 below). Thus, the protein at the latter simulation is not strongly retained in its position and may be more mobile.

FIGURE 6.

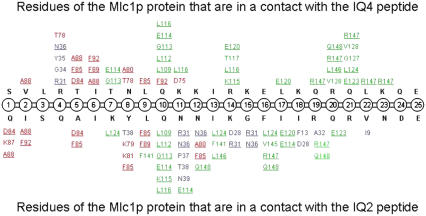
Contacts (<4 Å) between residues of the Mlc1p protein and the bound IQ peptides obtained from the MD simulations at t > = 6 ns. Data regarding the Mlc1p-IQ4 structure simulation (60) are presented at the upper half of the illustration, whereas data regarding the Mlc1p-IQ2 structure simulation are presented at its lower half. The IQ peptides, the N-lobe of the protein, the interdomain of the protein, and the C-lobe of the protein are colored in black, blue, red, and green, respectively. Residues of the Mlc1p protein that interact with both peptides are underlined. Only contacts that persist at least 80% of the examined period are presented.

The electrostatic field around the IQ peptides

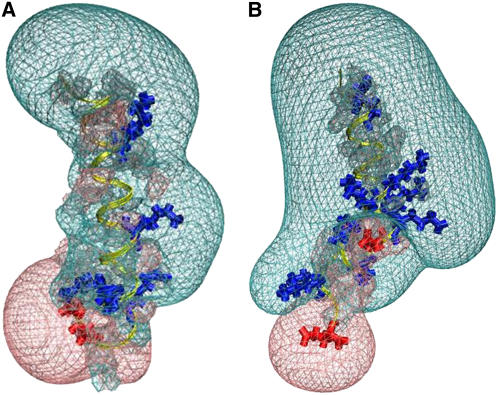
The Mlc1p-IQ protein-peptide complexes are composed of the same protein, and similar, although not identical, peptides. Yet, the protein-peptide complexes differ one from the other by their crystalline structures (Fig. 1, A and C), and to some extent by the simulated structures obtained by means of MD simulations (Fig. 1, B and D). Evidently, the differences between the structures of the protein-peptide complexes reflect the variation sequence of the bound IQ peptides. To account for the difference between the peptides, we calculated the electrostatic field surrounding the IQ2 and IQ4 peptides. The volumes of the averaged (for the timeframe t = 10 until t = 12 ns) positive and negative electrostatic fields of both peptides are presented in Table 1, while in Fig. 5 we show the Coulomb cages of the IQ peptides at the last snapshot (t = 12 ns) of the simulations. The positive (transparent blue) and negative (transparent red) domains are drawn where the electrostatic potential equals 1 k_BT/e. The C-α traces of both peptides are colored in yellow, while their positive and negative residues are shown in blue and red, respectively. The potential field of the IQ peptides consists of two main lobes, one positive and the other negative. However, although the IQ2 and IQ4 peptides are both basic, α-helical, 25-amino-acids long, they produce different electrostatic fields around them. The volume of the positive Coulomb cage around the IQ2 peptide is 4257.12 ± 264.48 ų, while the volume of its negative Coulomb cage is 2080.56 ± 147.25 ų. The volume of the positive Coulomb cage around the IQ4 peptide is 10180.42 ± 426.12 ų, while the volume of its negative Coulomb cage is 796.02 ± 144.94 ų.

TABLE 1.

The electrostatic field around the IQ peptides

	IQ2 peptide	IQ4 peptide
Charge	+2	+6
Positively-charged residues	K-7, K-14, R-19, R-21	R-4, K-11, K-12, R-14, K-15, K-18, R-20, K-23
Negatively-charged residues	D-24, E-25	E-16, E-25
Volume of the positive Coulomb cage (Å3)	4257.12 ± 264.48	10180.42 ± 426.12
Volume of the negative Coulomb cage (Å3)	2080.56 ± 147.25	796.02 ± 144.94
Total volume of the Coulomb cage* (Å3)	6337.69 ± 395.11	10976.76 ± 498.02

^*Calculated by summation of the volumes of the positive and the negative Coulomb cages.

FIGURE 5.

The electrostatic potential surface around the IQ2 peptide (A) and the IQ4 peptide (B). Both peptides are presented in yellow with the same orientation, while their positive and negative residues are drawn in blue and red, respectively. The Coulomb cages for the positive (transparent blue) and negative (transparent red) domains are drawn at the distance where the electrostatic potential equals 1 k_BT/e.

The differences between the electrostatic fields surrounding the peptides are caused by variations in their local charge and charge distribution. The total charge of the IQ2 peptide is Z = +2, while that of the IQ4 peptide is Z = +6. The peptides differ not only in their total net charge, but in the distribution of the charges along them as well. Four positive residues (K-7, K-14, R-19, and R-21) are scattered along the IQ2 peptide, while its negative residues (D-24 and E-25) are concentrated at its C-terminal edge. The IQ4 peptide consists of a series of four positive residues (K-11, K-12, R-14, and K-15) located in its middle section, whereas its other positive residues (R-4, K-18, R-20, and K-23) are distributed along it. The midcluster of positive charge contributes to the high-volume positive Coulomb cage bulb at the center of the peptide. The differences between the electrostatic fields of the two peptides may suggest that electrostatic forces play a major key role in the protein-peptide interactions.

The protein-peptide interaction free energies

To analyze the energetics of peptide binding to the Mlc1p protein, the various components of the interaction free energy of the two protein-peptide complexes were evaluated during the last 2 ns for each simulation. This timeframe corresponds with the stable MD-derived solution structures of the protein-peptide complexes at both simulations, from which we can calculate the energy associated with protein-peptide interaction. The detailed results of the energetic analysis are presented in Table 2.

TABLE 2.

Components of the Mlc1p-IQ interaction free energy

	Mlc1p-IQ2 complex	Mlc1p-IQ4 complex
〈ΔEelectrostatic〉	−590.77 ± 49.96	−1534.02 ± 84.28
〈ΔEVdW〉	−664.18 ± 25.2	−547.7 ± 25.88
〈ΔEMM〉	−1254.95	−2081.72
〈ΔGpolar,solvation〉	678.25 ± 41.85	1594.88 ± 78.84
〈ΔGnonpolar,solvation〉	−58.69 ± 5.59	−53.98 ± 5.48
〈ΔGsolvation〉	619.56	1540.9
−TΔS	75	372
ΔGinteraction	−560	−169

Energies are presented in kJ/mol. The calculations present the average values obtained from t = 10 until t = 12 ns for both Mlc1p-IQ simulations. Angle brackets (〈 〉) denote an average over a set of snapshots along an MD trajectory. Atomic charge and radii values were taken from the PARSE parameter set (108). Definitions of the energetic components are as follows: (〈ΔE_{electrostatic}〉), electrostatic molecular mechanics energy; (〈ΔE_VdW〉), VdW molecular mechanics energy; (〈ΔE_MM〉), total molecular mechanics energy defined as 〈ΔE_MM〉 = (〈ΔE_int〉 + 〈E_{electrostatic}〉 + 〈ΔE_VdW〉); 〈ΔG_{polar,solvation}〉, electrostatic contribution to the solvation energy calculated by the PB approach; 〈ΔG_{nonpolar,solvation}〉, nonpolar contribution to the solvation energy; 〈ΔG_solvation〉, total solvation energy defined as (〈ΔG_{polar,solvation}〉 + 〈ΔG_{nonpolar,solvation}〉); TΔS, solute entropic contribution; and (ΔG_interaction), total free energy of interaction defined as (〈ΔE_MM〉 + 〈ΔG_solvation〉 − (TΔS)).

The analysis was based on the MM-PBSA approach (46), in which the interaction free energy, (ΔG_interaction), for each of the complexes is composed of three energetic terms: The molecular mechanics energy term (〈ΔE_MM〉), the solvation energy term (〈ΔG_solvation〉), and the solute entropic contribution (TΔS). The first term includes internal (〈ΔE_int〉), VdW (〈ΔE_VdW〉), and electrostatic (〈ΔE_{electrostatic}〉) components. The second term consists of electrostatic (〈ΔG_{polar,solvation}〉) and nonpolar (〈ΔG_{nonpolar,solvation}〉) contributions. Solute entropies were determined at the last snapshots of the MD trajectories. Note that the internal component of the molecular mechanics energy, (〈ΔE_int〉), is set per definition as zero and thus cancels out, making no contribution at all (53,55,56).

On combining the (〈ΔE_MM〉) with the (〈ΔG_solvation〉) and the (TΔS) terms, we end up with interaction free energy, (ΔG_interaction), for the complexes' formation. The estimated interaction free energy of the Mlc1p-IQ2 and the Mlc1p-IQ4 complexes is ∼−560 kJ/mol and ∼−169 kJ/mol respectively, consistent with their observed stability. These data represent a balance between enthalpy and entropy in which, according to our calculations, the complexes' formation is an enthalpically driven process and is entropically unfavorable. The favorable formation of both Mlc1p-IQ complexes is driven by the electrostatic (〈ΔE_{electrostatic}〉) and the VdW (〈ΔE_VdW〉) terms of the molecular mechanics energy and the nonpolar component of the solvation energy (〈ΔG_{nonpolar,solvation}〉).

Of particular interest is the total solvation energy, (〈ΔG_solvation〉), composed of polar (〈ΔG_{polar,solvation}〉) and nonpolar (〈ΔG_{nonpolar,solvation}〉) terms. The total solvation energy is unfavorable at both complexes (619.56 kJ/mol for the Mlc1p-IQ2 complex, and 1540.9 kJ/mol for the Mlc1p-IQ4 complex). Thus, considering the solvation energy, it appears that the protein-peptide complexes would rather not be formed at all. Yet, the molecular mechanics energy component of the interaction energy strongly favors the complexes over the unbound molecules.

Electrostatic interactions were assumed to play a dominant major role in the interaction between CaM and target peptides (11,88–90). This view emerged from x-ray structures of complexes showing close proximity between the negatively charged CaM and positively charged peptides (8–16). Accordingly, electrostatic interactions have been anticipated to be significant in the Mlc1p-IQ systems, as the Mlc1p-IQ complexes also present a close distance between a negatively charged protein and highly positively charged peptides. It is of high importance to consider the electrostatic component of the molecular mechanics energy, (〈ΔE_{electrostatic}〉), together with the electrostatic contribution to solvation, (〈ΔG_{polar,solvation}〉), when examining the role of electrostatics in the protein-peptide complexes formation. At both protein-peptide complexes, the nature of the electrostatic interactions is similar: The molecular mechanics electrostatic term per se favors the bound state of the complexes (〈ΔE_{electrostatic}〉 < 0), while the electrostatic PB solvation energy favors the unbound state of the protein-peptide complexes (〈ΔG_{polar, solvation}〉 > 0). As the latter is dominant (|〈ΔG_{polar,solvation}〉| > |〈ΔE_{electrostatic}〉|), their sum, representing the total electrostatic energy, opposes the formation of the protein-peptide complexes. Thus, the positive solvation energy electrostatic term penalty paid by the electrostatics of solvation is not completely covered by favorable electrostatic interactions within the resulting protein-peptide complexes. Evidently, the same phenomenon was also demonstrated by numerous studies (53,55,56,81,91–93), in which the total electrostatics between two interacting molecules un-favors their bound state over the unbound due to intense solvation forces. Interestingly, the electrostatic energy terms (〈ΔE_{electrostatic}〉) and (〈ΔG_{polar,solvation}〉) are more prominent in the Mlc1p-IQ4 complex compared to the Mlc1p-IQ2 complex by approximately a factor of 3, which is proportional to the charge of the peptides (the charges of the IQ2 and IQ4 peptides are +2 and +6, respectively). Hence, the differences in charges between the protein and the peptide are more substantial in the Mlc1p-IQ4 complex, and consequently its electrostatic terms are more profound.

It is not surprising that, at both complexes, the entropic term does not support the interaction between the protein and the peptide. The Mlc1p proteins, as well as the IQ peptides, are characterized by higher entropy in their unbound states. In its free state, the lobes of the Mlc1p protein can tumble more or less independently of one another, constrained only by the interdomain. However, in the bound state, its lobes interact with the peptide, and hence, are at relatively fixed positions. Similarly, the free IQ peptides may also acquire more structural freedom when they are not constrained by the protein.

Our energy calculations agree fairly well with isothermal titration calorimetry (94,95) and NMR relaxation (96) experiments, in which it was found that the binding of a peptide to Holo-CaM is favored by enthalpy and opposed by entropy. Our results are also in accord with an MD study of Holo-CaM complexed with a target peptide suggesting that the protein-peptide free energy is enthalpy-dependent and not entropy-dependent (97). As pointed out by these authors, identification of changes in entropy (94,96) or enthalpy (97) upon complex formation is fraught with difficulty. Therefore, the qualitative agreement between our calculations regarding the Mlc1p-IQ complexes obtained by computer simulations, and experimental and theoretical calculations regarding Holo-CaM peptide complexes, is encouraging and promising.

Finally, it must be stressed that the values given in Table 2 are model-dependent and reflect all of the approximations implemented in the MM-PBSA formalism. Thus, the numerical values should be taken as indicative, representing qualitative trends rather than actual quantitative ones. The consistency of the results with the observed stability of the complexes supports the acceptance of this mode of calculation as a proper representation of the operating forces.

Owing to the opposite charges of the protein and the peptide, the electrostatic interactions may serve as the initial driving force for long-range molecular recognition between the Mlc1p protein and the IQ peptides. On the other hand, the highly charged protein and peptides strongly interact with the solvent, leading to intensive solvation forces. Upon formation of the protein-peptide complexes, the Mlc1p protein approaches a close vicinity to the IQ peptides. This desolvation process, which is unfavorable, is accompanied by a release of water molecules from their interfaces, replacing solute-solvent interactions by intracomplex interactions. The unfavorable change in the electrostatics of solvation is mostly, but not fully, compensated by the favorable electrostatic charge-charge interactions within the resulting Mlc1p-IQ complexes. The close interaction of the Mlc1p protein with the IQ peptides is grossly mediated by the Lennard-Jones (LJ) interactions, whereas their opposite highly charged surfaces contribute to their initial attraction. The major role played by the molecular mechanics VdW interactions demonstrates how inter-residues contacts, where the tight fitting of the surface atoms occurs, contribute to the LJ stabilization energy term and consequently to the stability of the complexes. In conclusion, electrostatic interactions seem to operate mostly during the long-range attraction between the protein and the peptides before the complexes are formed. Once protein-peptide contact occurs, VdW and nonspecific hydrophobic interactions stabilize the Mlc1p-IQ structures, whereas the contribution of salt bridges is relatively negligible.

The contacts between the protein and the peptides

The detailed interactions between individual residues of the Mlc1p protein and the IQ peptides were followed during the last half of the simulations (6–12 ns). Residues of the peptides, which were in a contact (<4 Å) with the Mlc1p protein, were listed. The rapid motion of the residues during the simulations led to numerous encounters, but most of them were temporary and made a marginal contribution to the protein-peptide interaction. To account for that, we selected only those contacts, between residues of the IQ2 or the IQ4 peptides with the Mlc1p protein, which were present in at least 80% of the snapshots. These lasting interactions are presented in Fig. 6.

Altogether, 51 contacts between the peptide and the protein were found at the Mlc1p-IQ2 simulation. Fifteen of these contacts involve the N-lobe of the protein (blue), 14 the interdomain (red), and 22 the C-lobe (green). Similarly, at the Mlc1p-IQ4 simulation, 42 contacts were found between the peptide and the protein (60). Only four of these contacts involve the N-lobe of the protein (blue), 13 the interdomain (red), and 25 the C-lobe (green). It is of interest to point out that 20 residues of the Mlc1p protein interact with both IQ peptides (underlined in Fig. 6); 12 of its residues interact only with the IQ2 peptide; and seven of its residues exclusively interact with the IQ4 peptide. Residues 24–25 of both IQ peptides made no contact with the Mlc1p protein in either of the simulations.

The IQ2 peptide has four positive residues (K-7, K-14, R-19, and R-21), and two negative residues (D-24 and E-25) located in its C-terminal edge. These negative residues repel the negatively charged Mlc1p protein, and hence only one residue of the protein (I-9) interacts with the last five residues of the IQ2 peptide. In comparison, the IQ4 peptide is more positive. It has a substantial cluster of positive residues (K-11, K-12, R-14, K-15, K-18, R-20, and K-23) located at its mid- and C-terminal parts. These positive residues are bound to the C-lobe of the Mlc1p protein mainly through hydrophobic interactions (i.e., R-14–L-116 and R-20–V-128), but two salt bridges are also present (K-11–E-114 and R-14–E-120).

The different binding modes of the two peptides are reflected by their different regions of contact with the Mlc1p protein at each simulation. At the Mlc1p-IQ2 simulation, the mid- and C-terminal regions of the peptide (residues 13–25) interact with eight residues of the N-lobe and 12 residues of the C-lobe of the protein. On the other hand, at the Mlc1p-IQ4 simulation, the mid- and C-terminal regions of the peptide (residues 13–25) do not interact with the N-lobe of the protein as they are bound to 17 residues of its C-lobe. The fact that the mid- and C-terminal sections of the IQ2 peptide interact with the N-lobe of the protein, while those regions of the IQ4 peptide do not interact with it, is manifested by the various orientations of the peptides when bound to the protein (Fig. 1, B and D).

Although the protein and the peptides are highly charged in opposite charges, out of the 51 contacts between the IQ2 peptide and the Mlc1p protein, only two involve electrostatic interactions (K-7–E-114 and K-14–D-28). Similarly, out of the 42 contacts between the IQ4 peptide and the Mlc1p protein, only two involve electrostatic interactions (K-11–E-114 and R-14–E-120). Besides these few electrostatic interactions, all the other protein-peptide interactions are hydrophobic in nature. Matter of fact, even the positive residues of the peptides interact with the positive residues of protein (K-14–R-31 and R-19–R-147 for the Mlc1p-IQ2 protein-peptide complex; R-4–R-31, R-14–K-115, R-19–R-147, and K-23–R-147 for the Mlc1p-IQ4 protein-peptide complex). Considering the repulsive force between positive charges, the interactions between the basic residues are clearly hydrophobic. These data are consistent with the findings regarding the dominant role played by the LJ component of the molecular mechanics energy and the nonpolar component of the solvation energy in the stabilization of the protein-peptide complexes (Table 2).

The structure of the LCBD of myosin V

Myosin V is a versatile motor involved in the short-range transport of vesicles in the actin-rich cortex of the cell. Its long neck domain, serving as a lever arm (98,99), gives rise to a step size of ∼36 nm, the largest step size thus far measured for a myosin motor. This LCBD neck of myosin V consists of six tandem IQ motifs, which constitute the binding sites for light chain proteins, such as the CaM and the Mlc1p. The primary function of the light chains is to regulate the ATPase activity of the globular head of myosin V (43,44,100). The crystal structures of the Mlc1p-IQ2, Mlc1p-IQ4, and Mlc1p-IQ2/3 complexes had been determined by Terrak and co-workers (61,87). On the basis of these crystal structures and sequence similarity among the six IQ motifs, Terrak and co-workers suggested a model for the LCBD in a recent publication (62). According to their model, the six IQ motifs, that constitute the neck domain of the myosin V, adopt a straight long α-helical configuration. Moreover, two of the light chains retain an extended configuration, in which their N-lobe does not interact with the IQ motif, as determined by the crystalline form of the Mlc1p-IQ4 complex. This proposed model of the LCBD does not take into account the conformations that the proteins may reveal in solution; rather, it is constrained by the packing forces of the Mlc1p-IQ crystal structures. The elucidation, by MD simulations, of the solution structures of two Mlc1p-IQ complexes calls for reevaluation of the Mlc1p-LCBD model structure.

In this study, and in the previous one (60), we simulated two structures of complexes formed between the Mlc1p protein with the IQ motif peptides of the LCBD. We noticed that the simulated structures of the complexes can grossly deviate from the x-ray crystallography-resolved ones. Of the two simulated solution structures, that of the Mlc1p-IQ2 complex holds a conformation very close to that of its crystal structure. On the other hand, the simulated structure of the Mlc1p-IQ4 complex is remarkably different from its crystalline structure. The simulated Mlc1p protein is curved since its interdomain is bent, whereas the IQ4 peptide exhibits a ∼90° kink. The tight engulfing of the protein around the peptide and the bending of the latter, point out the difficulty of predicting the solution structure of a large protein-peptide complex based on crystal structures of some of its isolated components. Therefore, the schematic description of the IQ motifs as constitutes of a rigid straight α-helix is not consistent with the dynamics of the complex. Hence, we propose that the light chains of the myosin, namely the CaM and the Mlc1p proteins, may maintain a compact conformation as their interdomain is bent. Their N-lobe is probably not free to engage in protein-protein interactions as proposed by Terrak and co-workers, but instead interacts with the IQ peptides, coming into a close contact with their C-lobe. In addition, and not less important, we claim that the IQ peptides may curve when bound to the light chain proteins. Consequently, the neck domain should reveal a considerable structural flexibility associated with its walking over the actin filament.

A wide range of experimental results supports our view about the LCBD. The predicted ∼90° curvature of the myosin's IQ4 motif neck domain resembles that observed in the crystal structure of scallop's myosin S1 (101). It was found that the lever arm of the scallop's myosin S1 does not move as a rigid body, but rather flexes when the myosin is in motion. In addition, fluorescence imaging with one-nanometer accuracy (102–104) and time-resolved single-molecule fluorescence polarization studies (105) suggest a fundamental role to the elasticity of the LCBD during the movement of the myosin V. Myosin V “walks” using an asymmetric hand-over-hand mechanism, where its heads alternate leading and trailing positions along the actin filament, analogous to the hands of a rope climber. In the course of its stride, a conformational change was demonstrated during the transition of the lever-arm from a pre-stroke to post-stroke state. This change is manifested by a tilting of the LCBD between two distinct conformations, a straight one and a bent one. The angle of the LCBD's rotation deduced from these experiments is in a very good accord with the one predicted in our MD studies. Furthermore, when actin-bound myosin V was imaged by electron microscopy (106,107), a bent lever arm was observed. The leading head was curved backward, whereas the rear head was straighter, resembling a skier in a telemark stance. Thus, the electron microscopy data confirmed the bowlike shape of the LCBD of the lead-head pre-stroke state.

Evidently, the solution structure of the LCBD of myosin V is more complicated than the one based on crystal structures of some individual Mlc1p-IQ complexes, as predicted by Terrak and co-workers. When our simulations are taken into account together with the experimental data presented above, it is reasonable to conclude that the LCBD is not a passive structural device but a dynamic proteinous machinery. We argue that a mutual structural flexibility of the light chain proteins and the IQ peptides represents a more realistic model of the neck region of myosin V.

CONCLUDING REMARKS

This study provides a fundamental understanding of the Mlc1p protein's solution behavior in a complex with IQ peptides by sampling the conformational space of two Mlc1p-IQ complexes. Our findings suggest that, although the IQ2 and the IQ4 peptides share similar sequence and structure, the fine details of each individual IQ sequence determine its binding mode to the Mlc1p protein. The ability of the Mlc1p protein to assume different conformations, which is driven by the specific IQ peptides, is crucial. The flexibility of the protein and the dominance of its nonspecific hydrophobic interactions with the IQ peptides are probably correlated with its ability to bind a wide range of targets. Besides describing the structure and dynamics of the protein in the presence of the peptides, we analyze the interaction free energy that governs the protein-peptide binding. Using a combination of energies derived from MD simulations in an explicit solvent, a continuum solvent model, and solute entropies contributions derived from normal mode analysis, we have obtained approximate values for the protein-peptide interaction energy of both complexes. We found that favorable molecular mechanics energy contribution profoundly supports this protein-peptide interaction, while the polar solvation energy and the entropy oppose it. Given our results, and the previously suggested simulated structure of the complex between the Mlc1p protein and the IQ4 peptide (60), we propose a dynamic solution model of the LCBD of myosin V, involving mutual modulations of the structures of the light chain proteins in respect to the IQ peptides of the myosin's neck toward each other. Such a model may have important implications regarding the structure-function relationship of the lever arm of myosin V.