Fiber Depolymerization

Abstract

Depolymerization is, by definition, a crucial process in the reversible assembly of various biopolymers. It may also be an important factor in the pathology of sickle cell disease. If sickle hemoglobin fibers fail to depolymerize fully during passage through the lungs then they will reintroduce aggregates into the systemic circulation and eliminate or shorten the protective delay (nucleation) time for the subsequent growth of fibers. We study how depolymerization depends on the rates of end- and side-depolymerization, k_end and k_side, which are, respectively, the rates at which fiber length is lost at each end and the rate at which new breaks appear per unit fiber length. We present both an analytic mean field theory and supporting simulations showing that the characteristic fiber depolymerization time 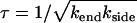depends on both rates, but not on the fiber length L, in a large intermediate regime 1 ≪ k_sideL²/k_end ≪ (L/d)², with d the fiber diameter. We present new experimental data which confirms that both mechanisms are important and shows how the rate of side depolymerization depends strongly on the concentration of CO, acting as a proxy for oxygen. Our theory remains rather general and could be applied to the depolymerization of an entire class of linear aggregates, not just sickle hemoglobin fibers.

INTRODUCTION

The assembly of particular proteins, or other monomers, into long polymeric fibers is of great importance in the function of the living cell as well as chemistry in general. This polymerization process can often be reversible, as in actin filaments or microtubules (1) or living polymers, such as wormlike surfactant micelles (2). Whereas the phenomenon of polymerization has been studied in great detail, that of depolymerization has received rather less attention. This is despite the fact that depolymerization processes are now believed to play an important role in sickle cell disease and may even be relevant in amyloid-based diseases if they affect the persistence of fibrils.

We believe that the theoretical analysis that we present in this article could have rather wide application in understanding depolymerization processes in general. However, this study was initially motivated by experiments that demonstrated the feasibility of measuring the depolymerization of individual sickle cell fibers (3). New quantitative data is now available that is suitable for comparison with our theory, as we will report below. We hope that the connection that our model makes with microscopic kinetic rates may motivate future experiments on depolymerization of other polymers, perhaps including amyloid fibrils.

Sickle hemoglobin fibers are sometimes formed by mutant hemoglobins (HbS), e.g., when they are deprived of oxygen. These fibers rigidify red blood cells and are a primary, initiating cause of sickle cell disease (4). It is important to understand the kinetics that control both the polymerization and depolymerization of these fibers as both of these processes are important in controlling the effects of the disease. We will consider only depolymerization in the remainder of this article.

The association kinetics of sickle hemoglobin fibers have been well characterized and have been shown to be described by the double-nucleation model of Ferrone et al. (5,6). In this model the initial nucleation of fibers is homogeneous and highly cooperative with a rate that is a high power of the protein concentration. Subsequently, new fibers are also formed by heterogeneous nucleation on the surfaces of existing fibers, so that the rate of new fiber formation is proportional to the mass of fiber already present, leading to exponential kinetics. All fibers grow by addition of monomers at fiber ends.

In sickle cell disease, polymers form under deoxygenating conditions and depolymerize if the oxygen concentration is high. If depolymerization is slow, sickle fibers may fail to dissolve during their passage through the oxygenating conditions provided by the lungs, typically lasting 1–3 s (7). As we will discuss below, slow depolymerization may often be associated with conditions in which the fibers depolymerize by loss of materials from their ends (only), a process which we will refer to as end-depolymerization. If depolymerization is slow, residual polymers may pass into the systemic circulation, eliminate the protective nucleation-dependent delay time, and thus may predispose the patient to acute sickle cell crises. As we will discuss below, an additional mode of depolymerization, which we will refer to as side-depolymerization, is also possible and can greatly decrease the time required for fibers to fully depolymerize. The side-end depolymerization mechanism, which involves loss of material from fiber midsections, may apply to other biological polymers and may thus have bearing on normal physiology as well as pathophysiology. We therefore suggest that the results of our theoretical analysis may be relevant to scientists who are interested in polymer kinetics in general.

Recent experiments by Agarwal et al. (3) clearly show that sickle hemoglobin fibers can depolymerize both by loss of monomers from the fiber ends and by side depolymerization, which involves loss of material from midsections of the fiber. Electron micrographs of partially depolymerized fibers presented in this earlier study seem to suggest that side-depolymerization may correspond to the formation of breaks in the fiber. The fiber may not always break as cleanly as these micrographs suggest, but may leave ends that resemble, e.g., sharpened sticks. This is natural, given that sickle hemoglobin fibers are made up of a twisted bundle of seven double strands of HbS and those proteins residing in the outermost strands may leave before those in the inner strands. However, provided the length of any resulting tapered section near the end remains small compared to the average length of the fiber fragments, we can neglect such details, treating the polymer as a quasi-one-dimensional object in what follows. Finally, it may be worth noting that end-depolymerization appears to occur at the same rate at both (all) ends of the fiber.

The new pairs of ends that result from the formation of such breaks in the fiber would then provide new sites for the loss of material via end-depolymerization. Clearly, if there are many such breaking events during the course of the depolymerization of a typical fiber, then the kinetics will depend crucially on both the rates of end- and side-depolymerization (3). In this article, we aim to provide a quantitative analysis of this effect. Clearly, similar depolymerization mechanisms may be important in other fibrillar protein aggregates.

It is worth noting that, in a sense, our depolymerization model mirrors that of polymerization: For depolymerization, there is nucleation of holes, whereas in polymerization, there is the nucleation of aggregates. We study depolymerization (alone) in this article by restricting our attention to thermodynamic (chemical) conditions in which net association is negligible, as can be easily achieved for sickle hemoglobin and other so-called living polymers.

THEORY

We consider a fiber of length L that, at time t = 0, starts to depolymerize via two mechanisms: 1), end-depolymerization at rate k_end in units of μm s⁻¹; and 2), side-depolymerization, described by the formation of breaks (new pairs of ends) at random positions with a rate k_side in units of μm⁻¹ s⁻¹ (see Fig. 1). This second process is assumed to involve the formation of holes of constant initial size d, equivalently the loss of a segment of fiber of length d. Once created, the holes then grow via end depolymerization of the newly created end pairs. A complete mathematical treatment must deal not only with the creation of ends but also their annihilation, which occurs whenever any small segment of fiber vanishes by shrinkage of its ends to a point. Such events may occur frequently for fibers that have significant side-depolymerization rates, as we will show below.

FIGURE 1.

Schematic figure showing a typical distribution of fiber segments present some time after the onset of depolymerization. The thin horizontal line indicates the original extent of the polymer. All the ends (eight are present in this realization) are losing material at a constant rate k_end and new breaks are appearing randomly with a rate k_side per unit length of remaining polymer. The kinetics of the resulting depolymerization are analyzed mathematically in this article.

The kinetics of the depolymerization process that result from this model are as follows: For fibers that are subject to a very slow breaking rate, fiber shrinkage occurs via depolymerization at its two original ends (only), leading to fiber disappearance on the timescale

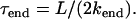(1)

This has been observed (3) to occur with a rate k_end ≈ 0.5 μm s⁻¹. As the breaking (side-depolymerization) rate k_side increases, controlled by, e.g., an increase in oxygen (or CO) concentration, the appearance of breaks remains rare on average, until the dimensionless parameter χ given by

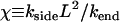(2)

reaches 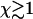. At this point, the average maximum number of extra ends formed in time τ_end, given by 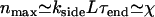, exceeds unity and thus hole formation cannot be neglected when 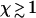. The characteristic timescale on which the fiber disappears then remains well approximated by

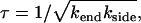(3)

provided 1 ≪ χ ≪ (L/d)², with d the initial size of holes, probably of the order of the fiber thickness. We will fully justify this result, and its regime of validity, in what follows. This timescale has the striking feature that it does not depend on the initial fiber length L. Finally, the side-depolymerization rate may becomes so large that the entire fiber disappears rapidly by simultaneous side-depolymerization of all its segments on the timescale

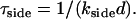(4)

This is the fastest mechanism when τ_side ≪ τ, which only occurs when χ ≫ (L/d)², thereby justifying the upper bound of the intermediate regime defined above.

For long fibers, the intermediate regime 1 ≪ χ ≪ (L/d)² in which the depolymerization time τ depends intimately on both rate constants can be extremely large. Similar results are well known from nucleation-and-growth models (8,9), including those restricted to one dimension (10,11).

The results described above are straightforward to verify except those leading to the appearance of the timescale τ in the intermediate regime 1 ≪ χ ≪ (L/d)², which we will now analyze. We assume that, in this regime, the average fiber experiences many hole-formation (breaking) events before it has completely depolymerized, a fact that can be verified a posteriori, see, e.g., Fig. 2 below. This justifies a mean field description of the fiber's fragmented state during depolymerization, which corresponds to retaining information only on the average length of the fiber segments, rather than the full segment length distribution.

FIGURE 2.

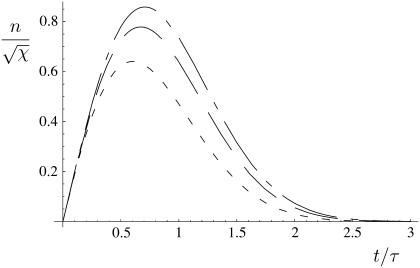
The number of polymer ends n present at time t after the onset of depolymerization. Shown are the results for finite χ, as analyzed in Appendix 1, χ = 10 (short dashes), χ = 100 (long dashes), and the asymptotic behavior in the large χ limit (short and long dashes), which gives a good approximation for the overall depolymerization time for all values 1 ≪ χ ≪ (L/d)² as given in Eq. 8.

We propose that the rate of change of φ, the total length of fiber remaining at time t, is

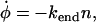(5)

subject to the boundary condition that φ(0) = L. This equation captures the physics that the fiber depolymerizes at a rate proportional to the number of ends n present, with n(0) = 2. Additionally, there is another differential equation that determines n(t), the number of ends present:

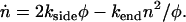(6)

The first term on the right-hand side of Eq. 6 takes account of the rate of production of pairs of ends (single holes) as the product of the length of polymerized fiber remaining and the breaking rate. The second term on the right-hand side of Eq. 6 takes account of the rate of annihilation of fiber fragments when their two retracting ends meet. The mean field rate at which ends are annihilated is proportional to the rate at which each segment of fiber shrinks (2k_end) and inversely proportional to the mean length of each remaining segment (2φ/n), which is how far a typical segment has to shrink before it disappears. It is also proportional to the number of fiber segments (n/2) that are shrinking, with an extra factor of 2 since two ends are lost each time a segment reaches zero length. The following are approximate solutions to the above differential equations with 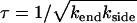, as discussed in Appendix 1:

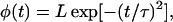(7)

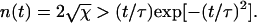(8)

Thus, the characteristic timescale on which the fiber depolymerizes is τ (see Appendix 2 for further discussion). It can also be seen that the kinetics is indeed dominated by the large number of depolymerizing ends typically present, peaking 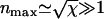at at 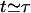. The evolution of the total number of fiber ends and the total length of fiber remaining are shown in Figs. 2 and 3, respectively.

FIGURE 3.

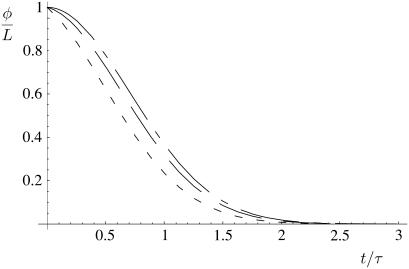
The total length of remaining fiber φ divided by the initial length L is the proportion of fiber still remaining at time t after the onset of depolymerization. Shown are the results for finite χ, as analyzed in Appendix 1, χ = 10 (short dashes), χ = 100 (long dashes), and the asymptotic behavior in the large χ limit (short and long dashes), which give a good approximation for the overall depolymerization time for all values 1 ≪ χ ≪ (L/d)² as given in Eq. 7.

Verification of mean-field results by simulation

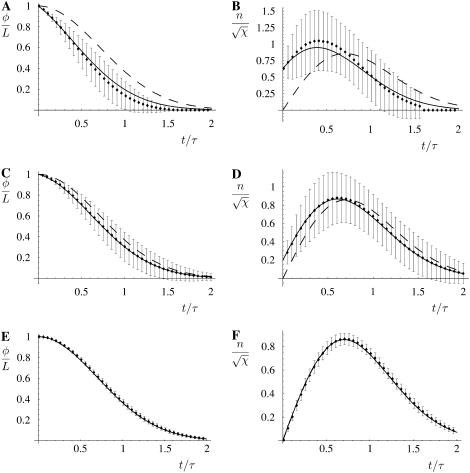
A Monte Carlo simulation routine was constructed to simulate stochastic fiber decomposition. In this routine an initial fiber was permitted to depolymerize deterministically from its ends while the side-depolymerization, or breaking, events were simulated stochastically with an appropriate breaking probability per unit time. The simulation results, including averages over 1000 simulation runs, are shown in Fig. 4, A–F. These results show that the analytic mean-field solution is remarkably accurate, probably being sufficient for most purposes even for 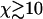. The stochastic uncertainty represented by the vertical bars in the simulation data are seen to diminish as χ increases. These are not error bars per se but are rather the variation that should be expected between similar realizations of the stochastic depolymerization process. It is seen that the asymptotic-mean field result in the χ → ∞ limit yields an excellent approximation to both the simulation data and the finite χ-mean field results, provided χ is large.

FIGURE 4.

(A–F) The variation of the total length fraction of remaining fiber φ/L (A, C, and E) and the number of ends present, shown the rescaled end density 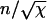(B, D, and F) as a function of the time after the onset of depolymerization in units of the characteristic timescale τ defined in Eq. 3. The curves show the mean-field solution, both for finite values of χ as derived in Appendix 1 (solid line) and for χ → ∞; see Eqs. 7 and 8 (dashed line). Also shown is the data from the simulations of the fiber depolymerization process: the points show the average over 1000 simulations and the vertical bars represent the 1-SD stochastic variation for a single realization. Shown are χ = 10 (A and B), χ = 10² (C and D), and χ = 10⁵ (E and F). It can be seen that even for χ-values as low as 10 there is good agreement between the mean-field result and the simulation mean and a relatively large stochastic variation about the mean between individual simulation runs. As the value of χ increases, we see both that the mean-field estimate asymptotically converges to the mean of the simulations, but that the stochastic variation diminishes as well. This can be understood in terms of the fact that the larger the χ, the more breaks a typical fiber experiences, and the better the statistics that emerge from a single simulation run.

The excellent agreement between the mean-field results of the previous section, in which a single characteristic mean fiber length is retained, and those obtained by simulations, which involves the full length distribution, hints that only a single length scale is needed to parameterize the distribution. In turn, this suggests that the distribution is monoexponential throughout most of the depolymerization process. This can be confirmed, either by inspection of the length distribution obtained by simulation, or by an approximate analytic approach (R. W. Briehl, unpublished).

COMPARISON WITH EXPERIMENT

Materials and Methods

Differential interference contrast (DIC) microscopy

The Materials and Methods used in this study are as per Agarwal et al. (3) and the reader is referred there for additional technical details. In brief, HbS was purified chromatographically and prepared at 3.75 mM on slides prepared in a glove bag containing from 1% to 100% CO in nitrogen. Fibers and gels were observed at room temperature by video-enhanced differential interference contrast (DIC) microscopy with mercury arc illumination at 546 nm. Deoxygenation and polymerization were induced by photolysis of COHbS by epi-illumination at 436 nm. Once a gel was formed, it was selectively depolymerized by changing epi-illumination intensity (and hence fractional deoxygenation) and the region photolyzed until only an isolated fiber in free solution remained. This procedure of fiber surgery is necessitated by the nucleation-dependent nature of gelation: when sufficient intensity is used to overcome the high barrier to nucleation, extensive further polymerization occurs very rapidly, with formation of a dense cross-linked gel, precluding creation of individual fibers free of the network. Hence, fibers in free solution cannot be produced in the initial gelation stage; they require selective dissolution of a previously formed gel. After the desired fibers were formed, they were held at constant length within the photolyzed regions to allow solution CO transients to diffuse. The circular photolysis spots were usually 15 but sometimes 25, 10, or 6 μm in diameter. All experiments were at room temperature. Depolymerization in circular spots was initiated by extinguishing the photolytic epi-illumination.

Interpretation

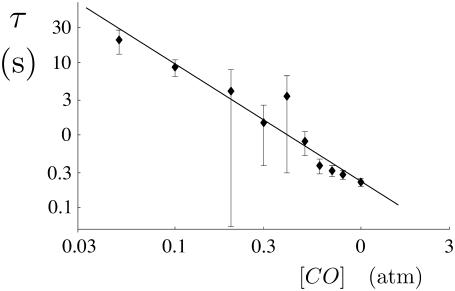
It was already established in an earlier study (3) that fiber end-depolymerization rates, as observed under DIC microscopy, vary only slightly with the concentration of CO. The typical end-depolymerization rate is k_end ≈ 0.5 μm/s. The overall timescale on which the fiber disappears is, however, observed to vary substantially. A fully quantitative analysis of this process, including side-depolymerization, is made possible by the combination of theory and experiment reported here. To calculate the variation of the side-depolymerization rate we carried out repeated observations of the depolymerization of single sickle hemoglobin fibers using DIC video microscopy. This allowed us to estimate the disappearance time of the fiber, after the removal of photolysis, under different CO concentrations; see Fig. 5. As we will now discuss, this provides the first quantitative probe of how the rate of the side-depolymerization process scales with the concentration of CO, acting as a proxy for oxygen. A least-squares fit to the experimental data points of Fig. 5 indicates a slope of −1.6, giving the scaling of

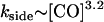(9)

from Eq. 3. This represents the first quantitative evidence for a substantial cooperative influence of oxygen on the side-depolymerization rate. As discussed in Agarwal et al. (3), in which a limited number of similar experiments were reported, there is some question that CO diffusion may influence the rate for the most rapidly depolymerizing fibers, leading to slower side-depolymerization than the underlying rate at that (bulk) concentration. However, the data shown on Fig. 5, for concentrations [CO] ≥ 0.5 atm, were obtained using both a small (21 repeats) and a large (38 repeats) optical photolysis field of 6- and 15-μm diameter, respectively. The fact that there was rather little consistent difference between the two field sizes helps to support the hypothesis that any artifacts associated with the diffusion of CO to the fiber may be rather minor.

FIGURE 5.

The variation of the lifetime of the fiber τ with the concentration of CO, as estimated from DIC video microscopy. The best-fit line has the slope α = −1.62, characterizing the power law τ ∼ [CO]^α. The error bars show the variation of our measurements about the mean (1 SD) over a total of 86 measurements taken over nine different CO concentrations. Aside from the large intrinsic stochastic variations, which the error bars mostly reflect, our assessment of the underlying experimental errors is that they are mainly associated with the imprecision in measuring the depolymerization times by subjective inspection of the video and might typically be 10–20%, i.e., rather small compared to the stochastic variation.

Electron microscopy measurements

In this section we reanalyze previously published data. In Fig 8 of Agarwal et al. (3), a fiber is shown in various stages of depolymerization and strongly resembles Fig. 1 of this article. In this case, depolymerization was induced by dilution, rather than CO photolysis (the reader is referred to Agarwal et al. (3) for experimental details). We have no overall timescale for the process of depolymerization, merely a snapshot of the state of the fiber at an unknown time after the onset of depolymerization. Although this means we cannot extract absolute values of k_end and k_side, we can estimate their relative values, as we now demonstrate. The left frame in Fig. 8 of Agarwal et al. (3) shows a fiber with φ ≈ 0.6 L having five segments (n = 10) in an L = 1-μm section. From Fig. 3, we have t ≈ 0.8 τ and, from Fig. 2, 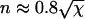. From the definition of χ ≡ k_sideL²/k_end we have

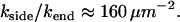(10)

Thus, under these conditions, side-depolymerization plays an important role for any fibers that are longer than ∼80 nm, corresponding to .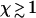

CONCLUSIONS

We have shown how the rate of fiber depolymerization can depend on the geometric mean of both the end- and side-depolymerization rates. In particular the timescale for fiber depolymerization τ need not depend on the initial length of the fiber. Our mean-field results for finite values of the parameter χ, controlling the relative rate of the side- and end-depolymerization processes, are fully quantitative, being in excellent agreement with our corresponding Monte Carlo simulations. When compared with experiments, our mean-field results give information about the two kinetic rates controlling depolymerization. As we have discussed, the process of depolymerization may play an important role in the pathology of sickle cell disease. We show that one of the rates, controlling the formation of new fiber breaks, scales with roughly the third power of oxygen concentration. Our theory is actually rather general and should describe the depolymerization of all linear aggregates that shed monomers from their ends as well as via the formation of short breaks.

APPENDIX 1: SOLUTIONS TO EQS. 5 AND 6

We can obtain a second-order nonlinear ODE for φ by substituting for n from Eq. 5 into Eq. 6,

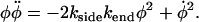(11)

We now identify the characteristic timescale 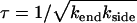and use the identities 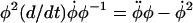and 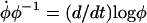to write the differential equation for log φ,

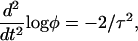(12)

which has the general solution of

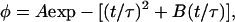(13)

and hence, from Eq. 5

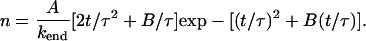(14)

The particular solution of interest to us here is determined by the boundary conditions φ(0) = L and n(0) = 2 corresponding to A = L and 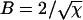and hence the solutions (Eqs. 13 and 14) above. However, in the regime 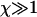of interest, the solutions are well approximated by Eqs. 7 and 8, as given in the Theory section.

APPENDIX 2: INTERPRETATION OF THE CHARACTERISTIC FIBER DEPOLYMERIZATION TIME τ

The fact that the fiber depolymerizes according to Eq. 7 implies that the fiber has substantially depolymerized after a time of the order of τ. Indeed, any experimental probe that is sensitive to the length of fiber remaining will register the fiber as having completely disappeared after a few (two, say) times τ. Nonetheless, one can ask, What is the terminal fiber depolymerization time τ* after which the very last fiber segment disappears on average? It is a delicate matter to estimate this timescale from our mean-field approach as our treatment starts to break down in the late stage of depolymerization, when there are no longer many segments present. Nonetheless, an appropriate estimate can be constructed as follows.

Define τ* to be the time at which there is O(1) segment remaining. Thus setting n = 2 in Eq. 8, we have

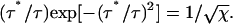(15)

This is a transcendental equation for τ*/τ but is dominated by the exponential term and, neglecting logarithmic corrections, is approximately satisfied when

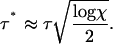(16)

The additional time it takes for this final segment to depolymerize by end-depolymerization alone is of the order of φ(τ*)/(2k_end) ≈ τ/2, which is smaller than τ* in the regime χ ≫ 1. Thus we estimate that the fiber completely disappears on the timescale τ* which, for all practical values of χ, is not much greater than τ. For example, with χ = 100 we obtain τ* = 1.5τ from Eq. 16 and find that τ* only exceeds 10τ for completely unrealistic values of χ > 10⁴³.