Control of Electrical Alternans in Canine Cardiac Purkinje Fibers

Abstract

Alternation in the duration of consecutive cardiac action potentials (electrical alternans) may precipitate conduction block and the onset of arrhythmias. Consequently, suppression of alternans using properly timed premature stimuli may be antiarrhythmic. To determine the extent to which alternans control can be achieved in cardiac tissue, isolated canine Purkinje fibers were paced from one end using a feedback control method. Spatially uniform control of alternans was possible when alternans amplitude was small. However, control became attenuated spatially as alternans amplitude increased. The amplitude variation along the cable was well described by a theoretically expected standing wave profile that corresponds to the first quantized mode of the one-dimensional Helmholtz equation. These results confirm the wavelike nature of alternans and may have important implications for their control using electrical stimuli.

Electrical alternans is a phenomenon characterized by a beat-to-beat alternation in the duration of the cardiac action potential (APD) [1]. Because heart cells are refractory to further stimulation during an action potential, alternans of APD results in an alternans of refractoriness, the magnitude of which may vary across different regions of the heart. Several studies have shown that the resulting spatial dispersion of refractoriness facilitates the development of local conduction block [2–5], which may in turn cause the normally planar wave of electrical excitation in cardiac tissue to break and form spiral waves [6]. If the spiral waves also encounter regions of disparate refractoriness, they may disintegrate into multiple wavelets, which may account for the onset of the lethal heart rhythm disorder ventricular fibrillation [7–9].

Given that APD alternans may be mechanistically linked to the onset of reentrant arrhythmias, its elimination might be an effective antiarrhythmic strategy. Initial work in that direction showed that closed-loop feedback methods could be used to suppress a type of alternans (known as atrioventricular-nodal conduction alternans) with period-doubling dynamics that are related to those of APD alternans [10–13]. More recently, it was shown that a related control method could terminate APD alternans in isolated frog hearts [14,15]. The latter studies showed clearly that perturbations to the electrical stimulus interval could be used to eliminate APD alternans in a system that does not have spatiotemporally varying repolarization and wave-propagation dynamics (the frog sections were small enough that there were no apparent spatial variations in dynamics).

However, modeling work has suggested that, due to the complex spatiotemporal dynamics of electrophysiological repolarization, control of larger tissues might require stimulation from multiple sites [16]. More recently, Echebarria and Karma found in simulations that control from a single site was limited by an inability to influence alternans dynamics in tissue distant from the stimulating electrode, with control efficacy decreasing as pacing rate increased [17]. Furthermore, these authors showed analytically [17] that control failure from single-site pacing is a direct consequence of the wave nature of alternans elucidated in an earlier theoretical study of alternans [18]. In particular, they showed that the linear stability eigenmodes of the paced cable are governed by the standard one-dimensional Helmholtz equation with a spatial coupling term originating from the diffusive electrical coupling between cells and an additional spatially uniform external forcing imposed by the feedback control [17]. While control can stabilize the state with a spatially uniform amplitude of alternans, it fails to control higher quantized modes with a spatially varying amplitude that are present even when the conduction velocity is constant along the cable. Remarkably, these modes are directly analogous to the ubiquitous vibrational standing wave modes associated with the Helmholtz equation in many physical contexts (such as sound harmonics in an open pipe).

In the present study, we sought to determine the extent to which alternans control can be achieved in real cardiac tissue as well as to test experimentally the wave nature of alternans. To approximate the one-dimensional, homogeneous cables analyzed in [17], free-running, unbranched cardiac Purkinje fibers (superfused with Tyrode solution) were studied (1.5–2.5 cm long × 2–3 mm wide; n = 8 fibers from 8 animals). The fibers were obtained from either ventricle of deeply anesthetized adult mongrel dogs. The studies were approved by the Institutional Animal Care and Use Committee of the Center for Research Animal Resources at Cornell University. Pacing stimuli (2 ms duration) were delivered to either end of the fiber via a bipolar electrode. Action potentials were recorded [sampled at 1 kHz with 12-bit resolution [19] ] simultaneously from 6 sites along the fiber using standard microelectrode techniques. Following 60 minutes of equilibration at a pacing cycle length (T_*) of 300 ms, T_* was decreased progressively by 10 ms decrements to induce alternans—concordant (i.e., all spatial regions alternate in phase) at slower pacing rates and discordant (i.e., distinct spatial regions alternate out of phase) at faster pacing rates. The pacing protocol subsequently was repeated with the application of the control algorithm at each T_*. Both the pacing and control stimuli were applied to the same end of the fiber.

As in previous alternans control studies, the interstimulus interval was adjusted for each stimulus according to:

$$T_n=\{\begin{array}{cc}{T}_{*}+\mathrm{\Delta }{T}_n& \text{if\hspace{0.17em}}\mathrm{\Delta }{T}_n<0,\\ T_{*}& \text{if\hspace{0.17em}}\mathrm{\Delta }{T}_n\ge 0,\end{array}$$ (1)

where

$$\mathrm{\Delta }{T}_n=(\gamma /2)(A_n-A_{n-1}),$$ (2)

T_* is the pacing cycle length without control, γ is the feedback gain (which typically ranged from 0.6 to 1.0, and was held constant for the duration of each experiment), A is the APD at the proximal microelectrode (‘‘Lead 1’’ in Figs. 1 and 2) and n is the interval number. No significant differences in the ability to control alternans were detected for different γ values between 0.6 and 1.0.

FIG. 1.

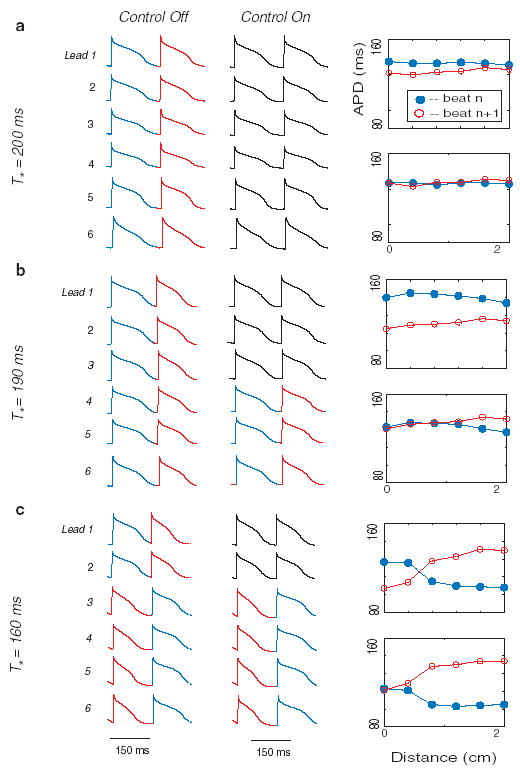
(color). Data from two consecutive action potentials recorded from 6 microelectrodes spaced along the length of a Purkinje fiber (Lead 1 is proximal; Lead 6 is distal) in one representative control experiment. Stimulation was applied to the proximal end of the fiber near microelectrode 1 (x = 0 cm). For each of the three rows [(a), (b), and (c)]: (1) T_* is shown on the left, (2) membrane potential vs time for microelectrodes 1 through 6 (which correspond to x = 0 and 2 cm, respectively) are shown in the left column (before control) and middle column (during control), and (3) the right column shows APD values computed from the six microelectrodes for the same alternate beats before (top panels) and during (bottom panels) control. During control, stimulation was adapted according to Eq. (1). In the middle column, action potentials for which control failed to eliminate alternans are shown in red and blue, while those in which alternans was suppressed are shown in black.

FIG. 2.

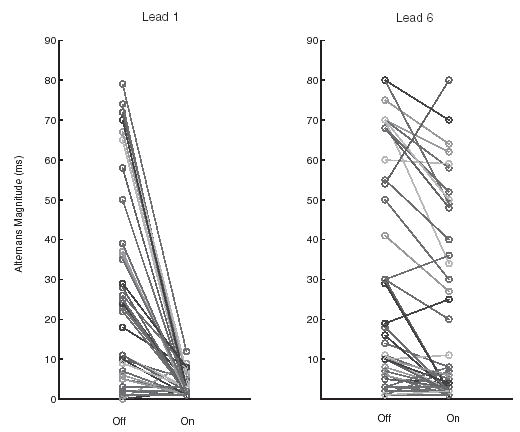
Alternans magnitude, as recorded by microelectrodes 1 (Lead 1, left panel) and 6 (Lead 6, right panel) from Fig. 1, before control (‘‘Off’’) and during control (‘‘On’’). Periodic pacing and control were applied to the proximal end of the fiber (near microelectrode 1).

The algorithm was similar to that used for control of APD alternans in Refs. [14,17], although the approaches used in those studies did not impose any conditions on ΔT_n, (i.e., T_n = T_* + ΔT_n for all ΔT_n). The conditions of Eq. (1) were used in this study for two reasons. First, such an implementation is more electrophysiologically realistic than the unconditional approach. In an intact heart, in which the underlying pacing is the result of native electro-physiological activity rather than external stimulation, it is not possible to prolong an interstimulus interval [13,20]. Second, algorithms using only negative perturbations have been shown analytically to have a larger successful-control regime than those that apply both positive and negative perturbations [12,21]. However, a disadvantage of the former is that they achieve control slower (i.e., more beats are required to suppress alternans after control is activated).

In this study, in the absence of control [as described in detail previously [5,22,23] ], progressive shortening of T_* produces a stereotypical sequence of APD dynamics, including a period-doubling bifurcation that initially takes the form of concordant APD alternans and subsequently is converted to discordant alternans at the shortest T_*. Examples of such uncontrolled dynamics are shown in Fig. 1. They include: (1) concordant alternans at T_* = 200 ms, during which APD for all sites on the fiber alternate in phase [leftmost column of Fig. 1(a)]; (2) increased magnitude of alternans at the site of stimulation at T_* = 190 ms, with a reduction of alternans magnitude at more distal sites [leftmost column of Fig. 1(b)]; (3) discordant alternans at T_* = 160 ms, during which the alternans of APD at the proximal and distal ends of the fiber are out of phase [leftmost column of Fig. 1(c)].

Control was attempted at 5 different T_* values for each of the n = 8 fibers. Two control trials were excluded because of loss of microelectrode impalement, leaving a total of m = 38 control trials. Although quantitative control results varied between fibers, qualitative features were common to all trials. For any given fiber, control results were correlated to pacing period T_* and the corresponding degree (i.e., magnitude and concordance) of alternans. Specifically, for relatively small-amplitude concordant alternans, successful control (i.e., elimination of alternans) could usually be achieved for the entire length of the fiber [e.g., Fig. 1(a)]. For larger-amplitude concordant alternans (resultant from a smaller T_*), successful control extended beyond the proximal end of the fiber, but not all the way to the distal end of the fiber [e.g., Fig. 1(b)]. For discordant alternans, successful control could be achieved only at, or very near, the proximal end of the fiber; moreover, during control, discordant alternans was converted to concordant alternans [e.g., Fig. 1(c)].

A summary of the extent to which control was achieved at the site of stimulation and at the site furthest from the site of stimulation during concordant alternans is shown in Fig. 2. In 35/38 cases alternans magnitude was reduced to less than 7 ms at the site of control [Fig. 2(a)], regardless of the magnitude of alternans prior to the onset of control. In contrast, reduction to less than 7 ms was achieved in only 17/38 cases at the distal sites [Fig. 2(b)]. Moreover, control at the distal site was effective only when the magnitude of alternans in the absence of control was less than 30 ms.

The effect of control is strikingly similar in the experiments and in previous simulations of the Noble model in a cable geometry, as can be seen by comparing Fig. 1 of the present Letter with Fig. 4 (which used a 5 cm cable) of Ref. [17]. Furthermore, the analysis of Echebarria and Karma Ref. [17] predicts that the amplitude of alternans should be given to a good approximation by

$$a(x)\approx \frac{a(L)}{2}\left[1-cos\frac{\pi x}{L}\right],$$ (3)

where x measures the position along a cable of length L paced at x = 0, and a(x) is defined by writing the APD at beat n and position x in the form A_n(x) = A* + (−1)ⁿa(x) where A* is the APD of the unstable spatially uniform state without alternans. More accurate expressions for a(x) that resolve the very small amplitude of alternans at the pacing site are unnecessarily accurate for interpreting the present experiments that do not resolve this amplitude. Control suppresses concordant alternans and discordant alternans with antinodes (maximum amplitude) at the two ends of the cable. However, it fails to stabilize the standing wave mode described by Eq. (3) with a node (antinode) at the pacing site (other end of the cable), which is a solution of a forced Helmholtz equation [17]. Hence, spatial attenuation of control away from the pacing site is reflected in the appearance of this mode, which is most clearly observed experimentally for large alternans magnitude in Fig. 1(c). A quantitative comparison of a(x) corresponding to Eq. (3) and five control trials is shown in Fig. 3. The five control trials were selected because they were paced at similar cycle lengths and had similar APD profiles prior to alternans control. The departure of the experimental profiles from a pure sinusoid can be attributed to variations of conduction velocity along the cable that are neglected for simplicity in the analysis leading to Eq. (3), but included in the ionic model cable simulations, which exhibit a similar departure when the cable length is long enough for the conduction velocity to vary [see Fig. 4(e) in Ref. [17] ].

FIG. 3.

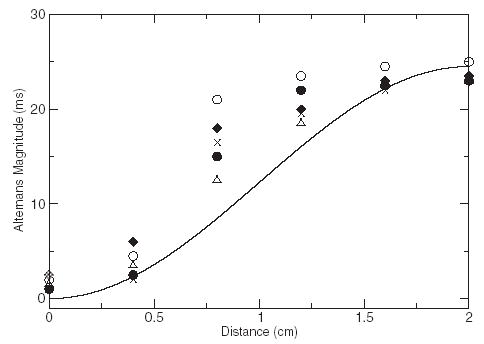
A quantitative comparison of a(x) corresponding to Eq. (3) (solid curve) and five control trials (symbols). For the control-trial data, the APD values for consecutive beats were subtracted and divided by two for each of the six spatial electrodes.

In summary, this study has shown that in ≈2 cm Purkinje fibers, spatially extended control of alternans in Purkinje fibers is possible if alternans magnitude is small. However, in agreement with past theoretical predictions [17], as alternans magnitude increases, control becomes attenuated spatially due to the appearance of a standing wave mode of alternans that is unaffected by the present control scheme. These results intimately link spatiotemporal alternans dynamics in cardiac tissue with a wide range of physical wave phenomena and provide a fundamental basis for developing new control strategies.

Although this study demonstrates that control of cardiac alternans from a single electrode is spatially limited, control nonetheless has some antiarrhythmic effect by decreasing the magnitude of the spatial gradient of APD. Without control, this magnitude is largest in the state of discordant alternans shown in the top panel of Fig. 1(c), which is directly analogous to the state that has been shown to promote the initiation of high-frequency reentrant spiral waves in ventricular tissue [2–5]. In contrast, this magnitude is reduced in the standing wave mode induced by feedback control shown in the bottom panel of Fig. 1(c). An attractive future prospect is to control such modes by exploiting their quantized nature and their sensitivity to boundary conditions. An alternative approach might be to eliminate alternans using multiple dispersed controllers spaced at distances less than the maximum controllable tissue distance [dispersed controller approaches have been used to control spatiotemporal dynamics in physical systems [24–26], and in simulated cardiac monolayers for the control of spiral-wave reentry or fibrillation [16,27] ].

Support is acknowledged from the Whitaker Foundation (RG-02-0369), NSF (PHY-0513389), the NIH (R01RR020115), and the Kenny Gordon Foundation (D. J. C. and C. A. C.); the NIH (HL62543) (M. L. R., R. F. G.); the NSF (IGERT) (J. J. F.); and the NIH (SCOR in Sudden Cardiac Death P50-HL52319) (A. K.). The authors wish to acknowledge the Aspen Center for Physics for holding the Waves in Biological Excitable Media workshop (2002), at which ideas for this work were spawned.