Ensemble molecular dynamics yields submillisecond kinetics and intermediates of membrane fusion

Abstract

Lipid membrane fusion is critical to cellular transport and signaling processes such as constitutive secretion, neurotransmitter release, and infection by enveloped viruses. Here, we introduce a powerful computational methodology for simulating membrane fusion from a starting configuration designed to approximate activated prefusion assemblies from neuronal and viral fusion, producing results on a time scale and degree of mechanistic detail not previously possible to our knowledge. We use an approach to the long time scale simulation of fusion by constructing a Markovian state model with large-scale distributed computing, yielding an understanding of fusion mechanisms on time scales previously impossible to simulate to our knowledge. Our simulation data suggest a branched pathway for fusion, in which a common stalk-like intermediate can either rapidly form a fusion pore or remain in a metastable hemifused state that slowly forms fully fused vesicles. This branched reaction pathway provides a mechanistic explanation both for the biphasic fusion kinetics and the stable hemifused intermediates previously observed experimentally. Our distributed computing and Markovian state model approaches provide sufficient sampling to detect rare transitions, a systematic process for analyzing reaction pathways, and the ability to develop quantitative approximations of reaction kinetics for fusion.

The kinetic and mechanistic details of membrane fusion are extremely challenging to observe in a physiological context (1–3) because the rate-limiting steps of biological fusion likely precede and are much slower than the fusion reaction itself (4). This experimental challenge makes membrane fusion an ideal target for simulation studies, but simulating lipid vesicle fusion in atomic detail is extremely challenging computationally because of the long time scales and large system sizes needed to understand the process. To reach the time scale of interest and attain statistical significance, orders of magnitude greater computational power would be needed, far greater than possible with even the world’s fastest supercomputers. Recent advances in coarse-grained simulation methodology have brought the simulation of individual fusion events on the 100-ns time scale within reach (5), but these studies have to date not included sufficient sampling to make precise quantitative predictions for membrane fusion.

To overcome these barriers, we have developed a Markovian state model (MSM)-based approach, consisting of a set of algorithms and computational paradigms for long time scale dynamics (Fig. 1). Using this method and a large-scale distributed computing approach, we predict the fusion behavior of pairs of 14-nm-diameter vesicles (comprising >500,000 atoms) on the hundred-microsecond time scale. This time scale is comparable to the fastest experimental measurements of the fusion process [≈200 μs (6)] and is 10,000-fold longer than most atomic-resolution molecular dynamics simulations. This simulation method makes possible our subsequent kinetic and mechanistic analysis of membrane fusion.

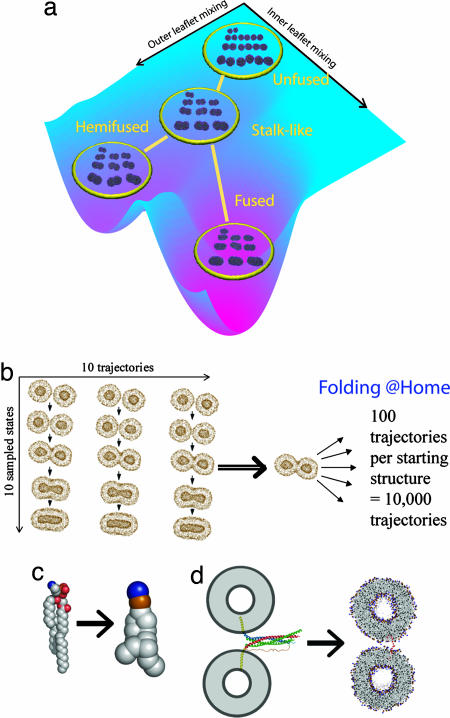
Fig. 1.

Methodological advances for the simulation of vesicle fusion. (a) The clustering of reaction snapshots into states and the linking of these clusters using MSM to derive a kinetic model for fusion reactions over long time scales. Ten randomly selected structures are rendered for each state, with lines representing transitions between states. The state-transition rendering is generated from the equilibrium distribution of states and overlaid on a surface schematizing the free energy landscape for fusion projected onto outer- and inner-leaflet lipid mixing reaction coordinates. (b) The ensemble-simulation scheme that we use with the Folding@Home distributed computing system. (c) A single POPE lipid using a unified-atom and a coarse-grained model (10, 11). (d) The analogy by which a chemical crosslinker is used to model a fusion protein such as the trans-SNARE complex, which is rendered based on an extrapolation from the crystal structure (35).

The theoretical underpinning for these techniques (the MSM approach) has been developed for simple model systems (7, 8), and here we demonstrate the application of MSM approaches to large, complex systems. The power of this technique is that, in addition to predicting rates and mechanisms, we obtain a robust kinetic model that extends the time scale of accurate measurement to hundreds of microseconds and beyond, limited only by the fidelity of the computational representation and the uncertainty levels in the initial rate calculations (see Methods). Because this approach simulates a very large ensemble of reaction trajectories, it makes predictions with high statistical power and strong error estimation, greatly exceeding the quantitative accuracy of previous molecular dynamics simulations.

To build an MSM, we perform molecular dynamics simulations of 10,000 separate fusion reactions by using the Folding@Home distributed computing project (9), thus creating a statistical ensemble of reaction trajectories unprecedented in membrane fusion studies. We use 10 initial simulation runs to seed 10,000 independent molecular dynamics runs (Fig. 1b and Methods); we then sample the reaction trajectories at regular intervals and cluster these sampled “microstates” into a discrete set of “macrostates” to derive an MSM (7, 8) describing the kinetics and thermodynamics of membrane fusion (Fig. 1a and Methods). The resulting >85,000 structures are systematically grouped into states by k-means clustering (Fig. 6, which is published as supporting information on the PNAS web site), and a transition probability matrix (p_ij) is constructed by using the trajectories, setting p_ij to the frequency that a trajectory in state i will visit state j in the next snapshot. This probability matrix allows modeling of the long time scale kinetics of the reaction ensemble (7, 8).

At the individual simulation level, we use the Marrink-Mark coarse-grained molecular dynamics method (10, 11) (Fig. 1c) to achieve a quantitative approximation of atomic behavior while easing the computational requirements for simulation. Our simulation is designed to mimic experimental conditions while still maintaining a model simple enough to analyze the relevant driving forces for fusion. We use molecular dynamics with an explicit representation for lipids, ions, and solvent. Simulation trajectories evolve according to explicit physical forces rather than methods such as dissipative particle dynamics that use soft-core potentials (12, 13). The Marrink-Mark force field allows a 4-fold reduction in the number of particles represented and a 40-fold increase in the time step interval compared with unified-atom simulations (see Methods).

We generated a starting configuration that we hypothesize may correspond to a fusion-active complex: two highly curved 14-nm vesicles composed of 1-palmitoyl 2-oleoyl phosphatidylethanolamine (POPE) lipids that are positionally restrained by a crosslinker molecule corresponding approximately to the intermembrane distance predicted for the fusion-active soluble N-ethylmaleimide-sensitive factor attachment protein receptor (SNARE) complex. This crosslinker serves as a local positional restraint on the vesicles in the region of fusion, analogous to the prefusion states of HIV gp41, influenza hemagglutinin, or trans-SNARE complexes (Fig. 1d). The 14-nm vesicles are of comparable size to the smallest experimentally observed lipid vesicles (14). The highly curved fusogenic lipid context is designed to reproduce additional factors believed necessary for fusion in biological systems (15, 16). Indeed, fusogenic phosphatidylethanolamine lipids have been extensively used as experimental model systems for studying fusion intermediates (17, 18). Fig. 1d shows the analogy by which this starting configuration was designed to mimic hypothesized fusion-active conformations from neuronal and viral fusion.

Results and Discussion

Using these combined computational advances, we have constructed a reaction diagram for vesicle fusion from a starting configuration designed to approximate the fusion-active complexes formed by SNAREs and viral fusion peptides (Figs. 2 and 3a). Construction of MSMs for membrane fusion has required extension of the underlying methodology, as typical reaction coordinates used for protein folding problems (such as rmsd between aligned structures) fail to capture the structural transitions involved in fusion (Fig. 7, which is published as supporting information on the PNAS web site). We use measures of lipid and vesicle contents mixing to capture the reaction coordinates for fusion, monitoring the progression of the reaction from two separate and unfused vesicles through the formation of fusion intermediates and ultimately progression to full fusion. Clustering of trajectory snapshots (or microstates) via the k-means algorithm applied to lipid and contents mixing data yields reaction intermediates in an automated and systematic manner. The intermediates (or ensemble macrostates) can be broadly classified as unfused, stalk-like, hemifused, and fully fused vesicles based on inspection of the clustered states (Table 1, which is published as supporting information on the PNAS web site). We find fusion simulation trajectories to be Markovian at our 20-ns sampling interval (Fig. 8, which is published as supporting information on the PNAS web site), thus validating the use of the MSM analytic approach.

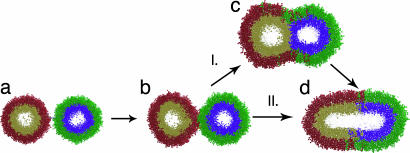
Fig. 2.

Branching reaction pathway for vesicle fusion. Pathway I shows the canonical progression from an unfused starting state (a) through a stalk-like early intermediate (b) and a hemifused late intermediate (c) to the fully fused state (d). Pathway II shows the additional reaction pathway observed in our simulations: rapid fusion from the stalk-like intermediate to the fully fused state. All renderings are of snapshots from observed reaction trajectories; lipids are colored to distinguish the outer (red and green) and inner (gold and blue) leaflets of each vesicle. Explicit water is present in all simulations but not rendered.

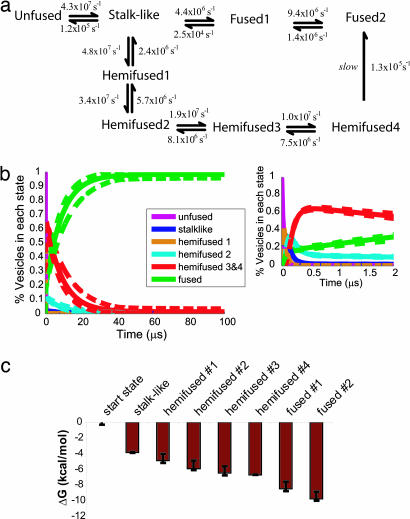
Fig. 3.

Vesicle fusion reaction mechanism and kinetics. (a) A schematic of the fusion reaction mechanism as determined by MSM. All reactions with probabilities >5% are shown with rates as calculated from the MSM transition matrix. In our simulations, fusion proceeds via a stalk-like intermediate state. We also observe a long-lived off-pathway intermediate that is hemifused, which slowly converts to the fused state (dashed line). Error estimation for calculated rates is given in Table 2, which is published as supporting information on the PNAS web site. (b) The reaction kinetics for fusion over multimillisecond time scales as determined from our simulations. The hemifused intermediate state dominates on the microsecond time scale, with a decay t_1/2 of 6.3 μs. On the 10-μs time scale, the fused state dominates. (Inset) The formation of transient intermediates at early times. Dashed lines show 90% confidence bounds. (c) Free energy values calculated from the long-time scale kinetic model for each state identified via k-means clustering. Error bars denote 90% confidence intervals.

We observed rapid depletion of the unfused starting state with formation of transient intermediates on the 100-ns time scale. These transient intermediates have a stalk-like conformation similar to that previously proposed as an early fusion intermediate (19–21). On the submillisecond time scale, long-lived hemifusion intermediates dominate; this population decays over a time scale of several microseconds (t_1/2 = 6.3 μs) to yield fully fused vesicles. We find that fusion proceeds via two distinct pathways (Fig. 2) from the stalklike state: rapid formation of a fused state and formation of a metastable hemifused state that slowly decays to form a fused state. The metastable hemifused intermediates that we observed resemble hemifused structures that have previously been suggested as fusion intermediates (22–24) and have been observed experimentally as long-lived intermediates in fusion-impaired systems (24, 25). Recently, a cell-based fusion assay has been shown to produce a large fraction of stable and metastable hemifusion intermediates, thus supporting our computational analyses (26). Our results are consistent with these findings; furthermore the reaction scheme we derive provides a mechanistic explanation for such experimental observations. In our simulations, ≈20% of vesicles rapidly fuse from the stalk state; the others fuse via slow decay of the hemifused population, resulting in a biphasic pattern for completion of the fusion reaction (Figs. 3b and 4d).

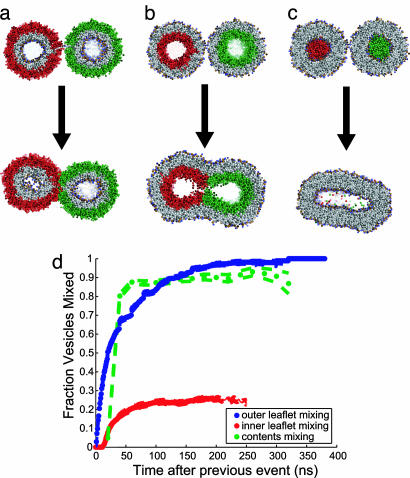
Fig. 4.

Measuring the progress of fusion via analogue to experiment. Progress of the vesicle fusion reaction is assessed via lipid and vesicle contents mixing, as have been measured in experimental assays (23, 28, 29). (a) Mixing of outer leaflet lipids. (b) Mixing of inner leaflet lipids. (c) Mixing of vesicle contents. (d) The fraction of vesicles that have mixed inner leaflet lipids, outer leaflet lipids, and contents, measured for each mixing event as a function of Δt from the time of the previous mixing event. Outer leaflet mixing is rapid and complete, but on the time scale of individual trajectories, only 26% of inner leaflets fuse; the remaining vesicles fuse at a much slower rate, dependent on the decay of off-pathway intermediates. Upon inner leaflet fusion, formation of a fusion pore and contents mixing is again rapid and complete. Dashed lines represent one standard deviation of the mean. Intravasicle lipid mixing between leaflets was observed in <2% of trajectory snapshops (Fig. 13, which is published as supporting information on the PNAS web site).

Our approach also allows the calculation of free energies of fusion intermediates by using statistical mechanics (Fig. 3c), using rates for both forward and reverse reactions (such as blinking of the fusion pore) from our observed trajectories. Free energies are calculated by using the kinetic model derived from these forward and reverse transition probabilities. The energetics of membrane fusion have received considerable attention in the literature (reviewed in ref. 27); the advantages of free energy calculations using an MSM approach are that intermediate states are derived from the reaction and energies are based on molecular interactions from molecular dynamics simulation rather than continuum membrane models. The energies calculated depend on the fusion system being simulated, but this powerful and general approach can be repeated to calculate free energies for any given fusion model. We observe a 3.8 kcal/mol decrease in free energy on formation of the stalk-like state from the starting configuration, consistent with a reaction driven by vesicle crosslinking. The hemifused state is more stable than the stalk-like state (ΔG of −3.3 kcal/mol), whereas the fused state is, as expected, the most stable state, with a ΔG of −6.0 kcal/mol from the stalk-like state and −2.6 kcal/mol from the hemifused state (see Methods). Our clustering of macrostates does not explicitly address pore expansion, as both newly opened and expanded pores cocluster within the fused states. Thus the calculated free energy value for the fused state does not fully reflect the energy of fusion pore expansion, which will be considerable for the fusion of two small and highly curved vesicles.

We have also assessed vesicle fusion by performing computational measurements analogous to experimental fusion assays. Schematized in Fig. 4, these measurements are outer leaflet lipid mixing between vesicles, inner leaflet mixing, and contents mixing, which have been assessed experimentally for vesicle fusion via fluorescence dequenching and FRET assays (23, 28, 29). In full fusion, these mixing events are thought to happen sequentially, as shown in model systems (30) and in our simulations (Fig. 9, which is published as supporting information on the PNAS web site). We have therefore measured the fraction of simulations that have progressed to the next mixing stage as a function of time after the previous stage (Fig. 4d). Because we measure mixing via a threshold for the number of molecules mixed rather than via percent dilution (see Fig. 9), the diffusional processes limiting mixing for a given vesicle geometry will not depend on vesicle size. We observe rapid (t_1/2 = 20 ns) and complete (100% of vesicles) initiation of outer leaflet mixing from the unfused state. Subsequent to outer leaflet mixing, 26% of vesicles rapidly (t_1/2 = 30 ns) progress to inner leaflet mixing; our MSM analyses indicate that essentially all of the vesicles that mix outer leaflets go on to fuse, but on a much slower time scale (τ = 8.9 μs, biexponential fit to Fig. 3b). After the onset of inner leaflet mixing, contents mixing and full fusion are again relatively fast (t_1/2 < 40 ns) and complete (93% of vesicles).

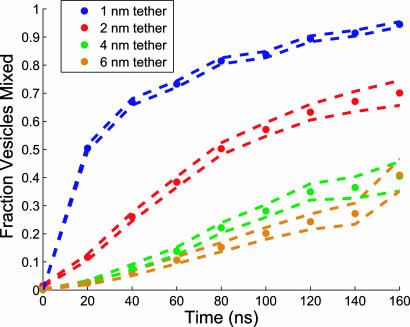
Because lipid mixing calculations provide results in terms of experimental parameters but at higher time resolution than measurable with current experimental techniques, they are especially useful in probing the determinants of membrane fusion. In this manner, we have tested the length of the intervesicle crosslinker required for fusion. Increasing the length of the crosslinker decreases the probability of outer leaflet mixing (Fig. 5) but, once the outer leaflets have mixed, inner leaflet mixing and contents mixing occur with the same rates at all crosslinker lengths (Fig. 10, which is published as supporting information on the PNAS web site). We have also computed MSM simulations for a 2-nm crosslinker configuration corresponding to the minimal predicted width of a prefusion (trans)-SNARE complex; these simulations show formation of the fused state on a 13-μs time scale (Fig. 11, which is published as supporting information on the PNAS web site).

Fig. 5.

Dependence of vesicle fusion rates on crosslinker length. To assess the effect of crosslinker length on vesicle fusion rates, the fraction of vesicles that have mixed outer leaflets is plotted as a function of time for crosslinker lengths of 1, 2, 4, and 6 nm. Simulations with a crosslinker length of 2 nm have a t_1/2 of 80 ns for outer leaflet mixing, compared with 20 ns for simulations with a 1-nm crosslinker. Simulations with crosslinker lengths of 4 and 6 nm remain at <50% fused after 150 ns. Dashed lines represent one standard deviation of the mean.

These results suggest that intermembrane crosslinking (and likely the analogous tethering activity of fusion proteins) are important in initiating formation of stalk-like intermediate structures between highly curved membranes but that membrane crosslinking does not participate in later stages of the fusion reactions, although experiments on fusion protein mutants suggest that the fusion apparatus still promotes fusion at this stage (24, 25). Because both transmembrane domain mutants of both SNAREs and several viral fusion peptides and glycosylphosphatidylinositol-anchored influenza hemagglutinin (24, 25) have been shown to generate long-lived hemifused states, it is likely that the transmembrane regions of fusion proteins decrease the free energy of the fused state, perhaps by affecting lipid organization. Our results, in combination with these experimental findings, highlight the manner in which physiological regulation of fusion may occur via the modulation of the kinetic and energetic balance between fusion intermediates.

Physiologic measurements of vesicle fusion have detected fusion at the submillisecond range (6, 31, 32); however, our simulations suggest that fusion of closely apposed membranes occurs >20-fold faster than these measurements. Factors such as vesicle curvature and lipid composition differ between our model system and physiological fusion and likely modulate fusion kinetics. However, based on our findings, we suggest that the rate-limiting steps in physiological fusion, such as the entry of enveloped viruses and neurotransmitter release, are those leading to the formation of the activated “encounter complex” that comprises our start state rather than the mechanics of fusion itself.

Conclusions

By using powerful MSM simulation techniques, we were able to calculate the reaction kinetics and free energies for membrane fusion in a chemically defined and biologically relevant system. Our simulation design represents a major step forward in sampling accuracy for predicting membrane fusion mechanisms: our simulations feature large (n = 10,000) ensembles of molecular simulations that yield a qualitatively greater degree of information regarding the biophysics of membrane fusion on time scales of physiologic fusion (time scales 1,000-fold longer than previously simulated by molecular dynamics). In addition, our use of a chemical crosslinker begins to capture the requirements for synthetically induced fusion in biological systems.

These advances have made possible calculations of sufficient detail and statistical rigor to address kinetic questions, such as rates and mechanism, in a quantitative and physically based manner. Our simulations provide a systematic, statistically significant, kinetic model of membrane fusion at near-atomic resolution, thus representing a major advancement of computational methodology. We use this model to predict rates for the fusion of two apposed, highly curved membranes after formation of an activated prefusion complex, a key step in membrane fusion that is not directly observable by current experimental techniques. We predict that this reaction proceeds in a biphasic fashion and on a 6- to 9-μs time scale via a branching reaction pathway with a metastable hemifusion intermediate. Previous simulations of fusion have observed multiple fusion pathways (5); our approach adds mechanistic specificity in that we predict fusion via a metastable hemifused intermediate in one instance and rapid fusion directly from a stalk-like state in the other. Furthermore, our MSM simulation approach can be extended to include the simulation of the long time scale behavior of large molecular assemblies in general and specifically the investigation of protein–lipid interactions and explicit models of biological fusion proteins.

Methods

Simulation Setup.

The coarse-grained lipid and water parameter set of Marrink and coworkers (10, 11) was used to model fully hydrated POPE vesicles with coarse-grained explicit water molecules. This parameter set includes explicit representations of electrostatic interactions and polarity (11). Molecular dynamics simulations were performed with GROMACS (33, 34) using simulation parameters as described (10, 11). A 4-fold time scale normalization factor was applied as in previous reports (10, 11); additional validation is presented in Fig. 12, which is published as supporting information on the PNAS web site.

Starting coordinates for individual vesicles were as described (10) with the vesicles then placed ≈1 nm from each other. A crosslinker was formed by a solvent-exposed polar group covalently bonded to the phosphate group of one POPE molecule from the outer leaflet of each vesicle, with an equilibrium interphosphate distance of 1, 2, 4, or 6 nm. One crosslinker molecule was sufficient to induce vesicle fusion in our simulations (Fig. 2).

Computation of Molecular Dynamics Trajectories.

To compute the large number of simulations required for ensemble dynamics, we harnessed the distributed computing power of the Folding@Home project (9). Ten initial simulation runs were used to seed 10,000 independent molecular dynamics runs (Fig. 1b) as follows: 10 400-ns simulations were performed and sampled once at the starting state, eight times at 12-ns intervals, and once at >180 ns to generate 100 sets of starting coordinates. Folding@Home was used to calculate 100 independent molecular dynamics trajectories for each set of starting coordinates, yielding 10,000 total trajectories of up to 500 ns in length (Fig. 1b).

Development of an MSM for Vesicle Fusion.

We built an MSM based on molecular dynamics trajectories as described (7) by sampling the trajectories at 20-ns intervals, clustering the sampled “snapshots” into macrostates according to kinetically relevant criteria, and constructing a transition count matrix A from the trajectory data such that a_ij = count [Tr_k(t) = i, Tr_k (t + Δt) = j], for all trajectories Tr_k and times t, where Tr_k (t) is the state that trajectory k is in at time t and Δt = 20 ns. Lipid and contents mixing were selected as metrics that well capture the reaction coordinates of vesicle fusion, and state clustering was performed in the Euclidean space defined by these metrics. Cluster centroids are listed in Table 1.

The resulting kinetic-state model was tested for Markovian characteristics by comparing transition count matrices calculated from the trajectory data at different time intervals Δt. For any transition probability matrix P(Δt) such that p_ij ≥ 0 and Σ_jp_ij = 1, the likelihood that the matrix P(Δt) is the underlying probability matrix that generated an observed transition count matrix A is proportional to

We can sample transition probability matrices from the likelihood distributions for each time interval. For a Markov process, the following two equations hold:

and

where λ_i are the eigenvalues of the matrix P. We assessed the degree to which the above equations held for these sampled transition matrices by calculating the eigenvalues of each sampled P_s(Δt) for Δt = 20, 40, 60, 80, and 100 ns, and s = 1–50.

We compared these eigenvalues by using a linear fit to the logarithms of the values (Fig. 8a). Because the eigenvalue uncertainty increases with time interval, we used weighted least-squares linear fitting where the weight for each point was equal to the inverse of the variance at that point. We could calculate the degree of eigenvalue linearity as the weighted rmsd from the fitted line to the sampled eigenvalues. The results of this process showed good agreement with the Markovian expectation.

To calculate long-time scale dynamics of vesicle fusion using the kinetic model derived above, we started with all vesicles in the unfused state (the cluster corresponding to the “starting state” for molecular dynamics trajectories as described above): we set the initial state vector v_i(0) = 1 for starting state i, v_j(0) = 0, ∀j ≠ i. The kinetic model was then propagated by using the sampled transition probability matrix as follows: v_s(t + 1) = P_s^T∗v_s(t) for any time t. A matrix K of first-order rate constants may be calculated from the transition probability matrix by the following relation: K = log(P)/Δt. Uncertainties in K and v(t) caused by sampling errors were determined by calculating K_s and v_s(t) for many sampled transition probability matrices P_s at a constant Δt and computing 90% confidence intervals. Other potential sources of uncertainty include misclustering and the degree to which trajectories sample rare transitions.

As an additional test of Markovian characteristics, we calculated mean first passage times (MFPTs) for vesicle fusion by using the sampled transition probability matrices P_s(Δt) for different time intervals Δt. The MFPT between state A and B is defined as the average time taken to move from A state to B. We were interested in the average time to reach the fused states from the unfused state, because it reflects the rate of fusion. In the MSM model, the MFPT has a simple analytic form (7). The following set of linear equations define the MFPT from any state to a given final state (denoted MFPT_F).

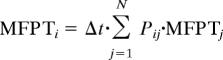For our system, the MFPTs from the unfused state are constant to within sampling error across time intervals (Fig. 8b), lending further confirmation to our Markovian assumption.

Calculation of Free Energies from Ensemble Molecular Dynamics.

The extremely large number of molecular dynamics trajectories that we computed allowed us to calculate free energy values based on statistical mechanics. As our molecular dynamics simulations were performed under NPT conditions (constant number, pressure, and temperature), the appropriate expression for free energy is G = −k_BT ln(Z), where Z is the isobaric-isothermal partition function. For a macrostate (or cluster) M, we can approximate Z as Σ_m∈M/Σ_∀m for microstates m, which is equivalent to the fraction of microstates that are in macrostate M at equilibrium and can be calculated directly from the Markovian transition probability matrix given a starting distribution of macrostates. This calculation is not limited to individual macrostates, and we can also consider the sets of macrostates corresponding to unfused, stalk-like, hemifused, and fully fused vesicles. Error estimation for free energy calculations was performed by resampling the Markovian transition matrix as above to calculate a distribution of partition function values. This method estimates sampling error; an additional source of error derives from misassignment of microstates to macrostates in the clustering process. Because clusters are contiguous in state-space, a small clustering misassignment could result in erroneous measurement of reverse transitions over a boundary. Given a small but nonzero frequency of misassignment, this error becomes a substantial factor only for transitions with very high free energies; the higher the free energy, the larger the effect of a potential misclustering.

Abbreviations

MSM

Markovian state model

SNARE

N-ethylmaleimide-sensitive factor attachment protein receptor

MFPT

mean first passage time

POPE

1-palmitoyl 2-oleoyl phosphatidylethanolamine.