Theoretical model of temperature regulation in the brain during changes in functional activity

Abstract

The balance between metabolic heat production, heat removal by blood flow, and heat conductance defines local temperature distribution in a living tissue. Disproportional local increases in blood flow as compared with oxygen consumption during functional brain activity disturb this balance, leading to temperature changes. In this article we have developed a theoretical framework that allows analysis of temperature changes during arbitrary functional brain activity. We established theoretical boundaries on temperature changes and explained how these boundaries depend on physiology (blood flow and metabolism) and external (heat exchange with the environment) experimental conditions. We show that, in regions located deep in the brain, task performance should be accompanied by temperature decreases in regions where blood flow increases (activated regions) and by temperature increases in regions where blood flow decreases (deactivated regions). The sign of temperature effect may be reversed for superficial cortex regions, where the baseline brain temperature is lower than the temperature of incoming arterial blood due to the heat exchange with the environment. Importantly, due to heat conductance, the temperature effect is not localized to the activated region but extends to a surrounding tissue at rest over the distances regulated by the temperature-shielding effect of blood flow. This temperature-shielding effect quantifies the means by which cerebral blood flow prevents “temperature perturbations” from propagating away from the perturbed regions. For small activated regions, this effect also substantially suppresses the magnitude of the temperature response, making it especially important for small animal brains.

Basic mechanisms underlying global temperature regulation in humans and animals have attracted substantial attention from scientists, and considerable progress has been achieved in this area both in health and disease (see, e.g., refs. 1–4). However, information on brain temperature regulation, especially its relationship to function, is conflicting. Indeed, although, numerous experimental studies have demonstrated changes in the brain temperature of humans and animals upon functionally induced changes in brain activity, the magnitude and even sign of reported temperature changes vary substantially. For example, localized temperature variations from 0.01°C to 0.2°C were observed in animal brains (5–13) under different stimuli (visual, auditory, somatic). As reported in ref. 6, the sign of temperature response to visual stimulation in cats depends on the frequency of flashing light; for low frequencies (2–12 Hz), the temperature increases, whereas at high-frequencies (42–62 Hz) the temperature decreased. Negative temperature changes, on average −0.2°C, were observed in the deep regions of the visual cortex in conscious intact human subjects by a magnetic resonance method (14), whereas positive temperature changes up to 0.15°C were observed during visual stimulation on the human head surface by infrared temperature measurements (12). Also, functionally induced positive temperature changes ranging from 0.04–0.08°C (15) to 0.7°C (16) were detected on the brain surface by means of infrared cameras on surgically operated human subjects after craniotomy and dural opening.

Although the processes responsible for temperature changes during functional brain activity have not been studied systematically yet, previous experimental and theoretical studies have provided important insights. A basic theory of brain temperature changes in functionally activated regions was developed in ref. 14, where these changes were attributed to disproportional increases in blood flow as compared with oxygen consumption during changes in brain functional activity, an effect observed previously (17). Accordingly, in the absence of heat exchange with the surrounding nonactivated regions, the local temperature within the activated region decreases as the cooling effect of elevated blood flow exceeds the heating effect of increased oxygen metabolism. Experimental measurements (14) in the visual cortex of humans were consistent with this prediction.

Whereas under normal physiological conditions tissue temperature in the deep brain regions is expected to be higher than the temperature of arterial blood, the situation can be inverted near the brain surface due to the heat exchange with the environment (18–20). Quantitatively, this phenomenon is regulated by the “temperature-shielding effect of blood flow” (20, 21) that quantifies the means by which cerebral blood flow (CBF) prevents “extracranial cold” from penetrating deep brain structures. Although brain insulation by cerebrospinal fluid, skull, scalp, and hair is also important (see detailed discussion in ref. 20), these effects are especially significant in small animals and/or in case of exposed brain, where direct intraoperative temperature measurements (15, 22–25) demonstrated that the superficial brain temperature is lower than the deep brain temperature by several degrees. A computer model of temperature changes in the human calcarine fissure during functional activation (26) predicted that the temperature changes in this structure could be both positive and negative, depending mostly on the distance from the brain surface. The fact that the sign of temperature response to functional brain activation depends on the tissue/arterial blood temperature differential was recognized previously (6); it was demonstrated that the task-induced temperature response changed its sign (from positive to negative) after the brain tissue had been artificially heated and the baseline temperature became higher than the arterial blood temperature. This result is important for understanding temperature response to changes in brain activity.

Despite all this progress, a number of important questions still remain unanswered: What are the major parameters determining brain temperature changes during functional activation? How localized is the temperature change with respect to the activated region? How do temperature effects depend on the shape and position of the activated region in the brain? And what are the physiological limits of temperature changes during functional activation? These and other questions are addressed in the current paper. Recently, substantial attention was drawn to the fact that, during changes in functional activity, some regions of the brain actually exhibit decreases in activity (decreases in blood flow) or deactivations (27, 28). Possible temperature responses in deactivated regions will also be studied herein. Although our analysis deals mostly with the human brain, we also tackle the problem of brain temperature distribution in small animals and discuss how brain size and condition (awaked vs. anesthetized) affect the temperature response to changes in functional activity. We show that the small brain size favors positive temperature responses, especially under anesthesia. However, the small size of activated regions results in substantial suppression of the magnitude of this effect.

Theoretical Approach

The major mechanisms contributing to brain temperature regulation are metabolic heat production, heat removal by blood flow, heat conductance, and heat exchange with the environment. The balance between these factors defines temperature distribution in the brain. Functionally induced local changes in the regional blood flow and metabolic processes might upset this balance and lead to changes in the brain temperature.

Whereas the blood flow response is relatively fast and usually requires only several seconds, the brain temperature response should be much slower because it depends on the rate of “heat delivery” by blood flow, F. A characteristic time constant is t_T = c_T/(ρ_bc_bF) (14), where ρ_b is the density of blood, and c_t and c_b are the specific heat of tissue and blood, respectively. For normal human subjects and small animals, this time is on the order of tens of seconds, which is in agreement with experimental findings that the maximal temperature response during visual stimulation was reached in ≈40–60 sec and then was maintained for the duration of stimulation (6). A similar result was obtained recently in a rat model (13), in which the maximal temperature change was achieved ≈1 min after the stimulation onset. Here we consider only temperature distributions in a steady state (activated or deactivated).

It is convenient to classify possible “temperature responses” to changes in brain activity based on the general concept of a physiologically defined baseline state (28). The main feature of this baseline state (achieved when normal subjects rest quietly but awake with eyes closed) is the relative uniformity of the oxygen extraction fraction (OEF) across the brain, despite significant differences in the blood flow and oxygen consumption in different brain regions (29, 30). As shown in ref. 14, in the absence of heat exchange with the surrounding tissue and the environment, the heat balance between heat generation by metabolic processes and heat removal by blood flow results in the brain temperature T_b exceeding the arterial blood temperature T_a by the quantity T_m, which depends on the OEF:

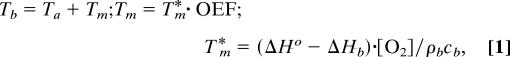where ΔH^o = 470 kJ/mol of O₂ is the enthalpy of the net chemical reaction of oxygen and glucose (31), ΔH_b = 28 kJ is the energy used to release oxygen from hemoglobin (32), and [O₂] is oxygen concentration in arterial blood. Thus, brain temperature is expected to be higher than that of arterial blood by the “metabolic temperature shift” T_m (MTS). By using numerical values of the parameters known from literature, c_b = 3.8 J/(g·°C), ρ_b = 1.05 g/cm³, [O₂] = 8 μmol/ml (a typical oxygen concentration in arterial blood), OEF = 40%, one obtains under normal physiological conditions T_m = 0.36°C. This quantity is in good agreement with experimental data (8, 33). The uniformity of the OEF in the resting state leads to the uniformity of the baseline temperature (temperature in the resting state) in the deep brain regions. Small local variations in the OEF [global-to-local ratio varies from 0.887–1.01 (28)] could lead to variations in the baseline brain temperature with an amplitude of ≈0.1°C.

Upon changes in functional activity, OEF changes: OEF → OEF′ (hereafter, all “primed” parameters correspond to the activated or deactivated state). Therefore, according to Eq. 1, the local brain temperature should also change. Assuming that the temperature of arterial blood does not change, we get:

As blood flow increases in activated regions to a larger extent than the oxygen consumption, the OEF decreases (17), leading to local decreases in brain temperature (14). In deactivated regions, the OEF increases (28), and brain temperature should increase.

The above consideration, however, accounts only for the local heat balance within an activated (or deactivated) region. Due to the heat conductance, any local temperature change leads to temperature change in the surrounding tissue as well. It is also important that the inhomogeneity of temperature distribution takes place not only upon changes in functional activity but is characteristic to the baseline temperature even in the resting state; the uniformity of the baseline temperature distribution is broken near the brain surface due to the heat exchange with the environment (18–20). These effects are important because they can alter brain temperature response to functional activation (26).

To incorporate heat conductance within the brain and heat exchange with the environment, we use an approach based on a static bio-heat equation originally proposed by Pennes (34) for description of the temperature distribution in organs. We present this equation in the following form, specific for the brain:

where T = T(r) describes the temperature distribution in the brain as a function of position r, K is tissue thermal conductivity. The second term in Eq. 3 describes heat generated by metabolic processes and is determined by the local blood flow F, oxygen concentration [O₂] in blood, and OEF (14):

where ρ is the tissue density. The third term in Eq. 3 represents the heat removed by blood flow. Under the assumption that the blood temperature equilibrates with the tissue temperature in the capillary bed (34), this term is proportional to the temperature difference between arterial blood, T_a, and brain tissue, T:

If heat conductance is ignored, the first term in Eq. 3 vanishes, and the equilibrium temperature obtained from Eq. 3 coincides with that obtained previously (Eq. 1).

As demonstrated in ref. 20, the problem of temperature distribution in the brain can be substantially simplified by the following consideration. According to Eq. 3, any temperature inhomogeneities in the brain have a characteristic length Δ depending on the blood flow F:

Typically, Δ is approximately several millimeters. For large animals that have head diameter of several centimeters or higher (this includes adult humans, diameter of ≈15 cm; neonates, diameter of ≈6 cm; most primates, etc.), the temperature distribution near the brain surface can be treated as a one-dimensional problem, temperature depending only on the distance from the brain surface. This consideration leads to the temperature in the resting brain T₀(r) (baseline for our problem) being (i) practically homogeneous except for a narrow (≈Δ) region in the vicinity of the brain surface and (ii) practically independent of specific brain geometry. Indeed, numerical calculations of T₀(r) for adult and neonatal head (18, 19) clearly demonstrate that T₀(r) is nonuniform only near the brain surface.

Within the brain, the characteristic length Δ defines the extent of the area, surrounding any specifically defined region of altered blood flow or heat generation, in which a substantial temperature change can be observed. Outside this area, the temperature distribution in the brain remains practically unchanged. The genesis of the “temperature shielding effect” resides in the efficient removal by CBF of heat diffusing in the tissue due to temperature gradients. The existence of such a “shielding effect” allows a crucial simplification (from a mathematical point of view) of the problem of temperature distribution in the brain; for any local perturbation in blood flow or heat generation, there is no need to analyze the temperature distribution across the whole brain (which can be done only numerically and requires a very complicated computer modeling; see, e.g., ref. 26). Instead, the analysis can be restricted to a small area surrounding such an altered-flow region (AFR). For instance, if an AFR is located deep in the brain (at a distance from the surface much larger than Δ), surface effects can be neglected and temperature changes will take place only in the AFR and surrounding tissue at a distance of ≈Δ. However, if an AFR is located at the brain surface, the temperature distribution is expected to be changed only at a distance on the order of Δ from the surface. Note that the existence of the shielding effect also leads to a very important conclusion: Any small details of brain structure (smaller than the characteristic size Δ) are practically “invisible” from the temperature distribution point of view (see section Results).

During changes in functional activity, blood flow and oxygen consumption change in one or another region of gray matter (GM) that might be located either in cerebral cortex or within GM nuclei. Our analysis shows that the most important geometrical parameters defining temperature changes during changes in functional activity are the distance from the brain surface and the size of the AFR, with the specific shape of the latter playing a secondary role. In what follows, we analyze the task-induced temperature response for two different locations of AFR: a deep-brain located AFR and an AFR in the superficial cortex. The aforesaid blood flow-induced shielding effect leads to a significant simplification of mathematical modeling in these cases and allows a rather simple analytical solution to the problem.

Results

To analyze brain temperature response to changes in functional activity in deep GM nuclei, we use a model in which an AFR is mimicked by a sphere of radius R. The distance from the brain surface is assumed to be substantially larger than Δ, therefore surface effects (heat exchange with the environment) can be ignored. Blood flow and the OEF within the AFR are denoted F_i and OEF_i, respectively. In surrounding tissue, these parameters are F_e and OEF_e. In this model, the temperature distribution depends only on the distance r from the center of the AFR:

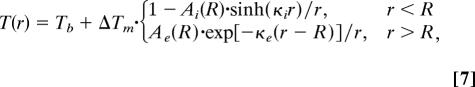where ΔT_m = T_mi − T_me, T_mi = OEF_i·T_m*, and T_me = OEF_e·T_m* are the metabolic temperature shift within and outside the AFR, parameters κ_i,e = (ρF_i,eρ_bc_b/K)^1/2 represent inverse characteristic lengths: Δ_i = κ_i⁻¹ and Δ_e = κ_e⁻¹ (see details and definition of coefficients A_i,e in Supporting Text, which is published as supporting information on the PNAS web site).

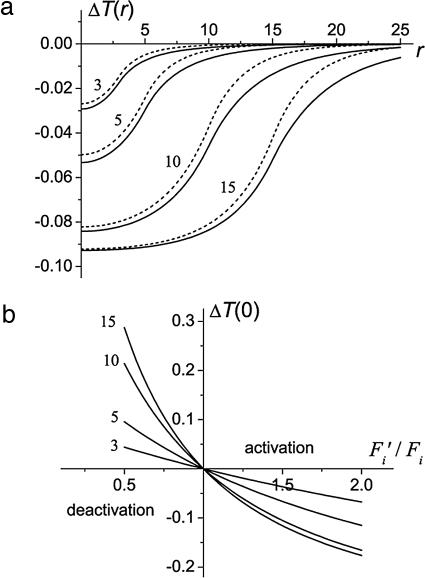
Eq. 7 allows analysis of the changes in the brain temperature distribution under arbitrary variations in local blood flow and oxygen consumption. In the analysis that follows we use some typical values of resting state CBF: F_W = 3.8·10⁻³ ml/(g·sec) in white matter (WM) and F_G = 11.2·10⁻³ ml/(g·sec) in GM. For these values of CBF and K = 5·10⁻³ W/(cm·°C) (35) (other typical values of the parameters used for calculation are given above; see also Table 1, which is published as supporting information on the PNAS web site), the characteristic length in WM, Δ_W = 6.2 mm is approximately two times longer than that in GM, Δ_G = 3.6 mm. We consider two different situations: (i) a small AFR of GM lies completely within a WM structure; in this case, blood flow in resting state is different inside and outside the AFR, F_i = F_G, F_e = F_W; and (ii) the AFR is a small GM region surrounded by GM, in this case, blood flow in resting state is the same inside and outside the AFR, F_i = F_e = F_G. Fig. 1a illustrates changes in the temperature distribution in the activated region for these cases. The temperature change at the center of the AFR, ΔT(0), as a function of the ratio F′_i/F_i for different R is shown in Fig. 1b. The intervals F_i′/F_i > 1 and F_i′/F_i < 1 correspond to the activation and deactivation, respectively. It is important to note that the sign of temperature change in the AFR is opposite to the sign of blood flow change; blood flow increases cause temperature decreases and vice versa.

Fig. 1.

Temperature change in the deep brain AFR. (a) The distribution of temperature change, ΔT(r) = T(r) − T_b (in °C) (r, distance from the center of AFR in millimeters) at F_i′ = 1.5·F_i, q′_i = 1.1·q_i for different R. Solid and dashed lines correspond to the following cases: (i) AFR of GM surrounded by WM and (ii) AFR of GM surrounded by nonactivated GM. (b) ΔT(0) (in °C) as a function of the ratio F_i′/F_i for q′_i = q_i for different radii of the AFR, R (numbers next to the curves are in millimeters). The default values (see Table 1) of other parameters are assumed.

For the AFRs located in the superficial cortex, heat exchange with the environment should be taken into account. In this case, the temperature distribution in the cortex and surrounding regions is inhomogeneous not only upon changes in functional activity but when already at rest. The thickness of the adult human cortex is ≈2–3 millimeters, which is comparable with the characteristic length Δ, whereas the typical surface extent of the AFR may be several centimeters. Accordingly, an AFR in the cortex will be modeled by a “flat” model, assuming that its thickness d is much smaller than its surface extent. In this case, the temperature distribution can well be described as one-dimensional. For this flat model, the temperature depends only on the coordinate z normal to the brain surface:

Details and definitions of coefficients B_i,e are given in Supporting Text. These coefficients depend on the ambient temperature T_ext and the “effective” heat transfer coefficient h, accounting for an insulation of the brain from the environment by intermediate layers of cerebrospinal fluid, skull, and scalp (20). In the resting state, when metabolic temperature shifts in GM and WM are the same, T_mi = T_me, Eq. 8 describes the baseline temperature distribution, (T₀(z) − T_b) ∼ −exp(−κz).

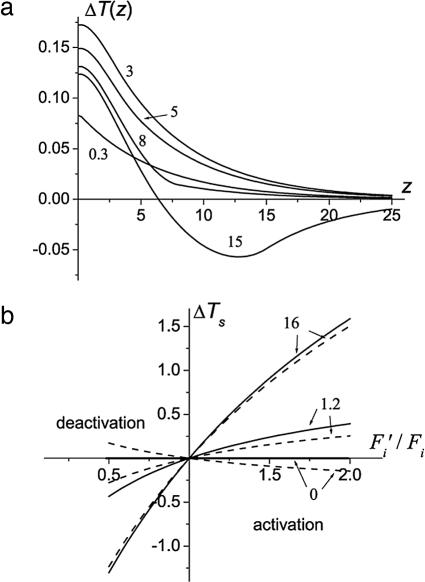
The spatial distribution during changes in brain activity ΔT(z) − T₀(z) is shown in Fig. 2a for F_i′ = 1.5·F_i, q′_i = 1.1·q_i and different thickness (d) of the AFR. For a typical cortex thickness of ≈3 mm, the temperature increase upon activation is monotonic and has a maximum at the brain surface. The behavior is similar for a thicker AFR, up to d ∼ 1 cm. However, for d = 1.5 cm, it becomes nonmonotonic: ΔT(z) is positive at small z and negative for larger z. Such a behavior is similar to that obtained in ref. 26 by means of computer simulations for the model of functional activation in the human visual cortex.

Fig. 2.

The temperature change in the cortex-located AFR. (a) ΔT(z) = T(z) − T₀(z) (in °C; z in millimeters) for different thicknesses d (numbers next to the curves are in millimeters) of the AFR; F_i′ = 1.5·F_i, q′_i = 1.1·q_i and the default values of other parameters (see Table 1). (b) ΔT_s (in °C) as a function of the ratio F_i′/F_i for different values of the effective heat transfer coefficient [numbers next to the curves are in 10⁻³ W/(cm²·°C)] for OEF′_i = OEF_i (solid lines) and q′_i = q_i (dashed lines).

In Fig. 2b we plot the temperature change at the brain surface, ΔT_s, as a function of the ratio F_i′/F_i in two extreme (from the physiological point of view) cases: (i) the oxygen consumption in the AFR is unchanged upon changes in functional activity (dashed lines), q′_i = q_i (correspondingly, the OEF is changing inversely proportional to the blood flow, OEF′_i/OEF_i = F_i/F_i′); (ii) the OEF remains unchanged (solid lines), OEF′_i = OEF_i (the oxygen consumption is changing proportionally to blood flow, q′_i/F_i′ = q_i/F_i). The curves are presented for h = 0, h = 1.2·10⁻³ W/(cm²·°C) (this value is typical for the human brain, and hereafter will be considered the default value), and h = 16·10⁻³ W/(cm²·°C). The latter case can be anticipated with the brain exposed to the environment, where h can be very high due to the evaporative contribution. Note that ΔT_s is greater in the case when the OEF does not change. In fact, the area between the solid and dashed lines (for a given h) provides the interval of possible temperature changes.

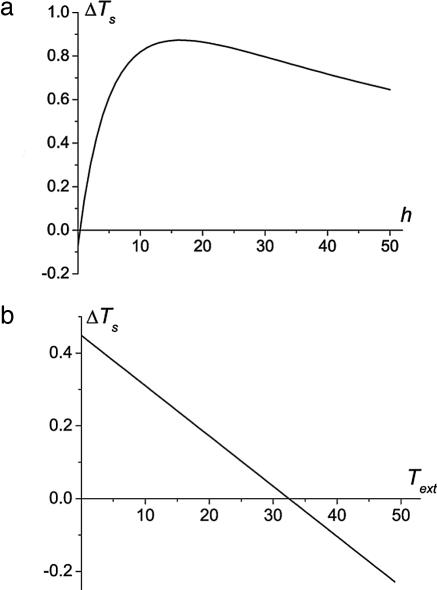
The temperature change in the cortex-located AFR strongly depends on h and T_ext. The dependencies of ΔT_s on these parameters are shown in Fig. 3.

Fig. 3.

ΔT_s as a function of the effective heat transfer coefficient h [in 10⁻³ W/(cm²·°C)] (a) and of the ambient temperature T_ext for F_i′ = 1.5·F_i, q′_i = 1.1·q_i (b). The default values of other parameters and d = 3 mm are assumed.

Discussion

Numerous findings suggest that even small temperature changes in the brain may play an important role in brain function. For instance, it is well appreciated that temperature substantially affects the affinity of hemoglobin for oxygen [blood oxygen saturation level, sO₂, may change by several percent per 1°C (36)], and the rate of chemical reactions [the average van’t Hoff temperature coefficient in the brain, Q₁₀, is 2.3 (1)]. The latter effect is especially pronounced for the activation rate of heat-evoked membrane currents [Q₁₀ up to 25.6 (37)]. It was reported that small temperature variations could have profound effects on brain integrative functions by affecting protein geometry, protein assembly, and alterations in protein expression (38, 39). Another interesting recent finding reveals dramatic changes in spine number on mature hippocampal dendrites with alterations in temperature (40). All these data indicate that changes in the brain temperature may play an active role in brain functioning and can possibly shed a light on the still unexplained fundamental discovery that the blood flow to activated regions of the normal human brain increases substantially more than the oxygen consumption (17).

According to the default mode concept of brain function in the resting state (28) and the relationship between brain temperature and OEF (14), the baseline temperature in the deep brain is uniform and exceeds the arterial blood temperature by the metabolic temperature shift determined by the OEF (≈0.3–0.4°C in humans). During changes in functional activity in deep brain regions, the temperature change ΔT depends on the change in the OEF within the AFR. If blood flow and oxygen consumption increase or decrease proportionally, their ratio and the OEF remain unchanged, and ΔT = 0. The maximal temperature effect is reached in the extreme (from a physiological point of view) case when blood flow changes, whereas oxygen consumption (and, as a result, heat generation) remains unchanged. The assumption that the fractional change in blood flow is always greater than the change in oxygen consumption leads to the conclusion that the sign of temperature change is always opposite to the sign of blood flow change; when blood flow in the activated region increases, the temperature decreases, whereas when blood flow in deactivated region decreases, the temperature increases.

The maximal temperature change achieved at the center of the AFR crucially depends on its size, R. If R ≈ Δ_i (Δ_i ∼ 3–4 mm in the normal human brain), the temperature only slightly deviates from T_b. For an AFR of a large size (R ≥ Δ_i), the temperature at the center becomes independent of the region’s size and parameters of the surrounding tissue and is defined by Eq. 2. Under the normal physiological conditions, ΔT(0) ≈ (OEF_i − OEF′_i)·0.9°C. Hence, the temperature changes by ≈0.1°C for each 10% change in the OEF.

A profoundly different picture of the temperature response to changes in functional activity is expected in regions located in the superficial cortex. Due to the heat exchange with the environment, the baseline temperature distribution is inhomogeneous, the characteristic length of this inhomogeneity being determined by blood flow in the cortex. This characteristic length changes during an increase in functional activity and ΔT ≠ 0, even if the OEF remains unchanged. Furthermore, the temperature response in the cortex-located regions depends considerably on the ambient temperature T_ext and the effective heat transfer coefficient h.

For sufficiently high h [including the default value h = 1.2·10⁻³ W/(cm²·°C)], the magnitude of the surface temperature change increases with blood flow increases. The predicted increase of local temperature in the AFRs located in the superficial brain cortex (rather than decrease for the deep brain regions) has a simple explanation. Deep in the brain, due to metabolic heat generation, the baseline brain temperature T_b is higher than the arterial blood temperature T_a, T_b = T_a + ΔT_m > T_a, i.e., blood flow plays the role of brain cooler. As a result, an increase in blood flow in activated regions cools the brain more efficiently, leading to decreases of the brain temperature. Whereas in the superficial cortex, the baseline brain temperature near the surface can be lower than T_a, hence blood flow plays the role of a brain heater. Oxygen consumption resulting in metabolic heat generation always “works” as a heater. Hence, in deep brain, an increase in blood flow and in metabolic heat generation upon functional activation work in opposite directions, with flow being dominant, leading to brain cooling. In the superficial cortex, however, both the contributions work in the same direction, increasing brain temperature in activated regions.

For the default value of h, the task-induced temperature change in the superficial cortex is several tenths of degree Centigrade, whereas for higher h it can reach several degrees Centigrade. This result explains why most of the animal and human data obtained on the exposed brain show an increase in brain temperature during functional activation. However, for sufficiently small h (poor heat exchange with the environment), ΔT is predicted to be negative in the activated region (and positive in the deactivated region). In the limit of no heat exchange with the environment, h = 0, the baseline temperature distribution in surface regions of the brain is homogeneous, and T₀(z) = T_b > T_a, as in the case of deep-located activated regions; hence, a decreased temperature should be expected in activated regions and increased in deactivated regions with the amplitude of temperature change that cannot exceed ΔT_m.

For normal environmental conditions and typical changes in blood flow and oxygen consumption in the AFR (Fig. 3a), the temperature change on the brain surface may achieve a maximum of 0.85°C at a rather high value of the effective heat transfer coefficient, h ∼ 1.6·10⁻² W/(cm²·°C). This result is in a good agreement with an experimentally observed temperature increase of 0.7°C during prolonged functional activation (16), where temperature was measured by means of infrared technique on the brain surface after craniotomy and dural opening. Obviously, in this experimental situation, heat exchange with the environment is extremely high both due to the direct brain exposure and, most importantly, due to the evaporative contribution. Infrared study of functionally induced (5-sec light flashing) temperature changes on the surface of the intact human head (12) revealed substantially smaller ΔT (0.08–0.14°C). The difference can be explained by the short duration of the stimulus (much shorter than the time needed to achieve a stationary temperature distribution, which is approximately tens of seconds) and also the nature of measurement (head surface vs. brain surface). Note also that, in another infrared study (15), observed temperature changes (0.04–0.08°C) on the surface of the exposed brain during functional activation were much smaller than those in ref. 16. The discrepancy between these experimental findings may be associated with differences in stimuli duration and possibly with different air conditions in operating facilities because the heat transfer coefficient substantial depends on the ambient humidity.

Another important parameter affecting the thermal response in functionally AFRs in the superficial cortex is the ambient temperature T_ext. If T_ext is lower than a certain threshold (see Fig. 3b), there is a region near the surface where the baseline temperature is lower than T_a. Hence, within this interval, blood plays the role of a heater, and temperature increases in activated regions and decreases in deactivated regions. However, if T_ext exceeds this threshold, such an interval disappears (or becomes too small), and the temperature response is inverted; temperature decreases in activated regions and increases in deactivated regions.

Experimental results (e.g., refs. 41 and 42) suggest that, during changes in functional brain activity, the size of the AFR is usually larger than the size of the neuronal activity region. As we have demonstrated here, the spatial region, in which the temperature is changing during changes in functional activity, is even bigger than AFR; it extends over the characteristic length Δ_e into the surrounding tissue. This result is in accordance with the computer simulations (26). Because WM has slower blood flow and correspondingly longer characteristic length, it is affected by temperature changes in the AFR to a greater extent than GM.

The previous estimates are based on the brain size and CBF typical for adult humans. Despite the differences in brain dimension and in some of the anatomical structures between human and other mammals, the vascular networks supplying the brain have great similarities providing a dense blood flow distribution throughout the brain. From this point of view, the theory introduced here is broadly applicable. It should be pointed out, however, that some differences of vascular structures compared between the brain of animals and humans may change the thermal parameters used in the theoretical model. One such example is a carotid rete, a compact network of intertwined arteries that lies within a venous lake. It has been found in cat, sheep, goat, ox, and pig, but not in human, rabbit, or rat brains (43). The carotid rete allows constant heat exchange between incoming arterial blood and outgoing venous blood, which leads to a lower incoming arterial blood T_a than that of the body core temperature T_body. However, the carotid rete is located only in the initial region of the brain’s arterial supply; it should not change the temperature distribution and the theoretical model discussed in our study.

However, the size of the brain may play an important role in the temperature response to changes in the brain functional activity. In small awake animals, such as rats and mice, due to higher blood flow the characteristic length Δ determining the region where the baseline temperature is nonuniform is ≈1–2 mm. Because this characteristic size is usually bigger than the size of AFR in small animals (≈1 mm or smaller), the task-induced temperature response may be substantially suppressed due to the heat exchange with the surrounding tissue. That is why most experiments on small animals have revealed rather small local changes in brain temperature upon changes in functional activity. The situation can be dramatically different under anesthesia when the blood flow may be much lower than in the awaked state, and the characteristic length becomes bigger (3–4 mm). Because this characteristic length is comparable with the size of small animal brain, the baseline temperature distribution may become inhomogeneous across the whole brain and can lead to significant global baseline temperature decreases in the entire brain (25). This effect can be exaggerated if the brain is exposed to the environment. In this case, a substantially stronger positive temperature response to functional activation can be expected with a character of temperature changes similar to that in the superficial cortex of humans.

In the above discussion, we considered a local temperature changes due to local changes in functional activity. It should, however, be noted that there is another type of brain temperature changes, namely global changes caused by an increase (or decrease) in the temperature of arterial blood, which can result from global changes in the body temperature. Significant brain temperature changes of such a type were observed, for instance, during feeding, sleeping, after cold saline injection, or anesthesia in the monkey (8). A similar temperature response was also observed in rats under strong changes in environmental conditions, such as exposure to various stressful, emotionally arousing stimuli (44–46). Such strong and lasting external stimuli lead to temperature increases not in a small portion of the brain but across the whole brain. Corresponding changes in arterial blood temperature can be readily incorporated in the above-derived equations.

Conclusion

An analytical theory of task-induced brain temperature regulation is developed, making it possible to predict local temperature responses upon changes in functional activity in both activated and deactivated regions of the brain. The temperature effect substantially depends on the relationship between changes in the blood flow and oxygen consumption. Also, the size and the position of the AFR influence the temperature change in the brain both quantitatively and qualitatively. The temperature change reaches the maximal magnitude for large AFRs and may become negligible for small AFRs. We demonstrate that the temperature effect is not localized to the AFR only; surrounding tissue at rest is also affected by the temperature changes. Due to the shielding effect of blood perfusion, the extent of these affected regions is on the order of the characteristic shielding length Δ. For the AFR located in the deep brain, the maximal temperature change is achieved at the center of the region and depends only on the task-induced change in the OEF, the temperature change being negative in activated regions and positive in deactivated regions. The situation is substantially different for changes in functional activity in the superficial cortex, where the sign of temperature change can vary with distance from the brain surface and depends not only on changes in blood flow and oxygen consumption but is crucially determined by the effective heat transfer coefficient and the ambient temperature. In small animals (especially under anesthesia), the shielding length can be on the order of the brain size leading to a substantial body/brain temperature differential, temperature inhomogeneity, and consequently a possible strong positive response to changes in functional activity.

Abbreviations

AFR

altered-flow region

CBF

cerebral blood flow

GM

gray matter

OEF

oxygen extraction fraction

WM

white matter.