Abstract
Extreme animal movements are usually associated with a single, high-performance behavior. However, the remarkably rapid mandible strikes of the trap-jaw ant, Odontomachus bauri, can yield multiple functional outcomes. Here we investigate the biomechanics of mandible strikes in O. bauri and find that the extreme mandible movements serve two distinct functions: predation and propulsion. During predatory strikes, O. bauri mandibles close at speeds ranging from 35 to 64 m·s−1 within an average duration of 0.13 ms, far surpassing the speeds of other documented ballistic predatory appendages in the animal kingdom. The high speeds of the mandibles assist in capturing prey, while the extreme accelerations result in instantaneous mandible strike forces that can exceed 300 times the ant’s body weight. Consequently, an O. bauri mandible strike directed against the substrate produces sufficient propulsive power to launch the ant into the air. Changing head orientation and strike surfaces allow O. bauri to use the trap-jaw mechanism to capture prey, eject intruders, or jump to safety. This use of a single, simple mechanical system to generate a suite of profoundly different behavioral functions offers insights into the morphological origins of novelties in feeding and locomotion.
Keywords: biomechanics, evolutionary origins, feeding, locomotion
Multifunctional morphology is an ubiquitous theme in biology. Evolutionary tradeoffs, evolutionary origins, and higher rates of lineage diversification all have been attributed to this fundamental feature (1–6). Evolutionary novelty is widely thought to arise when existing structures are co-opted for shared or novel functions (3, 7, 8). Examples range from feathers, which aid in both thermoregulation and flight, to bird beaks, which facilitate both feeding and sound production. One relatively unexplored and surprising example of multifunctionality is found in the extremely rapid mandible strikes of trap-jaw ants (Fig. 1).
Fig. 1.
Trap-jaw ants control the explosive release of stored energy through a combination of sensitive trigger hairs on the mandibles and an internal latch mechanism (9, 10). (a) A dorsal view of an O. bauri worker with mandibles cocked in preparation for a strike. (b) Left and right mandibles showing the dorsal surfaces (Upper) and leading edges (Lower). (Scale bar: 0.5 mm.)
Trap-jaw ants are best known for phenomenally fast predatory strikes during which they fire their mandibles over very short timescales (9, 11). Yet some biologists also have observed trap-jaw ants using their mandibles for propulsion, specifically to jump or physically expel small intruders (12). Although the use of the mandible strike for prey-capture is widely accepted, natural history observations of mandible propulsion have stimulated discussions as to whether the jumps are the results of accidental mandible firing or intentional behaviors used for body propulsion (12, 13). In one of the few experimental studies of this phenomenon, Carlin and Gladstein (13) documented Odontomachus ruginodis using mandible strikes in a defensive behavior, specifically to eject ant intruders away from the nest entrance. However, no subsequent studies, to our knowledge, have visualized and analyzed the mechanics of these propulsive movements, particularly the use of the mandibles for self-propulsion. Furthermore, the mandibles close over such short timescales that previous studies were unable to visualize a complete strike using available imaging technology (9, 11).
Here we examine the biomechanical interface of the extremely fast predatory mandible strikes of trap-jaw ants and their use in body propulsion. Through high-speed imaging, mechanical analyses and behavioral observations, we show that the predatory strikes of Odontomachus bauri generate such extreme accelerations that these ants can and do use their mandibles in a novel mode of body propulsion. In addition, we provide complete visualizations of jaw propulsion mechanics and mandible strike kinematics, which have not been reported previously. The goals of this study were as follows: (i) to calculate the kinematics and force generation of trap-jaw strikes; (ii) to use high-speed videography to determine the behavioral context of jaw propulsion; and (iii) to analyze the mechanics and aerial trajectory of ballistic jaw propulsion as a novel mode of locomotion.
Results
Mandible Strike Kinematics.
During trap-jaw strikes, the mandibles closed with remarkable speeds and accelerations. Closing speeds averaged 38.4 m·s−1 (SD ±7.5) with peak speeds ranging from 35.5 to 64.3 m·s−1. All of the strikes generated accelerations on the order of 105 × g, and peak angular velocities ranged from 2.85 × 104 to 4.73 × 104 rad·s−1. The average duration of a strike was 0.13 ms (SD ±0.05) with a minimum observed duration of 0.06 ms.
With high-resolution video images, we observed asynchronous movements of the mandibles. In all strikes, the left and right mandibles closed sequentially, with one mandible following the other after an average delay of 0.05 ms (SD ±0.02) (Fig. 2). Most individuals did not preferentially start with one particular mandible. The average strike duration of the first mandible was 0.13 ms (SD ±0.02); that of the second mandible was 0.12 ms (SD ±0.03). The second mandible, on average, closed 5 m·s−1 faster than the first mandible. The durations and speeds of the first and second mandibles were not significantly different when compared within strikes using a t test (P > 0.05).
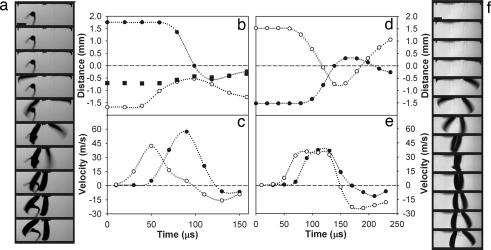
Fig. 2.
The high-speed kinematics of trap-jaw strikes. (a) High-speed video images show a typical strike when an object is between the mandibles (20 μs between each frame). (b) The first mandible to move in a (open circles) strikes an object (filled squares, scaled to size) and pushes it toward the second mandible (filled circles). Zero represents the midline of the ant. (c) The second mandible to fire (a and b) (filled circles) attains a higher velocity than the first mandible (open circles). Movement opposite to the original direction of the strike is represented as negative velocity. (d) Corresponding to the images of an unobstructed strike (f), the first mandible to fire (open circles) scissors past the second (filled circles) as they cross the midline (at zero). (e) Corresponding to f, the second mandible to fire achieves a slightly higher velocity. (f) High-speed images show an unobstructed strike (20 μs between each frame). (Scale bars: 0.5 mm.) See Movie 1, which is published as supporting information on the PNAS web site.
Both mandibles decelerated before reaching the midline, meaning that maximal force generation occurs before the mandibles cross. The first mandible typically began to decelerate 25° from the midline (SD ±25; n = 13 strikes across 7 individuals). The second mandible began to decelerate at 28° before crossing the midline (SD ±18; n = 23 strikes across 7 individuals). The mandibles were ≈0.5 mm from the midline at the onset of deceleration. Thus, a prey item would experience maximal force if it was wider than 1 mm in the plane of the mandible’s movement (Fig. 2).
By modeling the mandibles as simple beams rotating around a fixed point, we calculated that the average instantaneous strike force of a single mandible was 47 mN (SD ±12); maxima ranged from 51 to 69 mN. Therefore, a single mandible could potentially generate a force that is 371–504 times the ant’s body weight.
Jaw Propulsion Behavior.
We observed two distinct mandible strike behaviors in O. bauri that resulted in the ballistic propulsion of the ants’ bodies (see Movies 2–5, which are published as supporting information on the PNAS web site). The most frequently observed behavior consisted of simultaneous attack and body propulsion, previously termed the “bouncer defense” (13) or “retrosalience” (11) (Figs. 3 and 4). In these cases, the ants, either alone or as a group, approached a large intruding object, struck it, and simultaneously propelled themselves away from the intruder. We also observed cases in which a smaller intruder (another ant or small spider) was attacked, and both the ant and intruder were propelled away from each other. The initial stages of these bouncer defense jumps followed a stereotypical series of behaviors (Fig. 3) similar to those observed in previous studies of predatory mandible strikes (14, 15) and defensive attacks against intruders (13).
Fig. 3.
Bouncer defense and escape jumps are characterized by distinct head orientations during mandible firing. (a) In a bouncer defense jump (see Movie 2), an ant approaches an “intruder” (plastic strip outlined in gray at 0.00 ms) with its jaws cocked and open. The jaws are then closed against the intruder (0.67 ms), propelling the ant’s head and body upward (1.33 and 5.00 ms, respectively). (b) In an escape jump (see Movie 3), an ant aligns its cocked jaws perpendicularly to the substrate (0.00 ms). When it strikes (0.33 ms), the head and body are propelled upward (0.66 and 4.33 ms, respectively). (Scale bars: 1 cm.)
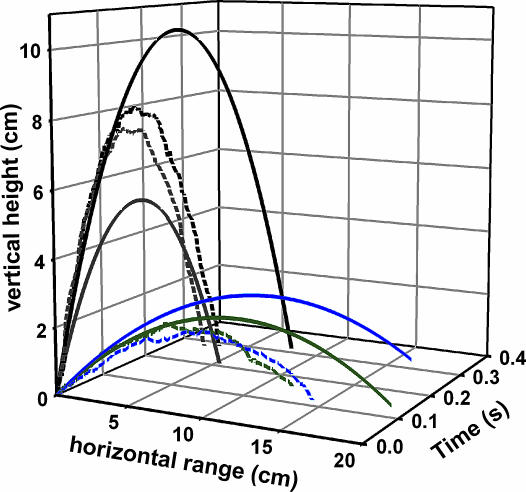
Fig. 4.
The predicted and observed trajectories of bouncer defense and escape jumps. Dashed lines represent actual digitized trajectories of four typical jumps. Solid lines depict “drag-free” trajectories based on the initial conditions of the jumps. Escape jumps (gray and black lines) yielded greater heights and, on average, double the airborne duration observed in bouncer defense jumps (blue and green lines). On average, the ranges of bouncer defense jumps were seven times greater than escape jumps. Digitized data were sampled at intervals of 17 ms from the high-speed video sequences, which were filmed at 3,000 frames per second (see Movies 3–5).
The second category of jaw propulsion was an “escape jump.” In contrast to bouncer defense jumps, in which the ants approached and attacked intruders, escape jumps were characterized by ants avoiding the intruder and propelling themselves vertically into the air by firing their mandibles against the substrate (Figs. 3–5). In a stereotypical series of behaviors, an escape-jumping ant first oriented its head and antennae perpendicularly to the substrate with mandibles cocked and open (Fig. 3). It then rocked its body and lifted at least one leg vertically into the air. Finally, the mandibles struck the substrate, jerking the ant’s head upward and flinging its body into the air in a rapid spinning motion (Fig. 5). At the conclusion of both types of jumps, ants landed haphazardly back onto the substrate.
Fig. 5.
A high-speed image sequence of an escape jump using jaw propulsion in response to the presence of a larger heterospecific competitor (O. erythrocephalis) in the filming arena. Shown starting in the top-right image, the ant indicated by an arrow directs and fires its cocked mandibles against the substrate. The ant is propelled upward through the air toward the left of the page. The ant descends to the left of the page in the second half of the trajectory. Images are shown at 13.3-ms intervals (see Movies 3 and 5). (Scale bar: 1 cm.)
Jaw Propulsion Kinematics.
Bouncer defense and escape jumps had distinct kinematic parameters (Table 1) (see Movies 2–5). Bouncer defense jumps yielded mean take-off angles of 27°, whereas the angles of the more vertically directed escape jumps averaged 76°. The mean horizontal range of defense jumps was 22.3 cm (5.3–39.6 cm), compared with 3.1 cm in escape jumps. Escape jumps yielded greater heights of 6.1–8.3 cm compared with bouncer defense jumps, which reached heights of 0.8–5.7 cm. The ants spun dramatically throughout the trajectories of both jump types. Revolution rates during the first half of escape jump trajectories were greater (average: 63 rev·s−1) than the comparable trajectories of bouncer defense jumps (average: 36 rev· s−1). Furthermore, the mean duration of escape jumps (0.253 s) was nearly double the mean bouncer defense jump duration (0.128 s). Bouncer defense jump parameters (Table 1) were not correlated with body size (linear regression; P > 0.05).
Table 1.
Kinematics of the ballistic trajectories generated during bouncer defense and escape jumps
| Trajectory parameter | Bouncer defense | Escape jump |
|---|---|---|
| Projection angle, ° (θ0) | 27 ± 8 (15–53) | 76 ± 5 (69–82) |
| Initial velocity, m·s−1 (v0) | 1.7 ± 0.4 (1.1–2.3) | 0.24 ± 0.04 (0.20–0.29) |
| Body acceleration (a), × g | 680 ± 401 (137–1,324) | 472 ± 286 (241–880) |
| Range, cm (d) | 22.3 ± 11.5 (5.3–39.6) | 3.1 ± 2.1 (0.2–5.0) |
| Height, cm (h) | 3.1 ± 1.3 (0.8–5.7) | 7.3 ± 1.1 (6.1–8.3) |
| Duration, s (t) | 0.128 ± 0.035 (0.068–0.195) | 0.253 ± 0.022 (0.220–0.268) |
| Duration to peak height, s | 0.067 ± 0.018 (0.027–0.098) | 0.115 ± 0.008 (0.108–0.123) |
| Spin rate during first half of trajectory (rev·s−1) | 36 ± 15 (8–60) | 63 ± 3 (60–67) |
| Spin rate during second half of trajectory (rev·s−1) | 21 ± 7 (12–36) | 24 ± 2 (21–27) |
Trajectory parameters are presented as mean ± SD (minimum–maximum). Bouncer defense jump parameters were measured in 20 jumps from 20 different individuals. Mean duration was calculated from 10 jumps only, and final spin rate was calculated from 13 jumps only, because the range exceeded the camera’s view in some jumps. Escape jumps were calculated from four jumps by four different individuals.
Drag forces appeared to reduce the horizontal distance traveled during bouncer defense jumps. The trajectories of actual jumps compared with their predicted output were markedly different (Fig. 4) in terms of both height and range. Across all bouncer defense jumps, the predicted range based on the takeoff angle and initial velocity (Eqs. 4–6 in Methods) exceeded the actual range by an average of 20%.
Discussion
O. bauri generated strike speeds that were exceptional by comparison with any other predatory movements driven by internal energy storage mechanisms. With speeds of 35.5–64.3 m·s−1 and accelerations of 105 × g, trap-jaw strikes exceeded the extreme predatory movements performed by mantis shrimp (104 × g, 23 m·s−1) (16), nematocyst stylet speeds (106 × g, 18.6 m·s−1) (17), fungal ballistospore launch accelerations (104 × g, 1.5 m·s−1) (18), and previous speed estimates from trap-jaw ants (17 m·s−1) (9, 11). Contrary to previous research (9, 11), we found that the mandibles closed asynchronously, with the second mandible to close achieving higher velocities than the first (Fig. 2). Asynchronous closure patterns may be caused by limits to the speed of signal conduction between the mandible trigger muscles. In addition, we confirmed that the mandibles decelerate before crossing the midline, thereby possibly reducing damage to the mandibles when they miss a target and impact each other (Fig. 2) (9, 11).
As a direct result of these extraordinary accelerations, the small, low-mass mandibles of O. bauri can produce substantial instantaneous strike forces relative to body weight. Indeed, a single O. bauri mandible, with an average mass of 129 μg accelerating at 105 × g, can generate a force 371–504 times the ant’s body weight. These estimated mandible forces are on the high end of the feeding forces documented in other animal systems (19–21). Of even greater relevance, these forces are more than sufficient to propel an ant’s body into the air.
By snapping their mandibles against hard objects, O. bauri achieved ballistic trajectories that rival leg-jumping ants (22–24) as well as other propulsive arthropods (12, 25–28). O. bauri’s bouncer defense jumps yielded low heights (1–6 cm) and substantial horizontal trajectories ranging from 5–40 cm, whereas escape jumps covered shorter ranges (<1–5 cm) and reached greater heights (6–8 cm) (Table 1 and Fig. 4). Drag forces are known to disproportionately reduce the jump range of small insects relative to larger insects (29), and the actual ranges of the bouncer defense jumps were 20% less than predicted by ideal ballistic trajectory calculations. In one of the escape jumps (Fig. 4), the actual height exceeded the predicted dragless height of the trajectory, possibly due to lift generated by the high spin rate of the body (25).
Although trap-jaw strikes are effective for prey capture and processing (30), and bouncer defense behaviors are effective for ejecting small intruders (13), the relative performance and survival rates of ants using jaw propulsive jumps remain to be determined. Given that O. bauri do not appear to direct their escape jumps toward a particular landing site, unlike the directed trajectories of backward-gliding ants (31), they are likely attempting to evade potential predators. For example, many lizard species use rapid tongue strikes with durations ranging from 0.11 to 0.28 s to capture ants (32), so that a well timed escape jump (0.22 to 0.27 s duration) (Table 1) would be sufficient to keep an ant airborne during a lizard’s predatory strike. In addition, the “popcorn-effect” of multiple ants performing escape jumps (A.V.S. and B.L.F., unpublished data) may serve to confuse potential predators. We also observed groups of ants performing bouncer defense attacks on large intruders, perhaps with a function similar to the deterrent mobbing behaviors observed in birds and other animals. Propulsive behaviors may be especially important given that O. bauri builds nests in leaf litter, rather than below ground (33). Because this species does without the subterranean strongholds typical of many ants, temporary escape from predators and ejection of intruders may be essential for survival.
The extreme performance of the wide diversity of trap-jaw mandibles implies a high degree of specialization for speed that is correlated with specific predatory strategies (10, 11, 34–37). Yet the propulsive use of these strikes by some trap-jaw ant species (12, 13, 30, 38, 39) suggests that this system is also behaviorally versatile. All of the ant species in which jaw propulsion has been observed have relatively short, robust mandibles more suitable for generating large forces than producing large displacements (Fig. 1) (Ponerinae: Odontomachus and Anochetus; Myrmicinae: Orectognathus and Strumigenys; (A.V.S. and S.N.P., unpublished data and refs. 12, 13, and 38). Indeed, O. bauri forages on other ants and termites rather than on elusive prey and uses large strike forces to squash insects or stun chemically defended prey before it can emit noxious or toxic secretions (33). Thus, although the use of the mandible strike for body propulsion in trap-jaw ants is nonintuitive and surprising, it is possible that mandibles with a short out-lever (i.e., force-modified) have evolved to support the multiple functions of prey capture, intruder defense (13), and body propulsion. The degree to which the ants vary and control the force vectors of their mandibles in these distinct behaviors remains to be determined.
The unexpected and context-dependent multifunctionality of trap-jaws demonstrates that high-speed predatory movements can be co-opted for distinctly different functions due to a fundamental physical principle: High acceleration can yield both high speed and high force. At some point in the history of these taxa, jaw propulsion may simply have been an epiphenomenon of high-speed predatory strikes. Now, the versatility of trap-jaw strikes offers an excellent example of contingency and co-option in evolutionary origins (3, 4, 40–42). In conclusion, the extreme accelerations of mandible strikes produce highly effective mechanisms for both prey capture and propulsion. The multiple independent origins of trap-jaws (11, 34, 35) and the co-option of feeding strikes for use in a novel locomotor mode offers insights into the origins and potential multifunctionality of extreme animal movements.
Methods
Mandible Closure.
O. bauri (Formicidae: Ponerinae) workers were collected in Costa Rica, at La Selva Biological Station (10°25′N, 84°01′W) on October 26, 2004, with Ministry of Environment and Energy Permit 122-2004-OFAU. The seven ants used in the mandible strike kinematic analyses ranged in body mass from 12.1 to 14.9 mg. Their mandibles were 1.24–1.38 mm long, with masses ranging from 111 to 145 μg (DFC350 FX digital camera and MZ 12.5 microscope from Leica Microsystems, Wetzlar, Germany, analytical balance, resolution 0.1 mg, Adventurer AR0640 from Ohaus, Pinebrook, NJ; microbalance, resolution 0.1 μg, Toledo MX5 from Mettler, Columbus, OH). This information was used for the calibration of kinematic analyses described below and in measurements of strike speed and force.
We filmed three to nine mandible strikes by each of these individuals (5 × 104 frames per second, 8–11 μs shutter, Ultima APX high-speed video from Photron USA Inc., San Diego, CA; Leica Microsystems MZ 12.5 microscope) and used custom digital image analysis programs (Matlab, Version 7.0.1; Mathworks, Natick, MA). Each ant was mounted on the end of a thin rod with its head positioned perpendicularly to the camera. We tracked specific points on each mandible across each image sequence in which the mandibles stayed perpendicular to the camera’s axis and the movement remained unobstructed throughout the sequence. We measured the distance moved by the mandibles across each video frame; speed and acceleration were calculated as derivatives of the arc distance and speed traversed by the tip of the mandible, respectively. When the mandible’s movement was blurred in an image, we tracked the leading edge of the mandible that was not blurred, thereby potentially underestimating the maximum speed by an average of 39% (±13%). Derivatives of distances provided average speeds and accelerations rather than instantaneous values along the trajectory, thereby also underestimating the speeds and accelerations of the mandible. Each strike was digitized three times, and the results were averaged for each strike. Digitizing error was on average ±3% from the mean value.
To calculate the peak instantaneous force generated by the mandibles, each mandible was modeled as a thin rod of uniform density, which rotates about a fixed axis through one end. The moment of inertia (I) of the mandible was thus calculated (43) as
where M is the mass of the mandible, and R is the length of the mandible.
Torque (τ), the force generating rotation perpendicular to the long axis of the mandible, is
where Fm is the perpendicular force generated by the tip of the mandible. Analogous to F = ma, τ is equal to Iα, such that we can solve for Fm as follows:
The peak instantaneous mandible strike force was calculated for the maximum angular accelerations (α) produced during each strike.
Jaw Propulsion.
Jaw propulsion was elicited by (i) presenting the ant with a threatening object (typically, a thin strip of plastic or metal), which the ants attacked with their jaws and simultaneously propelled themselves away (bouncer defense); or (ii) introducing a potential biological predator (heterospecific ant or predatory spider), which caused the trap-jaw ants to either attack the predator or perform a jaw-propelled escape response by closing their mandibles against the substrate (escape jump). Forty jaw-initiated ballistic trajectories were filmed; the kinematic parameters of primary interest were visible in 4 escape jumps and 18 bouncer defense trajectories produced by 22 different individuals. Body mass of these individuals ranged from 9.3 to 14.6 mg, with an average mass of 12.1 mg (analytical balance, resolution 0.1 mg; Ohaus Adventurer AR0640).
Two high-speed imaging systems were positioned perpendicular to each other and captured the trajectory and any off-axis movements of the jaw jumps. A lateral camera recorded the initial conditions and subsequent trajectory of the jaw jumps (3,000 frames per second, 125 μs shutter speed, 1024 × 1024 pixel resolution; APX-RS, Photron USA Inc.). Digitizing error was on average ±3.5% from the mean value. A dorsal camera captured images, which we used to correct for off-axis movements relative to the side-view camera’s focal plane (500 frames per second, 2 ms shutter speed, 720 × 480 pixel resolution; MotionMeter; Redlake, Tucson, AZ). The overall trajectory of the jump was tracked by digitizing the head/thorax joint position in every fifth lateral video frame (1.67-ms intervals). Custom computer programs in Matlab (Version 7.0.4; Mathworks) were used for digital image analysis.
Eight measurements were collected from each jaw propulsion trajectory as follows: (i) projection angle, θ0, which is the initial angle with which the ant’s body launched relative to the horizontal substrate; (ii) initial velocity, v0, the take-off velocity of the body during launch; (iii) body acceleration, a, the acceleration from the mandible strike to maximum velocity; (iv) range, d, the horizontal distance traversed between launch and landing; (v) height, h, the maximum vertical distance achieved during the trajectory; (vi) duration, t, the elapsed time between take-off and landing; (vii) spin rate, rev/s, the number of body revolutions per second during the jump; and (viii) correction angle, θc, the angle formed between the side-view camera’s plane of view and the horizontal line of the ant’s trajectory. Custom computer programs in Matlab (Version 7.0.4; Mathworks) were used for digital image analysis.
Ballistic Trajectories: Predictions and Empirical Tests.
The initial conditions of the jaw jumps were used to predict the theoretical output of the system in the absence of drag forces. Predicted trajectories were compared with actual trajectories, and the proportional effects of drag were assessed (25). Assuming negligible drag, and given the initial velocity of the ant, the actual digitized trajectory of the ant’s body can be compared with its predicted position over time with the following two equations:
where x is the horizontal position, y is the vertical position, v0y is the initial vertical velocity, v0x is the initial horizontal velocity, and g is the acceleration due to gravity (43).
The range of the trajectory (d) is calculated as the distance at which y = 0 for the first time since takeoff using the above equations. Or, the range can be calculated by using
With the outputs of these equations, we calculated the percent of actual range relative to the predicted range. We also compared the paths of the actual parabolic trajectories with those of the theoretical, drag-free jumps calculated with Eqs. 4 and 5.
Statistical Analyses.
Statistical analyses were conducted by using packaged software (JMP; Version 5.0.1; SAS Institute, Inc., Cary, NC). t tests were used to compare kinematic differences between first and second mandible closures. Least-square linear regressions tested for correlations between body size and the kinematic parameters of the jumps. Body sizes were log-transformed before regression analyses to reduce the dependence of the variance on the mean.
Supplementary Material
Acknowledgments
We thank S. Combes, R. Dudley, M. Koehl, C. Nunn, K. Padian, S. Sane, J. Spagna, and the University of California at Berkeley Biomechanics group for comments and discussions; two anonymous reviewers for their insightful comments; Alex Wild for providing the photograph for Fig. 1; and the Hebets and Dawson laboratories for use of their microscope and balances. The Dudley laboratory loaned us one high-speed video camera. This work was supported by a Research Initiative Seed Grant from the Beckman Institute for Advanced Science and Technology (University of Illinois at Urbana–Champaign).
Footnotes
Conflict of interest statement: No conflicts declared.
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Nowicki S., Westneat M., Hoese W. Semin. Neurosci. 1992;4:385–390. [Google Scholar]
- 2.Patek S. N., Oakley T. H. Evolution (Lawrence, Kans.) 2003;57:2082–2100. doi: 10.1111/j.0014-3820.2003.tb00387.x. [DOI] [PubMed] [Google Scholar]
- 3.Gould S. J., Vrba E. S. Paleobiology. 1982;8:4–15. [Google Scholar]
- 4.Lauder G. V. Paleobiology. 1981;7:430–442. [Google Scholar]
- 5.Barel C. D. N. Acta Biotheor. 1993;41:345–381. [Google Scholar]
- 6.Podos J. Nature. 2001;409:185–188. doi: 10.1038/35051570. [DOI] [PubMed] [Google Scholar]
- 7.Ganfornina M. D., Sanchez D. BioEssays. 1999;21:432–439. doi: 10.1002/(SICI)1521-1878(199905)21:5<432::AID-BIES10>3.0.CO;2-T. [DOI] [PubMed] [Google Scholar]
- 8.Muller G. B., Wagner G. P. Annu. Rev. Ecol. Syst. 1991;22:229–256. [Google Scholar]
- 9.Gronenberg W., Tautz J., Hölldobler B. Science. 1993;262:561–563. doi: 10.1126/science.262.5133.561. [DOI] [PubMed] [Google Scholar]
- 10.Paul J. Comp. Biochem. Physiol. A. 2001;131:7–20. doi: 10.1016/s1095-6433(01)00458-5. [DOI] [PubMed] [Google Scholar]
- 11.Gronenberg W. J. Comp. Physiol. A. 1995;176:391–398. [Google Scholar]
- 12.Wheeler W. M. Biol. Bull. 1922;42:185–201. [Google Scholar]
- 13.Carlin N. F., Gladstein D. S. Psyche. 1989;96:1–19. [Google Scholar]
- 14.Ehmer B., Gronenberg W. Cell Tissue Res. 1997;290:153–165. doi: 10.1007/s004410050917. [DOI] [PubMed] [Google Scholar]
- 15.Ehmer B., Gronenberg W. J. Comp. Physiol. B. 1997;167:287–296. [Google Scholar]
- 16.Patek S. N., Korff W. L., Caldwell R. L. Nature. 2004;428:819–820. doi: 10.1038/428819a. [DOI] [PubMed] [Google Scholar]
- 17.Nüchter T., Benoit M., Engel U., Özbek S., Holstein T. W. Curr. Biol. 2006;16:R316–R318. doi: 10.1016/j.cub.2006.03.089. [DOI] [PubMed] [Google Scholar]
- 18.Pringle A., Patek S. N., Fischer M., Stolze J., Money N. P. Mycologia. 2005;97:866–871. doi: 10.3852/mycologia.97.4.866. [DOI] [PubMed] [Google Scholar]
- 19.Patek S. N., Caldwell R. L. J. Exp. Biol. 2005;208:3655–3664. doi: 10.1242/jeb.01831. [DOI] [PubMed] [Google Scholar]
- 20.Taylor G. M. Proc. R. Soc. London Ser. B; 2000. pp. 1475–1480. [Google Scholar]
- 21.Alexander R. M. J. Exp. Biol. 1985;115:231–238. doi: 10.1242/jeb.115.1.231. [DOI] [PubMed] [Google Scholar]
- 22.Ali T. M. M., Urbani C. B., Billen J. Naturwissenschaften. 1992;79:374–376. [Google Scholar]
- 23.Mercier J.-L., Lenoir A. Comptes Rendus L’Academie Sci. Ser. III Sci. de la Vie. 1999;322:661–667. doi: 10.1016/s0764-4469(99)80105-x. [DOI] [PubMed] [Google Scholar]
- 24.Urbani C. B., Boyan G. S., Blarer A., Billen J., Ali T. M. M. Experientia. 1994;50:63–71. [Google Scholar]
- 25.Vogel S. J. Biosci. 2005;30:167–175. doi: 10.1007/BF02703696. [DOI] [PubMed] [Google Scholar]
- 26.Burrows M., Morris O. J. Exp. Biol. 2003;206:1035–1049. doi: 10.1242/jeb.00214. [DOI] [PubMed] [Google Scholar]
- 27.Brackenbury J., Hunt H. J. Zool. 1993;229:217–236. [Google Scholar]
- 28.Wauthy G., Leponce M., Banai N., Sylin G., Lions J. Proc. R. Soc. London Ser. B; 1998. pp. 2235–2242. [Google Scholar]
- 29.Bennet-Clark H. C., Alder G. M. J. Exp. Biol. 1979;82:105–121. doi: 10.1242/jeb.82.1.105. [DOI] [PubMed] [Google Scholar]
- 30.Dejean A., Bashingwa E. P. Insectes Sociaux. 1985;32:23–42. [Google Scholar]
- 31.Yanoviak S. P., Dudley R., Kaspari M. Nature. 2005;433:624–626. doi: 10.1038/nature03254. [DOI] [PubMed] [Google Scholar]
- 32.Meyers J. J., Herrel A. J. Exp. Biol. 2005;208:113–127. doi: 10.1242/jeb.01345. [DOI] [PubMed] [Google Scholar]
- 33.Ehmer B., Hölldobler B. Psyche. 1995;102:215–224. [Google Scholar]
- 34.Gronenberg W., Brandão C. R. F., Dietz B. H., Just S. Physiol. Entomol. 1998;23:227–240. [Google Scholar]
- 35.Gronenberg W. J. Exp. Biol. 1996;199:2021–2033. doi: 10.1242/jeb.199.9.2021. [DOI] [PubMed] [Google Scholar]
- 36.Moffett M. W. Insectes Sociaux. 1986;33:85–99. doi: 10.1007/s00040-011-0151-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Gronenberg W., Holldobler B., Alpert G. D. J. Insect Physiol. 1998;44:241–253. doi: 10.1016/s0022-1910(97)00145-5. [DOI] [PubMed] [Google Scholar]
- 38.Carlin N. F. Pysche. 1981;88:231–244. [Google Scholar]
- 39.Weyer V. F. Zool. Anzeiger. 1930;90:49–55. [Google Scholar]
- 40.Arnold E. N. In: Phylogenetics and Ecology. Eggleton P., Wright R. I. V., editors. London: Academic; 1994. pp. 124–168. [Google Scholar]
- 41.Bock W. J. Evolution (Lawrence, Kans.) 1959;13:194–211. [Google Scholar]
- 42.Koehl M. A. R. Annu. Rev. Ecol. System. 1996;27:501–542. [Google Scholar]
- 43.Ohanian H. C. Physics. New York: Norton; 1989. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.