On a classical limit for electronic degrees of freedom that satisfies the Pauli exclusion principle

Abstract

Fermions need to satisfy the Pauli exclusion principle: no two can be in the same state. This restriction is most compactly expressed in a second quantization formalism by the requirement that the creation and annihilation operators of the electrons satisfy anticommutation relations. The usual classical limit of quantum mechanics corresponds to creation and annihilation operators that satisfy commutation relations, as for a harmonic oscillator. We discuss a simple classical limit for Fermions. This limit is shown to correspond to an anharmonic oscillator, with just one bound excited state. The vibrational quantum number of this anharmonic oscillator, which is therefore limited to the range 0 to 1, is the classical analog of the quantum mechanical occupancy. This interpretation is also true for Bosons, except that they correspond to a harmonic oscillator so that the occupancy is from 0 up. The formalism is intended to be useful for simulating the behavior of highly correlated Fermionic systems, so the extension to many electron states is also discussed.

Planck ushered in quantum mechanics with the proposal that matter be regarded as a collection of harmonic oscillators. Dirac (1) showed that this description is in fact exact, fully consistent with the (then) new quantum mechanics, if every quantal state of the system is represented as an oscillator. Solving the time-dependent Schrödinger equation for the system is then equivalent to solving the classical dynamics of these fictitious harmonic oscillators. This scheme is, of course, practical if the system can sample only a finite number of states. When the system is in a stationary state, the corresponding oscillator is uncoupled to others. In theoretical chemistry (2, 3) and in quantum optics (4), this correspondence has been used to considerable advantage, because solving classical equations of motion, which are local and first order in time, is computationally much more tractable then solving the quantum ones.

In both chemistry and solid-state physics, electrons can be highly correlated, and special methods need to be developed (5). We recently encountered this problem in connection with the onset of metallic behavior (6) in assemblies of quantum dots (7). To discuss the transport properties of electrons in such arrays, one must allow electrons to move from one site to the other, subject to the limitations of the Pauli principle and to the Coulomb repulsion of electrons. This repulsion depends on where in space any two different electrons are and so is not well approximated in terms of a mean field (because of the average positions of the other electrons) in which a given electron moves. On the other hand, when the repulsion between two electrons on the same site is not high, there are numerous possible electronic states for the system. This is because ionic states, which are typically higher in energy, need to be included. As an example, even in a simple model (one spatial orbital per dot) of a completed hexagonal array of 19 nanodots, there are over 2 billion states in a narrow energy range, so replacing each electronic state by a classical degree of freedom is not quite an advantage.

In this paper, I discuss a simple approach whereby a classical limit is useful. The starting point is an orbital picture, long familiar to chemists. Because electron correlation will be fully taken into account, this starting point is not necessarily a limitation. There are at least as many orbitals (or, strictly speaking, spin orbitals) as there are electrons, but there can easily be more orbitals than electrons. There are usually more states than orbitals, and in the model of quantum dots that motivated this work, the number of spin orbitals is twice the number of sites. For the example of 19 sites, there are 38 spin-orbitals vs. 2,821,056,160 doublet states.

The point of the formalism is that it ensures that the Pauli exclusion principle is satisfied, namely that no more than one electron occupies any given spin-orbital. Note that the occupancy can be below one and need not be either zero or one. The idea that an orbital is either full or empty belongs to simple orbital pictures and need not be the case when electron correlation is allowed. In both stationary and time-evolving states, a partial occupancy is possible both in quantum mechanics and in the classical limit that we consider here.

The orbitals that are used as a basis can be chosen in different ways, depending on the physics of the problem and also on the question. For an extended array, they can be site orbitals, but they can also be self-consistent-field delocalized orbitals [which are coupled by the residual interaction (8)]. Other examples where orbitals are coupled by residual interactions include, e.g., the Auger process and other instances of electronic autoionization, electronic energy transfer, etc. The different choices are made possible by a unitary transformation of the Hamiltonian. We will address the question of different classical limits below. Two other points that will be discussed are: (i) the extension of the formalism to many electron systems where, in addition to the exclusion principle, it is also necessary to satisfy the requirement of antisymmetry of the state under exchange, and (ii) an active point of view where the states are left unchanged, and it is the operators that are transformed to a classical limit.

The Spin States

The essential idea is that the z component of a spin, in units of ℏ/2, has a range from −1 to +1. Therefore the variable (1 + S_z)/2 has values in the range 0 to 1 and so provides an analog for the occupation number of an orbital by a Fermion. This is not just an analog, and we argue below that this is a consequence of the result that the Pauli spin matrices (9, 10) (Eq. A.2 of the Appendix) realize the same anticommutation relations as the Fermionic creation and annihilation operators (denoted by a carat):

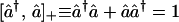1

The intended application of the theory is to the dynamics of correlated many-electron systems. It is then the case that the occupancy of a spin orbital need not be either 0 or 1 but can be any number in between. We therefore need to consider states where the occupancy is fractional. For this purpose, we define a spin state |χ〉 as follows.

The spin state |χ〉 that has a definite component ℏ/2 along a unit vector u specified by the polar angles θ and φ can be written as (10):

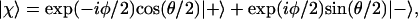2

where the two basis vectors, |+〉 and |−〉, are the two eigenstates of the operator Ŝ_z. Eq. 2 is derived in the Appendix. The derivation shows that the state |χ〉 can be regarded as a “coherent spin state” (11).

One can also define spin up, Ŝ₊, and down, Ŝ_{_}, operators Ŝ_± ≡ (Ŝ_x ± iŜ_y)/2, which will be the realization of the Fermionic creation annihilation operators, [Ŝ₊, Ŝ₋]₊ = 1, such that

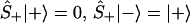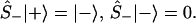3

Then,

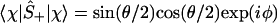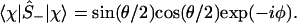4

And, by explicit evaluation by using Eq. 3 or by using Ŝ₊Ŝ₋ = (1 + Ŝ_z)/2, one can express the orbital occupancy, n, as the expectation value of the number operator n̂ = â^†â

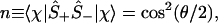5

which manifestly satisfies the Pauli exclusion, 0 ≤ n ≤ 1. Another manifestation of there being a place for at most one electron in the orbital is that two electrons cannot be added or removed 〈χ|Ŝ_±Ŝ_±|χ〉 = 0. Also, because Ŝ_x² = Ŝ_y² = Ŝ_z² = I, we have the result 〈χ|Ŝ_z²|χ〉 = 1, etc. (Note that the result is 1 and not ℏ²/4, because we measure the spin in units of ℏ/2.)

For application in many electron systems, note that the state |χ〉, which is a state where the spin is “up” along the unit vector u specified by the polar angles θ and ϕ can be regarded as the state |+〉, where the spin is “up” along the z axis, which is rotated to the required direction (10)

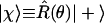6

Using Eq. 6 as a starting point allows the introduction of an “active” point of view in which it is the operators rather than the state that are rotated. This is discussed, with a worked-out example, in the Appendix.

The Anharmonic Oscillator

An anharmonic oscillator has a finite number, say N, of excited bound vibrational states. Typically, the lower the number of bound states, the higher the anharmonicity, and this relation is particularly simple for the Morse oscillator for which the anharmonicity, [ω_ex_e in the notation of Herzberg (12)] is exactly 1/2N. For the Morse and other anharmonic oscillators whose vibrational spectrum is quadratic in the vibrational quantum number n, the expectation values of the raising and lowering operators scale as (13) , with the harmonic limit corresponding to N → ∞. The correspondence, Eq. 5, n = cos²(θ/2) allows Eq. 4 to be written as

7

Thereby we conclude that, whereas a Bosonic degree of freedom corresponds to a harmonic oscillator (which has a countable infinite number of bound states), a Fermionic degree of freedom corresponds to an anharmonic oscillator with exactly one bound state, in addition to the ground state. Because we identify the vibrational quantum number with the occupancy, this corresponds to the possibility of a Bose–Einstein condensation, n → ∞, on the one hand and to the Pauli exclusion principle, 0 ≤ n ≤ 1, on the other.

The Schwartz inequality implies that 〈χ|Ŝ₊Ŝ₋|χ〉 ≥ 〈χ|Ŝ₊|χ〉〈χ|Ŝ₋|χ〉, and this is explicitly n ≥ n(1 − n) with equality only when the oscillator is in the ground state, n = 0.

The correspondence with an oscillator also suggests that n and φ can be regarded as a pair of classical action-angle variables. There are well known (14, 15) problems with the definition of an angle (or phase) operator even in the harmonic case, and these are associated with the spectrum of n being bounded from below. Here the spectrum is bounded from both ends. Therefore, it is not possible to start from a quantum mechanical commutator of the operators and conclude that the classical Poisson bracket satisfies {n, φ} = 1.

The Classical Limit

The classical limit is taken by replacing operators by their expectation values in the spin state |χ〉, where the expectation value is regarded as a function of the classical (action-angle variables) n, n = cos²(θ/2) = (1 + cos θ)/2, and φ. Specifically, the classical Hamiltonian is defined by

8

and the classical equations of motion are Hamiltonian

9

where the dot signifies a time derivative. From these, one can derive equations of motion for other variables such as θ rather than n.

The classical limit is an approximation because, as we noted, the classical limit of a product of operators is not necessarily equal to the product of the classical limits. The importance of this can be examined by comparing the quantal and classical equations of motion. Take the number operator n̂ as an example. Quantum mechanically, ∂n̂/∂t = i[Ĥ, n̂], where here the square bracket is the usual commutator. Consider first an isolated system, with an electronic Hamiltonian Ĥ = ωn̂. Then both quantum mechanically and classically, the number is conserved while the phase changes classically as φ̇ = ω. Quantum mechanically, ∂â/∂t = i[Ĥ, â] = −iωâ, so that taking expectation of both sides ∂a_cl/∂t = −iωa_cl = −iω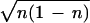 exp(−iφ), which is consistent with the classical equations. To perturb the system, we add an external field, f(t)(â^† + â), to the Hamiltonian. Now [(â^† + â), n̂] = −â^† + â, so taking expectation values, the external field changes n as i∂n_cl/∂t = f(t)〈χ|â − â^†|χ〉 = −2if(t)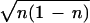 sin φ. The classical equation of motion is, from Eq. 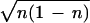9, ṅ = −f(t)∂〈χ|â^† + â|χ〉/∂φ = −f(t) sin φ. There is agreement, because in all the examples so far, the commutator in the quantum mechanical equation of motion is linear in the operators.

The reader familiar with group theory will recognize that the operators Î (the identity), Ŝ₊, Ŝ₋, and Ŝ_z are the four generators of the Lie group SU(2). This means that they form a collection of operators that is closed under the binary operation of (ordinary) commutation.‡ So as long as the Hamiltonian is linear in these generators, the classical equations of motion will be exact, because the commutator of H with any one of the generators will be linear in the generators. Even further, bilinear products such as Ŝ₊Ŝ₋ or Ŝ_x², Ŝ_y², and Ŝ_z² are also closed under commutation with the generators. So Hamiltonians that are bilinear in certain combinations of generators will also admit of an exact classical limit. Other examples where such closure was used to advantage have been discussed elsewhere (18). Work is in progress (19) on the numerical solution of the classical equations of motion in the many-electron case. What is already clear is that for shorter time dynamics, which is what one is really interested in, the classical limit works quite well.

Finally, we comment that the classical limit can also be taken in the active point of view in which it is the Hamiltonian that is rotated:

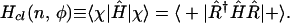10

An explicit example for the rotation of the raising operator is worked out in the Appendix. Any other function of the creation and annihilation operators can be worked out from it by matrix multiplication, because, e.g., R̂^†Ŝ₊Ŝ₋R̂ = R̂^†Ŝ₊R̂R̂^†Ŝ₋R̂.

The expert will know that, because the operator R̂ is an element of the group [R̂ = exp(−iθS ⋅ u) (10)], by the Campbell–Baker–Hausdorff theorem (9), if the original Hamiltonian contains only generators then so will the rotated Hamiltonian.

Many-Electron Systems

Once we have more than one electron, the restrictions on the wave function go beyond the Pauli exclusion principle. As is very well known, the wave function needs to be antisymmetric under the exchange of two electrons, which means that creation (or annihilation) operators of different orbitals also need to anticommute, e.g., [â_r, â_s]₊ = 0, where r and s refer to different sites. This can be achieved in the following way. First, the orbitals (or sites) are arranged in a fixed order, 1, 2, 3, … , n. Then a Slater determinant is built up from these orbitals such that, as usual, each row corresponds to a different orbital, and each column corresponds to a different electron. Therefore, the rth orbital corresponds to a fixed row in the determinant. Then, the operation of â_r on such a determinant is given by the following known rules: in the determinant, interchange the row where the rth orbital appears with each row above it where, by construction, these are rows with orbital indices below r. Continue until the row of the rth orbital is at the top of the determinant. This gives a phase factor (−1)^r−1. Strike out the first row and the last column. Normalize the resulting (n − 1) ⋅ (n − 1) determinant. Symbolically,

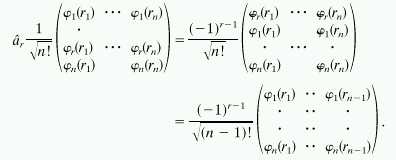11

In the final (n − 1) ⋅ (n − 1) determinant, the r − 1 row is followed by the r + 1 row. The rth row was struck out. Consider next the action of the product â_râ_s and say that s > r. Then the action of â_râ_s results in the phase factor (−1)^r+s and an (n − 2) ⋅ (n − 2) determinant in which the rows r and s are absent. Next consider the action of â_sâ_r. The resulting determinant is the same as for the action of â_râ_s, but the phase factor is now (−1)^r+s−1 because the first action by â_r has brought the row s up by one position. For n Fermions, the n ⋅ n Slater determinants form a complete set (20), and hence we have in general that since the action of two bilinear operators is the same up to a phase factor of −1, â_râ_s + â_sâ_r = 0.

In a single Slater determinant, an orbital is either occupied or is empty. The general wave function is, however, a linear combination of Slater determinants, and so an orbital can have partial occupancy. The spin states required to represent this are introduced in the next section.

Therefore, in the case of n orbitals, where the orbitals are arranged in a specified order, one can define the action of the creation and annihilation operators in one of two ways. One can associate with the action of â_r (or of â_r^†) the phase factor ϕ_r = (−1)^(Σ_j<rn_j), or one can explicitly write such an operator that gives rise to the desired phase factor. We need a factor of −1 for each occupied orbital below r, no phase factor if an orbital below r is unoccupied, and no phase factor for all orbitals above r. An n orbital spin operator that will do so is

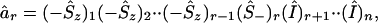12

where the subscript is that of the orbital on which the operator acts, and Î, as before, is the identity operator. The realization of â_r^† will be the same, except that for the rth orbital the factor will be (Ŝ₊)_r and not (Ŝ₋)_r.

In quantum chemistry, one is often not concerned with changing the number of electrons in the system.§ The operators that typically appear in the Hamiltonian will therefore conserve the total number of electrons. They will be either number operators, such as â_r^†â_r, for which the phase factor is unity or shift operators, such as â_r^†â_s + â_s^†â_r. The phase factor associated with a shift operator is (−1)^n_rs, where n_rs is the number of orbitals that, in our prearranged ordering of orbitals, appear between r and s (20). An n ⋅ n matrix representation for each such shift operator is a matrix with zeros everywhere except for a single entry of unity in the r, s position (20). In group theory literature, this is usually known as a Gelfand representation for the generators of the unitary group.

The Many-Electron Spin States.

The states that the n orbital operators act on are the so-called occupation number representation. A typical such state is the list of occupancies of each orbital in the prearranged set. The coordinate space representation of each such state is a Slater determinant. Using, as before, + and − to denote an occupied and an empty orbital, one such possible state is |+〉₁|−〉₂⋅⋅|+〉_r⋅⋅|+〉_n. To generate the states that have the spin in a direction specified by the unit vector u_r, which is possibly different for different orbitals, we rotate each state, as in Eq. 6, so that the particular occupation number state above leads to the state

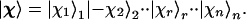13

The expectation values of creation and annihilation operators in such a state can now be computed as for the one-electron case. In terms of a completely empty state, usually denoted as |vac〉, with vac standing for vacuum, and by analogy to Eq. 6

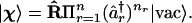14

Here R̂ is an n site rotation, and one can use this form to show that the classical limit can also be taken directly in the occupation number basis set by rotation of the operators rather than the state. This active point of view is discussed further, with an example, in the Appendix.

Coupled Orbitals

In general, a Hamiltonian resulting from electrostatic interactions can directly couple up to four different sites (21, 22) so that, indirectly, all sites can be coupled. Often direct coupling of two sites is sufficient for a description that is realistic but not accurate to chemical standards. A widely used form of such a Hamiltonian is that attributed to Pariser, Parr, and Pople, (21) and is also known in solid state physics as a Hubbard Hamiltonian (22):

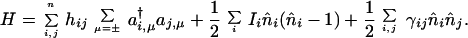15

To avoid any possible confusion, note that each orbital is indexed by a space (i, j, etc.) and a spin label, and n̂_i counts the total population in orbital i, summing over both directions of the spin. The space and spin labels together specify a spin orbital, and it is each spin orbital that is represented by a spin state |χ〉, such that its occupancy is characterized by the two polar angles θ and φ. The classical Hamiltonian is obtained as the expectation value of the quantum mechanical Hamiltonian in the many-electron spin states.

A (possibly oversimplified) Hamiltonian is the Hückel one:

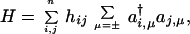16

which can be diagonalized exactly by the introduction of molecular orbitals as linear combination of site orbitals (22, 23)

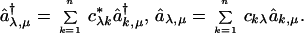17

If the coefficients c are chosen so as to diagonalize the matrix h, then the Hückel Hamiltonian is diagonal, H = Σ_λⁿ ɛ_λ Σ_μ=± a_λ,μ^†a_λ,μ. The point to examine is whether one can take the classical limit in either orbital basis. Now the transformation of the site orbitals to yield the molecular orbital (MO) ones is a linear operation. So for any Slater determinant (which is equivalent to a state in the occupation number representation), the expectation number of the operators in the MO basis is a linear combination of the expectation values of the site operators. Hence, using an active point of view in which it is the operators (rather than the state) that are rotated (see the discussion in the Appendix), any finite linear combination of operators can be rotated term by term. Even when the n orbital wave function is not a single Slater determinant but is a linear combination of determinants, one can still take the classical limit term wise.

Concluding Remarks

The dynamics of electrons in highly correlated systems is of current interest but is not easy to discuss quantitatively because many states are coupled. It is here suggested to approximate the dynamics by a classical limit based on orbitals rather than on states. Such a description needs to satisfy Fermi statistics, which include the Pauli exclusion principle for the limitation on the occupancy of a single orbital. A way of taking the classical limit where the statistics is inherently satisfied is discussed. The limit is based on the equivalence between the requirements of the Pauli principle and the up component of the spin of a (fictitious) electron. This is then generalized to the many-electron case. Technically, the limit is taken by using coherent spin states that are obtainable by rotation. It is also possible to take the limit in an active way, where it is the operators that are changed by (a counter) rotation. Realistic Hamiltonians and relevant observables (such as the number operator or shift operators) for which the classical limit can be an exact description are discussed.

An “Active” Transformation

In this Appendix we show, with an explicit example, how rotation of an operator can provide a complementary “active” route to the classical limit. Because we realize the creation and annihilation operators as spin raising and lowering operators, the rotation operator R̂ needs to be written explicitly in the {|+〉, |−〉} basis. The derivation of the matrix representation of R̂ follows (10). For a rotation by an angle α about a unit vector v,

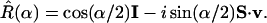A.1

The Pauli matrices have the form

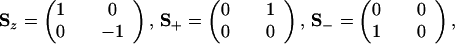A.2

and it is readily verified that the realization of â^† and â by Ŝ₊ and Ŝ₋ satisfies the anticommutation relation, Eq. 1.

Coherent Spin States.

S ⋅ v is the matrix representing the spin along the unit vector v. For the unit vector u of direction angles θ and φ, one has

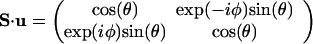A.3

with two eigenfunctions, |χ〉, as given by Eq. 2 and the opposite component

The Spin-Rotation Matrix.

The unit vector u of direction angles θ and φ is obtained from a unit vector along the z axis by a rotation through an angle θ about a vector v whose components are (−sin φ, cos φ, 0). So

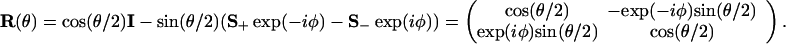A.4

An Active Point of View.

Rather than rotating the state and keeping the operators fixed, as in Eqs. 4 and 5, one can take an active complementary point of view of keeping the states (as up or down along the z axis) and counter rotate the operators, e.g.,

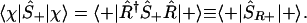A.5

Because in the {|+〉, |−〉} basis the action of Ŝ₊ is like that of |+〉〈−|, the operator Ŝ_R+, Ŝ_R+ ≡ R̂^†Ŝ₊R̂ can be written as R̂^†|+〉〈−|R̂. Note that this is a counter rotation to the rotation of the state, Eq. 6. Using the matrix representation (A.4) and its Hermitian adjoint,

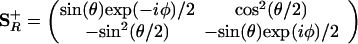A.6

Using Eq. A.6, we recover the earlier result, Eq. 4, for 〈χ|Ŝ₊|χ〉, but now computed as the matrix element of the rotated operator in the unrotated, {|+〉, |−〉}, basis. Because the rotation operator is unitary, the matrix representation of the rotation of any function of Ŝ₊ can be evaluated by matrix products, R̂^†f(Ŝ₊)R̂ = f(R̂^†Ŝ₊R̂). Rotation of the operators is therefore a viable alternative to rotation of states. In the many-electron case, rotations of different spins will commute. Hence for the product rotation operator that is needed in Eq. 14, one can either use a product of the matrices, each operating on a different spin, or a single 2n ⋅ 2n rotation matrix with entries along the diagonal.