A hypothesis for vulnerable plaque rupture due to stress-induced debonding around cellular microcalcifications in thin fibrous caps

Abstract

In this article, we advance a hypothesis for the rupture of thin fibrous cap atheroma, namely that minute (10-μm-diameter) cellular-level microcalcifications in the cap, which heretofore have gone undetected because they lie below the visibility of current in vivo imaging techniques, cause local stress concentrations that lead to interfacial debonding. New theoretical solutions are presented for the local stress concentration around these minute spherical inclusions that predict a nearly 2-fold increase in interfacial stress that is relatively insensitive to the location of the hypothesized microinclusions in the cap. To experimentally confirm the existence of the hypothesized cellular-level microcalcifications, we examined autopsy specimens of coronary atheromatous lesions using in vitro imaging techniques whose resolution far exceeds conventional magnetic resonance imaging, intravascular ultrasound, and optical coherence tomography approaches. These high-resolution imaging modalities, which include confocal microscopy with calcium-specific staining and micro-computed tomography imaging, provide images of cellular-level calcifications within the cap proper. As anticipated, the minute inclusions in the cap are very rare compared with the numerous calcified macrophages observed in the necrotic core. Our mathematical model predicts that inclusions located in an area of high circumferential stress (>300 kPa) in the cap can intensify this stress to nearly 600 kPa when the cap thickness is <65 μm. The most likely candidates for the inclusions are either calcified macrophages or smooth muscle cells that have undergone apoptosis.

The rupture of the thin fibrous cap overlying the necrotic core of a vulnerable plaque is the principal cause of acute coronary syndrome. It has been widely assumed that plaque morphology is the major determinant of clinical outcome (1–6). Several pathological studies of ruptured plaques have provided morphological descriptions of the high-risk, or vulnerable, coronary plaque that is prone to rupture or erosion as a positively remodeled lesion rich in vasa-vasorium, containing a lipid-rich core with an overlying thin fibrous cap infiltrated by macrophages (7–10). Virmani et al. (6) described thin-cap fibroatheroma with a large necrotic core and a fibrous cap of <65 μm as a more specific precursor of plaque rupture due to tissue stress.

Despite the above observations, the mechanism of vulnerable plaque rupture has remained a mystery because ruptures often occur in regions where computational finite element (FEM) and fluid structure interaction (FSI) models do not predict maximal stress. Forty percent of ruptures occur in the central part of the cap rather than regions of high curvature at the shoulders of the lipid core where FEM models predict maximum tissue stresses (11–13). Similarly, the latest study by Tang et al. (14), using an FSI model applied to 3D MRI images of sample plaques, predicts that maximal stress often appears at healthy parts of the vessel where the vessel wall is thinner than the wall on the diseased plaque side or where vessel wall curvature is large. Finally, millimeter-size or larger calcifications beneath or adjacent to a lipid-laden necrotic core, which can be easily observed by intravascular ultrasound (IVUS) or optical coherence tomography (OCT), have been theoretically predicted to be stabilizing (15, 16). Our hypothesis was conceived to explain these paradoxical observations and computational predictions.

In this article, we propose a hypothesis for the rupture of thin-cap fibroatheroma, namely that it is due to stress-induced debonding of minute calcifications, the size of a single cell whose mass is six or more orders of magnitude smaller than the millimeter or larger calcifications observed in MRI, IVUS, and OCT mentioned previously. At first glance, it might seem highly implausible that such minute inclusions are destabilizing when FEM models predict, as noted earlier, that much larger calcifications are stable (15, 16). Our hypothesis is inspired by the classical theoretical studies of Goodier (17), who examined the effect of minute solid spherical impurities in rubber tires as a cause of their failure. Subsequent experiments by Gent and Park (18) showed that debonding occurred at the interface between the solid impurity and rubber because of the large mismatch in hardness of the materials and the local stress concentrations that develop at the poles of the impurity along the tensile axis as a result of this mismatch.

Goodier's classical analysis describes a small spherical impurity in an infinite medium. In the present study, we are interested in the case where the dimensions of the solid inclusion (10 μm) are a significant fraction of the cap thickness and where the location of the impurity within the fibrous cap can be arbitrary. The problem we are interested in is basically that of a rigid spherical inclusion asymmetrically positioned in a thin elastic layer subject to uniaxial tension at infinity. This is a classical unsolved problem in the mechanics literature. The problem was of considerable interest in the 1970s when investigators were studying the fatigue fracture of high-hardness steels with spherical inclusions or voids. The effect of a solid impurity near a free surface in a semiinfinite medium was first studied by Tsutsui and Saito (19). Subsequently, Tsuchida et al. developed a solution for spherical voids in plates (20) and then extended the solution approach to treat a spherical solid inclusion of varying hardness (21) along the centerline of the plate. The solutions for a spherical void showed large variation of stress concentration as a function of inclusion position, suggesting that a similar behavior might occur for a solid inclusion. The asymmetric problem, where the solid inclusion is arbitrarily positioned in the thickness direction, is treated herein. Our solutions predict that there is a near-doubling of the interface stress at the poles of the calcified inclusion and that this doubling is only modestly affected by the positioning of the calcification within the cap thickness. Furthermore, the results of this analysis predict, quite remarkably, the critical cap thickness of 65 μm proposed by Virmani et al. (6) for vulnerable plaque rupture.

Having demonstrated the quantitative feasibility of our microcalcification hypothesis, we explored in vitro imaging techniques whose resolution far exceeded conventional MRI, IVUS, and OCT approaches to confirm that the proposed cellular-level microcalcifications actually exist. To this end, we examined autopsy specimens of coronary atheromatous lesions using confocal microscopy combined with calcium-specific stains and micro-computed tomography (CT) imaging. At the end of the article, we present images of microcalcifications in fibrous caps. As anticipated, the minute inclusions in the cap are very rare compared with the numerous calcified macrophages observed in the necrotic core. The most likely candidates for the inclusions are either calcified smooth muscle cells or macrophages that have undergone apoptosis while crossing the cap in their migration into or out of the necrotic lipid core.

Theoretical Model for Hypothesis

Most existing models of fibrous cap rupture (11–13, 15, 22, 23) have been based on FEM calculations of calcified tissue cross-sections with a lipid core where the detailed geometry has been obtained from histology or IVUS imaging. A single element in such calculations would be larger than the cellular-level impurity in our hypothesis. In this article, we develop an infinite series solution for the stress concentration around a minute impurity in a thin tissue layer whose thickness is typically 2–10 times the diameter of the impurity and whose location is arbitrary in the cap thickness direction. The convergence of this solution is confirmed by using numerical FEM methods (data not shown). The purpose of the model is to test the quantitative feasibility of the hypothesis and provide a framework for understanding the importance of the size of the impurity and its location.

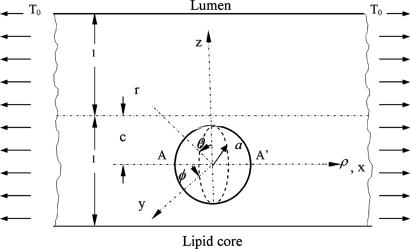
Our 3D theoretical model, shown in Fig. 1, consists of a rigid inclusion eccentrically located between the top (lumen) and bottom (lipid core) boundaries (Fig. 1). The circumferential tensile stress in the fibrous cap is modeled by unidirectional tension, T₀, applied at infinity; the top and the bottom boundaries are considered to be stress-free. Let the origin of coordinates be at the center of the inclusion with the z axis normal to the surfaces. The spherical and cylindrical coordinates are denoted by (r, φ, θ) and (ρ, φ, z), respectively. For convenience, r, z, ρ, and all other lengths are made dimensionless by scaling relative to the half-thickness of the tissue layer. In such notation, the upper (lumen) and lower (lipid core) surfaces of the fibrous cap are represented by z = ±1 + c, where c, the eccentric distance between the origin and the midline of the plate, is <1 − a. To solve the problem, we apply the Navier–Lame equations of linear elasticity for the case of equilibrium with no action-at-a-distance forces:

where u(u,v,w) is the displacement vector and λ and μ are the Lame constants. Eq. 1 is solved subject to stress-free boundary conditions at z = ±1 + c, perfect bonding conditions at the rigid spherical inclusion–tissue interface at r = a, and the condition that the normal stress in the plate in the x direction tend to a uniform stress T₀ as x tends to ±∞. The mathematical expressions for these boundary conditions are given in Supporting Appendix, which is published as supporting information on the PNAS web site.

Fig. 1.

Mathematical model: geometry and coordinate system. Shown is a perfectly bonded rigid spherical inclusion with radius a in a fibrous cap.

Although the above boundary value problem is 3D, it can be solved analytically without resort to numerical methods. The approach is patterned after the solution technique developed by Tsuchida et al. (20) for the problem of an eccentric spherical cavity under uniaxial tension. In the latter problem, the authors were interested in the stress concentration around a void space created by a spherical bubble. According to their approach, components of the displacement u(u,v,w) are first expressed in terms of six cylindrical harmonic functions, φ₀, φ₁, φ₂, φ₃, φ₄, and λ₃, which satisfy boundary conditions (2) and the normal stress condition (4) at infinity. These functions are defined in Supporting Appendix. The cylindrical harmonics are then expressed in terms of spherical harmonics that are also required to satisfy the stress-free boundary conditions (2). The boundary conditions at the inclusion–tissue interface (3) lead to an infinite system of linear equations for the unknown coefficients of the spherical harmonics which are then truncated to provide the desired numerical convergence. After solving for the coefficients, one can calculate the stresses and deformations at any point within the tissue layer. A more detailed outline of the solution is given in Supporting Appendix.

Results

Local Stress Concentration Around Minute Spherical Inclusions Embedded in a Fibrous Cap.

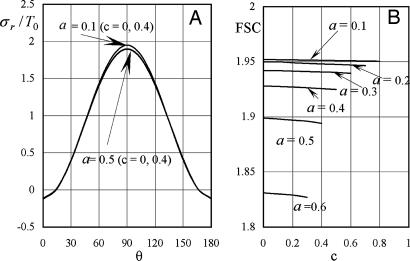
The quantitative feasibility of our hypothesis was explored by using the theoretical model in Fig. 1 to predict the factor of stress concentration surrounding a spherical inclusion in the fibrous cap. Fig. 2A shows the distribution of calculated radial stress concentration, σ_r/T₀, at the matrix–inclusion interface when the dimensionless radius of the inclusion is a = 0.1 or a = 0.5 and the eccentric distance is c = 0 or c = 0.4 and φ = 0°. One observes from the figure that the presence of a perfectly rigid inclusion almost doubles the tension (adhesion stress) at the “poles” A and A′ (θ = 90°, φ = 0°, and φ = 180°; Fig. 1) in the direction of the applied tension, T₀. In the classical theory of Goodier (17) for a rigid spherical inclusion in an infinite medium, the adhesion stress at the poles would exactly double. Surprisingly, the tensile-stress intensification is scarcely affected by the relative size of the inclusion because the curves in Fig. 2A corresponding to inclusion radii a = 0.1 and a = 0.5 are very close to one another and can be distinguished only at θ ≈ 90°, and the curves for c = 0 and 0.4 are indistinguishable. The effect of a free surface on the stress concentration is demonstrated in Fig. 2B for a = 0.1, 0.2, 0.3, 0.4, 0.5, and 0.6. Maximum tensile stresses at A and A′ tend to decline slightly as the inclusion approaches a free surface; the tendency is more noticeable for larger inclusions. One also notes that the larger inclusions are more stable and that the value of factor of stress concentration decreases with increasing size. This behavior is similar to the much larger calcifications observed in IVUS where FEM calculations predict greater mechanical stability when calcified plaques are present (15). This strengthening occurs because the model does not allow for debonding and the calcification is more rigid than the surrounding material.

Fig. 2.

Stress concentration in a fibrous cap due to the presence of a rigid spherical inclusion. (A) Distribution of radial stress concentration, σ_r/T₀, at the matrix–inclusion interface for the cases of a = 0.1, a = 0.5, and c = 0, 0.4 (φ = 0°). (B) Effect of a free surface on factor of stress concentration for a = 0.1, 0.2, 0.3, 0.4, 0.5, and 0.6.

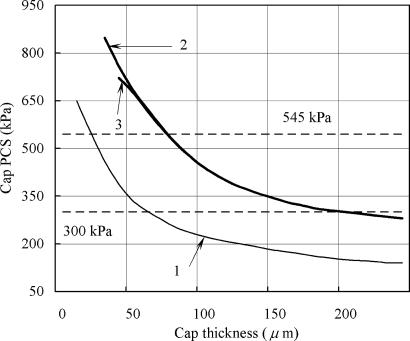
The theoretical model also allows us to estimate the peak circumferential stress (PCS) in the fibrous cap of atherosclerotic plaque arising from the presence of a calcified macrophage or smooth muscle cell. Finet et al. (22) have performed FEM calculations to predict the effect of cap thickness on the stability of fibrous cap atheroma based on typical in vivo IVUS images. The predictions of this model, which are given by line 1 in Fig. 3, show that PCS increases exponentially and will exceed the average maximum circumferential stress in ruptured plaques of 545 kPa (11) for plaque geometry 1 in Fig. 1 of their article when the fibrous cap thickness is ≈25 μm. These predictions are based on the material properties used by Cheng et al. (11). The stresses indicated by line 1 are the PCS for a lumen pressure of 14.6 kPa (110 mmHg) in the absence of a calcified macrophage. Lines 2 and 3 show how this PCS would increase if rigid inclusions 10 and 20 μm in diameter, respectively, approached to within 5- and 10-μm distances, in that order, from the lipid pool. Results of the calculations presented in Fig. 3 provide a plausible explanation of the paradox that most plaque ruptures occur close to a region of high circumferential tensile stress, defined as a stress of >300 kPa, but ruptures are not necessarily located at the points of maximum stress. According to Fig. 3, a calcified macrophage located in an area of high circumferential stress (>300 kPa) can intensify this stress nearly 2-fold to ≈600 kPa when the cap thickness is <65 μm.

Fig. 3.

Changes in cap PCS with cap thickness for the case when cap tissue is homogeneous (line 1) and when it contains a rigid inclusion 10 and 20 μm in diameter (lines 2 and 3, respectively).

Confocal Microscopy Evidence of Microcalcifications in the Fibrous Cap.

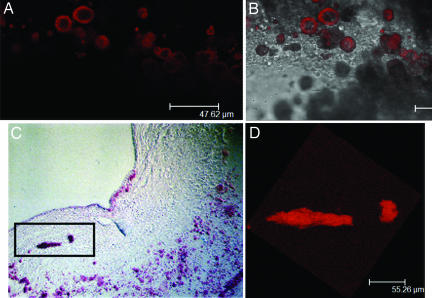
The results of our theoretical model were the catalyst for an intensive search for cellular-level solid inclusions within the cap proper. We have developed a confocal laser scanning microscopy technique using a Leica DM IRE2 microscope and Alizarin red S stain to demonstrate the presence of microscopic calcific inclusions in atherosclerotic plaques from human arteries. As shown in Fig. 4, the Alizarin red S staining technique provides high contrast in confocal images, with near negligible levels of background fluorescence. Fig. 4A shows a necrotic core containing orange-red features from individual confocal optical sections obtained by using Alizarin red S-specific detection. Fig. 4B is obtained by overlaying the Alizarin confocal images with interference contrast images. The numerous cellular- and subcellular-level calcifications observed in the lipid core in Fig. 4A reveal two characteristic calcifications, spherical calcifications with dimensions comparable with an entire macrophage or smooth muscle cell, and subcellular calcifications as small as 1–2 μm that either are of vesicular origin and extracellular or are intracellular calcified organelles. This image shows that Alizarin red S is quite sensitive to very small deposits of ≈10 μm. In some cases, the Alizarin dye incompletely penetrated the calcification and an annular staining pattern was evidenced when the optical section sampled an intersecting plane (calcifications in center of Fig. 4A).

Fig. 4.

Confocal microscopy images of calcific deposits stained with Alizarin red S in coronary artery lesions. (A) Numerous cellular- (≈10 μm) and subcellular-level calcifications in the necrotic core. (B) Overlay of A with a transmission image. (C) Calcified inclusions in the fibrous cap appear red in a section stained with Alizarin red S. (D) A 3D confocal imaging reconstruction of section C within the slide thickness.

Fig. 4 C and D shows experimental evidence for the existence of cellular-level calcifications in a fibrous cap. Fig. 4C shows two Alizarin red S-stained calcifications in close proximity, one the size of a single cell (≈10 μm) and the other an elongated calcification that is several times the diameter of the single-cell inclusion. Because we were unable to reconstruct a 3D image for this histological section, it is not possible to determine the full inclusion shape; however, the confocal imaging technique allows us to perform a 3D reconstruction of the two calcifications within the section thickness (≈30 μm). This partial reconstruction is shown in Fig. 4D.

Micro-CT Assessment of Cellular-Level Calcifications in Fibrous Caps of Atherosclerotic Lesions.

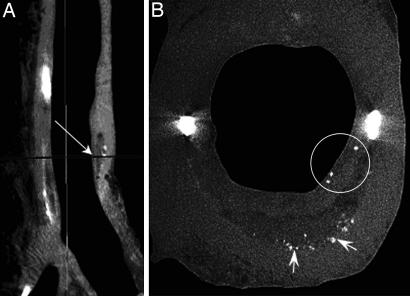
Micro-CT images provide precise plaque visualization based on relative grayscale attenuation differences within the lesions. Fig. 5A shows a sagittal section of a 25-mm coronary segment, in which different tissue constituents within the sample can be readily distinguished. In particular, air (black), soft tissue (light gray), mineral (white), and lipid (dark gray) are resolved. Initial analysis of coronary-segment reconstructions with 35-μm resolution detected five advanced atheromatous lesions with fibrous caps and lipid cores. Further reconstructions of these soft plaques at 7-μm resolution revealed the presence of cellular-level calcifications in a thick cap of one of these lesions. Fig. 5B shows a cross-section corresponding to the plane indicated by the arrow in Fig. 5A with three microcalcifications (circled) in a thick cap (≈250 μm). Similar to the confocal images shown in Fig. 4, this micro-CT image demonstrates that these cellular-level calcified inclusions in the cap are rare compared with the numerous calcifications seen at the bottom of the necrotic core (Fig. 5B, arrows). The cross-section also shows two nearly spherical macrocalcifications, ≈300 μm in diameter, at the plaque shoulders.

Fig. 5.

Micro-CT detection of cellular-level microcalcifications in a fibrous cap. (A) Sagittal view of a coronary artery segment with microcalcifications in the thick cap (35-μm resolution). (B) A cross-section of the lesion (arrow in A) corresponding to the plane marked by an arrow in A with cellular-level microcalcifications ≈10- to 20-μm diameter in the cap (circled) and numerous calcific deposits at the bottom of the lipid pool shown by arrows (7-μm resolution).

Discussion

Our hypothesis that minute cellular-level microcalcifications of typically 10-μm diameter in the fibrous cap can cause its rupture provides an important insight into the mechanism of fibrous cap rupture and also resolves a long-standing paradox as to why rupture does not always occur at the location of what was previously thought to be maximal tissue stress. The model predicts that minute spherical calcifications can increase the local stress around the embedded particle by nearly a factor of two at the poles of the tensile axis and that this amplification, quite surprisingly, is nearly independent of the size of the particle and relatively insensitive to its position in the fibrous cap. One of the striking results of the theoretical model is that it predicts that cap rupture can occur in the center of a fibrous cap whose thicknesses is <65 μm, in close agreement with the empirical observations of Virmani et al. (6).

Our hypothesis provides a plausible explanation for the paradoxical observation that ≈40% of ruptures are observed in the center of the cap, and not at the plaque shoulders where FEM calculations predict the maximum values of circumferential stress (9, 11). Using FEM analysis, Cheng et al. (11) calculated the stress distribution in specific coronary artery lesions that caused lethal myocardial infarction at a mean intraluminal pressure of 110 mmHg and compared it with the stresses in control stable lesions. The average maximum circumferential stress in ruptured plaques without cellular-level solid inclusions was significantly higher, 4,091 ± 1,199 mmHg (545 ± 160 kPa), than the average maximum stress found in stable specimens, 1,444 ± 485 mmHg (193 ± 65 kPa), but not all plaque ruptures occurred at the region of the highest stress. In 7 of 12 ruptured lesions, rupture coincided with the location of the maximum circumferential stress, whereas in 10 of 12, lethal lesions rupture occurred where calculated stress was not maximal but was >2,250 mmHg (300 kPa). The near-doubling of the local stress due to the presence of minute calcifications in fibrous caps of these lesions can explain why rupture often occurs in secondary stress concentration regions. Our theoretical analysis predicts that the presence of a calcified cellular inclusion in the shoulder would be even more dangerous than in the central portion of the cap because the background stress here is greater and its doubling would make this region especially vulnerable. Thus, we propose that the site of cap rupture depends on the relative location of both the circumferential stress concentration and whether minute cellular-level microcalcification is present in the cap. Furthermore, the average maximum stress of 545 kPa could be the rupture stress of the cap if no cellular-level solid inclusions are present.

The recent study by Tang et al. (14) revealed another paradox in the assessment of plaque vulnerably. Their 3D MRI-based computational model with multicomponent plaque structure and FSI predicts that global maximal stress often appears at healthy parts of the vessel where vessel walls are thinner than the diseased plaque side or vessel curvature is large, although rupture does not occur at these sites. To resolve this paradox, the authors advance a “local maximal stress hypothesis” suggesting that local maximal stress values at critical locations may be more closely related to possible plaque rupture and should be used for more accurate mechanical plaque assessment. Preliminary results based on calculating the stress-based computational plaque vulnerability index (CPVI) showed a good correlation with plaque stability assessment given by histopathological analysis. This index is consistent with our hypothesis because a cellular-level calcification located at the critical site can nearly double their computed stress. Although these microcalcifications cannot currently be detected by standard imaging techniques (the present resolution of IVUS is ≈120 μm and OCT 15 μm), future development of the OCT technique might allow in vivo detection of these inclusions in thin fibrous caps. Such microcalcification assessment combined with advanced in vivo image-based FEM/FSI models will provide more accurate quantitative assessment of plaque stability.

Our theoretical prediction that cellular-level calcifications can be responsible for plaque rupture might seem counterintuitive at first because much larger punctate calcifications (10⁶ times the mass of a single cell) have been shown to be stabilizing by FEM calculations (15, 16). Computational analysis applied to typical ruptured or stable human coronary atherosclerotic lesions reveals that millimeter-size or larger calcifications deeper in the intima do not increase fibrous cap stress in the lesions (15). In contrast to a lipid pool, which dramatically increases cap stresses, bulk calcification does not seem to decrease the mechanical stability of the coronary atheroma. The most recent 3D FEM calculations of the longitudinal stress distribution within atherosclerotic plaques based on a simplified axisymmetric geometry demonstrated that superficial millimeter-size calcified plaques adjacent to the lipid core led to a decrease in the peak longitudinal stress value at the fibrous cap just above the lipid core (16). Our model also predicts that the larger inclusions are more stable and that the value of circumferential stress concentration decreases with increasing size. This behavior is similar to the much larger calcifications observed in IVUS where FEM calculations predict greater mechanical stability when calcified plaques are present (15). This strengthening occurs because the model does not allow for debonding and the calcification is more rigid than the surrounding material. Larger calcifications are also frequently observed beneath or at the edges of lipid pools, as seen in Fig. 5B, where the wall is thicker. For these larger calcifications, the stress is also nearly doubled, but the background stress is much lower, and even with a 2-fold increase in stress, the total stress would not exceed the threshold stress of 300 kPa.

The presence of small cellular- and subcellular-level calcified inclusions in necrotic cores of advanced atherosclerotic lesions has been reported in a number of histological studies (6, 24, 25). These microcalcifications have been mentioned in several intravascular imaging studies as a coronary calcification pattern that is extremely difficult to detect. For instance, Friedrich et al. (26) describe microcalcifications as small flecks of calcium with a single fleck size of ≤50 μm in their IVUS study of intralesional calcium patterns. Only 17% of these microcalcification lesions were detected correctly by intracoronary ultrasound in contrast to 89% of all dense calcified plaques. Similarly, a frequency-based spectral analysis of unprocessed ultrasound data (27) demonstrated that although microcalcifications reflect slightly more ultrasound energy than moderate fibrosis and less than dense fibrosis, the echoreflectivity of the plaque cannot be used alone to identify microcalcification from moderate fibrosis. These cellular-level calcifications in the necrotic core are not dangerous from a mechanical standpoint because they reside within a viscous lipid pool that does not support significant tensile stress. They are essentially floating debris without interface stresses. This is the exact opposite of a microcalcification that would occur in the fibrous cap as shown by our theoretical model.

Our hypothesis for fibrous cap rupture is inspired by the classical theoretical studies of Goodier (17), who examined the effect of minute solid spherical impurities in rubber tires as a cause of their failure. Failure will not occur unless there is debonding (failure at the tissue–particle interface). The most frequent cause of debonding is the formation of a minute cavitation bubble at the interface, which then rapidly expands. Experiments by Gent and Park (18) showed that debonding occurred at the interface between the solid impurity and rubber because of the large mismatch in hardness of the materials and the local stress concentrations that develop at the poles of the impurity along the tensile axis as a result of this mismatch. Classical experiments with spherical impurities in elastomeric materials clearly demonstrate the creation of these cavitation bubbles (28, 29). The maximum circumferential stress of 4,091 ± 1,199 mmHg (545 ± 160 kPa) estimated by Cheng et al. (11) in ruptured plaques is almost equivalent to 6 atm (1 atm = 101.3 kPa) and, thus, far greater than needed to produce a negative pressure or vacuum at the failure interface. We emphasize that the present theoretical analysis does not incorporate debonding per se but clearly demonstrates the possibility that this can occur. Future experimental studies are needed to demonstrate the possibility of such failure in coronary arteries with microcalcifications.

Another example of the influence of inclusions on the strength of materials is the reduction in fatigue strength of steels due to the stress concentration introduced by an inclusion. In high-hardness steel, cracks often initiate preferentially from nonmetallic inclusions either on or beneath a free surface of a specimen and lead to final fracture. Since the 1933 classical study of Goodier (17), numerous theoretical or experimental investigations have been performed to obtain a better understanding of the stress fields due to inclusions in an elastic medium. However, most of the studies had been focused on inclusions within an infinite medium, and thus the results could not be applied to the analysis of fractures of high-hardness steels where a free surface has a strong influence on the stress field. Tsutsui and Saito (19) were the first to analyze the problem of a semiinfinite body containing a perfectly bonded spherical inclusion under axisymmetric tension to see the effect of a free surface on the stress field. Their calculations showed that the effect of a free surface is significant when the inclusion is soft. On the other hand, if the inclusion is rigid, the maximum tensile stress appears to be insensitive to its position within the semiinfinite plate and tends to decline slightly as the inclusion approaches a free surface similar to our observations in Fig. 2B. Shortly after this, Nakahara et al. (21) developed solutions for a symmetrically located spherical inclusion under uniaxial tension and showed large variation of the stress concentration as a function of its hardness. The 3D asymmetric problem, where a rigid spherical inclusion is arbitrarily located within a thin plate, is treated herein. A closed-form truncated series solution for stresses and displacements is represented by a combination of a solution that is regular outside of the inclusion and a solution that is regular in an infinite plate. This solution is derived by using an approach similar to that proposed by Tsuchida et al. (20) for the problem of an eccentric spherical cavity under uniaxial tension.

The predictions of our theoretical model were the catalyst for an experimental search for probable weakening factors in the cap responsible for creating stress levels sufficient for its rupture. There were no prior reports, to our knowledge, of cellular-level solid inclusions in the cap proper. Our initial effort was to develop a confocal laser scanning microscopy technique that would clearly identify calcium. This approach was suggested by the fact that macrophages and smooth muscle cells in the necrotic core were observed to calcify after apoptosis. Therefore, it seemed plausible that both of these cell types could undergo apoptosis and calcification in migrating across the fibrous cap of the lesion. Having obtained confocal imaging evidence for the presence of cellular-level microcalcifications in the cap proper, we sought a 3D nondestructive imaging technique that would allow a systematic analysis of intact and unprocessed coronary artery segments. Recently, Langheinrich et al. (30) demonstrated the feasibility of using micro-CT for morphological and quantitative analysis of macroscopic atherosclerotic lesions. Micro-CT imaging provides an accurate characterization of lesion morphology due to the difference in density between air, soft tissue, lipid, and mineral. In contrast to histologic processing, which requires fixation, dehydration, and/or some degree of decalcification before paraffin embedding to allow sectioning, micro-CT imaging can be performed in unprocessed coronary arteries. This approach prevents mechanical and physiochemical artifacts, such as shrinkage of the specimen, and retains true calcification morphology because no decalcification is involved. Another problem with histological analysis is the difficulty of obtaining adjacent sections and avoiding distortion during the sectioning process. Histologic microscopy also does not provide 3D information and, as a destructive technique, is limited to a small number of 2D sections. With micro-CT, a complete digital data set of the whole vessel is available. By using tomographic reconstruction algorithms, 3D images of the vessel wall can be generated that allow total stereoscopic visualization of the 3D microarchitecture. Because of all of these advantages combined with reliable and clear mineral detection, micro-CT imaging appears to be the best method to assess the presence of microcalcifications in the cap of fibroatheroma lesions in vitro.

Finally, it should be emphasized that the purpose of the present experimental study was simply to confirm our hypothesis that microcalcifications do indeed exist in fibrous caps and not just in the necrotic core. It is clear that a large-scale statistical study is needed to quantify and compare the likelihood of cellular-level microcalcifications in the cap of ruptured and nonruptured plaques and to further validate our proposed hypothesis for fibrous cap rupture. Our initial experimental data show that these calcifications are very rare compared with the numerous cellular- and subcellular-level calcifications observed in the lipid core (Figs. 4 and 5). If there were many such calcifications, one might anticipate that there would be a high risk of cap rupture and thrombus formation even if not all ruptures lead to occluding thrombi (31). We also emphasize that cap rupture is very likely a multifactorial event, and variation in material properties of the cap could play a role. For instance, this might provide a predilection for the cellular-level calcifications being more likely to occur in some regions of the cap rather than others. Local material properties could have a significant effect on macrophage apoptosis.

Methods

Fluorescent Confocal Imaging.

Human coronary segments obtained at autopsy time, <12 h after death, were pressure-fixed with 10% formalin and later stained with 2% aqueous solution of Alizarin red S (A5533–25G; Sigma, St. Louis, MO) at pH 4.2 for 5 min (32). After staining, the samples were washed twice with deionized H₂O followed by 70% ethanol to remove the excess stain from the tissue. The segments were examined by using a confocal laser scanning microscope system (DM IRE2; Leica, Deerfield, IL) with an oil-immersed objective (index of refraction, n = 1.4; magnification level, ×63). To examine the signals arising from calcifications stained with Alizarin red S relative to potential autofluorescence, confocal spectral imaging was used to verify the presence of Alizarin-derived signals with expected emission maxima at 650 nm. The detection window selected by using the Leica acousto-optical beam splitter ranged from 645 to 665 nm for these measurements (633-nm HeNe laser excitation). For reference, interference contrast images were collected by using the Leica tube optics HC 1X/B apparatus with a focusing Bertrand lens for setting the contrast.

Micro-CT Imaging Technique.

Formalin-fixed human coronary segments (≈25 mm in length, n = 24) obtained at autopsy were scanned by using the eXplore SP Pre-Clinical Specimen Micro-CT acquisition and analysis system (GE Healthcare, Piscataway, NJ). For image acquisition, 720 consecutive x-ray projections were taken, obtaining 7-μm isotropic voxel resolution images. Mineral density was calibrated by using a phantom containing hydroxyapatite, air, and water. The detailed experimental protocol is given in Supporting Methods, which is published as supporting information on the PNAS web site.

Abbreviations

CT

computed tomography

FEM

finite element

FSI

fluid structure interaction

IVUS

intravascular ultrasound

OCT

optical coherence tomography

PCS

peak circumferential stress