Mg²⁺–RNA interaction free energies and their relationship to the folding of RNA tertiary structures

Abstract

Mg²⁺ ions are very effective at stabilizing tertiary structures in RNAs. In most cases, folding of an RNA is so strongly coupled to its interactions with Mg²⁺ that it is difficult to separate free energies of Mg²⁺– RNA interactions from the intrinsic free energy of RNA folding. To devise quantitative models accounting for this phenomenon of Mg²⁺-induced RNA folding, it is necessary to independently determine Mg²⁺–RNA interaction free energies for folded and unfolded RNA forms. In this work, the energetics of Mg²⁺–RNA interactions are derived from an assay that measures the effective concentration of Mg²⁺ in the presence of RNA. These measurements are used with other measures of RNA stability to develop an overall picture of the energetics of Mg²⁺-induced RNA folding. Two different RNAs are discussed, a pseudoknot and an rRNA fragment. Both RNAs interact strongly with Mg²⁺ when partially unfolded, but the two folded RNAs differ dramatically in their inherent stability in the absence of Mg²⁺ and in the free energy of their interactions with Mg²⁺. From these results, it appears that any comprehensive framework for understanding Mg²⁺-induced stabilization of RNA will have to (i) take into account the interactions of ions with the partially unfolded RNAs and (ii) identify factors responsible for the widely different strengths with which folded tertiary structures interact with Mg²⁺.

Mg²⁺ ions strongly stabilize RNA tertiary structures under conditions that only weakly affect RNA secondary structure stability, a phenomenon first studied in the folding of transfer RNA (1, 2). Although the sensitivity of RNA folding to Mg²⁺ has been amply documented for many RNAs, it is still unknown how this sensitivity is quantitatively related to the strengths of Mg²⁺–RNA interactions. Thus, for most RNAs, the magnitude of the intrinsic RNA instability is unknown, nor is it known how much more favorably Mg²⁺ interacts with the native RNA structure than with structures from which folding takes place. Lacking this fundamental overview of Mg²⁺–RNA interaction free energies, it has not been possible to carry out extensive evaluations of theoretical models that seek to explain Mg²⁺-induced RNA folding in terms of the underlying physical interactions (3, 4).

In this article, we parse the tertiary folding of two different RNAs into the intrinsic free energy of folding in the absence of Mg²⁺ and the free energies of Mg²⁺ interactions with folded and partially folded states. To obtain the relevant free energies, we devised a practical experimental method for measuring the effect of RNA on Mg²⁺ ion activities and derived the equations necessary for extracting Mg²⁺–RNA interaction free energies from the experimental data. The two RNAs have vastly different stabilities in the absence of Mg²⁺ and correspondingly large differences in the favorable interactions of the native RNA structures with Mg²⁺. Clearly, different RNAs use different strategies to achieve stable tertiary structures. By using rigorous thermodynamic measurements to define the scope of the Mg²⁺–RNA interaction problem, this work provides an experimental context for further development of theoretical accounts of ion–RNA interactions.

Background

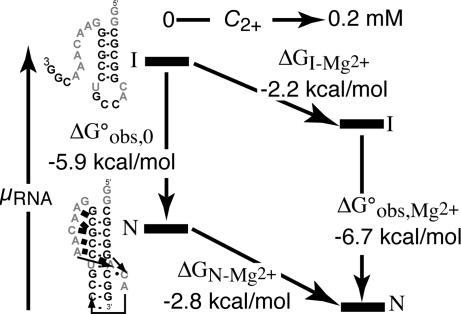
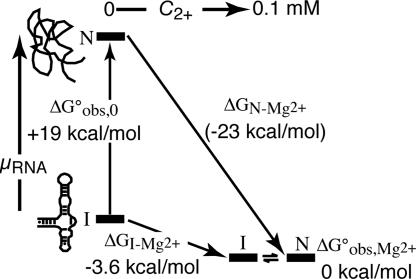
A scheme depicting the stabilization of an RNA tertiary structure (a pseudoknot) by Mg²⁺ is shown in Fig. 1. By following a standard formulation of RNA folding pathways (5, 6), we denote the fully folded RNA with “N” (native) and the partially folded form of the RNA with “I” (intermediate). For most RNAs, the I state is an ensemble of different secondary-structure conformations rather than a unique structure. (Fully unfolded RNA is usually found only under strongly denaturing conditions. Because this article is concerned with the formation of RNA tertiary structure, “folding” will be used to refer to the I→N reaction in the rest of the article.) In Fig. 1, the different forms of the RNA are placed along the vertical axis according to their relative chemical potentials (free energies); going horizontally from left to right corresponds to the addition of MgCl₂. The arrows of the folding pathways decompose Mg²⁺-induced RNA folding into the RNA-folding reaction itself (Fig. 1, vertical arrows) and Mg²⁺–RNA interactions (Fig. 1, sloping horizontal arrows). For the pseudoknot illustrated in Fig. 1, folding in the presence of monovalent ions only is a favorable reaction (ΔG_obs,0^°, the left vertical arrow, is negative). Upon addition of MgCl₂, the chemical potentials of the I and N states decrease (ΔG_N-Mg²⁺ and ΔG_I-Mg²⁺ are both negative). The N state interacts more strongly with Mg²⁺ ions than the I state; therefore, a net stabilization of the pseudoknot structure takes place. As discussed in Results in relation to an rRNA fragment, the N- and I-state positions for many RNAs are reversed in the absence of Mg²⁺ (ΔG_obs,0^° is unfavorable).

Fig. 1.

Thermodynamic cycle for Mg²⁺-induced RNA folding. The cycle separates the folding reaction (vertical arrows) from Mg²⁺ association (sloping horizontal arrows), where I is a partially folded state of the RNA and N represents the native structure. Experimental free energies for BWYV RNA are associated with each reaction arrow. The I and N states have been positioned in the vertical dimension approximately to scale according to the chemical potential (relative free energy) of the particular state. Free energies refer to buffers containing 54 mM Na⁺, 10 mM Mops (pH 7.0), and Cl⁻ anion at 25°C.

A useful quantity related to the thermodynamic cycle in Fig. 1 is ΔΔG_Mg²⁺, the change in RNA-folding free energy afforded by a given concentration of Mg²⁺. This free energy is defined as

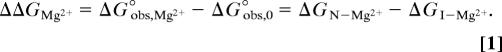The two ways of expressing ΔΔG_Mg²⁺ are equivalent because the free energy in going from the I-state RNA in the absence of Mg²⁺ to the N state in the presence of Mg²⁺ must be the same by either of the two possible paths.

Of the four free energies defined in Fig. 1, ΔGobs,Mg2+° is the only one that is routinely determined experimentally (e.g., from melting experiments). ΔGobs,0° is not directly accessible for the majority of RNA tertiary structures, which are unstable in the absence of Mg2+. ΔGN-Mg2+ and ΔGI-Mg2+ can only be obtained by measuring the extent of Mg2+ interaction with an RNA, for instance by equilibrium dialysis. These kinds of measurements have been done for only a few folded tRNAs (2, 7,8–9) and one rRNA fragment (10). Thus, for most RNAs, we do not know the overall contribution of Mg2+ to RNA folding (ΔΔGMg2+) or the degree to which Mg2+ affects the free energies of folded and partially folded forms.

Most formulations of the effects of Mg²⁺ on RNA folding transitions have considered Mg²⁺ as a ligand that binds stoichiometrically to sites in the folded forms of the RNA, e.g., I + nMg²⁺ ⇌ N·(Mg²⁺)_n (11–13). This approach oversimplifies the complex set of interactions taking place between RNA, Mg²⁺, monovalent cations, and anions (6). A more useful starting point for considering the influence of ions on nucleic acid equilibria has been to ask how the chemical potentials of the nucleic acid species change as a function of salt concentration, which does not introduce any assumptions about the nature of the interactions taking place (14, 15). (The sloping horizontal lines in Fig. 1 represent this dependence of I or N RNA chemical potential on Mg²⁺ concentration.)

The relationship between RNA chemical potential and changing salt concentration can be derived in terms of an experimentally accessible quantity sometimes called the ion interaction coefficient (15). The coefficient for Mg²⁺–RNA interactions taking place in the presence of excess monovalent salt is referred to here as Γ₂₊. Consider a single RNA molecule in solution. On and near the RNA, Mg²⁺ ions are at high concentrations, which decrease with distance until the effects of the RNA electrostatic field are negligible; the ions are then at their “bulk” concentrations. Γ₂₊ is the difference in the number of ions present in a large volume surrounding the RNA and the number of ions in an equivalent volume far from the RNA, or the “excess” Mg²⁺ ions accumulated per RNA at a given bulk Mg²⁺ concentration. Γ₂₊ also can be thought of as half the number of RNA negative charges neutralized by Mg²⁺; the remaining charges are neutralized by excess monovalent cations (Γ₊) and a deficiency of anions (Γ₋). As derived in Supporting Text, which is published as supporting information on the PNAS web site, the free energies of Mg²⁺–RNA interaction in Fig. 1 (ΔG_N-Mg²⁺ and ΔG_I-Mg²⁺) are obtained by integrating the values of Γ₂₊ obtained when an RNA is titrated with MgCl₂ (m₄) while keeping the monovalent ion concentration constant:

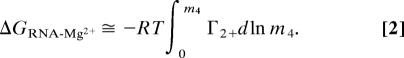Eq. 2 applies only if (i) the concentration of NaCl or KCl is in large enough excess over MgCl₂ that the Cl⁻ concentration is nearly constant during the titration and (ii) Γ₂₊ is evaluated at dilute RNA concentrations, at which RNA–RNA interactions are negligible and m₄ is equivalent to the bulk Mg²⁺ concentration (molal units), as defined above. The correspondence of Γ₂₊ and m₄ with experimental quantities is made in Mg²⁺–RNA Titrations Monitored by a Fluorescent Dye and in Supporting Text.

We emphasize that this formulation of Mg²⁺–RNA interactions in terms of Γ₂₊ is completely general. In the case of strong ligand binding at specific sites on a macromolecule, the interaction coefficient Γ becomes the number of bound ligands per macromolecule (binding density). But in the case of ions and RNA, the long-range nature of electrostatic interactions means that an RNA interacts with all of the ions in solution; “bound” and “free” ions cannot be rigorously distinguished. Free energies calculated from Γ₂₊ by using Eq. 3 include all Mg²⁺–RNA interactions, whether from site-bound ions or ions distant from the RNA. We will refer to Γ₂₊ as the “excess” number of ions per RNA to distinguish it from the more familiar binding density.

Linkage analysis developed by Wyman (16) and described in Supporting Text gives the following approximate relationship between Γ₂₊ for the N- and I-state RNAs and the way the free energy of the folding reaction changes with Mg²⁺ concentration:

where C₂₊ is the molar Mg²⁺ concentration and the concentration of monovalent salt is held constant. This relationship assumes that there is an excess of monovalent ions over Mg²⁺, that there is a large excess of Mg²⁺ over RNA phosphates, and that the folding transition is described by a two-state equilibrium.

Results

Mg²⁺–RNA Titrations Monitored by a Fluorescent Dye.

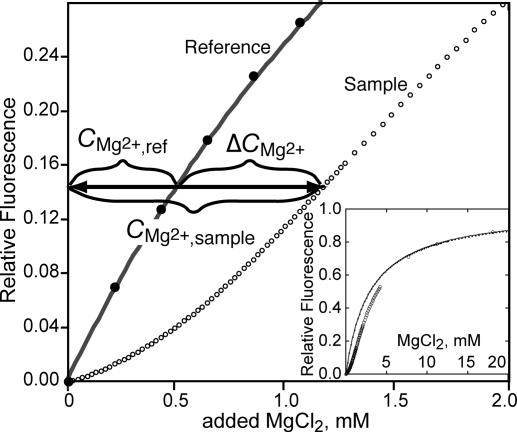
Indicator dyes have been used as a means to monitor the effective concentration of Mg²⁺ in the presence of tRNA (2) or homopolymer RNA (17). A Mg²⁺ chelator, 8-hydroxyquinoline-5-sulfonic acid (HQS), is convenient for this purpose; Mg²⁺ binding causes a large shift in its visible wavelength absorption maximum and an ≈40-fold increase in its fluorescence intensity (18). Fig. 2 shows parallel MgCl₂ titrations of reference and sample solutions containing HQS. The solutions are buffered identically and have the same concentration of KCl. RNA, previously equilibrated with the same buffered salt solution, has been added to the sample. The reference titration yields an HQS–Mg²⁺-binding curve that is fit by a single-site-binding isotherm over the entire range of Mg²⁺ concentrations used (Fig. 2 Inset). A distinct lag is seen in the sample solution titration curve: For a particular Mg²⁺ concentration in the reference solution, an excess amount of Mg²⁺, ΔC_Mg²⁺, has been added to the sample solution to attain the same effective Mg²⁺ concentration. (Note that HQS is being used to monitor the Mg²⁺ thermodynamic activity in these experiments and that cation–RNA interactions are reflected in a reduced activity coefficient of the ion. HQS is not counting bound ions.) For instance, the horizontal arrow in Fig. 2 shows that the HQS fluorescence intensity obtained after addition of 0.5 mM MgCl₂ to the reference solution (C_Mg²⁺,ref; henceforth referred to as C₂₊) is observed only after 1.2 mM MgCl₂ has been added to the sample (C_{Mg²⁺,sample}). The excess Mg²⁺ concentration measured at a particular effective Mg²⁺ concentration is normalized to the RNA (C_RNA) or nucleotide (C_nt) molar concentration used in the experiment:

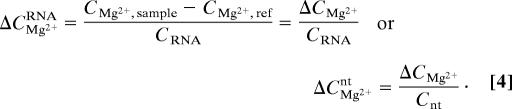In Supporting Text, it is shown that when KCl or NaCl is in excess over added MgCl2, ΔCMg2+RNA ≈ Γ2+ and the bulk Mg2+ concentration is approximately the effective Mg2+ concentration, m4 ≈ C2+. These experimental quantities, ΔCMg2+RNA and C2+, can therefore be substituted, respectively, for Γ2+ and m4 in Eq. 3 to calculate ΔGRNA-Mg2+.

Fig. 2.

Representative titration of an indicator dye, HQS, with MgCl₂ in the presence (open circles) or absence (closed circles) of 4.18 mM A1088U RNA nucleotides in otherwise identical buffers (60 mM K⁺/10 mM Mops, pH 7.0/Cl⁻ anion). The two data sets have been normalized to the same extrapolated maximum fluorescence intensity. The ordinate is the total molarity of added Mg²⁺. The solid line has been fit to the HQS alone titration with a single-site-binding isotherm, K = 337 M⁻¹. The horizontal arrow shows the relationship between the bulk Mg²⁺ concentration (C_Mg²⁺,ref) and the value ΔC_Mg²⁺ = C_{Mg²⁺,sample} − C_Mg²⁺,ref (see text).

The approximation that ΔCMg2+RNA ≈ Γ2+ also assumes that RNA does not affect the sensitivity of HQS to Mg2+ ions (by directly binding the dye, for instance); other assumptions are mentioned in Supporting Text. Inadequacy of any one of these assumptions would be manifested as a dependence of ΔCMg2+RNA on RNA concentration. No such trend in ΔCMg2+RNA values has been observed with the RNAs discussed here (see Supporting Text).

Beet Western Yellow Virus (BWYV) Pseudoknot Folding.

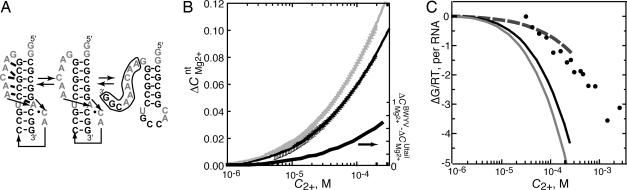
A pseudoknot RNA from BWYV induces ribosome frameshifting. High-resolution crystal structures of the RNA (19, 20) show extensive hydrogen bonding of loop bases in the grooves of the two Watson–Crick helices (Fig. 3A). Nixon and Giedroc (21) used UV melting and scanning calorimetry of a series of variants to show that full denaturation takes place in three two-state transitions; the first two are shown in Fig. 3A. We have reproduced the UV melting curves obtained by these workers and found that the RNA remains fully folded at Na⁺ concentrations as low as 24 mM (at 25°C).

Fig. 3.

Energetics of BWYV RNA folding in 54 mM Na+ (pH 7.0) at 25°C. (A) Unfolding pathway of BWYV pseudoknot RNA. Bold nucleotides connected by thin lines are Watson–Crick pairs; lines with arrowheads indicate 5′–3′ connectivity of nucleotides; thick bars represent tertiary hydrogen bonds as deduced from a crystal structure (19). Thermal denaturation causes a first loss of tertiary hydrogen bonding followed by denaturation of the shorter Watson–Crick helix, as deduced from thermodynamic studies of variant sequences (21). 3′ nucleotides (boxed in the hairpin structure) have been changed to U in the variant termed U-tail. (B) ΔCMg2+nt curves for BWYV (gray circles) and U-tail (black circles) RNAs at 54 mM Na+. Error bars are derived from the average of three independent titrations. The solid lines are polynomials fit to the data as described in Materials and Methods. The difference between the two polynomials, ΔCMg2+BWYV − ΔCMg2+Utail, is also plotted (right ordinate, expressed in ions per RNA). (C) Free energy changes upon addition of MgCl2 to BWYV RNA (ΔGN-Mg2+, gray curve) or U-tail RNA (ΔGI-Mg2+, black curve), as calculated from titration data in B; the difference between these two curves is plotted as the dashed curve, ΔΔGMg2+. Circles are values of ΔΔGMg2+ calculated from unfolding free energies derived from melting experiments (see Materials and Methods).

Because the BWYV pseudoknot is stable in the fully folded (N state) form at low concentrations of monovalent salt, its interactions with Mg2+ ions can be studied without the complication of Mg2+-induced folding. To measure the effect of Mg2+ on an I-state RNA, an altered BWYV sequence was used in which nine residues at the 3′ terminus were changed to U (“U-tail” RNA). This modification prevents formation of any secondary structure except the single hairpin shown on the right side of Fig. 3A. ΔCMg2+nt has been measured for both BWYV and U-tail RNAs as a function of C2+ (Fig. 3B). The difference between these two curves, ΔCMg2+BWYV − ΔCMg2+Utail, also is plotted in Fig. 3B (right ordinate, expressed as Mg2+ ions per RNA). To the extent that U-tail RNA mimics the partially unfolded I state of BWYV RNA, this difference curve represents the increased number of excess Mg2+ ions in the N-state RNA relative to the I state, ΔΓ2+. ΔΓ2+ necessarily approaches zero at very low C2+, and smoothly rises to ≈0.75 ions per RNA molecule at the highest Mg2+ ion concentrations used in these experiments.

As discussed above, the area under a plot of ΔCMg2+nt vs. log(C2+) is related to the change in free energy of the RNA due to its interactions with Mg2+ ions. These free energy changes, ΔGI-Mg2+ and ΔGN-Mg2+ as marked by the sloping horizontal arrows in Fig. 1, are plotted in Fig. 3C. The difference between these two ion–RNA free energies, ΔΔGMg2+, is the stabilization energy afforded to the N-state (folded) RNA by Mg2+ (Eq. 1). This free energy also is plotted in Fig. 3C (dashed line). Mg2+ interacts with the partially unfolded RNA only marginally less strongly than with the folded pseudoknot; hence, ΔΔGMg2+ is small compared with ΔGI-Mg2+ or ΔGN-Mg2+.

The free energies of the folding reactions indicated by the vertical arrows in Fig. 1, from a single hairpin to the native pseudoknot, correspond to the sum of the free energies of the first two unfolding transitions shown in Fig. 3A. The free energies of these transitions have been measured by UV melting experiments carried out in increasing concentrations of Mg2+ at a constant Na+ concentration (data not shown). The difference between the RNA folding free energies measured in the presence and absence of Mg2+ (ΔGobs,Mg2+° − ΔGobs,0°) is the same Mg2+ stabilization free energy as calculated from the difference between the areas under the ΔCMg2+RNA curves (ΔΔGMg2+) (Eq. 1). The values of ΔΔGMg2+ calculated from melting experiments (plotted as points in Fig. 3C) are in reasonable agreement with the ΔΔGMg2+ curve derived from titration experiments, over the range in which the two data sets overlap.

Fig. 1 summarizes the free energies relevant to Mg2+-induced stabilization of the BWYV pseudoknot at a single set of conditions (54 mM Na+ at 25°C with or without 0.2 mM Mg2+). All four free energy changes in the thermodynamic cycle have been measured independently, the two Mg2+–RNA interaction free energies from titrations monitored by HQS and the two folding free energies from melting experiments. ΔΔGMg2+ derived from melting experiments (vertical arrows) is −0.8 kcal/mol, which is consistent with the ΔΔGMg2+ of −0.6 kcal/mol derived from the HQS-monitored Mg2+–RNA titrations. This agreement is within the inherent error of these measurements, which we estimate as ±0.1 kcal/mol in each case. There also are potential sources of error due to differences in the I-state RNAs in the two different experiments (U-tail RNA may have a different conformation than thermally unfolded BWYV RNA, with an unknown effect on Mg2+–RNA interactions) and a small uncertainty in the polynomial extrapolation of ΔCMg2+nt values to the x axis in Fig. 3B.

Folding of a 58-mer rRNA Fragment.

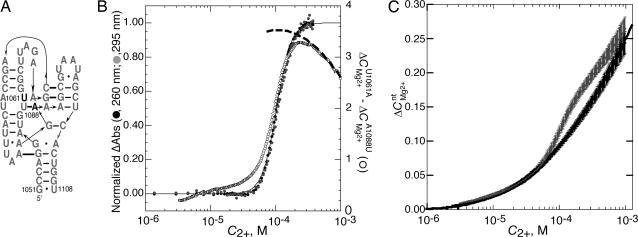
A 58-nt fragment of 23S rRNA constitutes an independently folding domain of the ribosome that binds protein L11. The structure of the domain has been resolved by crystallography of protein-bound rRNA fragments (22, 23). The native structure has an extensive set of tertiary hydrogen bonds that constrain the RNA in a compact conformation (Fig. 4A). The sequence used for folding studies in this work, U1061A RNA, is a particularly stable variant of the Escherichia coli rRNA in which a base pair that competes for tertiary structure formation (U1061/A1077) is disrupted (24). Titration of this RNA with MgCl₂ causes a cooperative folding transition under the conditions used here (Fig. 4B). Identical folding curves are observed whether hypochromicity at 260 nm or hyperchromicity at 295 nm is monitored. Because changes at 295 nm in this RNA originate solely from formation of tertiary structure (24) and have a distinct origin from the base-stacking interactions that cause hypochromic changes at shorter wavelengths (25), the coincidence of the two curves is evidence in favor of a two-state folding transition.

Fig. 4.

Energetics of folding a 58-mer rRNA fragment in 60 mM K+ (pH 6.8) at 15°C. (A) Nucleotides 1051–1108 of the E. coli 23S rRNA showing secondary structure (thin lines) and base–base tertiary interactions (thick bars) found in a crystal structure (22). The positions of two variants of the E. coli sequence are shown in outline, one stabilizing (U1061A) and the other destabilizing (A1088U). The I-state form of this RNA presumably retains most of the shown secondary structure interactions but almost certainly differs in detail. (B) Mg2+-induced 58-mer RNA folding as monitored by (left ordinate) UV absorbance at 295 (gray circles) or 260 (black circles) nm, after subtraction of baselines and normalization (see Materials and Methods). The solid line is a plot of the Hill equation in which the midpoint of the transition is at 0.103 mM and the exponent is 3.99. The right ordinate indicates the difference between ΔCMg2+RNA measured for U1061A and A1088U RNAs, taken from C and reported per RNA molecule (open circles). The dashed line (right ordinate) is an extrapolation of ΔΓ2+ from ΔCMg2+RNA data between 0.4 and 1.0 mM C2+ (see Materials and Methods). (C) ΔCMg2+nt measured for U1061A (gray curve) and A1088U (black curve) RNAs. Averaged data points and error bars are calculated from six independent titrations.

ΔCMg2+nt was measured for two variants of the 58-mer rRNA fragment from E. coli (Fig. 4C). One is the stable variant discussed above, U1061A RNA. A second variant of the 58-mer rRNA fragment, A1088U, lacks a key tertiary interaction and shows no Mg2+-induced structure formation under the same solution conditions used to fold U1061A RNA (melting experiments not shown). In measurements of ΔCMg2+nt, A1088U RNA gives a monotonic curve similar to those obtained for the BWYV pseudoknot variants. ΔCMg2+nt curves for U1061A and A1088U RNAs nearly coincide at low Mg2+ concentrations, as expected if the two RNAs have similar partially unfolded structures (Fig. 4C). However, U1061A RNA undergoes a transition to a form with larger ΔCMg2+nt values at ≈0.1 mM Mg2+. At higher Mg2+ concentrations, ΔCMg2+nt values for the two RNAs start to approach each other. This behavior is consistent with Γ2+ curves calculated for tRNA, which suggest that the difference between the number of excess ions associated with I- and N-state RNAs starts to decline when Γ2+ exceeds ≈0.2 ions per nucleotide (4).

To show that the U1061A RNA transition detected by ΔCMg2+nt measurements indeed represents the formation of tertiary structure, the difference between ΔCMg2+RNA curves for U10601A and A1088U RNAs is compared with the UV-monitored folding curve in Fig. 4B. The scales of the two curves have been adjusted to show that the midpoints of the two transitions are essentially identical. Apparent differences between the curves at low Mg2+ concentrations are within the experimental error of the measurement (see error bars in Fig. 4C).

ΔΓ2+ can be found from Wyman linkage analysis (Eq. 4) of the normalized UV-monitored folding data in Fig. 4B; at the transition midpoint (C2+ = 0.10 mM) its value is 3.9 ± 0.1 ions per RNA (see Materials and Methods). An independent estimate of ΔΓ2+ at the same C2+ can be obtained from the HQS-monitored titration curves in two ways. Because half the RNAs are folded at the transition midpoint, ΔΓ2+ is twice the difference ΔCMg2+U1061A − ΔCMg2+A1088U evaluated at 0.10 mM Mg2+, i.e., 4.4 ± 0.4 ions per RNA. Alternatively, ΔCMg2+U1061A data obtained at values of C2+ > 0.4 mM, where the RNA is expected to be fully folded, were extrapolated to lower Mg2+ concentrations (see Materials and Methods) and compared with ΔCMg2+A1088U to obtain the dashed curve in Fig. 4B. This exercise suggests that ΔΓ2+ reaches a maximum of 3.5 ± 0.4 ions at the transition midpoint. Although the uncertainties are large, it is nevertheless reassuring that independent experiments which measure ΔΓ2+ by monitoring either effective Mg2+ concentration or the extent of RNA folding give consistent values.

A thermodynamic cycle for Mg2+-induced folding of U1061A RNA is shown in Fig. 5. Data presented in Fig. 4 B and C define two of the free-energy changes for the cycle. For convenience, all of the free energies in Fig. 5 have been evaluated at the folding transition midpoint, C2+ = 0.10 mM, at the monovalent salt concentration used in these experiments. ΔGobs,Mg2+° is thus zero at this point. Integration of the ΔCMg2+nt curve for A1088U RNA gives −3.6 kcal/mol for the value of ΔGI-Mg2+ at the transition midpoint. The intrinsic free energy of RNA folding in the absence of Mg2+, ΔGobs,0°, can be estimated from a previous study of another variant of the same 58-mer rRNA fragment (10). It was found that the tertiary structure can be induced to fold in the absence of Mg2+ by very high (1.6 M) monovalent salt concentrations and that methanol behaves as a protective osmolyte by preferentially stabilizing the tertiary structure of this RNA in monovalent salt concentrations as low as 0.3 M. Extrapolation of the salt and methanol dependencies of the tertiary unfolding transition yielded an estimate of ΔGfold,int° as +19 kcal/mol RNA under the experimental conditions of Fig. 5, 60 mM KCl and 15°C.

Fig. 5.

Thermodynamic cycle and energy level diagram for Mg²⁺-induced folding of a 58-mer rRNA fragment. Labeling of RNA states and their positioning in the vertical dimension according to their relative free energies is as in Fig. 1. Three of the free energies are derived from experiment; the one in parentheses is calculated from the other three. Free energies refer to buffers containing 60 mM K⁺, 10 mM Mops (pH 6.8), and Cl⁻ anion at 15°C.

The remaining unmeasured free energy of the Fig. 5 cycle is ΔGN-Mg2+. Because a significant concentration of folded U1061A RNA exists only at Mg2+ concentrations above the folding transition, the form of the N-state ΔCMg2+nt curve is largely undetermined; therefore, a direct experimental measurement of ΔGN,Mg2+ is not possible. However, this free energy is constrained by the other three free energies of the thermodynamic cycle (Eq. 1) to be approximately −23 kcal/mol at the transition midpoint (Fig. 5). Although the extrapolation needed to estimate ΔGfold,int° introduces some uncertainty in this calculation, it is clear that ΔGN-Mg2+ must be a number of times larger than ΔGI-Mg2+ in order for this RNA to fold.

Discussion

To begin to understand the problem of Mg²⁺-induced RNA folding at a fundamental level, it is necessary to measure the separate free energies of Mg²⁺ interaction with folded and unfolded conformations of an RNA. Only a few measurements relevant to this problem have been made in the past, in part because it is difficult to separate the intrinsic free energy of RNA folding from the free energy of Mg²⁺–RNA interactions in most RNAs. In the work presented here, we have obtained a complete overview of the free energies of RNA folding and Mg²⁺–RNA interactions for two different RNAs, as summarized by the free energy diagrams in Figs. 1 and 5. For a pseudoknot RNA (Fig. 1), all four free energies of the thermodynamic cycle were independently measured and are self-consistent. For folding of the rRNA fragment diagrammed in Fig. 5, three free energies of the cycle were experimentally determined, from which the fourth free energy was calculated.

Attempts to measure the interactions of Mg2+ ions with RNAs in the partially structured conformations from which tertiary folding takes place (the I state) have been made previously only with tRNA at high temperatures (2, 7) and a mutant intron domain at 2 M NaCl (26). In contrast, the ΔCMg2+nt curves for variant RNAs unable to fold tertiary structure (Figs. 3 and 4) provide a look at Mg2+ association with I-state RNAs under conditions typically used to fold RNA. In terms of the extent to which RNA negative charges are neutralized by excess Mg2+, I-state RNA does not differ dramatically from the native RNA: Γ2+ for BWYV RNA is only incrementally larger than Γ2+ for the I-state mimic (≈25% at 0.1 mM Mg2+), and at the 58-mer RNA folding transition midpoint Γ2+ increases from 5.3 to 8.8 ions. Thus, the properties of the I state are an important aspect of the folding reaction. For instance, a mutation affecting the distribution of I state conformations could change ΔΓ2+ and ΔΔGMg2+, even if the mutation has not affected Mg2+ interactions with the N-state RNA. Therefore, any quantitative accounting for Mg2+-induced RNA folding will have to incorporate a model of Mg2+ interactions with an ensemble of I-state conformations that adequately reproduces ΔCMg2+RNA as a function of C2+ for the RNA. Our preliminary investigations suggest that a “generic” I-state model, such as a segment of helix (4), will not be adequate; specific features of an RNA will have to be taken into account.

In contrast to the small variations in Γ₂₊ among the RNAs considered here, the Mg²⁺–RNA interaction free energies (ΔG_RNA-Mg²⁺) and the intrinsic RNA stabilities (ΔG_obs,0^°) vary dramatically. At the moderate monovalent salt concentrations used in these sets of experiments, the rRNA fragment is extremely unstable (+19 kcal/mol), whereas the pseudoknot is stably folded (−5.9 kcal/mol). In addition, the folded rRNA fragment interacts ≈25-fold more strongly with Mg²⁺ ions (on a per-nucleotide basis) than does the pseudoknot. Calculations have suggested that a single Mg²⁺ ion chelated within a pocket of the rRNA fragment contributes a significant fraction of the Mg²⁺-induced stabilization under some conditions (3); no similarly buried Mg²⁺ is found in the BWYV pseudoknot crystal (20). Because the energetics of all of the ions interacting with an RNA are strongly coupled (3), the free energy of Mg²⁺–RNA interactions can only be derived from a full accounting of the ways all ions are distributed among all environments in and near an RNA (6). An understanding of the contrasting stabilities and Mg²⁺-interaction strengths of these two RNAs will therefore have to wait for theoretical treatments to complement structural studies.

The work presented here suggests that some caution is necessary with regard to two common practices in Mg²⁺-induced RNA folding studies: The buffer is frequently the only source of monovalent cations and anions, and the exponent of the Hill equation is used as an approximation of ΔΓ₂₊ (5, 13, 27). Linkage analysis can indeed be used to derive ΔΓ₂₊ from the dependence of a two-state equilibrium constant for folding on C₂₊, but only if an ≈30-fold or greater excess of KCl or NaCl over added MgCl₂ is present (see Supporting Text, Eq. 7). In addition, the value of ΔΓ₂₊ calculated from linkage analysis applies only to the narrow range of Mg²⁺ concentrations over which the analysis is carried out. It is apparent from the data presented here (Figs. 3B and 4B) and theoretical considerations (4) that ΔΓ₂₊ can vary widely with Mg²⁺ concentration. Thus, a mutation could alter ΔΓ₂₊ simply because RNA folding is being observed in a different Mg²⁺ concentration range and not because Mg²⁺–RNA interactions have been perturbed in any fundamental way.

In this article, we have shown how the thermodynamics of Mg²⁺-induced RNA folding may be experimentally parsed into the separate free energies of RNA folding and Mg²⁺ interactions with N and I states. The results with just two different RNA tertiary structures reveal large differences in both the intrinsic stabilities of the structures and their free energies of interaction with Mg²⁺; the full range of possibilities may yet remain to be explored. These experimental free energies now provide constraints for theoretical attempts to account for Mg²⁺-induced RNA folding (3, 4), which may in turn provide insight into the physical origins of the different Mg²⁺–RNA free energies measured here.

Materials and Methods

BWYV RNA, the 58-mer rRNA fragment, and their variants were prepared by transcription with T7 RNA polymerase from plasmid DNA as described for the 58-mer fragment (28) or from a double-stranded synthetic DNA template for BWYV RNAs (29). RNAs were purified either by chromatography under denaturing conditions on ion exchange columns or by denaturing gel electrophoresis. Before use, RNAs were extensively equilibrated with buffer containing 10 mM Mops (adjusted to pH 7.0 with 4 mM NaOH) and 50 mM NaCl (BWYV RNAs) or 20 mM Mops (adjusted to pH 6.8 with 5.7 mM KOH), 54.3 mM KCl, and 20 μM EDTA (rRNA fragments) by using Centricon filter units (Millipore, Billerica, MA). Titrations in the presence of HQS were carried out in an Aviv ATF-105 fluorimeter. Additions of MgCl₂ (in the identical buffer as used to equilibrate the RNA) were made into 1-cm² cuvettes by computer-controlled Hamilton (Reno, NV) titrators (rRNA fragments) or by manual additions into 2- × 10-mm cuvettes (BWYV RNAs). Details of RNA purification, equilibration with buffer, titration procedures, and data analysis are described elsewhere (18). Automated titrations of 58-mer rRNAs with MgCl₂ monitored by UV absorption were carried out in a Cary 400 spectrophotometer, and melting experiments with BWYV RNA were performed in the same instrument.

Extraction of unfolding free energies as a function of Mg2+ concentration from melting profiles was as described (30); enthalpies were first calculated for each melting profile individually, and then the average enthalpy from all experiments was used in calculating free energies from the fitted Tms. Plots of ΔCMg2+nt as a function of ln(C2+) were fit by least squares to a polynomial that asymptotically approaches the abscissa, y = b(x − a)2 + c(x − a)3 + d(x − a)4. The fitted polynomials were integrated to find free energy changes according to Eq. 2. The same polynomial was fit to ΔCMg2+RNA data for U1061A RNA at C2+ values > 0.4 mM to extrapolate ΔΓ2+ to the folding transition midpoint (plotted in Fig. 4B).

Data from UV-monitored titrations of the rRNA fragment were collected from ≈2 to 400 μM added MgCl2. Linear dependencies of the OD at low and high Mg2+ concentrations were subtracted from the data, from which the fraction of RNA in the folded state was then calculated. ΔCMg2+RNA, measured under identical solution conditions, was then used to correct the total added MgCl2 concentration for the excess Mg2+ present with the RNA. The resulting data were transformed into a plot of ΔGobs,Mg2+° as a function of ln(C2+). Eq. 3 was applied to the linear portion of this curve around the transition midpoint, C2+ = 80–136 μM, to obtain ΔΓ2+.

Abbreviations

BWYV

beet western yellow virus

HQS

8-hydroxyquinoline 5-sulfonic acid.