Towards genome-scale structure prediction for transmembrane proteins

Abstract

In this paper we briefly review some of the recent progress made by ourselves and others in developing methods for predicting the structures of transmembrane proteins from amino acid sequence. Transmembrane proteins are an important class of proteins involved in many diverse biological functions, many of which have great impact in terms of disease mechanism and drug discovery. Despite their biological importance, it has proven very difficult to solve the structures of these proteins by experimental techniques, and so there is a great deal of pressure to develop effective methods for predicting their structure. The methods we discuss range from methods for transmembrane topology prediction to new methods for low resolution folding simulations in a knowledge-based force field. This potential is designed to reproduce the properties of the lipid bilayer. Our eventual aim is to apply these methods in tandem so that useful three-dimensional models can be built for a large fraction of the transmembrane protein domains in whole proteomes.

1. Introduction

A wide range of fundamental biological processes such as cell signalling, transport of membrane-impermeable molecules, cell–cell communication, cell recognition and cell adhesion are mediated by membrane proteins. Not surprisingly, therefore, understanding the structure and function of membrane proteins is of great importance in biological and pharmacological research.

Analysis of the complete genomic sequences for several organisms indicates that 20–25% of all genes code for transmembrane proteins (Jones 1998; Wallin & von Heijne 1998). Despite their large number and their importance only less than 1% of all three-dimensional protein structures deposited in the Protein Data Bank (PDB) are of membrane proteins (Berman et al. 2000), probably because they are not easy to crystallize and are hardly tractable by nuclear magnetic resonance (NMR). It appears therefore of particular importance to develop efficient theoretical structure prediction methods for transmembrane proteins.

2. Biological membranes

To understand how transmembrane protein structures can be predicted, it is important to understand the properties of biological membranes, which are composed of a lipid bilayer. Membranes serve to separate different compartments of the cell or the cell from its environment, and to achieve this, the lipid bilayer is impermeable to polar (soluble in water) molecules and ions.

A space-filling model of a lipid bilayer is shown in figure 1 (Heller et al. 1993). Each phospholipid is composed of a negatively charged phosphate group and two tails, which are two highly hydrophobic hydrocarbon chains. The hydrophobic effect ensures that the tails of the phospholipids in each layer orient towards each other creating a highly hydrophobic environment within the membrane. The charged phosphate groups face out into the hydrophilic environment.

Figure 1.

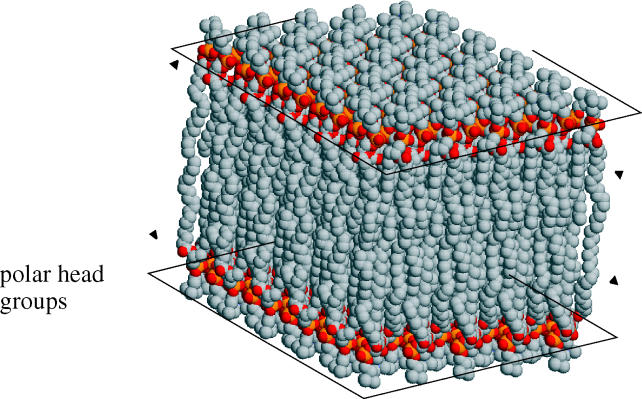
A space-filling model of a typical phospholipid bilayer.

3. Membrane protein classes: structures and functions

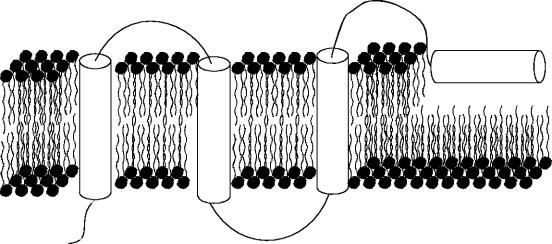
All of the active processes involving membranes are carried out by proteins within the membrane environment. These proteins are usually classified as being either peripheral (membrane associated proteins) or integral on the basis of how readily they can dissociate from the membrane. Peripheral membrane proteins are loosely associated with the membrane and usually interact with the polar head groups of the membrane phospholipids. These proteins can therefore be solubilized under relatively mild conditions, such as an environment of high ionic strength. Integral membrane proteins, on the other hand, are found to interact extensively with the hydrocarbon chains of the membrane lipids (figure 2) and can therefore be solubilized only by using detergents or an organic solvent. They are embedded in the phospholipid bilayer, often membrane spanning, although some unilateral ones can be embedded in only one leaflet (see figure 2).

Figure 2.

Diagrammatic representation of an integral membrane (transmembrane) protein. The first two helices fully span both leaves of the bilayer, but the third helix (typically an amphipathic helix) is shown not fully penetrating the bilayer.

(a) Integral membrane proteins

The principle that underlies the structure and stability of membrane proteins is the high energetic cost of dehydrating the peptide bond during its transfer into a non-polar phase (White 2001). This has two consequences. First, and perhaps most obviously, most of the amino acid side chains found within transmembrane segments should be non-polar. Second, the polar groups of the polypeptide backbone of the transmembrane segments must participate in hydrogen bonds in order to lower the energetic cost. This second constraint is typically accomplished by exploiting two structural motifs: the membrane-spanning α-helix bundle and the β-barrel (White & Wimley 1999). In the α-helical structure, the peptide bonds are internally bonded with hydrocarbon bonds whereas β-strands form a closed structure termed the β-barrel.

(b) β-Barrel integral membrane proteins

The β-barrel proteins, also called porins, consist of β-strands spanning the membrane connected by short loops facing the periplasm and larger loops protruding outside the outer membrane (von Heijne 1996). The β-strands are amphiphilic, i.e. the side chains of the strand residues are alternately polar and hydrophobic with polar residues projecting into a central pore. Thus, the structure forms a pore with a polar environment. All β-barrel membrane proteins form oligomers (Seshadri et al. 1998).

The porins are found in the outer membrane of Gram-negative bacteria and in the outer membrane of chloroplasts and mitochondria. Their function is to facilitate diffusion of salts and polar compounds.

(c) α-Helical integral membrane proteins

In the α-helical proteins, the transmembrane segments are arranged in helices of 17–25 residues length and may cross the membrane once or several times (figure 3). Bi-topic proteins (or membrane-anchored proteins) are α-helical membrane proteins, which cross the membrane once (or sometimes twice), exposing globular domains on the extracellular and cytoplasmic surfaces. They typically act as cell surface markers, adhesion factors or receptors. The cytoplasmic domains often play a role in cell signalling (e.g. tyrosine kinases) or may connect to the cellular cytoskeleton. Polytopic (multi-spanning) α-helical membrane proteins have more than one α-helical transmembrane segment and the helices are arranged into a bundle (see figure 4). Possible driving forces for helix–helix association in the lipid bilayer are van der Waals interactions and inter-helical polar interactions, including hydrogen bonds and electrostatic interactions (Popot & Engelman 2000).

Figure 3.

An example of an α-helical bundle integral membrane protein (halorhodopsin from Halobacterium salinarum).

Figure 4.

A plot of the potentials of the bilayer potentials (in units of kcal mol⁻¹) for the charged amino acids.

When polytopic α-helical membrane proteins are grouped according to their topology, differences between various species can be observed. In general, eubacteria, archaea, fungi and plants have large collections of membrane proteins built of 6 and 12 transmembrane segments, whereas in Caenorhabditis elegans and human proteins with seven transmembrane segments are preferred (Wallin & von Heijne 1998).

Perhaps the most biologically important example of polytopic proteins (at least with respect to pharmacology) is the superfamily of G-protein-coupled receptors (GPCRs), which includes receptors for hormones, neurotransmitters, growth factors, light and many other kinds of ligands (Dewji & Singer 1997). Other families of this superfamily function as channel and pore forming proteins involved in membrane transport (Singer 1990).

4. Helix-bundle integral membrane protein folding

The folding process of helix-bundle membrane proteins consists of two stages. The first stage involves formation of stable helices across the hydrophobic region of the membrane lipid bilayer. In the second stage, the helices interact to give a functional membrane protein (Popot & Engelman 1990). The assembly is carried out by a translocon apparatus involving the transient attachment of an active ribosome to a translocon embedded in the membrane. As soon as the protein is synthesized into the translocon and transferred into the membrane, the apparatus disassembles leaving the folded protein within the membrane (White & Wimley 1999).

5. Experimental studies of helix-bundle integral membrane; membrane helix locations and topology

As mentioned above, elucidation of the three-dimensional structure of membrane proteins is a difficult task. Therefore, other approaches for studying the structure of the proteins are being employed. One such approach is to determine the protein topology, i.e. the inside–outside location of the N and C termini relative to the membrane, and the number and positions of the membrane spanning regions. Knowing a protein's topology is a significant step towards determining both its structure and function. Topology assignments are also sometimes referred to as ‘low resolution structures’ (Kernytsky & Rost 2003), but there is clearly no actual three-dimensional information produced.

Several experimental approaches can be used to determine transmembrane topology:

1. Fusion proteins: a protein segment that can be detected while it is translocated through the membrane is fused to the predicted loops of the tested protein (van Geest & Lolkema 2000).

2. Proteolytic digestion in situ: proteolytic enzymes can be used to cut the loops outside the membrane. It is then possible to run the segments remaining in the membrane by SDS-PAGE (Kuroiwa et al. 1996).

3. Antibody binding: antibodies specific to the loops are used to locate the loops outside the membrane (Amstutz et al. 2001).

6. Predicting transmembrane helix-bundle protein topology

Given the amount of information that can be potentially obtained from topology assignment and the relative difficulty in obtaining this information experimentally, it is not surprising that a great deal of attention has been paid to prediction of transmembrane topology from sequence.

Transmembrane protein topology prediction methods rely on two major topological features. The first is that, as already discussed, transmembrane helices are ultimately formed by hydrophobic stretches, the second is primarily the bias towards positively charged residues in the regions flanking the hydrophobic stretches, especially on the intracellular side of the membrane. The feature is commonly known as ‘the positive-inside rule’ where short loops are found to be enriched with Lys and Arg residues on the intracellular side and depleted on the outside (Wallin & von Heijne 1998; von Heijne 1999).

More than 30 methods have been developed for predicting the topology of helix-bundle membrane proteins (Kernytsky & Rost 2003) and here there is only space to mention a few of them. Below is a brief summary of the main representative methods developed and the advances made over the last two decades.

In the earliest transmembrane prediction methods, simple hydrophobicity scales were used (e.g. Kyte & Doolittle 1982) to detect probable transmembrane segments. These scales classify amino acids according to their preference to be found in polar or non-polar environments. Thus, a high hydrophobicity value indicates a preference for a non-polar environment, i.e. the lipid bilayer. Kyte & Doolittle used a ‘sliding window’ approach to identify membrane segments where a fixed window of width 19 residues is moved along the protein sequence and the sum or average hydrophobicity is calculated for amino acids within the window. Using these mean hydrophobicity values, a threshold can be identified for deciding whether the centre of the window is within a membrane spanning membrane helix or not. The Kyte & Doolittle method, along with other similar approaches, predict the occurrence of transmembrane segments only and were not designed to predict the inside–outside location of the segments relative to the membrane.

The first major advance in transmembrane topology prediction was the TopPred method proposed by von Heijne (1992). TopPred still made use of hydrophobicity scales and a sliding window to predict transmembrane segments, but combined these predictions with a simple topological rule: the so-called ‘positive-inside rule’. The observation that there was a strong bias for positively charged residues on the inside facing segments of a transmembrane protein provided a means for identifying which predicted topology is correct from a small number of alternatives. Even though the starting point to TopPred was a basic hydrophobicity plot, it was nonetheless the first transmembrane topology prediction method.

The MEMSAT method of Jones et al. (1994) was the first prediction method to fully integrate the prediction of transmembrane topology with the prediction of transmembrane segments. Rather than simply deciding between a few possible topological models, MEMSAT was able to calculate the most probable length, location and topological orientation for each transmembrane segment, guaranteeing a mathematically optimal solution. The method made use of statistical tables (log likelihood ratios) compiled from membrane protein data and a dynamic programming algorithm to search through all possible topological models by a process of expectation maximization. The propensity of each amino acid to be in one of five states (inside loop, outside loop, inside helix end, helix middle and outside helix end) was calculated from experimentally well-described membrane proteins and was represented as a log-likelihood ratio. This approach can clearly be seen as a forerunner of more recent approaches which are based on formal Hidden Markov Models.

PHDhtm (Rost et al. 1996) was the first method to use neural networks for prediction of transmembrane helix topology. It used multiple sequence alignments to do a consensus prediction of the target protein, and then predicted topology by using a neural network trained on proteins with experimentally characterized topologies.

TMHMM (Sonnhammer et al. 1998) and HMMTOP (Tusnady & Simon 1998) are methods which are both based on Hidden Markov models. TMHMM implements a cyclic model with seven states for transmembrane helix, whereas HMMTOP uses a Hidden Markov model which distinguishes between five structural states (helix core, inside loop, outside loop, helix caps (C and N) and globular domains). The states are connected by transition probabilities. As with the earlier MEMSAT approach, dynamic programming is used to match a sequence against the model in order to find the most probable match.

DAS-Tmfilter (Cserzo et al. 2004) is based on computing a dot plot between the query protein and a library of known transmembrane proteins. The result is a hydrophobicity profile.

Finally, in line with recent developments in methods for predicting globular protein structure, consensus methods have started to appear. The first such approach has been developed by Nilsson et al. (2002), and uses the consensus of five topology prediction methods (TMHMM, HMMTOP, MEMSAT, PHD, TopPred). They find that approximately 90% of partial consensus topologies are correctly predicted in membrane proteins from both prokaryotic and eukaryotic organisms, which is a higher accuracy than can be achieved by any single component method. They further go on to show that a consensus topology can be predicted for 70% of all membrane proteins in a bacterial genome and for ca 55% of all membrane proteins in eukaryotic genome. These accuracy estimates were surprisingly low compared to some of the values quoted in the original method papers, which was further confirmed by Melen et al. (2003). One possible reason for this is the low reliability of experimentally determined topology information available when the first prediction methods were developed. Another possibility is that earlier accuracy estimates were biased by the lack of proteins with unusual three-dimensional structures in the testing sets used. As more high resolution structures are determined for transmembrane proteins, more accurate benchmarking of methods should be possible and hopefully this will stimulate further developments in the field.

7. Predicting tertiary structure of helix-bundle membrane proteins

At present there is no general-purpose method for three-dimensional structure prediction for transmembrane proteins, though of course the same can be said for globular proteins. As with globular proteins, the most reliable method for deriving a three-dimensional model for a protein is that of comparative modelling. Unfortunately, the reputation of comparative modelling for membrane proteins suffered slightly from the efforts made in the early 1990s to model proteins in the seven-helix GPCR superfamily based on templates derived from bacteriorhodopsin. The subsequent crystal structure of rhodopsin showed that despite similarities in the overall topology and approximate positioning of the helices, the structure of bacteriorhodopsin was substantially different in terms of the helix packing arrangements. The very remote sequence similarity observed between the GPCR sequences and bacteriorhodopsin also contributed to the inaccuracy of the models which were built, and so in hindsight the attempts to build useful models of the GPCRs by comparative modelling must be seen as failures.

Even ignoring the difficulties in identifying remote evolutionary relationships between membrane proteins and the difficulties in arriving at accurate alignments, a much more fundamental problem is the lack of structural templates available. Given the difficulties in experimentally determining structures for integral membrane proteins, it is not surprising that so few structures are currently available in the structure databases. At the time of writing, there are 95 sequence-unique membrane proteins in the current release of PDB (Berman et al. 2000), compared to 20 000 or so globular proteins. The chance of finding a suitable template structure for transmembrane proteins is consequently very small in comparison to that of globular proteins, though a little higher than might otherwise be expected due to the dominance of very large families such as the GPCRs.

In view of the difficulties in applying comparative modelling to transmembrane proteins, a number of groups have looked into the problem of structure prediction for these proteins without the requirement for a template structure, and several studies have been published on analysing the important structural features of helix-bundle membrane proteins that can be used for the prediction of their structure.

As discussed earlier, topology prediction methods give some spatial information, but as a first step towards full three-dimensional modelling of proteins with multiple transmembrane segments, information on the orientations of each transmembrane helix is required. After topology, the next most readily predicted feature of each transmembrane helix is the relative orientations of the helix around its own axis, i.e. the identification of which residues are exposed to the lipid phase and which are packed against the interior of the transmembrane bundle.

Early attempts were made to predict relative helix orientation by using the concept of the hydrophobic moment (Eisenberg et al. 1984; Rees et al. 1989). The hydrophobic moment is essentially a vector pointing from the helix axis to the most hydrophobic surface of the helix. In these methods, the angular orientations of transmembrane helices could be predicted by assuming that the helical hydrophobic moments should point out into the lipid phase. Later, however, it was found that hydrophobic moments are poor indicators of the angular orientation of the transmembrane helices due to the fact that hydrophobic residues often face both the core of the protein and the lipid (Stevens & Arkin 1999; Rees & Eisenberg 2000).

In later work, a statistical analysis was conducted on known high-resolution structures of integral membrane proteins in order to find the lipid exposure propensities of the different residues (Cronet et al. 1993; Donnelly et al. 1993). The work of Donnelly was particularly important in that it described very clearly the importance of sequence conservation in discriminating between lipid exposed and buried residues. Lipid exposed residues, while needing to be highly hydrophobic are also under no significant steric constraints and so are often seen to be evolutionarily quite variable. Buried residues, on the other hand, while also being typically hydrophobic are also subject to steric constraints and so are commonly seen to be highly conserved in sequence alignments. As an alternative to the evolutionary approach, Pilpel et al. (1999) proposed a knowledge-based scale for the propensity of residue orientation in the transmembrane segments. The authors made the assumption that residues which tend to be exposed to the membrane will be more frequent in the transmembrane segments of single spanning transmembrane proteins than in multi-spanning proteins, whereas residues that prefer to be buried in the transmembrane bundle interior would show the opposite trend.

Using this kind of knowledge, some attempts have been made to develop prediction methods for membrane protein three-dimensional structure. Taylor et al. (1994) adapted some programs originally developed for the prediction of globular protein structures to derive a method for predicting integral membrane protein structures. The method uses the ‘variphobicity’ (evolutionarily variable and hydrophobic) faces of transmembrane helices to predict the structure and was successfully applied to two protein family sequence alignments (bacteriorhodopsin and rhodopsin).

Nikiforovich et al. (2001) developed a modelling approach which was a combination of helical packing, based on the bacteriorhodopsin template, and selection of low-energy conformers for loops that are closest to the known X-ray structure of bacteriorhodopsin. Using this method, the authors were able to accurately reproduce the bacteriorhodopsin structure.

Fleishman & Ben-Tal (2002) used data on residue environment preferences to predict the likely arrangement of transmembrane helices, and this method was used to predict successfully the native structure of transmembrane protein glycophorin A. In the same year, Ledesma et al. (2002) produced a model for uncoupling protein 1 (UCP1), using a computational docking method, and in 2003, Chen & Chen used a Monte Carlo method for protein folding and successfully predicted the seven helix bundle structure of rhodopsin I.

Pellegrini-Calace et al. (2003) developed a method (FILM) for predicting small membrane protein structures based on a method previously developed for predicting tertiary structure of globular proteins. The method is based on the assembly of super-secondary structural fragments taken from a library of proteins with known structure, using a standard simulated annealing algorithm. The method was applied to small membrane proteins of known structure and was able to predict at reasonable accuracy level the helix topology and the conformation of a number of these proteins. We give a brief outline here of the FILM method.

8. FILM: Membrane potential definition

At the core of the FILM method was a simple approach to modelling the physicochemical constraints of the lipid bilayer. Globular protein structure prediction is simplified by the assumption that the water which surrounds the folding protein is essentially isotropic. Indeed, many successful globular protein prediction methods treat the effects of the solvent as an implicit term, e.g. by altering the dielectric constant in an application of Coulomb's Law.

The lipid bilayer (see figure 1) clearly cannot be treated as an isotropic environment, and so some means is needed to model its effects in a realistic way. Although in theory the lipid bilayer could be incorporated in atomic detail in a molecular dynamic simulation (e.g. Heller et al. 1993), this would require far too much computational power, and so FILM makes use of a very simplistic model of the bilayer properties in the form of membrane potentials.

Membrane potentials (MPs) were defined by a statistical analysis carried out on a set of 640 transmembrane helices, belonging to 133 membrane proteins extracted from the SWISSPROT database (Bairoch & Apweiler 1996) and having an experimentally defined topology at the very least. We would have preferred to limit our analysis to transmembrane proteins of known three-dimensional structure, but there are currently insufficient structures to allow this.

The membrane bilayer was modelled as an infinite slab 60 Å in thickness made of a 30 Å core and a 15 Å interface at both periplasmic and cytoplasmic sides. The z-axis was taken as the direction perpendicular to the Cartesian plane formed by the bilayer surface. A simplifying assumption here is that we assume that membrane physicochemical properties are variable only along the z-axis and are constant across each plane parallel to the membrane surface. The core region was then divided along the z-axis into 21 ‘layers’ with a layer thickness of 1.5 Å (corresponding to the translation per residue of a right-handed α-helix), with z=0 being right at the centre of the membrane. Arbitrarily, we defined the cytoplasmic direction as being in the negative z-direction.

The relative frequencies of occurrence for each naturally occurring amino acid within each layer of the core region were calculated by analysing the sequences of the 640 transmembrane helices, giving a total dataset of 17 162 residues. The midpoint of each helix was considered to be positioned at the middle of the membrane (z=0), and sequence positions (0, …, n) were transformed into z-coordinates (z) as follows:

$$z=\frac{c(i-\frac{1}{2}h)}{h},$$

where i is the position number, h is the helix length and c is the membrane core thickness.

Periplasmic and cytoplasmic interfaces were divided into three layers each, with a larger step size of 3 Å, as we assume that the backbone is more likely to be extended at that level (the observed span per α-carbon in an extended polypeptide is ca 3.6 Å). The three amino acids leading into both ends of the transmembrane helices were considered in calculating the frequencies of occurrence within the interface layers (sequence positions again have been transformed as above).

Finally, the inverse Boltzmann equation was applied so that, given an amino acid type a at a specified z-coordinate (z) inside of the slab, its membrane propensity (MP) was calculated according the equation:

$$\text{MP}(z)=-RT\text{ln}\frac{f_{\text{a}}(z)}{f(z)},$$

where f_a(z) is the observed relative frequency of occurrence of amino acid type a at z, f(z) is the observed relative frequency of occurrence of all amino acids found at z, and RT is taken to be 0.582 kcal mol⁻¹.

As an example, figure 4 shows the calculated bilayer potentials for the charged amino acids. The main features of the potentials concur with what is expected from our knowledge of amino acids and their occurrence in transmembrane segments. The well-known positive inside rule (von Heijne 1992) shows itself in the clear preference for the positively charged residues to be located at z-coordinates between −25 and −18, which correspond to the cytoplasmic facing helix cap regions. Other trends, such as the preference for aromatic residues to be located close to the polar head groups, also show up in their respective potentials.

9. FILM: Prediction method

(a) Energy function

In addition to the membrane potentials, further terms are needed in the complete potential function. FILM was based on the FRAGFOLD method used for globular protein folding (Jones 1997) and so the core of the used objective function is a set of pairwise potentials of mean force representing both short range and long range interresidue interactions. These potentials were determined by a statistical analysis of highly resolved protein X-ray crystal structures and again the application of the inverse Boltzmann equation, along with a solvation potential (E_solv).

In FILM, the solvation energy is set to zero at the membrane core and smoothed at interfaces by a factor SF as follows:

$$\text{SF}=\frac{\left|z\right|-L}{U-L},$$

where z is any interface z-coordinates (i.e. 15 Å<|z|<30 Å), L is the positive lowest interface z-coordinate (15 Å) and U is the positive higher one (30 Å). In this way, the traditional ‘water’ solvation potential has no effect within the bilayer, but does have an effect outside of the membrane environment.

All other terms in the FILM potential function (e.g. hydrogen bonding and steric terms) are the same as currently used by FRAGFOLD. The total potential value is obtained by summing the membrane potentials (E_mem) and then added to the other potential terms with an appropriate weight, e.g.

$$E_{\text{tot}}=a{E}_{\text{short}-\text{range}}+b{E}_{\text{long}-\text{range}}+c{E}_{\text{solv}}+d{E}_{\text{mem}}+e{E}_{\text{steric}}+f{E}_{\text{hbond}},$$

a–f are the adjustable weights.

FILM was tested on a number of small transmembrane proteins. The requirement that targets be relatively small and have both known three-dimensional structure and known transmembrane topology limits the number of available targets to a small handful. Figure 5 shows the results of applying FILM to three such targets (glycophorin A, subunit C of the F1Fo ATPase and major fd coat protein). In all cases, FILM produced a final model with the correct topology and a reasonable approximation of the chain conformation (RMSDs between 3.6 and 4.8 Å). Unfortunately, there are almost no other targets available on which the method could be tested, and the lack of suitable small transmembrane targets is a critical restriction in testing and developing methods for folding transmembrane proteins. Although FILM appears to be a useful method, further benchmarking will be needed on newly solved targets before its performance can be accurately assessed.

Figure 5.

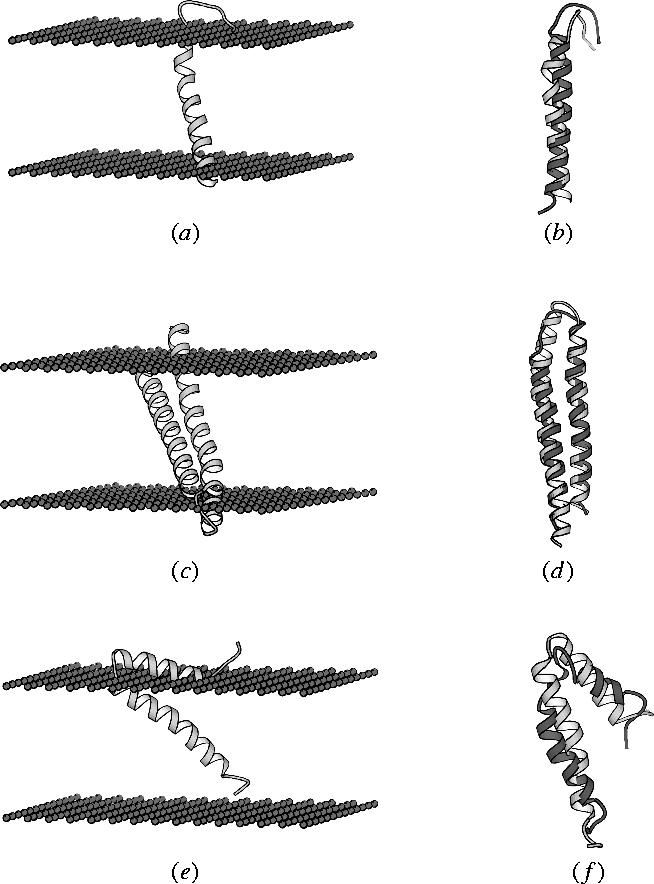
(a) FILM model for glycophorin A (predicted transmembrane helix from T93 to I118); (b) superposition of FILM model with NMR model (RMSD=3.6 Å); (c) FILM model of subunit C of the F1Fo ATPase (predicted transmembrane helices from E2 to R41 and from L48 to A77); (d) superposition of FILM model with NMR model (RMSD=4.2 Å); (e) FILM model of major fd coat protein (predicted transmembrane helix from W49 to T69 and predicted amphipathic helix from A32 to A41); and (f) superposition of FILM model with NMR model (RMSD=4.8 Å).

10. Further Development of the FILM Method

Although the FILM method appears to be effective in predicting the fold and topological arrangement of small transmembrane proteins, the method was not able to predict the conformations of larger transmembrane proteins. The main limitation of FILM is that the potential function is not able to reproduce the compactness of transmembrane bundles. Transmembrane helix bundles are usually not optimally compact, although neighbouring helices are closely packed. Bacteriorhodopsin, for example, is an elongated two-layer bundle of seven helices and not a compact bundle with a circular cross-section. We have been trying to improve the prediction of these large bundles by incorporating the prediction of lipid exposure from variphobicity analysis into the FILM potential function.

In order to develop better potential functions for folding larger multihelical transmembrane proteins, we have recently started making use of a set of decoy structures. Decoy sets have been widely used to validate and optimize potential functions for folding globular proteins (e.g. Park & Levitt 1996), and a number of globular protein decoy sets can be downloaded from the Decoys ‘R’ US web site (http://dd.stanford.edu/). To date, however, no decoy sets have been developed for evaluating potential functions designed to fold transmembrane proteins.

We employed the polyhedral modelling approach of Taylor et al. (1994) to make a set of challenging decoy sets for transmembrane protein scoring functions. The approach is briefly summarized in figure 6. Firstly, for a given topology (number of transmembrane helices and direction with respect to inside/outside phasing) all possible windings are generated on a hexagonal close-packed lattice. Windings which violate topological rules (e.g. short crossing loops) are then eliminated and the remaining windings are transformed into regularized three-dimensional coordinates firstly by generating a ‘stick model’ of the structure where each helix is represented by a single vector. These vectors are rotated slightly to allow for helix packing and then an alpha-carbon trace is generated by alternating rounds of distance geometry and real space refinement.

Figure 6.

An outline of the decoy generation procedure using a polyhedral model of transmembrane helix bundles (Taylor et al. 1994). In the first step, different tracings are generated through a hexagonal close packed lattice (packed cylinder model). Tracings that violate obvious structural constraints (e.g. loops too short to make a particular connection) are eliminated. Given a tracing through the lattice, helix axes are generated taking into account the normal packing angles between helices in close packed helix bundles. Finally, using these axes, alpha-carbon coordinates are generated by means of distance geometry and real-space refinement.

Figure 7 shows the results of applying one of our simplified scoring functions to the decoys generated for bacteriorhodopsin and rhodopsin. The scoring function is the same as previously described for the FILM method, with the addition of a weighted term for variphobicity as defined by Taylor et al. (1994). As can be seen, this simple scoring function is reasonably effective in assessing the quality of the transmembrane models. In the case of bacteriorhodopsin, the best generated model (6 Å RMSD from native) has the lowest pseudo-energy sum out of all the decoys. One slight problem is that the model in fact scores slightly better than the crystal structure in this case, which underlines the fact that the scoring function is still not fully accounting for all aspects of protein stability in a bilayer. In the case of rhodopsin, the crystal structure enjoys a much more pronounced gap between its own energy and that of the next closest decoy structure. However, in this case, the best model is not the model which produces the lowest pseudo-energy sum, though the lowest energy model is close to the native (7 Å RMSD) and the model with lowest RMSD is the next best.

Figure 7.

Validation results for FILM2 potential function applied to decoy sets based on (a) bacteriorhodopsin and (b) rhodopsin.

11. Classifying transmembrane proteins using predicted structural features

Over the past 15 years there has been a great deal of progress in the classification of proteins both by sequence (Sonnhammer et al. 1997; Mulder 2005) and by structure (Murzin et al. 1995; Orengo et al. 1997). In both cases, improvements have been driven by the rapid explosion in sizes of both sequence and structure data banks, and these improvements have led to better and more comprehensive annotations of genome sequences.

With the limited available structural data for transmembrane proteins and the large fraction of transmembrane families for which there is little or no functional information, it is not surprising that annotations for membrane-associated genome sequences are relatively sparse. Automatic sequence clustering techniques have a particular problem with transmembrane proteins because of the sequence constraints on the transmembrane helices. Put simply, one transmembrane protein sequence looks very similar to many others. Nevertheless, basic sequence analysis techniques are a good starting point. Liu & Engelman (2002) have classified polytopic membrane proteins in 26 genomes, according to their number of transmembrane helices and sequence similarities, into 637 families. Classification based on similarity of amino acid sequences can be very informative when very significant sequence similarity exists; however, it is known that the impact of amino-acid sequence similarity on protein evolutionary or functional relationships is rather limited in the cases when the similarity between sequences is low. Moreover, we know from globular protein domains that sequence comparisons fail to identify many of the relationships that emerge from the comparison of protein structures.

With little prospect of vast numbers of transmembrane structures being solved experimentally over the next few years, we have to focus on predicted structural features to improve existing transmembrane classifications. The aim of some of our recent work on transmembrane protein sequence analysis has therefore been to classify proteins according to their predicted structural features, i.e. residue and helix orientation, as opposed to classifying them by sequence similarity alone. Examining predicted transmembrane topology is one very crude way in which uncharacterized transmembrane proteins can be grouped into meaningful families using structural clues (e.g. Jones 1997). However, we are already very aware that transmembrane proteins of identical topology can have dissimilar folds (e.g. the case of bacteriorhopsin and rhodopsin), and should therefore not be clustered into the same superfamily.

The aim of some of our recent work on transmembrane protein sequence analysis has been to classify proteins using a greater variety of predicted structural features. For example, by classifying membrane proteins according to their packing and orientation of their helices we hope to be able to improve on the classifications carried out to date, which have been based just on sequence and topology.

One powerful structural feature we have been examining is again the variphobicity signal which can be deduced from a multiple sequence alignment, and this has been found to provide a strong signal which can be used to correctly segregate transmembrane sequence clusters that would otherwise be grouped together.

As an example of using variphobicity analysis to distinguish topologically similar families of transmembrane proteins, we set up a simple experiment to see whether we can correctly cluster a mixture of bacteriorhodopsin and rhodopsin-like protein sequences using variphobicity alone. Of course, a great deal of work remains to be done in constructing an optimal clustering method based around variphobicity scoring, but we show here an example which is intended to serve as a minimal proof of principle.

As a first step, the MEMSAT method (Jones et al. 1994) was used to predict the topology of each protein along with the transmembrane segment locations and lengths. As expected, all of the proteins were predicted to have the same overall topology (seven transmembrane segments with the N-terminus on the outside). For each of the transmembrane segments, we calculated a measure of variphobicity (Taylor et al. 1994). As discussed by Taylor et al., transmembrane segments having a high variphobicity score suggests that the helix has a high lipid exposure, whereas a low score suggests that the helix is not likely to be exposed to lipid (and is consequently like to be packed into the core of the protein).

Table 1 shows the resulting variphobicity scores for the seven transmembrane segments in each of the target proteins. Five of the proteins (BAC1_HALS1, BACH_HALSP, BACH_HALSS, BACR_HALHA, BACS_HALHA) come from the bacteriorhodopsin family, eight from the family of opsins and one from a distant member of the GPCR superfamily (sphingosine 1-phosphate receptor; EDG1_HUMAN). For each pair of proteins we derive a metric of similarity by calculating the (Pearson) correlation coefficient for the variphobicity scores. Our expectation is that proteins with the same approximate ranking of variphobicity across their transmembrane helices are more likely to share a common folding pattern. A distance matrix was formed by subtracting each pairwise correlation coefficient from 2.0, and then weighted pair group clustering was used to cluster the proteins. Figure 8 shows the results of this clustering in the form of a dendrogram.

Table 1.

Calculated transmembrane helix variphobicity scores for the five bacteriorhodopsin-like sequences, the seven opsin sequences and a sphingosine-1-phosphate receptor.

	TM1	TM2	TM3	TM4	TM5	TM6	TM7
BACA_HALS1	0.42	0.32	0.02	0.31	0.35	0.23	0.31
BACH_HALSP	0.20	0.24	−0.01	0.30	0.37	0.28	0.20
BACH_HALSS	0.28	0.24	−0.01	0.30	0.33	0.28	0.20
BACR_HALHA	0.37	0.33	0.04	0.30	0.40	0.25	0.29
BACS_HALHA	0.21	0.22	0.05	0.27	0.32	0.19	0.19
EDG1_HUMAN	0.29	0.01	0.30	0.64	0.67	0.43	0.22
OPS1_CALVI	0.72	0.05	0.18	0.46	0.06	0.50	−0.12
OPS2_DROME	0.70	0.09	0.22	0.40	0.14	0.53	−0.11
OPS3_DROME	0.68	0.12	0.19	0.17	0.49	0.50	0.08
OPS4_DROME	0.57	0.06	0.06	0.32	0.48	0.51	0.00
OPSB_HUMAN	0.61	0.06	0.19	0.31	0.27	0.43	0.03
OPSD_BOVIN	0.83	0.10	0.20	0.23	0.36	0.67	−0.07
OPSG_HUMAN	0.67	0.04	0.28	0.30	0.54	0.52	−0.12
OPSR_HUMAN	0.66	0.04	0.27	0.27	0.54	0.54	−0.05

Figure 8.

Dendrogram of the sequences shown in table 1 based solely on the pairwise correlation coefficients of the variphobicity scores.

The results obtained are very close to the results that would be obtained from clustering these proteins by sequence similarity. However, in this case, the proteins are represented merely by a vector of seven variphobicity values and the similarity by a crude calculation of correlation. Based just on these variphobicity patterns, the proteins form three distinct clusters (with EDG1_HUMAN forming a singleton group) suggesting that the relative variphobicity of the transmembrane segments is indeed a useful ‘fingerprint’ for a structurally similar family of transmembrane proteins.

We expect that a robust method for clustering transmembrane proteins of unknown structure will need to take into account a number of different features. For example, the lengths and physicochemical characteristics of connecting loops might be very informative. With the right combination of features it should be possible to get a clearer picture of the as yet uncharacterized transmembrane proteins found in completed genomes than can be obtained by using sequence similarity alone.

12. Conclusions

Despite a significant amount of progress in recent years in the prediction of globular protein structure from amino acid sequence, particularly in the areas of fold recognition and distant homology modelling, technology for the prediction of transmembrane protein structure is clearly lagging some way behind. In this paper we have described a number of recently developed methods for transmembrane protein structure prediction which we hope will eventually form parts of a ‘pipeline’ for automatically building structural models for all of the transmembrane proteins in a genome.

The main bottleneck to progress in improving transmembrane modelling methods is clearly the lack of experimentally determined structures for integral membrane proteins. This not only limits our ability to calculate reliable statistics for our knowledge-based approaches, but also limits our ability to test them. A common feature of all the methods discussed in this paper is that they have been designed to extract maximum value from what little experimental data is available. Were there to be a lot more available structural data then we would have made different decisions in the design of our algorithms.

Although there has clearly been some progress in increasing the efficiency of structure determination for membrane proteins, it is apparent that the lack of data will be the limiting factor for some considerable time to come. However, we prefer to look on this as a challenge for bioinformatics rather than an explanation for failure. The true value of bioinformatics has always been in maximizing the potential for exploitation of limited amounts of data, and the structural characterization of membrane proteins has to be seen as a perfect example of doing just this. We hope, therefore, that this paper will at the very least serve as a rallying call to both the experimental and bioinformatics community to develop imaginative new approaches to predicting the structure of transmembrane proteins which effectively and efficiently combine theory with experimental data.