A rapid genome-scale response of the transcriptional oscillator to perturbation reveals a period-doubling path to phenotypic change

Abstract

Perturbation of the gated-synchrony system in yeast with phenelzine, an antidepressant drug used in the treatment of affective disorders in humans, leads to a rapid lengthening in the period of the genome-wide transcriptional oscillation. The effect is a concerted, genome-scale change in expression that is first seen in genes maximally expressed in the late-reductive phase of the cycle, doubling the length of the reductive phase within two cycles after treatment. Clustering of genes based on their temporal patterns of expression yielded just three super clusters whose trajectories through time could then be mapped into a simple 3D figure. In contrast to transcripts in the late-reductive phase, most transcripts do not show transients in expression relative to others in their temporal cluster but change their period in a concerted fashion. Mapping the trajectories of the transcripts into low-dimensional surfaces that can be represented by simple systems of differential equations provides a readily testable model of the dynamic architecture of phenotype. In this system, period doubling may be a preferred pathway for phenotypic change. As a practical matter, low-amplitude, genome-wide oscillations, a ubiquitous but often unrecognized attribute of phenotype, could be a source of seemingly intractable biological noise in microarray studies.

The idea that the cell is an oscillator, an attractor, and that time is an essential variable of the information content of cellular systems, although well supported by both theory and experimental findings, is still something of a novelty in genomics (1–4). Before the development of genome-wide assays, experimental support for viewing the cell as an oscillator was limited to measuring single constituents or to analyzing macroscopic events such as DNA replication or cell division after an intentional perturbation (5–7). We now have the capacity to follow the transcriptional patterns of all expressed genes to construct a system-wide dynamic network. By assessing the temporal pattern of gene expression in all of the transcripts closely through time after perturbation, we can derive the first measurements of coupling strength among genes. Such information is essential to constructing a detailed formal representation of the cellular attractor. Network representations based on two-hybrid, chip–chip, or mass spectrometry interactions (8–13) give us a sparse mapping of genes that interact but have not offered clear insights into dynamic connectivity among genes and their transcripts. Our effort here is to bring together genome-wide changes through time and the more traditional gene-centered, steady-state network perspective to uncover the dynamic architecture of phenotype.

Lithium and phenelzine (PZ) are among the oldest of the mood-stabilizing or antidepressant psychoactive drugs used in the treatment of bipolar and other affective disorders in humans. It has long been known that one of the effects of these agents is a slight lengthening of the period of the circadian rhythm in both normal volunteers and patients under controlled settings (14, 15). In humans, as well as experimental systems as disparate as rodents and the plant Kalanchoe, treatment with these agents increases the period of the circadian clock by an amount just under an hour (16). In the budding yeast Saccharomyces. cerevisiae, there is a similar 30- to 40-min increase in period (17). Thus, in yeast, the period of the oscillation in the respiratory/reductive cycle is nearly doubled from 40 to ≈70 min. Close examination of the benchmark oscillation in dissolved oxygen (DO) in the gated synchrony system described here indicates that the reductive phase is exactly doubled whereas the length of the respiratory phase is unchanged by the drug.

The presence of a genome-wide pattern of oscillation favors a view of the organization of cellular phenotype as a globally coupled dynamic structure. Representative genes from the three observed clusters (early reductive, late reductive, and respiratory) trace out a 3D structure. Collectively, all of the transcripts of the system can be pictured in concentration phase space as circling the steady state at a few opposed and equally spaced phase angles (18–23). The great strength of this view is that systems with large numbers of variables can be visualized in rather simple low-dimensional figures. These systems have a mathematical basis that has been well understood for some time (18). The rules of behavior are specific, and predictions can be readily tested in well controlled biological systems.

Results

In a previous study using Affymetrix chips and close time series sampling (every 4 min/32 chips/through three cycles), we showed that oscillations are a ubiquitous property of yeast transcripts (4). The temporal organization that gives rise to the well characterized 40-min oscillation (24–28) in DO is manifested in the sequestering of transcripts into those maximally expressed in the reductive phase and those maximally expressed in the respiratory phase. The reductive phase is roughly twice the length of the respiratory phase, and expression maxima are largely restricted to three equally spaced intervals in the cycle, one in the respiratory phase and two in the reductive phase. We have suggested that this transcriptional-respiratory-attractor cycle (TRAC) is responsible for the temporal organization of phenotype and for the timing of developmental processes such as the cell cycle.

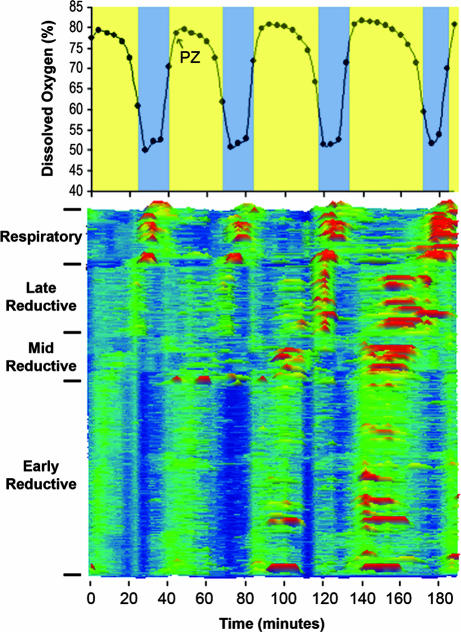
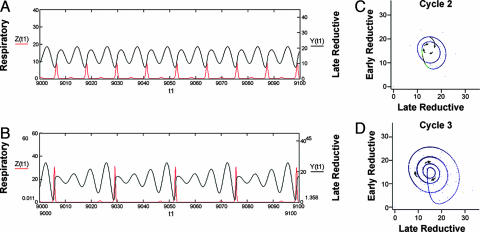
By mapping the genome-scale response to a perturbation known to change the oscillation period, some evidence of the dynamic structures underlying cellular phenotype may be revealed. Based on experiments following the changes in only the DO, carbon dioxide (CO₂), and hydrogen sulfide (H₂S) oscillations in response to PZ treatment (Fig. 6, which is published as supporting information on the PNAS web site), it was thought that the response, although rapid might, through close time sampling, allow a measure of the coupling strength and connectivity among genes and their transcripts. Treatment of cultures synchronous with respect to the TRAC and showing an ≈40-min DO oscillation results in a rapid response to PZ at doses between 0.5 and 3 mM. Lower doses have little effect on the period. The DO oscillation in response to 1 mM PZ showed that the period increased by 1.72. This increase was due to a nearly perfect doubling of the reductive phase (no oxygen utilization; high DO values), with little to no change in the duration of the respiratory phase (Figs. 1, 6, and 7, which is published as supporting information on the PNAS web site).

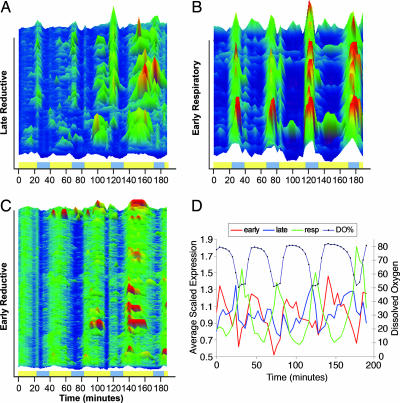
In the color intensity map of Fig. 1, all expression values for each gene were scaled to the average expression of the pretreatment cycle (samples 1–10). All genes were then ordered for their time of maximum expression according to this scaling. Three major classes of transcripts are apparent-early reductive, late reductive, and respiratory, as described earlier (4). Overall, the effect of PZ treatment seems to be a transient delay in the maximum expression of reductive phase transcripts with respect to DO. The duration of the respiratory phase and the patterns of expression in the respiratory phase transcripts are not altered by the treatment except that the time of maximum expression shifts in response to the lengthening of the reductive phase (Figs. 2B and 8, which is published as supporting information on the PNAS web site). Similarly, in the early-reductive phase, oscillations in transcripts do not show the same genome-scale changes until after the expansion of the late-reductive period, as can be seen in Fig. 1 and in the expanded map of the late-reductive phase transcripts in Fig. 2A and early and respiratory phase transcripts (Fig. 2 B and C). The increase in the duration of the reductive phase is accompanied by a doubling in the number of peaks or maxima in expression in early and late-reductive phase transcripts in the third cycle after PZ treatment, thus transiently moving transcripts into the respiratory phase of the DO curve (Fig. 2D). By the fourth cycle, the DO curve lengthens and the reductive phase transcripts come closer to coordination with DO again. Transcripts maximally expressed in the late-reductive phase, as opposed to early-reductive, showed the most notable changes in phase of maximum expression. The net effect is a doubling in the duration of the reductive phase.

Fig. 1.

Period increase in DO and transcription in response to PZ treatment. Samples for Affymetrix expression array analysis were taken at 4-min intervals through four cycles of the oscillation as indicated by the black circles on the DO curve (Upper). Bands overlying the DO oscillation indicate the respiratory phase (azure) and reductive phase (yellow). After one complete cycle of sampling, PZ was added at 1 mM at the time indicated in the figure. Transcripts were classed according to their time of maximum expression in the cycle by scaling expression to the average of the first 10 samples (control cycle) (Lower). Expression intensity is scaled from <0.2 (dark blue) to >4 (red orange). The black arrow represents the time of PZ treatment.

Fig. 2.

Late-reductive, early-reductive, and early-respiratory transcripts. (A–C) Change in phase relationships and period of transcripts after perturbation color intensity maps of the three major classes of transcripts were expanded to show the patterns after treatment. The x axis in A and B represents time in minutes. As in Fig. 1, intensity was scaled from 0.2 (dark blue) to >4 (red-orange). In D, the average expression level of all transcripts maximally expressed in early-reductive phase (red), late-reductive phase (blue), and respiratory phase (green) are shown relative to the DO curve (black). Bands indicate the respiratory phase (azure) and reductive phase (yellow).

Measures of Periodicity in the Transcriptional Cycle.

Fast Fourier transform filtering.

To provide further support for the genome-wide nature of the oscillation in both the control and PZ-treated cultures, two standard methods, fast Fourier transform and singular value decomposition (SVD), were used to characterize transcript changes through time. Fourier filtering was used to class the transcripts according to where in the cycle they were maximally expressed and to determine whether maximum power was in the 40-min range in the first three cycles. Before beginning this classification, a decision rule for calling a particular transcript present was established. In our original study (4), we classed a transcript as present if it was present in at least 3 of the 11 samples taken for each cycle of the control series, leading to 5,432 transcripts being included in the analysis. If we raised the standard for inclusion to require that the transcript be present in all 32 samples, the number fell to 4,425 transcripts being classed as present. Using a similar classification system in this study and the default Affymetrix standards for a present call, we found that 5,328 were present in the PZ-treated experimental series when scored as present if present in at least three samples. If we raised the requirement to present in all samples, the number of transcripts scored as present fell to 4,429. Of these, 4,328 showed maximum power in the 40-min range by fast Fourier transform analysis (Fig. 9, which is published as supporting information on the PNAS web site). This amount is very similar to the number (4,311) found with maximum power at 40 min in the previously published control series. This analysis suggests that 4,328 (97.7%) of the 4,429 expressed genes show maximal power in the 40-min range.

SVD.

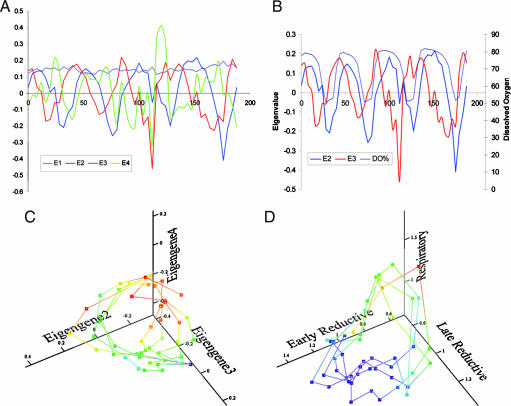
SVD has seen wide use in the analysis of expression array data and has proven to be a useful method for developing a global representation of expression profiles (29, 30). In our earlier study (4), shown here as the control, SVD uncovered the artifact in the data set that was caused by sampling from two different cultures with slightly different periods (Fig. 10, which is published as supporting information on the PNAS web site). The ability of the SVD application to find small differences between the two data sets in that series because of differences in phase and amplitude of the oscillation is a measure of its utility in studies of the transcriptional cycle. Having established the global pattern in the control series described in the earlier study (4), we next examined the information content of the Eigengenes (equivalent to eigenvectors 29,30) in the PZ-treated series involving a total of 5,328 expression patterns through 48 samples taken at 4-min intervals through four cycles of the oscillation. If SVD uncovers the details of the period-doubling response by a method designed to detect global features of the data, support for this finding would be enhanced. Information in the PZ-treated cultures is collected into the first four Eigengenes (Fig. 3A). Typically, the first Eigengene serves to normalize the data set. The results of the analysis are expanded in Fig. 3B, where Eigengenes 2, 3, and 4 capture the envelope of the reductive phase transcripts. In contrast to the smooth pattern seen in Eigengenes 3 and 4 in the control series (Fig. 10), Eigengenes 3 and 4 in the PZ-treated sample show sharp discontinuities after treatment. Eigengene 3 captures the period-doubling response of the early-reductive transcripts. A reconstruction of the attractor can be seen in the plot of the principle Eigengenes 2, 3, and 4 (Fig. 3C). One difference between this map and that for the control series (Fig. 11, which is published as supporting information on the PNAS web site) lies in the greater excursion of the map in the second and third cycles after PZ treatment and in the folds in the posttreatment cycles. This difference is consistent with an increase in the cycle time of all expressed transcripts, further indicating that the information content of the transcript expression as a whole is best represented as cyclical. It should be emphasized that other projections of the 3D figure show better the folding in the surface (Fig. 12, which is published as supporting information on the PNAS web site).

Fig. 3.

Reconstructing the transcriptional oscillator. (A) The first four principal Eigengenes are shown for the 48 samples ordered through time from 0 to 188 min for all 5,328 genes from the PZ time series for all four cycles. Eigengenes E1–E4 as indicated by the color code in the figure contain >80% of the information. (B) Just the E2 and E3 vectors are shown to make clear the increase in the number of maxima in E3 after treatment. Plots of Eigengenes E2, E3, and E4 are shown in C as a 3D projection that emphasizes the globally cyclic nature of expression. The expansion of the trajectory in the third cycle and the increase in the number of maxima in expression seen in A and B and captured principally by Eigengenes 3 and 4 are seen in the Figs. 13 and 14. For comparison, a 3D reconstruction of the trajectory of transcript concentration from the averages of the scaled data of three major temporal clusters from Fig. 2D above is shown. The projection emphasizes the globally cyclic nature of the system.

For comparison, a more transparent method was used. The average of the three major temporal clusters of Figs. 1 and 2 are shown in Fig. 2D and plotted together in Fig. 3D as a 3D reconstruction of the trajectories through concentration phase space of the four cycles of the experiment (Fig. 3D). The increase in the amplitude of the respiratory and late-reductive phase transcripts is expressed in the greater excursion of the late-reductive transcripts in the third and forth cycles after treatment. This projection emphasizes the cyclical nature of the system as a whole but does not show the folding of the surface that would be expected from a period-doubling response (Fig. 13, which is published as supporting information on the PNAS web site).

A third independent assessment of the genome-wide behavior of the TRAC was made by using self-organizing maps (SOM) and is presented in Movie 1 (which is published as supporting information on the PNAS web site) as an animation showing the cyclic pattern of changes through all four cycles of the experiment in transcripts clustered (31) using GEDI software (Fig. 14, which is published as supporting information on the PNAS web site).

Concerted and Sequential Response to Perturbation.

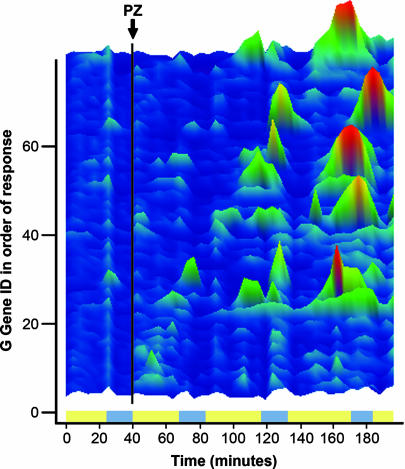
The period-doubling response seems to involve the entire genome and to take place rapidly, making an assessment of the sequence of specific changes difficult despite the frequent sampling. Nevertheless, one can assess those gene transcripts that change first and that change most dramatically as an indication of their immediacy in the drug response. In a globally coupled system, there is the expectation that those transcripts that are most tightly coupled to the initial responders will be the next to change and so on until the system as a whole has settled into a new basin of attraction. For the great majority of transcripts, the response was to show an increase or decrease in expression at the expected time rather than showing a phase shift. Transcripts were first sorted into groups based on their phase of maximum expression in the pretreatment cycle, as described in Figs. 1 and 2. The groups provide a cluster of gene transcripts with relatively low pretreatment variability. The grouped transcripts were then ordered according to the similarity of their scaled expression to the average scaled expression in the group as a whole in the pretreatment (control) cycle. To adjust for slight phase differences or other variance unrelated to the PZ treatment, the sum of the squares difference of each transcript from the average of the pretreatment cycle was calculated and used to normalize the variance. Then, a three sample-wide measure of the variance was windowed through the entire series after treatment. Genes ordered in this way were then sorted according to their difference from the average of the treated series as a function of time after treatment. This differential difference in position was plotted as a measure of which genes changed first and most rapidly after PZ treatment, as shown in the intensity map of Fig. 4 and in Table 1, which is published as supporting information on the PNAS web site. Among the early responders with the greatest changes after treatment are found a number involved in mitochondrial function and RNA transcription and processing, along with some seemingly involved in drug response. In particular, along with YOR211c (MGM1) are YHR046C/INM1, a gene known to respond to lithium and other drugs used in the treatment of depression (32). Most dramatic is the increase in YOR153W/PDR5, a short-lived membrane ATP binding cassette involved in drug transport and resistance. One might speculate that tPDR5, which elevates expression soon after treatment and remains high through the experiment, is, like many in this small group, not a good example of the period-doubling response. However, as Fig. 7 shows, it acts to prevent PZ transport into the cells within 30 min of PZ addition and thus causes the response to be transient. In general, there are two types of responses that are favored by the method of selection: transcripts that show very large changes in level of expression throughout the experiment and those that show a phase shift in the time of maximum expression relative to their pretreatment phase maximum. It is worth emphasizing that few transcripts showed phase changes distinct from those of their pretreatment control group.

Fig. 4.

First response changes in expression of late-reductive phase transcripts. The transcripts found to be the early strong responders to PZ are shown ordered according to the time after PZ when they are maximally different from the cluster as a whole. Scaling and color mapping are as described in Fig. 1. Gene IDs and descriptions are in Table 1. Bands indicate the respiratory phase (azure) and reductive phase (yellow).

Modeling the Dynamic Architecture of Phenotype.

Qualitative similarities in the behavior of transcriptional oscillations described here to the trajectories taken by the variables in the systems of ordinary differential equations originally developed by Rössler (33) to represent biochemical or macromolecular regulatory loops are hard to ignore. The trajectory of the Rössler attractor was modified by translation into the positive quadrant and rotated to produce a model that more closely represented the behavior of the TRAC (Fig. 5 and Appendix 1, which is published as supporting information on the PNAS web site). First, there are just three major basins into which all of the transcripts of the yeast cell settle. One of these, the respiratory phase cluster, is notably more periodic than the other two and moves from essentially background intensity to brief high amplitude expression and returns quickly to background. This behavior is similar to that of the z component of the attractor drawn here (red line in Fig. 5A). The two reductive phase clusters tend to show more nearly sinusoidal oscillations, a roughly 2-fold average variation, and maintain a high level throughout the cycle similar to the x and y variables of the Rössler.

Fig. 5.

Mapping period doubling onto a low-dimensional surface. A sketch of proposed paths in concentration phase space of the transcripts is shown based on the Rössler attractor. (A and B) A simulation of the starting and period doubled states is shown for the late-reductive genes (black) and the respiratory gene transcripts (red). Arrows in C indicate the path that would be followed by late-reductive transcripts to reach the levels seen in the first cycle after treatment cycle 2. (D) The continuing path and the state reached by the late-reductive transcripts by cycle three (second cycle after treatment). A sample simulation is shown in Appendix 1.

The increase in period of the oscillation occurs exclusively through a doubling of the reductive phase with the doubling in the number of peaks in expression during this time (Fig. 5 A and B). From the model, we would expect that, before treatment, there would be peaks in expression of early-reductive, late-reductive, and then respiratory transcripts. Following the period-doubling response, the sequence should be early-reductive, late-reductive, and then early-reductive again and late-reductive, followed by respiratory transcripts. Individual transcripts and, less clearly, the averages of all transcripts from the three major clusters show the trend (Figs. 2D and 14, which is published as supporting information on the PNAS web site). It seems the SVD analysis captures this response in the third and forth cycles after treatment (Fig. 3 A and B). An example of a single transcript showing the period-doubling pattern is shown in Fig. 14. A sketch (arrows in Fig. 5C) shows the proposed path from the pretreatment cycle to the first cycle after treatment during which the late-reductive phase transcripts are either phase advanced or reduced in their expression and the increase in the number of cycles through the reductive phase (Fig. 5D) before entering the respiratory phase. It was surprising to find that an “off-the-shelf” attractor, modified only slightly, served to model this complex experimental system so well. However, the correspondence is imperfect, and, at this time, the sampling resolution is not sufficient to test a more detailed mapping. Given that we are in the early stage of dynamic systems biology, the specific system of differential equations chosen to represent the phenomenon will doubtless evolve.

Discussion

The gated synchrony system described here provides a unique opportunity to do true time series analysis. In this coherent population, all of the transcripts oscillate. Given this genome-wide oscillation, the only plausible way to think about a cell is as an oscillator, an attractor. Upon perturbation, the system shows a period-doubling response, one of the expected behaviors of deterministically noisy attractors. The envelope that contains the trajectories of all transcripts through phase space is similar to that described by the Rössler attractor.

The TRAC oscillation is an expression of a complex, biological system with >5,000 transcripts and many more variables in toto. In dynamic systems theory, the formal representations that show the phenomenon of period doubling typically result from a change in the value of one of the parameters of the system equations, in which there are usually only three variables. To better represent this multivariable system, we earlier modeled the genome-wide properties of transcription by coupling multiple attractors each taken to represent a genetic regulatory loop of one or a few genes and their products and end products (22, 23). With yeast continuous cultures, we may now have a starting point for an experimental model for the period-doubling phenomenon and a means of testing some of the predictions of the simulations. If it can be generalized, the period-doubling phenomenon may represent a common pathway for differentiation. The idea that such phenotypic changes can be stably maintained as a consequence of their settling into a new stable basin of attraction or canal is not new (1). Because the period-doubling effect is confined to the reductive phase, the relative length of time spent in the reductive as opposed to the respiratory phase is increased. It is known that the ratio of respiration to glycolysis in this system is an accurate measure of the Warburg ratio, the relative amount of energy derived from glycolysis as opposed to respiration. It is reasonable to speculate that period doubling is a means by which the Warburg ratio is increased in other systems.

Unrecognized Oscillations and the Reproducibility of Expression Microarrays.

Concern has been growing that high through-put technologies, particularly expression microarrays (34), have shown a persistent barrier in sensitivity leading to the idea that there is a 2-fold boundary for change in the expression level of any gene transcript. Below the 2-fold boundary, calls are less certain. Although there is general agreement that the barrier within a particular microarray assay system is biological, no ready solution has been offered beyond increased numbers of biological replicates (34, 35). Doing more replicates might work if the cells or tissues are truly random in time or making transient excursions away from the steady state. However, taking increasing numbers of replicates, as many as 12 in some instances, has unexpected consequences if the system is universally oscillatory. If cells show highly organized temporal patterns of expression that go unrecognized, then repeated sampling and statistical analysis will yield a time-averaged value that is near the steady state of the oscillatory system but is not a value taken at any time during the oscillation. It is an artifact and guarantees that most of the genes with regular trajectories through concentration space will fall below the values needed to make a change call. Perfect randomness is likely to be as rare as perfect synchrony, and cells are not at a steady state. From the steady-state statistical perspective, it is not possible to show, on a gene by gene basis, that each gene transcript oscillates. However, in dynamic systems theory, there are classic papers that make the case that, in a coupled system where some of the elements are shown to oscillate, the likelihood that the system as a whole oscillates increases rapidly as the number of elements is increased beyond a rather small fraction of the total (36, 37).

Conservation of Period.

The temporal coordination manifested by the TRAC seems to involve essentially all cellular functions thus far examined. Given the alternation of the redox state, it should not be surprising to find that the alternation of respiration and reduction also extends to the functional state of the mitochondria (4, 38). Of current interest is the role that these high amplitude oscillations play in protein synthesis, degradation, and functional state. Transcripts for ubiquitin-proteosome function are made at just one phase of the cycle, suggesting that protein catabolism is temporally organized and oscillatory (4). This temporal organization extends to the synchronous gating of cells into S-phase. DNA replication in these cells begins abruptly at the end of the respiratory phase as oxygen consumption decreases and H₂S levels rise. The restriction of DNA replication to the reductive phase of the cycle is seen as an evolutionarily important mechanism for preventing oxidative damage to DNA during replication. Moreover, conserved genes, those whose rate of substitution is in the lowest third of all genes, are transcribed almost exclusively in the reductive phase of the cycle.

The idea that certain functional domains are conserved through great evolutionary distances is the core of our understanding of modern molecular evolution (39). Moreover, a number of papers have appeared showing that the rate of evolution of a protein is related to the number of measurable interactions, and the argument has been made that evolutionary changes may occur largely by coevolution (16). What has rarely, if ever, been considered is the idea that a dynamic property of the system might impose similar or greater constraints on its variation over time (40). An argument can be made for this idea based on the rapid genome-scale change in expression shown here. If, as we show, “everything oscillates,” then it is likely that, to a greater of lesser extent, every gene product interacts with some or many other gene products. In such a globally coupled system, the constraints on period change might be expected to be extreme. To put it another way, there may be a very limited path through which such change occurs and constraints on that path might be expected to follow a period-doubling bifurcation. Period mutants of the circadian clock and quantized generation times in cultured mammalian cells tend to cluster at a somewhat restricted set of values in the ≈4-h range (40, 41). The gating of yeast cells in the continuous synchrony cultures used here would seem to be another manifestation of this underlying timekeeper. In particular, ≈40 min, ≈80 min, and ≈240 min (4 h) are the most frequently seen. However, a recent study using a different yeast strain grown in limiting glucose and under high oxygen tension showed an ≈5-h DO oscillation and a similar pattern of transcriptional oscillations to that reported here and earlier (42, 43). In nonlinear dynamic systems, the TRAC and most of the temporal organization associated with it seem to be maintained through the period-doubling process. This path is significant in representing period doubling and, perhaps, period three bifurcations. An intriguing question is whether this behavior generalizes to mammalian cells and to stem cell differentiation.

Methods

Medium and Culture Conditions.

The fermenter (650 ml) was inoculated with 2 × 10⁷ cells of the yeast strain IFO0233 and grown as described (4) except glucose monohydrate was added at 19.25 g/liter (Sigma, St. Louis, MO). Antifoam A was added at 0.2 ml/liter, and the pH was maintained at 4.0. To maintain oscillations, cultures were shifted from batch to continuous mode at a dilution rate of 0.086/h. Phenelzine (cat. no. 156136; MP Biomedicals, Solon, OH) was added at the reductive phase.

RNA Preparation.

RNA was purified and processed for Affymetrix GeneChip analysis as described in Supporting Methods, which is published as supporting information on the PNAS web site. RNA yield differences between samples were normalized by adding Affymetrix poly(A) standards to the cell pellets at the beginning of RNA isolation.

Data Analysis.

Results were quantified and analyzed by using MicroArray Suite 6.1 and GCOS software. Excel files were created to permit further processing and then put into Mathcad (Mathsoft Inc., Cambridge, MA), Mathematica (Wolfram Research, Champaign, IL), SigmaPlot, or in MatLab (Mathworks Inc., Natick, MA). Intensity values for each of the verified ORFs in the S98 chip and the yeast S2 chip were linked to the Saccharomyces Genome Database (SGD) site, and both their genetic and physical map locations were associated with the intensity values for each gene as described (4). The results for all ORFs scored as present by using the default Affymetrix settings were identified according to the original sample number and the phase in the DO oscillation at which the maximum expression occurred. Expression patterns were then mapped according to the time of maximum as a starting point for presentation. Further analysis was performed for all ORFs present in all samples in each of the four cycles. Of the 5,443 ORFs scored as present in at least 3 of the 48 samples, 5,254 had P values <0.01 and the remainder had P values <0.035 (detailed methods and sample calculations are available in Supporting Methods). Original data are available from the National Center for Biotechnology Information/Gene Expression Omnibus web site.

Abbreviations

PZ

phenelzine

SVD

singular value decomposition

DO

dissolved oxygen

TRAC

transcriptional-respiratory-attractor cycle.