Abstract
Molecular simulations are carried out on the Immunoglobulin 27 domain of the titin protein. The energy landscape is mapped out using an implicit solvent model, and molecular dynamics simulations are run with the solvent explicitly modeled. Stretching a protein is shown to produce a dynamic energy landscape in which the energy minima move in configuration space, change in depth, and are created and destroyed. The connections of these landscape changes to the mechanical unfolding of the Immunoglobulin 27 domain are addressed. Hydrogen bonds break upon stretching by either intrabasin processes associated with the movement of energy minima, or interbasin processes associated with transitions between energy minima. Intrabasin changes are reversible and dominate for flexible interactions, whereas interbasin changes are irreversible and dominate for stiff interactions. The most flexible interactions are Glu-Lys salt bridges, which can act like tethers to bind strands even after all backbone interactions between the strands have been broken. As the protein is stretched, different types of structures become the lowest energy structures, including structures that incorporate nonnative hydrogen bonds. Structures that have flat energy versus elongation profiles become the lowest energy structures at elongations of several Angstroms, and are associated with the unfolding intermediate state observed experimentally.
INTRODUCTION
The energy landscape formalism has become widely used to describe the properties of proteins (1–6). The central idea underlying this approach is that the energy landscape of a protein has many local energy minima of various depths. The protein dynamics can be considered as the sum of vibrational-like motion within individual energy minima, and transitions between energy minima (7,8). The transitions between energy minima lead to the more interesting and complex dynamics, such as protein folding, and have been modeled with master equation approaches (9–14).
Previous energy landscape studies have addressed proteins that are mechanically isolated from their environment. In some physiological processes, such as muscle contraction and cell adhesion, the mechanical coupling of the protein to its environment is an essential feature of the protein function. For example, the mechanical properties of the protein titin play an important role in muscle function (15–17).
The stretching of single molecules of titin has been investigated experimentally using atomic force microscopy (18) and optical tweezers techniques (19,20). Titin is a very large protein composed of hundreds of modular domains, and these experiments show that the domains unfold one-by-one as the protein is stretched. Experiments on engineered proteins composed only of repeats of the 27th immunoglobulin domain of titin (Ig27) show that these domains undergo reversible transitions to intermediate states before they unfold (21).
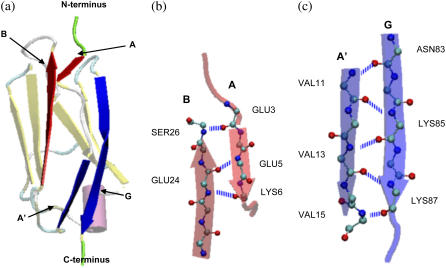
The mechanical unfolding of Ig27 has been elucidated on an atomic level by molecular simulations (22–30). The structural features that control mechanical unfolding are the interstrand A-B hydrogen bonds near the N-terminus of the protein, and the interstrand A′-G hydrogen bonds near the C-terminus; these interactions are shown in Fig. 1. The A-B interactions break first upon stretching, and the strength of the protein with respect to unfolding is determined by the force required to break the A′-G interactions.
FIGURE 1.
Structure of the Ig27 domain of titin (31). Interactions between the A and B strands (shown in red), and between the A′ and G strands (shown in blue), govern the resistance to unfolding. This figure was created with the VMD software package (44).
This investigation addresses the mechanical unfolding of Ig27 in terms of the energy landscape. In particular, the energy landscape approach is used to elucidate the ways that the relevant hydrogen bonds break as Ig27 unfolds.
METHODS
Simulations are carried out on the titin Ig27 domain (designated 1TIT in the protein data bank (31)), which consists of 89 residues and 1379 atoms. The Amber force field (version ff99) is used in the simulations (32,33). The simulations are carried out with the Amber molecular modeling package (34).
Two types of simulations are carried out. First, molecular dynamics (MD) simulations and energy minimizations are used to probe the energy landscape as Ig27 is stretched, with the aqueous environment represented by the generalized Born implicit solvent model (35,36). Second, MD simulations are carried out to determine the relevance of the landscape analysis at finite temperature and with the aqueous environment explicitly modeled.
The quasi-static simulations probe the changes in energy minima of Ig27 with stretching. Starting from an initial configuration (discussed below), an energy minimization is carried out with the end-to-end distance R1N constrained by a harmonic energy penalty function to be near a desired value R1N,x (R1N is defined as the distance between the alpha carbon atoms of the first and last residues). The value of R1N,x is then increased or decreased in increments of 0.1 Å, and after each change in R1N,x the minimum energy structure is found using an energy minimization procedure that starts from the minimum energy structure at the previous value of R1N,x. Very high precision is required to fully characterize the stretching-induced changes in the minimum energy structures, which necessitates 30,000–100,000 energy evaluations for each energy minimization; these energy minimizations are therefore much more computationally intensive than steered molecular dynamics simulations at stretching rates of 0.1 Å/ps (which require ∼1,000 energy evaluations per elongation increase of 0.1 Å).
The initial configurations for the quasi-static simulations are taken from instantaneous configurations during MD simulations with R1N constrained by a harmonic energy penalty function. The procedure used is as follows. An MD simulation is first run starting from the initial 1TIT structure. Instantaneous configurations from this MD simulation are used as starting points for quasi-static stretching trajectories (described above). Then, configurations from these quasi-static stretching trajectories are used as starting points for further MD simulations with different constrained values of R1N, which in turn give strating points for more quasi-static stretching trajectories. This process of alternating MD simulations with quasi-static stretching trajectories is repeated a number of times to obtain an ensemble of energy minima at a range of R1N.
MD simulations are also carried out to establish the relevance of the energy landscape results in regard to both finite temperature and a more accurate explicit representation of the aqueous environment. The MD simulations are carried out with the protein end-to-end distance R1N constrained by a harmonic energy penalty function; the harmonic spring constant is 5 kcal/mol Å2. The MD simulations begin from structures obtained in the quasi-static trajectory described above, and are carried out at 300 K. The simulations include a 10 Å shell of water around the starting coordinates of the Ig27 structure; the number of water molecules included in the simulation depends on the elongation of Ig27, and ranges from 1480 to 1684.
RESULTS
Energy landscape distortions upon stretching
The most important features of the energy landscape are the local minima. Here we determine how stretching affects local minima of Ig27, using the quasi-static procedure described above starting from the 1TIT structure.
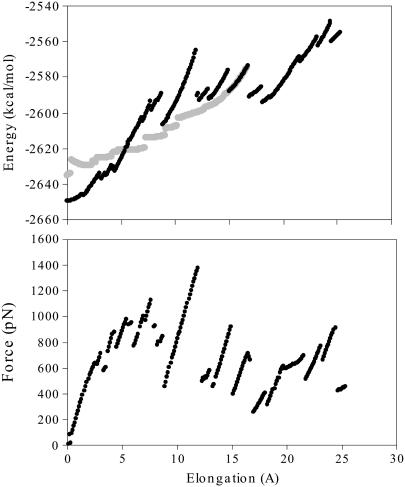
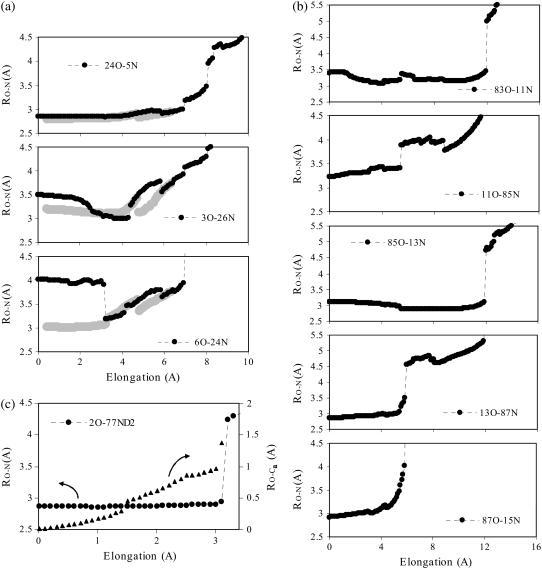
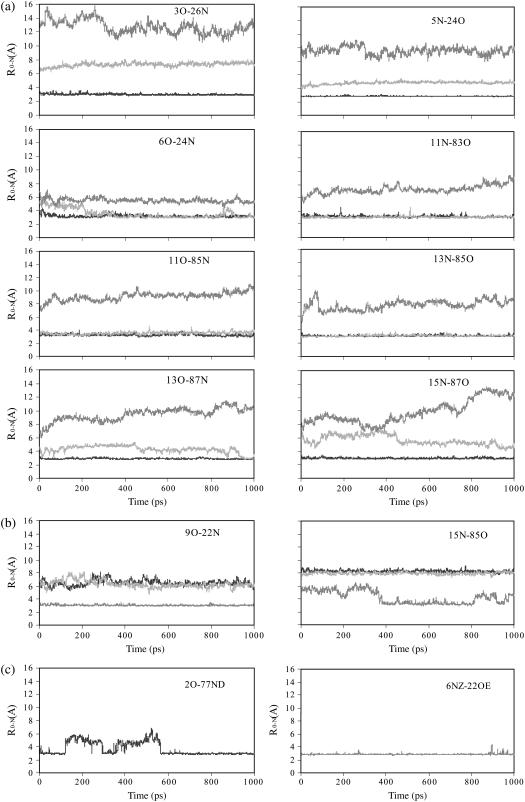
The local minima are characterized by their energy and their position in configuration space (i.e., the atomic level structure). The local minima can also be characterized by the force with which it resists stretching (i.e., the derivative of the energy at the minimum with respect to the end-to-end distance). The changes in energy and force are shown in Fig. 2. In regard to the position in configuration space, the most relevant structural features are the hydrogen bonds that control mechanical unfolding; the changes in these hydrogen bond lengths are shown in Fig. 3. As Ig27 is stretched, all properties usually change continuously, but these continuous changes are punctuated by discontinuous changes. These results show that stretching distorts the energy landscape as follows:
Stretching moves the positions of local minima in configuration space, and changes the depth of the energy minima. These intrabasin effects lead to continuous changes in the energy, force and hydrogen bond distances, and are fully reversible when the stretching is reversed.
Stretching causes local minima to disappear and new local minima to be created. After a local minimum disappears, net forces on the atoms move the protein along the steepest descent path to another local minimum, which leads to discontinuous changes in the energy, force and hydrogen bond distances. This stress-induced destruction of local minima has been demonstrated in more detail in simpler systems through studies of changes in the height, position and curvature of energy minima and energy barriers (37,38). Local minima are destroyed upon both increasing and decreasing elongation (see Fig. 2 a), so that local minima are stable for only finite ranges of elongation; the destruction of a local minimum upon decreasing elongation can be equivalently described as the creation of that local minimum upon increasing elongation.
FIGURE 2.
Properties of energy minima of Ig27 during stretching. (a) Energy. Note that gray lines are results as stretching is reversed. (b) Force.
FIGURE 3.
Structure at energy minima of Ig27 during stretching, as characterized by hydrogen bond donor-acceptor distances. (a) A-B backbone hydrogen bonds. Note that gray lines are results as stretching is reversed. (b) A′-G backbone hydrogen bonds. (c) A hydrogen bond involving a side chain.
These results show that mechanical coupling to the environment produces a dynamic energy landscape. When end atoms of the protein are constrained, the energy depends on the positions of the free atoms, and parametrically on R1N, i.e., E = E(r2, r3, r4,…,rN−1; R1N) (note that the energy is independent of 2 these internal degrees of freedom, due to rigid-body rotation about the axis connecting the end atoms). Changes in R1N alter the dependence of the energy on the free atom positions, and thus distort the reduced-dimensioned E(r2, r3, r4,…,rN−1) energy landscape. These distortions cause energy minima to move in configuration space and become deeper or shallower, and energy minima to be repeatedly created and destroyed. Although not explicitly addressed here, the heights of barriers also change as a protein is stretched—the destruction of an energy minimum necessarily implies that the height of a barrier decreases to zero (38).
Whereas previous work attributed the breaking of hydrogen bonds to activated transitions between energy minima, the results in Fig. 3 show that hydrogen bonds can in some cases weaken and gradually break even when the system remains in a single energy minimum, due to the movement of energy minima in configuration space. For example, the A′-G hydrogen bond closest to the C-terminus (87O-15N) breaks by this type of process, as shown in Fig. 3 b. The factors that allow this gradual breaking of hydrogen bonds, as well the relationship of this result to previous simulations, is addressed in the Discussion section.
For hydrogen bonds involving side chains, the relaxation of side chains allows hydrogen bonding to remain optimal even when the backbone atoms of the residues move significantly. For example, Fig. 3 c shows that even though the residues on the A and B beta strands separate by >1 Å, the side chain hydrogen bond distance changes by <0.04 Å. After the side chain has been pulled taut, the relevant energy minimum is destroyed and the hydrogen bonds break. Many of the discontinuous changes in energy and force curves (Fig. 2) are due to such breaking of hydrogen bonds involving side chains. However, two salt bridges, Glu-22-Lys-6 and Glu-24-Lys-6, remained intact to the maximum elongations investigated (>25 Å).
In regard to the force-elongation curve, the force increases nearly linearly with elongation when an energy minimum remains stable, and the force decreases after the energy minimum is destroyed. Analogous landscape effects underlie yielding and plastic deformation in glassy materials (39,40). The magnitude of the force peak in this quasi-static trajectory, 1400 pN, is similar to results of ∼1200–1400 pN from previous quasi-static simulations (29), but is significantly larger than the experimental result of 210 pN (29)—this difference from experiment is addressed in the following section.
Ensemble of energy minima
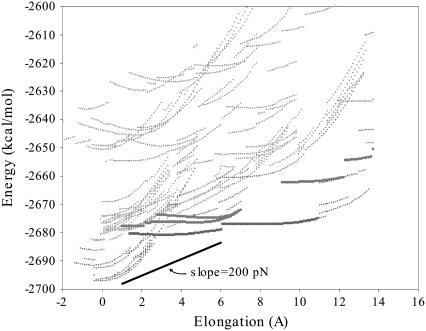
A sample of energy minima visited by the system during MD simulations was obtained at fixed elongations at T = 200 K, with the implicit solvent model (simulations were run at 200 K because the native structure was unstable in MD simulations with the implicit solvent model at 300 K; the instability of the native structure indicates inaccuracies in the implicit solvent model, but these inaccuracies are relatively minor since the native structure was stable at temperatures below 250 K). The changes in these energy minima with both increasing and decreasing elongation were then determined using the quasi-static procedure described above. In total, over 3100 minimum energy structures were examined, and the results for the energies are shown in Fig. 4.
FIGURE 4.
Energies for ensemble of minimum energy structures. The larger points highlight particular states discussed in the text. The diagonal solid line at the bottom of the figure represents a slope of 200 pN.
We emphasize that this ensemble of minimum energy structures is far from a complete or even representative catalog of the possible energy minima. Furthermore, due to the crude force field with the implicit solvent representation, the relative energies of all states cannot be expected to be accurately modeled.
These ensemble results elucidate the magnitude of the force necessary to unfold Ig27. As shown in the previous section, the quasi-static force required to unfold Ig27 is much higher than the experimental value (1400 pN vs. 210 pN). The reason for the much lower value of the force in experiments can be understood in terms of the ensemble of energy minima shown in Fig. 4. During slow stretching, the protein will equilibrate among the low energy states at the current elongation. The energy of these lowest-lying states increases with elongations with a much smaller slope than the energy of a single state. Since the force is determined by the slope of the energy with respect to elongation, the force to stretch Ig27 will significantly smaller when it is able to equilibrate between the lower lying states than when it is confined to the quasi-static trajectory. The slope of the low-lying energies is consistent with a value on the order ∼200 pN, although a particular value cannot be determined from this relatively crude set of data (for reasons discussed in previous paragraph).
The types of energy minima that represent the low energy states changes as the protein is stretched. In particular, we note that important changes characterize the structures corresponding to the lowest lying states:
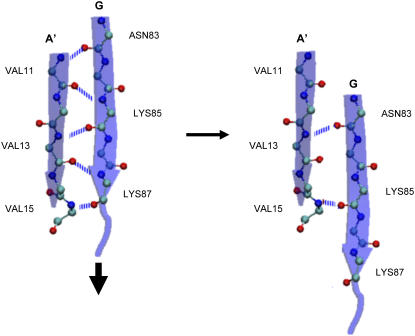
States with nonnative hydrogen bonds become lower in energy than the native state as the protein is stretched. In particular, the lowest-energy states at elongations between 3 and 12 Å include nonnative hydrogen bonds between residues 9 and 22 (both 9N-22O and 9O-22N), and shifting of the register of the A′-G interactions to include 13N-83O and 15N-85O hydrogen bonds. The shifting of the register of the A′-G interactions is shown in Fig. 5.
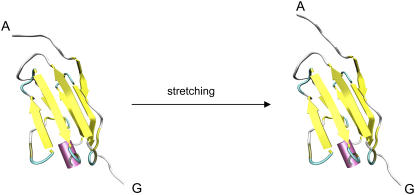
States with “flat” energy versus elongation profiles become the lowest energy states after elongations of a few Angstroms. These states were examined in more detail. As shown in Fig. 6, the A strand is detached in these states, and stretching proceeds by movement of the detached A strand without much distortion of rest of the protein. We believe that these energy minima underlie the intermediate state observed experimentally for the following reason: experiments show that the intermediate state involves an abrupt and reversible extension of several Angstroms (21), which would correspond to the behavior expected for states that have the flat energy versus elongation properties shown in Fig. 4.
FIGURE 5.
Nonnative hydrogen bonds in the A′-G region that form as the protein is stretched. These bonds correspond to a shift in the register of the A′ and G strands by two residues.
FIGURE 6.
Mechanism of deformation of states with “flat” energy versus elongation profiles. Note that the deformation is dominated by the movement of the detached A strand.
We note that this methodology, which combines stretching and reversal of stretching with MD simulations, is more efficient at finding lower energy states than steered MD simulations. The use of strain cycles to guide a system to lower energy states has been observed in experiments (41) and simulations (42) of colloidal systems, where cycles of mechanical strain are found to accelerate the rate of aging.
Molecular dynamics simulations with explicit solvent
Molecular dynamics simulations with explicit solvent are carried out to determine the relevance of the energy landscape results presented above. The simulations are carried out at a temperature of 300 K, for Ig27 constrained to elongations of 0 Å, 9 Å, and 13 Å (relative to the minimum energy end-to-end distance)—note that elongations of 9 Å and 13 Å are slightly before and slightly after the force peak in the quasi-static simulations (Fig. 2 b). Each simulation is run for 1 ns.
The MD results for the backbone hydrogen bonds are shown in Fig. 7 a. All native A-B and A′-G backbone hydrogen bonds remain intact in the 0 Å elongation MD simulations, and all are broken in the 13-Å elongation simulations, as expected from the energy landscape analysis. In the 9-Å elongation simulations, two of the A-B hydrogen bonds and the A′-G hydrogen bond closest to the C-terminus are broken throughout the entire 1 ns trajectory, also as expected from the energy landscape analysis.
FIGURE 7.
MD simulation results for hydrogen bond donor-acceptor distances in Ig27 at 300 K, and with an explicit solvent representation of the aqueous environment. These plots show running averages over 1ps. Black represents results for 0-Å elongation, light gray represents results for 9-Å elongation, and dark gray represents results for 13-Å elongation. (a) Backbone hydrogen bonds. (b) Nonnative backbone hydrogen bonds. (c) Two hydrogen bonds involving side chains. The 2O-77ND interaction results are for the 0-Å elongation, and the 6NZ-22OE interaction results are for the 13-Å elongation.
The 6O-24N and 13O-87N hydrogen bonds reform during the MD simulation at 9-Å elongation. In terms of the energy landscape picture, these bonds reform by thermally activated interbasin transitions between energy minima. Note that experimental results have shown that the transition to the folding intermediate is reversible (21), and so the reforming of these hydrogen bonds is not surprising.
Nonnative hydrogen bonds formed in the simulation at 13-Å elongation, as shown by the results in Fig. 7 b. These nonnative hydrogen bonds, 15N-85O and 9N-22O, were anticipated from the energy landscape analysis described in the above section.
The MD results show that the hydrogen bonds involving side chains often break (and sometimes reform) in the finite temperature/explicit solvent simulations, as shown in Fig. 7 c. In terms of the energy landscape, these changes correspond to thermally activated interbasin processes. For the hydrogen bonds that break permanently, the energy landscape distortions discussed above will not have much relevance. However, the landscape distortions will be relevant for the hydrogen bonds that break and reform (e.g., the 2O-77ND hydrogen bond shown in Fig. 7 c).
In the energy landscape analysis, it was found that the Glu-22-Lys-6 salt bridge between the A and B strands remains intact to large elongations, even when the A and B strands are “detached”. The MD results show that this effect is valid at 300 K and with the solvent explicitly modeled—as shown in Fig. 7 c for the 13-Å elongation simulation, the salt bridge remains intact throughout the entire 1-ns simulation. This salt bridge acts as a tether—i.e., a strong but extremely flexible connection—between the A and B strands, where the long side chains allow extreme flexibility and the charged end-groups make the interaction strong.
DISCUSSION
Mechanical coupling to the environment generates a dynamic energy landscape, for which nontrivial structural change can occur by the movement of the position of energy minima in configuration space (an intrabasin process), as well by transitions between energy minima (an interbasin process). In contrast, for a static landscape, nontrivial structural change can only occur by transitions between energy minima. The way that the structural change occurs has implications in regard to the mechanical response: Intrabasin structural changes are fully reversible, whereas interbasin structural changes are inherently irreversible.
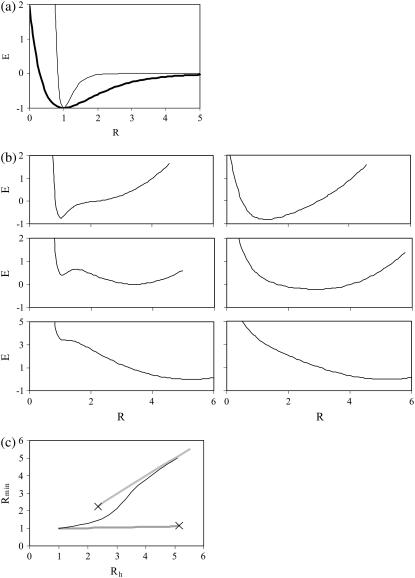
A simple model demonstrates that the stiffness of a bond determines whether the bond breaks by an intrabasin or interbasin process. In this model a bond is represented by a Morse potential, Em(R) = Dm[exp(−2αm(R − Rm)) − 2exp(−αm(R − Rm))], where Dm, Rm and αm describe the binding energy, minimum-energy distance, and stiffness of the bond, respectively. The coupling of the bond to the environment is modeled by a harmonic interaction, Eh(R) = ½kh(R − Rh)2, and stretching is simulated by increasing the value of Rh. Energy landscapes, E(R) = Em(R) + Eh(R), of systems with identical Dm and Rm, but different αm, are shown in Fig. 8 b. The flexible system (αm = 1) has one energy minimum for all values of Rh, whereas the stiff system (αm = 4) has two local minima for 2.35 < Rh < 5.15 (the minimum at small R is destroyed at Rh = 5.15, and the minimum at large R is destroyed at Rh = 2.35). The positions of these energy minima as a function of Rh are shown in Fig. 8 c. The bond distance corresponds to the position of the energy minimum (if two energy minima exist, the bond corresponds to the energy minimum at smaller R). For the flexible bond, the bond distance increases gradually with stretching and the bond breaks by an intrabasin process (the bond is considered broken when the bond distance exceeds an arbitrary value). For the stiff bond, the bond distance is insensitive to stretching until the bond suddenly breaks by an interbasin processes, when either thermal fluctuations or the destruction of the energy minimum cause the system to move to the energy minimum at large R.
FIGURE 8.
(a) Morse potentials with Dm = 1, Rm = 1; thick line is αm = 1, and thin line is αm = 4. (b) Energy landscapes for systems with Dm = 1, Rm = 1, kh = 0.5. Left panels are for the αm = 4 system, and right panels are for the αm = 1 system, with αm = 1. The panels from top to bottom represent Rh = 2, Rh = 3.4, and Rh = 5.25. (c) Positions of energy minima as a function of Rh; the dark line is for the αm = 1 system, and the gray lines are for the αm = 4 system. The X's denote the points where energy minima are destroyed.
In regard to the mechanical unfolding of Ig27, these results show that hydrogen bonds can weaken and break even when the system remains in a single energy minimum, due to the movement of energy minima in configuration space. For example, the 87O-15N hydrogen bond can weaken and break while in a single energy minimum, whereas the 85O-13N hydrogen bond cannot (Fig. 3 b). According to the analysis in the previous paragraph, this behavior occurs because the 87O-15N interaction is more flexible than the 85O-13N interaction. The higher flexibility of the 87O-15N interaction is consistent with the MD results of Lu and Schulten (24), which show that the 87O-15N interaction undergoes much larger fluctuations than the 85O-13N interaction (e.g., Fig. 12 of Lu and Schulten (24)).
Models for protein unfolding have been developed based on simple representations of hydrogen bonds (e.g., (26,29)). In these models, hydrogen bonds break by interbasin processes—i.e., the hydrogen bond remains intact until it suddenly breaks. These results show that more complete models would also allow for the breaking of hydrogen bonds by intrabasin processes, in which the hydrogen bonds gradually lengthen until the interaction becomes negligible.
These results also have implications in regard to the interpretation of results of Gō protein models in regard to mechanical unfolding (30,43). Gō models are coarse-grained models in which each reside is represented by one site, and hydrogen bonds between residues are only included when such interactions occur in the native state. The advantage of Gō models is their computational efficiency—much longer timescales can be addressed with Gō models than with fully atomistic models. However, these results show that nonnative hydrogen bonds may be important in the slow mechanical unfolding—for example, the shifting of the A′-G hydrogen bonds as shown in Fig. 6.
CONCLUSION
Physiological processes such as muscle contraction and cell adhesion involve proteins that are mechanically coupled to a changing environment. The mechanical coupling produces a dynamic energy landscape for the protein, in which energy minima move in configuration space, change in depth, and are created and destroyed. These landscape distortions guide the mechanical response of the protein at all temperatures and stretching rates.
This energy landscape and MD analysis elucidates the mechanical unfolding of Ig27 as follows:
Hydrogen bonds can break not only by thermally activated transitions between energy minima, but also by a gradual nonactivated process associated with the stretching-induced motion of energy minima in configuration space.
Nonnative hydrogen bonds can form during the mechanical unfolding process. These nonnative bonds will be important in the slow stretching regime relevant experimentally, in which the protein can equilibrate among low energy states.
States in which the A and B strands are detached can stretch with very small energy penalty—i.e, the energy mimima are “flat” with respect to elongation. This result concurs with the experimental evidence for an intermediate state in regard to mechanical unfolding (21).
Hydrogen bonds involving side chains can act as flexible tethers that remain intact even after backbone interactions between strands have broken. Glu-Lys salt bridges form especially effective tethers due to the long side chains and strong interactions associated between the polar ends.
The experimentally observed force for unfolding, ∼200 pN, can be rationalized in terms of the ensemble of energy minima. During slow stretching, the protein will equilibrate among the low energy states. The energy of these lowest-lying states increases with elongations with a much smaller slope than the energy of a single state. The slope of the low-lying energies is consistent with a value on the order of ∼200 pN, although a particular value cannot be determined from the available data.
Acknowledgments
This material is based upon work supported by the National Science Foundation under grant No. DMR-0402867.
References
- 1.Frauenfelder, H., S. G. Sligar, and P. G. Wolynes. 1991. The energy landscapes and motions of proteins. Science. 254:1598–1603. [DOI] [PubMed] [Google Scholar]
- 2.Onuchic, J. L., Z. Luthey-Schulten, and P. G. Wolynes. 1997. Theory of protein folding: the energy landscape perspective. Annu. Rev. Phys. Chem. 48:545–600. [DOI] [PubMed] [Google Scholar]
- 3.Wales, D. J., M. A. Miller, and T. R. Walsh. 1998. Archetypal energy landscapes. Nature. 394:758–760. [Google Scholar]
- 4.Frauenfelder, H. 2002. Proteins: Paradigms of complexity. Proc. Natl. Acad. Sci. USA. 99:2479–2480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cheung, M. S., L. L. Chavez, and J. N. Onuchic. 2004. The energy landscape for protein folding and possible connections to function. Polym. 45:547–555. [Google Scholar]
- 6.Angell, C. A. 2005. Energy landscapes for cooperative processes: nearly ideal glass transitions, liquid-liquid transitions and folding transitions. Philos. Trans. R. Soc. Lond. A. 363:415–430. [DOI] [PubMed] [Google Scholar]
- 7.Stillinger, F. H., and T. A. Weber. 1984. Packing structures and transitions in liquids and solids. Science. 225:983–989. [DOI] [PubMed] [Google Scholar]
- 8.Debenedetti, P. G., and F. H. Stillinger. 2001. Supercooled liquids and the glass transition. Nature. 410:259–267. [DOI] [PubMed] [Google Scholar]
- 9.Becker, O. M., and M. Karplus. 1997. The topology of multidimensional potential energy surfaces: theory and application to peptide structure and kinetics. J. Chem. Phys. 106:1495–1517. [Google Scholar]
- 10.Westerberg, K. M., and C. A. Floudas. 1999. Locating all transition states and studying the reaction pathways of potential energy surfaces. J. Chem. Phys. 110:9259–9295. [Google Scholar]
- 11.Mortenson, P. N., and D. J. Wales. 2001. Energy landscapes, global optimization and dynamics of the polyalanine Ac(ala)(8)NHMe. J. Chem. Phys. 114:6443–6454. [Google Scholar]
- 12.Levy, Y., J. Jortner, and R. S. Berry. 2002. Eigenvalue spectrum of the master equation for hierarchical dynamics of complex systems. Phys. Chem. Chem. Phys. 4:5052–5058. [Google Scholar]
- 13.Zhang, W., and S.-J. Chen. 2003. Master equation approach to finding the rate-limiting steps in biopolymer folding. J. Chem. Phys. 118:3413–3420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Evans, D. A., and D. J. Wales. 2004. Folding of the GB1 hairpin peptide from discrete path sampling. J. Chem. Phys. 121:1080–1090. [DOI] [PubMed] [Google Scholar]
- 15.Wang, K., J. McClure, and A. Tu. 1979. Titin: major myofibrillar components of striated muscle. Proc. Natl. Acad. Sci. USA. 76:3698–3702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Erickson, H. P. 1994. Reversible unfolding of fibronectin type-iii and immunoglobulin domains provides the structural basis for stretch and elasticity of titin and fibronectin. Proc. Natl. Acad. Sci. USA. 91:10114–10118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Linke, W. A., and M. C. Leake. 2004. Multiple sources of passive stress relaxation in muscle fibres. Phys. Med. Biol. 49:3613–3627. [DOI] [PubMed] [Google Scholar]
- 18.Rief, M., M. Gautel, F. Oesterhelt, J. M. Fernandez, and H. E. Gaub. 1997. Reversible unfolding of individual titin immunoglobulin domains by AFM. Science. 276:1109–1112. [DOI] [PubMed] [Google Scholar]
- 19.Kellermayer, M. S. Z., S. B. Smith, H. L. Granzier, and C. Bustamante. 1997. Folding-unfolding transitions in single titin molecules characterized with laser tweezers. Science. 276:1112–1116. [DOI] [PubMed] [Google Scholar]
- 20.Tskhovrebova, L., J. Trinick, J. A. Sleep, and R. M. Simmons. 1997. Elasticity and unfolding of single molecules of the giant muscle protein titin. Nature. 387:308–312. [DOI] [PubMed] [Google Scholar]
- 21.Marszalek, P. E., H. Lu, H. Li, M. Carrion-Vazquez, A. F. Oberhauser, K. Schulten, and J. M. Fernandez. 1999. Mechanical unfolding intermediates in titinmodules. Nature. 402:100–103. [DOI] [PubMed] [Google Scholar]
- 22.Lu, H., B. Isralewitz, A. Krammer, V. Vogel, and K. Schulten. 1998. Unfolding of titin immunoglobulin domains by steered molecular dynamics simulation. Biophys. J. 75:662–671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lu, H., and K. Schulten. 1999. Steered molecular dynamics simulation of conformational changes of immunoglobulin domain I27 interprete atomic force microscopy observations. 1999. Chem. Phys. 247:141–153. [Google Scholar]
- 24.Lu, H., and K. Schulten. 2000. The key event in force-induced unfolding of titin's immunoglobulin domains. Biophys. J. 79:51–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Paci, E., and M. Karplus. 2000. Unfolding proteins by external forces and temperature: the importance of topology and energetics. Proc. Natl. Acad. Sci. USA. 97:6521–6526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Makarov, D. E., P. K. Hansma, and H. Metiu. 2001. Kinetic Monte Carlo simulation of titin unfolding. J. Chem. Phys. 114:9663–9673. [Google Scholar]
- 27.Fowler, S. B., R. B. Best, J. L. Toca Herrera, T. J. Rutherford, A. Steward, E. Paci, M. Karplus, and J. Clarke. 2002. Mechanical unfolding of a titin Ig domain: structure of unfolding intermediate revealed by combining AFM, molecular dynamics simulations, NMR and protein engineering. J. Mol. Biol. 322:841–849. [DOI] [PubMed] [Google Scholar]
- 28.Li, P.-C., and D. E. Makarov. 2003. Theoretical studies of the mechanical unfolding of the muscle protein titin: bridging the timescale gap between simulation and experiment. J. Chem. Phys. 119:9260–9268. [Google Scholar]
- 29.Eom, E., P.-C. Li, D. E. Makarov, and G. J. Rodin. 2003. Relationship between the mechanical properties and topology of cross-linked polymer molecules: parallel strands maximize the strength of model polymers and protein domains. J. Phys. Chem. B. 107:8730–8733. [Google Scholar]
- 30.Cieplak, M., T. X. Hoang, and M. O. Robbins. 2004. Thermal effects in stretching of Go-like models of titin and secondary structures. Proteins. 56:285–297. [DOI] [PubMed] [Google Scholar]
- 31.Improta, S., A. S. Politou, and A. Pastore. 1996. Immunoglobulin-like modules from titin I-band: extensible components of muscle elasticity. Structure. 4:323–337. [DOI] [PubMed] [Google Scholar]
- 32.Wang, J., P. Cieplak, and P. A. Kollman. 2000. How well does a restrained electrostatic potential (RESP) model perform in calculating conformational energies of organic and biological molecules? J. Comput. Chem. 21:1049–1074. [Google Scholar]
- 33.Ponder, J. W., and D. A. Case. 2003. Force fields for protein simulations. Adv. Protein Chem. 66:27–85. [DOI] [PubMed] [Google Scholar]
- 34.Case, D. A., T. A. Darden, T. E. Cheatham III, C. L. Simmerling, J. Wang, R. E. Duke, R. Luo, K. M. Merz, B. Wang, D. A. Pearlman, M. Crowley, S. Brozell, V. Tsui, H. Gohlke, J. Mongan, V. Hornak, G. Cui, P. Beroza, C. Schafmeister, J. W. Caldwell, W. S. Ross, and P. A. Kollman. 2004. AMBER 8. University of California, San Francisco.
- 35.Hawkins, G. D., C. J. Cramer, and D. G. Truhlar. 1995. Pairwise solute descreening of solute charges from a dielectric medium. Chem. Phys. Lett. 246:122–129. [Google Scholar]
- 36.Hawkins, G. D., C. J. Cramer, and D. G. Truhlar. 1996. Parametrized models of aqueous free energies of solvation based on pairwise descreening of solute atomic charges from a dielectric medium. J. Phys. Chem. 100:19824–19839. [Google Scholar]
- 37.Malandro, D. L., and D. J. Lacks. 1998. Molecular-level mechanical instabilities and enhanced self-diffusion in flowing liquids. Phys. Rev. Lett. 81:5576–5579. [Google Scholar]
- 38.Lacks, D. J. 2005. Energy landscape distortions and the mechanical unfolding of proteins. Biophys. J. 88:3494–3501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Malandro, D. L., and D. J. Lacks. 1999. Relationships of shear-induced changes in the potential energy landscape to the mechanical properties of ductile glasses. J. Chem. Phys. 110:4593–4601. [Google Scholar]
- 40.Osborne, M. J., and D. J. Lacks. 2004. Inherent structure analysis of the thermal history dependence of yielding in glasses. J. Phys. Chem. B. 108:19619–19622. [Google Scholar]
- 41.Viasnoff, V., and F. Lequeux. 2002. Rejuvenation and overaging in a colloidal glass under shear. Phys. Rev. Lett. 89:065701. [DOI] [PubMed] [Google Scholar]
- 42.Lacks, D. J., and M. J. Osborne. 2004. Energy landscape picture of overaging and rejuvenation in a sheared glass. Phys. Rev. Lett. 93:255501. [DOI] [PubMed] [Google Scholar]
- 43.West, D. K., P. D. Olmsted, and E. Paci. 2006. Mechanical unfolding revisited through a simple but realistic model. J. Chem. Phys. 124:154909. [DOI] [PubMed] [Google Scholar]
- 44.Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD: visual molecular dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]