Predicting the consequences of carry-over effects for migratory populations

Abstract

Migratory animals present a unique challenge for predicting population size because they are influenced by events in multiple stages of the annual cycle that are separated by large geographic distances. Here, we develop a model that incorporates non-fatal carry-over effects to predict changes in population size and show how this can be integrated with predictive models of habitat loss and deterioration. Examples from Barn swallows, Greater snow geese and American redstarts show how carry-over effects can be estimated and integrated into the model. Incorporation of carry-over effects should increase the predictive power of models. However, the challenge for developing accurate predictions rests both on the ability to estimate parameters from multiple stages of the annual cycle and to understand how events between these periods interact to influence individual success.

1. Introduction

Migratory animals present a unique challenge for predicting population abundance because individuals, by definition, occupy two or more geographically distinct areas during the course of the annual cycle. Populations can be influenced by events that occur during the over-wintering, migration and breeding periods, and regulation can occur by a combination of mechanisms operating in one or more of these seasons (Sillett et al. 2000). In a general two-season model, a migratory population will be at equilibrium when the per capita net breeding output (reproduction−mortality) during the breeding season equals the per capita mortality during the wintering season (Fretwell 1972; Sutherland 1996). In such a model, habitat loss or deterioration on either the breeding or wintering grounds will displace these relationships causing a subsequent drop in population size (Sutherland 1996, 1998).

In addition to changes in per capita rates within a season, non-fatal effects on individuals during one period of the annual cycle can influence success and per capita rates during the following period, a phenomenon termed the carry-over effect (Webster et al. 2002; Runge & Marra 2005). Despite empirical support at the individual level (e.g. Marra et al. 1998; Gill et al. 2001; Morrison & Hobson 2004), we still lack estimates of non-fatal carry-over effects for populations that can be integrated into predictive models. Here, we show how carry-over effects can be incorporated into a two-season equilibrium model developed to predict the effect of habitat loss and deterioration on migratory populations (Sutherland 1996, 1998). We then present estimates of carry-over effects from migratory birds that can be integrated into this model.

2. The model

Sutherland (1996) showed that the relative strength of density-dependence between the wintering (d′) and breeding grounds (b′) can be used to predict the change in population size (x) following loss of average quality habitat (L) in either area. For small changes in habitat, d′ and b′ can be considered linear (figure 1a). Habitat loss on the wintering grounds, for example, displaces d′ by L_w, where L_w=initial equilibrium population size E × proportion of habitat lost (figure 1b). The change in population size due to habitat loss on the wintering grounds (x_w) can then be expressed by (Sutherland 1996)

$$x_{\text{w}}=L_{\text{w}}\frac{d^{\prime }}{d^{\prime }+b^{\prime }}.$$ (2.1)

When E is influenced by changes in mean habitat quality, the displacement of d′ can instead be represented by τ, the vertical shift in the intercept of the density-dependent function (figure 1c); where τ=original mortality rate × change in the mean habitat quality. The change in population size resulting from τ, therefore, is

$$x_{\text{w}}=\tau \frac{1}{d^{\prime }+b^{\prime }}.$$ (2.2)

Carry-over effects occur when individual success is influenced by habitat quality in the previous season and can influence x_w through τ, thereby affecting per capita rates in the following season. Let τ, displace b′ by τ × c_w, where c_w is the carry-over effect constant that represents the per unit change in b′ related to the change in d′, and varies from −∞ to ∞ (figure 2). Solving for x_w gives

$$x_{\text{w}}=\frac{\tau (1+c_{\text{w}})}{d^{\prime }+b^{\prime }}.$$ (2.3)

In cases where the decline or increase in habitat quality can only be measured by a change in population size, L_w (Sutherland 1998), carry-over effects can be incorporated into equation (2.1) by

$$x_{\text{w}}=L_{\text{w}}\frac{d^{\prime }}{d^{\prime }+b^{\prime }}(1+c_{\text{w}}).$$ (2.4)

Here, the change in population size, L_w, is due only to habitat deterioration, not loss.

Figure 1.

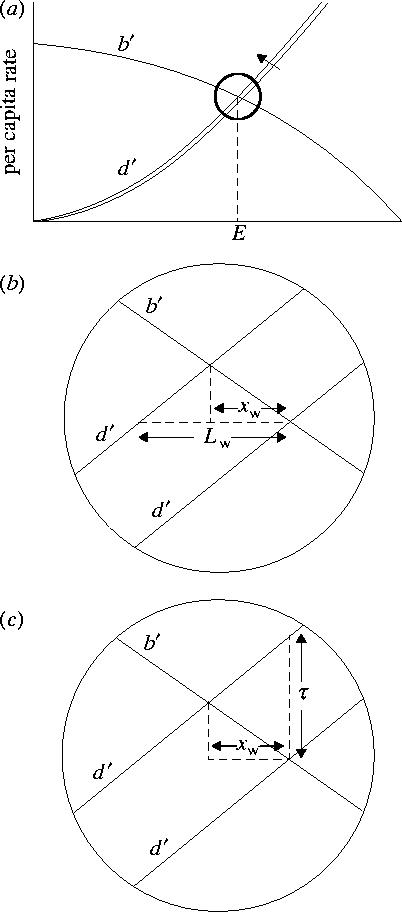
(a) Loss of winter habitat increases the strength of density-dependent winter mortality and displaces d′, lowering equilibrium population size, E. Over short time periods, losses of habitat are typically small relative to total habitat available, in which case the relationship between d′ and b′ can be considered linear as in (b), where loss of winter habitat displaces d′ by L_w. The change in population size, x_w is related to the relative strength of d′ and b′ (equation (2.1)). (c) x_w caused by a change in the overall quality of habitat is represented by a vertical shift in d′, expressed as τ (equation (2.2)).

Figure 2.

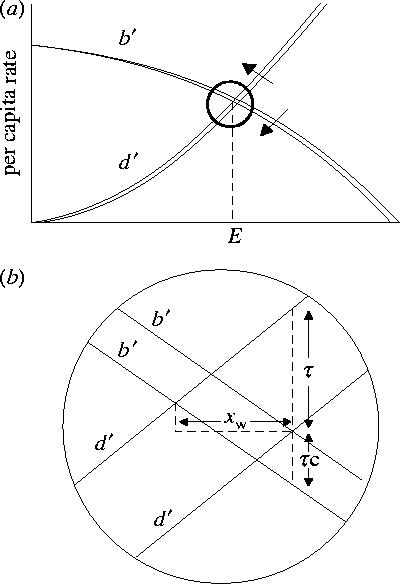
(a) Carry-over effects from winter to summer influence population abundance via a shift in b′, further reducing E. As in figure 1, small changes can be considered linear. (b) Carry-over effects influence population size when there is a change in the mean quality habitat available, τ. In the model, the carry-over effect is expressed as a shift in b′, where its strength is determined by the carry-over effect constant, c, times τ (equation (2.3)).

Equations (2.1) and (2.3) can be used independently to predict x_w in relation to L_w, and τ, respectively. In cases where there is habitat loss as well as a change in the mean quality of habitat, equations (2.1) and (2.3) can be combined into a single model. For the wintering grounds

$$x_{\text{w}}=L_{\text{w}}\left(\frac{d^{\prime }}{d^{\prime }+b^{\prime }}\right)+\frac{\tau (1+c_{\text{w}})}{d^{\prime }+b^{\prime }}.$$ (2.5)

An analogous situation exists for the case when there is a change in the quantity or quality of habitat on the breeding grounds (τ_S) and a carry-over effect from breeding habitat quality to wintering survival (c_S). In this case, x_S can be predicted as

$$x_{\text{S}}=L_{\text{S}}\left(\frac{b^{\prime }}{d^{\prime }+b^{\prime }}\right)+\frac{{\tau }_{\text{S}}(1+c_{\text{S}})}{d^{\prime }+b^{\prime }}.$$ (2.6)

When mean habitat quality declines, c will have a negative impact on population size and when mean habitat quality increases, c will have a positive impact on population size. Changes in τ may occur independently or in accordance with habitat loss. If the majority of habitat lost is low quality, population declines will be less than predicted from loss of the same amount of average quality habitat (Sutherland 1996) because a greater proportion of high quality habitat remains. As with habitat loss, we assume that c operating through a shift in b′ or d′ is linear over small changes in τ.

3. Estimating carry-over effects

The strength of the carry-over effect (c) can be estimated by the slope of the relationship between habitat quality and individual success in the subsequent season. Estimates of variation in habitat quality may be based on annual means (e.g. climate indices), or from individuals occupying a range of habitats. The former requires data from multiple years and the latter requires information from individuals in multiple seasons (see electronic supplementary material). The following examples from migratory birds illustrate these approaches.

Example 1. Barn swallows (Hirundo rustica) are colonial nesting passerines that breed throughout Europe and winter in sub-Saharan Africa. Saino et al. (2004) reported the relationship between reproduction and primary productivity on the wintering grounds (measured by normalized difference vegetation index; NDVI). They found that a difference in ±2 s.d. NDVI resulted in a difference of ±1.1 offspring produced per female (effects on first and second broods combined). We assume that ±2 s.d. NDVI represents the annual variation in habitat quality on the wintering grounds and that this is linearly related to winter mortality. Based on the mean and variance of offspring fledged in Barn Swallows (7.8±1.6 s.d.; Moller 1989), we calculated the standardized (Z-score) number of offspring produced that would be equivalent to ±2 s.d. NDVI (±offspring=(7.8±1.1)−7.8/1.6=±0.69). The slope of the line between NDVI and reproductive output, therefore, is estimated as c_w=0.34.

Example 2. Regulated hunting on the spring staging grounds in the St Lawrence River estuary has been recently used as a method to control population growth in greater snow geese (Chen caerulescens atlantica; Calvert & Gauthier 2005). Mainguy et al. (2002) reported a 30% reduction in the potential clutch size (the sum of developing and post-ovulatory follicles which is a strong indicator of clutch size; Choinière & Gauthier 1995) of females captured on the high-Arctic breeding grounds in years with spring hunting compared to years without hunting. This result suggests that management on the staging grounds not only increases mortality but lowers the reproductive success of individuals in the following season. To calculate the carry-over effect from the staging grounds to the breeding grounds, we normalized hunting intensity scores for each year reported in Mainguy et al. (2002) using a mean of zero (equal to years with no hunting) and a standard deviation calculated from kill rates of a longer term dataset (Calvert & Gauthier 2005). These values represent the range of habitat quality on the staging grounds related to hunting intensity. After normalizing potential clutch size (Mainguy et al. 2002), the slope of relationship between hunting intensity on the staging grounds and potential clutch size in the Arctic is estimated as 0.61. To estimate the slope between hunting intensity and number of offspring produced, we multiplied this estimate by mean egg survival (89.7%) and mean hatchability (92.8%; Lepage et al. 2000) resulting in c_w=0.51.

Example 3. American redstarts (Setophaga ruticilla) are migratory passerines that breed in North America and winter throughout Central American and the Caribbean. Stable-carbon isotopes (δ¹³C) values of redstarts indicate the type of habitat occupied during the non-breeding season (Marra et al. 1998) and signatures in red-blood cells of individuals upon arrival at the breeding grounds can be used as an indicator of the winter habitat quality. Using path analysis, Norris et al. (2004) found that ±1 s.d. change in δ¹³C values was equivalent to ±1 s.d. change in the number of young fledged × 0.31 (total effect from standardized partial regression coefficients). The carry-over effect, c_w, therefore, is estimated as 0.31.

4. Discussion

We show how non-fatal carry-over effects (c) can be incorporated into a model predicting population size due to change in habitat quality and how this is related to habitat loss (Sutherland 1996). Mechanistically, carry-over effects occur at the individual level when events during one period have non-fatal effects on individuals in the following period (Norris 2005; Runge & Marra 2005). It is important to note that the presence or strength of c alone does not affect population size. Instead, c influences population size when there is a change in the proportion of individuals experiencing either a positive or negative carry-over effect, and this occurs via a shift in the mean quality of habitat available (τ). Changes in τ could be influenced by global climate patterns (e.g. NDVI in barn swallows), large-scale management practices (e.g. hunting of greater snow geese), or losses of key habitats (e.g. mesic tropical forests for American redstarts).

Our model, along with the accompanying examples, suggests that carry-over effects may play an important role in population dynamics. Changes in the amount of habitat will likely be concordant with disproportional changes in the quality habitat available (i.e. τ≠0), as opposed to loss of average quality habitat or loss of habitat with an overall mean that is average quality (τ=0) that previous models have assumed (Fretwell 1972; Sutherland 1996). The incorporation of carry-over effects, therefore, should improve the predictive power of population models in migratory animals.

Carry-over effects can act in conjunction with or in the opposite direction to regulatory mechanisms. For example, suppose that habitat loss in winter increases the per capita breeding output the following season through regulatory mechanisms. If the same habitat that is lost is primarily high quality, this can result in a higher proportion of individuals occupying lower quality winter habitat. Given winter habitat quality affects net breeding output (i.e. c>0), the per capita reproduction will decrease the following season because a greater proportion of individuals originate from poor quality habitat. In this way, regulatory mechanisms and carry-over effects can act in opposite directions. In contrast, loss of low quality winter habitat may result in a higher proportion of individuals occupying high quality habitat which increases the per capita breeding output (given c>0), resulting in these processes acting in the same direction. The relationship between the two will depend on the relative strength of regulation between seasons and the strength of c. Given strong regulation, c may have minimal impacts on population size. Empirical studies are needed to test this idea, as well as how different regulatory mechanisms (crowding, site-dependence) may interact with c.

Our model applies to small, annual changes in habitat represented by a linear displacement of b′ or d′ (as in Sutherland 1996, 1998). We also assume a linear relationship between changes in τ and the degree of displacement of b′ or d′. However, unlike habitat quantity which is typically lost or gained in relatively small amounts per year (e.g. <1%), habitat quality may shift more dramatically, particularly if quality is linked to large-scale processes (e.g. climate). In such cases, it will be critical to determine the functional relationship between τ and the subsequent change in per capita rates the following season.

We stress that the examples presented here are rough estimates intended to illustrate different approaches to determining carry-over effects. The challenge will be to derive accurate empirical estimates of c, in conjunction with estimates of b′ and d′. For b′ and d′, it will critical to determine the specific mechanism behind density-dependence, which includes quantifying the amount and quality of habitat (Rodenhouse et al. 1997). In many cases, the estimation of c will require the application of novel techniques to track individuals between periods of the annual cycle. If the estimates calculated here are close to realistic, then carry-over effects may be vitally important for predicting population size. Surprisingly, however, we still lack the empirical data to completely parameterize even a general migratory population model, such as the one presented in this paper.