HIV recombination: what is the impact on antiretroviral therapy?

Abstract

Retroviral recombination is a potential mechanism for the development of multiply drug resistant viral strains but the impact on the clinical outcomes of antiretroviral therapy in HIV-infected patients is unclear. Recombination can favour resistance by combining single-point mutations into a multiply resistant genome but can also hinder resistance by breaking up associations between mutations. Previous analyses, based on population genetic models, have suggested that whether recombination is favoured or hindered depends on the fitness interactions between loci, or epistasis. In this paper, a mathematical model is developed that includes viral dynamics during therapy and shows that population dynamics interact non-trivially with population genetics. The outcome of therapy depends critically on the changes to the frequency of cell co-infection and I review the evidence available. Where recombination does have an effect on therapy, it is always to slow or even halt the emergence of multiply resistant strains. I also find that for patients newly infected with multiply resistant strains, recombination can act to prevent reversion to wild-type virus. The analysis suggests that treatment targeted at multiple parts of the viral life-cycle may be less prone to drug resistance due to the genetic barrier caused by recombination but that, once selected, mutants resistant to such regimens may be better able to persist in the population.

1. Introduction

Viral resistance to antiretroviral therapy presents a major challenge to the long-term treatment of HIV-infected patients, both at the level of the individual who fails specific therapy regimens and also at the level of the population in which individuals may become infected by viral strains already resistant to antiretroviral therapy. If patients are able to take their antiretroviral medication as prescribed, treatment failure may result from the accumulation of multiple point mutations, each conferring a degree of resistance to one or more antiretroviral drugs. Due to the large viral population size and the error-prone nature of retroviral replication, the response of HIV viral quasi-species to selection pressures imposed by antiretroviral drugs can be very rapid.

The aim of this manuscript is to explore the impact of retroviral recombination (viral sex) on the dynamics of resistance. Most previous quantitative analyses have assumed that variation is generated solely by point mutations (Bonhoeffer & Nowak 1997; Ribeiro et al. 1998; Ribeiro & Bonhoeffer 2000; Fraser et al. 2001; Phillips et al. 2001). However, HIV virions include two separate RNA strands so that HIV may properly be regarded as diploid. Cross-over during reverse transcription appears to arise up to one hundred times more frequently than mutation (Hu & Temin 1990; Jetzt et al. 2000; Zhuang et al. 2002; Levy et al. 2004).

Recombination offers the potential to link together point mutations that have arisen independently. It is possible to create experimental circumstances in which recombination can hasten the emergence of drug resistant strains (Gu et al. 1995; Kellam & Larder 1995; Moutouh et al. 1996), leading some to suggest that this must also be the case in vivo (Burke 1997; Wain-Hobson et al. 2003). This contrasts sharply with the predictions of a population genetic model which suggest that, in most circumstances, recombination will act to delay the appearance of drug resistance during therapy (Bretscher et al. 2004). This occurs because, while recombination can combine separate drug resistance mutations, it can also separate them. This effect is well known in the evolutionary literature as one of the ‘costs of sex’, specifically known as recombinogenic load (Barton & Charlesworth 1998). Indeed, such are these costs that controversy still exists as to the evolutionary advantages of sex that allow it to emerge. In this context the study of retroviruses may be important since they are among the simplest organisms to exhibit sexual reproduction (albeit isogamous). In a previous analysis, Boerlijst et al. (1996) examined the role of retroviral recombination on quasi-species evolution (but not specifically antiretroviral resistance) and found that the net effect was to flatten the effective fitness landscape, thus promoting greater quasi-species diversity.

A key prerequisite for viral recombination to take place is the co-infection (or super-infection) of cells. Recent data indicate that, at least in the spleen, the multiplicity of cell infection (MOI) may be startlingly high (over three proviruses per infected cell on average; Jung et al. 2002). The frequency of cell co-infection might be expected to depend on viral load, which varies over many orders of magnitude during antiviral therapy. One might naively expect linear dependence of the form f∝v, where f is the frequency of co-infection and v is the viral load. However, evidence from in vitro and animal studies point to a quadratic dependence of co-infection frequency (and also resulting recombinant products) on the total viral load of the form f∝v² (Levy et al. 2004). Bretscher et al. (2004) on the other hand assumed a constant rate of cell co-infection during therapy (f∝const.), as might arise due to strong spatial sequestration of virus in the lymph nodes or spleen. I will study the general case of dependence of the form f∝v^a, where a is an unknown exponent and show that the effect of recombination on antiretroviral resistance depends critically on this exponent. Bretscher et al. (2004) also assumed a constant total viral population size v (as is common in population genetic models). The rapid thousand-fold or more decay in virus that occurs during therapy (Ho et al. 1995; Wei et al. 1995) suggests, however, that the effect of changing population size could be important, though these changes may be less dramatic in lymphatic tissues (Hockett et al. 1999). I will thus consider recombination within a population dynamic model where the viral load v is a dynamical variable.

Thus, the approach taken is to first focus in detail on the observed distribution of cell infection rates (Jung et al. 2002) and to discuss potential mechanisms that can generate this distribution, a question recently discussed by Dixit & Perelson (2004). I then show that the pre-treatment frequencies of resistant viruses can be calculated analytically for any arbitrary distribution, and explore the impact of recombination and other important factors on these frequencies. I then analyse a full dynamical model of viral replication that includes recombination and study the dynamics of the response to antiretroviral treatment. Results were found to critically depend on how the multiplicity of infection changes in response to decaying virus levels. If this dependence is linear, or quadratic as suggested in Levy et al. (2004), then recombination has almost no effect on the emergence of drug resistance during therapy. This is because reduced viral load translates into a reduced infection rate for cells and, thus, reduced opportunities for recombination. If, on the other hand, the multiplicity of infection does not change, then the effect of recombination is always to slow the emergence of drug resistance, independent of epistasis.

These effects can be dramatic resulting in bi-stability, so that recombination can completely prevent a fitter resistant strain from emerging. Bi-stability has been previously noted in general models of retroviral recombination (Boerlijst et al. 1996). The prediction of bi-stability is found to be more robust after primary HIV infection (i.e. not dependent on the multiplicity of infection). Recombination can prevent reversal to wild-type virus in resistant infections and, conversely, wild-type virus can persist even when resistant strains acquire compensatory fitness-enhancing mutations. I focus on the simplest possible system of retroviral evolution that exhibits both mutation and recombination, namely a two-locus system in which each locus has a wild-type and a resistant allele. This system exhibits most of the interesting phenomena attributable to retroviral recombination.

2. The genetics of drug resistance and recombination

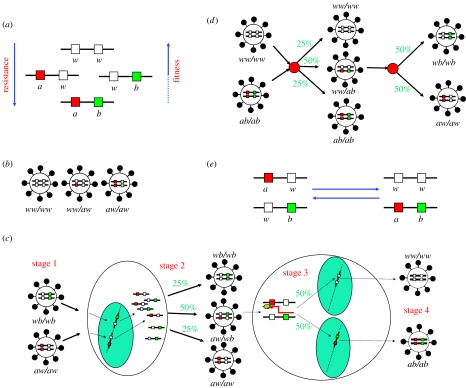
Consider two linked loci, each with a wild-type and a resistant allele, resulting in four possible genotypes consisting of wild-type alleles (genotype ww), a mixture of wild-type and resistant alleles (aw or wb) and resistant alleles (ab; illustrated in figure 1a). Typically, the two-point mutant genotype ab will be associated with a higher degree of resistance, with resistance to more classes of antiretroviral agents or with a higher fitness than either of the one-point resistant mutants. Each virion packs two full HIV RNA genomes so that HIV may be regarded as diploid. As a result, there are ten possible combinations of viral strains resulting from the four basic genotypes above, three of which are illustrated in figure 1b.

Figure 1.

The genetics of HIV drug resistance and viral sex. (a) The four basic genotypes. (b) Three of the ten possible genotype combinations for the free virus. (c) The stages of viral sex. (d) Reversibility of recombination. (e) Summary of the non-silent recombination processes for this two-locus two-allele system.

Retroviral recombination occurs during the process of reverse transcription (during which the two RNA genes are transcribed into a single DNA provirus) and is a result of the reverse transcriptase jumping from one RNA strand to the other. The rate at which reverse transcriptase crosses from one strand to the other has been estimated experimentally, with recent estimates indicating that this is up to one hundred times more frequent than mutation (i.e. a transcription error). This results in up to 3.3 cross-overs for every kilo base pair (kbp) transcribed (or 30 cross-overs for the whole 9.2 kbp HIV genome), depending on the target cell type (Jetzt et al. 2000; Zhuang et al. 2002; Levy et al. 2004).

There are two non-silent recombination events for the two-locus two-allele system, which, since they result in an increase and decrease in the frequency of the two-point mutant genotype, we call forward and back recombination. The biological processes which drive forward and back recombination are illustrated in figure 1c,d, respectively. We see that recombination requires two full viral life-cycles for two one-point mutant viruses to produce a two-point mutant virus. Figure 1e summarizes these into a single reversible balance ‘reaction’ process, from which it is possible to intuit the counterintuitive effects of recombination, known as the recombinogenic load (Barton & Charlesworth 1998). If the two-point mutant virus is fittest but infrequent, its growth will be hindered by constant recombination with the wild-type virus.

3. Inbreeding and the multiplicity of infection

The first stage of viral sex is infection of a single target cell by more than one virion (figure 1c,d). For a singly infected cell producing a virus, all transcribed viral RNA will be copied from the same single strand of proviral DNA. As a result, all virions produced from this cell will be inbred, in the sense of being progeny of a single infecting virus. For virions thus produced, recombination will never generate new genotypes (I ignore the issue of mutations arising during DNA to RNA transcription, since this process has a much higher fidelity than reverse transcription, the main source of mutations). However, single infection is not the only state from which an inbred virus may be produced. Virions produced from a multiply infected cell may still contain two copies of the same provirus. Specifically, if a cell contains k proviruses, the probability that any two randomly chosen RNA transcripts are copies of the same provirus, resulting in inbred virus is 1/k. If the proportion of all infected cells that are k-fold infected (denoted π_k) is known, then it is possible to compute the proportion of all virus produced that is inbred, that is, the coefficient of inbreeding, as follows:

$$h={\pi }_1+\frac{{\pi }_2}{2}+\frac{{\pi }_3}{3}+\frac{{\pi }_4}{4}+\cdots .$$ (3.1)

A complicating factor would be the production of multiple proviral reverse transcripts from a single infecting virion but this does not appear to arise (Jones et al. 1994).

4. The multiplicity of infection: a biological interpretation

The in vivo multiplicity of infection has been characterized in spleenic CD4+ T-cells isolated from two patients (Jung et al. 2002). More than three proviral copies per cell were found on average from 216 infected cells. The distribution of multiplicities of infection, π_k above, was found to have a similar shape for both patients. Our analysis shows that this distribution is well described by a modified Poisson distribution (figure 2a). From this, we can compute the maximum likelihood estimate for the coefficient of inbreeding, h, of 45%.

Figure 2.

The in vivo multiplicity of cell infection. (a) The distribution of proviral copies per cell in spleenic CD4+ T-cells recovered from two patients (from Jung et al. 2002) and the best-fit model distribution. This was found to be an inflated, shifted Poisson distribution ${\pi }_k=ϵ{\delta }_{1k}+(1-ϵ){\lambda }^{k-1}{\text{e}}^{-\lambda }/(k-1)$! This distribution fit significantly better than a regular Poisson distribution, a shifted Poisson distribution or an inflated Poisson distribution. The maximum likelihood estimates for the parameters were ϵ=0.13 and λ=2.4, so the mean multiplicity of infection was computed as $ϵ+(1-ϵ)(1+\lambda )\approx 3.11$. The coefficient of inbreeding for this distribution, derived using the series in equation (3.1), was computed as $h=ϵ+(1-ϵ)(1-{\text{e}}^{-\lambda })/\lambda \approx 0.45$. The coefficient σ was numerically computed to be ≈0.27. (b) An illustration of a biological process that gives rise to the above distribution.

This statistical analysis yields insight into the biological process of multiple HIV cell infections. The mechanistic model illustrated in figure 2b generates the distribution described in figure 2a. In this model, when a CD4+ T-cell is first infected, there is an ϵ=13% chance that the viral RNA will be immediately transcribed to a provirus with no further infections. If the virus is not immediately transcribed, the cell remains susceptible for a fixed period of time T during which it may be super-infected with hazard γ and, after this period, reverse transcription will produce one provirus from each infecting virion. A mean of λ=2.4 additional infections occur during this time period. Since λ=γT is large, this implies that if the time period is short, then the hazard of super-infection must be very large or, conversely, that if the hazard is low, then the time period must be very long. A large hazard of cell super-infection could be a feature of very spatially localized viral replication—a particular possibility in the spleen. It would be of interest to determine the distribution π_k in other body compartments. A long delay T before RNA integration does arise in some cells (Stevenson et al. 1990), but that this should occur after 1−ϵ=87% of infections seems implausible.

Dixit & Perelson (2004) have recently analysed this distribution and proposed a very similar modified Poisson distribution, ${\pi }_k=ϵ{\delta }_{1k}+(1-ϵ){\lambda }^k{\text{e}}^{-\lambda }/(k!(1-{\text{e}}^{-\lambda }))$, which fits slightly less well than the one used here but results from a quite different biological model. They suggested that multiple infections could arise in lymphatic tissues because of the simultaneous transmission of multiple proviruses during direct cell–cell infection. While there is currently little evidence for this, this would have important consequences because, as the authors argue, the diversity of proviruses in cell would not reflect the diversity of the viral population as a whole. Within the framework used here, the result would be a very large increase in the coefficient of inbreeding and, thus, a commensurate reduction in the opportunities for recombination. This possibility needs further experimental exploration but our framework is sufficiently robust for such a modification.

A further important caveat is that the MOI could be very different in other body compartments and our estimates, based on the spleen, may need to be appropriately re-adjusted in the light of further experimental work. It is likely that, overall, many cells are singly infected and that the coefficient of inbreeding h may be much higher than suggested here, in which case the impact of recombination would be commensurately reduced.

A key determinant of the dynamics of the emergence of resistance during therapy is the dependence of this distribution on viral load. Levy et al. (2004) extensively measured the dependence of the proportion of co-infected cells in vitro and in an animal model (=1−π₁) and found a quadratic dependence on viral load. In contrast, the two distributions of the MOI shown in figure 2a are extremely similar for the two patients, despite an over twenty-fold difference in peripheral viral load. In addition, patient R (with the higher viral load) was receiving antiretroviral therapy (AZT+ddI; A. Meyerhans, personal communication). This similarity could arise either because of a viral disconnection between blood plasma and the spleen or because of a mostly viral load-independent mechanism of cell super-infection (consistent with spatially focused viral replication), or simply by chance since these are only two observations. More in vivo data are required.

5. The frequency of drug resistance in untreated antiretroviral-naive patients

The main reason for the rapid failure of antiretroviral therapy based on the administration of a single drug is not due to the lack of efficacy, but rather the limited number of mutations that are required to move from wild-type to fully resistant virus (Bonhoeffer & Nowak 1997; Ribeiro & Bonhoeffer 2000). All one- and two-point mutants, though less fit than wild-type, are predicted to be present at low frequencies in all HIV-infected patients, even untreated antiretroviral therapy-naive patients (Bonhoeffer & Nowak 1997; Ribeiro et al. 1998). This prediction is based on mathematical models since current experimental assays are not capable of detecting very infrequent viral strains. The models, however, assume that all resistant strains are generated by a process of point mutation. Bretscher et al. (2004) explored by simulation the dependence of these frequencies on the rate of recombination and found that the key determinant was epistasis, measured by the parameter E=f_wwf_ab−f_awf_wb, where f is the relative fitness of each strain. For synergistic epistasis (E<0), recombination increases the frequency of two-point mutants, while this frequency is decreased for antagonistic epistasis (E>0). Put more simply, the effect of recombination is to reduce the dependence on fitness differences.

The evolution of retroviruses is complicated by so-called ‘phenotypic mixing’, where fitness differences are associated with the proviral stage. Viruses of different genotypes produced from the same cell can have the same phenotype (Novick & Szilard 1951; Bretscher et al. 2004), which we assume is the mean of fitness values associated with each genotype.

The basic method for calculating gene frequencies was presented in Bretscher et al. (2004). I note, however, that it is possible to derive approximate analytical solutions for the gene frequencies (denoted p_..), even with an arbitrary distribution of infection multiplicity:

$$\begin{array}{l}{p}_{ww}\approx 1,\hfill \\ p_{aw}\approx \frac{m}{1-{\tilde{f}}_{aw}},\hfill \\ p_{wb}\approx \frac{m}{1-{\tilde{f}}_{wb}},\hfill \\ p_{ab}\approx \frac{m^2+m({\tilde{f}}_{aw}{p}_{aw}+{\tilde{f}}_{wb}{p}_{wb})+r(1-h)p_{aw}{p}_{wb}}{1-{\tilde{f}}_{ab}+r(1-h)},\hfill \end{array}\}$$ (5.1)

where m is the point mutation rate per bp and r is the recombination probability, that is, the probability of an odd number of crossovers between the two loci. f_aw, f_wb and f_ab are the fitness of resistant genotypes relative to wild-type. ${\tilde{f}}_{aw}$ is the fitness value adjusted for the attenuating effect of phenotypic mixing, given by ${\tilde{f}}_{aw}=(1-h)+h{f}_{aw}$, with similar definitions for ${\tilde{f}}_{wb}$ and ${\tilde{f}}_{ab}$. A more accurate but less biologically instructive approximation is given by equation (A 17).

The appearance of the coefficient of inbreeding h in equation (5.1) can be understood intuitively by noting that recombination is ‘suppressed’ (relative to panmixis) in inbred virions since these are descended from an identical provirus. This naturally leads us to define the quantity ρ=r(1−h) as the effective recombination rate, which takes into account both the molecular recombination rate arising during reverse transcription and the opportunities for recombination that arise due to multiple cell infections. As already noted, the effective recombination rate could be lower than estimated here due to lower rates of multiple cell infection in body compartments other than the spleen.

Equation (5.1) reveals the balance illustrated in figure 1e between forward recombination, appearing in the numerator, and back recombination, which appears in the denominator. As recombination becomes more frequent, the dependence of the frequency of two-point mutant genotype on the fitness of one-point mutants is slightly accentuated, while the dependence on the fitness of the two-point mutant is markedly reduced. The dependence on these relative fitness parameters is illustrated for several assumptions in figure 3. It is worth noting that the epistasis E only approximately predicts the threshold where recombination does not affect the frequency of two-point mutants (which is model dependent, as seen in figure 3c); a more accurate estimate is given by equation (A 21). For the realistic case where differences in fitness are not too large (specifically, 1+f_ab≈f_aw+f_wb), the approximation is good.

Figure 3.

The kinetics of drug resistance in antiretroviral therapy-naive patients. (a) The frequency of each of the one-point mutants as a function of their fitness f₁ relative to wild-type, which is independent of the recombination probability r. (b) The frequency of the two-point mutant as a function of the fitness f₁ of the one-point mutants relative to wild-type, assuming that these are identical and that the fitness of the two-point mutants f₂=0.8. (c) The frequency of the two-point mutant as a function of the fitness f₂ of the one-point mutants relative to wild-type, assuming that these are identical and that the fitness of the two-point mutants f₁=0.9. For both (b) and (c) the dashed line signifies no recombination (r=0) and the solid line signifies maximum recombination (r=1/2).

In the absence of recombination (r=0), the equilibrium resistant gene frequencies given by equation (5.1) are formally identical to previous results (Ribeiro et al. 1998). The formal similarity hides an important difference, namely that the fitness parameters themselves are affected by cell co-infection. The minimum effective fitness value is 1−h and all resistant gene frequencies are increased by co-infection, a result already noted by Bretscher et al. (2004). An interesting question that needs further exploration is the possibility of dominance relations between genotypes. For example, what is the fitness of a virus produced from a cell infected by one wild-type and one resistant provirus? We have assumed that it is just the average of the two but there is no reason that one or the other genotype could not dominate. This needs further experimental elucidation.

6. The dynamics of drug resistance

Next I turn to the problem of describing antiretroviral treatment failure due to the emergence and outgrowth of resistant viral strains and analysing how recombination affects these predictions. To describe the dynamics of gene frequencies, we must properly use a mathematical model of viral replication which allows for changes in viral load as well as relative frequencies. This causes some difficulty: writing a model which includes an arbitrary MOI is a technical challenge due to the proliferation of different possible genotype combinations. I propose to use a model that approximates this system, in which we assume that cells can be infected a maximum of three times. The super-infection parameters are adjusted such that the pre-treatment equilibrium distribution of multiple cell infections is π₁=0.1, π₂=0.3 and π₃=0.6, that is, the mean multiplicity of infection is 2.5 and the coefficient of inbreeding is h=45%. While this corresponds to more multiply infected cells than indicated in figure 2a, the effective reproduction rate is the same. The model then builds upon the ‘basic model of viral dynamics’, reviewed by Nowak & May (2000), and its structure is illustrated in figure 4. A key modification which allows the dependence of the MOI on viral load during therapy is the introduction of a scaling exponent (a) such that the rate of cell super-infection is proportional to v^a, where v is the viral load. A constant co-infection rate, as assumed by Bretscher et al. (2004), is obtained when a=0. Mass-action dynamics are recovered when a=1 and when the quadratic dependence measured by Levy et al. (2004) corresponds to a=2.

Figure 4.

A model of viral dynamics with recombination. A dynamical model of viral replication with recombination is presented in stages. (a) Cell infection: x is the density of target cells, =N prior to infection, and their turnover rate is μ. The force of infection for genotype α is Λ_α and is then multiplied by a constant b_m for the mth infection, and scales with viral load v with exponent a. $y_{\alpha }^{(1)}$ is the density of cells singly infected with virus of genotype α and similar for doubly and triply infected cells $y_{\alpha \beta }^{(2)}$ and $y_{\alpha \beta \gamma }^{(3)}$. (b) Viral production: v_αβ is the density of virus of genotype αβ produced at constant rate k. f_α is the fitness of genotype α and e_α is the efficacy of treatment against that genotype (e_α=0 corresponds to 100% efficacy). Phenotypic mixing occurs since virions of different genotypes can have the same fitness when produced from the same cell. Virions are produced from a single cell in Hardy–Weinberg ratios with respect to proviral gene frequencies. (c) Force of infection: heterozygous virions with genotype αβ contribute half to the force of infection for each genotype α and β, apart from v₁₄ and v₂₃ for which recombination can occur with probability r. (d) Resistance mutations occur with probability m, are reverted with probability m_b and are implemented by mixing the force of infections Λ_α. The equations for this model are presented in Appendix B with the added complication that infected cells are stratified into long-lived latent and short-lived productive states.

First, starting with the assumption that viral load is independent of the multiplicity of infection (a=0), when antiretroviral treatment is insufficient in suppressing replication of the two-point mutant strain, and treatment fails, the impact of recombination is always to slow the emergence of the resistant strain (figure 5a–c). These simulations include the case of positive (a), negative (b) and null (c) epistasis, and thus differ from the earlier predictions of Bretscher et al. (2004). The dependence on epistasis is explored in further detail in figure 5f, where it shown over a large range of values of epistasis (from −3 to +3) that recombination always slows the appearance of two-point mutants. Figure 5c illustrates a special outcome, explored in more detail below, where recombination actually prevents the two-point mutant from emerging. This counter-intuitive result arises due to the interaction between population dynamics and natural selection, and need not have an evolutionary benefit. Selection by antiretroviral therapy is fundamentally different from selection in more normal circumstances where the population genetic assumption of constant population size is appropriate and leads to different outcomes as shown here.

Figure 5.

The dynamics of treatment failure. If the multiplicity of infection is independent of viral load (a=0), the effect of recombination is generally to slow the appearance of resistance mutations. This is illustrated for the case of both positive (a) and negative (b) epistasis. If, on the other hand, the multiplicity of infection depends on the viral load (d), then recombination has almost no effect on the viral dynamics (shown here for a=1). For all these, the solid lines assume no recombination (r=0), the dashed lines assume intermediate recombination (r=0.25) and the dotted lines assume maximal recombination (r=0.5). The number of wild-type, one-point mutant and two-point mutant viral RNA copies are plotted in blue, green and red, respectively. The basic reproductive number is R₀=5 so that a minimum of 80% of replication of any strain must be blocked by therapy to ensure treatment success. Therapy is assumed to block 90% of wild-type replication, so that the reproduction number is reduced from five to R_t=0.5, but only 51% of replication of the two-point mutant, so that its reproduction number is only reduced to 2. In (a) post-therapy epistasis is negative (E=−1), corresponding to 75% treatment efficacy against both one-point resistant mutants. In (b) post-therapy epistasis is instead positive (E=+1), corresponding to 81% treatment efficacy against both one-point resistant mutants. (c) is as (b) but with increased treatment efficacy of 63% against the two-point mutant, corresponding to a reproduction number of 1.5. In this case, treatment still fails in the absence of recombination but not when recombination is included: this is an example of bi-stability. Frequent recombination with wild-type virus prevents the two-point mutant strain from causing treatment failure. (e) illustrates the threshold reproduction number below which recombination can prevent the emergence of resistance as a function of the recombination rate. In cases where recombination has an effect (a=0), recombination usually slows the emergence of resistance (except for very large negative epistasis). Epistasis is a determinant of the time to failure (defined by reaching viral load >10⁴ copies per ml; f). However, the exponent (a), which determines the relation between viral load and multiple infection rates, is the most dominant determinant of the impact of recombination (g). In all graphs, the other model parameters are μ=0.1, d=1, k=1000, c=10, f_L=10⁻⁴ and d_L=0.01. The relative fitness of one-point mutants is 0.9 and that of two-point mutants is 0.81. Epistasis E is defined with a relative fitness of 1 for wild-type virus, even during therapy.

It has hitherto proved difficult to match the relatively slow time-scale of treatment failure observed in clinical trials with the mathematical predictions based on the rapid turnover of virus (see, for example, Phillips et al. 2001 for discussion of these issues). This suggests that predictions may be more realistic with the inclusion of the effects of recombination. Next, turning to viral load dependent multiplicity of infection (a=1 or a=2), recombination was not found to play a discernable role in determining the outcome of therapy (figure 5d). To explore this more systematically, the time to treatment failure is illustrated as a function of the scaling exponent a (figure 5g). Only when the scaling exponent is very small (a<0.1) does recombination have any discernible effect on the outcome of therapy. It is thus plausible to suggest that recombination will have no effect whatsoever on the rate of treatment failure. In vivo experimental measurements of a are needed to answer this question. This differs sharply with predictions of bi-stability (below) which are independent of the exponent a.

7. The action of recombination against infrequent emerging strains

An intriguing feature of the dynamics of retroviral evolution is the existence of hysteresis, or bi-stability (Boerlijst et al. 1996). Long-term viral dynamics depend on initial conditions, with increasing levels of recombination tending to give an advantage to frequent viral strains over fitter ones. Figure 5c illustrates the first paradoxical outcomes caused by this effect. All other factors remaining unchanged, recombination can prevent the emergence of a resistant viral strain that would otherwise cause treatment failure (provided the multiplicity of infection is viral load independent). This is not a peculiar outcome associated with special parameter values. Figure 5e illustrates for a different model assumption the threshold fitness value below which recombination prevents the emergence of the two-point mutants. This effect occurs because the two-point resistant strain is too often lost by recombining with wild-type virus. It is a frequency-dependent effect. If the amount of resistant virus were somehow boosted, it would pass a threshold where it could emerge and cause treatment failure.

The bi-stable nature of the dynamics can be seen more clearly by considering the persistence of the founding viral population in primary infections of untreated individuals. Figure 6a illustrates the case of a two-point mutant strain that is associated with a fitness gain relative to wild-type. If the infecting inoculum is predominantly wild-type then recombination will allow the wild-type virus to persist despite the presence of a fitter competitor. Figure 6a also illustrates the converse scenario. If an individual is infected with a resistant virus that carries a fitness cost relative to wild-type virus, then recombination can cause the resistant virus to persist simply because it is more common.

Figure 6.

Bi-stability: a strong founder effect. (a) A person is infected with a two-point resistant virus that is less fit than a wild-type but recombination prevents reversion to wild-type virus. Parameters are as in figure 5. This situation can equally be thought of as a person infected with wild-type virus with recombination preventing the emergence of fitter resistant strains. (b) The steady-state gene frequency p_ab is plotted as a function of fitness f_ab, illustrating the two coexisting equilibria for intermediate values of f_ab (plotted in black). The analytical approximation of equation (A 17) is also plotted (thick red line), showing excellent agreement, even when f_ab>1.

Figure 6b illustrates the range of this effect by plotting the eventual frequency of the two-point mutant within the viral population, depending on whether an individual was first infected with wild-type or the mutant. With high levels of recombination the most common strain can persist even in the face of a competitor with a 74% fitness advantage. If the fitness differential is larger, then the fittest strain will always win. Figure 6b also shows excellent agreement between the analytical result for the gene frequencies and the full dynamical model. The results of figure 6 are independent of the exponent a, that is, of what assumptions are made regarding the dependence of super-infection on viral load. They are also independent of the fitness of the one-point mutants and, thus, of epistasis. They are, however, dependent on the multiplicity of infection via the effective recombination rate. The prediction of bi-stability is thus a robust prediction of the model and valid for a wide range of parameter values.

The model presented in figure 3 and defined in Appendix B was extended to consider three resistance loci and up to four-fold infected cells without substantially altering any of the conclusions (analysis not shown).

8. Conclusions

Resistance to antiretroviral therapy is a major barrier to the long-term management of HIV-infected patients. Understanding the underlying mechanisms required to generate resistance is a crucial step in the rational design of therapy regimens that minimize the probability of resistant viral strains emerging. Because the dynamics of resistance involve changes in gene frequencies over many orders of magnitude, mathematical models are an essential tool for the study of resistance. Genetic sequencing can only focus on the most common genotypes at any point in time. This study shows that when the MOI is high, as recent data indicate is the case, recombination can have a dramatic impact on these dynamics. It is important to note that this impact can be large even when the observed rate of recombination is very low. If recombination were to prevent a multi-point resistant strain from emerging then the recombinant strains may not be seen, since most viruses would be wild-type. In fact, it may be only after treatment failure, when recombination has less impact, that recombination would be observed.

The analysis highlights the importance of the multiplicity of infection and its dependence on viral load. A plausible biological mechanism that could generate the distribution of the pro-viral copies per infected cell observed in cells collected from spleens of HIV-infected individuals was discussed (figure 2b). The within-host coefficient of inbreeding and its corollary, the effective recombination rate, were introduced as powerful tools for capturing the effect of the distribution of cell infection multiplicity on recombination. The analysis could thus easily be updated as more data are gathered from different patients and body compartments.

The outcome of therapy, in terms of the likely emergence of resistance, was shown to primarily depend on how the multiplicity of infection changes during therapy. If cell co-infection falls rapidly with decreasing viral load, as has been recently suggested (Levy et al. 2004), then recombination should have no discernible impact on the dynamics of resistance. If this is instead constant, as suggested by Jung et al. (2002) and Bretscher et al. (2004), then the impact of recombination is always to slow or even arrest the emergence of drug resistant strains. The resolution of this discrepancy should be a priority for future experimental study and could be achieved by, for example, measuring the in vivo changes in the MOI during therapy.

A second prediction is that recombination creates a strong founder effect, favouring the frequent over the fit virus (up to a point). It can thus prevent reversion to wild-type infection in resistant infections (which could easily be mistaken for the presence of compensatory fitness enhancing mutations) as well as prevent the emergence of fit resistant strains that have acquired such compensatory mutations. This prediction is independent of how the multiplicity of infection changes with viral load and is thus more robust than the first. The range of parameters over which the founder effect operates is, however, strongly dependent on the effective rate of recombination and may be smaller than suggested here if multiple cell infection is uncommonly frequent in the spleen, the only source of data to date.

The principal conclusion to this study is that the clinical response to a particular antiretroviral drug regimen depends on the location of the associated resistance mutations on the HIV genome. More distant mutations will have more recombination. The analysis suggests that all other things being equal, an antiretroviral drug regimen that targets multiple stages of the virus life cycle associated with more distant parts of the genome may, because of the effect of recombination, be less liable to fail due to the emergence of resistant viral strains. This suggests additional benefits beyond the obvious pharmacodynamic advantages to regimens with multiple drug classes. This could in part explain the apparently low efficacy of triple nucleoside reverse transcription inhibitor therapy (Gerstoft et al. 2003; Gulick et al. 2004) as these regimens may provide a low genetic barrier to viral resistance compared with regimens containing medications from multiple classes of antiretroviral agents. Conversely, when mutants of more unlinked loci emerge, reversal to wild-type could be slowed or halted by recombination, particularly in newly infected individuals. The application of this analysis to real genetic data is simple, since location information is encoded in the resistance genetics nomenclature (Fraser et al. 2003).1 The predictions of the theory are experimentally testable and have clinical consequences.

By requiring a precise formulation of the assumptions of the model, the analysis highlights areas of uncertainty in antiretroviral genetics, particularly with regards to the fitness of viral strains. These should be addressed by future experimental work. On the theoretical level, the model must be developed with increasing practicality, including a realistic number of resistance loci and other factors that determine treatment success such as drug efficacy, patient adherence, immune cell dynamics and stochasticity. Measuring the MOIs in body compartments other than the spleen, and in HIV-infected patients with good viral suppression during antiretroviral therapy, would provide more insight into the role of retroviral recombination in antiretroviral resistance.

Appendix A. Equilibrium frequencies of resistant viral strains in antiretroviral therapy-naive patients

A.1 Definitions

We denote the four (single strand) genotypes: 1=ww, 2=aw, 3=wb and 4=ab. We use the symbol α (ranging from 1 to 4) to denote an arbitrary genotype. We denote the four gene frequencies as p_α. We denote the frequency of virus of (two-strand=diploid) genotype αβ as $p_{\alpha \beta }^v$. We denote the proportion of k-fold-infected cells that are infected with proviruses of genotypes α₁ through to α_k as $p_{{\alpha }_1\dots {\alpha }_k}^{(k)}$. Finally, we denote the proportion of infected cells that are k-fold-infected as π_k.

A.2 The frequency of infected cell genotypes as a function of the gene frequencies

If each time a cell is infected, it is infected with genotype α with probability equal to the gene frequency (p_α), then the frequency of k-fold-infected cells is given by the multinomial expansion:

$$\sum _{({\alpha }_1\dots {\alpha }_k)}{p}_{{\alpha }_1\dots {\alpha }_k}^{(k)}{x}_{{\alpha }_1}\dots x_{{\alpha }_k}={\left(\sum _{\alpha }{p}_{\alpha }{x}_{\alpha }\right)}^k.$$ (A 1)

The right-hand side of this expression is a sum over the four genotypes, whereas the left-hand side is a sum of all possible ordered combinations of k genotypes. x_α are dummy variables. Biologically, equation (A 1) states that the k infection events which results in k-fold-infected cells occur with identical gene frequencies p_α.

A.3 The fitness of viral genotypes, including the effect of phenotypic mixing

We define a single measure of viral fitness which averages over the whole replication cycle and assume without much loss of generality that this acts at the point of viral production. We assume the fitness of virus produced from a k-fold-infected cell with genotype α₁α₂…α_k is the arithmetic mean of the basic fitness values associated with each genotype. We do not address the interesting question of what might arise with other plausible assumptions, such as a geometric mean or dominance relationships between genotypes. The fitness of virus produced from a k-fold-infected cell with proviral genotypes α₁α₂…α_k is thus

$$f_{{\alpha }_1{\alpha }_2\dots {\alpha }_k}^{(k)}=\frac{f_{{\alpha }_1}+f_{{\alpha }_2}+\cdots +f_{{\alpha }_k}}{k},$$ (A 2)

where f_α is the fitness associated with the individual proviral genotype.

A.4 The frequency of free virus genotypes as a function of infected cell genotypes

Suppose a k-fold-infected cell is infected i times by provirus of genotype α and j times by provirus of genotype β, such that i+j≤k. Viruses produced from this cell will be produced with genotypes αα, αβ and ββ with Hardy–Weinberg relative frequencies:

$$p_{\alpha \alpha }^{(v)\text{cell}}:p_{\alpha \beta }^{(v)\text{cell}}:p_{\beta \beta }^{(v)\text{cell}}=\frac{i^2}{k^2}:\frac{2ij}{k^2}:\frac{j^2}{k^2}.$$ (A3)

The overall rate of virus production will be weighted by the fitness of the overall cell genotype (A 2).

To proceed further with the calculation, we assume that a hierarchy of gene frequencies exists at equilibrium, so that the wild-type genotype is much more common than either of the one-point mutants and the two one-point mutant genotypes are both more common than the two-point mutant genotype, that is,

$$p_1\gg p_2,p_3\gg p_4,$$ (A 4)

so that when calculating gene frequencies, we only consider leading-term contributions. It follows from equation (A 4) that p₁≈1. We now relate the viral genotype frequencies to the gene frequencies via the intermediary of cell genotype frequencies as follows. For the wild-type 1/1=ww/ww genotype, it follows from equation (A 4) that

$$p_{11}^v\approx 1.$$ (A5)

For heterozygous wild-type resistant genotypes, these are dominantly produced from k-fold-infected cells that have k−1 wild-type proviruses and 1 resistant genotype, so that

$$p_{1\alpha }^v=\sum _{k=2}^{\infty }{\pi }_k{f}_{1\dots 1\alpha }^{(k)}{p}_{1\dots 1\alpha }^{(k)}\left(2\frac{k-1}{k}\frac{1}{k}\right)=\sum _{k=2}^{\infty }{\pi }_k\left(\frac{(k-1)f_1+f_{\alpha }}{k}\right)(k{p}_{\alpha })\left(2\frac{k-1}{k^2}\right)=2p_{\alpha }\sum _{k=1}^{\infty }{\pi }_k\left\{\frac{{(k-1)}^2+f_{\alpha }(k-1)}{k^2}\right\}=2p_{\alpha }\sum _{k=1}^{\infty }{\pi }_k\left\{1-\frac{2}{k}+\frac{1}{k^2}+f_{\alpha }\left(\frac{1}{k}-\frac{1}{k^2}\right)\right\}=2p_{\alpha }\{1-2h+\sigma +f_{\alpha }(h-\sigma )\},$$ (A6)

where

$$h=\sum _{k=1}^{\infty }\frac{{\pi }_k}{k}$$ (A7)

is the coefficient of inbreeding and

$$\sigma =\sum _{k=1}^{\infty }\frac{{\pi }_k}{k^2}$$ (A8)

is another summary statistic that can be readily be computed from the multiplicity of infection distribution. A similar calculation applies for a homozygous resistant virus:

$$p_{\alpha \alpha }^v=\sum _{k=1}^{\infty }{\pi }_k{f}_{1\dots 1\alpha }^{(k)}{p}_{1\dots 1\alpha }^{(k)}\left(\frac{1}{k}\frac{1}{k}\right)=\sum _{k=1}^{\infty }{\pi }_k\left(\frac{(k-1)f_1+f_{\alpha }}{k}\right)(k{p}_{\alpha })\left(\frac{1}{k^2}\right)=p_{\alpha }\sum _{k=1}^{\infty }{\pi }_k\left\{\frac{1}{k}-\frac{1}{k^2}+f_{\alpha }\frac{1}{k^2}\right\}=p_{\alpha }\{h-\sigma +f_{\alpha }\sigma \}.$$ (A9)

A heterozygous virus will be produced from k-fold-infected cells that have k−2 wild-type proviruses and one of each of the resistant genotypes

$$p_{\alpha \beta }^v=\sum _{k=2}^{\infty }{\pi }_k{f}_{1\dots 1\alpha \beta }^{(k)}{p}_{1\dots 1\alpha \beta }^{(k)}\left(2\frac{1}{k}\frac{1}{k}\right)=\sum _{k=2}^{\infty }{\pi }_k\left(\frac{(k-2)f_1+f_{\alpha }+f_{\beta }}{k}\right)(k(k-1)p_{\alpha }{p}_{\beta })\left(\frac{2}{k^2}\right)=2p_{\alpha }{p}_{\beta }\sum _{k=1}^{\infty }{\pi }_k\left\{\frac{(k-1)(k-2)f_1+(k-1)(f_{\alpha }+f_{\beta })}{k^2}\right\}=2p_{\alpha }{p}_{\beta }\sum _{k=1}^{\infty }{\pi }_k\left\{1-\frac{3}{k}+\frac{2}{k^2}+(f_{\alpha }+f_{\beta })\left(\frac{1}{k}-\frac{1}{k^2}\right)\right\}=2p_{\alpha }{p}_{\beta }\{1-3h+2\sigma +(f_{\alpha }+f_{\beta })(h-\sigma )\}\equiv 2p_{\alpha }{p}_{\beta }S[f_{\alpha }+f_{\beta }],$$ (A10)

where the function S[x] is defined as

$$S[x]=1-3h+2\sigma +x(h-\sigma ).$$ (A11)

A.5 Gene frequencies, as a function of free virus genotypes

The next step is to relate gene frequencies to viral genotype frequencies by examining the force of cell infection. It is useful to define intermediary steps. First, allow for a single round of recombination with probability r of cross-over between the loci.

$$\begin{array}{l}{p}_{\alpha \beta }^r=p_{\alpha \beta }^v,\hfill \\ \text{except}\hfill \\ p_{14}^r=(1-r)p_{14}^v+r{p}_{23}^v,\hfill \\ p_{23}^r=r{p}_{14}^v+(1-r)p_{23}^v.\hfill \end{array}\}$$ (A12)

We denote the relative magnitude of the genotype-specific force-of-infection terms as ${\lambda }_{\alpha }$. The leading-term contributions are

$$\begin{array}{l}{\lambda }_1\approx p_{11}^r,\hfill \\ {\lambda }_2\approx m{p}_{11}^r+\frac{1}{2}{p}_{12}^r+p_{22}^r,\hfill \\ {\lambda }_3\approx m{p}_{11}^r+\frac{1}{2}{p}_{13}^r+p_{33}^r,\hfill \\ {\lambda }_4\approx m^2{p}_{11}^r+m\left(\frac{1}{2}{p}_{12}^r+p_{22}^r+\frac{1}{2}{p}_{13}^r+p_{33}^r\right)+\frac{1}{2}{p}_{14}^r+p_{44}^r.\hfill \end{array}\}$$ (A13)

It follows that

$$\begin{array}{l}{\lambda }_1\approx 1,\hfill \\ {\lambda }_2\approx m+\frac{1}{2}{p}_{12}^v+p_{22}^v=m+p_2[1-2h+\sigma +f_2(h-\sigma )]\hfill \\ +p_2[h-\sigma +f_2\sigma ]=m+{\tilde{f}}_2{p}_2,\hfill \\ {\lambda }_3\approx m+\frac{1}{2}{p}_{13}^v+p_{33}^v=m+{\tilde{f}}_3{p}_3,\hfill \\ {\lambda }_4\approx m^2+m({\tilde{f}}_2{p}_2+{\tilde{f}}_3{p}_3)+\frac{r}{2}{p}_{23}^v+\frac{1-r}{2}{p}_{14}^v+p_{44}^v\hfill \\ =m^2+m({\tilde{f}}_2{p}_2+{\tilde{f}}_3{p}_3)+rS[f_2+f_3]p_2{p}_3\hfill \\ +{\tilde{f}}_4{p}_4-rS[1+f_4]p_4,\hfill \end{array}\}$$ (A 14)

where we have defined the ‘average’ fitness values for each genotype as

$${\tilde{f}}_{\alpha }=1-h+h{f}_{\alpha }.$$ (A15)

A.6 The steady-state gene frequencies

If we assume that cell infection occurs at these frequencies at each round of infection (for multiply infected cells), then these are also the gene frequencies:

$${\lambda }_{\alpha }=p_{\alpha }.$$ (A16)

The gene frequencies then follow from equation (A 14):

$$\begin{array}{l}{p}_1=1,\hfill \\ p_2=\frac{m}{1-{\tilde{f}}_2},\hfill \\ p_3=\frac{m}{1-{\tilde{f}}_3},\hfill \\ p_4=\frac{m^2+m({\tilde{f}}_2{p}_2+{\tilde{f}}_3{p}_3)+r{p}_2{p}_{3}S[f_2+f_3]}{1-{\tilde{f}}_4+rS[1+f_4]}.\hfill \end{array}\}$$ (A 17)

This reduces to the standard formulae when there are no multiply infected cells, that is, π₁=h=σ=1, namely,

$$\begin{array}{l}{p}_1=1,\hfill \\ p_2=\frac{m}{1-f_2},\hfill \\ p_3=\frac{m}{1-f_3},\hfill \\ p_4=\frac{m^2+m(f_2{p}_2+f_3{p}_3)}{1-f_4}.\hfill \end{array}\}$$ (A18)

In the case where there is no recombination but there are still multiply infected cells the formulae are algebraically similar, that is,

$$\begin{array}{l}{p}_1=1,\hfill \\ p_2=\frac{m}{1-{\tilde{f}}_2},\hfill \\ p_3=\frac{m}{1-{\tilde{f}}_3},\hfill \\ p_4=\frac{m^2+m({\tilde{f}}_2{p}_2+{\tilde{f}}_3{p}_3)}{1-{\tilde{f}}_4},\hfill \end{array}\}$$ (A19)

the difference being that fitness differences are reduced by phenotypic mixing with wild-type virus, that is, ${\tilde{f}}_{\alpha }=1-h+h{f}_{\alpha }\ge f_{\alpha }$. Approximation (5.1) presented in the text is valid when all relative fitness values are close to unity, so that we can assume $S[1+f_4]\approx S[f_2+f_3]\approx S[2]=1-h$.

A.7 Generalized epistasis

The aim here is to identify a parameter describing the interaction between the resistance loci which predicts whether recombination will increase or decrease the frequency of the two-point mutant. If viruses were freely mixing, the epistasis parameter would be $E=f_1{f}_4-f_2{f}_3=f_4-f_2{f}_3$. For negative epistasis (E<0), recombination increases the frequency of two-point mutants while for positive epistasis (E>0), recombination decreases their frequency. For this model, the complex population structure of the viruses and their phenotypic mixing leads to more complex predictions. The frequency of two-point mutants in (A17) takes the general form (A+Br)/(C+Dr) and, thus, the derivative of this with respect to r has the same sign as the discriminant BC−AD. To match the above definition, we define an alternative epistasis parameter E′=K(AD−BC), where K is an arbitrary positive constant.

$$E^{\prime }=K\{(m^2+m{\tilde{f}}_2{p}_2+m{\tilde{f}}_3{p}_3)S[1+f_4]-(p_2{p}_{3}S[f_2+f_3])(1-{\tilde{f}}_4)\}=m^{2}K\left\{\left(1+\frac{{\tilde{f}}_2}{1-{\tilde{f}}_2}+\frac{{\tilde{f}}_3}{1-{\tilde{f}}_3}\right)S[1+f_4]-\frac{S[f_2+f_3](1-{\tilde{f}}_4)}{(1-{\tilde{f}}_2)(1-{\tilde{f}}_3)}\right\}=\frac{m^{2}K}{(1-{\tilde{f}}_2)(1-{\tilde{f}}_3)}\{(1-{\tilde{f}}_2{\tilde{f}}_3)S[1+f_4]-(1-{\tilde{f}}_4)S[f_2+f_3]\}.$$ (A20)

We fix $K=(1-{\tilde{f}}_2)(1-{\tilde{f}}_3)/m^2$ so that

$$E^{\prime }=(1-{\tilde{f}}_2{\tilde{f}}_3)S[1+f_4]-(1-{\tilde{f}}_4)S[f_2+f_3].$$ (A 21)

This formula allows us to see the impact of both population structure and phenotypic mixing. In the limit of panmixis, when cells are highly multiply infected and there is no population structure, h≈σ≈0 and S[x]≈1; thus, the epistasis function takes the algebraically familiar form $E^{\prime }\approx {\tilde{f}}_4-{\tilde{f}}_2{\tilde{f}}_3$, but fitness differences become marginal due to extreme phenotypic mixing so that ${\tilde{f}}_2\approx {\tilde{f}}_3\approx {\tilde{f}}_4\approx 1$. In the alternative limit of singly infected cells, h≈σ≈1, S[x]≈0 and ${\tilde{f}}_{\alpha }\approx f_{\alpha }$, and while epistasis takes its regular form the overall effects of recombination are suppressed. Finally, in the case where the differences in relative fitness are not too large or, more specifically, 1+f₄≈f₂+f₃, then the expression (A 21) reduces to $E^{\prime }\propto {\tilde{f}}_4-{\tilde{f}}_2{\tilde{f}}_3$.

A.8 The range of bi-stability

The numerical analysis presented in figure 6a shows that the analytical approximation presented in equation (A 17) is extremely accurate and, furthermore, that where the equilibrium is positive, it is locally stable. The range of stability can thus be derived by requiring

$$1-{\tilde{f}}_4+rS[1+f_4]>0.$$ (A22)

This can be re-written as

$$f_4<\frac{h+r(1-2h+\sigma )}{h-r(h-\sigma )}.$$ (A23)

In the presence of maximal levels of recombination r=1/2, this becomes

$$f_4<\frac{1+\sigma }{h+\sigma }.$$ (A 24)

For our parameter estimates this yields a maximum relative fitness of 1.74, as stated in the text. Equation (A 24) can also be used to explore the effect of higher h values that might arise if our estimates based on observations in the spleen are unrepresentative of the body as a whole.

Appendix B. A mathematical model of viral dynamics with drug resistance and recombination

We limit ourselves to two resistance loci, each with a wild-type and resistant allele, and a maximum of three proviral copies per cell. The notation and structure of this model is defined in figure 3 with the added complication that we allow for long-lived latently infected cells. The dynamical state variables consist of uninfected cells x; singly, doubly and triply productively infected cells of each genotype $y_{\alpha }^{(1)}$, $y_{\alpha \beta }^{(2)}$ and $y_{\alpha \beta \gamma }^{(3)}$, respectively, where the indices α≤β≤γ label the four basic genotypes: singly, doubly and triply infected long-lived latently infected cells of each genotype $y_{\text{L}\alpha }^{(1)}$, $y_{\text{L}\alpha \beta }^{(2)}$ and $y_{\text{L}\alpha \beta \gamma }^{(3)}$, respectively, and free virus v.

The equation for susceptible cells is

$$\frac{\text{d}x}{\text{d}t}=\mu (1-x)-b_{1}x\Lambda ,$$ (B1)

where μ is the rate of turnover of uninfected cells, b₁ is the rate of susceptible cell infection and Λ is the force of infection. The equations for singly infected cells are

$$\begin{array}{l}\frac{\text{d}{y}_{\alpha }^{(1)}}{\text{d}t}=(1-f_{\text{L}})b_{1}x{\Lambda }_{\alpha }-d{y}_{\alpha }^{(1)}-b_2{y}_{\alpha }^{(1)}{\Lambda }^a+d_{\text{L}}{y}_{\text{L}\alpha }^{(1)},\hfill \\ \frac{\text{d}{y}_{\text{L}\alpha }^{(1)}}{\text{d}t}=f_{\text{L}}{b}_{1}x{ϵ}_{\alpha }{\Lambda }_{\alpha }-d_{\text{L}}{y}_{\text{L}\alpha }^{(1)}-b_{\text{L}2}{y}_{\text{L}\alpha }^{(1)}{\Lambda }^a,\hfill \end{array}\}$$ (B2)

where f_L is the proportion of cell infections that lead to latent infection, Λ_α is the force of infection of genotype α (note $\Lambda ={\sum }_{\alpha }{\Lambda }_{\alpha }$), d is the death rate of short-lived productively infected cells, d_L is the rate at which long-lived latently activated cells are reactivated, b₂ is the rate at which singly infected short-lived cells are re-infected, b_L2 is the rate at which singly infected long-lived cells are re-infected and a is the exponent governing how the rate of multiple cell infections changes with viral load. a=1 is the naively expected mass-action dependence while a=0 leads to viral load-independent multiplicity of infection and a=2 results in quadratic dependence.

The equations for doubly infected cells are

$$\begin{array}{l}\frac{\text{d}{y}_{\alpha \alpha }^{(2)}}{\text{d}t}=(1-f_{\text{L}})b_2{y}_{\alpha }^{(1)}{\Lambda }^{a-1}{\Lambda }_{\alpha }-d{y}_{\alpha \alpha }^{(2)}-b_3{y}_{\alpha \alpha }^{(2)}{\Lambda }^a+d_{\text{L}}{y}_{\text{L}\alpha \alpha }^{(2)},\hfill \\ \frac{\text{d}{y}_{\alpha \beta }^{(2)}}{\text{d}t}=(1-f_{\text{L}})b_2{\Lambda }^{a-1}(y_{\alpha }^{(1)}{\Lambda }_{\beta }+y_{\beta }^{(1)}{\Lambda }_{\alpha })-d{y}_{\alpha \beta }^{(2)}-b_3{y}_{\alpha \beta }^{(2)}{\Lambda }^a\hfill \\ +d_{\text{L}}{y}_{\text{L}\alpha \beta }^{(2)},\hfill \\ \frac{\text{d}{y}_{\text{L}\alpha \alpha }^{(2)}}{\text{d}t}=f_{\text{L}}{b}_2{y}_{\alpha }^{(1)}{\Lambda }^{a-1}{\Lambda }_{\alpha }+b_{\text{L}2}{y}_{\text{L}\alpha }^{(1)}{\Lambda }_{\alpha }-d_{\text{L}}{y}_{\text{L}\alpha \alpha }^{(2)}-b_{\text{L}3}{y}_{\text{L}\alpha \alpha }^{(2)}{\Lambda }^a,\hfill \\ \frac{\text{d}{y}_{\text{L}\alpha \beta }^{(2)}}{\text{d}t}=f_{\text{L}}{b}_2{\Lambda }^{a-1}(y_{\alpha }^{(1)}{\Lambda }_{\beta }+y_{\alpha }^{(1)}{\Lambda }_{\beta })+b_{\text{L}2}{\Lambda }^{a-1}(y_{\text{L}\alpha }^{(1)}{\Lambda }_{\beta }\hfill \\ +y_{\text{L}\beta }^{(1)}{\Lambda }_{\alpha })-d_{\text{L}}{y}_{\text{L}\alpha \beta }^{(2)}-b_{\text{L}3}{y}_{\text{L}\alpha \beta }^{(2)}{\Lambda }^a,\hfill \end{array}\}$$ (B3)

where α<β, b₃ is the rate at which doubly infected short-lived cells are re-infected and b_L3 is the rate at which doubly infected long-lived cells are re-infected.

The equations for triply infected cells are

$$\begin{array}{l}\frac{\text{d}{y}_{\alpha \alpha \alpha }^{(3)}}{\text{d}t}=(1-f_{\text{L}})b_3{y}_{\alpha \alpha }^{(2)}{\Lambda }^{a-1}{\Lambda }_{\alpha }-d{y}_{\alpha \alpha \alpha }^{(3)}+d_{\text{L}}{y}_{\text{L}\alpha \alpha \alpha }^{(3)},\hfill \\ \frac{\text{d}{y}_{\alpha \alpha \beta }^{(3)}}{\text{d}t}=(1-f_{\text{L}})b_3{\Lambda }^{a-1}(y_{\alpha \alpha }^{(2)}{\Lambda }_{\beta }+y_{\alpha \beta }^{(2)}{\Lambda }_{\alpha })-d{y}_{\alpha \alpha \beta }^{(3)}+d_{\text{L}}{y}_{\text{L}\alpha \alpha \beta }^{(3)},\hfill \\ \frac{\text{d}{y}_{\alpha \beta \beta }^{(3)}}{\text{d}t}=(1-f_{\text{L}})b_3{\Lambda }^{a-1}(y_{\alpha \beta }^{(2)}{\Lambda }_{\beta }+y_{\beta \beta }^{(2)}{\Lambda }_{\alpha })-d{y}_{\alpha \beta \beta }^{(3)}+d_{\text{L}}{y}_{\text{L}\alpha \beta \beta }^{(3)},\hfill \\ \frac{\text{d}{y}_{\alpha \beta \gamma }^{(3)}}{\text{d}t}=(1-f_{\text{L}})b_3{\Lambda }^{a-1}(y_{\alpha \beta }^{(2)}{\Lambda }_{\gamma }+y_{\alpha \gamma }^{(2)}{\Lambda }_{\beta }+y_{\beta \gamma }^{(2)}{\Lambda }_{\alpha })-d{y}_{\alpha \beta \gamma }^{(3)}\hfill \\ +d_{\text{L}}{y}_{\text{L}\alpha \beta \gamma }^{(3)},\hfill \\ \frac{\text{d}{y}_{\text{L}\alpha \alpha \alpha }^{(3)}}{\text{d}t}=f_{\text{L}}{b}_3{y}_{\alpha \alpha }^{(2)}{\Lambda }_{\alpha }+b_{\text{L}3}{y}_{\text{L}\alpha \alpha }^{(2)}{\Lambda }^{a-1}{\Lambda }_{\alpha }-d_{\text{L}}{y}_{\text{L}\alpha \alpha \alpha }^{(3)},\hfill \\ \frac{\text{d}{y}_{\text{L}\alpha \alpha \beta }^{(3)}}{\text{d}t}=f_{\text{L}}{b}_3{\Lambda }^{a-1}(y_{\alpha \alpha }^{(2)}{\Lambda }_{\beta }+y_{\alpha \beta }^{(2)}{\Lambda }_{\alpha })+b_{\text{L}3}{\Lambda }^{a-1}(y_{\text{L}\alpha \alpha }^{(2)}{\Lambda }_{\beta }\hfill \\ +y_{\text{L}\alpha \beta }^{(2)}{\Lambda }_{\alpha })-d_{\text{L}}{y}_{\text{L}\alpha \alpha \beta }^{(3)},\hfill \\ \frac{\text{d}{y}_{\text{L}\alpha \beta \beta }^{(3)}}{\text{d}t}=f_{\text{L}}{b}_3{\Lambda }^{a-1}(y_{\alpha \beta }^{(2)}{\Lambda }_{\beta }+y_{\beta \beta }^{(2)}{\Lambda }_{\alpha })+b_{\text{L}3}{\Lambda }^{a-1}(y_{\text{L}\alpha \beta }^{(2)}{\Lambda }_{\beta }\hfill \\ +y_{\text{L}\beta \beta }^{(2)}{\Lambda }_{\alpha })-d_{\text{L}}{y}_{\text{L}\alpha \beta \beta }^{(3)},\hfill \\ \frac{\text{d}{y}_{\text{L}\alpha \beta \gamma }^{(3)}}{\text{d}t}=f_{\text{L}}{b}_3{\Lambda }^{a-1}(y_{\alpha \beta }^{(2)}{\Lambda }_{\gamma }+y_{\alpha \gamma }^{(2)}{\Lambda }_{\beta }+y_{\beta \gamma }^{(2)}{\Lambda }_{\alpha })\hfill \\ +b_{\text{L}3}{\Lambda }^{a-1}(y_{\text{L}\alpha \beta }^{(2)}{\Lambda }_{\gamma }+y_{\text{L}\alpha \gamma }^{(2)}{\Lambda }_{\beta }+y_{\text{L}\beta \gamma }^{(2)}{\Lambda }_{\alpha })-d_{\text{L}}{y}_{\text{L}\alpha \beta \gamma }^{(3)},\hfill \end{array}\}$$ (B4)

where α<β<γ and no new parameters are introduced.

To ensure a similar distribution of cell infection multiplicity in resting and productively infected cells in the untreated equilibrium, we can impose the conditions

$$b_{\text{L}k}=\frac{d_{\text{L}}}{d}{b}_k\text{for}k=1,2,3.$$ (B5)

Next, for viral production, we begin by rescaling the density of infected cells according to the relative fitness and drug efficacy:

$$\begin{array}{l}{\overline{y}}_{\alpha }^{(1)}=e_{\alpha }{f}_{\alpha }{y}_{\alpha }^{(1)},\hfill \\ {\overline{y}}_{\alpha \beta }^{(2)}=\frac{e_{\alpha }{f}_{\alpha }+e_{\beta }{f}_{\beta }}{2}{y}_{\alpha \beta }^{(2)},\hfill \\ {\overline{y}}_{\alpha \beta \gamma }^{(3)}=\frac{e_{\alpha }{f}_{\alpha }+e_{\beta }{f}_{\beta }+e_{\gamma }{f}_{\gamma }}{3}{y}_{\alpha \beta \gamma }^{(3)},\hfill \end{array}\}$$ (B6)

where f_α is the relative fitness value for genotype α and e_α is the drug efficacy acting against genotype α (1 corresponds to no inhibition and 0 to 100% inhibition). Viral production follows Hardy–Weinberg ratios

$$\begin{array}{l}\frac{\text{d}{v}_{\alpha \alpha }}{\text{d}t}=k\left(\begin{array}{l}{\overline{y}}_{\alpha }^{(1)}+{\overline{y}}_{\alpha \alpha }^{(2)}+\frac{1}{4}\left(\sum _{\beta <\alpha }{\overline{y}}_{\beta \alpha }^{(2)}+\sum _{\beta >\alpha }{\overline{y}}_{\alpha \beta }^{(2)}\right)\\ +{\overline{y}}_{\alpha \alpha \alpha }^{(3)}+\frac{4}{9}\left(\sum _{\beta <\alpha }{\overline{y}}_{\beta \alpha \alpha }^{(3)}+\sum _{\beta >\alpha }{\overline{y}}_{\alpha \alpha \beta }^{(3)}\right)\\ +\frac{1}{9}\left(\begin{array}{l}\sum _{\beta <\alpha }{\overline{y}}_{\beta \beta \alpha }^{(3)}+\sum _{\beta >\alpha }{\overline{y}}_{\alpha \beta \beta }^{(3)}+\sum _{\beta <\gamma <\alpha }{\overline{y}}_{\beta \gamma \alpha }^{(3)}\\ +\sum _{\beta <\alpha <\gamma }{\overline{y}}_{\beta \alpha \gamma }^{(3)}+\sum _{\alpha <\beta <\gamma }{\overline{y}}_{\alpha \beta \gamma }^{(3)}\end{array}\right)\end{array}\right)-c{v}_{\alpha \alpha },\hfill \\ \frac{\text{d}{v}_{\alpha \beta }}{\text{d}t}=k\left(\begin{array}{l}\frac{1}{2}{\overline{y}}_{\alpha \beta }^{(2)}+\frac{4}{9}({\overline{y}}_{\alpha \beta \beta }^{(3)}+{\overline{y}}_{\alpha \alpha \beta }^{(3)})\\ +\frac{2}{9}\left(\sum _{\gamma <\alpha }{\overline{y}}_{\gamma \alpha \beta }^{(3)}+\sum _{\alpha <\gamma <\beta }{\overline{y}}_{\alpha \gamma \beta }^{(3)}+\sum _{\gamma >\beta }{\overline{y}}_{\alpha \beta \gamma }^{(3)}\right)\end{array}\right)-c{v}_{\alpha \beta },\hfill \end{array}\}$$ (B7)

where α<β, k and c are the viral production and clearance rates, respectively. It remains to define the force of infection, including viral fitness, recombination and point mutation. First, allow for recombination

$$\begin{array}{l}{v}_{\alpha \beta }^r=v_{\alpha \beta },\hfill \\ \text{except}\hfill \\ v_{14}^r=(1-r)v_{14}+r{v}_{23},\hfill \\ v_{23}^r=r{v}_{14}+(1-r)v_{23},\hfill \end{array}\}$$ (B8)

where r is the recombination probability (specifically, the probability of an odd number of cross-overs occurring between the two resistance loci during reverse transcription). Effect reverse transcription to translate viral densities into force of infection terms

$${\Lambda }_{\alpha }^{(0)}=v_{\alpha \alpha }^r+\frac{1}{2}\left(\sum _{\beta <\alpha }{v}_{\beta \alpha }^r+\sum _{\beta >\alpha }{v}_{\alpha \beta }^r\right),$$ (B9)

where ‘(0)’ denotes that it is the force of infection obtained prior to mutations arising. Finally, account for point mutation

$$\begin{array}{l}{\Lambda }_1={\Lambda }_1^{(0)}(1-2m)+m({\Lambda }_2^{(0)}+{\Lambda }_3^{(0)})+m^2{\Lambda }_4^{(0)},\hfill \\ {\Lambda }_2={\Lambda }_2^{(0)}(1-2m)+m({\Lambda }_1^{(0)}+{\Lambda }_4^{(0)})+m^2{\Lambda }_3^{(0)},\hfill \\ {\Lambda }_3={\Lambda }_3^{(0)}(1-2m)+m({\Lambda }_1^{(0)}+{\Lambda }_4^{(0)})+m^2{\Lambda }_2^{(0)},\hfill \\ {\Lambda }_4={\Lambda }_4^{(0)}(1-2m)+m({\Lambda }_2^{(0)}+{\Lambda }_3^{(0)})+m^2{\Lambda }_1^{(0)},\hfill \end{array}\}$$ (B10)

where m is the mutation probability (assumed symmetric going from wild-type to resistant and vice versa).

Most of the parameters can be estimated from the literature. However, parameters relating to relative fitness may depend on each genotype and are difficult to estimate. The primary infection parameter b₁ can be related to the basic reproduction number R₀ of the virus as follows:

$$b_1=\frac{dc{R}_0}{k}.$$ (B11)

Super-infection parameters determine the multiplicity of infection and can be estimated as

$$\begin{array}{l}{b}_2=\frac{d}{{\hat{v}}^a}\frac{1-{\hat{\pi }}_1}{{\hat{\pi }}_1},\hfill \\ b_3=\frac{d}{{\hat{v}}^a}\frac{{\hat{\pi }}_3}{{\hat{\pi }}_2},\hfill \end{array}\}$$ (B12)

where $\hat{v}$ is the steady-state (pre-treatment) viral load, approximately equal to

$$\hat{v}=\frac{\mu k}{dc}\frac{R_0-1}{R_0},$$ (B13)

and ${\hat{\pi }}_1$, ${\hat{\pi }}_2$ and ${\hat{\pi }}_3=1-{\hat{\pi }}_1-{\hat{\pi }}_2$ are the steady-state (pre-treatment) relative frequencies of singly, doubly and triply infected cells, respectively.

Thus, the model has four evolutionary parameters, r, m, ${\hat{\pi }}_1$ and ${\hat{\pi }}_2$, and seven dynamical parameters, R₀, d, d_L, μ, k, c and f_L, that we estimate from the literature. There remain the three relative fitness values, f₂, f₃ and f₄, the exponent, a, and the four drug efficacies, e₁, e₂, e₃ and e₄. We explore the sensitivity to these latter parameters in the analysis of the model.