Singular value decomposition with self-modeling applied to determine bacteriorhodopsin intermediate spectra: Analysis of simulated data

Abstract

An a priori model-independent method for the determination of accurate spectra of photocycle intermediates is developed. The method, singular value decomposition with self-modeling (SVD-SM), is tested on simulated difference spectra designed to mimic the photocycle of the Asp-96 → Asn mutant of bacteriorhodopsin. Stoichiometric constraints, valid until the onset of the recovery of bleached bacteriorhodopsin at the end of the photocycle, guide the self-modeling procedure. The difference spectra of the intermediates are determined in eigenvector space by confining the search for their coordinates to a stoichiometric plane. In the absence of random noise, SVD-SM recovers the intermediate spectra and their time evolution nearly exactly. The recovery of input spectra and kinetics is excellent although somewhat less exact when realistic random noise is included in the input spectra. The difference between recovered and input kinetics is now visually discernible, but the same reaction scheme with nearly identical rate constants to those assumed in the simulation fits the output kinetics well. SVD-SM relegates the selection of a photocycle model to the late stage of the analysis. It thus avoids derivation of erroneous model-specific spectra that result from global model-fitting approaches that assume a model at the outset.

A general problem in spectroscopy is the dissection of spectra of mixtures of unknown composition into the spectra of the pure constituents, thereby determining the relative amount of the components. In a typical experiment, many spectra are measured, and the variation of an experimental parameter provides a systematic change in the contribution of the pure components to each mixture spectrum. The spectra are arranged in a matrix so that the experimental parameter varies along one of the dimensions. Various algebraic procedures can be used to determine the number of pure components (equal to the effective rank) of the data matrix and to reduce the random noise content at the same time. Principal component analysis (PCA) yields orthonormal spectral eigenvectors, and the corresponding combination coefficients are determined as dot products between the eigenvectors and the mixture spectra (1). Singular value decomposition (SVD) derives the same orthonormal eigenvectors as well as another orthonormal vector set, which, when multiplied by the singular values, provides the same combination coefficients as does PCA (2).

The condition that fluorescence or absorption spectra have no negative intensities permits their normalization before the analysis, ensuring that the derived spectra of the pure components also are normalized (3). The combination coefficients of the normalized spectra of a rank-two matrix are points along a normalization line, as one coefficient is plotted versus the other. The combination coefficients of the pure spectra are sought on the same line beyond the points corresponding to measured spectra during self-modeling (SM) (3, 4). When three pure forms are present, points defined by the combination coefficients of mixture spectra fall within a triangle on the normalization plane in three-dimensional space. The sides represent two component mixtures, and the vertices represent the pure components, as in a phase diagram (5–11). Once the SM procedure locates the spectra of the pure components, reverse normalization provides their actual amplitude.

We describe an application of SVD-SM (analogous to PCA-SM) to the determination of the spectra of the intermediates in the bacteriorhodopsin photocycle. On light excitation, bacteriorhodopsin (BR), the light-driven proton pump in the cell membrane of Halobacterium salinarium, exhibits a series of spectrally distinct metastable intermediates labeled as J, K, L, M, N, and O before returning to the initial state (BR) (for reviews, see refs. 12, 13). Although transitions between the intermediates appear to be first-order reactions, back reactions and/or parallel pathways result in mixtures rather than pure intermediates at all times during the photocycle. Moreover, the intermediate spectra strongly overlap in the visible spectral range. Hence, decomposing the measured difference spectra into difference (and absolute) spectra of the intermediates, and their time-dependent concentrations (kinetics), is a mathematically underdetermined problem (14, 15). Global model fits are in principle capable of determining the spectra and the kinetics simultaneously, but in practice they are hampered by spurious local minima of the optimization routines in the case of noisy data (15). In addition, errors in the models lead to model-specific erroneous spectra optimally adjusted to fit the assumed kinetics sequence. The goal in this and the following paper (16) is to determine accurate model-independent spectra of the intermediates at the outset, thereby defining their time evolution. Relegation of the selection of the best model for the kinetics to the final step should enhance the understanding of the proton transfer mechanism.

RESULTS

Generation of Simulated Data.

SVD-SM was tested on simulated data resembling the simpler case of the photocycle of the Asp-96 → Asn (D96N) mutant BR with four spectrally distinct intermediates, K, L, M₁, and M₂, in the submicrosecond to 100-millisecond range. The data were generated by modification of the procedure described in ref. 17. A measured visible absorption spectrum of light-adapted BR was shifted on the wavenumber scale to provide spectra at appropriate energies for the K, L, and M₁ intermediates. The amplitudes of the new spectra were changed, and their half widths were modified by convolution with Gaussians to yield spectra consistent with previous information. M₁ was shifted by 6 nm to the blue, and its amplitude was decreased by 5% to generate the M₂ spectrum. The two Ms were originally introduced to fit a kinetic model for the wild-type protein (18) and to account for the slight spectral shift of the maximum of measured difference spectra on D96N BR during the rise of the amount of M (19). Time-dependent concentrations of the intermediates were simulated by integration of the rate equations corresponding to the photocycle scheme K ⇌ L₁ ⇌ L₂ ⇌ M₁ → M₂ → BR plus M₁ → BR. The two L forms were assumed to be spectrally indistinguishable. This scheme is adapted from ref. 20, with the additional branch from M₁ to BR introduced here to account for the new finding of biphasic BR recovery kinetics in the D96N mutant (16). Table 1 shows the rate constants used in the simulation.

Table 1.

Input and recovered rate constants

Reaction	Input k, s−1	Output k, s−1
K → L1	5.00 × 105	5.13 × 105
K ← L1	1.00 × 105	1.00 × 105
L1 → L2	5.00 × 103	5.13 × 103
L1 ← L2	1.00 × 103	1.00 × 103
L2 → M1	1.00 × 107	1.23 × 106*
L2 ← M1	1.00 × 107	1.17 × 106*
M1 → M2	1.00 × 103	1.00 × 103
M2 → BR	2.00 × 100	2.09 × 100
M1 → BR	2.00 × 102	1.48 × 102

Output rate constants were obtained by fitting the SVD-SM-derived output kinetics for the noisy simulated spectra to the input reaction scheme. Rate constants denoted with an asterisk are minimum values. 

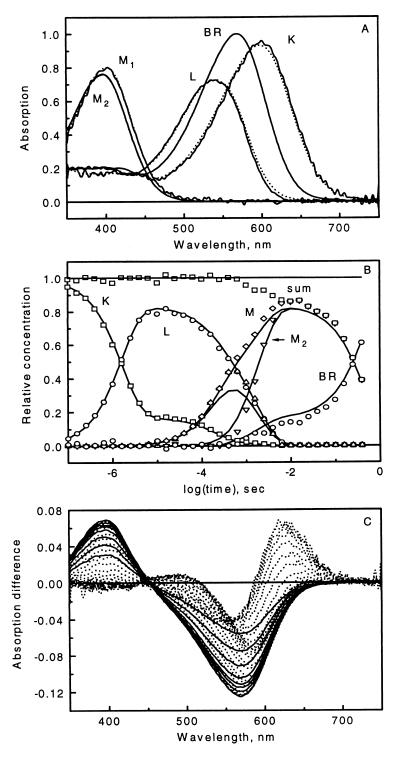
Products of the difference spectra between the pure intermediates and BR and their kinetics, sampled at logarithmically quasiequidistant time points, provided mixture-difference spectra. These were attenuated by a photocycling ratio (PCR) of 0.15, corresponding to excitation of 15% of the sample to create the noise-free data matrix with the difference spectra arranged as column vectors. The individual mixture spectra were further multiplied with factors deviating from 1 by normally distributed random numbers, with mean 0 and variance 0.01, to account for variations of the laser intensity, as in the case of measured data. Finally, normal distribution random noise was added to the data points to yield a simulated noisy data matrix. This spectral noise has increasing amplitudes toward the blue and red ends of the spectrum as well as decreasing amplitudes in five steps with increasing time. The former models lower light intensity at both ends of the experimental spectra, and the latter models the increasingly longer gate pulses (and, therefore, longer light integration times) with increasing delay times of the optical multichannel analyzer instrument (21). Fig. 1 shows the input absorption spectra, the input intermediate kinetics, and the noisy data matrix.

Figure 1.

Input absorption spectra (A, dotted lines) and time evolution (B, solid lines) of the photocycle intermediates used in the simulation. Combination of the input spectra and kinetics, with noise added, yielded the mixture difference spectra (C), with solid lines representing the final decay of the signal. Output intermediate spectra (A, solid lines) and kinetics (B, symbols) were obtained from the analysis of the data in C. In B, “sum” means the total intermediate concentration, and “M” means M₁ + M₂ .

Analysis of Simulated Data: SVD.

SVD of the noise-free data matrix recovers four significant components, with the rest containing fluctuations reflecting rounding errors. SVD of the noisy data matrix provides eigenvectors with nonmonotonously varying autocorrelations beyond the first three. This is the result of the assumed nonuniform noise along both the spectral and time dimensions. The rotation algorithm of Henry and Hofrichter (2) was used to reorder eigenvectors 4–8. A new fourth vector pair was obtained that carries significant signal as revealed by its high autocorrelation. Subsequent eigenvectors contain only random noise. The data matrix was reconstructed with reduced noise by using these first four eigenvectors. SVD treatment of this matrix provided new, orthonormal eigenvectors (the orthonormality was lost during the rotation procedure):

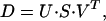1

where D (n × m) is the reconstructed data matrix whose elements, D_ij = D(λ_i,t_j), are the absorption difference values at wavelength λ_i and time t_j after the start of the photocycle. Matrices U (n × 4) and V (m × 4) consist of the orthonormal spectral eigenvectors and the orthonormal kinetics vectors, respectively, and the S (4 × 4) diagonal matrix contains the significant singular values. The product

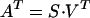2

defines the A (m × 4) matrix, which is equivalent to the combination coefficient matrix in PCA-SM and whose elements were designated previously as α_j, β_j, γ_j, and δ_j (6).

The Stoichiometric Plane.

The elements of the data matrix are products of the difference spectra, Δɛ_k, of the pure intermediates and their time-dependent concentrations, c_k:

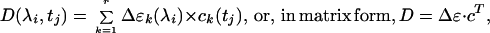3

where r is the number of intermediates, generally greater than or equal to the rank of matrix D. Both the difference spectra and the concentrations on the right-hand side of Eq. 3 are unknown. There exists an unknown transformation T, however, that converts the SVD basis sets to the respective real spectra and kinetics:

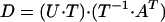4

so that

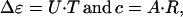5

where R is the transpose of the inverse of matrix T. Up to a certain time in the photocycle, no recovery of the BR initial state takes place, and the sum of the intermediate concentrations is constant, or is unity with proper normalization:

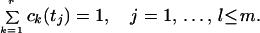6

Eqs. 5 and 6 together yield for the combination coefficients:

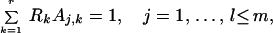7

where R_k = ∑_i=1^r R_k,i are time-independent constants for k = 1, …  , r.

The set of Eq. 7 is analogous to the equation of a plane in three-dimensional space. We therefore designate the r-1 D surface of points that obey Eq. 7 the stoichiometric plane (SP). Before the onset of the recovery of the initial state in the photocycle, each point in this space that corresponds to a mixture difference spectrum must fall on the SP. Accordingly, the combination coefficients belonging to the unknown difference spectra of the pure intermediates also must fall on this plane. The stoichiometric criterion for the pure intermediate spectra introduced by Nagle et al. (22) is a consequence of Eq. 7.

Identification of the SP is based on the combination coefficients contained in matrix A. Because its columns contain increasing amounts of noise, a new transformation is helpful in the accurate determination of the SP, which, by properly mixing the columns of A (and U), provides new combination coefficient vectors with more evenly distributed noise while the new spectral basis vectors obtained from U are still orthonormal:

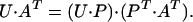8

For a three- and four-component system, respectively, the corresponding P matrices are as follows:

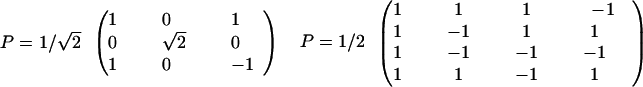9

After this transformation, the first 4, 5, …  , m equations in the Eq. 7 are solved consecutively for R_k in the least squares sense, and, in each case, the standard deviations of the corresponding 4, 5, … , m points from the derived SP are calculated. The parameter l, i.e., the number of spectral points before any recovery of the initial state, is identified as the one before the deviations start to systematically increase. In other words, l corresponds to the number of spectra that gives the minimum standard deviation of the spectral points from the least squares plane defined by these points. Although this approach reveals the early BR recovery for noise-free data, it yields the incorrect result of no BR recovery until the 27th data point, when the entire spectral region of the noisy input data is analyzed. This result is attributable to the small difference between the M spectra. Therefore, the SP was searched for on truncated data matrices in the >540-nm range, where the two M − BR difference spectra are identical and the matrices behave as robust, three-component systems.

Table 2 shows the standard deviation from unity of the left-hand side of Eq. 7, as fitted to the first 11, 12, … , 34 spectral points of the noisy data. An early increase of this deviation is followed by a plateau before the final increase. For the noise-free and the noisy truncated data, the number of data points before the early recovery was estimated as 18 and 20, and the R_k parameters in the equation of the SP (Eq. 7) for l = 18 and l = 20, respectively, were determined. The standard deviation before the early recovery of BR for the noisy data is consistent with the standard deviation from unity introduced in the simulation to model the laser intensity fluctuations.

Table 2.

The stoichiometric plane and BR recovery

No. of spectra	Standard deviation	No. of spectra	Standard deviation
11	0.011186	23	0.018126
12	0.014940	24	0.019683
13	0.014354	25	0.021780
14	0.013981	26	0.023265
15	0.013530	27	0.023681
16	0.013372	28	0.026399
17	0.013183	29	0.030809
18	0.013412	30	0.036071
19	0.013085	31	0.044445
20	0.012974	32	0.061808
21	0.014920	33	0.088526
22	0.017599	34	0.124710

Standard deviation of the stoichiometric plane fits to the combination coefficients of the first 11, 12, …, 34 noisy difference spectra. Bold numbers represent the last point considered to be on the plane and the point where the main phase of BR recovery starts. 

Estimation of the Photocycling Ratio.

The PCR (also considered unknown, as in the case of real experiments) was obtained in a general way without using the pure M₂ − BR difference spectra that are expected in the millisecond time domain in the D96N mutant. In the first method, the PCR was varied until the best SP was found in the least squares sense that fits the first 20 (18 for noise-free data) truncated difference spectra augmented with the PCR-scaled negative of the BR absorption spectrum, in the spectral range 540–750 nm. The latter is equivalent to the pure M − BR difference spectra in this spectral interval and should fall on the SP of the first 20 mixture spectra when scaled by the proper PCR. The second method calculates the dot product between the truncated (−BR) spectrum and the first three spectral eigenvectors (columns of U) from the SVD output of the first 20 truncated difference spectra. The resulting combination coefficients are substituted into Eq. 7 to yield the reciprocal of the PCR. The averages of these values, 14.99% for the noise-free data and 14.43% for the noisy data, were accepted as the true PCR.

The pure M₂ absorption spectrum was obtained from the average of the late SVD reconstructed difference spectra of the full data matrix by using the criterion that adding a properly scaled BR absorption spectrum to the difference spectra contributed by M₂ alone should give uniform baseline for wavelengths >540 nm. Normalization by the scaling factor provides the M₂ absorption spectrum with the proper amplitude.

SM.

SM, as tailored here for the BR problem, is the technique of searching for the pure intermediate spectra on the SP by using geometric criteria as well as criteria regarding the relative displacement on the wavelength axis of the pure intermediate spectra. First, a truncated matrix consisting of difference spectra 1–20, augmented with the negative of the BR spectrum times the PCR, was created for the 540- to 750-nm spectral region. The last column of this matrix represents the pure M₁ − BR difference spectrum, and the remaining 20 represent varying mixtures of the K − BR, L − BR, and M₁ − BR spectra. SVD on this matrix for both the noise-free and the noisy data returned a rank of 3, as expected. The parameters for the SP follow from Eq. 7.

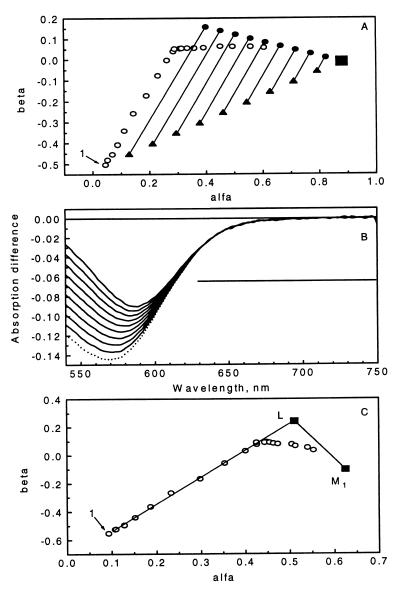
Fig. 2A shows the plot of the second combination coefficient versus the first one (the third coefficient is automatically determined by the equation of the SP). Early points show a progression from K toward L, mostly; then, a turn represents the onset of the accumulation of M. The LM side of the triangle corresponding to pure L + M₁ mixtures was located first. The line connecting the first and the last (pure M₁) points was divided to yield nine equidistant starting points on the SP, and a direction was determined that roughly corresponds to the tangent of the trajectory of the early spectral points (a good approximation of the KL line). This direction represents decreasing amounts of K and increasing amounts of L anywhere within the KLM triangle. Moving in this direction along the parallel lines in Fig. 2A should lead to points on the LM line. The search for these points was based on the expectation that there is a spectral region in which both M and L absorptions (and any combination thereof) are negligible and only K (and, potentially, BR) absorbs. This region was varied from 610–730 to 690–730 nm, and the standard deviation of the calculated spectra minus the negative of the BR absorption spectrum times the PCR was determined. The smallest standard deviation along each search line defines potential L + M mixtures, and the smallest overall standard deviation was initially monitored to determine the appropriate tail region for L. This parameter leveled off beyond a certain wavelength for both the noise-free and the noisy data. Selection of the final region in which the L spectrum does not contribute was optimized as follows: For each region, the calculation described below was completed, and the resulting trial K, L, M₁, and M₂ spectra were used to fit the data matrix in the least squares sense, with the restriction of nonnegative intermediate concentrations. The best overall fit identifies the region in which only K and BR contribute and, consequently, the final LM line. This line, along with the nine points that determine it, is shown in Fig. 2A. Fig. 2B shows the corresponding nine difference spectra as well as the M₁ − BR spectrum.

Figure 2.

Demonstration of self-modeling on noisy simulated data. (A) α-β projection of the stoichiometric plane fitted in the 540- to 750-nm region of the first 20 difference spectra augmented with the photocycling ratio times the negative of the BR spectrum. Open circles, input spectra, the first one marked as 1; solid triangles, initial nine points in the LM line search along the parallel lines; full circles, the nine points found on the LM line; solid square, pure M₁ − BR. (B) Difference spectra corresponding to the nine points on the LM line (solid lines) and the pure M₁ − BR difference spectrum (dotted line) in the 540- to 750-nm range. The horizontal bar represents the estimated interval where the L absorption is zero (630–750 nm). (C) α-β projection of the stoichiometric plane fitted to the first 20 difference spectra (full wavelength scale) augmented with the pure M₁ − BR spectrum. Open circles, input spectra, the first one marked as 1; solid squares, pure M₁ − BR and L − BR vertices. The LM and KL lines also are shown.

These truncated spectra were fitted with the spectral eigenvectors obtained from the SVD treatment of the first 20 columns of the original, full data matrix. Only the appropriate region (540–750 nm) of the full length (351–750 nm) SVD spectral eigenvectors was used in the least squares fit. The resulting combination coefficients multiplied by the SVD spectral eigenvectors (full length) yield the nine difference spectra defining the LM line as well as the pure M₁ − BR difference spectrum, now over the full spectral interval.

Linear regression of the nine combination coefficient triplets with the M vertex fixed provided the parameters of the LM line. The pure L − BR spectral point was sought by moving along this line away from the M vertex. The constraint used to define the L − BR point for the noisy data is the expectation that a spectral region (351–410 nm) exists where the L intermediate has approximately the same extinction as BR. The simulated input spectra were constructed in this way, based on low-temperature and room-temperature spectra determined earlier for L (23, 24). Thus, the vertex corresponding to the pure L − BR difference spectrum was identified as the point along the LM line that results in a difference spectrum whose average over the 351- to 410-nm interval is zero.

The criterion used to locate the LM line is not applicable in the search for the KL line because all mixtures of K and L have nonzero absorption throughout the entire spectral range. However, this line must contain the L vertex, and, because no contribution from M is expected at the earliest times, it must include the first (several) spectral points. Fig. 2C shows the first two combination coefficients of the first 20 data points (noisy matrix, full wavelength), the location of the pure M₁ − BR and L − BR vertices, the LM line, and the KL line, the latter determined by connecting the L vertex with the average of the first 3 spectral points. In fact, were it not for the noise, the first several spectral points alone could be used to locate the KL line. Then, the L vertex could be found at the intersection of the KL and LM lines, or, more generally, as an extrapolated intersection to time zero even if a little M already contributes to the earliest spectral points. Although this method worked for noise-free data, in the noisy case the intersecting points scatter too much (i.e., no clear progression is obtained with time), so the above method based on the L absorption in the blue region was preferred.

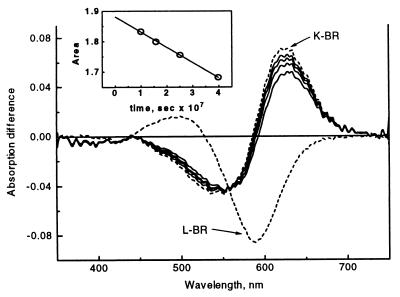
The pure K spectral point is determined by extrapolation of the early spectra to time zero. This was accomplished in two steps. First, the integral of the initial four difference spectra of the data matrix in the 600- to 750-nm interval minus that of the pure L − BR spectrum yields areas proportional to the concentration of K. Extrapolation to the parameter value of K at time zero is achieved by assuming single exponential decay (see Fig. 3 Inset). In the second step, the K vertex is found by moving along the KL line beyond the first spectral point until the corresponding integral parameter reaches the extrapolated value. The first four difference spectra, the L − BR spectrum, and the extrapolated K − BR spectrum are plotted in Fig. 3.

Figure 3.

The first four mixture difference spectra (solid line), the pure L − BR spectrum (dashed), and the extrapolated pure K − BR spectrum (dashed line). (Inset) The extrapolation to time zero of the logarithm of the integral parameter used to locate the K spectral point.

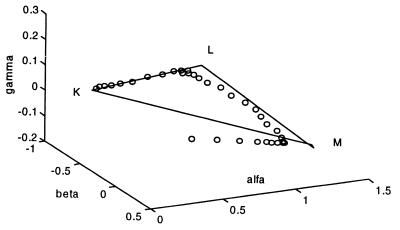
A final SVD treatment of the entire data matrix augmented by the pure K − BR, L − BR, M₁ − BR, and M₂ − BR difference spectra was followed by determining the final “SP” in the four-dimensional space of this rank-4 matrix. This surface was calculated from the combination coefficients of the four pure intermediates by simple matrix inversion rather than by least squares fit. Fig. 4 shows the α, β, γ plot of the combination coefficients of all 34 spectra from the noisy data matrix as well as that of the pure intermediate difference spectra, defining a tetrahedron in three-dimensional space. The origin corresponds to BR, and the adherence of the first 20 points to the “SP” as well as the subsequent deviation from it as BR recovers is demonstrated in this three-dimensional projection of the four-dimensional space.

Figure 4.

α, β, γ plot of the combination coefficients of the entire noisy data matrix (open symbols) plus the pure K − BR, L − BR, M₁ − BR, and M₂ − BR spectra as vertices of the stoichiometric tetrahedron. The adherence of the data points to the stoichiometric surface is demonstrated. The M₁ and M₂ points are very close to each other because of their spectral similarity.

Comparison of the Input and Output Spectra and Kinetics.

The pure absorption spectra of the intermediates are obtained by addition of the BR spectrum, scaled by the PCR, to the pure difference spectra corresponding to the vertices of the tetrahedron in Fig. 4. The recovered spectra for the noisy simulated data set are shown in Fig. 1A. The time evolution of the intermediates follows directly from the location of the spectral points within the tetrahedron in Fig. 4. It also can be computed by linear least squares fitting of the mixture spectra by the pure intermediate spectra, with the non-negativity constraint for the concentrations. The output kinetics for the noisy simulated data set are shown in Fig. 1B. The output pure spectra and kinetics obtained with the above procedure by using noise-free input spectra are visually indistinguishable from the pure spectra and kinetics used in the simulation (data not shown). The RMS noise content of the input difference spectra varies between 4.0 × 10⁻³ and 2.9 × 10⁻⁴ (higher noise in the earlier spectra). The RMS deviations between the noise-free input spectra and the output noisy spectra of the intermediates (all scaled by PCR) are 2.5 × 10⁻³, 2.1 × 10⁻³, 1.4 × 10⁻³, and 2.0 × 10⁻⁴ for K, L, M₁, and M₂, respectively.

The output kinetics from the noisy data were fitted to the same reaction scheme used to generate the input data. The rate constants are listed in Table 1. The error of the fit is low, and all but the M₁ → BR rate constant agree very well with the input rates. With the noise-free data, all recovered rate constants are essentially identical to those used in the simulation (data not shown). SVD-SM on a noisy data matrix generated similarly to the one discussed, but without the M₁ → BR step, resulted in the correct spectra and kinetics lacking the early BR recovery (data not shown).

DISCUSSION

Multichannel and single wavelength kinetic absorption measurements have been published in numerous articles on bacteriorhodopsin (14, 17–21, 24–29). Various strategies have been applied to obtain the ultimate information, the time dependence of the photocycle intermediates, which is essential to the elucidation of the mechanism and energetics of light energy conversion by this protein. Global model fitting on such data has generally returned ambiguous results, with spectra of the intermediates possessing unusual properties, such as more than one absorption band, incorrect baselines, etc. (25, 26).

L.Z. and J.K.L. have pursued the strategy of a model-independent determination of the pure intermediate spectra first, followed by calculation of the intermediate concentrations in the second step. The original trial-and-error method (27, 28) was improved by a grid search algorithm (17) and more recently by a Monte Carlo-based procedure to obtain the spectra (24). Pure intermediate spectra were found approximately by narrowing the limits imposed on various spectral parameters: for instance, the height, the width, and the negative value tolerance. Factor analysis (analogous to PCA) combined with similar spectral criteria applied simultaneously on visible and Fourier transform IR spectra was used by others to dissect the photocycle (29).

SVD was applied to chromoprotein spectra to estimate the number of spectrally independent components, to eliminate random noise, and to store spectral information in a compressed form (17, 30, 31). The kinetics vectors of the SVD output were fitted by sums of exponentials, yielding phenomenological rates and amplitudes. Such information can be used to obtain microscopic rate constants by the fitting of photocycle models. SVD alone tends to underestimate the number of components from noisy data, which is usually more accurately determined by the multiexponential fit, if the pure component spectra are not clearly distinguishable (or are not linearly independent) (32). However, the advantage of SVD is utilized here and in the following paper (16), where SVD is combined with the application of self-modeling: i.e., the search for the pure intermediate spectra in the SVD eigenvector space. Most of the assumed, empirical spectral criteria that were essential in earlier methods are rendered unnecessary by SVD-SM, which takes advantage of the stoichiometric behavior of the photocycle.

D.F.S. and J.S. have applied PCA with self-modeling in photochemistry in resolving absorption and fluorescence spectra of mixtures of unknown composition (4, 6–11). The original SM procedure (33) used no other constraint regarding the location of the pure forms on the combination coefficient normalization planes (lines) than the inner limits defined by the most extreme measured spectral points and the outer limits required by non-negative absorption. This procedure often results in a wide range of acceptable pure component spectra. Unique solutions can be obtained by applying additional constraints dictated by the known chemistry of each system. The introduction of the global Stern-Volmer constant optimization constraints for fluorescence spectra (9) is an illustration.

Adaptation of the procedure to BR requires several modifications. Normalization of spectra is abandoned because the input data are difference rather than absolute spectra. The stoichiometric condition is used instead. The advantage of relying on stoichiometric relationships is that they reveal as part of the analysis the time of the onset of BR recovery and the photocycling ratio. Self-modeling, performed on the stoichiometric plane, readily yields the LM side of the KLM triangle because only K contributes at the red edge of the spectra. The location of M on this line is based on its lack of absorption over most of the visible wavelength range. Because in the blue region of the visible spectrum there is no wavelength range in which any intermediate has zero absorption, two additional criteria are introduced outside the usual framework of SM to locate the remaining pure intermediate spectra: The absorption of intermediate L is considered the same as that of BR in the blue region (this constraint is not needed for the analysis of noise-free simulated spectra), and the spectrum of K is estimated by extrapolation to time zero. A single time-dependent exponential function is used in the extrapolation as the most reasonable choice.

Analysis of noise-free simulated data returns the input spectra almost exactly. Closer examination reveals a slight shift of the output M₁ spectrum toward M₂ and a minor discrepancy between the tails of the input and output L spectra (data not shown). Both are caused by imposing the three-component approximation to the first 18 mixture spectra. Although the stoichiometric condition holds up to the 18th spectrum, there is a small amount of M₂ present after the 15th spectrum. SVD of the noise-free input matrix reveals this, but, with the noisy matrix, the presence of trace M₂ is concealed. When SVD-SM analysis is performed on the noise-free matrix with only the first 15 mixture spectra included, the slight spectral discrepancies disappear. The same procedure does not succeed with the noisy data matrix because the level of noise and the small accumulation of M prevent the location of the proper SP when only 15 spectra are considered.

The small spectral discrepancies cause more visible deviations between input and output kinetics, the latter computed by non-negative least squares fitting the input mixture spectra with the output pure spectra. However, despite the noise level introduced here, the fit of the same reaction scheme to the output kinetics as the input photocycle model gives very good agreement, and with only minor differences in the rate constants. Only the M₁ → BR rate deviates by ≈25%, mostly because of the 3% underestimation of the PCR in the case of the noisy data.

The overall agreement of the input simulated spectra and kinetics with those recovered by SVD-SM shows that this approach, while avoiding the imposition of subjective spectral constraints, significantly narrows the range of potential solution spectra relative to earlier approaches based on the grid search and on the Monte-Carlo method. In the accompanying paper, we demonstrate that SVD-SM leads to more accurate intermediate spectra and kinetics in cases of real experimental data as well.

ABBREVIATIONS

BR

bacteriorhodopsin

PCA

principal component analysis

PCR

photocycling ratio

SM

self-modeling

SP

stoichiometric plane

SVD

singular value decomposition