Bacteriophage-mediated competition in Bordetella bacteria

Abstract

Apparent competition between species is believed to be one of the principal driving forces that structure ecological communities, although the precise mechanisms have yet to be characterized. Here we develop a model system that isolates phage-mediated interactions by neutralizing resource competition with a large excess of nutrients, and consists of two genetically identical Bordetella strains that differ only in that one is the carrier of phage and the other is susceptible to the phage. We observe and quantify the competitive advantage of the bacterial strain bearing the prophage in both invading and in resisting invasion by the bacterial strain sensitive to the phage, and use our experimental measurements to develop a mathematical model of phage-mediated competition. The model predicts, and experimental evidence confirms, that the competitive advantage conferred by the lysogenic phage depends only on the phage pathology on the sensitive bacterial strain and is independent of other phage and host parameters, such as the infection-causing contact rate, the spontaneous and infection-induced lysis rates and the phage burst size. This work combines experimental and mathematical approaches to the study of phage-driven competition, and provides an experimentally tested framework for evaluation of the effects of pathogens/parasites on interspecific competition.

1. Introduction

Pathogens usually damage their host organisms and reduce their fitness, and thus a host carrying a pathogen is generally regarded as less competitive relative to its natural opponents (Anderson & May 1991; Dickmann et al. 2002). An exception is found in the phenomenon of apparent competition where a host harbouring and transmitting a pathogen can be a superior rival to a more vulnerable host (Park 1948; Bonsall & Hassell 1997; Hudson & Greenman 1998; Thomas et al. 2005). Apparent competition, together with direct resource competition, is generally accepted as a major force in the formation of ecological community structure.

There are a few excellent illustrative examples of apparent competition from the laboratory and field studies of ecological assemblage (Park 1948; Bonsall & Hassell 1997; Hudson & Greenman 1998; Thomas et al. 2005) and even from the history of human diseases (Simpson 1980). However, due to the complexities originating from dynamical interactions among multiple hosts and multiple pathogens, it is not always easy to single out and quantitatively measure the effect of pathogen-mediated competition in nature. In a system of bacteria and bacteriophage, it is relatively easy to manipulate both host resistance mechanisms and pathogen virulence, and thus this is one of the most suitable systems for the exploration of pathogen-mediated competition. In recent studies (Bohannan & Lenski 2000a,b), chemostat communities of Escherichia coli bacteria and lytic bacteriophage have been used as model systems for phage-mediated competition. However, in these studies, resource- and lytic phage-mediated competition was strongly intertwined and the role of lysogenic phage on apparent competition was not addressed. As lysogenic phage can turn sensitive bacteria into resistant phage carriers, the dynamics and stationary outcome of lysogenic phage-mediated competition can be remarkably different from that of lytic phage-mediated competition.

Here we establish an infection system with bacteria and lysogenic bacteriophage, in which resource competition is neutralized by using a large nutrient excess, and examine competition between bacterial strains that differ only in their sensitivity to the phage. Particularly, we use Bordetella bronchiseptica (Bb), a causative bacterium of mammalian respiratory disease, and its natural virus (BPP-1), a temperate phage that can either incorporate its DNA into the genome of Bb (lysogeny) or replicate itself and lyse the host bacterium (lysis). We demonstrate and quantify, both experimentally and theoretically, the existence of a competitive advantage conferred by this virus in a bacterial population. We observe that the bacterial strain bearing the prophage has an advantage in both invading and resisting invasion by bacteria sensitive to the phage and that the steady-state outcome of lysogenic phage-mediated competition depends solely on the pathology of the lysogenic phage on the sensitive bacterial strain, and is independent of the values of the kinetic parameters of the system. The theoretical representation of these interactions should have broad application to pathogen-mediated competition at many levels.

2. Material and methods

(a) Culture techniques and competition experiments

Bordetella bronchiseptica strains (BbGm, Bb$\mathrm{\Delta }prn$Gm, Bb::Φ and BbGm::Φ) were derived from the same wild-type parental B. bronchiseptica strain RB50 (Bb) (see table 1). All strains were grown on Bordet–Gengou (BG) agar plate, and incubated for 3 days at 37 °C. Then two to three colonies of each strain were inoculated in 4 ml of Stainer Sholte media with supplements, and grown at 37 °C overnight to mid log phase. For competition experiments, two B. bronchiseptica strains were subcultured together in 10 ml of Stainer Sholte media at the appropriate concentrations. The co-culture was incubated at 37 °C with continuous agitation. To determine the concentration of a bacterial strain in the culture at various time points, 100 μl of the culture was taken out, serially diluted in PBS, and spread on three plain BG agar plates and on three other BG plates treated with gentamicin. The average and the standard deviation of concentration of each bacterial strain were calculated from the number of colony forming units (CFU) on three plates from a single experiment; figure 3a,b presents results on nine plates from three replicate experiments. The phage-sensitivity of host bacteria and the lack of host diversity mechanisms of ΦΔorf5 were tested at various time points during the competition experiments as described previously (Liu et al. 2004).

Table 1.

Notations and characteristics for the bacterial and phage strains used in this study.

notations	characteristics	references
Bb	wild-type B. bronchiseptica bacterial strain	Cotter & Miller (1994)
BbGm	Bb with a gentamicin antibiotic marker	Liu et al. (2004)
Bb::Φ	Bb containing a prophage (lysogen), which is resistant to Φ and ΦΔcI infection	Liu et al. (2004)
BbGm::Φ	Bb with a gentamicin antibiotic marker and containing a prophage, which is resistant to Φ and ΦΔcI	Liu et al. (2004)
BbΔprnGm	mutant Bb with an in-frame deletion in the gene encoding pertactin, which is resistant to ΦΔorf5 infection	Liu et al. (2004)
BPP-1 Φ	lysogenic phage	Liu et al. (2004)
ΦΔcI	mutant phage with an in-frame deletion of the cI repressor required for lysogeny (lytic phage), which lyses BbGm, but cannot infect Bb::Φ and BbGm::Φ	Liu et al. (2004)
ΦΔorf5	mutant phage with an in-frame deletion of the orf5 gene encoding the reverse transcriptase necessary for the tropism switching mechanism, which is unable to infect BbΔprnGm	Liu et al. (2004)

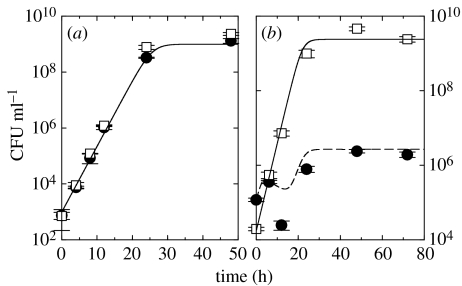
Figure 3.

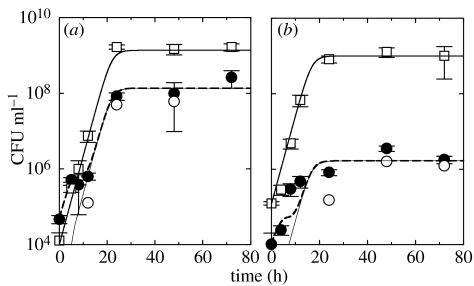
In vitro experiments (symbols) and numerical simulations (lines) of (a) the invasion of the strain (Bb::Φ) exogenously and endogenously carrying the lysogenic phage to the susceptible strain (BbGm) and (b) the protection of Bb::Φ against the invading BbGm. Symbols and lines represent Bb::Φ (open squares, thick solid line), BbGm::Φ (open circles, thin solid line) and the total BbGm (filled circles, long-dashed line), respectively. BbGm::Φ are newly resistant bacteria which initially belonged to the sensitive strain, yet later became resistant by incorporating the prophage into their genome. See the text for the parameter values used for simulations. The error bars denote the standard deviation of the number of colony forming units (CFU) of each bacterial strain.

(b) Theoretical model

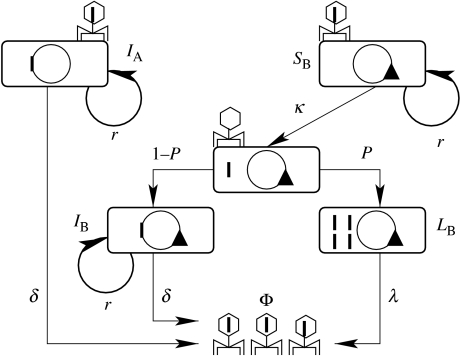
We constructed a theoretical model of lysogenic phage-mediated competition based on susceptible-infectious models describing the impact of directly transmitted pathogens on the dynamics of multiple hosts (Holt & Pickering 1985; Begon et al. 1992; Holt & Lawton 1994; Bowers & Turner 1997; Greenman & Hudson 1997). We consider the dynamically interacting system of five subpopulations: (i) bacterial strain A (Bb::Φ) which bears the prophage, bacterial strain B (BbGm) which can be in one of (ii) susceptible, (iii) latent, or (iv) lysogenic states and lastly (v) the bacteriophage (Φ). The interactions between subpopulations are diagrammatically represented in figure 1. All bacterial strains divide with a constant rate a and bacterial populations grow with a density-dependent rate r. Susceptible bacteria (BbGm) become infected with the phage at an infection-causing contact rate κ. Upon infection the lysogenic phage can take either lytic pathway or lysogenic pathway (Ptashne 1992). In a fraction P of infected BbGm, i.e. in latent bacteria, the phage replicate and then lyse the host bacteria after an incubation period 1/λ, during which the latent bacteria do not divide (Ptashne 1992). Alternatively, the phage lysogenize a fraction 1−P of their hosts, by incorporating their genome into the DNA of the host. Thus, the concentration of newly lysogenic bacteria (BbGm::Φ) provides a measure of the density of the phage taking the lysogenic pathway. The parameter P characterizes the pathogenicity of the phage on the sensitive bacterial strain. The lysogens (Bb::Φ and BbGm::Φ) are spontaneously lysed at a rate δ, thus they grow with a net growth rate r−δ. Lysogens replicate prophage as a part of the host chromosome, and are Φ-resistant.

Figure 1.

Schematic of phage-mediated competition between two bacterial strains. The phage (Φ) is represented by a hexagon carrying a small thick line (Φ DNA). Bacteria are represented by a rectangle containing an inner circle (bacterial DNA), while the lysogens (Bb::Φ and BbGm::Φ) are represented by rectangles containing Φ DNA integrated into bacterial DNA. Gm indicates gentamicin resistance marker. All bacterial populations grow with identical growth rate r; lysogens are spontaneously lysed with a rate δ and have a net growth rate of r−δ. κ is the infection-causing contact rate, λ is the infection-induced lysis rate and P the pathogenicity of the phage.

We assume homogeneous mixing among all subpopulations, justified by vigorous stirring of the culture growth tube on an agitator. The time-evolution of each subpopulation is determined by the rates of incoming and outgoing flow in subpopulations, quantified by the rates given in figure 1, and follows

$$\begin{array}{l}\frac{\text{d}{I}_{\text{A}}(t)}{\text{d}t}=(r(t)-\delta )I_{\text{A}}(t),\hfill \\ \frac{\text{d}{S}_{\text{B}}(t)}{\text{d}t}=(r(t)-\kappa \Phi (t))S_{\text{B}}(t),\hfill \\ \frac{\text{d}{L}_{\text{B}}(t)}{\text{d}t}=P\kappa \Phi (t)S_{\text{B}}(t)-\lambda L_{\text{B}}(t),\hfill \\ \frac{\text{d}{I}_{\text{B}}(t)}{\text{d}t}=(1-P)\kappa \Phi (t)S_{\text{B}}(t)+(r(t)-\delta )I_{\text{B}}(t),\hfill \\ \frac{\text{d}\Phi (t)}{\text{d}t}=\chi (\delta (I_{\text{A}}(t)+I_{\text{B}}(t))+\lambda L_{\text{B}}(t))-\kappa \Phi (t)S_{\text{B}}(t),\hfill \end{array}\}$$ 2.1

where I(t), L(t) and S(t) are the concentrations of the infected, latent and susceptible bacteria at time t, $N(t)=I_{\text{A}}(t)+I_{\text{B}}(t)+S_{\text{B}}(t)+L_{\text{B}}(t),r(t)=a(1-N(t)/N_{\text{max}})$ is the density-dependent growth rate of bacteria and $N_{\text{max}}$ is the maximum concentration of bacteria supported by the nutrient broth environment.

3. Results

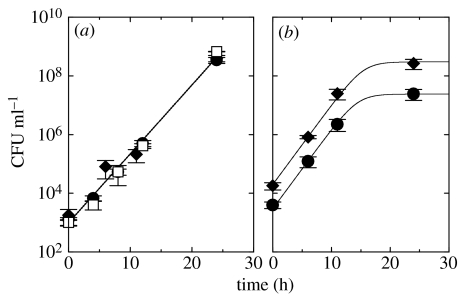
The quantitative assessment of pathogen-conferred competitive advantage is usually hampered by the existence of direct competition over resources (Park 1948; Bonsall & Hassell 1997; Hudson & Greenman 1998; Thomas et al. 2005). To address this concern, we use a large excess of nutrients to neutralize resource competition. To examine the possibility of nutrient-dependent competition, we observed the in vitro growth rates of three bacterial strains: Bb, BbGm and Bb::Φ. When grown separately, all three strains grew exponentially in nutrient-rich medium over a range of cell densities from less than 1000 to over 10⁹ CFU ml⁻¹ (see figure 2). This indicates that there is little evidence of direct resource competition for the first 24 h. Note that the net growth rate of the lysogens (Bb::Φ) is the difference between their division rate and their spontaneous lysis rate, and the latter is about 10³ times smaller than the former. When co-cultured, Bb and BbGm grew at the same rate within statistical errors, indicating that the Gm resistance marker does not affect the growth rate of the host bacteria.

Figure 2.

The in vitro growth curves of B. bronchiseptica strains. (a) The three B. bronchiseptica strains, Bb::Φ (open squares), BbGm (filled circles) and Bb (filled diamonds), grow exponentially when grown separately. The straight line corresponds to a doubling time of 77 min. (b) Bb and BbGm grow at the same rate when co-cultured. We fit the growth curves of the two bacterial strains by using the theoretical model of equation (2.1) in the absence of lysogens and phage. The error bars denote the standard deviation of the number of colony forming units (CFU) of each bacterial strain.

We then examined competition between the sensitive bacterial strain (BbGm) and the resistant strain (Bb::Φ) mediated by the lysogenic bacteriophage Φ. The interactions involved in this competition experiment are represented in figure 1 and described in detail in §2. We directly measured the values of five parameters, a, δ, λ, χ and $N_{\text{max}}$, and estimated the others; the relevant ranges of all parameters are given in table 2. Upon infecting the sensitive bacteria, the lysogenic phage take either a lysogenic pathway with a probability 1−P or a lytic pathway with a probability P. Here, the parameter P characterizes the phage pathology, incorporating multiple aspects of phage–host interactions resulting in damage to host fitness. Both the number of phage produced (burst size χ) and the phage pathology P may depend on the culture conditions (Ptashne 1992).

Table 2.

Parameters used for the numerical simulation of the phage-mediated competition in B. bronchiseptica. (a is determined from the measured doubling time of Bb bacteria in mid-log phase in figure 1. δ is measured from a competition experiment mediated with spontaneously induced lysogenic phage (see figure 1 of the electronic supplementary material). λ is determined from the observed phage incubation period (6–12 h). χ is measured from the difference in the phage concentrations between 0 and 12 h of Φ and Bb co-culture. The two undetermined parameters P and κ are estimated by comparing the experimental results with those of the theoretical model and by minimizing discrepancies.)

parameter	name	range	resources
a	(free) growth rate	0.54	measured
δ	spontaneous lysis rate	0≤δ≪a	measured
λ	Φ-induced lysis rate	0.08–0.17	measured
χ	burst size	10–50	measured
P	phage pathology	0≤P≤1	estimated
κ	contact rate	κ>0	estimated
Nmax	holding capacity	∼109	measured

To experimentally observe phage-mediated competition between two strains, Bb::Φ and BbGm were co-cultured in vitro. Since spontaneous induction of the phage from Bb::Φ is inevitable, yet can take place at different time points (see the electronic supplementary material), we added exogenous phage to induce phage-mediated competition at an earlier time, while bacteria are in the log growth phase. One thousand CFU per ml of Bb::Φ and approximately 10³ plaque forming units (PFU) ml⁻¹ of lysogenic phage were added to a culture containing 10⁴ CFU ml⁻¹ of BbGm. As shown in figure 3a, the population of the strain with the Gm marker increased with the same initial growth rate as Bb::Φ, but suddenly dropped at about 8–12 h post-infection. After 24 h, the initial 1 : 10 ratio of the concentration of Bb::Φ to that of the Gm-marked strain was reversed to approximately 10 : 1, indicating a 100-fold relative increase in the proportion of Bb::Φ. To observe the advantage of the lysogens in resisting invasion by the strain susceptible to the phage, 10³ CFU ml⁻¹ of BbGm was added to a culture containing 10⁴ CFU ml⁻¹ of Bb::Φ and approximately 10⁴ PFU ml⁻¹ of lysogenic phage in figure 3b. The initial 10 : 1 ratio of Bb::Φ to the strain with the Gm marker was amplified to approximately 1000 : 1, indicating again a 100-fold increase in the proportion of Bb::Φ to the Gm-marked strain. In figure 3a,b, the concentration of newly resistant bacteria (BbGm::Φ), which the sensitive bacterial strain (BbGm) has turned into, provides a measure of the density of the phage taking the lysogenic pathway. At later times there are only resistant bacteria (Bb::Φ and BbGm::Φ) growing exponentially at a net growth rate equal to their doubling rate minus their spontaneous lysis rate.

To simulate the competition experiments, we chose a set of parameters within the range provided in table 2: spontaneous lysis rate $\delta =5.4\times {10}^{-4}$ h⁻¹ per bacterium, infection induced lysis rate $\lambda =0.081$ h⁻¹, phage burst size χ=15, contact rate $\kappa =1.08\times {10}^{-5}$ ml h⁻¹ per CFU, phage pathology P=0.98. The agreement between numerical and experimental results in figure 3 validates our choice of theoretical model and kinetic parameters. Minor discrepancies between experiments and simulations are noticeable in the concentrations of the bacterial strain with the Gm marker, especially BbGm::Φ. These are likely due to our assumption of homogeneous mixing of phage particles and bacterial hosts.

Using the theoretical model, we find that the final ratio of the two bacterial concentrations depends only on the phage pathology P and on the ratio of their initial concentrations, regardless of the values of the kinetic parameters κ, δ, χ and λ:

$$r_{\text{AB}}(\infty )\simeq \frac{r_{\text{AB}}(0)}{1-P},$$ 3.1

where A≡Bb::Φ, B≡BbGm, $0\le P<1$, $r_{\text{AB}}(t)=N_{\text{A}}(t)/N_{\text{B}}(t)$ and N_A[N_B] is the total concentration of bacterial strain A[B] and $N_{\text{A}}(\infty )+N_{\text{B}}(\infty )=N_{\text{max}}$. In the electronic supplementary material, we provide the derivation of equation (3.1) in the limit of a fast infection process ($\kappa S_{\text{B}}(0)\gg a$ and $\lambda \gg a$), i.e. when susceptible bacteria are rapidly infected by phage particles and lysed immediately after infection. Using extensive numerical simulations, we also verified the validity of equation (3.1) in a much broader parameter range, including a slow infection process. The invasion criterion, defined as the condition of the invading strain A becoming dominant in number over the strain B, is provided as $r_{\text{AB}}(\infty )>1$ or $r_{\text{AB}}(0)>1-P$, and thus depends only on the phage pathology on the sensitive bacterial strain.

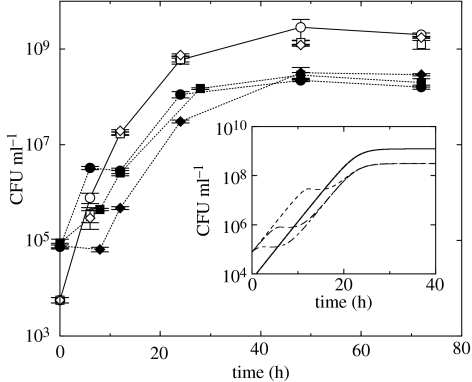
The above analysis predicts that neither different initial phage concentrations nor different contact rates affect the steady-state outcome of the lysogenic phage-mediated competition, while either can modify the transient dynamic behaviour of the two bacterial strains (see the inset of figure 4). To validate this prediction, we performed the same competition experiments as in figure 3 with three different initial concentrations of the lysogenic phage. As shown in figure 4, higher initial phage concentration results in a larger drop of the Gm-marked population size between 0 and 12 h. However, regardless of initial phage concentration, the stationary concentrations of Bb::Φ and the Gm-marked bacterial strain converge to the same values, within statistical errors, after 48 h. This verifies the independence of the steady-state outcome of the lysogenic phage-mediated competition on the initial phage concentration, i.e. the validity of the invasion criterion in equation (3.1). This also provides justification for the addition of exogenous phage to the system for the competition experiments in figure 3a,b.

Figure 4.

Independence of the steady-state outcome of phage-mediated competition on the initial phage concentration. Main: in vitro competition experiments of Bb::Φ (open symbols connected by a solid line) and the Gm-marked strain (filled symbols, dotted lines) with exogenously added phage concentrations of 10 (filled circles), 10⁴ (filled squares) and 10⁵ (filled diamonds) PFU ml⁻¹. Inset: numerical simulations of the competition of Bb::Φ (solid line) and the total BbGm with three different initial phage concentrations of 10¹ (long-dashed line), 10⁴ (dashed line) and 10⁵ (dot-dashed line) PFU ml⁻¹. We used the same parameter values as in figure 3a. The error bars denote the standard deviation of the number of colony forming units (CFU) of each bacterial strain.

The success of our theoretical model in capturing the dynamic behaviour of the bacteria–phage system in various scenarios enables us to use it to explore cases that are not addressed by experiments. We investigated theoretically the steady-state outcome of the lysogenic phage-mediated competition when the two bacterial strains differ in their susceptibility (κ) to the phage and in their resulting pathology (P). In this case, the final ratio of the concentrations of two strains is given as

$$r_{\text{AB}}(\infty )\simeq r_{\text{AB}}(0)\frac{(1-P_{\text{A}})}{(1-P_{\text{B}})},$$ 3.2

where P_A[P_B] is the phage pathology on strain A[B]. The final ratio of two strains depends only on the phage pathologies and on the initial ratio of two strains, independently of the values of the kinetic parameters κ, δ, χ and λ. In the electronic supplementary material, we verify the validity of equation (3.2) both analytically and numerically.

Next we investigated one of possible bacterial resistance mechanisms against the pathogenicity of the phage. A simple mutation can take place in the receptor complex of the host bacteria that renders the mutant bacterial strain (BbΔprnGm) no longer susceptible to mutant phage (ΦΔorf5) lacking the tropism switching mechanism. We co-cultured 10³ CFU ml⁻¹ of BbΔprnGm with 10³ CFU ml⁻¹ of Bb::ΦΔorf5 containing the prophage ΦΔorf5 and approximately 10³ PFU ml⁻¹ of ΦΔorf5. As shown in figure 5a, both strains grow without any sign of phage-mediated competition and maintain the initial ratio of the two bacterial concentrations for more than 24 h. This indicates that there is no phage-mediated competition when the phage are not infectious to either of the two bacterial strains.

Figure 5.

Dependence of phage-mediated competition on the phage pathology P is observed in in vitro experiments (symbols) and numerical simulations (lines). Presented are time-evolutions of (a) the co-cultured BbΔprnGm (filled circles, solid line) and Bb::ΦΔorf5 (open squares, dashed line) in the presence of exogenously added mutant phage (ΦΔorf5) and (b) the co-cultured Bb::Φ (open squares, solid line) and the Gm-marked strain (filled circles, dashed line) in the presence of exogenously added lytic phage (ΦΔcI). The parameters used for the numerical simulations are the same as in figure 3a, except κ=0 (and thus P=0) in figure 5a, and P=1 for lytic phage and P=0.98 for lysogenic phage in figure 5b. The error bars denote the standard deviation of the number of the colony forming units (CFU) of each bacterial strain.

Finally, we experimentally investigated the effect of the phage pathology on the amount of the phage-mediated competition by co-culturing 10⁵ CFU ml⁻¹ of BbGm with 2×10⁴ CFU ml⁻¹ of Bb::Φ and approximately 10⁴ PFU ml⁻¹ of lytic phage (ΦΔcI). The competition between Bb::Φ and BbGm is mediated both by the lytic phage externally added to the system and by the lysogenic phage spontaneously released from Bb::Φ. The two phage are assumed to have the same values of κ, δ and χ. We modify our theoretical model to incorporate the effects of both the lysogenic phage (P=0.98) and the lytic phage (P=1) on the sensitive bacteria (BbGm) (see the electronic supplementary material). As shown in figure 5b, the experiments clearly corroborate the numerical simulation results. The mixture of the lytic and the lysogenic phage confers an approximately 1000-fold advantage to Bb::Φ over the strain with the Gm marker. The Gm-marked bacteria that survive after 24 h appear to carry lysogenic phage, which are evidently induced from Bb::Φ. Our theoretical model indicates that the stationary outcome of this two phage-mediated competition can be described by equation (3.1) with an effective phage pathology $P_{\text{eff}}$, where $0.98\le P_{\text{eff}}\le 1$. $P_{\text{eff}}$ is determined by the initial concentration of lytic phage; $P_{\text{eff}}\to 0.98$ as the initial concentration of lytic phage decreases while $P_{\text{eff}}\to 1$ as it increases. In the electronic supplementary material, we show that the steady-state outcome of a general two-phage-mediated competition between two bacterial strains is given by equation (3.2) in the limit of a fast infection process. We also demonstrate that all the detailed kinetic interactions of two-phage-mediated competition are condensed into a single parameter, the effective phage pathology, that depends on the values of the kinetic parameters.

4. Discussion

In summary, we quantitatively assessed phage-mediated competition, using both mathematical analysis and in vitro competition experiments between two bacterial strains. We have demonstrated that the complex concept of phage-mediated competition is essentially described by a single parameter, the phage pathology, that can be regarded as the probability of survival upon phage infection.

Our study has important implications in relation to the long-term advantage of bearing multiple pathogens. An a priori view might have been that the heavier pathogen load might reduce fitness relative to a competitor. This view is directly contradicted by the findings of this study, in which the advantages of bearing a pathogen are conspicuously associated with the relative pathology of the pathogen on the hosts. There are at least two other examples supporting the advantages of bearing pathogens. First, bacteriocins, bacteriocidal protein moieties toxic to bacteria closely related to the producing strain, are analogous to bacteriophage and may play a critical role in mediating competition in microbial populations (Riley & Wertz 2002). Second, lysogenic cells bearing prophage are immune against infection by homologous phage and the phage may confer morphological, metabolic or immunogenic properties to the host. A spectacular example of phage conversion is Vibrio cholerae strains, which only cause cholera when they are infected with a lysogenic phage carrying the cholera-causing toxin (Waldor & Mekaianos 1996; Weinbauer & Rassoulzadegan 2004). Thus, further studies of laboratory communities of lysogenic phage and bacteria may provide insights on ecological and evolutionary aspects of the formation of microbial communities.

The conclusion of our study may be extended to a more general framework of pathogen-mediated competition in nature, since there exist pathogens analogous to lysogenic phage that confer hereditary resistance to a few selected individuals in the sensitive host population (Anderson & May 1991; Dickmann et al. 2002), and since it is usually possible to condense the detailed host–pathogen interactions that affect the host survival into the pathogen pathology.1 There are certain limitations to such an extrapolation. First, the assumption that host populations and pathogens are well mixed may be better suited in vitro than in nature. However, the theoretical model and experimental manipulation of phage concentrations suggest that the ultimate effect of pathogen-mediated competition does not depend on the rate of contact, and successful pathogens are, by their nature, very efficient at transmission. Second, infection processes are discrete, stochastic and spatial in nature and might not be completely described by differential equations. Stochastic models can deal with this limitation; our preliminary results indicate that the conclusion obtained from the differential equation model is robust against inherent stochastic fluctuations. Third, pathogens can be transmitted without killing hosts in general infection processes, and the birth and death events in other hosts can be markedly different from bacterial growth. However, most pathogens play the same role of reducing their carriers' fitness (i.e. the probability of the survival of the host), usually by decreasing the net growth rate of the host. Therefore, the concepts learned from this study may be applicable to more general circumstances of pathogen-mediated competition.

Supplementary Material

Derivation numerical verification of invasion criteria for phage-mediated competition

Section 1 and appendix figure 1 present experimental evidence of spontaneous induction of phage from lysogens. Section 2 provides the derivation of the invasion criterion as shown in equation (3.2) for a generalized model of phage-mediated competition. Section 3 and appendix figures 2 and 3 provide numerical verification of the invasion criteria in equations (3.1) and (3.2) in the main text. Section 4 and appendix figure 4 give a detailed analysis of two-phage-mediated competition.