Homology modeling using parametric alignment ensemble generation with consensus and energy-based model selection

Abstract

The accuracy of a homology model based on the structure of a distant relative or other topologically equivalent protein is primarily limited by the quality of the alignment. Here we describe a systematic approach for sequence-to-structure alignment, called ‘K*Sync’, in which alignments are generated by dynamic programming using a scoring function that combines information on many protein features, including a novel measure of how obligate a sequence region is to the protein fold. By systematically varying the weights on the different features that contribute to the alignment score, we generate very large ensembles of diverse alignments, each optimal under a particular constellation of weights. We investigate a variety of approaches to select the best models from the ensemble, including consensus of the alignments, a hydrophobic burial measure, low- and high-resolution energy functions, and combinations of these evaluation methods. The effect on model quality and selection resulting from loop modeling and backbone optimization is also studied. The performance of the method on a benchmark set is reported and shows the approach to be effective at both generating and selecting accurate alignments. The method serves as the foundation of the homology modeling module in the Robetta server.

INTRODUCTION

The millions of proteins that have been sequenced to date appear to have domains that are limited in the topologies they adopt to perhaps only a few thousand folds. Homology modeling, also called comparative modeling, takes advantage of topologically equivalent experimental structures and frequently is the best method for obtaining an accurate model of a protein. Identification of the correct relationship between similar regions of the two proteins, the alignment step, is critical to the accuracy of the model, and has proven difficult to accomplish well consistently for distant relatives. As a consequence, structural genomics initiatives, which will attempt to provide experimental structures or homology models for all proteins in genomes of interest, will have to solve many more structures experimentally in order to provide a reliable basis set of close homologs upon which to model the remainder of sequences (1). A homology modeling method that could provide higher quality models at greater evolutionary distance would allow for far fewer experimental structures to be solved, significantly reducing the expenditure of resources. The efforts in this study are focused on analyzing methods for improving the alignments between remote protein pairs.

The best techniques currently for remote homolog detection and alignment start with the comparison of acceptable residue substitutions (a frequency ‘profile’) at each position determined from multiple sequence alignments (2–11), because such methods better span evolutionary space than single sequence comparisons. Fold-recognition methods, which attempt to identify topologically similar structures that are not necessarily evolutionarily related to the query, often also utilize structural information to their benefit. They incorporate such terms as predicted secondary structure (12–14), solvent accessibility (13,15), use information from structurally aligned homologs (16) or score alignments with threading potentials (17,18).

Additionally, groups have investigated the ability to obtain improved alignments and models through generation of ensembles by genetic (19,20), suboptimal (21–26) and parametric (24,27–29) approaches. Such approaches have the goal of first generating high-quality alignments, and then selecting the best in the set, usually by evaluating the resultant models for protein-like characteristics (19,20,26,29,30). These methods primarily select from their ensembles by evaluating the models (also called ‘decoys’) with various energy functions, and do not incorporate consensus information.

Other methods, rather than generating their own set of alignments, utilize a set of models from fold-recognition servers to develop a consensus from which models are either selected or derived (31–36). The principle behind these methods is essentially one of increasing the signal-to-noise: there are so many incorrect folds, that if several different methods report similar fold assignments, then that fold is far more likely to be correct.

Once a fold and an alignment to it is obtained, modeling the complete protein including insertion and deletion events and other variable regions requires turning to other techniques to find the conformation of such missing portions. Various methods exist for this task, commonly called ‘loop modeling’ (37–41), from purely de novo to application of fragments from experimental structures.

It is commonly accepted that sequence changes more rapidly than structure. However, this statement is mostly made from a low-resolution perspective, such as the consideration of the topology of a protein domain. One complication present in homology modeling, especially when the scaffold utilized is a distant relative of the query protein, results from the perturbations to the backbone that result from differing sequences. Even in the circumstance that two proteins share the same topology and approximate arrangement of residues in the core, the local and global perturbations that result from the specific sequence may make identification of the true conformation challenging. Clashes may exist between contacting residues, or bad backbone torsional arrangements may arise such as from changing a residue at a given position from a glycine or proline (37). Such imperfections, although the model may be topologically correct, require ‘refinement’ of the model to make it more native-like (42–44).

Here we describe a method for aligning sequences to known structures by parametrically generating an alignment ensemble and its derivative model ensemble. The method includes a novel approach for incorporation of information about regions likely to be obligate to a given fold. We generate very large ensembles that are quite diverse and usually approach the approximate upper bound obtainable with a structure–structure alignment between the query native structure and the best parent structure. In addition to sampling better alignments, these large ensembles allow for derivation of a more reliable consensus that provides for the ability to select quite good models from each ensemble. Additionally, we have investigated the ability to discriminate the best models using hydrophobic burial and energy functions based on low- and high-resolution representations and have examined techniques for combining these approaches to allow for improved selection. The impact of loop modeling and backbone optimization on model quality and selection is also studied. The approach has many different inputs and stages, and we therefore chose to call our method ‘K*Sync’, inspired by the expression ‘everything but the kitchen sink’.

MATERIALS AND METHODS

Availability

K*Sync is integrated into the Robetta server (http://robetta.org/), and can be used there as the foundation of the homology modeling protocol. Additionally, the K*Sync program itself and supporting programs are freely available to non-commercial users under license, and can be downloaded from the Robetta server.

Modeling complete domains

Complete domains are the best scaffolds to use for homology modeling (15). Extra pieces from peripheral domains, or incomplete scaffolds, may mislead both alignment methods and the ability to discriminate models using energy methods that expect well-formed cores. Therefore, after a parent structure has been detected, we apply a consensus structure-based parsing method that we have developed which applies Taylor's domain parsing method (45) to the parent and PSI-BLAST (4,47) detectable structural homologs (D. Chivian, manuscript in preparation) to automatically divide the parent structure into domains. Even when using an experimental structure to assign the domains of a protein chain, the exact definition of the locations of the domains varies depending on the method used or the member of the protein family examined. The application of consensus to the parses determined from a set of homologous structures allows for a more consistent definition of the edges of the domains within the protein family (and sometimes even the number of domains). We compared the agreement between our consensus based on homologous structures with the domain definitions in the CATH domain structure database (46) (which itself uses a consensus obtained with several domain parsing methods), and found our agreement to be improved over the already quite good agreement from domain parsing with a single structure (D. Chivian, manuscript in preparation). Fortunately, most of the disagreement between methods is with regard to the precise boundary (∼30% of boundaries with an identical edge definition, ∼67% within 5 residues and ∼85% within 20 residues), so large errors in the alignment that result from inaccurate domain boundaries are usually not introduced.

Further modeling considers the entirety of those domains from the homologous parent structure that the detection method indicates are present in our query. This has the advantage of including regions of the parent that may be obligate to the fold, but may not have been included in the detection. Additionally, knowledge of the domain boundary allows us to perform an alignment that favors the ends of the parent structure to be aligned for those positions that are found to be obligate to the fold in a multiple alignment. We therefore refer to alignments that are ‘local’ (not penalizing unaligned ends) with respect to the query and ‘global’ (penalizing unaligned ends) with respect to the parent as ‘domain’ scope alignments.

Detection of suitable parents

We use established methods for the detection of parent scaffolds to use for modeling. PSI-BLAST (4,47) is used for the more closely related proteins, FFAS03 (48) for the detection of intermediate distance proteins that are not detectable with a reasonable confidence by PSI-BLAST and the 3D-Jury (32) consensus method for the most remote fold-recognition regime (thresholds for confidence are given in the description of the LiveBench-8 set below). The K*Sync alignment method then seeks to generate alignments better than those produced by the detection method.

Single K*Sync default alignment

The K*Sync default method uses dynamic programming (49–54), together with a combination of sequence-based and structure-based scoring terms. We used the K*Sync default method in CASP4 and CASP5, as described previously (55). It uses a linear combination of terms derived from (i) sequence profile to sequence profile comparison, (ii) matches of predicted secondary structure of the query to known secondary structure of the parent and (iii) matches of regions that appear to be obligate in multiple alignments. Also included are (iv) gap terms: a base gap initiation and extension penalty, as well as a term to avoid gapping in regular secondary structure of the parent as well as regions that appear to be contiguous in multiple alignments.

1. Sequence information: PSI-BLAST generated position-specific residue substitution profiles (from searching for sequence homologs in the NR non-redundant sequence database from the NCBI) for the query and the parent are compared by inner product in K*Sync's default mode. This produces a pair score distribution which is adjusted to possess a mean below zero (−0.12) and a standard deviation of 1.0 in the same fashion as FFAS (5,6). Residue profiles are adjusted to include counts from multiple structural alignments [either FSSP (56) alignments or our ‘StrAD-Stack’ alignments, see Supplementary Data] to allow for more distant residue sampling than might be available with sequence-only homolog detections (16). In all development and benchmarking, the query and its close sequence relatives are not included in the multiple structural alignment.

2. Secondary structure: Secondary structure is added into the pair scores by giving a bonus to matches of PSIPRED (57) predicted query regular secondary structure (helix and strand only) with DSSP (58) assigned parent regular secondary structure, with a penalty for mismatches, weighted by the confidence of the prediction. The base secondary structure pair score for each combination of positions ranges between −1.0 and 1.0.

3. Obligate elements: A novel pair term is included to attempt to match positions that appear to be obligate to the fold. Positions that are usually occupied in a multiple alignment are more likely to be obligate to the fold, whereas infrequently aligned positions are likely insertions (or at least conformationally variable). The ‘occupancy obligateness’ of a position in the parent sequence is therefore based on the fraction of aligned residues at that position in the multiple structural alignment, and with less reliability the occupancy in the PSI-BLAST multiple sequence alignment. A bonus is given to matches of occupancy obligate positions with each other and a penalty to matches of occupancy obligate positions with insertions, with weighting based on the degree of occupancy of the obligate position. The base obligate pair score for each combination of positions ranges between −1.0 and 1.0. Additionally, to increase the fidelity for obligate positions of the parent, a multiplier is applied to the sequence-based pair scores for such positions. Finally, the pair distribution is adjusted to restore the desired mean and standard deviation.

4. Gaps: Gaps are penalized with position-specific initiation and extension penalties for the query and parent. Each position starts with the base value that is appropriate to a sequence-only alignment (which are 4.02 for gap initiation and 0.40 for gap extension when using inner product for residue substitution profile comparison), to which are added the structurally determined penalties. In addition to penalizing the introduction of a gap into regular secondary structure in the parent, structural gap penalties are determined from the multiple alignments. Highly occupied positions that never have insertions between them are considered ‘contiguous obligate’. The values are adjusted to penalize failure to align obligate positions (by increasing the gap extension penalty at such positions) and for inserting a gap between two contiguous obligate positions (by increasing the gap initiation penalty between such positions). The gap initiation penalty is reduced for positions that tolerate insertions in the multiple alignment. The final distributions of gap values are not adjusted.

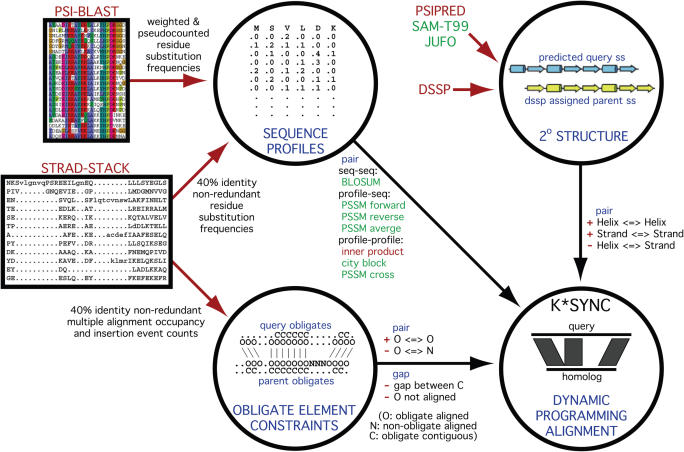
Dynamic programming is then performed to produce a single default alignment that captures all of the sequence and structural information that has been embodied in the pair and gap terms (Figure 1). Quantitative details for the pair and gap terms and the procedure for determining the weights on the individual terms are provided in Supplementary Data.

Figure 1.

Inputs to K*Sync alignment method. K*Sync combines sequence information with structural information to produce an alignment by dynamic programming. The inputs and weights on terms may be varied. The default alignment uses secondary structure predicted by PSIPRED and sequence comparison by the inner product of the residue substitution frequency profiles. In the diagram, ‘+’ indicates a bonus, ‘−’ a penalty, ‘<=>’ an alignment between two positions with the given characteristic.

Parametric alignment ensemble generation

Alignment ensembles for each of up to 5 parents are generated by varying the weights on each of the contributions to the alignment score, as well as the source of input information, following the approach we used to obtain alignment ensembles in CASP5 (55,59) and CASP6 (60). Weights on each structure-based pair and gap term are varied in isolation, taking on the values zero, half the optimal value for a single default alignment, the optimal value itself, 1.5 times the optimal value, and finally twice the optimal value. Additional variation comes from allowing the alignments to be either local–local or local–global in scope.

We also allow the method for sequence comparison to vary. Methods include a direct lookup from the BLOSUM62 score matrix (61) (single sequence against single sequence), looking up the score for the parent residue in the position-specific score matrix (PSSM) obtained for the query by several rounds of PSI-BLAST (profile against single sequence), or the reverse lookup of the query residue in the parent's PSSM (single sequence against profile), as well as the average of the scores from these latter two lookups. The profile–profile comparison methods that we use include the inner product of the pseudo-counted residue frequencies from PSI-BLAST or a city-block frequency vector comparison (with a distribution adjusted in a similar fashion as in the inner product method). Lastly, a ‘PSSM cross’ consisting of a linear combination of the PSSM scores for the query sequence with the effective frequencies for the parent sequence, and vice versa [similar to the approaches of PICASSO (7) and COMPASS (9)], was employed (see Supplementary Data).

Other means of obtaining variation are inspired by the inability to determine a priori the best method for secondary structure prediction for a given target, the best stringency for residue substitution profile generation, or the degree of structural variation to permit in the multiple structural alignment. We use three secondary structure prediction methods in the parametric ensemble generation, PSIPRED (57), SAM-T99 (62,63) and JUFO (http://www.jens-meiler.de/). Various residue frequency profiles are also obtained for the sequence comparisons, such as a stringent profile from two rounds of PSI-BLAST at an E-value for inclusion of 10⁻⁹, a looser profile started from the stringent checkpoint with one round at E-value 10⁻⁶, followed by another at E-value 10⁻³. Two even looser profiles, for a total of four PSI-BLAST multiple sequence alignments, are obtained by single additional rounds at E-value 10⁻³. In the case of multiple structural alignment derived profiles of the parent, we used FSSP multiple alignments for the early development of the method, but have switched over to our in-house StrAD-Stack method. With the FSSP multiple alignments, we used non-redundant structural homologs that had at least Z-scores of 10.0, 7.0 and 4.0 when aligned to the parent PDB structure. With StrAD–Stacdk alignments the Z-scores for non-redundant structures were 3.5, 2.5 and 1.5 (which are lower due to the tighter but more meaningful distribution as described in the Supplementary Data).

The above inputs and weights on terms are grid sampled as described above to produce initial alignment ensembles of 46 083 members for each parent [taking ∼10 min on a computer cluster with 54 AMD Athlon™ MP 1600+ processors], yielding initial ensembles with up to 230 415 members for those targets with five candidate parents. Alignment ensembles are then reduced to a non-redundant set, with redundancy defined as those alignments that are identical in all aligned and gapped positions to a given parent. This yields a non-redundant ensemble of typically a few thousand members per parent (e.g. in the LiveBench-8 set of targets, the ensembles for each parent were reduced, on average, to a size of ∼2500 members, with the greatest size being 8226 members, and the bulk of the distribution roughly between 500 and 4000 members). In order to minimize the expenditure of resources during more expensive modeling phases of the protocol, to allow for analysis less complicated by variable ensemble sizes, and potentially to enrich the consensus derived from the set of alignments for the more remote pairs (discussed for Figure 8 below), ensembles are further reduced to no more than 1000 members per parent (yielding combined ensembles no larger than 5000 members) by discarding alignments produced with information expected to be less likely to introduce diversity (such as profiles produced by intermediate rounds of PSI-BLAST) or less likely to be reliable for remote pairs (such as sequence comparison by straightforward BLOSUM lookup). For each parent, a series of reduction steps is applied until the ensemble size for each given parent is below the threshold of 1000, beginning with the variation in the bias term for highly occupied positions, followed by the variation of the weight on secondary structure gap terms, the inclusion of the sequence comparison by the BLOSUM matrix alone and so on (the full succession of stages is described in Supplementary Data).

Loop modeling

We have modified the Rosetta de novo fragment-replacement approach to make a hybrid loop modeling method (40) that models structurally variable regions that are not provided by the template.

Regions of the template that adjoin loop regions, called ‘stems’, are trimmed back to allow for spatially reasonable insertions. Since the ability to model a loop well often depends on the choice of which residues should be the edge of each stem, we added two variants to the trimmed ensemble for modeling. The first variant trims two residues into each stem, or as many as necessary to ensure that at least seven residues are unaligned in both the query and the parent. The second method trims back by at least one residue (extending until the modeled region corresponds to at least five residues for both the query and the parent), but continues to trim until it is at least one residue into a regular secondary structural element, since such ‘well-anchored’ positions are expected to usually be more stable within folds.

Loop regions are then modeled in the context of the fixed template using Rosetta (40). For short and medium loops (≤11 residues and ≤16 residues, respectively), ∼200 initial conformations are selected from a database of known structures using similarity of sequence, secondary structure and stem geometry. The closure of the loops is then optimized using cyclic coordinate descent (64), followed by optimization of the conformations in the context of the template by use of the standard Rosetta potential (65). PSI-BLAST level targets are optimized with a full-atom representation of the side-chains using a rotamer library (66). The loops of the more remote targets are optimized using the side-chain centroid representation. Conformations that have already passed filters based on their fit with the stems and the template are then selected in combination by simultaneous optimization starting from a random selection of initial conformations to try to achieve a combination of loop conformations compatible the other loops. Decoys that do not possess loops that close with the stem are removed from the ensemble. Long loops (≥17 residues) are then modeled using a modified version of Rosetta's de novo protocol similar to the short and medium loops, but without a starting conformation (40).

Modeling perturbations to the backbone

In an effort to make the models more similar to the query native structure and resolve steric clashes and bad backbone torsional arrangements, we have developed a protocol to allow for refining the entire model conformation using a low-resolution side-chain centroid-based energy function. The process begins by modifying the coordinates of the backbone structures to possess idealized bond lengths and angles to simplify sampling of conformations in torsional space. The entire length of the model is then perturbed in a Monte Carlo search procedure to find a lower energy conformation. In order to prevent the structure from diverging too far as a result of fragment-replacement or excessive expansion of the structure in an effort to alleviate steric clashes, distance restraints for non-local contacts based on the starting conformation are applied.

SCOP1.38 training and test sets

Following an earlier study (67), we built a training set of 524 mostly low identity pairs (<40% identity upon a structure–structure alignment) with one pair per family and one per superfamily from SCOP1.38 (68). This training set was used to obtain the optimal values for the sequence-only profile–profile pair score distribution mean and gap initiation and extension penalties, as measured by the similarity to ‘gold standard’ CE (69) structure–structure alignments between the query native and the parent native structures. Comparison of a predicted alignment with a ‘gold-standard’ alignment may be viewed from either the perspective of ‘accuracy’ (equivalent to ‘specificity’: the fraction of the predicted alignment that agrees exactly with the gold-standard alignment, with no tolerance for alignment to neighboring residues) or ‘completeness’ (equivalent to ‘sensitivity’: the fraction of the gold-standard alignment achieved exactly by the predicted alignment. Accuracy and completeness are discussed further in Supplementary Data). Since we wished our alignments to be both complete and accurate, we used the sum of the accuracy and completeness as the tuning metric. We then obtained the optimal values for the weights on the structural guidance terms (as described in Supplementary Data).

We also built a test set (that had no overlaps with the training set and were also mostly low identity) of 356 pairs from SCOP1.38 (168 families and superfamilies that were in the training set were not represented in the test set as they were the only pair in the family or superfamily). The single pair per family or superfamily requirement allowed us to avoid bias towards well-represented folds, in particular immunoglobulins and globins.

LiveBench-8 benchmark target set

In order to assess the performance of our ensemble generating and selection approach with a more standard benchmark, we turned to the set of targets from the LiveBench-8 experiment (70). These targets were newly released PDB structures that lacked BLAST-level similarity with any previously released structure. We selected for analysis those targets for which a homologous structure was detectable with sufficient confidence by PSI-BLAST (E-value ≤ 0.001), FFAS03 (ffas score ≤ −20.0) or 3D-Jury (3djury score ≥ 25.0). We additionally limited the targets to those for which the top confidence parent provided at least 40% of the query native structure by MAMMOTH's (71) implementation of MaxSub (72) (which reveals the percentage of the native structure that is captured by the model. Greater detail on MAMMOTH MaxSub is provided in Supplementary Data) so that spurious hits would not complicate our analysis. This left us with 98 targets: 27 targets at the most challenging 3D-Jury level, 9 targets at the intermediate FFAS03 level and 62 targets at the PSI-BLAST level (for the list of targets see Supplementary Table SI).

Ensembles built from multiple parents

While the highest confidence homolog provided by the detection method is often the best parent on which to build a homology model, there are situations where alternate parents that have detection confidence scores close to the top scoring parent may provide a scaffold that is more similar to the native structure of the query. When we allowed up to five non-identical parents that are not dramatically different in confidence but possesses as much diversity in sequence as possible from the top scoring parent (at least an E-value of 10⁻³ and within 10⁻¹⁵ of the top hit for PSI-BLAST detections, at least −8.0 and within 12.0 of the top confidence hit for FFAS03 detections, and at least 20.0 and within 30.0 of the top hit for 3D-Jury detections), we found that the best possible parent (as measured by the MAMMOTH MaxSub quality of the best 3D-Pair (73) structural alignment derived template) on average increased from 70.6 to 73.4% coverage for PSI-BLAST level targets, from 63.8 to 65.5% for FFAS03 level targets, and from 60.4 to 62.1% for 3D-Jury level targets. Thus, building ensembles derived from these parents is sometimes advantageous for improved sampling of near-native models.

Although the improvement from allowing alternate parents is not enormous when viewed with respect to the ability to optimally build a model, using multiple parents becomes more significant when generating and selecting from model ensembles. The ability of the parametric alignment protocol to sample the best alignments may be affected by the choice of parent. Additionally, selection from the model ensemble may be easier for some parents due to the details of the backbone and the arrangement of non-local contacts that may lend some parent scaffolds to be better suited upon which to drape the query sequence. Rather than attempt to determine the best parent at the outset with which to perform subsequent modeling, ensembles are built for each parent. Those ensembles are then simultaneously selected from using both an alignment consensus score and using energy functions (as discussed below in Results) with the hope that at least one of the parents has provided high-quality alignments and possesses a scaffold that fits well with the query sequence and therefore can be discerned. Additionally, as will be discussed in Results, multiple parents are particularly valuable when scoring alignments by consensus.

RESULTS

As described in Materials and Methods, the K*Sync default alignment method combines information from a broad range of sources, including sequence information from homologous sequences, predicted and known secondary structure, and information from multiple alignments that indicates regions corresponding to core elements that are required for the fold. Mathematically optimal alignments are found by dynamic programming (49–54), which may be compared from the perspective of ‘accuracy’ and ‘completeness’ with ‘gold-standard’ alignments achieved by structure–structure alignment methods (Supplementary Data), or by MAMMOTH MaxSub comparison of the model produced by the alignment with the native structure of the query (Supplementary Data). Alignments superior to the single default K*Sync alignment may be obtained parametrically by varying the source of the input information and the weights on terms in the alignment to produce an alignment ensemble (and its derivative model ensemble). Selection of superior models may be achieved by examination of the resultant models for protein-like characteristics as well as consistency with respect to the consensus of ensemble.

Below we test the default K*Sync method on a benchmark created from the SCOP1.38 (68) structure database using CE (69) structure–structure alignments as the ‘gold standard’. Then, employing a benchmark of targets from the LiveBench-8 (70) experiment, we evaluate the ability of the K*Sync parametric alignment ensemble approach to sample the best possible alignments, as measured by comparison to the native structure of the query. We then analyze strategies for selection of superior models from the ensemble. The impact on model quality and selection resulting from loop modeling and backbone refinement is also discussed.

Performance of K*Sync default method

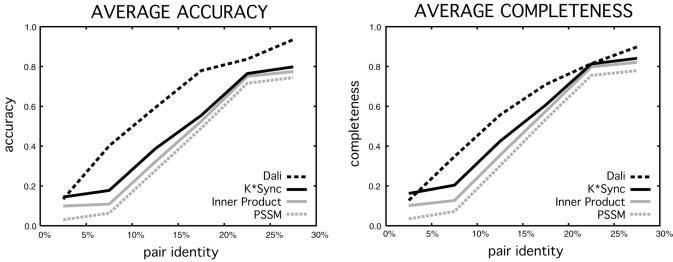
A sustained improvement in alignment quality was found by the application of our structural guidance terms. The performance on our SCOP1.38 test set (Materials and Methods) using ‘domain-scope’ alignments of baseline profile-sequence alignments (using a position-specific scoring matrix, or ‘PSSM’ built by PSI-BLAST), the baseline profile–profile alignments (using an inner product comparison of frequencies from PSI-BLAST) and the K*Sync default alignments is reported in Figure 2. The ‘accuracy’ and ‘completeness’ of alignments (as described in Materials and Methods under the SCOP1.38 training and test sets, as well as in Supplementary Data) are shown with respect to the CE structure–structure alignment between the query native and the parent structure. Also shown is the overlap of Dali structure–structure alignments (56) with the CE structure–structure alignments.

Figure 2.

Evaluation of K*Sync default alignments. Average accuracy and completeness of alignments for targets in SCOP1.38 test set with respect to a structure–structure alignment (CE) are shown for profile–sequence alignment (PSSM, in dashed gray), profile–profile alignment (Inner Product, in solid gray), the combination of profile–profile and structural information (K*Sync, in solid black), and another structure–structure alignment method (Dali, in dashed black). Targets are grouped into 5% identity bins (based on the CE alignment). Note that the Dali alignment diverges from the CE alignment as the pairs become more remote, owing to our strict alignment equivalence requirement.

As has been shown previously by other groups (3,5–11) alignment quality is improved on average for distant pairs by the use of profile–profile alignments over profile-sequence methods such as PSI-BLAST (4,47). We find that the addition of structural terms boosts this performance when measured by both accuracy and completeness. Although the K*Sync default alignment does improve over the sequence-only approaches in the remote regime, it is not at the level of similarity between the Dali and CE alignments, and even with these crude measures of alignment quality, it is clear that there is more room for improvement over the K*Sync default.

The Dali structural alignments do not agree exactly with the CE structural alignments as the sequences diverge. This discrepancy is due to the requirement in the accuracy and completeness measures that correctly aligned residues are exactly the same as in the ‘gold-standard’ alignment, and not aligned to neighboring residues. As the neighbor requirement is relaxed, the structure–structure alignment methods do show more agreement in accuracy and completeness (data not shown), indicating that the alignments are at least close (such as to neighboring residues on a helix) and highlighting the weakness with using agreement with a structure–structure alignment to measure of the quality of an alignment.

Comparison of the K*Sync default alignments with and without the obligate terms (Table 1) reveals that inclusion of obligate terms introduces the greatest variation in the remote identity regime. The impact seems to be greatest below 30% sequence identity, where ∼10–20% of alignments may benefit a significant amount (>5%) from the inclusion of the obligate terms at their default weighting. However, about an equal number of targets are better off without the use of the obligate terms. Not surprisingly, multiple alignments that lack sufficient variation in occupancy are responsible for the majority of the cases where the alignment is superior without the obligate terms. Unfortunately, not all of the cases where the alignment suffered from inclusion of the obligate terms at the default weighting could be explained by the occupancy information-poor targets, and it proved difficult to find a rule that works in all cases for when to include the obligate terms or how much to weigh them. Similar results were observed for the other terms and parameters in K*Sync and were the inspiration for considering alignment ensembles rather than single alignments.

Table 1.

Inclusion of obligate terms has greatest impact in low identity regime

Identity (%)	Targets	Threshold	Accuracy			Completeness
			Better	Unchanged	Worse	Better	Unchanged	Worse
0–5	22	0.05	3	18	1	4	17	1
		0.10	2	19	1	3	18	1
		0.20	1	21	0	1	21	0
5–10	69	0.05	11	49	9	10	45	14
		0.10	7	57	5	5	58	6
		0.20	3	65	1	3	64	2
10–15	58	0.05	11	38	9	10	38	10
		0.10	5	47	6	4	46	8
		0.20	1	53	4	1	55	2
15–20	47	0.05	5	38	4	4	40	3
		0.10	3	41	3	2	43	2
		0.20	2	43	2	1	44	2
20–25	35	0.05	1	32	2	1	32	2
		0.10	1	33	1	1	34	0
		0.20	0	35	0	0	35	0
25–30	27	0.05	3	23	1	2	25	0
		0.10	0	27	0	0	27	0
30–35	20	0.05	0	20	0	0	20	0
35–40	15	0.05	0	15	0	0	15	0

Evaluation of accuracy and completeness for K*Sync default alignments accomplished both with and without obligateness terms on SCOP1.38 test set. Targets are grouped into 5% identity bins, as in Figure 2. The number of ‘targets’ in each bin is reported. Also shown is the number of targets that have alignments that change in quality as a result of inclusion of the obligate terms with default weights. Change is defined as having an ‘accuracy’ or ‘completeness’ deviating by more than a given threshold than that of the default alignment without obligate terms, and are categorized as ‘better’, ‘unchanged’ or ‘worse’.

K*Sync alignment ensemble generation

Although it is certainly desirable for a method that produces, on average, improved alignments for remote protein pairs, often a still better alignment could have been achieved had one used a different way to score the sequence similarity of positions, a different scope of the alignment (local–local or local–global), different input information such as an alternate secondary structure prediction method, different stringencies and/or rounds of PSI-BLAST when generating the residue substitution profiles, different stringencies on which parents to include in the multiple structural alignment of the parent, or different weights on the structure terms when including them in the pair or gap scores of the alignment. We followed this approach (shown in Figure 1, and described in Materials and Methods) to parametrically generate large ensembles of alignments. We reasoned that adjusting the way in which the input information affects the alignment might allow us to obtain even better alignments and more dramatic variation than alignment methods based only on sequence information for more remote targets.

Sampling of the best possible alignment

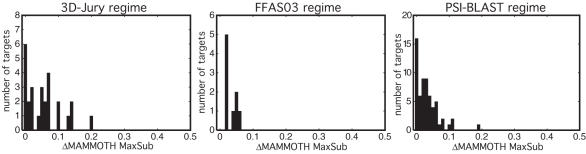
Examination of the quality of K*Sync ensembles reveals that they are quite good at sampling close to the best possible alignment. Figure 3 shows that, for the majority of targets in our LiveBench-8 benchmark, the ensemble samples alignments of quality equal to or quite close to the 3D-Pair structure–structure alignments between the query native structure and the best parent. Only for a few of the most challenging targets does the initial K*Sync ensemble not manage to sample near the best possible alignment. We find that for 21 of the 27 targets in the 3D-Jury regime, the K*Sync ensemble achieves at least one model of quality close to that of the model produced by the 3D-Pair alignment to the best parent (within ∼10% of the full query length by MAMMOTH MaxSub). In the FFAS03 regime, all 9 of the targets are within this threshold, and in the PSI-BLAST regime it is 58 of the 62 targets. These values contrast with the quality of the best models from the detection methods themselves, for which only 5 of the 27 targets are within 10% of the optimal in the 3D-Jury regime, 1 of 9 in the FFAS03 regime, and 27 of 62 in the PSI-BLAST regime. We discuss the most challenging targets in detail in Supplementary Data, and address some of the reasons for the failure of the K*Sync ensemble to sample near the best possible alignments in Discussion.

Figure 3.

Sampling of near best possible alignments. Histogram of number of targets with a member of the K*Sync ensemble with a model close in quality to the model derived from the 3D-Pair alignment of the query native structure to the structure of the best parent (that provides the most coordinates similar to the query). Horizontal axis represents the difference in the MAMMOTH MaxSub score of the 3D-Pair model and the best model in the ensemble (with values indicating the upper bound for the bin), and y-axis is the number of targets that are within that upper bound.

Improving the quality of model ensembles

Figure 4 shows the best and average MAMMOTH MaxSub quality of the K*Sync ensembles at various stages in the modeling process as well as the overall quality of models available from the detection methods and the quality of models derived from the 3D-Pair structure–structure alignments. The stages in the modeling process examined consist of obtaining the alignment ensemble, enriching the ensemble, loop modeling and, in the more remote regime, backbone optimization.

Figure 4.

Evaluation of ensemble quality. Comparisons in ensemble quality, as measured by MAMMOTH MaxSub (black, best in set; gray, average of set) are shown for 3D-Pair alignments between query native structure and parents from detection method, alignments from detection method (3D-Jury, FFAS03 or PSI-BLAST), and progressive stages in modeling.

In order to avoid expensive loop modeling for all members of the initial ensemble, we enriched the template-only ensemble using a combination of the simple hydrophobic burial and full-atom energy functions (see discussion of selection below). This enrichment reduced the size of each ensemble from up to 1000 members per parent for up to 5 parents (allowing initial ensemble sizes of up to 5000 members for each target) to the lowest scoring 500 members of the ensemble (requiring at least 50 members from each parent). This allows us to increase the average quality of the ensembles without a significant loss of the best members in the ensembles. Loop modeling of the shorter loops (≤16 residues) improves the best models, but does not alter the average quality of the ensembles, consistent with our expectation that a model must already be correct in alignment in the region of the loop to gain any benefit from loop modeling. Longer loops (≥17 residues) were then modeled for the more remote 3D-Jury and FFAS03 regime targets to allow for subsequent backbone optimization. Figure 4 shows that the addition of long loops to incomplete models does indeed improve the best models, in keeping with our results for shorter loops. Backbone optimization additionally modifies the models in the ensemble to provide more native-like conformations, but unfortunately also frequently disrupts native-like features that should have been retained, leading to a reduction in the average quality of the ensembles. Additionally, as will be discussed below, this disruption makes selection more challenging for many of the more remote targets. The improvement in quality tends to be from larger perturbations to the models, rather than finer shifts in conformation.

Selection from the ensemble

After generating an ensemble with high-quality alignments, we then need to be able to select out the best models. We examined the straightforward approach of rescoring the alignments after their creation using just the sequence scoring methods described above. Not surprisingly, although the sequence-based scoring methods were able to discriminate in the near regime, they were not as successful for the more remote targets, and did not compete with the consensus and energy-based evaluation approaches (data not shown), so were not considered further.

Comparison of strategies for selection

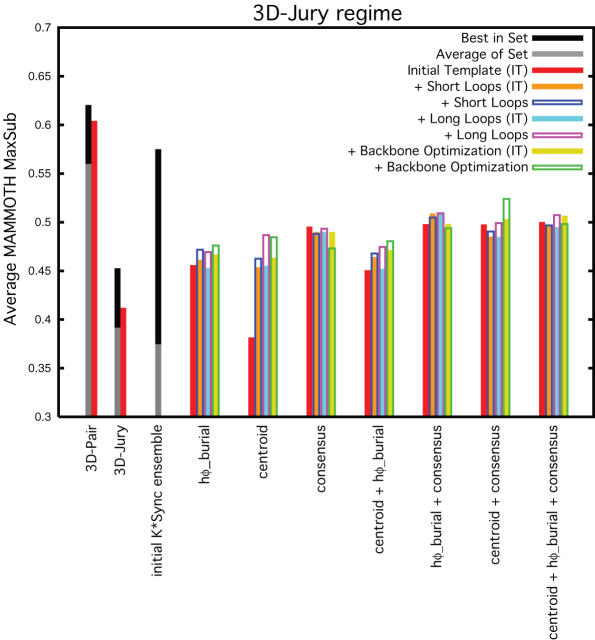
We investigated the ability of various strategies for selection of near-native models from the ensembles. Figure 5 reveals the performance of each of the techniques. On the left is the best and average quality of the 3D-Pair structure–structure alignments to all parents and to the most confident parent (where the best of the 3D-Pair alignments serves as the approximate upper-bound to template-only modeling), the best and average quality of the alignments from the detection methods, the quality of the top confidence alignment from the detection method, and the best and average quality of the initial non-redundant K*Sync ensemble. The quality of the default K*Sync alignment is shown. On the right is the average quality of the model selected by hydrophobic burial, the side-chain centroid representation energy function, the full-atom energy function, the consensus score from the alignment ensemble as well as ‘sum-of-rank’ combinations of these measures (measures discussed below). Selection measures are applied to the models before and after modeling of short loop regions. In order to distinguish the contribution to the quality of the selected model resulting from the addition of short loops, we also report the quality of the model that was selected after loop modeling but with a quality determined from the initial template without loops.

Figure 5.

Comparison of strategies for selection from the ensemble. Average MAMMOTH MaxSub scores for 3D-Pair set of alignments, detection method set of alignments, K*Sync ensemble set of alignments and models selected by various measures from K*Sync ensemble both before and after loop modeling. Best in set shown in black, average of set in gray, selection of a template-only model in red, selection of a model after modeling short loops (but with a quality evaluated prior to loop modeling) in orange, and selection of a model including short loops (and with a quality evaluated with the loops present) in blue. The average of the models resulting from the K*Sync default alignment is shown as well as those selected from the ensemble using the hydrophobic burial preference (‘hφ_burial’), the side-chain centroid representation energy function (‘centroid’), the full-atom representation energy function (‘full_atom’), and the alignment consensus score (‘consensus’). Also shown is the average of the models selected using sum-of-ranks combination scores of these measures (indicated by those scores with a ‘+’ in the name).

The impact of loop modeling on model quality and selection

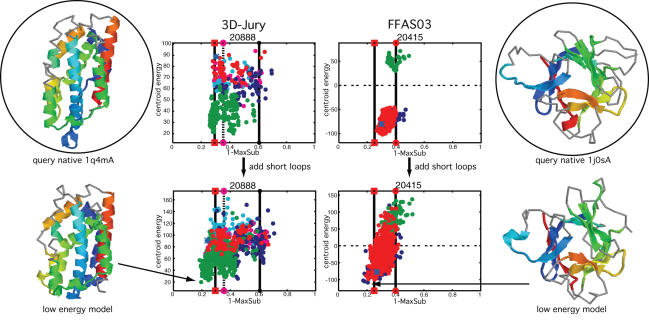
Figure 6 illustrates the impact that loop modeling can have on both the quality of the best models in the ensemble and the ability to select superior models. The plots report the side-chain centroid energy of each decoy (y-axis) versus structural similarity (x-axis), where 0.0 indicates a complete match to the native structure, and 1.0 no similarity (see the Supplementary Data for a more complete description and a discussion of the issues inherent to the MAMMOTH MaxSub evaluation measure). Two representative ensembles are shown, one from the 3D-Jury regime and one from the FFAS03 regime (a full set of plots is provided in Supplementary Data). The native structure of the query and the model with the lowest energy after loop modeling are shown, with those residues in the model that correspond to template positions (taken directly from the parent structure based on the alignment) shown with a colored cartoon representation, and those residues that were modeled using Rosetta indicated by a gray backbone trace.

Figure 6.

Loop modeling can improve both sampling and selection. The side-chain centroid energy score with respect the similarity of each model to the query's native structure, as measured by 1.0-MAMMOTH MaxSub (for description see Supplementary Data), both before and after modeling of short loops for targets 20888 (1q4mA) and 20415 (1j0sA). Each point represents a model, with the first parent shown with red points and up to four alternate parents with the other colors. For comparison, the quality of the model that would have resulted from the detection's alignment is shown with a vertical line with a circle on the end, with a solid line for the first parent and a dashed line for the best alternate (target 20415's first detection was the best). The vertical lines with boxes at the ends indicate the quality of the 3D-Pair alignment between the query native structure and the first parent (for both target 20888 and 20415 the first parent was the best) and approximates the upper bound. The quality of the model from the default K*Sync alignment is indicated with a blue asterisk. The native structure of each query and the lowest energy model after loop modeling are shown with colored cartoons for the template regions (with blue at the N-terminus and red at the C-terminus), and gray backbone representation for the regions that were modeled with loops in the low energy model.

As can be seen in these two examples, the majority of the core is provided by the template (with the exception of the green helix on the left of the low-energy model for target 20888), but even so the template-only models alone may not provide the ability to select the very best models. For regions of models where the alignment is accurate, loops that are reasonably well modeled will contribute additional native-like residues and this is what we observe for both target 20888 and target 20415, for which the very best models achieve MaxSub scores closer to the native after loop modeling (we used MAMMOTH MaxSub evaluation of the whole model rather than a more ‘loop-centric’ metric in order to focus on the effect on the overall quality of the models. The performance of the Rosetta loop modeling protocol itself is described in Rohl et al. (40)).

Additionally, and from the perspective of getting the alignment right, more importantly, the loops provide interactions that were not available in the template-only model. Although the loops in these examples are not all perfectly modeled, the burial they provide to otherwise exposed core positions and the additional pair interactions they offer contribute to improved discrimination of the most native-like models using energy functions. The whole of the protein (except for any long loops) becomes available for consistent evaluation and comparison of the models.

Selection using energy functions

We explored the use of energy-based measures to select out the native-like conformations from the ensemble. We utilized the Rosetta program (65,74) to evaluate the energies of template-only models with varying levels of detail: a coarse hydrophobic burial preference, a side-chain centroid representation that includes an empirical pair potential and van der Waals energies, and a full-atom representation in which side-chains are modeled using a backbone-dependent rotamer library (75) with a Monte Carlo conformational search procedure (66).

We compare the scores for ensembles of template-only models with their quality for three representative targets in Figure 7, one for each difficulty regime (a full set of plots is provided in the Supplementary Data). The coarsest energy function, called ‘hydrophobic burial’, captures hydrophobic-polar partitioning, and is often effective in discriminating the better models (for targets that are monomeric and globular) and is quite good at identifying the worst models that usually exhibit poorly formed hydrophobic cores. Figure 7a shows ensembles scored by hydrophobic burial. As can be seen in Figure 5, selection with the hydrophobic burial function is aided by loop modeling, probably owing to the additional interactions provided by the loops.

Figure 7.

Scoring of alignment ensembles. The similarity to the query native structure of each model in the initial template-only ensemble (before loop modeling) with respect to a selection score, with (a) the hydrophobic burial score, (b) the full-atom energy and (c) the consensus score. An example target in each of the three difficulty regimes (3D-Jury, FFAS03 and PSI-BLAST) is shown, in the same scheme as Figure 6. Targets are: 3D-Jury regime, 20906 (1uocA); FFAS03 regime, 20415 (1j0sA); and PSI-BLAST regime, 17597 (1iyzA). The negative of the consensus score is shown so the trend in (c) is similar to that in (a) and (b).

Figure 7b shows the same three targets, but evaluated using Rosetta's full-atom energy function. We see that there can be quite good correlation between the energy of the model and its quality, especially in the sequence detectable regime, when we expect the packing of the core is largely similar. Interestingly, even in the 3D-Jury regime, the full-atom energy can sometimes discriminate near-native from wrong models. We found that the discrimination with the full-atom energy improves upon reduction of the Lennard-Jones repulsive weight in the energy function because of clashes when placing the query sequence onto the parent backbone (this reduced repulsive form was used in all analysis). As with hydrophobic burial, selection using the full-atom energy function benefits from modeling of short loops (Figure 5).

Selection by consensus

Consensus is a powerful approach that has been applied by other protein structure prediction methods, both de novo (76,77) and fold-recognition (31–36,78,79). In the case of fold-recognition, it is based on the idea that since there are so many incorrect answers, the convergence is likely to indicate native features (essentially boosting signal-to-noise). The K*Sync alignment ensembles are well suited for obtaining consensus information and one can score each alignment from this perspective. Our approach consists of finding the frequency with which each position ‘i’ of the query maps to a given position ‘j’ in the parent. This signal can be increased by using multiple parents. The top confidence parent (the ‘reference’ parent) can be structurally aligned to the other parents, allowing alignments to alternate parents to be translated to the reference parent. This permits their rapid comparison without resorting to the more expensive, but otherwise essentially equivalent, process of structurally aligning each template-only model to the reference (e.g. our approach can score an ensemble of thousands of alignments in just a few seconds on a single processor). The consensus score is determined by summing the frequency of the observed mapping at each position that is aligned and then dividing by the length of the query. One advantage of this approach is that it allows some signal for alternate modes in the alignments, unlike approaches that give points only for the dominant mode. We also examined another approach for selection by consensus, in which alignments that did not possess the most dominant mappings were discarded, and found this approach to be inferior as it often resulted in discarding the best alignments, even when the dominant mode possessed a fairly high frequency of occurance in the ensemble (≥∼40%) (data not shown).

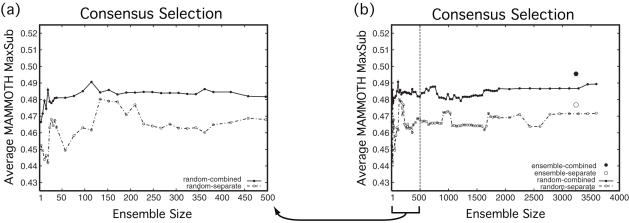
Figure 8 reveals that the performance is better and more stable when the consensus score is derived using alignments to multiple parents and when the number of alignments is above a few hundred. Figure 8 also shows that when we derive the consensus signal from a filtered ensemble that favors alignments expected to be better for more remote pairs (see Supplementary Data) instead of from a random set of the same size, the performance is slightly better for the more remote 3D-Jury targets. We find the performance from the filtered ensemble to be about the same for the intermediate FFAS03 targets, and slightly worse for the PSI-BLAST targets (data not shown).

Figure 8.

Consensus score as a function of ensemble size. Selection by consensus score for the 3D-Jury regime targets is shown, with consensus frequencies derived from a randomized ensemble. The ensemble from which models were selected was held constant, whereas the ensemble from which the consensus frequencies were derived was varied. The size of the randomized ensemble is varied (x-axis), so that the members of smaller ensembles are subsets of the larger ensembles, with the smallest ensemble comprised solely of the K*Sync default alignment to each parent. The y-axis reports the similarity to the query native structure of the selected model, as measured by MAMMOTH MaxSub. (a) Ensembles of size up to 500 members. (b) Ensembles of size up to ∼3500 members [so (a) is a ‘close-up’ of the first part of (b)]. The power of the consensus score when the frequencies are determined separately for each parent (‘random-separate’) or with respect to the reference parent (‘random-combined’) is shown. Also shown in (b) is the power of the consensus score when determined from the filtered ensemble, both with frequencies determined separately for each parent (‘ensemble-separate’) and with respect to the reference parent (‘ensemble-combined’). The ‘ensemble-combined’ is the form of the consensus score that was actually used.

Figure 7c shows the same three targets scored by our alignment consensus score. The correlation between consensus score and model quality can be quite strong, and may be almost linear for those targets for which the correct alignment is strongly dominant in the consensus mappings (owing to ensemble members receiving points for both quality and consensus score only from correct positions). Frequently, for targets that produce ensembles that are challenging to select from using energy functions, the consensus score can discriminate the superior models. Comparison of selection methods when used in isolation (Figure 5) reveals consensus to be the best single technique.

Selection by combining scores

In order to make selection of high-quality models even more consistent, we investigated several ways of combining the model scores and energies. As an example of improved selection by combining rankings, the full-atom score alone fails to consistently separate the better models from those that are very wrong for target 20906 (Figure 7b). Hydrophobic burial alone (Figure 7a), although better at separating the extremes than the full-atom energies, scores many of the middling quality alignments as among the lowest energy. Combination of these scores proves more robust. Rather than confront complications of scaling and weighting inherent in combining different measures, we implemented a straightforward ‘sum-of-ranks’ approach instead, where the scores are sorted and then summed, with the lowest summed rank being used for selection. We additionally investigated ‘purge-and-pick’ approaches, where the lower scoring ensemble members by one measure are discarded, followed by selection from the remaining set by another scoring method. We found that the purge-and-pick approach, although sometimes accomplishing the goal of improved selection, was not as robust as the sum-of-ranks approach (data not shown).

We also examined combining Rosetta energy functions with the consensus score using a sum-of-ranks approach and found such combinations were indeed very good at selection. The consensus score by itself provides such good discrimination that we did not find a huge improvement in selection upon combining it with the other measures when applied to the initial template models (Figure 5). However, the selection of models that have the loops modeled well does benefit somewhat from combining the energy functions with the consensus score, perhaps owing to subtle differences in the alignments and trimming of the stems that are not distinguishable with the consensus score alone, which may be responsible for the ability to better model the loops.

If we consider all three regimes in Figure 5, the single best approach appears to be the sum-of-ranks of the full-atom energy function with the hydrophobic burial preference and the alignment consensus score. This selection method significantly outperforms the alignments from the detection method and the default K*Sync method. Unfortunately, although a large improvement over the baseline methods, none of the selection measures by itself is able to consistently select the very best alignments that are present in the ensemble.

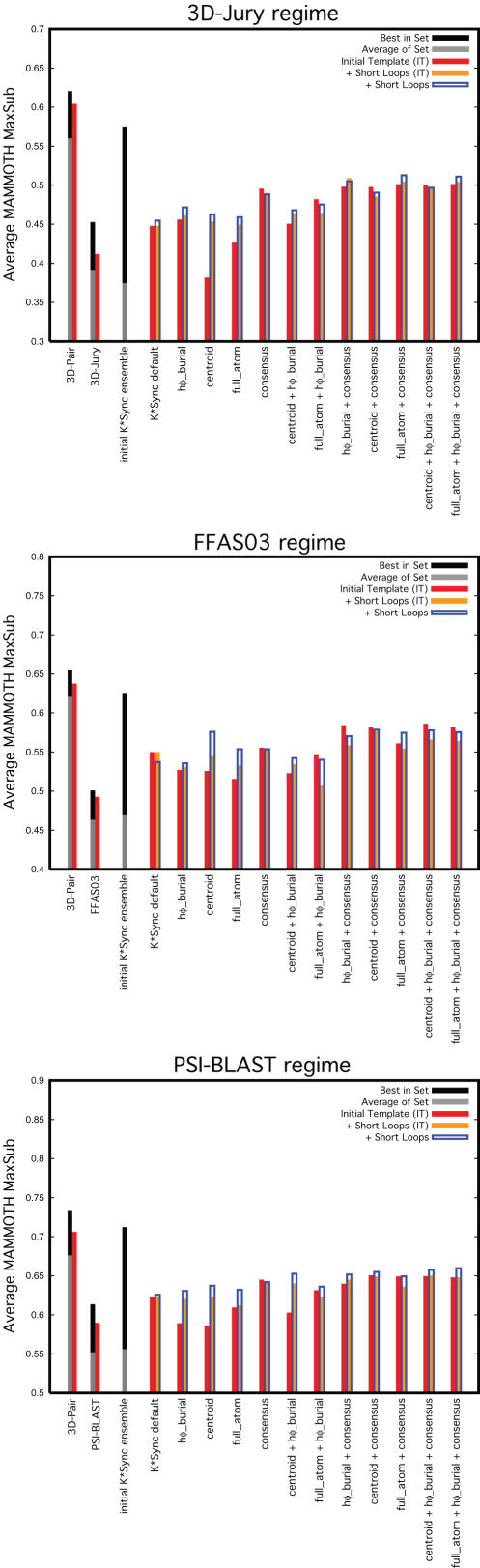
The impact of backbone optimization on model quality and selection

Figure 9 shows selection for the 3D-Jury regime targets after modeling of long loops and backbone optimization. For comparison, the template-only and short loop modeled stages are also reported. Also shown is the quality of the selected model at each stage, but as determined from the initial template before any loop modeling and backbone optimization of the entire model. We find that perturbation of the models allows for better selection with energy functions (full-atom energies were not examined as the backbone optimization was performed with the side-chain centroid energy function). Although the best overall selection of the optimized models is accomplished using the sum-of-ranks ‘centroid + consensus’ measure, we do not find improved selection by this combination of measures in the FFAS03 regime, where selection from ensembles that have undergone backbone optimization yields significantly inferior models to those selected from frozen-backbone templates (data not shown). Examination of the 3D-Jury targets reveals that the more distant pairs tend to be the ones that reap the greatest benefit from the backbone optimization (Supplementary Data). This is likely a consequence of the greater deviation between the more remote pairs that may be aided by backbone perturbation, whereas more similar pairs are already close to the correct conformation and can only be disrupted. PSI-BLAST regime targets were not examined due to the expense of the procedure combined with the large number of targets in this set, as well as the expectation that the more remote pairs would be the most likely to benefit from low-resolution backbone optimization.

Figure 9.

Selection from backbone optimized ensembles. Scheme is the same as that used in Figure 5, with additional average quality scores for models selected from ensembles after addition of long loops (‘+ Long Loops’, in magenta) and full-length backbone optimization (‘+ Backbone Optimization’, in green). Also shown are the quality of the initial template of the selected model for the long loop model (‘+ Long Loops (IT)’, in turquoise) and the initial template for the backbone optimized model (‘+ Backbone Optimization (IT)’, in yellow).

Instances of improved selection appear to have been mostly due to larger perturbations on unrestrained regions of the decoys, rather than high-resolution improvements. Other complications included targets that had a native structure and templates that did not possess tight hydrophobic cores. Optimization of the side-chain centroid energy function caused these structures to collapse in an attempt to bury the hydrophobic residues, misleading discrimination of the superior decoys. Combination of pre-optimization hydrophobic burial scores with post-optimization centroid energies also did not provide a consistent improvement (data not shown). The challenge presented by refinement of homology models remains an ongoing area of research.

DISCUSSION

We have pursued several avenues in our research with the goal of obtaining high-quality homology models. We found that we can improve alignments by the incorporation of structural guidance terms with sequence information, including a novel approach to utilize information about regions that are likely obligate to the fold. We generated large alignment ensembles by varying the contributions to the alignment cost function and found that the ensembles frequently sample near the best possible alignment from a structural perspective. We were able to select superior alignments from the ensembles by evaluating the models using energy functions. Completion of the models by loop modeling often had a positive impact on both model quality and selection, and to some extent so did adjusting the backbone to account for perturbations from the different sequences for more distant targets. We additionally developed an approach to derive a consensus score from the large K*Sync ensembles, and found that discrimination using our alignment consensus score benefited from having a large number of diverse alignments and became more accurate by building a consensus from ensembles derived from multiple parents. Additionally, combining different scoring techniques to select models proved the most robust. Although, on average, those combinations that included the consensus score were slightly better than consensus alone, the consensus score provided the majority of the signal with which better models were selected. In the following sections we discuss some of the issues in sampling and model selection that remain to be overcome.

Challenges in sampling

Although the K*Sync alignment ensemble generating approach is usually quite successful at producing alignments close to the best possible, it does not always manage to do so (Figure 3). When we investigated the causes for the most egregious of these failures (those >10% by MAMMOTH MaxSub away from the best possible), we found that our reduction of the ensemble size from the initial large ensemble to at most 1000 unique alignments per parent was not responsible (see Supplementary Data for the order in which the ensemble was filtered). Investigation of the most challenging targets in Figure 3 revealed that near best possible alignments were never sampled even in the initial large ensemble for these targets.

There proved to be several reasons for the failure of the K*Sync ensemble to sample near best possible alignments for some of the targets (for a detailed discussion of the most challenging targets see Supplementary Data). The most straightforward of these was when the parents were incorrect. Although we have not included in the analysis those targets that did not have a parent that provided a reasonable amount of backbone upon which to model, there were some examples where our threshold was exceeded even with a wrong parent, such as for a helical bundle with a mirror topology to the target (target 20436: 1p68A). There were also cases where the topology was fundamentally correct, but variations in the parents, such as the replacement of the C-terminal strand with an extra strand at the N-terminus for a canonical beta-propeller (target 17574: 1ofzA), proved insurmountable. Other variations in moieties (extra helices, dropped hairpins or even missing density), occasionally were not corrected for even in the best alignments.

Another misdirection in the alignments frequently resulted from inaccurate secondary structure predictions. Although not all alignments in the ensemble give full weight to the secondary structure predictions, it was telling that misalignment was consistently wrong in regions of targets with inaccurate secondary structure predictions by all three methods (PSIPRED, SAM-T99 and JUFO). In addition to incorrect guidance from the secondary structure predictions, the sequence signature itself was probably not reliable (hence the incorrect secondary structure predictions), exacerbating the difficulty to recover. This 2-fold challenge was especially pronounced for edge strands, where the hydrophobic patterning is often not as clear as for more central strands. The challenge of different hydrophobic patterning is especially great for those targets that are monomers but are being modeled with parents that are multimers (or vice versa). The residue substitution profiles in such cases will include polar residues for the exposed positions of the monomer, but may very well be hydrophobic for the multimer at positions that comprise a largely hydrophobic interface. Since the majority of the signal in producing the alignments derives from the hydrophobic patterning, the altered pattern can greatly disrupt the ability to obtain the correct alignment.

We were interested to discover that four of the seven most challenging targets (20436, 20241, 17574 and 18863) had alignment ensembles that did not possess any real agreement, yielding unusually weak consensus scores. In such easily identifiable circumstances (except for 20436, which does not have any correct parents), additional sampling by introduction of additional variation in weights and potentially by additional terms (such as predicted solvent accessibility or more specific conformational preferences than just 3-state secondary structure) may allow for better sampling of near best possible alignments which might be discriminated using energy functions even in the absence of alignment consensus.

The K*Sync ensemble generating approach has good success in generating optimal alignments, but frequently only obtains near best possible alignments, and for a small fraction of the targets does not manage to obtain high-quality alignments. Future modifications to the protocol, such as additional sampling that enforces greater diversity may remedy some of these cases.

Challenges in selection

Even in the circumstance that a high-quality alignment and model is generated, selection of the best models in the ensemble can be complicated by several factors. For example, sometimes a consensus is obtained that has a portion with the greatest frequency to an incorrect part of the parent. Sometimes a less frequent alternate mode (that is still somewhat common in the ensemble) is in fact the correct alignment. For this reason, our consensus score also gives points to alignments that are not necessarily the dominant frequency at all positions. In such circumstances, scoring the models in the ensemble using energy functions hopefully complements the misdirection from the alignment consensus, but is not always successful in doing so (e.g. target 20672, 1mzgA). Given that the consensus score is usually the most discriminating, and therefore should usually be included in selection of the best models, determining when to trust the consensus score and when to down-weight it has proven difficult (at least when it is above a reasonable threshold and indicates some degree of convergence in the alignment ensemble).

The energy functions have as their foundation the assumption that the proteins to be modeled are soluble monomeric domains with well-packed hydrophobic cores and largely soluble surfaces. The mostly non-hydrophobic surface assumption does not hold as well for targets that are obligate multimers with hydrophobic interfaces, and thus complicates selection of models using the hydrophobic burial score. Also, those targets that do not have tightly packed hydrophobic cores can mislead the burial energy score. Again, as with the consensus score, incorporation of the other scoring terms makes selection more robust, but does not work in all cases.

As discussed previously, van der Waals clashes and other high-energy features may result from placing a sequence onto a backbone that is not the same as that which determined the conformation of that backbone. Although we have alleviated this effect somewhat for the van der Waals clashes by reducing the repulsive term in the full-atom energy function used to evaluate such models, this ad hoc solution is not ideal as it sometimes misleads the energy function.

We also encountered some degree of favoritism for shorter templates in the energy functions when scoring models after loop modeling. If we are evaluating models that have frozen-backbone templates and loops that have been built under the influence of a given potential, then we must exercise caution that selection from among those models does not overly emphasize that same potential. The danger in so doing is that models that have fewer residues provided by the template (and correspondingly more residues optimized under the given potential) will be selected since the template regions have not been optimized under this potential, incorrectly yielding shorter and less complete alignments. Our goal is to further the early success shown here (Figure 9) in combining alignments that are both accurate and complete with conformational optimization to both template-derived and loop-modeled regions to consistently allow for selection of the most native-like models.

Comparison with other approaches

The protocol we have described has similarities to other methods. For example, generation of alignment ensembles and selection from them has been explored by other groups (19,20,26). However, we believe that the diversity of the initial ensembles generated by most of these methods may often not be as great as that available in the K*Sync ensembles due to the large degree to which we vary the input information and terms in producing the alignments, as well as our use of a novel approach for inclusion of obligate terms, as evidenced by the large number of unique alignments achieved by our parametric ensemble generation. This contrasts with those autonomous methods for ensemble generation that are largely dependent on variation of sequence-only terms for initial diversity. Additionally, most methods that autonomously generate their own ensembles rely upon selection approaches that only examine the models for protein-like features, and do not incorporate consensus information for scoring models.

Unlike K*Sync, other automatic consensus methods (31–34,36) are dependent on external fold recognition servers for their ensembles (with the exception of the local version of the SHOTGUN method (31)). They may therefore utilize more diverse initial ensembles than those available from variation of sequence-only alignment terms. However, we have found, at least in the case of our K*Sync ensembles, that the signal from the consensus score derived from an ensemble improves rapidly with the size of the ensemble and also when ensembles from multiple parents are considered. In our implementation, it usually does not stabilize until a fairly large number of alignments are considered, roughly on the order of several hundred (Figure 8). This is usually more than the number of alignments considered by existing consensus methods, which may have input on the order of up to 10 or so servers with usually up to ∼10 models from each server, frequently not all with the correct topology. Therefore, the ensembles used by other methods likely do not sample alignments to a degree that allows for as robust a consensus. This supposition is supported by comparison of the models from the 3D-Jury method with the K*Sync initial template-only consensus-selected models in Figure 5, which shows a significant increase in quality by the use of our consensus approach with K*Sync ensembles.

Additionally, most consensus methods do not incorporate model evaluation. To the best of our knowledge, only two other automated methods currently reported combine a consensus score directly with model evaluation to select the best models (33,36), but again, are limited in the pool from which they select and in the robustness of their consensus by the richness of the initial ensemble provided by external fold recognition servers. We hope to be able to compare the complete version of our method with other methods in future public benchmarking experiments.

The performance of the method in public benchmarking experiments

The K*Sync and Rosetta homology modeling protocol has been in development for several years. We have participated in several rounds of CASP using various incarnations of the method. We have also implemented the method, and updated it along the way, in the Robetta server (55,60,80). We have participated in both CASP and LiveBench with the Robetta server. We fared quite well in CASP4 with a mostly manual implementation of the K*Sync default method, placing in the top groups in both the comparative modeling (81) and the fold recognition (82) categories.

We then fully automated the K*Sync single default alignment and created the Robetta server and used it to participate in CASP5 and CAFASP3. Excitingly, Robetta was one of the better methods in the fold recognition regime in CASP5 (83), including human groups. Robetta also ranked highly in CAFASP3 (84), indicating that the K*Sync default method was performing very well. We also used K*Sync to generate alignment ensembles from which we selected from using a combination of energy functions and human intuition for our human group in CASP5 (59). This method proved among the best in the fold recognition regime (83), which supported our continued research into ensemble generation and selection.

We then implemented automatic ensemble generation (for the top confidence parent only) and selection using only energy functions in the Robetta server, returning the energy-picked model as the first model (burial for remote targets and full-atom + burial for PSI-BLAST detectable targets) and made model 2 the one from the default alignment. We then participated with Robetta in LiveBench-6, LiveBench-7 and LiveBench-8, (70,85) and did not fare as well as we had anticipated, ranking reasonably well in the remote regime for which we designed our method, but being outperformed by the meta consensus servers when just considering the first model. We attribute some of these less stellar results to the less robust energy selection that we were using and the fact that we were using only one parent. We did not include consensus, and for some targets did a poor job selecting the first model. When considering all models, Robetta was among the best methods.

We also participated in CASP6 and CAFASP4 with Robetta (again, with only the top confidence parent and without consensus scoring) and also with a newer version of the automatic protocol that we called ‘Robetta_04’ (60) that utilized multiple parents as well as backbone optimization, but did not utilize consensus scoring. Robetta ranked highest among the servers in CASP6 in the fold recognition category (86), and Robetta_04 was among the top 10 methods among all groups, including humans. Interestingly, although Robetta_04 compared favorably against other automated methods, Robetta was not evaluated by the CAFASP criteria as among the best servers in the CAFASP4 experiment (http://www.cs.bgu.ac.il/~dfischer/CAFASP4/), which may be attributable to the parents available at the time of execution of Robetta (when the targets were initially released by CASP, whereas other servers were run later for CAFASP) as well as the different scoring schemes used by each of the experiments. CASP uses several measures (primarily GDT_TS (87)) which can be forgiving for more low-resolution accuracy, whereas CAFASP uses the higher-resolution version of the MaxSub (72) method, which does not count positions that are not very close.

Based on the findings in this study, we have added generation of K*Sync ensembles using multiple parents and selection using our alignment consensus score and energy-based approaches to our development Robetta server that is participating in CASP7. We look forward to the results from CASP7, and will be making the method available to the public via the Robetta server soon.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.