Network frailty and the geometry of herd immunity

Abstract

The spread of infectious disease through communities depends fundamentally on the underlying patterns of contacts between individuals. Generally, the more contacts one individual has, the more vulnerable they are to infection during an epidemic. Thus, outbreaks disproportionately impact the most highly connected demographics. Epidemics can then lead, through immunization or removal of individuals, to sparser networks that are more resistant to future transmission of a given disease. Using several classes of contact networks—Poisson, scale-free and small-world—we characterize the structural evolution of a network due to an epidemic in terms of frailty (the degree to which highly connected individuals are more vulnerable to infection) and interference (the extent to which the epidemic cuts off connectivity among the susceptible population that remains following an epidemic). The evolution of the susceptible network over the course of an epidemic differs among the classes of networks; frailty, relative to interference, accounts for an increasing component of network evolution on networks with greater variance in contacts. The result is that immunization due to prior epidemics can provide greater community protection than random vaccination on networks with heterogeneous contact patterns, while the reverse is true for highly structured populations.

1. Introduction

Directly transmitted diseases spread across individual-to-individual contact networks as determined by the mode of transmission (e.g. aerosol versus sexually transmitted) and the social structure of the host population. Pathogen dynamics, therefore, fundamentally depend on the structure of the underlying contact network (McCallum et al. 2001; Meyers et al. 2005) as moulded by patterns of individual immunization through vaccination or prior exposure to the disease (Anderson & May 1990; Newman 2005; Pourbohloul et al. 2005). Immunized individuals are effectively removed from the network, thereby breaking possible chains of transmission and leaving a sparser residual network. An important principle in epidemiology is that an entire population can be protected by the immunization of a fraction of the hosts, the so-called herd immunity (Anderson & May 1990, 1991). The distribution of epidemiologically active contacts in a partially immunized network, and thus, the efficacy of herd immunity, will be shaped by the original network geometry and the source of immunization.

Immunization via vaccination differs from natural immunization in an important aspect. Epidemics preferentially infect (and subsequently immunize) highly connected individuals and contiguous clusters of individuals. In contrast, vaccination programmes, which target individuals randomly or are based on individual health considerations, do not necessarily select highly connected or interconnected portions of the network. Newman (2005) showed that the invasibility of a network that has been immunized through prior epidemic spread depends critically on the configuration of the original network and transmissibility of the first pathogen. Following Newman's results, we ask the question—is the geometry of the social contact network that results from previous infection more or less robust than that which results from random vaccination?

In the models of disease transmission on contact networks, the probability of exposure is determined by the connectivity (degree) of the individual (node). Thus, the most highly connected individuals in a contact network, the so-called ‘super-spreaders’, ‘hubs’ or ‘core group’, have both a higher probability of spreading infection through the population and a higher rate of exposure through social contacts. Heterogeneity in susceptibility, exposure or mortality is classically called ‘frailty’ in mathematical demography (Vaupel et al. 1979; Hougaard 1984). Applied in this context, high-degree nodes will tend to be the most frail nodes in the network (Barthelemy et al. 2005; Meyers et al. 2005). As an epidemic sweeps through a population, variation in frailty will lead to systematic structural changes in the active portion of the network (Barthelemy et al. 2005; Newman 2005). While the impact of network structure on the progression of an epidemic has been well studied (Newman 2002; Keeling 2005; Meyers et al. 2005), there has been relatively little work on network evolution during the course of an epidemic (recent notable exceptions are Barthelemy et al. (2005) and Newman (2005)).

In this paper, we show that the herd immunity of a network depends strongly on whether the source of immunization is exposure to a prior epidemic or randomly distributed vaccination. We investigate this phenomenon by considering the structural evolution of several classes of social networks—Poisson, scale-free and small-world—over the course of an epidemic. We introduce new analytical measures for tracking the evolution of network structure during an epidemic and use simulation to elaborate on the analytical results. In particular, we partition the structural impact of an epidemic into two components: (i) degree-dependent frailty and (ii) interference due to the accumulation of immune individuals. We show that the evolution of these quantities varies with the underlying geometry of the network (in terms of the degree distribution and the degree of clustering), and consequently, that natural immunization by epidemics can, for some networks, provide greater community-level protection than random vaccination.

2. Material and methods

(a) Modelling epidemic and vaccine-based immunization

We assume that disease spreads through a contact network in which each node represents an individual and the edges represent potentially infectious contacts. The number of edges emanating from a node is the degree of the node and the degree distribution is the distribution of this quantity across the population (Albert & Barabasi 2002). While the disease status of nodes may change during the epidemic (i.e. susceptible to infected), the edges that link nodes are assumed to be static. We performed stochastic simulations of the spread of disease on three classes of network geometry—small-world, Poisson and truncated scale-free networks—to investigate partial immunization of a population through both natural infection and random vaccination. These classes of networks have been well studied with respect to the spread of epidemics (Moore & Newman 2000; Volchenkov et al. 2002; Keeling 2005; Meyers et al. 2005) and have been shown to be the representative of a variety of animal and human social networks (Sjoberg et al. 2000). The small-world networks were generated using the algorithm described by Watts & Strogatz (1998) with rewiring probability of p=0.02. These networks are characterized by a degree distribution that is roughly symmetric about the mean, with a high degree of node clustering and a short characteristic path length (Watts & Strogatz 1998). For Poisson networks, the degree of each node was drawn randomly from a Poisson distribution and the edges were placed randomly with respect to the specified degrees. The scale-free networks are characterized by a highly skewed distribution of contacts such that most of the nodes are weakly connected and a small number of nodes have very high connectivity (Barabasi et al. 1999). In particular, the degree distribution follows a power law. As contact patterns have inherent limits on levels of connectivity, we generated networks using a truncated power-law degree distribution (a discretized Weibull distribution; Bonabeau et al. 1999) in which the probability that an individual has k contacts is given by $p(k)\propto a/b{(k/b)}^{a-1}{\text{e}}^{-{(k/b)}^a}$, where a is a shape parameter and b is a scale parameter. For both the Poisson and the power-law networks, nodes were connected at random with the restriction that self loops (nodes connected to themselves) and double edges between nodes were disallowed.

We simulated epidemics assuming a discrete time, chain binomial, susceptible–infected–removed (SIR) model (Bailey 1957). At each time-step, nodes are characterized as susceptible, infectious or removed. The susceptible nodes become infected in the next time-step with binomial probability 1−exp(−βI), where β is the rate of transmission across an edge, and I is the number of infected nodes to which the individual is connected. The infected nodes are assumed to recover in a given time-step and enter the immunized (removed) class with a probability γ=0.1, i.e. nodes are infectious for an average of 10 time-steps. Once in the removed class, a node is assumed to have lifelong immunity, and thus, no longer interact in the epidemiological network. These epidemic processes are analogous to many childhood infections (i.e. measles, chickenpox), which are highly infectious, have an infectious period of 1–2 weeks and convey lifelong immunity.

The basic reproductive ratio, R₀, depends on the first two moments of the degree distribution, 〈k〉 and 〈k²〉, i.e. mean and variance, by R₀=T(〈k²〉/〈k〉−1), where T is the average probability that an infected node will transmit disease to one of its neighbours (Meyers et al. 2005). For comparison, we standardize the degree distributions of the three classes of networks, hence 〈k²〉/〈k〉≈10, i.e. for a given transmissibility, R₀ is the same for all the three classes of network. The average degree in the small-world and Poisson networks is approximately 〈k〉=10 and in the scale-free networks, approximately 〈k〉=4.8.

To simulate natural immunization, we initially infected a randomly selected node and allowed the epidemic to run its course, resulting in a fraction, π of nodes immunized by exposure to the pathogen. We generated 300 networks of 1000 nodes for each of the network classes, and simulated 10 epidemics on each, varying the transmission rate, β, of the immunizing outbreak between 0.01 and 0.05 to achieve a range of immunized fractions, π. Using identical (pre-epidemic) contact networks, we then modelled a comparable level of vaccination by randomly removing a proportion, π of the nodes corresponding to one of the simulation runs. To compare the robustness (herd immunity) generated by these two immunization processes to subsequent outbreaks, we initiated secondary epidemics on the immunized networks. These secondary epidemics were initiated by infecting a randomly chosen node on the residual networks of susceptible nodes following the immunization. The transmission rate in these secondary epidemic simulations was β=0.05 and we assessed the epidemic size as the proportion of susceptible nodes that become infected.

(b) Quantifying the structural decay due to immunization

Following the mathematical framework developed in Newman et al. (2002), Meyers et al. (2005) and Newman (2005), we use percolation theory to study the predicted change in mean network degree due to the epidemic removal of nodes. For a node that never becomes infected during an epidemic, we can distinguish between its original degree, k, and its degree in the residual network consisting of all the nodes that remain uninfected by the epidemic, k_r. The original degree of a node indicates the potential exposure to infection, thus the change in network connectivity in terms of the original node degree gives a measure of the frailty of high-degree nodes. Remaining nodes in the residual network are partially protected by the removal of neighbours, and the concomitant reduction in degree, i.e. potential chains of transmission are interrupted. We call this process interference, which can be described in terms of difference between the original and the residual degree of nodes on the residual network (see formal definitions later). To understand the structural evolution of the network, we focus on three network statistics: the mean degree in the original network, 〈k〉; the mean original degree of individuals remaining in the residual network, 〈k〉_r; and the mean residual degree of the individuals remaining in the residual network, ${\langle k_{\text{r}}\rangle }_{\text{r}}$.

The mean degree in the original network is simply $\langle k\rangle ={\sum }_{k}k{p}_k$, where p_k is the frequency of nodes of degree k in the network. Assuming SIR dynamics on an undirected contact network, Meyers et al. (2005) derived the following formula for the probability that an individual of degree k will become infected during an epidemic: $v_k={(1-T+Tu)}^k$. Here, T is as mentioned earlier and $u={\sum }_{k}k{p}_k{(1+(u-1)T)}^{k-1}/{\sum }_{k}k{p}_k$ is the probability that the person at the end of a randomly chosen edge does not become infected during the epidemic, and can be calculated using numerical root finding methods (Meyers et al. 2005). If we define the infected edges as those through which the disease has spread during an epidemic, we can also calculate the probability of infection for a node that is reached by following an uninfected edge after an epidemic. If the degree of this node is k, then the probability that it was not infected is equal to the probability that it was not infected along one of its other k−1 edges. Thus, the probability that it was infected is ${\omega }_k=1-{(1-T+Tu)}^{k-1}$.

The frequency of the individuals, with original degree k, who remain in the residual network after an epidemic is given by $r_k=p_k(1-v_k)/{\sum }_j{p}_j(1-v_j)$, and thus, the mean original degree in the residual network is

$${\langle k\rangle }_{\text{r}}=\sum _{k}k{r}_k=\frac{\sum k{p}_k(1-v_k)}{\sum p_k(1-v_k)}.$$ 2.1

To calculate the residual degree, we partition the original network into the nodes that are infected during the epidemic and those that remain uninfected, and then calculate the fraction of edges in the original network that begin and end in the uninfected partition. Each edge in the network has two ends called stubs. Thus, the total number of stubs in the network is $N\sum k{p}_k$, where N is the number of nodes in the network. For every one of the approximately $N\sum p_k{v}_k$ nodes in the infected partition, disease transmission to that node would have occurred necessarily along an edge with both an origin and a destination stub (with the exception of the first infection; for simplicity, we ignore this exception). Thus, $N\sum p_k(k-2v_k)$ is the total number of stubs in the network excluding those that were a conduit for disease transmission during the epidemic. We refer to this quantity as the total number of uninfected stubs.

If we choose an uninfected stub at random, then the probability that it attaches to an uninfected node is given by

$$\frac{\sum k{p}_k(1-{\omega }_k)}{\sum p_k(k-2v_k)}.$$

If we now choose an uninfected edge (rather than stub) at random, the probability that it connects two uninfected nodes is given by the previous quantity squared,

$${\left(\frac{\sum k{p}_k(1-{\omega }_k)}{\sum p_k(k-2v_k)}\right)}^2.$$

1Thus, the average residual degree in the residual network is this probability multiplied by the total number of stubs and divided by the number of nodes in the residual network,

$${\langle k_{\text{r}}\rangle }_{\text{r}}={\left(\frac{\sum k{p}_k(1-{\omega }_k)}{\sum p_k(k-2v_k)}\right)}^2\left(\frac{N\sum p_k(k-2v_k)}{N\sum p_k(1-v_k)}\right)=\frac{{\left(\sum k{p}_k(1-{\omega }_k)\right)}^2}{\sum p_k(k-2v_k)\sum p_k(1-v_k)}.$$ 2.2

Although the approach we take is different, our estimate for the average residual degree is very similar to the one that would result by following the methods developed in Newman (2005). Our calculation discounts infected stubs when considering the uninfected (residual) portion of the network and appears to be a better estimate for average residual degree (see electronic supplementary material).

Finally, we define frailty as the difference between the mean original degree in the original network and the mean original degree in the residual network, scaled by the mean original degree,

$$\varphi =\frac{\langle k\rangle -{\langle k\rangle }_{\text{r}}}{\langle k\rangle }.$$ 2.3

This parameter quantifies the extent to which the high-degree individuals are preferentially infected during an epidemic. We define interference as the scaled difference between the mean original degree in the residual network and the mean residual degree in the residual network,

$$\theta =\frac{{\langle k\rangle }_{\text{r}}-{\langle k_{\text{r}}\rangle }_{\text{r}}}{\langle k\rangle }.$$ 2.4

This quantity is the extent to which the epidemic has cut-off connectivity among the remaining susceptible population.

To verify our analytical predictions for the end of an epidemic and study network evolution during the intermediate stages of an epidemic, we performed stochastic simulations of the spread of disease on small-world, Poisson and truncated scale-free networks (as described earlier). For comparison, the mean degree, 〈k〉, for all the three classes of network was set to 10 in these simulations. The transmission rate of β=0.05 and a recovery rate of γ=0.1 were used. We simulate epidemics on 100 replicate networks of 1000 nodes for each network class and compare the simulated residual network structure to the analytic predictions. We relate the per-contact transmission probability between an infected and a susceptible individual, T, to the simulation parameters, β and γ, in the manner, T=1−e^−β/γ. Note that we did consider additional values of β although the results did not change qualitatively and we do not present them here (e.g. figure 3; figure 2 in electronic supplementary material).

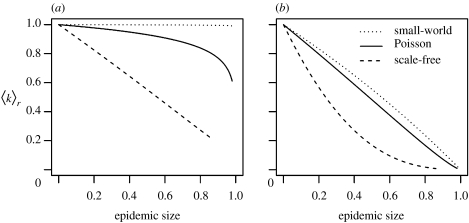
Figure 3.

(a) Mean original (scaled), 〈k〉_r, and (b) residual degree (scaled), ${\langle k_{\text{r}}\rangle }_{\text{r}}$, as a function of the epidemic size (proportion of nodes infected by the end of the epidemic) for the three types of networks.

3. Results

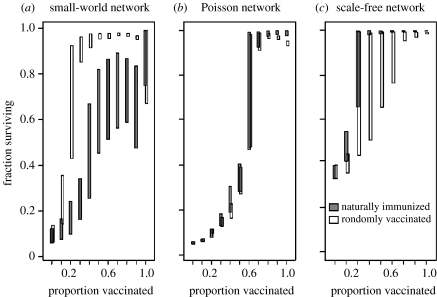
The robustness of residual networks to subsequent epidemic invasion is strongly dependent on the class of network, as shown in figure 1. Prior epidemics produce patterns of herd immunity nearly identical to that of random vaccination on Poisson networks (figure 1b). Natural immunization on scale-free networks results in residual networks that are more robust to epidemic attack compared to random vaccination at the same level (figure 1c). This pattern is consistent with previous observations that scale-free networks remain contiguous longer in the face of random compared to targeted attack (Albert et al. 2000). This pattern is reversed for small-world networks, where randomly vaccinated networks were considerably more robust to subsequent attack (figure 1a).

Figure 1.

Fraction of the immunized population that escaped infection as a function of the proportion immunized for small-world, Poisson and scale-free networks of 1000 nodes. Mean degree is scaled such that R₀=3.9 for the three classes of networks. Grey boxes indicate the central 50% simulation runs for populations immunized by a prior epidemic. White boxes indicate the same for randomly vaccinated populations. Note that boxes are offset for clarity.

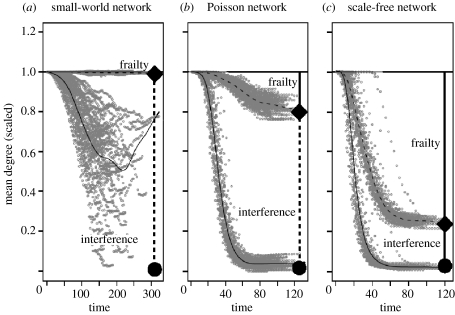
We can understand these differences in herd immunity for the three classes of network by considering the pattern of structural change in the degree distribution due to epidemic removal. Intuitively, all the networks become increasingly sparse as the epidemics progress (figure 2). However, the structural evolution of the networks differs in the relative contributions of frailty (the loss of high-degree individuals that are more vulnerable to infection) and interference (the reduction in the connectivity of the remaining susceptible individuals). Though all the three networks ultimately decrease to a similar residual mean degree, ${\langle k_{\text{r}}\rangle }_{\text{r}}$, the proportion of the decrease due to frailty increases with the contact heterogeneity of the initial network (figure 2). The analytical calculations of the mean original degree and the mean residual degree on the residual networks, 〈k〉_r and ${\langle k_{\text{r}}\rangle }_{\text{r}}$, respectively, match the simulation results for both the Poisson and the scale-free networks (figure 2). Overall, the congruence between analytical results and simulations holds on these networks for all the values of transmission rate (i.e. R₀), but is not presented here.

Figure 2.

Mean original degree and mean residual degree (scaled to 〈k〉=1) of the active epidemic network (susceptible and infectious nodes) for 100 simulated network epidemics and analytical predictions for (a) small-world, (b) Poisson and (c) scale-free networks of 1000 nodes. Each epidemic was simulated on a separate network with β=0.05. The dashed curve gives the mean original degree of nodes across all the networks and the solid curve gives the mean residual degree across time. Points indicate the simulated trajectories. The solid diamond indicates the predicted final mean original degree, 〈k〉_r, and the solid circle indicates the predicted mean residual degree, ${\langle k_{\text{r}}\rangle }_{\text{r}}$. The solid vertical bar indicates the predicted frailty and the dashed bar indicates the predicted interference.

Using equations (2.1) and (2.2), we can predict the mean original degree, 〈k〉_r, and the mean residual degree, ${\langle k_{\text{r}}\rangle }_{\text{r}}$, on the residual network following epidemics of varying sizes. For a given final epidemic size (i.e. 1 minus the proportion of nodes immunized), the resulting residual network has the lowest connectivity if the original degree distribution is scale-free and connectivity is highest if the original network is small-world (figure 3b). Again, the relative contribution of original node degree to the decay in connectivity (i.e. frailty) increases with contact heterogeneity in the network (figure 3a). The predicted mean residual degree for a network of arbitrary degree distribution with a fraction π of nodes randomly vaccinated is 1−π〈k〉 (see electronic supplementary material). Relative to the proportion immunized, there is less difference in the average residual degree on Poisson networks that have experienced prior epidemics (figure 3b) and that predicted for random vaccination. For a given proportion immunized by a prior epidemic, scale-free networks are more sparse and small-world networks less sparse than comparable randomly vaccinated networks (figure 3b), which explains the patterns of herd immunity seen in figure 1.

On small-world networks, the analysis and the simulations agree for 〈k〉_r but not ${\langle k_{\text{r}}\rangle }_{\text{r}}$. Simulations yield substantial variation in ${\langle k_{\text{r}}\rangle }_{\text{r}}$, consistently lower than the predicted analytic value (figure 1a). The percolation-based quantities derived for ${\langle k_{\text{r}}\rangle }_{\text{r}}$ are based on the assumptions that may not hold true for small-world graphs having a high degree of (non-random) clustering (also see Newman & Watts (1999), Volz (2004) and Newman (2005) for a discussion of analytical methods for clustered networks). The high degree of clustering also results in the greater variance in residual degree as epidemics occasionally fade out, leaving relatively contiguous and highly connected clusters of nodes. This clustering of nodes further explains the relatively low herd immunity on small-world networks due to prior epidemics; the susceptible nodes that have survived an epidemic tend to be contiguous and are of similar mean degree to the original network (figure 1a). Random vaccination, in contrast, removes nodes and edges homogenously throughout the community, thus conferring a higher degree of sparseness, and protection, throughout the residual network.

4. Discussion

The underlying pattern of contacts between individuals strongly impacts the susceptibility of a population to pathogen invasion (Pastor-Satorras & Vespignani 2001) and epidemic spread (Newman 2002; Barthelemy et al. 2005; Meyers et al. 2005). Less studied is the degree to which epidemic spread affects the structure of contac networks through node ‘death’ or immunization. Barthelemy et al. (2005) has characterized this pattern as a hierarchical cascade, in which the infection passes through nodes of progressively lower degree. As a result, the structure of the sub-network of interacting hosts will evolve towards lower mean degree and lower variance in degree. Here, we have shown that the structural evolution of communities experiencing epidemics can be characterized in terms of two quantities: frailty (the reduction in connectivity due to the selective removal of highly connected nodes) and interference (the reduction in connectivity due to the removal of neighbouring nodes).

Following an immunizing epidemic, we found the residual network to bear little signature of the original geometry; the result is usually a collection of weakly connected and largely isolated nodes. Newman (2005) showed that, in general, subsequent pathogens must be more transmissible to invade these previously exposed sparse networks. Interestingly, the structural evolution to this endpoint differs depending on the topology of the original network. Networks with highly skewed contact distributions are quickly homogenized due to the rapid cascade of infection through the highest degree (most frail) individuals (Barthelemy et al. 2005). In contrast, the comparatively homogenous Poisson and small-world networks are primarily shaped by interference as neighbouring nodes gain immunity effectively resulting in local cordons sanitaire.

The interaction between network geometry and structural evolution due to epidemic spread sheds light on the process of epidemic fadeout and the related problem of vaccine deployment. Albert et al. (2000) showed that scale-free networks are more susceptible to degree-ordered node removal than the Poisson networks. In our simulations, the frailty of high-degree nodes to epidemic spread effectively creates an ordered removal of nodes resulting in more rapid degradation of structure on skewed networks. The rapid homogenization of skewed networks under natural epidemics results in residual networks, which are robuster to secondary epidemics than randomly vaccinated networks. On Poisson networks, for which the structural evolution under natural epidemics is largely independent of node degree (i.e. interference), natural epidemic spread produces residual networks that are no more robust to subsequent epidemics than if randomly vaccinated. Intriguingly, random vaccination of small-world networks offers more protection than immunization by natural epidemic spread. This pattern can be attributed to the high degree of clustering on small-world networks (Watts & Strogatz 1998) as random vaccination tends to distribute some vaccinated nodes in all the clusters. While much of the discussion of social networks has focused on the degree distribution, these results suggest that higher order structural properties, such as clustering, can have important implications for the epidemiological evolution and robustness of populations.

Many pathogens exhibit recurrent outbreaks with a more or less regular inter-epidemic period (Anderson & May 1991). The intervening build-up of susceptible individuals, through births and loss of immunity, leads to the breakdown of herd immunity and increasing population vulnerability. Though typically described in terms of cycles in the number or density of susceptible and infectious hosts, these recurrent outbreaks should result in a concomitant cycling in the geometry of the active contact network. The build-up of susceptible nodes following an epidemic leads to an increase in the mean and variance of node degree (see electronic supplementary material). The contact network thereby becomes more susceptible to a subsequent outbreak, which will result in the breakdown of connectivity and begin the cycle anew. For recurring diseases, this suggests that vaccine priorities should be designed to complement naturally acquired immunity in the inter-epidemic periods, perhaps with special attention to the highly connected, and thus high-risk, individuals that have not recently been infected.

Supplementary Material

Analytical solutions for random vaccination and average residual degree.

Here we present analytical solutions for the mean original degree and mean residual degree of a network following random vaccination. Also we present the derivation of the average residual degree of a network following an epidemic and a comparison to the results of Newman 2005.

SIRS dynamics on a small world network.

This movie shows the change in the distribution of epidemiologically active network through time under SIRS dynamics.

SIRS dynamics on a scale free network.

This movie shows the change in the distribution of epidemiologically active network through time under SIRS dynamics.