The Number and Spatial Distribution of IP₃ Receptors Underlying Calcium Puffs in Xenopus Oocytes

Abstract

Calcium puffs are local Ca²⁺ release events that arise from a cluster of inositol 1,4,5-trisphosphate receptor channels (IP₃Rs) and serve as a basic “building block” from which global Ca²⁺ waves are generated. Important questions remain as to the number of IP₃Rs that open during a puff, their spatial distribution within a cluster, and how much Ca²⁺ current flows through each channel. The recent discovery of “trigger” events—small Ca²⁺ signals that immediately precede puffs and are interpreted to arise through opening of single IP₃R channels—now provides a useful yardstick by which to calibrate the Ca²⁺ flux underlying puffs. Here, we describe a deterministic numerical model to simulate puffs and trigger events. Based on confocal linescan imaging in Xenopus oocytes, we simulated Ca²⁺ release in two sequential stages; representing the trigger by the opening of a single IP₃R in the center of a cluster for 12 ms, followed by the concerted opening of some number of IP₃Rs for 19 ms, representing the rising phase of the puff. The diffusion of Ca²⁺ and Ca²⁺-bound indicator dye were modeled in a three-dimensional cytosolic volume in the presence of immobile and mobile Ca²⁺ buffers, and were used to predict the observed fluorescence signal after blurring by the microscope point-spread function. Optimal correspondence with experimental measurements of puff spatial width and puff/trigger amplitude ratio was obtained assuming that puffs arise from the synchronous opening of 25–35 IP₃Rs, each carrying a Ca²⁺ current of ∼0.4 pA, with the channels distributed through a cluster 300–800 nm in diameter.

INTRODUCTION

A major mechanism of calcium signaling in many cell types involves the liberation of Ca²⁺ ions sequestered in the endoplasmic reticulum (ER) through inositol 1,4,5-trisphosphate (IP₃) receptor channels (IP₃Rs) (1). The IP₃R channel opens upon the binding of both Ca²⁺ and IP₃, resulting in a regenerative mechanism of Ca²⁺-induced Ca²⁺ release (CICR), whereby Ca²⁺ ions released from an open channel can diffuse and open nearby IP₃Rs. However, the cytoplasm does not act simply as a continuous, homogeneous excitable medium in which the generation of repetitive Ca²⁺ waves can be explained in terms of the averaged population behavior of intracellular IP₃Rs. Instead, Ca²⁺ liberation occurs at discrete functional release sites, spaced a few micrometers apart, generating localized, transient Ca²⁺ signaling events (Ca²⁺ puffs) (2,3), which may both activate localized cellular processes and serve as the basis by which global Ca²⁺ waves propagate in a saltatory manner from release site to release site (4,5).

As originally described, puffs were thought to represent relatively stereotyped events (3). That is to say, repeated events at the same or different sites appeared to be of similar magnitude and time course, and could be considered as uniform “building blocks” in the generation of the global cellular signal. However, subsequent studies with improved resolution have revealed greater complexity, including detection of Ca²⁺ release events (“blips”) in Xenopus oocytes (6) and HeLa cells (7) that are yet smaller than the puffs. Blips are proposed to represent “fundamental” events of calcium signaling, arising through the opening of individual release channels, whereas the puffs represent “elementary” events involving the concerted activation of several tightly clustered channels by local calcium feedback (4,6,7). Thus, local IP₃-mediated Ca²⁺ signals represent a hierarchy of events of differing magnitude (8,9).

Important unresolved questions concern the number of IP₃Rs that open during a puff and the distribution of these channels within a cluster. Experimental estimates of the Ca²⁺ flux underlying a “typical” puff in Xenopus oocytes have been made from the signal mass of the fluorescence signal, yielding a corresponding Ca²⁺ current of ∼2.5 pA (8). On the assumption that the Ca²⁺ current through a single IP₃R channel under physiological conditions is 0.5 pA (10), this yielded a minimum estimate of five for the number of open channels in a puff. Independently, patch-clamp recordings from native IP₃Rs in Xenopus oocyte nuclei revealed a clustered spatial distribution, with a maximum of ∼8 IP₃Rs contained in the active patch regions (∼1 μm²) on the nuclear envelope (11).

The temporal and spatial limitations of optical microscopy limit resolution of the Ca²⁺ dynamics underlying puffs, but computational modeling offers a powerful tool to explore these processes at time and distance scales inaccessible to direct observation. Modeling of intracellular Ca²⁺ dynamics has proceeded along two distinct paths. In the first approach, IP₃R channels are assumed to be sufficiently close that Ca²⁺ concentrations can be considered homogeneous throughout the cluster, permitting use of an isolated dimensionless model (12–15). With such a tight cluster of stochastic IP₃R channels, Shuai and Jung (12) concluded that the variability of puff amplitudes, lifetime, and interpuff intervals mainly arise through stochastic variation in both the number of channels recruited and the duration of channel opening because of the stochastic IP₃R channel dynamics in the cluster. Shuai and Jung (16) further showed that a clustered channel distribution, in conjunction with stochastic channel dynamics, enhances the capability of intracellular Ca²⁺ signaling in response to weak IP₃ stimulation. Their model suggested that there are in total ∼16–50 IP₃Rs in a cluster. In the second approach, IP₃R channels are considered to be distributed more realistically in cytosolic space, and diffusion of Ca²⁺ ions within a cluster is explicitly simulated. Depending on the problems discussed, the puff simulation has been modeled either deterministically (17) or stochastically (18). Swillens et al. (18) concluded that a puff may be generated by the opening of ∼5 IP₃R channels, each passing a Ca²⁺ current of ∼0.1 pA, and that a typical Ca²⁺ release site contains in total some 20–30 IP₃Rs, packed closely together (∼12 nm spacing) to permit effective interchannel communication and, thus, synchronization.

Here, we reconsider the microarchitecture of puffs on the basis of new experimental findings that many puffs are preceded by small and transient “trigger” events (19). These events likely arise through the spontaneous initial opening of a single IP₃R channel, which provides sufficient Ca²⁺ to then recruit neighboring channels by CICR and thereby trigger a puff. Comparison of the amplitudes and spatial distributions of triggers and puffs then provides a useful yardstick by which to estimate the number and distribution of IP₃Rs active during a puff. Our simulations suggest that a cluster model of closely packed channels cannot be reconciled with these experimental observations. Instead, we obtain an optimal correspondence assuming that a puff involves the synchronous opening of some 25–35 IP₃Rs, distributed throughout a region 300–800 nm across, with each channel passing a Ca²⁺ current of ∼0.4 pA.

MATERIALS AND METHODS

Puff model

The model consists of two main parts; the Ca²⁺ release source from an ER pool through IP₃R channels, and the subsequent diffusion of Ca²⁺ through the cytosolic space. We simulate the propagation of Ca²⁺ throughout a cuboid cytosolic space with dimensions of (Fig. 1 A). The IP₃R channels are, for simplicity, assumed to be distributed on a square plane at the center of the cubic cytosolic space, i.e., the plane of (x, y, z = 3000 nm) (Fig. 1 B). In comparison to the large cytosolic volume, we treat the ER pool as a two-dimensional flat plane occupying no volume in the simulation, but acting as an infinite pool of releasable Ca²⁺. Control simulations showed that the size of the model space (Fig. 1 A) was sufficiently large that the results were not appreciably affected by boundary conditions, even when considering clusters as large as 1 μm².

FIGURE 1.

Design of the Ca²⁺ puff model. (A) Diffusion of Ca²⁺ within the cytosol is modeled within a cuboid space with dimensions . IP₃R channels are distributed on a square plane (solid) centered within the cubic cytosolic space, i.e., the plane of (x, y, z = 3000 nm). (B) Distribution of IP₃Rs (shaded circles) within a square cluster of length L. The ER pool is assumed to be a two-dimensional flat plane occupying no volume. (C) The point-spread function of the confocal microscopes is modeled as a weighted Gaussian distribution in all dimensions, with widths (FWHM) of 300 nm in the lateral (x,y) dimensions and 800 nm in the axial (z) dimension.

Each open IP₃R channel releases a Ca²⁺ current and thus the channel Ca²⁺ flux is

(1)

where , and is the small cubic grid volume around the channel pore with spatial grid step in the computation. Here we assume a constant Ca²⁺ current passing through each open IP₃R channel. A more realistic treatment would be to assume the Ca²⁺ flux to be proportional to the Ca²⁺ concentration difference between ER pool and cytosol in channel pore (12), but experimental results suggest there is little diminution in channel Ca²⁺ current during puffs or between temporally close puffs (20).

Our model necessarily incorporates several more simplifying assumptions. Among these, we did not consider Ca²⁺ pump dynamics because these are slow and relatively insignificant on the timescale (a few tens of ms) of the rising phase of puffs. Further, the experimental observations that we simulate utilized intracellular EGTA (300 μM) so as to inhibit the propagation of Ca²⁺ waves (19). This concentration of exogenous buffer is sufficiently high that any endogenous mobile buffers (which are, in any case, poorly characterized) can be reasonably ignored. Thus, the model includes the following species in the cytosolic space: free Ca²⁺ ions (FreeCa); stationary buffer in free (Stat) and Ca²⁺-bound forms (StatCa); exogenous mobile buffer EGTA in free (EGTA) and Ca²⁺-bound forms (EGTACa); and the Ca²⁺ fluorescent indicator in free (Fluo) and Ca²⁺-bound forms (FluoCa). FluoCa, in principle, represents any generic fluorescent Ca²⁺ indicator dye, but here we selected parameter values (Table 1) appropriate for Fluo-4-dextran, as this was used in the experimental studies we are modeling (19).

TABLE 1.

Standard parameter values used for simulations

Parameter	Value	Unit	References
Cytosol structure
Length of the cubic cytosol	6.0
IP3R Channel
Constant Ca2+ current,	0.4	pA
Free Ca2+
Diffusion coefficient,	200	μm2 s−1	21
Resting concentration	0.1		19
Fluo indicator (Fluo-4-dextran)
Diffusion coefficient,	15	μm2	21
Total concentration,	25		19
Dissociation constant,	2.0		19
On-rate,	150		37
Off-rate,	300
EGTA mobile buffer
Diffusion coefficient,	200	μm2 s−1
Total concentration,	300		19
Dissociation constant,	0.15		38
On-rate,	5		38
Off-rate,	0.75
Stationary buffer
Total concentration,	300		21
Dissociation constant,	2		24, 25
On-rate,	400		24, 25
Off-rate,	800.0

We consider the reactions of stationary buffer [Stat], mobile buffer [EGTA], and indicator [Fluo] with free Ca²⁺:

(2)

where X represents Stat, EGTA, or Fluo; the forward binding rate; and the backward binding rate.

The reaction-diffusion equations are then described as follows: for free Ca²⁺ with diffusion coefficient D,

(3)

in which the channel distribution function = 1 at the channel grids, otherwise (Fig. 1 B). For FluoCa with diffusion coefficient ,

(4)

For the Ca²⁺-bound EGTA mobile buffer with diffusion coefficient ,

(5)

and for the Ca²⁺-bound stationary buffer,

(6)

The total concentrations for Ca²⁺ indicator, EGTA buffer, and stationary buffer are , , and, respectively. Because each Ca²⁺ buffer, with or without Ca bound, has almost the same molecular weight, it is generally assumed that the diffusion coefficients of the free and Ca-bound forms of the indicator and mobile buffer can be considered to be equal (21–23). Thus, with a homogenous distribution of the total of the bound and free species as the initial condition, the sum will remain constant at all locations and times. The concentration at any location of the free species is then given by subtracting the concentration of the Ca-bound form from the total.

At the initial resting concentration of free Ca²⁺ ions , the resting concentrations of [FluoCa], [StatCa], and [EGTACa] are given, respectively, as , , and , where the dissociation constants κ_F, κ_S, and κ_E for Fluo Ca²⁺ buffer, stationary Ca²⁺ buffer, and EGTA are given by the respective ratios of their off and on binding rates.

Simulation of confocal fluorescence signals

The puff model simulates the distribution of [FluoCa] in three dimensions (x, y, z) as a function of time. To relate this to experimental observations of fluorescence signals imaged by confocal laser scanning microscopy (19), we assumed that the fluorescence is linearly proportional to [FluoCa] and calculated a weighted average of [FluoCa] throughout a volume corresponding to the microscope point-spread function (PSF) (21).

A representative PSF of the confocal microscope is illustrated in Fig. 1 C. The PSF resembles an American football, weighted as a Gaussian distribution in all dimensions, but with greater axial than lateral width. For our simulations, we assumed that the microscope was focused in the plane of the IP₃R (z = 3000 nm). Then, the confocal signal () that would result at any point (x₀, y₀, z₀ = 3000 nm) can be calculated as

(7)

with λ_x = λ_y = 0.0325 μm² and λ_z = 0.231 μm² chosen to match experimental PSF measurements of full width at half-maximal amplitude (FWHM) of 300 nm in the lateral and 800 nm in the axial dimension (21).

Deterministic simplification of complex channel dynamics

Our goal was to simulate cluster parameters (i.e., open channel number (N) during a puff and the cluster length (L)) that closely reproduced experimental observations of puffs and trigger events (19). These experimental data yielded the following average values: trigger amplitude = 1.26 ; trigger duration = 11.74 ms ; trigger width (FWHM) = 0.57 μm ; puff amplitude = 7.27 ; puff rise time = 18.97 ms ; puff FWHM = 1.51 μm.

As discussed by Rose et al. (19), the trigger event is presumed to arise through the opening of a single channel, whereas during the puff, some number, N, of IP₃Rs open and close with complex dynamics. Here, we apply a deterministic simplification of the average trigger and puff events rather than simulating stochastic channel dynamics. Specifically, we assume that a single channel at the center of the cluster initially opens for ΔT₁ = 12 ms, representing the trigger event. Subsequently, N IP₃R channels open simultaneously and remain open for ΔT₂ = 19 ms, representing the rising phase of the puff. The open IP₃R channels are evenly distributed on a square plane with a length of L. The distance between two nearby channels is thus (Fig. 1 B).

Confocal signal

Experimental confocal signals are typically expressed as fractional changes in fluorescence (F) above the resting baseline F₀, i.e., . Similar to the experimental procedure for calculating, we have , where _Rest is related to [FluoCa]_Rest. The confocal signal is rescaled by introducing a constant scaling parameter , such that the rescaled confocal fluorescence signal (Con), defined in the model as

(8)

has a scale similar to that of the experimental signal . Even though we cannot accurately simulate the absolute value of confocal signal in the model, we can use the trigger event for comparison with puff. The resulting ratio (puff amplitude/trigger amplitude) has a real meaning and can be directly compared with the experimental data.

Signal mass

Sun et al. (8) introduced the concept of “signal mass” for quantifying confocal fluorescence measurements of the Ca²⁺ flux underlying local Ca²⁺ release events. Signal mass (SM) is defined here as the integration of the one-dimensional confocal linescan fluorescence signal, , throughout three dimensions. Assuming that sequestration of liberated Ca²⁺ ions from the cytosol (e.g., by SERCA pumps) is negligible on the timescale considered, this provides a measure proportional to the total amount of Ca²⁺ liberated. Similar to the computation of signal mass from confocal linescan data, in the model we consider only a one-dimensional (along the x axis, as shown in Fig. 1 B) confocal signal in calculating SM:

(9)

Matching degree function

Our goal was to vary the cluster parameters (i.e., the open channel number N for a puff and the cluster length L) so as to most closely reproduce the experimental data of the mean triggered puff events (i.e., a puff with puff FWHM =1.5 μm, and a puff-to-trigger amplitude ratio (19)). We thus defined a matching degree function as follows:

(10)

The puff width and the puff/trigger amplitude ratio are obtained with the model for a given cluster with open channel number N during a puff and the cluster length L, and W₀ and R₀ are the corresponding experimental values. A perfect match corresponds to = 2.

Numerical method and parameters selection

Values for the “standard” parameters used in the model are given in Table 1. Some parameters (, ) correspond to the experimental conditions used by Rose et al. (19), whereas others are taken from the references listed in Table 1. The same parameters were used in a model by Shuai and Parker (21) that satisfactorily replicated imaging data of the single N-type Ca²⁺ channel on the oocyte membrane (22,23). The finite-difference method was used to solve the partial differential equations given above. At the boundaries of the cubic cytosol, the concentrations of all signal species are held constant at their resting states. Simulations used a time increment and spatial grid step nm. Although a spatial step of 40 nm was too coarse to accurately represent the concentration distribution of free Ca²⁺ around the channel pore, our principle aim was to model the broader distributions of the [FluoCa] and confocal signals. Tests using smaller values of = 20 nm and (data not shown) validated that the use of coarser steps (necessary for computational efficiency) did not significantly distort these signals.

RESULTS

Simulation of trigger and puff amplitudes

Fig. 2 outlines our simulation procedure. This is illustrated for N = 25 open IP₃R channels homogeneously distributed throughout a square with L = 520 nm because, as described later, these values provide a good agreement with experimental data. A central channel (as shown in Fig. 1 B) opens for ΔT₁ = 12 ms representing a trigger event, followed by the opening of N = 25 IP₃R channels for ΔT₂ = 19 ms, corresponding to the rising phase of the puff; after which all channels simultaneously close (Fig. 2 A).

FIGURE 2.

Deterministic simulation of a typical triggered puff. (A) The event is assumed to arise through the opening of a single IP₃R channel for 12 ms (from time 0 to time T₁) that gives rise to the trigger, followed by the simultaneous opening of a total of 25 channels for 19 ms (times T₁ to T₂), corresponding to the rising phase of the puff. The plot shows number of open channels (N_open) as a function of time. Simulations in Figs. 3 and 4 also assume the same number and kinetics of channel openings. (B) Resulting changes in free [Ca²⁺] in the grid element centered within the channel cluster and containing the trigger channel. (C) Corresponding changes in [FluoCa] at the same central grid element. (D) Simulated confocal fluorescence signal (Con) as would be recorded by a confocal spot centered on the trigger channel. The trace was derived from the distribution of [FluoCa] throughout the model space as a weighted average of the microscope point-spread function. (E) Graphical representation of the evolution of the trigger event. The panel shows a simulated linescan (x–t) confocal image, with increasing fluorescence signal (Con) depicted by increasingly “warm” colors and increasing height. (F) Corresponding simulated linescan image showing both the trigger and puff at reduced magnification.

The resulting changes in free Ca²⁺ concentration [FreeCa] at the central channel grid as a function of time are shown in Fig. 2 B. Notice that the local [FreeCa] stabilizes very rapidly, both after the initial opening of one channel, and after 25 channels open. It also decays quickly (by 90% within 1.5 ms) after channel closure. Corresponding changes in [FluoCa] at the same central channel grid are shown in Fig. 2 C. In contrast to the local free [Ca²⁺], the local concentration of Ca²⁺-bound indicator increases less rapidly during the opening of the trigger channel, quickly saturates after opening of the 25 channels, and falls much more slowly after the channels close. Finally, Fig. 2 D shows the predicted confocal signal Con, computed as an integral of [FluoCa] around the center of the cluster weighted by the microscope PSF. Despite the rapid saturation of Ca²⁺ binding to Fluo at the cluster center, the fluorescence averaged throughout the confocal volume approaches saturation more slowly. Nevertheless, indicator saturation introduces appreciable nonlinearity in the magnitude of the simulated fluorescence signals. Although the Ca²⁺ flux during the puff is 25-fold greater than during the trigger, the fluorescence amplitude (Con) is only ∼6 times greater.

These results are summarized graphically in Fig. 2, E and F, showing pseudocolored representations of the spatiotemporal evolution of a simulated trigger-puff event. The maximal spatial width of the trigger event immediately before the puff initiated (T₁ = 12 ms) is 0.61μm (FWHM), and the width of the puff at its peak (T₂ = 31 ms) is 1.46 μm.

Spatial distribution of the trigger and the puff signals

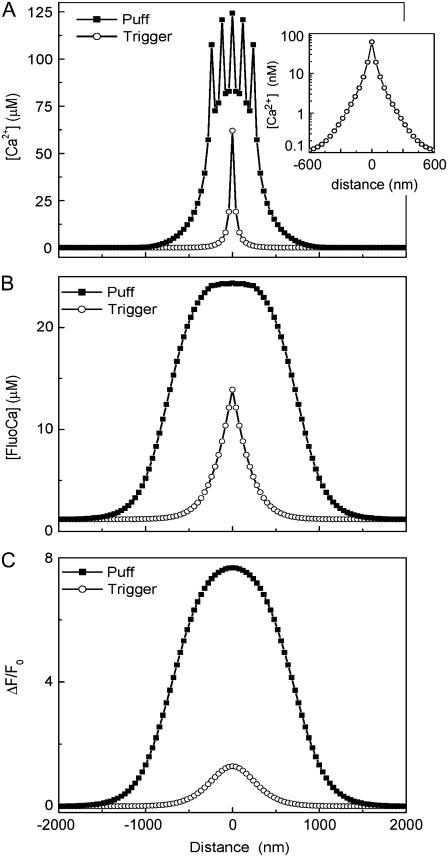
The spatial distributions of the trigger event at T₁, and of the puff at T₂, are shown in Fig. 3 for [FreeCa], [FluoCa], and Con (Fig. 3, A–C, respectively). The trigger event can be treated as a point-source of Ca²⁺ release. In that case the steady-state distribution of [FreeCa] diffusing passively from the channel is expected to approximate an exponential decay with increasing distance, as confirmed by the inset to Fig. 3 A, showing the spatial distribution of [FreeCa] at T₁ on a semilogarithmic scale. In marked contrast, the distribution of [FreeCa] during the puff shows a “crown” shape, with multiple peaks, each corresponding to an open channel site (Fig. 3 A). Moreover, as noted in Methods, the relatively coarse (40 nm) grid in our model does not accurately reproduce the distribution of [FreeCa] at small distance scales, and the true gradients around each channel are expected to be greater than indicated.

FIGURE 3.

Spatial distributions during the trigger event (○) at time T₁ and during the puff (▪) at time T₂ for [FreeCa] (A), [FluoCa] (B), and confocal signal Con (C). The spatial distributions are plotted along the x axis (see Fig. 1 A), centered on the triggering channel (x = 3000 nm). The inset in A shows the [FreeCa] distribution of the trigger replotted on semilogarithmic axes.

Because the Ca²⁺ binding and unbinding dynamics of Fluo-4 act as a spatial low-pass filter, the distribution of [FluoCa] for the trigger event is appreciably broader than for the underlying distribution of [FreeCa] (Fig. 3 B; open circles). This effect, together with local saturation of indicator binding also smoothes the distribution of [FluoCa] during the puff, so that individual peaks around each channel are no longer evident, and the spatial extent (FWHM) of [FluoCa] is about double that of [FreeCa] (Fig. 3 B, solid circles). Considering, finally, the distribution of Con, an interesting finding is that the trigger event at T₁ shows a broader spatial distribution than the underlying distribution of [FluoCa], whereas the distribution of Con for the puff event at T₂ is actually sharper than that of [FluoCa] (Figs. 3, B and C). This results from the confocal microscope acting as an ∼300-nm spatial-average filter, which broadens the trigger [FluoCa] signal with a FWHM of <300 nm, but slightly sharpens the flat-topped distribution of [FluoCa] during the puff.

Given the spatial distribution of [FreeCa], [FluoCa], and Con, we can calculate their corresponding spatial widths (FWHM) at different times (Fig. 4 A). The widths of the trigger event at T₁ are 57 nm, 318 nm, and 610 nm for [FreeCa], [FluoCa], and Con, respectively; whereas corresponding values for the puff at T₂ are 0.55μm, 1.54μm, and 1.46μm. The width of the free Ca²⁺ microdomain reaches a new steady-state value almost immediately after the opening of one channel during the trigger, and then after opening of several channels during the puff (Fig. 4 A, dashed line). During the duration of the trigger event, the FWHM of [FluoCa] is ∼½ that of Con, whereas shortly after puff initiation, the FWHM of [FluoCa] becomes slightly greater than that of Con (Fig. 4 A, dotted and solid lines, respectively).

FIGURE 4.

Spatial width and signal mass of the triggered puff event. (A) Changes in spatial widths (FWHM) of [FreeCa] (dashed line), [FluoCa] (dot-dashed line), and Con (solid line) as functions of time resulting from openings of IP₃R channels as shown in C. (B) Corresponding changes in signal mass of the fluorescence signal from the model, computed as a symmetrical integral of [FluoCa] in three dimensions from a one-dimensional section along the x axis centered on the trigger channel.

Signal mass

The signal mass derived by computing the integral of Con in three dimensions is plotted in Fig. 4 B as a function of time. During the trigger event and the puff rising phase, the signal mass increases nearly linearly with rates of 0.047 ms⁻¹ and 1.12 ms⁻¹, respectively. The ratio of these rates (1:23.8) should reflect the relative numbers of channels open, since the rate is expected to be proportional to Ca²⁺ flux; and, indeed, corresponds well to the 25 channels open during the puff in the simulation. Based on the same reasoning, we can also estimate the number of channels open during a puff from the signal mass at times T₁ and T₂—values that are easier to derive from experimental data. From the simulation in Fig. 4 B, the respective total signal masses are 0.52 and 21.0. Thus, considering the effect of the different time durations, the ratio (21.0/ΔT₂)/(0.52/ΔT₁) = 25.5 provides another estimate of the open channel number during a puff.

Varying the open IP₃R number

The simulations illustrated above used a value of N = 25 open IP₃R channels for a puff. Now, we consider how different numbers (4–121) of open IP₃R channels affect the puff behavior by simulating their behavior when distributed within clusters of dimensions L = 200, 520, and 1000 nm (Fig. 5). The FWHM of the puff at T₂, and the amplitude ratio R are plotted in Fig. 5, A and B, respectively, as functions of open IP₃R number N. With increasing N, the puff FWHM and the amplitude ratio both increase. Note that because the trigger event does not change, the absolute puff amplitude as a function of N is directly proportional to the ratio.

FIGURE 5.

Effects of changing open IP₃R number N on puff width at time T₂ (A), and on the amplitude ratio R between puff and trigger (B). Different clusters with lengths L = 200 nm (○), 520 nm (★), and 1000 nm (□) were simulated. For comparison, the dashed lines in A and B show the mean FWHM (W₀ = 1500 nm) and amplitude ratio (R₀ = 6) of experimental observations of puffs.

Fig. 5 shows that, for , further increases of N primarily result in an increase in puff FWHM rather than puff amplitude because [FluoCa] around the cluster approaches saturation. Thus, even if more channels open, the additional Ca²⁺ cannot bind to the free Fluo4 near the cluster area, but only to more distant free Fluo4 molecules.

Considering, then, puffs generated by only a few open channels, the simulations predict (Fig. 5) that small cluster dimensions (<520 nm) will generate puffs with both a smaller FWHM and a lower amplitude ratio as compared to experimentally observed means of a puff width of 1.6 μm and a ratio of 6.0. With more widely distributed clusters (e.g., L = 1000 nm), the model is able to match the puff FWHM of 1500 nm (Fig. 5 A), but the puff/trigger amplitude ratio R reduces to <3 (Fig. 5 B). Thus, using the “standard” parameters listed in Table 1, we were not able to reproduce the observed properties of experimental puffs in simulations employing relatively few (N < 10) open channels in the cluster.

However, Fig. 5 shows that the experimentally observed puffs can be mimicked by a cluster with a size of L = 520 nm or 200 nm and containing some 20–40 open channels during the puff. The optimal match to the averaged experimental puff is obtained for a cluster with = 520 nm and N = 25.

Varying the cluster dimensions

In Fig. 6 we explore further how the cluster length L affects the puff behavior for N = 9, 25, and 49 open channels in the cluster. For a given number N during a puff, increasing cluster dimension L results in an increase of puff FWHM and a decrease of the puff/trigger amplitude ratio. Because the trigger event does not change here, the puff amplitude again varies with L in direct proportion to the puff/trigger amplitude ratio.

FIGURE 6.

Effects of changing cluster dimensions (length L) on puff FWHM at time T₂ (A) and the amplitude ratio R between puff and trigger (B). Clusters containing 49 (○), 25 (★), and 9 (□) open channels were simulated. For comparison, the dashed lines in A and B show, respectively, the mean FWHM (W₀ = 1500 nm) and the amplitude ratio (R₀ = 6) of averaged experimental puffs.

In the case of a puff resulting from nine open channels, the simulation cannot replicate the parameters of the average experimental puff. If the channels are packed tightly (L < 200 nm) the puff/trigger amplitude ratio is ∼5, but the puff FWHM is only ∼1000 nm. Conversely, larger cluster dimensions (L ∼ 1000 nm) can replicate a puff width of ∼1500 nm, but the puff and trigger ratio reduces to <3 (Fig. 6, square data). A puff generated by 49 open channels results in a puff width >1700 nm, even for a tightly packed cluster (Fig. 6, circles). Thus, simulations of clusters containing either few (N < 10) open channels or many (N > 50) open channels fail to replicate the properties of experimental puffs. However, if we assume that a puff involves 25 open channels, the puff FWHM and puff/trigger amplitude ratio become less sensitive to changes in cluster length. An optimal match to the average experimental puff was obtained with cluster lengths between 300 nm and 800 nm (Figs. 5 and 6).

Influence of IP₃R single-channel Ca²⁺ current

Changes in IP₃R single-channel current are reflected in the behavior of both trigger events and puffs (Fig. 7). Increasing the IP₃R current results in the FWHM (Fig. 7 A) and peak amplitude (Fig. 7 B) of the simulated confocal signal increasing for both puff and trigger. However, the ratio of puff/trigger amplitudes decreases with increasing single-channel current (Fig. 7 C). This is because for a large IP₃R current, the puff amplitude ([FluoCa]) becomes saturated (Fig. 7 B), whereas the smaller amplitude of the trigger continues to increase.

FIGURE 7.

Influence of IP₃R channel Ca²⁺ current on puff FWHM at time T₂ (A), confocal image amplitude (B), and the amplitude ratio R between puff and trigger (C). Three different clusters are considered: open channel number N = 25 and cluster length L = 520 nm (★); N = 9, and L= 520 nm (○); and N = 9 and L = 200 nm (□). Additionally, solid triangles show the corresponding relationships for the trigger event at time T₁. For comparison, the dashed lines in A and C mark, respectively, the FWHM (W₀ = 1500 nm) and the amplitude ratio (R₀ = 6) of the mean experimental puff.

Our simulation predicts that if the channel current is as small as 0.1 pA, a puff/trigger ratio of ∼6.0 is achieved by few, tightly packed open channels (Fig. 7 C). However, this results in a puff FWHM of <1000 nm for clusters with and nm (Fig. 7 A), appreciably narrower than experimental observations. Conversely, large (>0.5 pA) single-channel currents also fail to replicate the mean experimental trigger-puff event. This is because a small puff/trigger ratio (<3) is obtained for a large IP₃R current (Fig. 7 C) as a result of the trigger amplitude being large in comparison with the saturated puff amplitude.

Effects of changing other model parameters

The choice of parameters used in the model may have strong effects on the simulation results. Some parameters in our simulation, such as the total concentration of Fluo4 and EGTA, were chosen to match the experimental conditions under which the triggers and puffs that we aim to model were observed (19); others, such as the diffusion coefficient for free Ca²⁺ ions are known with some accuracy. However, several important parameters listed in Table 1 remain poorly characterized. In this section, we explore the sensitivity of our conclusions to variations in some of these parameters.

Considering first the properties of the indicator dye Fluo-4-dextran, we assumed a dissociation constant K_d of 2 μM for Ca²⁺ binding. Small errors in this assumption are likely to be relatively unimportant, as experimental results using Fluo-4-dextrans with nominal dissociation constants of ∼3 μM or ∼0.8 μM showed only slight differences in puff and trigger characteristics (19). We thus examined how changes in K_d between 0.5 μM and 5 μM affected the conclusions from our model. We considered two simple ways of varying the affinity: by changing either the association (k_on) or dissociation (k_off) rate while keeping the other rate fixed. Increasing K_d from 0.5 μM to 5 μM causes the puff FWHM to decrease from 1700 nm to 1300 nm, whereas the puff/trigger amplitude ratio increases from 3 to 10 if the affinity is changed by altering k_on, and from 5 to 7.5 if k_off is changed. Thus, the puff characteristics are more sensitive to changes in k_on than in k_off of the indicator. Given that the Ca²⁺ association rate is likely to be diffusion-limited, differences in Fluo-4 affinity will primarily reflect differences in k_off, perhaps explaining why the experimental puffs were relatively insensitive to indicator affinity.

In the experimental studies, cytosolic EGTA concentrations of 90 μM or 300 μM were used to inhibit propagating Ca²⁺ waves (19). We assume these are sufficient to overwhelm the actions of any endogenous mobile buffers, and we thus modeled puffs considering 300 μM EGTA as the only mobile Ca²⁺ buffer. Further simulations with our standard parameters show that changing [EGTA] from 50 to 500 μM reduces the amplitudes of both triggers and puffs by similar extents, such that their ratio remains ∼6; moreover, the puff FWHM decreases only slightly from 1600 to 1400 nm. Thus, changes in [EGTA]_T within the range employed experimentally (19) have little effect on our estimates of IP₃R number and distribution.

Maximum likelihood determination of open-channel number and density within a cluster

As described above, our simulations suggest that a typical puff in the Xenopus oocyte arises from the opening of some 25 IP₃R channels distributed as a cluster with a width of ∼500 nm. To further validate this conclusion, and determine the range of model parameters over which a good fit could be obtained to the experimental observations, we simulated puffs generated across a wide region of parameter space and used a matching degree function (see Materials and Methods) to estimate the range of model parameters that result in simulated puffs that would be consistent with experimental observations.

The results are depicted graphically in Fig. 8 by contours of increasingly “warm” colors that signify an increasingly good match to the mean experimental puff parameters of puff/trigger ratio R₀ = 6 and puff width (FWHM) W₀ = 1.5 μm. If both the FWHM (W) and the amplitude ratio (R) of the model puff equal the experimental values W₀ and R₀ the matching degree is 2, which is depicted as red in Fig. 8. Other colors represent lower matching degrees, as indicated by the scale bar. As a guide, the entire colored regions (excluding black) correspond to simulated puffs with FWHM in the range of 1500 ± 300 nm and amplitude ratios of 6 ± 1.5; the red region corresponds to puffs with FWHM 1500 ± 100 nm and an amplitude ratio 6 ± 0.25.

FIGURE 8.

Matching degree function showing the correspondence between puffs simulated with various parameter values and the mean characteristics (puff/trigger amplitude ratio R₀ = 6 and FWHM W₀ = 1500 nm) of experimentally recorded puffs with triggers. In each panel, puffs were simulated across a wide parameter space of cluster length L and open channel number N. For any given pair of parameter values, the correspondence between the resultant simulated puff and the experimentally observed puff was calculated by a matching function (see text for details). A perfect correspondence (matching degree = 2) is depicted in red, with matching degrees <1.94 in black, and intermediate values on a pseudocolor scale as indicated by the color bar. (Left to right) Results assuming single-channel IP₃R currents of 0.2, 0.4, and 0.5 pA, respectively.

The central panel in Fig. 8 shows results of simulations where the dimensions of the cluster (L, horizontal axis) and number of channels opening during a puff (N, vertical axis) were varied while using standard values for other model parameters (Table 1). An optimal correspondence with the mean experimental puff is obtained by assuming the synchronous opening of ∼25–35 IP₃Rs distributed through a region of ∼400–700 nm across. However, the match is less sensitive to variation in cluster dimensions than to changes in open channel number, such that a reasonable fit is possible over a span of cluster lengths ranging from ∼200–900 nm.

Our standard value of single-channel current (0.4 pA) is based on extrapolations from experimental data (10), but is subject to considerable uncertainty, and smaller currents of ∼0.1 pA have been used in previous simulations (17,18,24,25). We thus investigated how changes in the channel current would affect our estimates of N and L. This is shown across the row of three panels in Fig. 8, illustrating results obtained with single-channel currents of 0.2 (left) and 0.5 pA (right) in comparison with the 0.4 pA data discussed above (center). Considering a channel Ca²⁺ current of 0.2 pA, only a very small area in the parameter space (corresponding to N ∼ 20 and L > 1000 nm) provided a match to the experimental data. For this reason, and because a sparse distribution of channels across a cluster with a diameter >1 μm may be expected to show detectable inhomogeneities in experimental linescan images of puffs, it seems unlikely that physiological single-channel IP₃R Ca²⁺ currents are as small as 0.2 pA. Conversely, a large IP₃R Ca²⁺ current (>0.5 pA) fails to permit a good match to the experimental data over any range of N and L (Fig. 8, right). Thus, the Ca²⁺ channel current appears to lie between 0.2 and 0.5 pA.

DISCUSSION

In this article, we estimate the single-channel IP₃R Ca²⁺ current and the number and spatial distribution of IP₃Rs that open during a Ca²⁺ puff by comparing simulated puffs in a deterministic model with experimental observations (19).

Number and distribution of open IP₃Rs underlying a puff

Our simulations were based on recent experimental findings that puffs in Xenopus oocytes are often preceded by brief trigger events that likely result from the initial opening of a single IP₃R channel (19). The trigger thus provides a yardstick by which to calibrate fluorescence Ca²⁺ signals in terms of the underlying number of channels that generate the Ca²⁺ flux. We sought to determine model parameter values yielding simulated puffs that matched experimental observations in terms of their relative amplitudes, spatial spread and time course. A good correspondence with the experimental data was obtained by assuming that a puff involves the synchronous opening of 25–35 IP₃Rs, distributed through a region 300–800 nm across. Both of these values are greater than several earlier estimates (12–15,17,24–26). These parameter ranges result in simulated puffs with widths of 1500 ± 300 nm and amplitudes relative to trigger events of 6 ± 0.25; as compared to respective mean experimental measurements of 1510 nm and puff/trigger amplitude ratio of 5.8 (19).

A different, more direct approach has been to estimate Ca²⁺ flux from the signal mass of fluorescence events associated with local Ca²⁺ signals (8,35,36). Indeed, calculations (Eq. 9) of the signal mass associated with the trigger and puff in our model of the integration yield a ratio of ∼25, consistent with our model setting that 25 channels open simultaneously during a puff. Experimental measurements (19) of the relative signal mass associated with triggers and puffs gave a higher ratio of ∼60, but are subject to considerable error owing to noise; which is not the case for deterministic simulations. Moreover, estimation of signal mass from experimental linescan images is based on assumptions that may break down if the size of the Ca²⁺ source (cluster dimensions) is as large as we conclude. One factor is that calculation from one-dimensional linescan data as defined in Eq. 9 assumes spherically symmetrical distribution of Ca²⁺ and fluorescence, which would not be the case for an extended two-dimensional source. Also, the signal mass was calculated from a Gaussian fit to the one-dimensional profile of fluorescence distribution. Specifically, the signal mass SM is assumed to be proportional to H × FWHM³; where H is the peak amplitude of the Gaussian, and FWHM is its width at half-peak amplitude (35). Applying this formula to our standard model data with 25 channels opening during a puff yields a ratio of (SM_puff at ΔT₂)/(SM_trigger at ΔT₁) = 52, a value discrepant with the true signal mass, but more concordant with the experimental measure of 60. Thus, the fluorescence signal distribution for large sources (i.e., 520 nm in our standard example) no longer matches the approximately Gaussian function expected from a point source.

By calculating the signal mass of fluorescence signals, and assuming that each channel passed a Ca²⁺ current of 0.5 pA, Sun et al. (8) estimated that a minimum of ∼5 IP₃R channels must open during a puff. Swillens et al. (18) then used that value when constructing a stochastic model of IP₃Rs within a cytoplasmic environment so as to gain mechanistic insights into the generation of these local Ca²⁺ signals. To ensure that ∼5 IP₃R channels open during a puff, they proposed that a typical Ca²⁺ release cluster contains 20–30 IP₃R channels in close contact. In their model, the Ca²⁺ current for each IP₃R was assumed to be 0.1 pA and interchannel distances were required to be as small as 12 nm to ensure adequate coupling between channels by CICR. Although the latter distance is incompatible with electron microscopy and single-particle analysis indicating that the IP₃R has a diameter of ∼30 nm (27), several subsequent modeling studies have followed the conclusions of Swillens et al. in assuming that a puff results from a few (<10) open IP₃R channels from a total of ∼20–30 IP₃R channels closely packed in a cluster with diameter <200 nm. (12–17,24–26).

Major differences between our model and the previous modeling studies are that we attempt to realistically simulate experimental measurements of the relative amplitude of the puff, as compared to the trigger, and we consider the spatial extent (FWHM) of these events. Moreover, we simulate the confocal imaging process by modeling the point-spread function of the particular microscope used to acquire the experimental data. By considering both amplitude and spatial parameters of the puff we were able to impose additional constraints on values of open channel number (N) and cluster width (L). For example, an amplitude ratio (puff/trigger fluorescence amplitude) mimicking the experimental mean of ∼6.0 could readily be obtained on the basis of a few closely packed IP₃R channels, each passing a current as little as 0.1 pA (Fig. 7 C), but the puffs obtained from such a tight cluster show a FWHM appreciably smaller than the experimental mean of 1500 nm (Fig. 7 A). Instead, we could only reproduce the experimental puff FWHM by increasing not only the open channel number and channel current, but also the cluster width.

Our model assumes, for simplicity, that a few tens of IP₃R channels remain continually open for the duration (∼19 ms) of the rising phase of a puff. This is probably unrealistic, as patch-clamp recordings of IP₃R channels in the oocyte nuclear envelope show mean open dwell times in the range of 4–10 ms, depending on [Ca²⁺] and [IP₃] (11,28). Thus, whereas our estimate of ∼25 open channels assumes that all are open simultaneously, it is likely that the actual number of channels that participate in a puff will be greater by a factor inversely proportional to the mean channel-open probability during the puff rising phase. For example, if the high local [Ca²⁺] during a puff rapidly inactivates IP₃Rs so that they open only once, the total number of channels opening may thus be more than twice our estimate; i.e., >60. Moreover, it is important to note that our model provides explicit information regarding only those channels that open; and not the total number of IP₃Rs in a cluster. The latter number is likely to be even higher, given that some receptors may fail to bind IP₃ or may become inactivated by Ca²⁺ before they have a chance to open.

Puffs without resolved trigger events

Experimental observations indicate that a proportion of puffs are not preceded by detectable trigger events; possibly because some triggers are too short and small to be resolved (19). Given the scan rate (2 ms/line) and noise level in those experiments, the minimal detectable fluorescence signal would have a duration of >4 ms and an amplitude (ΔF/F) > ∼0.5. Our model simulations (Fig. 2 D) indicate that a confocal signal with this amplitude would be generated by the opening of a single IP₃R channel for 3–4 ms. Thus, puffs that were evoked within ∼4 ms of the opening of an initial IP₃R channel would fail to show detectable triggers. It remains to be determined whether calcium-induced calcium release may occur sufficiently rapidly to recruit multiple IP₃Rs within a cluster on this timescale.

The IP₃R single-channel Ca²⁺ current

Direct measurements of Ca²⁺ currents through IP₃Rs in the presence of physiologically relevant ionic conditions have not yet been obtained. Nevertheless, our simulation results provide some inherent constraints on the likely single-channel Ca²⁺ current by taking into account both the magnitude and spatial distribution of the fluorescence signals during triggers and puffs. Specifically, Fig. 8 suggests that the observed puff characteristics cannot be replicated by single-channel currents <∼0.2 pA or >∼0.5 pA for any feasible combination of channel number and distribution. This range of currents falls within the widely varying estimates derived indirectly from experimental data. An early estimate of 0.47 pA was obtained based on extrapolation of recordings of IP₃R channels reconstituted into planar lipid bilayers to likely concentrations of ER and cytosolic Ca²⁺ (10), a value that was used in some early modeling studies (8,29,30) but is larger than assumed in other more recent simulations (17,18). Those experiments did not, however, consider the blocking of Ca²⁺ flux through the channel pore by Mg²⁺ ions in the cytosol (31). The magnitude of that effect can be extrapolated from data on ryanodine receptors (32), yielding a predicted Ca²⁺ current through IP₃R under physiological conditions of 0.1–0.2 pA (J. K. Foskett, C. White, K. H. Cheung, and D. O. D. Mak, unpublished data).

Moreover, our model assumes a constant Ca²⁺ current (flux) through an open IP₃R channel. An alternative approach, as applied in some models (12,15,16), assumes a Ca²⁺ flux that is proportional to the difference of free Ca²⁺ concentrations between the ER pool and the cytosolic space around the channel pore. Local depletion of Ca²⁺ in the ER pool may then reduce the Ca²⁺ flux throughout a release event, as proposed for sparks in cardiac and skeletal muscle (33,34). However, such luminal depletion appears to be minimal for isolated puffs in Xenopus oocytes, as observations of sequential puffs at intervals of a few hundred milliseconds show little diminution in amplitude of the second puffs (20). Thus, a simple assumption is to consider a fixed ER Ca²⁺ concentration (e.g., 500 μM). In that case, our simulations indicate the Ca²⁺ current approaches an almost constant value within 2 ms after channel opening; which can be well approximated by a constant Ca²⁺ flux, as used in our model.

Nanowaves within clusters?

For IP₃R molecules with a lateral extent of ∼30 nm (27), the maximum number of receptors that could be packed into a square cluster 300–800 nm on a side is 100–600. However, based on our predictions of ∼60 channels within a cluster of L = 500 nm, the coupling between channels would be relatively “loose”, with a mean spacing (center-to-center) of 70 nm. The free Ca²⁺ concentration across the cluster is thus expected to show a pronounced “crownlike”, multiple-peak distribution (Fig. 3 A). A further consequence of relatively large cluster dimensions (∼500 nm), is that spatial-temporal patterning of Ca²⁺ during puffs (resulting, perhaps, from inhomogeneous channel distribution or spreading activation of channels) may be experimentally resolvable. Indeed, Bootman et al. (7) have described propagating “microwaves” during puffs in HeLa cells; and, although our earlier studies in Xenopus oocytes suggested that puffs could be considered as point sources (<300 nm) of Ca²⁺ (8), recent imaging with higher resolution has revealed submicron shifts in Ca²⁺ release foci during puffs (A. Demuro and I. Parker, unpublished data).

CONCLUSIONS

We applied a deterministic simplification of average trigger and puff events to simulate the properties of puffs which, in reality, will display complex stochastic dynamics. For example, patch-clamp recordings of IP₃R channels in the oocyte nuclear envelope show mean open dwell times in the range of 4–10 ms (11,28), whereas we assumed that channels open simultaneously throughout the entire (19 ms) mean duration of the release event. Our estimate of 25 simultaneously open channels is therefore likely to underestimate the total number of channels that actually participate in a puff, by a factor inversely proportional to the mean channel open probability. Moreover, it is important to note that our model provides explicit information regarding only those channels that open; and not the total number of IP₃Rs in a cluster. The latter number is likely to be even higher, given that some receptors may fail to bind IP₃ or may become inactivated by Ca²⁺ before they have a chance to open. Nevertheless, the model provides a useful estimate of the mean number of simultaneously open channels and the dimensions of the cluster within which they are distributed. By using these parameters in a more realistic model of clustered, stochastic IP₃R channels we now aim to explore spatiotemporal dynamics of IP₃R recruitment and inactivation during puffs.