Structural Changes of Cross-Bridges on Transition from Isometric to Shortening State in Frog Skeletal Muscle

Abstract

Structural changes in the myosin cross-bridges were studied by small-angle x-ray diffraction at a time resolution of 0.53 ms. A frog sartorius muscle, which was electrically stimulated to induce isometric contraction, was released by ∼1% in 1 ms, and then its length was decreased to allow steady shortening with tension of ∼30% of the isometric level. Intensity of all reflections reached a constant level in 5–8 ms. Intensity of the 7.2-nm meridional reflection and the (1,0) sampling spot of the 14.5-nm layer line increased after the initial release but returned to the isometric level during steady shortening. The 21.5-nm meridional reflection showed fast and slow components of intensity increase. The intensity of the 10.3-nm layer line, which arises from myosin heads attached to actin, decreased to a steady level in 2 ms, whereas other reflections took longer, 5–20 ms. The results show that myosin heads adapt quickly to an altered level of tension, and that there is a distinct structural state just after a quick release.

INTRODUCTION

Muscle contraction is caused by the interaction of myosin heads, which hydrolyze ATP, with actin molecules in the thin filaments. Tension is generated by a conformational change of the myosin heads that are attached to actin (1). In a simplified version of a currently popular structural model of muscle contraction, a myosin head can take at least two conformations: one is a preworking-stroke conformation (PRE), in which the head does not actively produce force, and the other is a postworking-stroke conformation (POST), which exerts force (2). Transition from the PRE to POST conformation is the source of tension generation by muscle. The major structural difference between these two conformations is supposed to be the angle of the lever arm of a myosin head. In an isometrically contracting muscle, both of these conformations exist and there may be a quick equilibrium between them (3). After a quick release of an isometrically contracting muscle, tension drops instantaneously because the compliant elements, which reside in the cross-bridges and thin and thick filaments, shorten. Then, the equilibrium is shifted toward the POST conformation and the tension is quickly recovered. X-ray diffraction studies on the meridional reflection at 1/14.5 nm⁻¹ from myosin heads after a rapid length change of muscle fibers have provided structural evidence for this conformational change (4,5).

Recently, we measured intensity changes of other reflections, including the meridional reflections at 1/21.5 and 1/7.2 nm⁻¹, and layer lines at 1/36, 1/14.5, 1/10.3, and 1/5.9 nm⁻¹, after a quick release of frog sartorius muscle (6). Those at 1/21.5, 1/14.5, and 1/7.2 nm⁻¹ arise from the thick filament, and those at 1/36 and 1/5.9 nm⁻¹ from the thin filament. The intensity of the layer line at 1/10.3 nm⁻¹, which arises from myosin heads attached to actin, was measured for the first time at a time resolution higher than 1 ms. It was found that, although the gross intensity changes were consistent with an axial tilt of lever arms of attached heads, many details of the intensity changes were not readily explained by a simple model, especially those of the 21.5-nm and 7.2-nm meridional reflections and the (1,0) sampling of the 14.5-nm layer line.

In this experiment, we let the muscle shorten at a constant velocity to create a state of isotonic shortening. An initial quick release was imposed to adjust the tension in the elastic components other than cross-bridges (such as tendons and thin filaments) to the new level. Since the number of attached heads in isotonic shortening is lower than during isometric contraction, and more heads are in the POST configuration, we wished to determine how this new steady state is established at the beginning of shortening. It was found that the intensity drop of the 10.3-nm layer line was complete in 2 ms, showing that the heads adapt to the new condition quickly, and the slower intensity changes of other reflections suggest that there is a distinct structural state after a quick release. A biphasic intensity change of the 21.5-nm meridional reflection showed that the axial tilt of the lever arm of attached heads is restricted by the 43-nm periodicity in the thick filament.

METHODS

Most of the experimental techniques are the same as in our previous study (6).

Muscle preparations

Sartorius muscles of a small (body length 6–8 cm) bullfrog (Rana catesbeiana), ∼40 mm long and 5 mm wide, were used. The frogs were killed by decapitation followed by destruction of the brain and the spinal cord. The muscle was held vertically in a specimen chamber that had two Mylar windows to pass x-rays. The bottom (pelvic) end was connected to a strain gauge force transducer (resonance frequency ∼2 kHz) and the tendon end was connected to a servocontrolled motor (General Scanning, Watertown, MA). The sarcomere length was adjusted to 2.2 μm by laser diffraction. A Ringer solution (composition 115 mM NaCl, 2.5 mM KCl, 1.8 mM CaCl₂, 3.0 mM Hepes, pH 7.2) continuously flowed through the chamber. The temperature was kept at 4–5°C.

The muscle was stimulated supramaximally with electrical pulses (1 ms duration, 50 Hz) for 0.6 s. At ∼0.2 s after the beginning of the stimulation, when the tension had become steady, the motor was activated to change the muscle length. The tension and the motor position, together with other signals such as the frame timing of the x-ray detector, were recorded at 20-kHz sampling with a data acquisition system based on LabView (National Instruments, Austin, TX).

X-ray diffraction experiments

X-ray setup

The experiments were made using the SPring-8 synchrotron radiation facility (Harima, Hyogo, Japan) with a ring energy of 8 GeV and a stored current of 70–100 mA. The x-ray source of the beamline (BL40XU, high-flux beamline) (7) is an in-vacuum helical undulator with 132 magnetic poles and a 32-mm periodicity (8). The optics consists of two Rh-coated mirrors. The peak x-ray energy was 15.0 keV. The energy spread of the x-rays had a tail toward the low energy with a full width at half-maximum (FWHM) of ∼3%. The x-ray flux was ∼6 × 10¹⁴ photons/s. The beam size at the specimen was ∼0.35 mm horizontally and 0.15 mm vertically. The specimen-to-detector distance was 2.8 m. Most of the beam path was evacuated.

X-ray detector

The x-ray detector was an x-ray image intensifier coupled by a relay lens to a fast CCD camera, which has been described in detail (9). The image intensifier (V5445P, Hamamatsu Photonics, Hamamatsu City, Japan) (10) has a fast-decay phosphor (P46) in the exit window to reduce persistence. At 0.5 ms time resolution, the persistence in the image intensifier was negligible (<2%). The CCD camera (C7770, Hamamatsu Photonics) has three CCDs, which work alternately. In this experiment, the frame rate was 1890/s (0.53 ms per frame) with 640 × 72 pixels. Since intensity profiles along the meridian were measured with the muscle set vertically, the camera was rotated by 90° to have more pixels along the meridian.

Experimental protocols

Due to the very high flux of the beamline, if the same part of a muscle was kept irradiated, damage was recognizable after an exposure of 5 ms at 15 keV. To reduce the radiation damage, the specimen chamber was therefore moved downward at a speed of 100 mm/s (11). Before the windows of the chamber crossed the x-ray beam, electrical stimulation was begun. When the windows (5 mm in height) began to cross the beam, recording of the x-ray diffraction pattern was started. The motor was then activated to change the muscle length. The recording finished when the windows left the beam. For each specimen, the experiment was repeated several times with a horizontal shift of 0.5 mm. This ensured that the same part of the specimen was never exposed twice to x-rays.

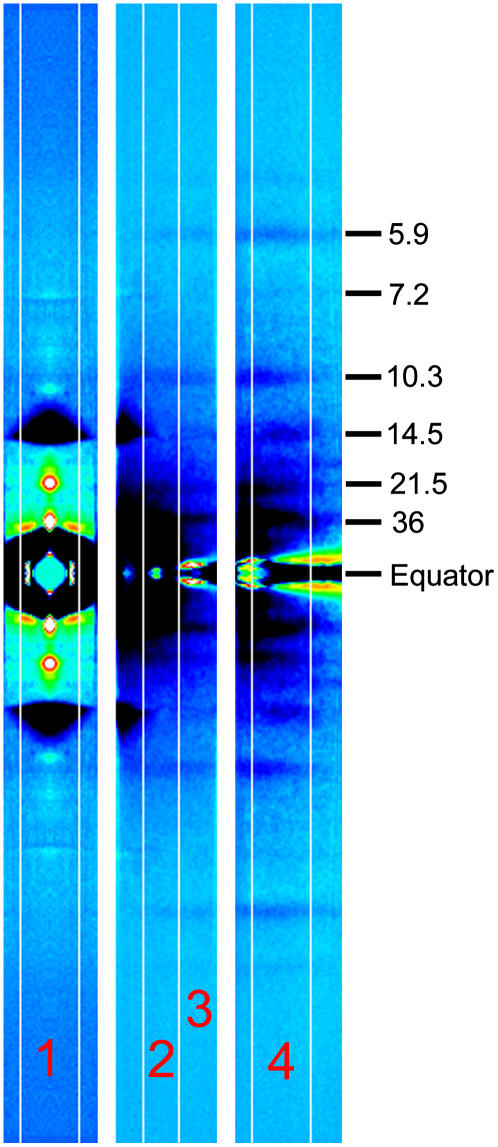
Since only part of the diffraction pattern can be recorded, the experiment was repeated with different shifts of the detector. The meridional region (0–0.03 nm⁻¹ in the equatorial direction, both sides of the meridian), the off-meridional region (0–0.46 nm⁻¹, one side only), and the layer-line region (0.026–0.063 nm⁻¹, one side only) were recorded in separate experiments (Fig. 1).

FIGURE 1.

Difference diffraction patterns recorded with different shifts of the detector. The difference was obtained by subtracting the pattern before the muscle release from that at 13 ms after the beginning of the release. The black-dark blue regions indicate decrease of intensity, whereas light blue-yellow-red-white regions indicate increase. The numbers in the right are approximate Bragg spacings. The pattern in the left is the meridional region (summation of 100 patterns from five muscles), which was obtained by averaging four quadrants. The middle pattern is the off-meridional region (100 patterns from nine muscles). The right pattern is the layer line region (107 patterns from 12 muscles). The contrast level is different for each image. The two sides of the equator were averaged in the off-meridional and layer line patterns. The vertical strips numbered 1–4 indicate the areas along which the intensity profiles were obtained. These patterns do not show the entire recorded area because part of the area was not usable for analysis due to the tilt of the muscle. The 7.2-nm meridional reflection looks enhanced due to the shift of its position. The 21.5-nm layer line indicates the position of the meridional reflection in region 1. The layer lines between 36 nm and 14.5 nm are at Bragg spacings of 23 nm and 18 nm, whose intensity was difficult to measure because they were so close to each other.

Data analysis

X-ray diffraction images for each specimen were summed frame by frame after correcting for orientation of the muscle using the two third-order myosin meridional reflections at 1/14.5 nm⁻¹ as markers of the meridional axis. When this reflection was not in the diffraction pattern, the strong equatorial scatter was used as a marker. The images obtained from each muscle were added, symmetric regions were summed, and the integrated intensity was measured as described below. The isometric intensity was obtained by averaging five frames obtained before the length change. The intensity after the length change was normalized to this isometric level. Results from different muscles were averaged. To determine the background intensity and the integrated intensity of a reflection, the intensity distribution along the meridian was obtained by summing the intensity in the equatorial direction. The integration range was as follows: 0–0.014 nm⁻¹ in the equatorial direction for the meridional reflections (Fig. 1, region 1), 0.022–0.038 nm⁻¹ for the (1,0) sampling of the third myosin layer line at 1/14.5 nm⁻¹ (region 2), 0.022–0.059 nm⁻¹ for the layer line at 1/10.3 nm⁻¹ (regions 2 and 3), 0.048–0.063 nm⁻¹ for the actin layer lines at 1/36 nm⁻¹ and 1/5.9 nm⁻¹ (region 4). For an intensity measurement, a linear background was drawn by connecting two background points on the two sides of the reflection. The integration above the background was used as the integrated intensity of the reflection.

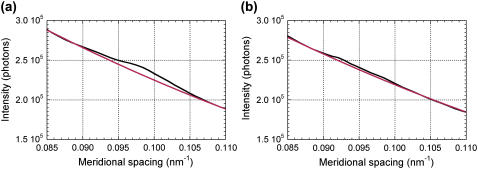
The simple method described above creates two problems with the layer line at 1/10.3 nm⁻¹: 1), the background is in fact not linear and the linear approximation tends to underestimate the integrated intensity when the reflection is as weak as the 10.3-nm layer line; and 2), the fourth myosin layer line at 1/10.8 nm⁻¹ overlaps with the 10.3-nm layer line. Thus, a different method of analysis was also tried. After diffraction patterns from all muscles were added together for each frame, an intensity distribution along the meridian was obtained as above. A background was then drawn by assuming a second-order polynomial function (Fig. 2). The net profile, which is the observed intensity minus the background, was fitted with two Gaussian peaks, one at 0.093 nm⁻¹ with a FWHM of 0.0071 nm⁻¹, and the other at 0.087 nm⁻¹ with a FWHM of 0.0043 nm⁻¹. These values were found to give the best least-square fit after searching for combinations of the parameters. Since the x-ray source used had an energy tail toward low energies, profiles of reflections are also expected to have a tail toward higher angles. However, since the layer lines are axially broad, the profile was mostly determined by the width of the layer line. For each frame, the heights of the two peaks were obtained and the integrated intensities of the peaks were calculated. A similar analysis was also tried on the actin 36-nm layer line, which is overlapped by the myosin 43-nm layer lines (12). However, lack of spatial resolution and high background in the small-angle region hampered the analysis.

FIGURE 2.

Axial intensity profiles in the region of the 10.3-nm layer line (a) before the muscle release, and (b) 13 ms after the beginning of the release.

Spacings of x-ray reflections were difficult to measure because the x-ray energy had a 3% spread. Thus, five data points around the peak of the intensity (0.0018 nm⁻¹ within the peak) were chosen and the center of gravity was calculated. This method has less precision than using the whole peak but is much less liable to be affected by intensity changes of other reflections. The spacing of the third meridional reflection from the thick filament was calibrated at 1/14.5 nm⁻¹ during isometric contraction, and that of the sixth reflection at 1/7.2 nm⁻¹.

Model calculation

A model of a thin filament decorated with myosin heads was constructed by using the model of acto-S1 in rigor (13) (Protein Data Bank accession code 1ALM). Occupancy of actin by the heads in the overlap region was set to 0.56 × 0.3. The ratio of myosin heads per actin monomer in the overlap region of the A-band is 0.56, and 0.3 is an estimate of the fraction of heads attached to actin in an isometric contraction (14,15). This occupancy was for the isometric contraction, and it was reduced after a quick release and during shortening. The calculation of intensity based on a model of decorated thin filaments was made as in the previous study (6).

The lever arm of a myosin head, which is assumed to consist of the 707–843 residues of the myosin heavy chain and the two light chains, was treated as a rigid structure around a vector connecting Cys-707 and Pro-830. The head in the original near-rigor conformation (13) was used as a poststroke structure (POST conformation). In the prestroke structure, the vector connecting Cys-707 and Pro-830 was tilted by 45° toward the M-line together with all atoms in the lever arm (PRE conformation). This angle was chosen to make the model more compatible with the ones used by others (5,16). In this study, each model had a mixture of attached heads with both PRE and POST conformations.

RESULTS

Tension response

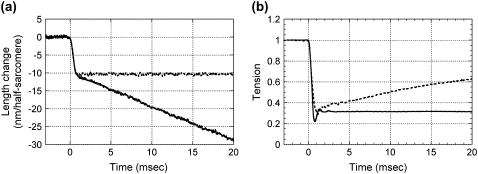
The muscle was allowed to shorten by ∼1% in 1 ms (Fig. 3 a) to cause a rapid tension drop to ∼30% of the isometric level. Then, the muscle was allowed to shorten at a constant velocity of ∼1.8 μm/sarcomere/s. The first rapid release was necessary because, without it, the tension would take much longer (>100 ms) to become steady. Shortening was continued for 25 ms, but the x-ray recording was often terminated earlier because the x-ray beam reached the upper edge of the window of the specimen chamber (see Methods). The tension initially showed oscillation due to the resonance in the force transducer (∼2 kHz, Fig. 3 b) and stayed constant during the shortening. Compared with the tension response in a quick-release experiment (6), the oscillation in tension we observed here is larger, probably because of slightly different damping of the force transducer.

FIGURE 3.

(a) Muscle length recorded by the encoder in the servo system. (b) Tension. The broken line is from the quick-release experiment (6). The tension is normalized by the isometric tension.

Meridional reflections

Fig. 4 summarizes the changes in the meridional reflections during a release and shortening. For comparison, intensity changes that were observed in the previously reported quick-release experiment (6) are shown as broken lines. Since the length control in the initial 1 ms was identical, differences during this period indicate lack of reproducibility. The third-order meridional reflection of the myosin periodicity, at 1/14.5 nm⁻¹, is the strongest meridional reflection during contraction, and its behavior has been studied extensively (4–6,17,18). As has been reported (6), its intensity began to decrease after a lag of 0.5 ms and then reached a minimum of ∼20% of the isometric intensity (Fig. 4 a). The initial decrease at 1 ms from the beginning of the release was 36% larger in the study described here. The intensity started to recover after 2 ms, as was the case in the quick-release experiment, but the recovery was only to 40% and this level was maintained during shortening. The lateral width of this reflection was ∼17% smaller during shortening, as found by others (12). Thus, the net intensity of this reflection during shortening was ∼33% of the isometric level (17).

FIGURE 4.

Intensity and spacing changes of meridional reflections. The data were obtained from 100 contractions of five muscles. The intensity is normalized by the average intensity in isometric contraction that is an average of five data points before the release. (a) Intensity of the 14.5-nm meridional reflection. The average isometric intensity of the five muscles was 9.6 × 10⁵ photons. (b) Peak Bragg spacing of the 14.5-nm reflection. The average isometric spacing was assumed to be 14.5 nm. (c) Intensity of the 7.2-nm meridional reflection. The average isometric intensity was 1.9 × 10⁴ photons. (d) Peak Bragg spacing of the 7.2-nm meridional reflection. The isometric spacing was assumed to be 7.2 nm. (e) Intensity of the 21.5-nm meridional reflection. The average isometric intensity was 3.8 × 10⁴ photons. The broken lines are from a previous quick-release experiment (6).

The axial Bragg spacing of the 14.5-nm reflection decreased by 0.17% (i.e., the peak shifted toward larger angles) during shortening. The spacing change at 1 ms after the beginning of the release was 0.12%. This spacing change is within the range that can be explained by filament compliance (19). After a small recovery, the spacing remained at the same level during shortening (Fig. 4 b). Piazzesi et al. (12) observed a spacing decrease of >1% at the end of 30-ms shortening at a load of 0.12T₀. Yagi and Takemori (20) found an ∼0.7% decrease in spacing averaged during shortening at a load of 0.3T₀. Thus, the change observed in this study is smaller than in our previous observations. Since the spacing change measured from the center of gravity of the entire axial intensity profile, not from the five pixels around the peak (see Methods), also decreased by only 0.4% during shortening, the method used to obtain the spacing was not the sole reason for the difference from the previous results.

The spacing change at 1 ms after the beginning of the release (0.12%) was about twice that in the previous quick-release experiment (6). In the previous experiment, the spacing change at the second point after the beginning of the release (between ∼0.5 and 1.0 ms) was 0.058 ± 0.0084% (n = 10, mean ± SE), whereas in this experiment it was 0.117 ± 0.034 (n = 5). Thus, although the average change was twice as large in this experiment, the difference from the previous result was not statistically significant. The size of the spacing changes was quite variable among specimens but the time courses were very similar. Thus, even though the point-to-point variation in the spacing is small in Fig. 4 b, the statistical deviation of each data value is larger than expected from the point-to-point variation. This is probably due to the variation in the length of tendon. Although the size of the release was adjusted to the length of each specimen, the actual response of muscle length to the release depended on the amount of elasticity in tendon. Even though the muscle length was controlled as in Fig. 1 a, the actual length of the muscle (without tendon) might not have changed in exactly the same manner. The spacing of the 14.5-nm meridional reflection seems to be the most sensitive to this variation because the tension at 1 ms after the beginning of the release had a standard error of the mean of only 5% relative to a tension drop of 70%.

The intensity of the sixth-order myosin meridional reflection at 1/7.2 nm⁻¹ increased promptly by 40% during and immediately after a release and returned to the isometric level within 3 ms of the release, remaining afterward at this level (Fig. 4 c). The intensity decay was faster in the shortening experiment than in a quick-release experiment, suggesting that continuous shortening accelerates the intensity decline. Its spacing decreased after a release and reached a steady level, which was ∼0.13% smaller than the isometric spacing, at ∼5 ms, when its intensity had returned to the isometric level (Fig. 4 d).

The intensity of the second-order meridional reflection of the myosin periodicity at 1/21.5 nm⁻¹ also increased promptly by 50% after a release. After a short plateau or a small decrease, it started to increase again at 2 ms (Fig. 4 e). It reached a steady level at ∼10 ms, which was about twice the intensity during isometric contraction. Thus, this study revealed that there are two components in the enhancement of this reflection. The initial intensity rise seems to have the same time course as that in the quick-release experiment (6), although its amplitude is much smaller in the study presented here. This can be due to the method of normalizing the intensity. Since the intensity of this reflection is quite low during isometric contraction, a small difference in the isometric intensity may cause an apparently large difference in the intensity change after the length change. Piazzesi et al. (12) found that the intensity of this reflection was almost zero in isometric contraction of a single frog muscle fiber. The presence of this reflection suggests that some of the fibers in the sartorius muscle that was used in this experiment were inactive. Since the number of inactive fibers may be variable from muscle to muscle, the intensity of this reflection in an isometric contraction may be different in each experiment, causing an apparent variation in the intensity increase. In fact, in the results presented here, the ratio of the isometric intensity of the 21.5-nm reflection to that of the 14.5-nm reflection was 0.039, whereas it was 0.016 in the previous experiment (6). The second component of the intensity rise probably corresponds to that observed previously (12,17,21), which was interpreted as due to detached myosin heads forming a helix around the shaft of the thick filament during shortening.

As is evident in Fig. 1, the meridional intensity at 1/38.5 nm⁻¹, where a reflection from troponin is expected, increased by a quick release and was kept high during shortening. However, the meridional intensity is influenced by the lateral width of the reflection. It was difficult to measure the lateral width of this reflection because of the high background. If its lateral width decreased like the 14.5-nm meridional reflection, it cannot be concluded that the peak at 1/38.5 nm⁻¹ is enhanced during shortening.

The intensity of the fourth-order meridional reflection of the myosin repeat (at 1/10.8 nm⁻¹) seemed to increase during shortening (Fig. 1). However, high background due to the tail from the 14.5-nm meridional reflection hampered quantitative intensity measurement.

Layer lines

The intensity of the 36-nm actin layer line increased slightly after a quick release and started to decrease at ∼2 ms (Fig. 5 a). It reached a steady level at ∼6 ms. Compared with the data from the quick-release experiment, the initial intensity increase seems to be truncated by the shortening that followed the release.

FIGURE 5.

Intensity changes of layer lines. The intensity is normalized by the average intensity in isometric contraction that is an average of five data points before the release. (a) Intensity change of the 36-nm layer line. The average isometric intensity was 1.5 × 10⁵ photons. (b) Intensity change of the 5.9-nm layer line. The average isometric intensity was 5.0 × 10⁴ photons. (c) Intensity change of the (1,0) sampling spot of the 14.5-nm layer line. The average isometric intensity was 2.3 × 10⁴ photons. (d) Intensity change of the 10.3-nm layer line obtained by linear background subtraction. The average isometric intensity was 7 × 10³ photons. (e) Intensity change of the 10.3-nm layer line obtained by the Gaussian fitting method assuming two peaks (see Methods). The open circles show the intensity of the peak at 0.087 nm⁻¹, corresponding to the fourth myosin layer line, and the solid circles that of the peak at 0.093 nm⁻¹ corresponding to the 10.3-nm layer-line. The average isometric intensity, obtained by adding the integrated intensity of the two peaks, was 5 × 10³ photons. Intensity changes shown in a and b were obtained from 100 contractions of nine muscles,and those in c–e from 107 contractions of 12 muscles. The broken lines are from a previous quick-release experiment (6).

The intensity of the actin layer line at 1/5.9 nm⁻¹ dropped in 1 ms after a release and decreased gradually further for ∼10 ms (Fig. 5 b). The intensity had dropped by ∼18% at 20 ms, which is similar to the reported value of ∼15% at a load of 0.3 T₀ (20). The intensity during unloaded shortening was ∼20% lower than in the isometric state (20).

The intensity of the off-meridional (1,0) lattice sampling spot of the 14.5-nm layer line increased after a delay of 0.5 ms and reached a maximum at 1.5 ms, which was ∼50% higher than the isometric intensity (Fig. 5 c). It then decreased to the isometric level in ∼6 ms and maintained this level during shortening. The maximum increase was smaller than that observed in the quick-release experiment (6), possibly because the isometric intensity of the diffraction spot, which is very low, was higher in this experiment, as was the case with the 21.5-nm meridional reflection.

The intensity of the 10.3-nm layer line, when a linear background was assumed, dropped, after a short delay, to ∼30% of the isometric level in 2 ms and stayed at that level during shortening (Fig. 5 d). When the background was subtracted using a second-order polynomial function, the integrated intensity was slightly higher. The center of gravity of intensity distribution after the background subtraction changed from 1/10.1 nm⁻¹ in the isometric state to 1/10.4 nm⁻¹ during shortening, suggesting that there are two layer lines in the range of the measurement. The intensity profile also suggested the presence of two peaks (Fig. 2). When Gaussian peaks were used to fit the profile, the one at the higher angle, which is supposed to be the 10.3-nm layer line, decreased in integrated intensity to ∼20% during shortening, whereas the one at the lower angle, which is supposed to be the fourth myosin layer line at 1/10.8 nm⁻¹, did not change in intensity (Fig. 6 e).

FIGURE 6.

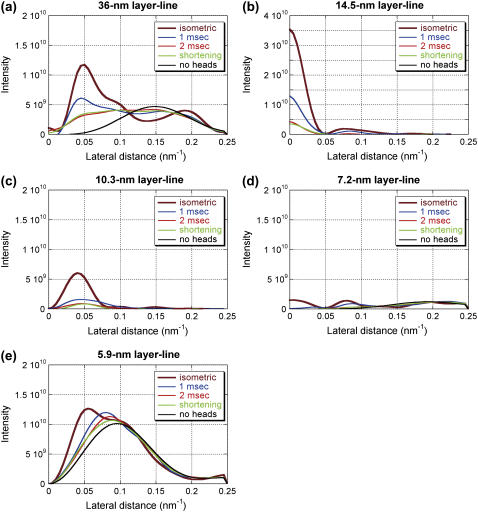
Intensity distribution along major layer lines calculated with various models of myosin attachment to the thin filament: (a) the 36-nm actin layer line; (b) the 14.5-nm myosin layer line; (c) the 10.3-nm actin-myosin layer line; (d) the 7.2-nm myosin layer line; and (e) the 5.9-nm actin layer line. The ordinate is in an arbitrary scale. The thick brown line is for a model with 80% PRE and 20% POST conformation with isometric occupancy (0.56 × 0.3), representing a cross-bridge state in isometric contraction. The red line is for a model with 20% PRE and 80% POST conformation with 70% isometric occupancy, representing a cross-bridge state at 1 ms after the beginning of the release. The thick green line is for a model with 20% PRE and 80% POST conformation with 50% isometric occupancy, representing a cross-bridge state at 2 ms after the beginning of the release. The black line is for a model with 30% PRE and 70% POST conformation with 38% isometric occupancy, representing a cross-bridge state in isotonic shortening. The blue line is for a model without myosin heads. To obtain intensity distribution along layer lines, background was subtracted by linearly connecting the intensity on the two axial sides of each layer line. The inner part of the 36-nm layer line has negative intensity due to the presence of a weak neighboring layer line. The 7.2-nm layer line includes not only the myosin layer line but also contribution from the actin 7.0-nm layer line.

Model calculation

Intensity distribution along major layer lines was calculated with various models of myosin attachment to the thin filament. The assumption in this calculation is that only two strong, stereospecific binding states before and after force generation (PRE and POST) contribute to the intensity. The weak binding states are regarded as nonstereospecific and not contributing to the intensity. The purpose of this calculation is to test whether or not this simple model can explain the observed intensity changes qualitatively and not to search a complete model. To simulate isometric contraction, a model with 80% PRE and 20% POST conformation with an occupancy of 0.56 × 0.3 (see Methods) was used. This is the model used in the previous article (6). The calculated intensity distributions along layer lines are shown in Fig. 6.

The calculated intensity was integrated in the region that was used in the data analysis of the experimental data (see Methods). When the intensities of the meridional reflections and layer lines are compared with each other, the 14.5-nm meridional reflection is more intense in the observation than in the calculation. In the observation, the intensity of the 14.5-nm meridional reflection was 10–20 times and 50–100 times higher than those of the 5.9- and 10.3-nm layer-lines, respectively. On the other hand, in the calculation it is only 3–6 times higher (see Fig. 8 in Yagi et al. (6)). However, since the meridional reflections are sampled by the filament lattice, direct comparison is difficult. Also, since the model does not include contributions from the myosin filament backbone and tropomyosin, the comparison of the relative intensities of these reflections may not be meaningful. Even so, it is still possible to compare the calculated time courses with the observations. Fig. 7 shows the observed intensity changes (the same as in Figs. 4 and 5) and the calculated integrated intensity.

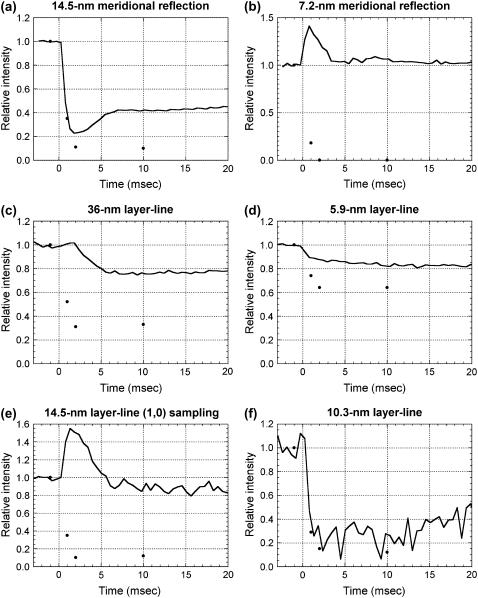
FIGURE 7.

Intensity changes at the beginning of and during shortening. The continuous lines are the observed intensities from Figs. 4 and 5. The black dots are from the calculation in Fig. 6. The calculated intensity for the isometric contraction is plotted at −1 ms and that for isotonic shortening at 10 ms. (a) The 14.5-nm meridional reflection. (b) The 7.2-nm meridional reflection. (c) The 36-nm actin layer line. (d) The 5.9-nm actin layer line. (e) (1,0) sampling on the 14.5-nm layer line. (f) The 10.3-nm layer line.

To simulate the cross-bridges at 1 ms after the beginning of the quick release, a model with 70% isometric occupancy, of which 20% was in PRE and 80% in POST conformation, was used. This occupancy was obtained from intensity recovery by restretch (6). The intensity of the 14.5-nm meridional reflection dropped to 40% of the isometric model. The intensity of the layer lines decreased, especially for the 10.3-nm layer line, which showed a 70% decrease. These changes are in agreement with the observation. The head in the POST conformation is more tilted toward the thin filament axis than that in the PRE conformation. Thus, the intensity distribution along layer lines generally shifts toward higher lateral angles because of the decreased radius of mass on the thin filaments.

For the cross-bridges at 2 ms after the beginning of the quick release, 50% isometric occupancy with 20% PRE and 80% POST conformation was used. This occupancy assumes that the PRE heads are shifting to the POST heads, and the POST heads that went through the working stroke are detaching while new heads are binding to actin in the PRE conformation. The 14.5-nm meridional reflection and the layer lines are further reduced in intensity.

For the cross-bridges in steady shortening, 30% PRE and 70% POST conformation with 38% isometric occupancy was used. This occupancy is based on the measurement of fiber stiffness (22), as discussed below.

Among the reflections studied here, the time courses of the intensity changes of the 14.5-nm meridional reflection and the 10.3-nm layer-line are predicted best by the model calculation. The intensity of the 14.5-nm meridional reflection goes too low but this may be due to the neglected contribution from the backbone and detached heads, as discussed below. The results of the model calculation show that the intensity is strongly affected by the number of attached heads. However, the intensities of the 14.5-nm meridional reflection and the 10.3-nm layer line decrease more than proportionally to the square of the number of attached heads (70% at 1 ms and 50% at 2 ms), showing that a conformational change of the attached heads also affects the intensities.

On the actin layer-lines, the time courses of the intensity changes were similar to the observation but the calculation predicted larger intensity drops than the observation. In the case of the 5.9-nm layer-line, reducing the number of attached heads during isometric contraction may solve this discrepancy. In the calculation, the intensity of the 5.9-nm layer-line is ∼1.5 times higher than that of the 10.3-nm layer-line but it is 4–5 times stronger in the experiment, also suggesting that the number of attached heads is too large in the calculation. However, this makes it necessary to assume fewer heads than suggested by the results from other experimental techniques (14). In the 36-nm layer-line, the predicted decrease during shortening is much larger than in the observation, because in the model, actin molecules do not contribute much to the region used for integration (0.048–0.063 nm⁻¹) (see Fig. 8 in Yagi et al. (6)). Together with the slow intensity decrease of the 5.9-nm layer line that is hard to explain from the model, these results suggest that the model of actin needs to be altered to fully account for the observation.

Other reflections that were studied here (the 7.2-nm meridional reflection and the (1,0) sampling of the 14.5-nm layer-line) show a transient increase in intensity in the experiment, but the calculation only predicted a large decrease. Together with the 21.5-nm meridional reflection, which is absent in the calculated diffraction pattern, the results for these reflections show that the model lacks a structural element that affects the intensity of these reflections after a quick release and during shortening, which is discussed below.

DISCUSSION

Overall intensity changes upon length change and shortening

The intensity changes of the three meridional reflections and the four layer lines that were closely examined in this study are different from each other. However, they may be classified into two types. In one type, after a transient intensity increase, the intensity during shortening is similar to that during isometric contraction. The 7.2-nm meridional reflection (Fig. 4 c) and the (1,0) sampling of the 14.5-nm layer line (Fig. 5 c) show this type of intensity change. In other reflections and layer lines, after a transient phase, the intensity reaches a level different from that in isometric contraction. The 14.5-nm and 21.5-nm meridional reflections (Fig. 4, a and e) and the 36-nm layer-line (Fig. 5 a) exhibit a clearly biphasic transient phase, whereas the 5.9-nm and 10.3-nm layer lines (Fig. 5, b and d) show a monotonic change. These results show that, during the transient phase, the conformation of the myosin heads is not a simple mixture of those in isometric contraction and isotonic shortening. In the following sections, we first discuss the conformation of myosin heads during shortening, and then their transient state.

Conformation of myosin heads during steady shortening

If we assume that there are only two conformations of myosin heads bound to actin, one before (PRE) and one after (POST) a working stroke (3), it is expected that the number of heads in each conformation differs in isometric and isotonic contractions. In the isometric state, the rate of transition from PRE to POST is slow because the strain is high. During isotonic shortening, the number of POST heads is expected to increase because the strain is lower. However, since the POST heads, especially those under negative strain, are supposed to have a higher rate constant for detachment (23), the number of POST heads is still not large. Overall, what is expected during shortening is a reduced number of bound heads and a shift of conformation from PRE to POST.

The muscle stiffness during steady shortening at a load of 0.3T₀ is ∼50% of the isometric stiffness (22,24). If 40% of the stiffness resides in myofilaments (25), the stiffness in cross-bridges is 38% of that in isometric contraction, assuming that compliance in myofilaments and cross-bridges is linear. This suggests that the number of cross-bridges during shortening at 0.3T₀ is ∼38% of that in isometric contraction.

Several groups measured the x-ray equatorial reflections during steady shortening (20,26–28). Although the experimental results were rather variable, the number of cross-bridges estimated from the ratio of intensities of the (1,0) and (1,1) equatorial reflections was larger than expected from the stiffness measurement. This may be due to the presence of weakly attached heads, which contribute neither to the stiffness nor to the axial diffraction pattern because of their nonstereospecific binding.

It is known that the heads detach after a quick release because of the high detachment rate of the POST conformation beyond a critical degree of shortening (29). The number of attached heads, estimated by the intensity recovery of the 10.3-nm layer line upon restretch at 1 ms, was ∼70% of the isometric number (6). Both with and without further shortening, the intensities of the 14.5-nm meridional reflection and the 10.3-nm layer line keep decreasing for another 1 ms (Figs. 4 a and 5 e). Since most of the heads are already in the POST configuration at 1 ms (30), this decrease is likely to be due to detachment.

If there are only 38% of attached heads compared with the isometric state during shortening at 0.3T₀, the intensity of the 14.5-nm meridional reflection during shortening (∼40% of the isometric intensity) is too high because the intensity is approximately proportional to the square of the number of attached heads (31). In fact, considering there are more POST heads during shortening, which give lower 14.5-nm intensity due to tilting of the heads toward the filament axis (5), the intensity is expected to be lower than the square of the number of attached heads (see Fig. 6 b). One possible explanation for the high intensity of the 14.5-nm meridional reflection is a contribution from the heads that assume the helical symmetry of the thick filament during shortening. The presence of such heads has been reported (12,17,21), and the intensity increase of the 21.5-nm meridian (Fig. 4 e) and that of the 10.8-nm meridional reflection (Fig. 1) in the results presented here also suggest that some heads are arranged according to the symmetry of the thick filament during shortening. However, this should cause a larger change in the 14.5-nm reflection, because the heads on the helical symmetry are known to give a meridional reflection at 1/14.3 nm⁻¹ (12). Also, the time courses of the intensity changes in the 14.5-nm and the 21.5-nm reflections are different (Fig. 4, a and c): the 21.5-nm reflection takes longer (10 ms) to reach a steady level. Thus, the contribution of helically arranged heads to the 14.5-nm reflection may not be large.

On the other hand, the intensity of the 10.3-nm layer line is ∼20% of the isometric level during shortening. This low intensity is consistent with a model that assumes that 38% of the heads relative to the isometric state are bound to actin (Figs. 6 c and 7 f).

Unique conformation after a quick release

From ∼2 ms after the quick release, the intensity of the 10.3-nm layer line stays almost constant during steady shortening (Fig. 5 e), suggesting that the myosin heads adapt promptly to the altered load. The myosin-based meridional reflection at 1/7.2 nm⁻¹ and the (1,0) sampling of the 14.5-nm layer line show a transient intensity increase after a quick release, which decays over several milliseconds regardless of the further shortening (Figs. 4 c and 5 c). Thus, the intensity rise is due to a transient state of myosin heads that exists only after a quick release. We suppose that it originates from heads that are attached to actin, because it is reversed when the muscle is stretched at 1 ms after the quick release (6). However, the decay of intensity of these reflections does not match the time course of the 10.3-nm layer line. This suggests that the high intensity of these myosin reflections is due to a part of a bound head that has only a small influence on the intensity of the 10.3-nm layer-line.

The intensity of the 21.5-nm meridional reflection increases without a delay upon a quick release of muscle (Fig. 4 e). Since 21.5 nm is the second order of the 43-nm periodicity in the thick-filament backbone, this suggests that an axial tilt of bound heads by the release is not uniform but differs at each of the three 14.5-nm levels of the 43-nm repeat. The presence of C-protein, which may be interacting with actin (32), possibly affects the freedom of axial flexibility of the lever arm of a bound head. If this occurs, the basic axial periodicity of bound heads becomes 43 nm, and all myosin-based meridional reflections would be expected to be enhanced, because they are on the order of 43 nm. Such an axial perturbation with different conformations of myosin heads has been shown to be the origin of the “forbidden” reflections at an order of 43 nm in relaxed vertebrate striated muscles (33–35). It was indeed found that the intensity of the fourth (at 1/10.8 nm⁻¹) and ninth (at 1/4.8 nm⁻¹) meridional reflections increased after a quick release (6). The only exception is the 14.5-nm meridional reflection, which is weakened by the axial perturbation in a relaxed muscle (34). On the other hand, the intensity of the 10.3-nm layer line is determined not by an axial mass distribution but by an overall conformation of the attached head to which the contribution of the tail region is only partial. Thus, the perturbation influences the 10.3-nm layer line only weakly. It is not clear how the intensity of the off-meridional part of the 14.5-nm layer line can be affected by the 43-nm periodicity. Since this region is also sensitive to a change in radial, rather than axial, mass distribution, a more detailed model calculation is required to understand it fully. For instance, the intensity in the area further along this layer line, around the (3,0) sampling, decreases on a quick release (6), showing the complicated nature of the intensity change.

The influence of the 43-nm periodicity seems to remain on the 21.5-nm meridional reflection even after the intensity of the 10.3-nm layer line reaches the isotonic level at ∼2 ms (Figs. 4 e and 5 e). The perturbation in the tail region of attached heads, which contributes only slightly to the intensity of the 10.3-nm meridional reflection, may persist until the perturbed heads detach from actin.

It is possible that the 43-nm repeat also influences the working stroke under isometric or isotonic condition. However, there is no evidence that shows the presence of the 43-nm periodicity in bound heads during shortening. Although the 21.5-nm meridional reflection is enhanced during shortening, it is supposed to be due to a helical arrangement of myosin heads around the shaft of the thick filament that takes 5–10 ms to form. If the 21.5-nm meridional reflection disappears during an isometric contraction in a fully activated fiber (12), the influence of the 43-nm repeat on the axial conformation of bound heads is likely to be specific to a large, sudden sliding between the thick and thin filaments.

Finally, the simple model used in this study does not explain the behavior of the actin layer lines and the myosin reflections other than the 14.5-nm meridional reflection (Fig. 7). Thus, the model should not be considered as a realistic one. The purpose of the calculation was to examine which part of the intensity changes can or cannot be explained by such a simple model, which is often used to explain the intensity changes of the 14.5-nm meridional reflection (5). The model assumes only a swing in the tail portion of a bound head and its detachment and reattachment. It qualitatively accounts for the intensity changes of the 14.5-nm meridional reflection and the 10.3-nm layer line, but not those of other layer lines, especially the actin layer lines. Thus, the calculation shows that additional assumptions such as a conformational change in actin or the 43-nm axial constraint are required to explain the observed intensity changes.