Abstract
We report that previous polymer chain scission experiments in strong flows, long analyzed according to accepted laminar flow scission theories, were in fact affected by turbulence. We reconcile existing anomalies between theory and experiment with the hypothesis that the local stress at the Kolmogorov scale generates the molecular tension leading to polymer covalent bond breakage. The hypothesis yields a universal scaling for polymer scission in turbulent flows. This surprising reassessment of over 40 years of experimental data simplifies the theoretical picture of polymer dynamics leading to scission and allows control of scission in commercial polymers and genomic DNA.
Keywords: bond breakage, drag reduction, polymer dynamics, Kolmogorov cascade, DNA rupture
Long-chain polymers undergo scission in strong flows because of the coupling of continuum-scale mechanical and atomic-scale chemical processes (1, 2). The interactions that connect these disparate scales are poorly understood. Yet, practically, polymer chain scission is a principal determinant of the performance of operations in many fields, including turbulent drag reduction for pipelines and ships (3), microfluidic handling of polymeric fluids (4), and gene therapy using plasmid DNA (5). Alternatively, chain scission underlies technologies such as the shotgun sequencing of DNA (6) and the generation of monodisperse polymer standards (7). The design and control of polymer scission in each of these flows is driven by the scaling relationship between the strength of the flow, as quantified by the fluid strain rate, and the scission product distribution, as quantified by the molar mass of ruptured polymer chains. Since Frenkel (8) published the first treatise on polymer chain scission more than 60 years ago, this fundamental issue has remained unresolved.
Scission theories for laminar flow hypothesize that the drag force, Fd, experienced by the chain induces a tension that breaks the molecule if it is greater than the critical strength of a polymer covalent bond. In a purely extensional flow, for example, the maximum tension is at the midpoint (9). If the extended chain is modeled as a slender rod, then the tension induced by the drag is Fd ∼ μVR ∼ με̇R2 (10). Here μ is the solvent viscosity, V is the relative velocity of the solvent flowing past the rod at its half-length R and ε̇ is the macroscopic fluid strain rate (∼V/R). Two laminar theories identify different regimes depending on the ratio of polymer relaxation time to flow residence time, the Deborah number (De). For the De ≪ 1 regime, such as in stagnation point flow of a cross-slot, chains are fully stretched such that R ∼ O(L), where L is the contour length of the chain (10). For the De ≫ 1 regime, such as in transient extensional flows generated in contraction-expansion geometries, chains adopt only a partially stretched conformation and R ∼ O(Rg), where Rg is the radius of gyration (11). These viscous flow models yield distinct scaling relationships: ε̇c ∼ L−2 for De ≪ 1 and ε̇c ∼ L−1 for De ≫ 1, where ε̇c is the critical strain rate for scission. The difference in scaling exponents is significant because L is very large for drag-reducing polymers (∼20 μm) and genomic DNA (∼40–1,600 μm). In fact, such large-L macromolecules are so prone to scission that they tend to rupture even in the flow generated by a manually operated syringe.
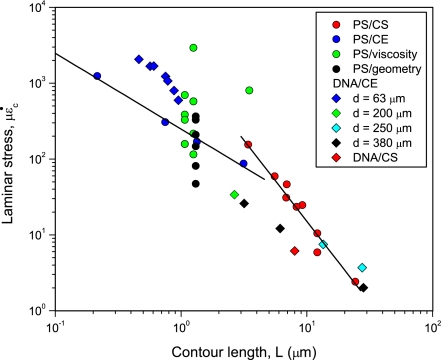
These two prevailing scission theories have been confronted with experimental data and judged successful (10, 12). Yet, a number of anomalies remain. First, in laminar flows, both theories predict that ε̇c ∼ μ−1 for a given polymer chain. However, contraction flow experiments in which viscosity was manipulated have found that ε̇c ∼ μ−0.25 (12). Second, scission experiments in converging flows show an unexplained dependence of the inlet diameter on scission strain rate (12). Third, recent evidence suggesting that the Reynolds number (Re) of the flow affects the laminar scaling exponents is inconsistent with the models (13). Fourth, bond strength estimates extracted from the laminar flow scission models are about two orders of magnitude lower (12) than recent density functional theory calculations (2). These anomalies in prior scission data (10, 12, 14–18) are apparent in Fig. 1. Fig. 1 reports the effective laminar stress for breakage, defined as με̇c, as a function of steady-state molar mass (see Methods), here reported as the contour length L (see Data Analysis).
Fig. 1.
Polymer chain scission scaling based on the assumption that the flow is laminar. Scission theories in laminar flows suggest that data plotted on these coordinates should yield universal behavior. Effective laminar stress represents the viscous stress on the chain, assuming that the flow is laminar. PS/CS and PS/CE represent the classical scaling data for polystyrene (PS) in cross-slot (CS) and contraction–expansion (CE) flows that were deemed to be in good agreement with the laminar flow scission theories. The lines denote the best fits for these data. Also shown are the anomalous experimental data that probed the effect of solvent viscosity (PS/viscosity, green circles) and geometry (PS/geometry, black circles) on chain scission. The anomalous geometric effect is also evident in scission data of DNA molecules in CE geometries of varied inlet dimensions (labeled d = 63–380 μm). Here ε̇c ≡ U/d. The details of the studies are given in Table 1.
Results and Discussion
Flow Visualization.
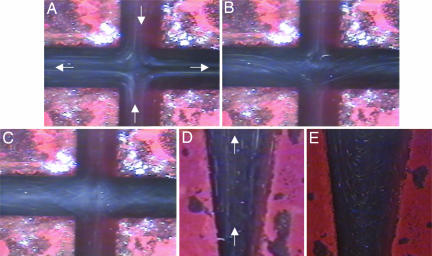
Given these anomalies, we questioned the assumption of laminar flow underpinning previous comparison between theory and experiment. Although not always discussed in the original literature, our analysis (Table 1) shows that scission experiments were conducted over a broad range of Re (≡ ρUd/μ, where U is the mean velocity, d is the geometric dimension, ρ is the fluid density, and μ is the fluid viscosity) where the flow may transition to turbulence. To address this issue, we examined flow field stability in the two most commonly studied geometries i.e., cross-slot (CS) and contraction–expansion (CE). Fig. 2 reports flow visualization of hydrodynamic instabilities in both the CS and CE geometries. We find that the onset Re for hydrodynamic instability in CS and CE geometries is 25 and 370, respectively. These values of the onset Re for inertial instabilities (Re*) agree well with literature reports for similar flow geometries (19–21) and are consistent with accompanying pressure drop measurements (data not shown). A comparison of Re* with the Re generated in chain scission experiments (see Table 1) suggests that all measurements reported to date have been affected by turbulence.
Table 1.
Summary of scission experiments
| Data set | Scission study | Geometry | d, mm | Re | Ref. |
|---|---|---|---|---|---|
| 1 | PS/decalin | CS | 0.30 | 2.5 × 101 to 1.6 × 103 | 10, L |
| 2 | PS/toluene | CS | 0.30 | 1.32 × 103 to 1.32 × 104 | 10, L |
| 3 | PS/decalin | CE | 0.50 | 4.53 × 103 to 6.4 × 104 | 12, L |
| 4 | PS/viscosity effect | CE | 0.50 | 2.1 × 102 to 2.1 × 105 | 12, L |
| 5 | PS/temperature effect | CE | 0.50 | 1.1 × 104 to 1.3 × 105 | 12, L |
| 6 | PS/geometry effect | CE | 0.35–1.0 | 2.3 × 102 to 2.4 × 105 | 12, L |
| 7 | PS/various solvents | RT | 72.5, 9 | 1.36 × 106 to 2.58 × 106 | 34, T |
| 8 | PEO/water | CS | 0.50 | 1.55 × 102 to 3.2 × 103 | 13, T |
| 9 | PEO/50% glycerol | CS | 0.50 | 8.0 × 101 to 5 × 102 | 13, T |
| 10 | PEO/water | CE | 0.50 | 2.93 × 103 to 3.07 × 103 | 13, T |
| 11 | PEO/water | CE | 10.9 | 4.0 × 104 to 2.81 × 105 | 33, T |
| 12 | PEO/water | RT | 60, 10 | 7.06 × 104 to 2.19 × 105 | *, T |
| 13 | PAM/water | CE | 10.9 | 4.37 × 104 to 1.93 × 105 | 33, T |
| 14 | PAM/water | RT | 60, 10 | 8.47 × 104 to 2.3 × 105 | *, T |
| 15 | DNA/buffer | OJ | 0.60 | 2.11 × 103 | 16, L |
| 16 | DNA/buffer | CE | 0.063 | 2.30 × 103 to 7.98 × 103 | 14, L |
| 17 | DNA/buffer | CE | 0.250 | 2.9 × 102 to 5.85 × 102 | 17, L |
| 18 | DNA/buffer | CE | 0.200 | 1.75 × 103 | 18, L |
| 19 | DNA/buffer | CE | 0.383 | 3.7 × 102 to −6.2 × 103 | 15, L |
| 20 | DNA/buffer | RT | 72.5 | 1.2 × 106 | 30, T |
PS, polystyrene; PEO, poly(ethylene oxide); PAM, polyacrylamide; CS, cross-slot; CE, contraction–expansion; RT, rotational turbulent; OJ, opposed jets. L and T in the Ref. column denote studies that were reported to have been conducted in laminar and turbulent flows, respectively;
* denotes current study.
Fig. 2.
Evidence for turbulence in CS and CE geometry. Shown are images of the flow at various Re in the two geometries. Re = 12 (A), 50 (B), 70 (C), 150 (D), or 370 (E). Flow is laminar in A and D and unstable in B, C, and E. The arrows (in white) indicate the direction of fluid flow. The CS is 500 μm in width and 7 mm in depth. The CE geometry has identical dimensions as CS with a tapered entrance/exit semi-angle of 7.5°.
Scaling Theory for Polymer Chain Scission in Turbulence.
Given this reevaluation, we formulate a simple scaling theory for chain scission that accounts for fluid turbulence and the effect of turbulent velocity fluctuations in particular. The interaction of a polymer chain with such fluctuations is a complex theoretical problem; however, good phenomenological descriptions of strain rate fluctuations in Newtonian homogeneous turbulence (the Kolmogorov cascade) and wall-bounded flows are available (22). Recently, the statistics of polymer stretching in isotropic homogenous turbulence have been studied theoretically for R ≪ L (23, 24), and the behavior of polymers in wall-bounded turbulence has been studied by direct numerical simulation (25–27). For our purposes, the interaction of extended polymer chains (R ∼ L) with turbulent velocity fluctuations is of interest because it is the extended chains that generate the highest tension, and thereby dominate the steady-state scission distributions reported in the literature and Fig. 1. Moreover, literature scission experiments have been exclusively conducted in wall-bounded flows. In such flows, near-wall velocity fluctuations are scaled on the inner variable uτ = , where uτ is the friction velocity and τw is the wall shear stress. On the other hand, in the flows' outer region, the Kolmogorov cascade is operative (28). Because the bulk of the volumetric flux in wall-bounded flows is through its outer region, we first consider interaction of extended polymer chains with turbulent fluctuations from the scaling perspective of the Kolmogorov cascade as previously applied to polymers (28, 29). We later consider scission in the inner region of wall-bounded flows.
We proceed as in the laminar flow scission theories by estimating the drag force experienced by the chain. However, now the drag force of interest is set by the turbulent cascade i.e., Fd ∼ μγ̇rR2 and γ̇r is the strain rate of velocity fluctuations associated with the length scale r of the Kolmogorov cascade. The scaling of the strain rate spectrum with r is shown in Fig. 3. At the largest length scale [r ∼ O(d)] corresponding to the mean flow, the strain rate is the smallest and is given by γ̇d ∼ U/d ∼ μRe/ρd2. In the so-called inertial range (d > r > η), the strain rate γ̇r ∼ Ur/r ∼ (μRe/ρd2)(r/d)−2/3 increases as r decreases toward η. Here η is the Kolmogorov length scale where energy is dissipated by viscosity, ur is the velocity scale corresponding to the length scale r, and Re is based on the mean flow. At r ∼ O(η), the velocity gradient is homogeneous: γ̇η ∼ ν/η2 ∼ μRe3/2/ρd2, where ν is the kinematic viscosity. In the above relationship we have made the common assumptions that the velocity fluctuation scale u′ ∼ U, that the largest eddy length scale l ∼ d, and that the Kolmogorov scale, η ∼ dRe−3/4 (22).
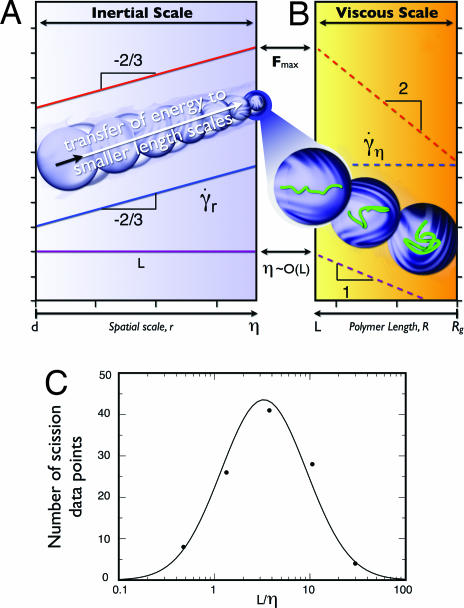
Fig. 3.
Maximum drag force on a polymer chain in the Kolmogorov cascade. The red, blue, and purple lines denote the variables: drag force, strain rate, and polymer length, respectively. (A) Interaction of inertial scales with polymer chain showing that the drag force peaks at r = η. The Inset shows an illustration of the Kolmogorov cascade. (B) Interaction of polymer chain with viscous scale. Here the drag force is maximum when R = L. The Inset shows a chain undergoing stretching from coiled to full extension. (C) Distribution of L/η for the various scission experiments listed in Table 1.
We now consider the interaction of a fully extended test chain with each spatial scale of the inertial range and estimate the drag force on the chain, i.e., Fd ∼ μγ̇rR2. Because the polymer extension is fixed (R ∼ L) and strain rate increases as r decreases, the drag force on the chain increases with decrease in spatial scale. This behavior is illustrated in Fig. 3A, where both the strain rate and the drag force scale identically with r. Further, Fig. 3A shows that the maximum drag force occurs at the Kolmogorov scale. Now consider how the polymer stretches at the viscous scale such that its extension is O(L) as shown in Fig. 3B. As R increases from Rg to L, the drag force increases as R2, just as in the classical theories, because the strain rate is fixed (γ̇ ∼ γ̇η) and the flow is homogeneous at the viscous scale. Both A and B of Fig. 3 suggest that the drag force experienced by a chain is maximum when η ∼ O(L), where the polymer chain is fully extended and the strain rate is the greatest. We test this condition [L/η ∼ O(1)] in Fig. 3C by calculating L/η (see Data Analysis) for all of the Table 1 scission experiments. The distribution is log-normal with mean at L/η ≈ 3. Encouraged by this result, we estimate the maximum drag force on the chain at the Kolmogorov scale.
Because midpoint scission is observed in turbulence (1, 10, 12, 30), we treat the chain as fully stretched with the drag of a rigid rod (31) in the homogeneous flow of the viscous scale. The drag force is then (32),
where a is the diameter of the chain and A is an O(1) constant that incorporates the proportionality of u′, l, and η to the combinations of the macroscopic quantities U, d, and the kinematic viscosity ν. The only way in which flow geometry enters the theory is through its effect on A. Substituting the earlier expression for γ̇η yields
Comparison of Scission Data with Scaling Theory.
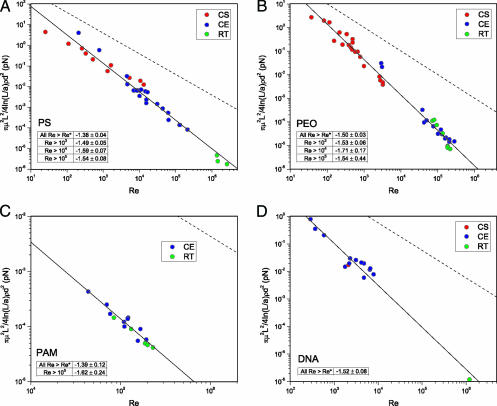
Eq. 1 contains parameters that are all experimentally available, except the O(1) constant A, and thus can be tested against the Table 1 data. To further increase the data set, we conducted additional scission experiments in turbulent flows (see Methods) with two different polymers, poly(ethylene oxide) (PEO) and polyacrylamide (PAM), and in three different flow geometries, CS, CE, and RT (rotational turbulent flow geometries that include Taylor–Couette and rotating disk apparatus flows). Eq. 1 suggests that plotting the quantity πμ2L2/4ρd2ln(L/a) vs. the Re of the flow will reduce the anomalous scission data of Fig. 1 and other scission data (13, 30, 33, 34) generated in turbulent flows (listed in Table 1) to a master curve for a given polymer. The range of the Fig. 4 data, spanning six decades in the ordinate and four decades in Re (∼102 to 106) for some of the polymers, is sufficient to stringently test the theoretically derived scaling. Fig. 4 shows that Eq. 1 successfully correlates these data. The scaling exponent for each of the four polymers, irrespective of the flow geometry, agrees remarkably well with the theoretical prediction of −1.5 (see Fig. 4 Insets). Analogously, we also found that when πμ2Re3/2/4ρd2ln(L/a) is plotted against the polymer contour length (L), all of the four polymers showed a scaling exponent close to −2 (see Data Analysis).
Fig. 4.
Universal polymer chain scission scaling in turbulent flows for the four polymers PS (A), PEO (B), PAM (C), and DNA (D) in three different flow geometries. The lines are the best fits for each of the polymers. The dashed line corresponds to chain scission scaling in laminar flows. The Insets each show a table listing the scaling exponents for various regimes of Re.
Thus, Eq. 1 is supported by the Fig. 4 data collected from 20 scission studies pertaining to four polymers in three different flow types, over a wide range of flow dimension d (63–72,500 μm), Re (25–2.6 × 106) and fluids of varied viscosity and solvent quality. The simplicity and sufficiency of the result supports its broad application in diverse areas. We conclude by addressing additional implications of the theory.
Implications of the Universal Scission Scaling.
The successful correlation of Fig. 4 data to Eq. 1 implies that literature reports of polymer scission are explained by polymer tension generated by velocity fluctuations at the Kolmogorov scale of turbulent flow. Such good agreement between theory and experiment leads to the following surprising implications: (i) polymer scission in wall-bounded turbulent flows is dominated by behavior in the outer (turbulent core) region rather than the inner (buffer) region; (ii) polymer scission in turbulent flows is affected by flow geometry only to within an O(1) constant; (iii) the Kolmogorov cascade theory is applicable to the literature scission data, even though many such experiments were conducted in very small geometries (∼102 μm); (iv) covalent bond strengths can be extracted directly from the fluid mechanics experiments of Table 1; and (v) scission of polymers in laminar flows is extraordinarily difficult to achieve. We provide additional tests and discussion of these implications below.
Relevance to Wall-Bounded Turbulent Flows.
All of the scission experiments reported in Table 1 have been conducted in wall-bounded flows. Because it is well known that turbulent velocity fluctuations are greatest near the wall (i.e., buffer region) of such flows, does an analysis based on turbulent wall scales describe the Fig. 4 data better than our analysis based on Kolmogorov scales? We address this question in the following way: We take the wall shear rate γ̇w ∼ uτ2/ν as the characteristic scale for near-wall velocity gradient fluctuations. We assume that near-wall turbulent velocity gradients determine the polymer tensile force in the same way that the strain rate at the Kolmogorov scale does for the cascade hypothesis, i.e., Fd ∼ ρuτ2L2. To link uτ with Re, we use friction factor–Reynolds number relationships available from the literature for the wall-bounded flows in question. The resultant polymer tensile force scaling is Fd ∼ Reα, where α varies from 1.75 to 1.87 depending on the geometry (see Data Analysis). Recall that for Eq. 1, α = 1.5. The data in Fig. 4 are of sufficient range and quality to discriminate between the wall scale and Kolmogorov scale hypotheses and to conclude that the latter mechanism better explains the scission measurements. How then can we reconcile this result with the fact that turbulent fluctuations in the inner region of wall-bounded turbulence are greater than in the outer flow where the Kolmogorov cascade is active? We suggest that scission in the outer region dominates the results because the volumetric flux in the inner region of wall-bounded turbulence is too small to be detected in the overall polymer molar mass distribution that is reported in scission experiments. For example, at Re = 104, only 10.2% of the volumetric flux is through the inner region of the turbulent boundary layer in pipe flow. At Re = 105, the inner region volumetric flux is only 1.0% of the total. Thus, although the wall-fluctuation-induced scission is a compelling hypothesis, we are led to the alternative conclusion that the Kolmogorov cascade drives scission in turbulent flows because it acts in regions of the flow that comprise the bulk of the volumetric flux. Direct numerical simulations of polymer solutions in wall-bounded flows would be helpful to further address this question, particularly with regards to the possibility of polymer modifications to turbulent velocity fluctuations.
Influence of Flow Geometry.
According to the Kolmogorov cascade theory, the small scales of turbulence are universal and independent of the mean flow (22). This property of the cascade has the unexpected implication that polymer scission scaling in turbulent flows is insensitive to the flow geometry used to generate turbulence. We find evidence for this intriguing observation in Fig. 4, because data from the three different flows are well correlated by the theory. To explore this point further, we calculate scaling exponents for each geometry irrespective of the polymer being ruptured (see Data Analysis). We obtain α = −1.26 ± 0.09, −1.43 ± 0.04, and −1.59 ± 0.13 for CS, CE, and RT geometries, respectively, which are close to the predicted exponent of α = 1.5. Thus, the effect of geometry on scission scaling is small. As further evidence, we note that the Eq. 1 proportionality constant A varies by no more than a factor of 2.09 ± 1.15 among the three flow geometries considered here. This variability of A is consistent with the expectation that its value should be of O(1).
Applicability of Kolmogorov Cascade to Scission Data.
To validate Eq. 1 in Fig. 4 we implicitly assumed the Kolmogorov cascade to be operative in the flows corresponding to Table 1 scission experiments. Do such classical turbulence ideas apply in the small geometries and Reynolds numbers characteristic of flow-induced chain scission? In general, for the cascade theory to be applicable a separation between the small scales characteristic of turbulent fluctuations and the large scales characteristic of the largest eddies and flow geometry is required (22). This separation of scales is determined by the magnitude of Re. To quantitatively address the separation of scales, we computed the quantity d/η for all of the experimental data of Fig. 4. We find that d/η > 102 for 97% of the Fig. 4 data, d/η > 103 for 72% of the data, and d/η > 104 for 39% of the data, suggesting that the scales are indeed well separated. In addition, the PS and PEO data were sufficient to extract scaling exponents corresponding to Re > 103 and Re > 104. The extracted scaling exponents do not exhibit strong Re functionality (see Insets of Fig. 4).
Bond Strength Estimates.
Eq. 1 implies it is possible to estimate bond strength values for each of the four polymers. We do so, by equating Fmax of Eq. 1 as the backbone bond strength (assuming A ∼ 1) and compare results to those of other methods. Our analysis yields 3.88 ± 0.10 nN, 2.30 ± 0.22 nN, 4.38 ± 0.16 nN, and 5.86 ± 0.18 nN for PS, PEO, PAM, and DNA bond strengths, respectively. The estimates for the synthetic polymers are in good agreement with C–C and C–O bond strengths of 4.1 and 4.3 nN, respectively, derived from density functional theory calculations (2). The DNA bond strength estimate agrees well with that of bond potential calculations, which predict a strength in excess of 5 nN (35) and resolves the discrepancy, highlighted by Bustamante et al. (35), between DNA bond strengths obtained from flow experiments and bond potential calculations.
Polymer Chain Scission in Laminar Flows.
With the availability of a scaling for chain scission in turbulence we now assess the conditions under which polymer chains break in laminar flows. We plot in Fig. 4 the predicted scission curve for laminar flows, i.e.,
by using the bond strength values obtained from turbulent scission scaling. Note that the polymer tensile force in laminar flows has a different dependence on Re compared with turbulent scission scaling. Let us consider the possibility of breaking a PEO chain in water by using a flow geometry with d = 500 μm. In such a scenario the laminar curve in Fig. 4B indicates that it is impossible to break PEO chains in laminar CS and CE flows because it requires chains with L > 150 μm (or molar mass >20 × 106 g/mol), which are not practically available. If the viscosity of the solvent were increased 100 times, then a chain of length at least 1.2 μm (or molar mass of 1.6 × 105 g/mol) is required to achieve scission in laminar CS and CE flows. However, in this case the characterization of scission products of chains with L > 1.2 μm in such viscous solvents becomes technically challenging. Fig. 4 can be used to derive similar conclusions for other polymers. Therefore it is extraordinarily difficult to simultaneously break and characterize polymer molecules in laminar flows. Thus, our turbulent scission analysis will suffice for the vast majority of flows encountered in practice.
Conclusions
Our findings show that the smallest scales of turbulence and the largest scales of polymer dynamics dominate the relationship between the strength of the flow and the longest polymer chain that can remain unbroken in that flow. Because both processes display universal behavior, the physics of polymer chain scission is thus itself explained by the universal properties of Eq. 1. The availability of this scaling is immediately useful to obtain scission-induced bounds on maximum drag reduction in turbulent flows. Further, this universal scaling would be a benchmark to assess flow-induced scission of polymer aggregates, which have been shown to provide enhanced turbulent drag reduction relative to single polymer chains (36). In conjunction with the bond strength estimates, the theory can be applied to design flow geometries and conditions that will break polymer chains into predictable sizes.
Methods
Flow Field Characterization.
Aqueous poly(ethylene glycol) (20,000 g/mol) solutions of various concentrations were used to generate Newtonian fluids of various viscosities (6–328 mPa·s) to cover a wide range of Re. Flow was visualized through a stereomicroscope by seeding a Newtonian fluid with mica flakes (∼0.1 g/liter) and recording the images by using a CCD camera.
Scission Experiments in Turbulent Flow.
Two methods exist to determine scaling for polymer chain scission. In the first, the critical strain rate for polymer scission is identified by varying the flow rate and tracking the onset of change in molar mass of a monodisperse polymer solution (10, 12). In the second, polydisperse polymer solutions are repeatedly passed through the flow geometry at a fixed flow rate until the molar mass distribution reaches a steady state (13). The steady-state molar mass distribution represents the population of the chains that survived the scission process at the given strain rate in the flow. The limiting weight-average molar mass (Mws) corresponding to the steady-state molar mass distribution is identified as the critical scission molar mass corresponding to the strain rate in the experiment. In our experiments we used the second method. The details of the experiments are given elsewhere (13). To plot data consistently between the two methods, we report in Figs. 1 and 4 the contour length corresponding to Mws. For scission data obtained by using the first method, Mws is half of the reported initial (undegraded) molar mass.
The details of the CS and CE flow geometries are given elsewhere (13, 33). The Taylor–Couette cell was custom-made with the radius of the inner cylinder, d1 = 6 cm, the height between the rotating cylinder and the bottom of the outer cylinder, d2 = 0.5 cm, and the gap between the inner and outer cylinder, d3 = 1 cm. The Re in this geometry is always based on d1; however the integral length scale is based on either d2 or d3, depending on whether the geometry is Taylor–Couette or rotating disk apparatus, respectively. The rotation of the inner cylinder was varied from ∼800 to 3,000 rpm. Critical scission molar masses of PEO and PAM solutions were obtained by constant rotation of the inner cylinder for >3 h.
Data Analysis.
To estimate L for PS, PEO, and PAM we used L = 0.82nlo (37), where n is the number of backbone bonds (= noMws/Mo, where no is the number of backbone bonds per monomer and Mo is the monomer molar mass) and lo is the C–C bond length (1.54 Å). For DNA we used 0.33 μm/kb to estimate L. We used 1 nm as the diameter of the chain for synthetic polymers (38) and 2 nm for DNA (31).
The Kolmogorov scale η (in Fig. 3C) was estimated by using the relationship η = dRe−3/4. The values of L and η for all of the reported experiments in Table 1 range from 0.21 to 43.3 μm and from 0.05 to 33 μm, respectively. The submicrometer viscous scale in some of the experiments results from the use of large Re (>2,000) in geometries with small dimensions (∼100 μm).
The scaling exponents reported for the various polymers in the Insets of Fig. 4 were obtained by fitting a power law to the data irrespective of the flow geometry. To extract the scaling exponents for the three flow geometries we normalized the data by the polymer bond strength to account for polymer variation and fit the resulting data to a power law. The mean of the prefactors associated with the resultant power-law fits is reported as the proportionality constant A. The errors from fitted values reported throughout the paper are SEM.
When we plot πμ2Re3/2/4ρd2 ln(L/a) vs. L, we find the scaling exponents for PS, PEO, PAM, and DNA to be −2.25 ± 0.12, −1.93 ± 0.13, −1.95 ± 0.15, and −2.24 ± 0.09, respectively. The range of L and the number of scission data points (N) used to generate the scaling exponents for the four polymers in Fig. 4 are the following: PS, L = 0.2–24.2 μm, N = 34; PEO, L = 4.0–43.3 μm, N = 42; PAM, L = 6.8–25.3 μm, N = 16; and DNA, L = 0.5–28.1 μm, N = 15.
The generalized friction factor law for Newtonian turbulence is f ∼ Re−β, where f ≡ uτ2/U2 and β is 0.13, 0.16, 0.22, and 0.25 for turbulent flow in Taylor–Couette (39), flat plate (22), rotating disk (40), and pipe (22) geometries, respectively. The tension for a polymer chain in the inner region of the turbulent flow is then Fd ∼ ρuτ2L2 ∼ μ2Re2−βL2/ρd2.
Acknowledgments
We thank D. R. Dowling, R. G. Larson, C. R. Doering, A. Roy, C. C. Hsieh for valuable discussions and an anonymous referee for suggesting the analysis based on wall scales. We thank C. R. Iacovella and C. J. Dibble for assistance with figure preparation. We acknowledge the support of the 3M Corporation and the Defense Advanced Research Projects Agency (Grants MDA972-01-1-0020 and N00014-01-1-0880) and a Rackham Predoctoral fellowship for S.A.V.
Abbreviations
- CE
contraction–expansion
- CS
cross-slot
- PAM
polyacrylamide
- PEO
poly(ethylene oxide)
- PS
polystyrene
- RT
rotational turbulent.
Footnotes
The authors declare no conflict of interest.
References
- 1.Horn AF, Merrill EW. Nature. 1984;312:140–141. [Google Scholar]
- 2.Grandbois M, Beyer M, Rief M, Clausen-Schaumann H, Gaub HE. Science. 1999;283:1727–1730. doi: 10.1126/science.283.5408.1727. [DOI] [PubMed] [Google Scholar]
- 3.Virk PS. AIChE J. 1975;21:625–656. [Google Scholar]
- 4.Groisman A, Enzelberger M, Quake SR. Science. 2003;300:955–958. doi: 10.1126/science.1083694. [DOI] [PubMed] [Google Scholar]
- 5.Levy MS, O'Kennedy RD, Ayazi-Shamlou P, Dunnill P. Trends Biotechnol. 2000;18:296–304. doi: 10.1016/s0167-7799(00)01446-3. [DOI] [PubMed] [Google Scholar]
- 6.Venter JC, Adams MD, Myers EW, Li PW, Mural RJ, Sutton GG, Smith HO, Yandell M, Evans CA, Holt RA, et al. Science. 2001;291:1304–1351. doi: 10.1126/science.1058040. [DOI] [PubMed] [Google Scholar]
- 7.Buchholz BA, Zahn JM, Kenward M, Slater GW, Barron AE. Polymer. 2004;45:1223–1234. [Google Scholar]
- 8.Frenkel J. Acta Physicochim USSR. 1944;19:51–76. [Google Scholar]
- 9.Perkins TT, Smith DE, Chus S. Science. 1997;276:2016–2021. doi: 10.1126/science.276.5321.2016. [DOI] [PubMed] [Google Scholar]
- 10.Odell JA, Keller A. J Polym Sci Part B: Polym Phys. 1986;9:1889–1916. [Google Scholar]
- 11.Rabin Y. J Non-Newtonian Fluid Mech. 1988;30:119–123. [Google Scholar]
- 12.Nguyen TQ, Kausch HH. Polymer. 1992;33:2611–2621. [Google Scholar]
- 13.Islam MT, Vanapalli SA, Solomon MJ. Macromolecules. 2004;37:1023–1030. [Google Scholar]
- 14.Thorstenson YR, Hunicke-Smith SP, Oefner PJ, Davis RW. Genome Res. 1998;8:848–855. doi: 10.1101/gr.8.8.848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bowman RD, Davidson N. Biopolymers. 1972;11:2601–2624. doi: 10.1002/bip.1972.360111217. [DOI] [PubMed] [Google Scholar]
- 16.Odell JA, Taylor MA. Biopolymers. 1994;34:1483–1493. [Google Scholar]
- 17.Levinthal C, Davison PF. J Mol Biol. 1961;3:674–683. doi: 10.1016/s0022-2836(61)80030-2. [DOI] [PubMed] [Google Scholar]
- 18.Wetmur JG, Davidson N. J Mol Biol. 1968;31:349–370. doi: 10.1016/0022-2836(68)90414-2. [DOI] [PubMed] [Google Scholar]
- 19.Lagnado R, Leal LG. Exp Fluids. 1990;9:25–32. [Google Scholar]
- 20.Kalashnikov VN, Tsiklauri MG. J Non-Newtonian Fluid Mech. 1993;48:215–223. [Google Scholar]
- 21.Drazin PG. Fluid Dynamics Res. 1999;24:321–327. [Google Scholar]
- 22.Pope SB. Cambridge, UK: Cambridge Univ Press; 2000. Turbulent Flows. [Google Scholar]
- 23.Balkovsky E, Fuxon A, Lebedev V. Phys Rev Lett. 2000;84:4765–4768. doi: 10.1103/PhysRevLett.84.4765. [DOI] [PubMed] [Google Scholar]
- 24.Chertkov M. Phys Rev Lett. 2000;84:4761–4764. doi: 10.1103/PhysRevLett.84.4761. [DOI] [PubMed] [Google Scholar]
- 25.Sureshkumar R, Beris AN, Handler RA. Phys Fluids. 1997;9:743–755. [Google Scholar]
- 26.Terrapon VE, Dubief Y, Moin P, Shaqfeh ESG, Lele SK. J Fluid Mech. 2004;504:61–71. [Google Scholar]
- 27.Gupta VK, Sureshkumar R, Khomami B. Phys Fluids. 2004;16:1546–1566. [Google Scholar]
- 28.Sreenivasan KR, White C. J Fluid Mech. 2000;409:149–164. [Google Scholar]
- 29.Tabor M, de Gennes PG. Europhys Lett. 1986;2:519–522. [Google Scholar]
- 30.Choi HJ, Lim ST, Lai PY, Chan CK. Phys Rev Lett. 2002;89 doi: 10.1103/PhysRevLett.89.088302. 0883021. [DOI] [PubMed] [Google Scholar]
- 31.Larson RG, Perkins TT, Smith DE, Chu S. Phys Rev E. 1997;55:1794–1797. [Google Scholar]
- 32.Batchelor GK. J Fluid Mech. 1970;44:419–440. [Google Scholar]
- 33.Vanapalli SA, Islam MT, Solomon MJ. Phys Fluids. 2005;17 095108. [Google Scholar]
- 34.Kim CA, Kim JT, Lee K, Choi HJ, Jhon MS. Polymer. 2000;41:7611–7615. [Google Scholar]
- 35.Bustamante C, Smith SB, Liphardt J, Smith D. Curr Opin Struct Biol. 2000;10:279–285. doi: 10.1016/s0959-440x(00)00085-3. [DOI] [PubMed] [Google Scholar]
- 36.Vlachogiannis M, Liberatore MW, McHugh A, Hanratty TJ. Phys Fluids. 2003;15:3786–3794. [Google Scholar]
- 37.Larson RG. New York: Oxford Univ Press; 1999. The Structure and Rheology of Complex Fluids. [Google Scholar]
- 38.Boyer RF, Miller RF. Macromolecules. 1977;10:1167–1169. [Google Scholar]
- 39.Lathrop D. P., Fineberg J, Swinney HL. Phys Rev Lett. 1992;68:1515–1518. doi: 10.1103/PhysRevLett.68.1515. [DOI] [PubMed] [Google Scholar]
- 40.Kalashnikov VN. J Non-Newtonian Fluid Mech. 1993;75:209–230. [Google Scholar]