A homeostatic rule for inhibitory synapses promotes temporal sharpening and cortical reorganization

Abstract

Experience with transient stimuli leads to stronger neural responses that also rise and fall more sharply in time. This sharpening enhances the processing of transients and may be especially relevant for speech perception. We consider a learning rule for inhibitory connections that promotes this sharpening effect by adjusting these connections to maintain a target homeostatic level of activity in excitatory neurons. We analyze this rule in a recurrent network model of excitatory and inhibitory units. Strengthening inhibitory→excitatory connections along with excitatory→excitatory connections is required to obtain a sharpening effect. Using the homeostatic rule, we show that repeated presentations of a transient signal will “teach” the network to respond to the signal with both higher amplitude and shorter duration. The model also captures reorganization of receptive fields in the sensory hand area after amputation or peripheral nerve resection.

Perhaps the most important proposition in the neuroscience of learning is Hebb's (1949) (1) famous postulate: when neuron A participates in firing neuron B, the strength of the connection from A to B is increased. An important consequence of Hebbian learning is that it tends to increase both the strength and the duration of the neural response elicited by a sensory stimulus. Consider a recurrent network of mutually excitatory neurons. Suppose there are initial connections of moderate strength among neurons and their near neighbors. When a transient signal is applied to a neuron, it and its neighbors will become activated, and, according to Hebb's rule, the excitatory connections between them will be strengthened. The strengthening will cause the network to respond with stronger, as well as longer, activation.

Increasing the duration of neural responses may have important benefits in many cases, but there are situations in which it may not be desirable, including cases in which it is necessary to follow a series of brief transient signals. Consider the situation confronting someone listening to fluent speech. The signal changes very rapidly, and important information for identification of many sounds is present in transients with durations <40 ms (2). If perceptual responses to speech become stronger and more robust with experience, this strengthening would reduce the network's ability to follow the sequence of changing temporal signals if the response became more temporally extended at the same time that it was strengthened.

A remedy to this problem would be to arrange neural circuitry so that the neural response not only becomes stronger, but it also becomes “sharper” (more temporally coherent or compact) with experience (3). This sharpening could have several beneficial effects. With experience, it would increase the overall temporal resolution of the system. It would produce more accurate discrimination of fine differences in timing of neural signals, which will allow the system to follow a series of signals arriving at a high rate. These benefits would co-occur with benefits at the neural level as well; for a given amount of total activation, higher temporal coherence should result in stronger postsynaptic depolarization of downstream receiving neurons, increasing their ability to excite such neurons sufficiently to induce downstream synaptic strengthening (4).

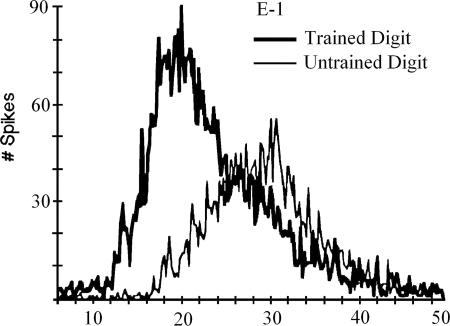
Just this sort of temporal sharpening in response to experience has been observed in an important series of experiments by Recanzone et al. (5–8). In these investigations, monkeys worked for reward to discriminate different frequencies of vibration applied to the skin surface of one finger. The difference between a 20-Hz standard and a higher frequency target was reduced as the monkeys improved in discriminating targets from standard stimuli in the task. Successfully trained monkeys showed an increase in the size of the population of neurons (and corresponding cortical surface) responding to each pulse of the stimulus. They also showed an increase in temporal coherence or sharpness of the response (see Fig. 1). Each monkey's behavioral performance was well predicted by the degree of coherence of its temporal response.

Fig. 1.

Temporal sharpening effect. [Reproduced with permission from ref. 8 (Copyright 1992, The American Physiological Society).]

Inspired by these findings and considerations, we have asked the following question: how might a neural system come to sharpen, rather than broaden, its response as the strengths of excitatory connections are increased? Based on analysis and simulations, we propose a remarkably simple answer. We suggest that the brain may achieve sharpening by adaptively modifying the strength of recurrent inhibition so as to conserve average neural activity. We also suggest that the same mechanism, augmented slightly, can address key findings in the literature on cortical reorganization after amputation (9–12).

Homeostasis, the idea that the brain conserves or regulates its average activity, has been proposed and supported previously (13), and recurrent inhibition has been explored as one of the factors that may play a role (14). We add the suggestion that, within the right architecture, the homeostatic adjustment of recurrent inhibition can promote temporal sharpening, along with regulation of total neural activity.

We present our argument in the following series of steps. First, we review some relevant physiology of the mammalian somatosensory systems thought to be the sites of the plastic changes under consideration. We then consider the effect of increasing the recurrent excitation in a simplified preliminary model of this system. We show that, to achieve temporal sharpening when the strength of the excitation is increased, the strength of recurrent inhibition must also be increased. We suggest a simple homeostatic mechanism for regulating the inhibition based on conserving average neural activity in the population of excitatory units “seen” by the inhibitory neuron, and we review data from systems-level experiments consistent with this homeostatic approach. We implement this mechanism in a model addressing the strengthening and sharpening of neural responses as revealed in the Recanzone et al. (5–8) experiments. Finally, we use the same model system to model cortical reorganization after peripheral alteration, adding a mechanism inspired by a proposal of Bienenstock et al. (15) for the regulation of homeostasis itself that may promote reorganization.

Sites of Cortical Plasticity

Sensory maps in cortex are regulated by experience, both during development and in adulthood. Whereas early studies focused on thalamocortical synapses as the primary site of plasticity, recent studies have identified intracortical excitatory synapses from layer 4 (L4) to L2/3 neurons and excitatory horizontal synapses across columns within L2/3 as sites of plasticity as well (9). It has been shown (16–22) that, in neonatal animals (<4 days old), thalamocortical synapses are likely to be a principal site of plasticity. In older animals, receptive field plasticity is most rapid in L2/3 and occurs only later, if at all, in L4. Based on these experimental findings, we examine a model in which the main sites of plasticity are recurrent horizontal connections among excitatory and inhibitory cells treated as a simplified model of somatosensory cortex layer L2/3.

Simplified Preliminary Model for Analysis

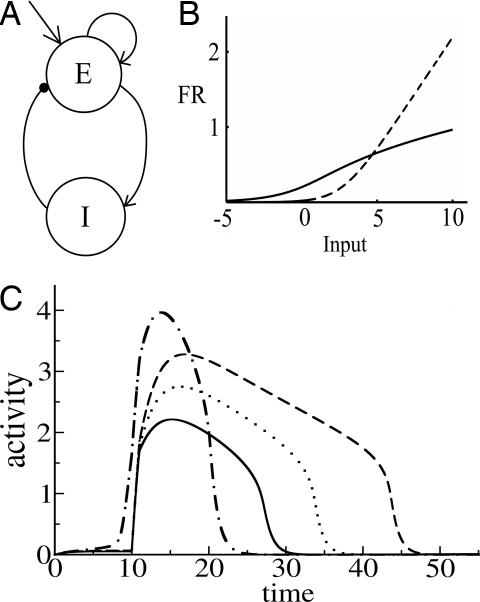
Excitatory neurons in layer L2/3 excite through direct excitatory projections and inhibit via inhibitory interneurons. Here, we consider a simplified model that relies on one excitatory and one inhibitory unit (Fig. 2A) to model the mean activities of these excitatory and inhibitory populations. To model recurrent excitation, we include a self-excitatory connection from the excitatory unit back to itself. Inhibition is modeled as an excitatory connection from the excitatory unit to the inhibitory unit, plus an inhibitory connection from the inhibitory unit back to the excitatory unit. Dynamics of unit activities are given by

E is the firing rate of the excitatory unit and I is the firing rate of the inhibitory unit. I_exte and I_exti are external inputs to the excitatory and inhibitory units, F_e and F_i are gain functions of the excitatory and inhibitory units, τ_e and τ_i are constants governing the response rate of each type of unit, and α, β, γ are parameters.

Fig. 2.

Simplified network: structure, gain functions, and dynamics. (A) The two-unit network. E and I are excitatory and inhibitory units. (B) Gain functions. The solid line represents the excitatory gain function and the dashed line is the inhibitory gain function; ε_e = 0.2; ε_i = 0.2; th_e = 1; th_i = 3. (C) The activity level of the E cell over time as a response to a transient stimulus. Solid, dotted, and dashed lines represent responses with increasing self-excitatory strength (α = 3, 3.5, and 4) and fixed inhibitory-to-excitatory strength (β = 1.2). Dot-dashed line represents response with both excitatory and inhibitory connections increased relative to the solid curve baseline (α = 5; β = 3). Other parameters were fixed with these values: τ_e = 1; τ_i = 20; ε_e = 0.2; ε_i = 0.2; th_e = 1; th_i = 2; I_exte = 5; γ = 1.

Somatosensory cortex produces a transient response to the onset of a stimulus with little or no sustained component (23, 24). It has been suggested (23, 24) that this effect is achieved in part by making the inhibitory unit respond more slowly that the excitatory unit. Accordingly, we set τ_i much larger than τ_e. To ensure that the response even to a sustained stimulus is transient, it has further been suggested that the inhibitory gain function must be much steeper than the excitatory gain function. Indeed, in the cortex, pyramidal neurons and interneurons show different f–I% curves (25). Regular-spiking (RS) excitatory pyramidal neurons show a continuous (type 1) f–I% curve with negative acceleration at high input levels. Fast-spiking inhibitory interneurons have a discontinuous (type 2) f–I% relationship, such that they do not fire below a critical input level but fire at much higher frequency than RS neurons at high input levels. We summarize these facts with the following gain functions (Fig. 2B) for the E and I units

Here th_e and th_i are thresholds and ε_e and ε_i are parameters describing the smoothness of the gain functions.

Given these features of the model, if we apply a strong stimulus to both units simultaneously, the excitatory unit will respond more quickly, but the activity of the inhibitory unit will eventually be much higher than the activity of the excitatory unit and so will come to suppress the excitatory unit, producing a transient response both to transient and sustained stimuli. Within this regime, we can now investigate how changes in connections may give rise to temporal sharpening of the transient response along with experience-dependent strengthening.

Model Analysis.

We implemented and analyzed the model using the XPPAUT package (26). To understand the effects of the strength of the excitatory and inhibitory connections, we observed the behavior of the network to changes in the strength of the connections (Fig. 2C). First, we recorded the network's response to a transient stimulus with baseline choices of the strengths for the E–E% and E–I% connections (Fig. 2C, solid line). As we increase the E–E% connection strength (α in the equations), the amplitude of activity of the E unit increases in response to a transient external stimulus (Fig. 2C, dotted line). However, as Fig. 2C shows, the response duration also increases. Further increases just amplify the effect (Fig. 2C, dashed line). Thus, strengthening of the self-excitatory loop alone results in a stronger but also longer lasting response. If we increase the inhibitory connection (parameter β) sufficiently along with the change in the excitatory connection, we can observe a response with higher amplitude and at the same time with shorter duration compared with baseline (Fig. 2C, dot-dash line). In general, our simulations indicate that, even with a positively accelerating inhibitory gain function and a negatively accelerating excitatory gain function, sharpening does not occur when only the excitatory connections are allowed to change. Sharpening along with strengthening can occur if the strength of the inhibitory loop is increased along with strengthening of the excitatory connection.

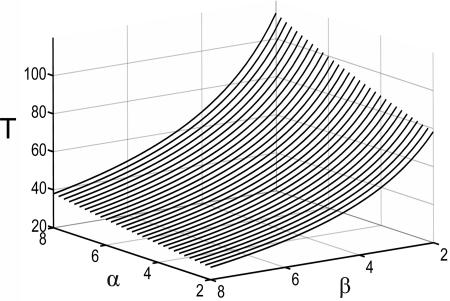
It was surprising at first that sharpening was not an automatic consequence of strengthening in this circuit, given the positive acceleration of the inhibitory gain function and the negative acceleration of the excitatory gain function. In supporting information, which is published on the PNAS web site, we investigate this issue and explore how changing parameters α and β can influence the amplitude and duration of the neural response. With the chosen gain functions and inhibition slower than excitation, the analysis shows that sharpening cannot occur with a change in the E–E% connection alone. The result can be proven for the case of inhibition much slower then excitation but also holds when τ_e and τ_i are not very different and holds for other choices of the gain functions as long as the excitatory gain function is negatively accelerating. Neurally realistic excitatory gain functions have this property, which is itself a basic requirement for stability. We have also shown that parameter α controls the amplitude of the response and its duration (increasing α increases both the amplitude and the duration of the response) and parameter β controls mainly the duration (increasing β shortens the duration). Finally (Fig. 3), we have shown that, for any increase in α, it is always possible to find a value of β such that the resulting response time will be shorter than the original response time before the change in α.

Fig. 3.

Response duration in the two-unit model as a function of the strength of the excitatory connection (parameter α) and the strength of the inhibitory connection (parameter β); τ_e = 1, τ_i = 10, γ = 2.5.

All the adjustments we have discussed so far have been performed manually. Now we ask: is there a simple policy whereby a network could adjust its inhibitory connections to produce temporal sharpening when the strength of the response becomes stronger? The key observation is the following: if the network adjusts its inhibitory connections to ensure that the time-averaged activity of the excitatory unit remains constant, then a higher-amplitude response will necessarily be briefer than the original low-amplitude response. We examine the implications of this observation through the use of a simple homeostatic learning rule for inhibitory connections in the somatosensory learning model described below.

Somatosensory Learning Model.

The model described in this section will be used to show how the homeostatic learning rule suggested above can produce sharpening along with strengthening as observed in the experiments of Recanzone et al. (5–8). It also addresses the expansion of the cortical area activated by the stimulus as a result of successful training in the Recanzone experiments (5–8). Finally, it addresses the reorganization of somatosensory receptive fields after amputation, a pattern for which others (9–12) have proposed a role for adaptive modification of inhibition as well as excitation.

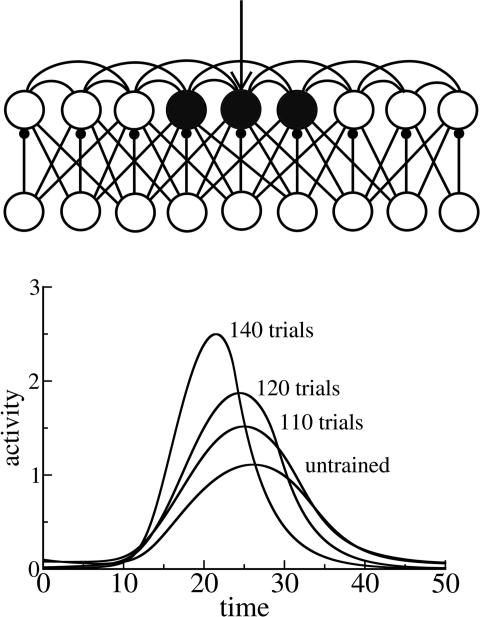
Our model is based on a recurrent network of excitatory and inhibitory units intended as a simplified representation of cortical neurons in layer L2/3 of mammalian somatosensory cortex (Fig. 4Upper). For each excitatory unit there is a corresponding inhibitory unit. There are connections from excitatory to excitatory units, from excitatory to inhibitory units, and from inhibitory to excitatory units. Excitatory connections to both excitatory and inhibitory units are scaled by a Gaussian function of distance. Each inhibitory unit projects only to the single corresponding excitatory unit. Both excitatory and inhibitory connections onto excitatory units are plastic. Connections to inhibitory units from excitatory units are fixed.

Fig. 4.

Somatosensory learning model: structure and dynamics. (Upper) Network of excitatory (upper row) and inhibitory (lower row) units used to model learning in somatosensory cortex layers 2/3. After training, several units are involved in the response to a transient stimulus applied to the trained unit, as indicated approximately by shading. (Lower) Activity levels of the trained unit as a function of time. Different curves represent activity change during training. Parameters were as follows: τ_e = 3; τ_i = 5; ε_e = 0.2; ε_i = 0.15; th_e = 0.1; th_i = 0.2; I_exte = 5; τ_syne = 300; τ_syni = 150; g_ee = 5; g_ei = 3.5; g_ie = 1; wijie = 1. The standard deviation of the Gaussian weight function r(i, j) is 3 for both excitatory-to-excitatory and excitatory-to-inhibitory connections.

As in the preliminary model, excitatory and inhibitory units are classical Wilson–Cowan rate units (27) with dynamics of activities described by equations

where u_i is the activity of ith excitatory unit; v_i is activity of ith inhibitory unit; F_e and F_i are the excitatory gain functions introduced in Eqs. 1 and 2; wijee, wiei, and wijie are synaptic weights; EE_i is the total synaptic input to excitatory unit i from other excitatory units; EI_i is the total synaptic input to excitatory unit i from inhibitory units; IE_i is the total synaptic input to inhibitory unit i from excitatory units; τ_e and τ_i are time constants; g_ee, g_ei, and g_ie are constants; Ieexteand Iiextiare external inputs to the excitatory and inhibitory units; and r_ij is a Gaussian function of distance between i and j.

Learning Rules.

Excitatory–excitatory connections.

We rely on a Hebbian (correlation-based) rule for modification of the connections among excitatory units. The rule includes an additional term that conserves the sum of the squares of the weights onto each neuron (28)

where ω is a constant, τ_syne is a time constant, and s_i=Σ_jw_ij^ee·uj. It is easy to show that the sum of the squares of the weights to unit i, Σ_j(w_ij^ee)², asymptotically approaches ω.

Inhibitory–excitatory connections.

The homeostatic learning rule for inhibitory connections is given by

where wiei is the synaptic weight to excitatory unit i from the corresponding inhibitory unit, θ_i is the homeostatic threshold, and τ_syni is the time constant. This rule strengthens the inhibitory connection if the activity level of the excitatory unit is higher than θ_i, decreasing the excitatory unit's activity, and weakens the inhibitory connection if the excitatory unit's activity is <θ_i, increasing its activity. We impose the restriction that wiei cannot become negative. To allow the homeostatic regulation to closely track changes in excitation, inhibitory learning happens on a faster time scale than excitatory learning, i.e., τ_syni < τ_syne.

Simulation of Strengthening, Sharpening, and Increased Cortical Area with Experience.

We used a network that consisted of 20 excitatory and 20 inhibitory units. We trained the network by applying a long series of transient stimuli to a chosen excitatory unit and its associated inhibitory unit.

Before training, the external stimulus activated the applied excitatory unit and not much activity was observed in adjacent units. The result of training is a spread of activity to adjacent units: a stimulus applied to the trained unit causes transient activity in a number of adjacent units, because of strengthening of recurrent excitatory connections. This spreading reproduces the increase of cortical area representing the trained digit in the Recanzone et al. (5–8) experiments: more neurons are participating in the representation of the trained digit.

The trained network also responded to a transient stimulus with higher amplitude and shorter duration (Fig. 4 Lower). As in our preliminary model, the higher amplitude of the response is due to the stronger excitatory–excitatory connections (in this case, among the stimulated unit and its neighbors), and the shorter duration is a result of homeostatic strengthening of the inhibitory connections.

The learning rule we have implemented for inhibitory connections naturally leads to temporal sharpening with training. According to the rule, the inhibitory connection stops changing once the activity of the excitatory unit is equal to the homeostatic value. But because the external stimulus is transient, activity is not fixed but changes in response to a transient stimulus. Thus, what the inhibitory learning rule does is maintain the total activity of the excitatory unit during each cycle of the response. We take an integral of the inhibitory weight change over a cycle of the stimulus T_C under the condition that the integral is zero:

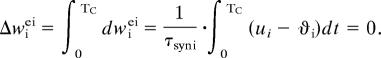It follows that the total activity of the excitatory unit is constant:

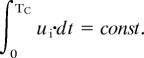Because the amplitude of the response increases due to changes in the excitatory connections, the only way the integral can be held constant is by shortening the response duration; this shortening is achieved by strengthening the inhibitory-to-excitatory connections. A similar effect would be achieved by using a similar homeostatic learning rule to modify the excitatory-to-inhibitory connections.

Simulation of Receptive Field Reorganization.

We have shown that, to observe temporal sharpening, it is necessary to allow plasticity in recurrent inhibition. This result raises a question: are there other phenomena besides temporal sharpening where plasticity in inhibitory pathways may play a role?

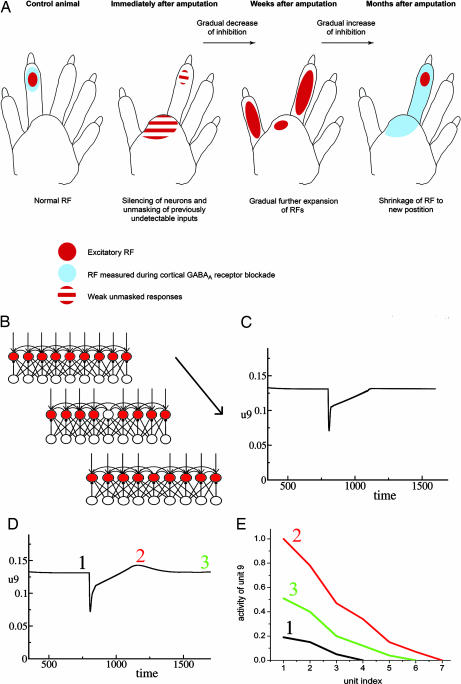
It is known that GABAergic (inhibitory) synapses influence receptive field size and participate in receptive field remapping after amputation (9–12). As summarized in Fig. 5A, reorganization after amputation proceeds through three phases. In phase 1, right after amputation, receptive field size increases. This increase is attributed to a reduction of inhibition because of the removal of afferent stimulation. In phase 2, there is a further gradual increase of receptive field size, because of a strengthening of horizontal excitatory connections onto the deafferented units together with a further, more gradual decrease in inhibition. In phase 3, the level of inhibition increases, establishing a more refined receptive field in a new location. We note that, in phase 2, the receptive field is larger than at any other phase, with the neuronal responses to skin stimulation at many sites being higher than in other phases.

Fig. 5.

Receptive field reorganization during amputation experiments. (A) Receptive field size is sensitive to the level of GABA antagonist. Remapping of receptive field (RF) location after amputation is accompanied by modulation of overall activity, which peaks part way through the recovery process. [Reproduced with permission from ref. 9 (Copyright 2004, Elsevier).] (B) Phases of the simulated amputation experiment. Baseline, external input is applied to all cortical units; amputation, input to one unit is removed, simulating amputation; recovery, the deprived unit's activation returns because of decreased inhibition and collateral excitatory inputs, which become stronger during recovery. (C) Activity of the deprived unit as a function of time during amputation experiment with the original inhibitory learning rule. (D) Activity of the deprived unit as a function of time during amputation experiment with the modified inhibitory learning rule. (E) Receptive field size of the deprived unit measured at three different times during receptive field remapping in the simulated amputation experiment (line 1, right before the amputation; line 2, during reorganization; line 3, after reorganization). Parameters are as follows: τ_e = 3, τ_i = 5, ε_e = 0.2, ε_i = 0.15, th_e = 0.1, th_i = 0.2, I_exte = 5, t_off = 800, τ_syne = 120, τ_syni = 30, τ_h = 1,000, g_ee = 1, g_ei = 2.5, g_ie = 2.5, wijie = 1, u₀ = 0.05, p = 2.1. The Gaussian weight functions r_ij have SD = 3 for both excitatory-to-excitatory and excitatory-to-inhibitory connections.

Our model as already described provides nearly all of the mechanisms required to simulate this three-phase pattern, as shown in a simulation experiment (Fig. 5B). To establish a baseline, we first applied a tonic stimulus to all excitatory units until connections stabilized in the network. Once activity reached equilibrium, we simulated the amputation by turning off the input to one unit, keeping inputs to the rest of the units intact. Before amputation (Fig. 5C), activity is maintained at the homeostatic level. After amputation (at time 800), activity drops down but then quickly shows a partial recovery. This recovery is due to weakening of the inhibitory connections according to the homeostatic inhibitory rule. Recovery is not complete because, even if there is no inhibition to the unit, inputs from adjacent units are not strong enough to activate the unit to the homeostatic level. Activity of the unit returns to the baseline level later on, because of strengthening of the recurrent excitatory connections. Once activity reaches a homeostatic level, the inhibitory-to-excitatory connections rebuild and maintain the activity of the “deprived” excitatory unit at the homeostatic level.

As previously noted, it seems that the overall cortical activity is greater during phase 2 of the remapping process than it is at steady state either before the amputation or at the end of the recovery process. In the form described thus far, however, the inhibitory learning rule we have implemented never allows the activity of the units to exceed the homeostatic level. As a result, after silencing following the amputation, the activity asymptotically approaches the homeostatic level but never overshoots it. Although there could be other explanations, we consider here the possibility that the homeostatic threshold might actually be raised during recovery to encourage reengagement and reorganization. To model this process, we adopt the notion from Bienenstock et al. (15) that the homeostatic set point of each unit is itself adjustable. Specifically, we employ the same homeostatic inhibitory learning rule as before:

We add the notion that the homeostatic set point depends on the average activity ū_i of the unit

The dynamics of ū_i follows

where u₀ specifies the desired long-run activity level of the unit, τ_h is a time constant much larger than any other time scale in the model, and p is a constant >1.

According to the new learning rule, the activity of each unit of the network will be adjusted based on the average activity of the unit over a long time. If the average activity of a particular unit is high during some time, then the homeostatic threshold will be lowered, which leads to stronger inhibitory connections. This learning rule provides an effective feedback mechanism that controls activity level of the units. This feature of the learning rule follows the sliding threshold mechanism of the Bienenstock–Cooper–Munro (BCM) learning rule (15). The BCM rule uses a threshold for excitatory-to-excitatory synapses, decreasing the threshold to encourage excitatory plasticity if the unit is not active enough. In our case, we adapt a threshold for inhibitory-to-excitatory connections, increasing the threshold so that inhibition is reduced when the unit is not active enough.

We simulated the amputation experiment a second time incorporating the adaptation of the homeostatic threshold. As before, a baseline period is followed by amputation at time 800 (Fig. 5D). As before, we observe an immediate drop in activity, followed by fast but incomplete recovery. This recovery reflects the direct adjustment of inhibitory connections in response to the removal of the input and takes place during a period that is much shorter than the period required for a change of the homeostatic threshold. In the next phase, we see the combined effects of Hebbian modification of excitatory-to-excitatory connections coupled with the effect of the slow adjustment of the homeostatic threshold. After amputation, the average activity of the deprived unit is much less than the homeostatic activity level. This shortfall of activity leads to a slow increase of the homeostatic threshold, allowing higher activity for the deprived unit during the recovery period. This process produces the overshoot of the activity at the time indicated by point 2 in Fig. 5D. The activity is higher than the homeostatic level because of the higher threshold. Once the long-run average activity of the unit increases back to its long-run target, the homeostatic set point returns to the original level.

We also measured receptive field size in our simulated amputation experiment (Fig. 5E). We stopped stimulations at three points within each phase: homeostatic, hyperactive, and recovered. We turned off all plasticity and external inputs and measured activity in the deprived unit while we stimulated one of the adjacent units. We plot activity of the deprived unit as a function of stimulus location. We can see that receptive field size increases during the hyperactive phase compared with the original homeostatic size, but at the final stage, the receptive field shrinks again. This nonmonotonic behavior of the receptive field size correlates with the experimental finding that the receptive field enlarges during remapping before it converges at a new location. Because the amputation affects one unit, the recovered receptive field is symmetrically placed around the site of the amputation. With a larger amputation, units to each side of the middle of the amputation will have receptive fields dominated by responses to surviving inputs on the same side of the center point of the amputation, resulting in new receptive fields concentrated on the corresponding side of the lesion.

We have run simulations using the modified learning rule and observed that it still leads to temporal sharpening under the conditions of our earlier sharpening simulation. In the modified learning rule, the time scale for changes of the threshold is much longer than the time scale for changes of inhibitory and excitatory synapses, so changes of the homeostatic threshold are slow and negligible during each cycle.

Discussion

Our work calls attention to important roles that the adjustment of inhibitory connections may play in regulating both the function and the structure of neural circuitry and highlights the consequences of using a homeostatic learning rule for inhibitory synapses. As noted earlier, others have emphasized homeostatic regulation as a broad principle of brain function (13, 14). Here, we add a specific observation on the homeostatic regulation of inhibition. In a regime where inhibition is slower than excitation, the homeostatic regulation of inhibition promotes a combined temporal sharpening and strengthening of neural activity. We note as well that the homeostatic regulation of inhibition may enhance spatial as well as temporal sharpening. Both forms of sharpening increase the resolution of the nervous system.

Future research should address, among other things, the role of adaptive modification of inhibitory connections in establishing neuronal selectivity during development. Inhibition may play a key role in the critical period observed in the development of ocular dominance columns (29). The stabilization of neuronal response properties during development, like their adaptive destabilization after injury, may be affected by plasticity in inhibitory connectivity.

Abbreviation

Ln

layer n.