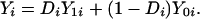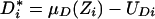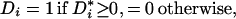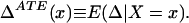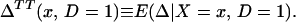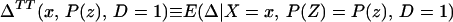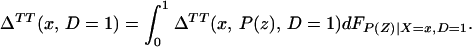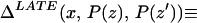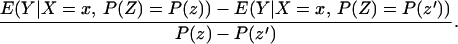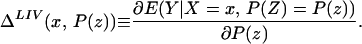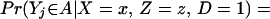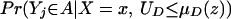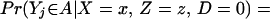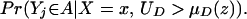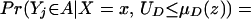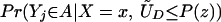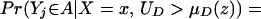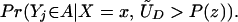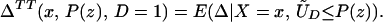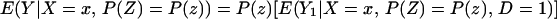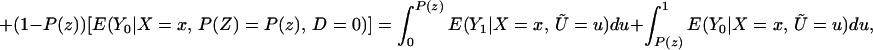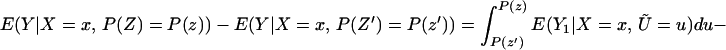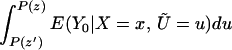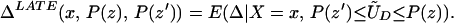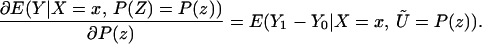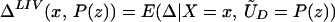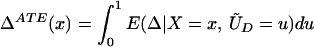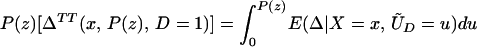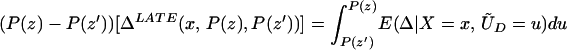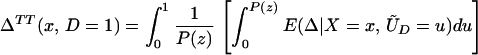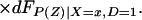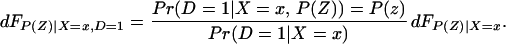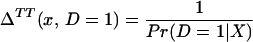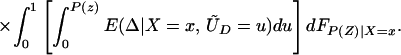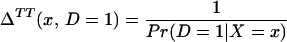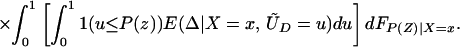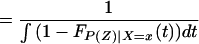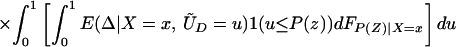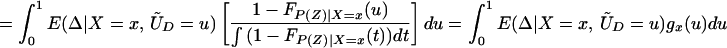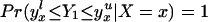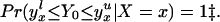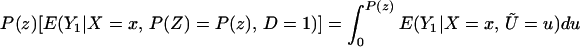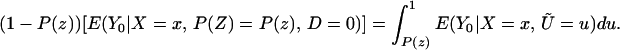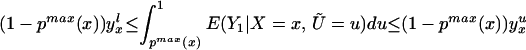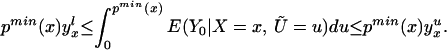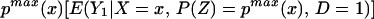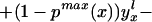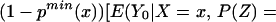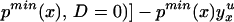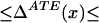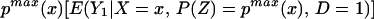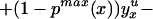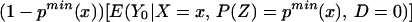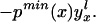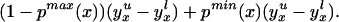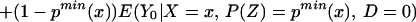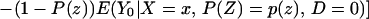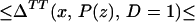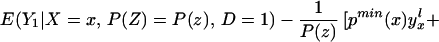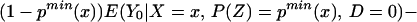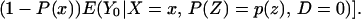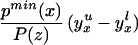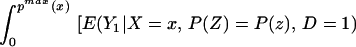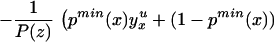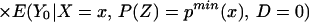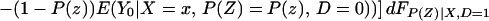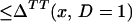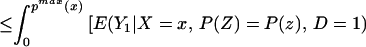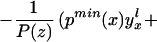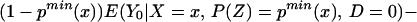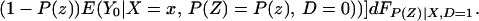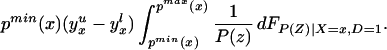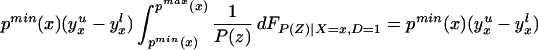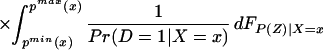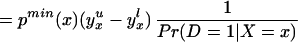Abstract
This paper examines the relationship between various treatment parameters within a latent variable model when the effects of treatment depend on the recipient’s observed and unobserved characteristics. We show how this relationship can be used to identify the treatment parameters when they are identified and to bound the parameters when they are not identified.
This paper uses the latent variable or index model of econometrics and psychometrics to impose structure on the Neyman (1)–Fisher (2)–Cox (3)–Rubin (4) model of potential outcomes used to define treatment effects. We demonstrate how the local instrumental variable (LIV) parameter (5) can be used within the latent variable framework to generate the average treatment effect (ATE), the effect of treatment on the treated (TT) and the local ATE (LATE) of Imbens and Angrist (6), thereby establishing a relationship among these parameters. LIV can be used to estimate all of the conventional treatment effect parameters when the index condition holds and the parameters are identified. When they are not, LIV can be used to produce bounds on the parameters with the width of the bounds depending on the width of the support for the index generating the choice of the observed potential outcome.
Models of Potential Outcomes in a Latent Variable Framework
For each person i, assume two potential outcomes (Y0i, Y1i) corresponding, respectively, to the potential outcomes in the untreated and treated states. Let Di = 1 denote the receipt of treatment; Di = 0 denotes nonreceipt. Let Yi be the measured outcome variable so that
This is the Neyman-Fisher-Cox-Rubin model of potential outcomes. It is also the switching regression model of Quandt (7) or the Roy model of income distribution (8, 9).
This paper assumes that a latent variable model generates the indicator variable D. Specifically, we assume that the assignment or decision role for the indicator is generated by a latent variable D*i:
where Zi is a vector of observed random variables and UDi is an unobserved random variable. D*i is the net utility or gain to the decision-maker from choosing state 1. The index structure underlies many models in econometrics (10) and in psychometrics (11).
The potential outcome equation for the participation state is Y1i = μ1(Xi, U1i), and the potential outcome for the nonparticipation state is Y0i = μ0(Xi, U0i), where Xi is a vector of observed random variables and (U1i, U0i) are unobserved random variables. It is assumed that Y0 and Y1 are defined for everyone and that these outcomes are independent across persons so that there are no interactions among agents. Important special cases include models with (Y0, Y1) generated by latent variables and include μj(Xi, Uji) = μj(Xi) + Uji if Y is continuous and μj(Xi, Uji) = 1(Xβj + Uji ≥ 0) if Y is binary, where 1(A) is the indicator function that takes the value 1 if the event A is true and takes the value 0 otherwise. We do not restrict the (μ1, μ0) function except through integrability condition iv given below.
We assume: (i) μD(Z) is a nondegenerate random variable conditional on X = x; (ii) (UD, U1) and (UD, U0) are absolutely continuous with respect to Lebesgue measure on ℜ2; (iii) (UD, U1) and (UD, U0) are independent of (Z, X); (iv) Y1 and Y0 have finite first moments; and (v) Pr(D = 1) > 0.
Assumption i requires an exclusion restriction: There exists a variable that determines the treatment decision but does not directly affect the outcome. Let FUD be the distribution of UD with the analogous notation for the distribution of the other random variables. Let P(z) denote Pr(D = 1|Z = z) = FUD(μD(z)). P(z) is sometimes called the “propensity score”, following ref. 12. Let ŨD denote the probability transform of UD: ŨD = FUD(UD). Note that, because UD is absolutely continuous with respect to Lebesgue measure, ŨD ≈ Unif(0,1). Let Δi denote the treatment effect for person i: Δi = Y1i − Y0i.
It is the index structure on D that plays the crucial role in this paper. An index structure on the potential outcomes (Y0, Y1) is not required, although it is both conventional and convenient in many applications.
Definition of Parameters
We examine four different mean parameters within this framework: the ATE, effect of treatment on the treated (TT), the local ATE (LATE), and the LIV parameter. The average treatment effect is given by:
From assumption iv, it follows that E(Δ|X = x) exists and is finite a.e. FX. The expected effect of treatment on the treated is the most commonly estimated parameter for both observational data and social experiments (13, 14). It is defined as:
From iv, ΔTT(x, D = 1) exists and is finite a.e. FX|D = 1, where FX|D=1denotes the distribution of X conditional on D = 1. It will be useful to define a version of ΔTT(X, D = 1) conditional on P(Z):
so that
From our assumptions, ΔTT (x, P(z), D = 1) exists and is finite a.e. FX,P(Z)|D=1. In the context of a latent variable model, the LATE parameter of Imbens and Angrist (6) using P(Z) as the instrument is
Without loss of generality, assume that P(z) > P(z′). From assumption iv, it follows that ΔLATE(x, P(z), P(z′)) is well defined and is finite a.e. FX,P(Z) × FX,P(Z). For interpretative reasons, Imbens and Angrist (6) also assume that P(z) is monotonic in z, a condition that we do not require. However, we do require that P(z) ≠ P(z′) for any (z, z′) where the parameter is defined.
The fourth parameter that we analyze is the LIV parameter introduced in ref. 5 and defined in the context of a latent variable model as
LIV is the limit form of the LATE parameter. In the next section, we demonstrate that ΔLIV(x, P(z)) exists and is finite a.e. FX,P(Z) under our maintained assumptions.
A more general framework defines the parameters in terms of Z. The latent variable or index structure implies that defining the parameters in terms of Z or P(Z) results in equivalent expressions. In the index model, Z enters the model only through the μD(Z) index, so that for any measurable set A,
Because any cumulative distribution function is left-continuous and nondecreasing, we have
Relationship Between Parameters Using the Index Structure
Given the index structure, a simple relationship exists among the four parameters. From the definition it is obvious that
Next, consider ΔLATE(x, P(z), P(z′)). Note that
so that
and thus
LIV is the limit of this expression as P(z) → P(z′). In Eq. 8, E(Y1|X = x, Ũ) and E(Y0|X = x, Ũ) are integrable with respect to dFŨ a.e. FX. Thus, E(Y1|X = x, P(Z) = P(z)) and E(Y0|X = x, P(Z) = P(z)) are differentiable a.e. with respect to P(z), and thus E(Y|X = z, P(Z) = P(z)) is differentiable a.e. with respect to P(z) with derivative given by†
From assumption iv, the derivative in Eq. 10 is finite a.e. FX,Ũ. The same argument could be used to show that ΔLATE(x, P(z), P(z′)) is continuous and differentiable in P(z) and P(z′).
We rewrite these relationships in succinct form in the following way:
and
Each parameter is an average value of LIV, E(Δ|X = x, Ũd = u), but for values of UD lying in different intervals. LIV defines the treatment effect more finely than do LATE, ATE, or TT.
ΔLIV(x, p) is the average effect for people who are just indifferent between participation or not at the given value of the instrument (i.e., for people who are indifferent at P(Z) = p). ΔLIV(x, p) for values of p close to zero is the average effect for individuals with unobservable characteristics that make them the most inclined to participate, and ΔLIV(x, p) for values of p close to one is the average treatment effect for individuals with unobservable characteristics that make them the least inclined to participate. ATE integrates ΔLIV(x, p) over the entire support of ŨD (from p = 0 to p = 1). It is the average effect for an individual chosen at random. ΔTT(x, P(z), D = 1) is the average treatment effect for persons who chose to participate at the given value of P(Z) = P(z); ΔTT(x, P(z), D = 1) integrates ΔLIV(x, p) up to p = P(z). As a result, it is primarily determined by the average effect for individuals whose unobserved characteristics make them the most inclined to participate in the program. LATE is the average treatment effect for someone who would not participate if P(Z) ≤ P(z′) and would participate if P(Z) ≥ P(z). ΔLATE(x, P(z), P(z′)) integrates ΔLIV(x, p) from p = P(z′) to p = P(z).
To derive TT, use Eq. 4 to obtain
Using Bayes rule, one can show that
Because Pr(D = 1|X = x, P(Z)) = P(z),
Note further that, because Pr(D = 1|X) = E(P(Z)|X) = ∫01 (1 − FP(Z)|X=x(t))dt, we can reinterpret Eq. 14 as a weighted average of LIV parameters in which the weighting is the same as that from a “length-biased,” “size-biased,” or “P-biased” sample:
where gx(u) = 1 − FP(Z)|X=x(u)/∫ (1 − FP(Z)|X=x(t))dt. Replacing P(Z) with length-of-spell, gx(u) is the density of a length-biased sample of the sort that would be obtained from stock biased sampling in duration analysis (16). Here we sample from the P(Z) conditional on D = 1 and obtain an analogous density used to weight up LIV. gx(u) is nonincreasing function of U. ΔLIV(x, p) is given zero weight for p ≥ pmax(x).
Identification of Treatment Parameters
Assume access to an infinite independently and identically distributed sample of (D, Y, X, Z) observations, so that the joint distribution of (D, Y, X, Z) is identified. Let 𝒫(x) denote the closure of the support P(Z) conditional on X = x, and let 𝒫c(x) = (0, 1)∖𝒫(x). Let pmax(x) and pmin(x) be the maximum and minimum values in 𝒫(x).
LATE and LIV are defined as functions (Y, X, Z) and are thus straightforward to identify. ΔLATE(x, P(z), P(z′)) is identified for any (P(z), P(z′)) ∈ 𝒫(x) × 𝒫(x). ΔLIV(x, P(z)) is identified for any P(z) that is a limit point of 𝒫(x). The larger the support of P(Z) conditional on X = x, the bigger the set of LIV and LATE parameters that can be identified.
ATE and TT are not defined directly as functions of (Y, X, Z), so a more involved discussion of their identification is required. We can use LIV or LATE to identify ATE and TT under the appropriate support conditions: (i) If 𝒫(x) = [0, 1], then ΔATE(x) is identified from ΔLIV. If {0, 1} ∈ 𝒫(x), then ΔATE(x) is identified from ΔLATE. (ii) If (0, P(z)) ⊂ 𝒫(x), then ΔTT(x, P(z), D = 1) is identified from ΔLIV. If {0, P(z)} ∈ 𝒫(x) then ΔTT(x, P(z), D = 1) is identified from ΔLATE.
Note that TT is identified under weaker conditions than is ATE. To identify TT, one needs to observe P(Z) arbitrarily close to 0 (pmin(x) = 0) and to observe some positive P(Z) values whereas to identify ATE, one needs to observe P(Z) arbitrarily close to 0 and arbitrarily close to 1 (pmax(x) = 1 and pmin(x) = 0). Note that the conditions involve the closure of the support of P(Z) conditional on X = x and not the support itself. For example, to identify ΔTT(x, D = 1) from ΔLATE, we do not require that 0 be in the support of P(Z) conditional on X = x but that points arbitrarily close to 0 be in the support. This weaker requirement follows from ΔLIV(x, P(z)) being a continuous function of P(z) and ΔLATE(x, P(z), P(z′)) being a continuous function of P(z) and P(z′).
Without these support conditions, we can still construct bounds if Y1 and Y0 are known to be bounded with probability one. For ease of exposition and to simplify the notation, assume that Y1 and Y0 have the same bounds, so that
and
For example, if Y is an indicator variable, then the bounds are yxl = 0 and yxu = 1 for all x. For any P(z) ∈ 𝒫(x), we can identify
and
In particular, we can evaluate Eq. 16 at P(z) = pmax(x) and can evaluate Eq. 17 at P(z) = pmin(x). The distribution of (D, Y, X, Z) contains no information on ∫pmax(x)1 E(Y1|X = x, Ũ = u)du and ∫0pmin(x) E(Y0|X = x, Ũ = u)du, but we can bound these quantities:
We thus can bound ΔATE(x) by§
The width of the bounds is thus
The width is linearly related to the distance between pmax(x) and 1 and the distance between pmin(x) and 0. These bounds are directly related to the “identification at infinity” results of refs. 9 and 18. Such identification at infinity results require the condition that μD(Z) takes arbitrarily large and arbitrarily small values if the support of UD is unbounded. The condition is sometimes criticized as being not credible. However, as is made clear by the width of the above bounds, the proper metric for measuring how close one is to identification at infinity is the distance between pmax(x) and 1 and the distance between pmin(x) and 0. It is credible that these distances may be small. In practice, semiparametric methods that use identification at infinity arguments to identify ATE are implicitly extrapolating E(Y1|X = x, Ũ = u) for u > pmax(x) and E(Y0|X = x, Ũ = u) for u < pmin(x).
We can construct analogous bounds for ΔTT(x, P(z), D = 1) for P(z) ∈ 𝒫(x):
The width of the bounds on ΔTT(x, P(z), D = 1) is thus:
The width of the bounds is linearly decreasing in the distance between pmin(x) and 0. Note that the bounds are tighter for larger P(z) evaluation points because the higher the P(z) evaluation point, the less weight is placed on the unidentified quantity ∫0pmin(x) E(Y0|X = x, Ũ = u)du. In the extreme case, where P(z) = pmin(x), the width of the bounds simplifies to yxu − yxl.
We can integrate the bounds on ΔTT(x, P(z), D=1) to bound ΔTT(x, D = 1):
The width of the bounds on ΔTT(x, D = 1) is thus:
Using Eq. 13, we have
Unlike the bounds on ATE, the bounds on TT depend on the distribution of P(Z), in particular, on Pr(D = 1|X = x) = E(P(Z)|X = x). The width of the bounds is linearly related to the distance between pmin(x) and 0, holding Pr(D = 1|X = x) constant. The larger Pr(D = 1|X = x) is, the tighter the bounds because the larger P(Z) is on average, the less probability weight is being placed on the unidentified quantity ∫0pmin(x) E(Y0|X = x, Ũ = u)du.
Conclusion
This paper uses an index model or latent variable model for the selection variable D to impose some structure on a model of potential outcomes that originates with Neyman (1), Fisher (2), and Cox (3). We introduce the LIV parameter as a device for unifying different treatment parameters. Different treatment effect parameters can be seen as averaged versions of the LIV parameter that differ according to how they weight the LIV parameter. ATE weights all LIV parameters equally. LATE gives equal weight to the LIV parameters within a given interval. TT gives a large weight to those LIV parameters corresponding to the treatment effect for individuals who are the most inclined to participate in the program. The weighting of P for LIV that produces TT is like that obtained in length biased or sized biased samples.
Identification of LATE and LIV parameters depends on the support of the propensity score, P(Z). The larger the support of P(Z), the larger the set of LATE and LIV parameters that are identified. Identification of ATE depends on observing P(Z) values arbitrarily close to 1 and P(Z) values arbitrarily close to 0. When such P(Z) values are not observed, ATE can be bounded, and the width of the bounds is linearly related to the distance between 1 and the largest P(Z) and the distance between 0 and the smallest P(Z) value. For TT, identification requires that one observe P(Z) values arbitrarily close to 0. If this condition does not hold, then the TT parameter can be bounded and the width of the bounds will be linearly related to the distance between 0 and the smallest P(Z) value, holding Pr(D = 1|X) constant.
Implementation of these methods through either parametric or nonparametric methods is straightforward. In joint work with Arild Aakvik of the University of Bergen (Bergen, Norway), we have developed the sampling theory for the LIV estimator and empirically estimated and bounded various treatment parameters for a Norwegian vocational rehabilitation program.
We conclude this paper with the observation that the index structure for D is not strictly required, nor is any monotonicity assumption necessary to produce results analogous to those presented in this paper. The index structure on D simplifies the derivations and yields the elegant relationships presented here. However, LIV can be defined without using an index structure (5); so can LATE. We can define LIV for different sets of regressors and produce relationships like those given in Eq. 11 defining the integrals over multidimensional sets instead of intervals. The bounds we present also can be generalized to cover this case as well. The index structure for D arises in many psychometric and economic models in which the index represents net utilities or net preferences over states, and these are usually assumed to be continuous. In these cases, its application leads to the simple and concise relationships given in this paper.
Acknowledgments
We thank Aarild Aakvik, Victor Aguirregabiria, Xiaohong Chen, Lars Hansen and Justin Tobias for close reading of this manuscript. We also thank participants in the Canadian Econometric Studies Group (September, 1998), the Midwest Econometrics Group (September, 1998), the University of Upsalla (November, 1998), the University of Chicago (December, 1998), the University of Chicago (December, 1998), and University College London (December, 1998). James J. Heckman is Henry Schultz Distinguished Service Professor of Economics at the University of Chicago and a Senior Fellow at the American Bar Foundation. Edward Vytlacil is a Sloan Fellow at the University of Chicago. This research was supported by National Institutes of Health Grants R01-HD34958-01 and R01-HD32058-03, National Science Foundation Grant 97-09-873, and the Donner Foundation.
ABBREVIATIONS
- LIV
local instrumental variable
- ATE
average treatment effect
- TT
effect of treatment on the treated
- LATE
local ATE
Footnotes
†See, e.g., Kolmogorov and Fomin (15), Theorem 9.8 for one proof.
‡The modifications required to handle the more general case are straightforward.
§The following bounds on ATE also can be derived easily by applying Manski’s (17) bounds for “Level-Set Restrictions on the Outcome Regression.” The bounds for the other parameters discussed in this paper cannot be derived by applying his results.
References
-
1.Neyman J. Stat Sci. 1990;5:465–480. [Google Scholar]
-
2.Fisher R A. Design of Experiments. London: Oliver and Boyd; 1935. [Google Scholar]
-
3.Cox D R. The Planning of Experiments. New York: Wiley; 1958. [Google Scholar]
-
4.Rubin D. Ann Stat. 1978;6:34–58. [Google Scholar]
-
5.Heckman J. J Human Resources. 1997;32:441–462. [Google Scholar]
-
6.Imbens G, Angrist J. Econometrica. 1994;62:467–476. [Google Scholar]
-
7.Quandt R. J Am Stat Assoc. 1972;67:306–310. [Google Scholar]
-
8.Roy A. Oxford Econ Papers. 1951;3:135–146. [Google Scholar]
-
9.Heckman J, Honoré B. Econometrica. 1990;58:1121–1149. [Google Scholar]
-
10.Maddala G S. Qualitiative and Limited Dependent Variable Models. Cambridge, U.K.: Cambridge Univ. Press; 1983. [Google Scholar]
-
11.Junker B, Ellis J. Ann Stat. 1997;25:1327–1343. [Google Scholar]
-
12.Rosenbaum P, Rubin D. Biometrika. 1983;70:41–55. [Google Scholar]
-
13.Heckman J, Robb R. In: Longitudinal Analysis of Labor Market Data. Heckman J, Singer B, editors. New York: Cambridge Univ. Press; 1985. pp. 156–245. [Google Scholar]
-
14.Heckman J, Lalonde R, Smith J. In: Handbook of Labor Economics. Ashenfelter O, Card D, editors. Amsterdam: Elsevier; 1999. , in press. [Google Scholar]
-
15.Kolmogorov A N, Fomin S V. Introductory Real Analysis, trans. Silverman, R. New York, NY: Dover; 1970. [Google Scholar]
-
16.Rao C R. In: A Celebration of Statistics. Feinberg S, editor. Berlin: Springer; 1986. [Google Scholar]
-
17.Manski C. Am Econ Rev. 1990;80:319–323. [Google Scholar]
-
18.Heckman J. Am Econ Rev. 1990;80:313–318. [Google Scholar]