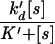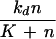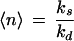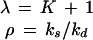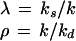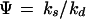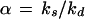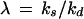Stochastic focusing: Fluctuation-enhanced sensitivity of intracellular regulation

Abstract

Many regulatory molecules are present in low copy numbers per cell so that significant random fluctuations emerge spontaneously. Because cell viability depends on precise regulation of key events, such signal noise has been thought to impose a threat that cells must carefully eliminate. However, the precision of control is also greatly affected by the regulatory mechanisms' capacity for sensitivity amplification. Here we show that even if signal noise reduces the capacity for sensitivity amplification of threshold mechanisms, the effect on realistic regulatory kinetics can be the opposite: stochastic focusing (SF). SF particularly exploits tails of probability distributions and can be formulated as conventional multistep sensitivity amplification where signal noise provides the degrees of freedom. When signal fluctuations are sufficiently rapid, effects of time correlations in signal-dependent rates are negligible and SF works just like conventional sensitivity amplification. This means that, quite counterintuitively, signal noise can reduce the uncertainty in regulated processes. SF is exemplified by standard hyperbolic inhibition, and all probability distributions for signal noise are first derived from underlying chemical master equations. The negative binomial is suggested as a paradigmatic distribution for intracellular kinetics, applicable to stochastic gene expression as well as simple systems with Michaelis–Menten degradation or positive feedback. SF resembles stochastic resonance in that noise facilitates signal detection in nonlinear systems, but stochastic resonance is related to how noise in threshold systems allows for detection of subthreshold signals and SF describes how fluctuations can make a gradual response mechanism work more like a threshold mechanism.

Internal regulation of biochemical reactions is essential for cell growth and survival. Initiation of replication, gene expression, and metabolic activity must be controlled to coordinate the cell cycle, supervise cellular development, respond to changes in the environment, or correct random internal fluctuations. All of these tasks are orchestrated by molecular signals whose concentrations affect rates of regulated processes. Because many of the regulatory kinetic mechanisms are insufficiently characterized for accurate quantitative analyses, they often are explicitly or implicitly approximated as Boolean step-functions, assuming that a regulated process switches on or off at a threshold signal concentration. How well Boolean approximations apply to real biochemistry depends on the underlying kinetic mechanisms' capacities for sensitivity amplification (1–3). Rates of simple reactions often respond far from Boolean to signal changes, and high sensitivity basically requires complicated control structures, as when signal molecules enter a reaction in many copies (cooperatively) or at many subsequent steps along a pathway.

Sensitivity analyses are generally phenomenological, assuming that concentrations change continuously and deterministically. However, signal molecules in genetic or metabolic networks are often present in a few to a few hundred copies (4) and the actual copy number in individual cells inevitably will fluctuate (4–13) because of the intrinsically random nature of chemical reactions (14–16). The relation between signal and response in intracellular processes is thus inevitably affected by noise. This noise can be exploited when nongenetic variation is selected for (6, 11), but its presence raises critical questions. How can cells respond in a reliable way to changes in conditions when signal molecule concentrations only represent these conditions in a probabilistic sense? Would not significant signal noise cause cells to frequently make the wrong decisions? Reports (4–13) that explicitly address these questions confirm the consensus that noisy signals reduce the reliability of control in intracellular regulatory networks by randomizing the response. However, these reports generally assume threshold kinetics and rarely take sensitivity into account.

It is unfortunate that sensitivity amplification and noise are treated as separate aspects of intracellular regulation because the two in fact are fundamentally connected. High sensitivity amplification is essential for reducing uncertainty in the timing of cellular events, and the significance of concentration noise is greatly affected by how formation and elimination rates respond to concentration changes. Conversely, random signal fluctuations can greatly affect the capacity for sensitivity amplification. For threshold-dominated control, fluctuations cause the signal to randomly jump back and forth across the threshold and thereby randomize the outcomes of the response reactions. Fluctuations thus turn the average response rates into more gradual functions of the average signal levels, i.e., reduces the sensitivity amplification. However, this is only a special case of the general principle that the average of a nonlinear function is not the same as the function of the average. When the kinetic mechanism itself is gradual so that the response is probabilistic also in the absence of signal fluctuations, the situation can be the opposite: random fluctuations can make it transcend all macroscopically predicted limits for sensitivity amplification. We term this phenomenon stochastic focusing (SF), and it applies quite generally to insensitive nonlinear regulatory mechanisms and signal noise that emerges spontaneously from biochemical reactions. An effect of SF is that cells can exploit signal noise to reduce the random variation in regulated processes.

Theory

Genetic and biochemical networks are complex systems, the parts of which cannot be properly analyzed in abstraction from the whole. Even so, Occam's razor is essential when making new kinetic design principles presentable, and this work therefore gives full precedence to simplicity.

Hyperbolic Inhibition and Sensitivity Amplification.

In the classification of biochemical regulatory mechanisms, hyperbolic control is commonly used as a standard (3). Hyperbolic activation is for instance described by the Michaelis–Menten equation (17), and for the complementary hyperbolic inhibition, the probability q of not inhibiting is given by

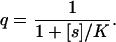1

Here [s] is the concentration of a signal molecule and K is an inhibition constant. The special position of hyperbolic control is warranted both by its simplicity and by the fact that it arises from ubiquitous reaction schemes, for instance simple branching reactions (see Appendix).

The standard measure of regulatory sensitivity (1–3) is the amplification factor, defined as the percentage change in the response q over the percentage change in the signal [s] or, identically, as the slope of a curve of log(q) as a function of log([s]). High sensitivity does not necessarily mean Boolean control in the strict sense that an activity switches from 0 to 1. However, the practical implications of switching between e.g. 10⁻³ to 10⁻¹ may be very similar; high sensitivity means sharp shifts between negligible and significant activities.

How sensitively q in Eq. 1 responds to changes in [s] depends on [s]/K, but the relative change in q is always smaller than the relative change in [s].

Signal Noise.

Internal noise does not reflect arbitrary irregularities that disturb an otherwise deterministic development. Chemical reactions are probabilistic by nature (14–16), and this randomness is the conceptual foundation also for macroscopic approaches. The mesoscopic molecular-level descriptions, based on chemical master equations, in fact provide the bases from which the corresponding phenomenological rate equations should be derived (16). All signal probability distributions used in the present work therefore were derived from biochemical reaction schemes (Appendix).

The Poisson distribution is widely used in theoretical analyses of chemical systems because it frequently arises at thermodynamic equilibrium (16) as well as when individual formation and elimination events are independent. However, intracellular processes are far from equilibrium and reactions are generally not even approximately independent. A more suitable paradigmatic distribution is then the negative binomial (NB) that ranges between Poissonian and very broad and skewed distributions depending on the kinetic parameters. The NB arises as the stationary distribution of many simple birth and death processes, including three prototypical kinetic designs of biochemical relevance:

1.

When individual signal molecules are synthesized independently but eliminated with Michaelis–Menten kinetics. Elimination may mean degradation into constituents, covalent modification, or incorporation into more complex molecules.

2.

When individual signal molecules are degraded independently but synthesized along two different pathways, one with zero and one with first-order rate (15, 16, 18). Apart from replicators, this approximately applies to systems with positive feedback, such as when a gene product binds to its own operator and increases the rate of transcription (Appendix).

3.

When individual signal molecules are degraded independently but produced in independent, instantaneous, geometrically distributed bursts. Constant competition rates of mRNA inactivation versus translation give a geometrically distributed number of proteins translated per mRNA (7, 9).

Modification of signal molecules often produces additional precursors for demodification, such as phosphorylation-dephosphorylation of a constant total number of molecules. When the individual reactions are independent, the stationary distributions are binomial. When molecules instead compete for modification-demodification enzymes, as for the zero-order ultrasensitivity mechanism (19), fluctuations can be much more significant. In the extreme where the rates are constant, the stationary distribution of the minority molecular configuration is a truncated geometric distribution.

Effective Probabilities.

The signal concentration is the number of signal molecules divided by the reaction volume (e.g. cell size), [s] = n/v. The expression for q in Eq. 1 is thus not only macroscopic, q(n) is also the reaction probability in cells with n signal molecules and therefore fluctuates randomly with n. However, because q is not a linear function of n, the average response probability is generally not the same as the response probability for the average signal, q(〈n〉). The macroscopic approach is then insufficient for describing average response rates, and because a population of cells cannot be seen as a single super-cell it does not even describe averages over infinitely large populations of identical, independent cells. The real average 〈q〉 is instead found by compounding q over all probabilities p_n for n signal molecules at the time of the reaction, assuming that n stays constant during the time window of an individual response reaction (Appendix).

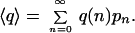2

When n fluctuates slowly, outcomes of subsequent signal-dependent reactions become correlated. The parameter 〈q〉 is then relevant because it determines average rates, but it is insufficient for describing the full impact of signal noise. However, when the signal fluctuates so rapidly that these response correlations are insignificant, 〈q〉 is not only an average over a cell population, but also the actual probability of every single reaction and thus determines the full random process so that the variance of q over the distribution p_n is irrelevant. The averaging procedure in Eq. 2 is then practical for kinetic modeling, but 〈q〉 is neither more nor less than a simple reaction probability.

Signal, Noise, and Ambiguities.

To inspect the impact that signal noise has on 〈q〉 it is tempting to simply relate 〈q〉 to the average signal 〈n〉 and compare results in the presence and absence of fluctuations around 〈n〉. For distributions that are completely determined by their average, like the Poisson, this approach works fine. However, when 〈n〉 does not uniquely determine the probability distribution, it is impossible to unambiguously track changes in 〈q〉 for changes in 〈n〉. The exact changes in the underlying kinetic parameters, such as rates of underlying reactions or binding constants, then must be specified because a change in two parameters such that 〈n〉 is kept constant can elicit a sharp change in the response 〈q〉. Taken over an entire cell population, the average signal then would not change at all while the average response rate could change with orders of magnitude.

Taking fluctuations into account and separating between different sources of changes in the average is not a subversive way of introducing additional layers of regulation. It instead reveals the true regulatory nature of a system where the full distribution over the internal states cannot be exchanged for the average. A state can be identified as the number of molecules of a given species, and conventional macroscopic kinetics relies on the approximate validity of replacing a set of possible states (internal noise) with a scalar mathematical abstraction: the average. Although trivial, it should be stressed that averages are defined from the distributions over the internal states, not vice versa, and a system's multivariate nature always precedes the macroscopic phenomena. In molecular biology, signal and response are mutually defining concepts, i.e., a concentration receives its signal character through the kinetics of the response reaction. By assuming that fluctuations in signal molecule concentrations obstruct reliable intracellular signal processing, without first carefully considering their impact on the response, one thus implicitly sequesters parts of the signal from the mechanism that defines it. The way to avoid these semantic but tangible problems of signal and noise is to return to the fully mesoscopic perspective where both the average and the fluctuations have their origin in the underlying kinetics.

Time-Correlated Noise.

When signal fluctuations are slow, outcomes of subsequent signal-dependent reactions are correlated. Long time periods with high signal-regulated intensity are then randomly succeeded by long time periods with negligible intensity. This can increase fluctuations in the regulated process greatly.

The significance of correlations between outcomes depends on how frequently the response reactions follow each other in time compared to how rapidly the signal probability distribution is reshuffled. Rapid signal fluctuations can be achieved by rapid degradation but also by equilibration between active and inactive configurations. High energy dissipation is thus not necessary to avoid response correlations.

Results

To illustrate the surprising impact that signal noise can have on intracellular regulation, we executed Monte Carlo simulations for some simple systems and calculated effective reaction probabilities.

Monte Carlo Simulation of a Branched Reaction.

We studied the scheme:

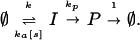3

The empty set ∅ denotes sources and sinks of molecules. It is unaffected by the reactions and does not affect the rates. I-molecules are produced constitutively with rate k and degraded or converted into P (product) with rates k_a[s] and k_p, respectively. Product molecules are individually degraded with normalized rate constant 1. I may be a constitutively synthesized replication preprimer (10) that can mature or be inhibited by signal molecules. However, scheme 3 can be given many interpretations, and I also may be a transcription complex, an active mRNA or an intermediate metabolite.

Noise in the signal concentration [s] arises from random synthesis and degradation of signal molecules S. Here we used

(corresponding to standard in Appendix) so that stationary signal fluctuations are Poissonian.

When the transition from I to ∅ or P is fast enough, the pool of I-molecules is insignificant, and [s] does not change significantly during the life span of an individual I-molecule. Scheme 3 then simplifies to

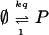with q from Eq. 1 and K = k_p/k_a so that the rate equation is d[p]/dt = kq − [p]. Simulations were made both for noise-free and noisy signal concentrations by using the Gillespie algorithm (20) with the rates above as transition probabilities per time unit. From the sum of rates, this algorithm iteratively generates exponentially distributed reaction times for the next event. The type of event is simulated with probabilities proportional to the respective rates.

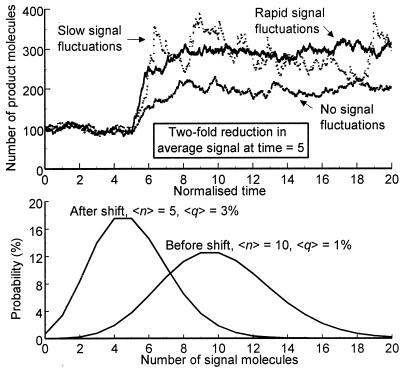
When signal noise is insignificant, a 2-fold decrease in signal can never result in more than a 2-fold increase in the average number of products due to the intrinsic limitation of hyperbolic inhibition (Eq. 1 and Fig. 1 Upper). However, Fig. 1 Upper shows that when signal noise is significant, a 2-fold decrease in the average signal concentration results in about a 3-fold increase in the average number of product molecules. Consequently, when the (stationary) signal molecule distributions overlap significantly (Fig. 1 Lower), the corresponding average reaction probabilities can in fact become more separated than when fluctuations are negligible: SF.

Figure 1.

(Upper) Number of product molecules as a function of time when product formation is inhibited by a noisy or noise-free signal (see main text). Product half-life is ln(2) time units, k = 10⁴ and 〈q〉 = 1%. To keep the same 〈q〉 before the shift for noisy and noise-free signals, the value of Kv, the inhibition constant multiplied by the reaction volume, is different in the two cases. After five time units the signal time average 〈n〉 = 10 shifts to 〈n〉 = 5 due to a 2-fold reduction in k_s from 10 k_d to 5 k_d. For slow fluctuations, k_d = 100. When k_s and k_d are 10 times higher, slow and rapid signal fluctuations give rise to almost indistinguishable processes for product formation (not shown). Rapid signal fluctuations correspond to insignificant time correlations. (Lower) Stationary signal distributions (Poissonian) before and after the shift in conditions in Upper. 〈q〉 (Eq. 2) is calculated by using the same Kv as in Upper.

The increased capacity for sensitivity amplification is the only effect of a rapidly fluctuating signal (Fig. 1 Upper). Stationary product fluctuations are then Poissonian regardless of signal noise. However, if signal fluctuations are slow (long signal half-life) and significant, product fluctuations may be considerably larger (Fig. 1 Upper), because of time correlations in the product synthesis rate. Their impact depends on the time scale of the regulated process, in this case the half-life of product molecules. Because time scales of intracellular processes span over many orders of magnitude, the effects of correlations can be anything from insignificant to extreme.

Effective Probabilities.

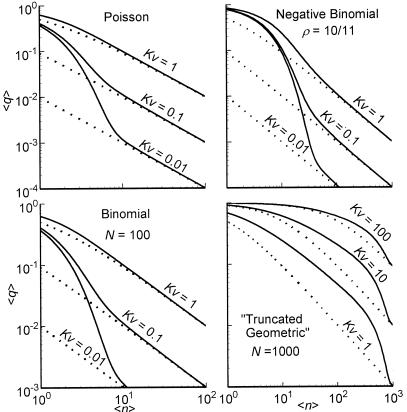
Fig. 2 shows 〈q〉 (Eq. 2) as a function of 〈n〉 for the four distributions inspected in the Theory section. The biological cause of the change in 〈n〉 depends on the underlying process (see Appendix). Only the Poisson is uniquely determined by its average. For the NB, one of the kinetic parameters is varied and the other is kept constant. For the binomial and truncated geometric distributions we keep the total number of molecules fixed and change the average number of signal molecules through the modification-demodification balance.

Figure 2.

〈q〉 (Eq. 2) for noisy (solid lines) and noise-free (dotted lines) signals as a function of the average number of signal molecules 〈n〉 in log-log scale. Kv is the inhibition constant multiplied by the reaction volume. For a mathematical specification of the distributions, see Eq. A3. For NB, the value of 〈n〉 is changed by changing λ for fixed ρ = 10/11. N in the lower two graphs is the upper limit in the number of molecules.

As can be seen in Figs. 2 and 3, all four distributions used for signal noise can significantly increase the sensitivity amplification. For Poisson and binomial distributions, fluctuations are only significant at very low averages so that low inhibition constants are required to get significant SF for hyperbolic inhibition (Figs. 2 and 3, Left). However, when fluctuations are larger, as for the NB or truncated geometric distributions, significant SF is possible in a much broader range of averages and inhibition constants (Figs. 2 and 3, Right). In these two cases, hyperbolic inhibition also can display stochastic defocusing, i.e., lower sensitivity than the response to a noise-free signal (Fig. 3, not shown for NB).

Figure 3.

Amplification factors (1–3) (the slope of the curves in Fig. 2 for other values of Kv) as functions of 〈q〉 in lin-log scale. The upper curve corresponds to noise-free signals.

Using Signal Noise to Attenuate Noise in Switching Delays.

High sensitivity amplification can be used for stricter control and reduced uncertainty in a regulated process (31). Signal noise thus can be used to attenuate response noise through SF. Here we exemplify this fundamental principle with a signal molecule that inhibits gene transcription. It is assumed that the signal synthesis rate decreases exponentially and that the signal concentration continuously relaxes to the changing steady state (Eq. A7). This can, for instance, be the case when synthesis depends on a rate-limiting precursor or enzyme that decays exponentially (with insignificant fluctuations). Defining switching delay as the waiting time before the first transcript appears, two questions are of particular interest. What is the average switching delay and how significant is random variation around the average?

The uncertainty in the number of signal molecules inevitably would increase the uncertainty in the switch delay if transcription were turned on at a threshold signal concentration. However, realistic regulatory mechanisms invoke random variation also in the response to noise-free signals. Like most mechanisms, hyperbolic inhibition has intrinsic shortcomings as a switching mechanism due to its limited capacity for sensitivity amplification. For a given initial transcription intensity, both the average and the variance of the switching delay have lower limits (Eq. A8) that cannot be transcended regardless of the choice of rate constants. Signal noise changes the scenario. Both the average and variance can then in fact be reduced indefinitely. A less dramatic example of this effect is shown in Fig. 4.

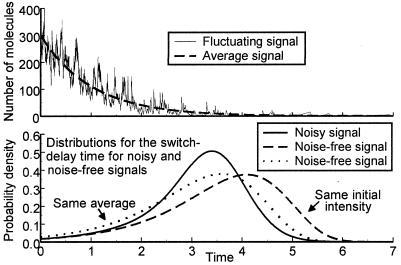
Figure 4.

(Upper) The number of signal molecules as a function of time. The synthesis rate constant decreases exponentially (Eq. A7). The quasistationary distribution of molecules is NB and the underlying random process is given by gene expression in Appendix. (Lower) The probability density for the switching delay time. The two curves for noise-free response corresponds to the minimal dispersion possible when all parameters can be chosen freely (Eq. A8), for the same initial intensity (dashed line) and the same average delay (dotted line) as the response (solid line) to the noisy signal, respectively. The noisy signal was NB-distributed with ρ = 10/11, as in Upper, Kv = 1 and assumed to fluctuate so rapidly that correlations are insignificant. The choice of underlying process does not change the result. See Appendix for a mathematical and numerical specification.

Fig. 4 Upper shows a fluctuating signal and its average as functions of time. The large fluctuations come from random bursts in signal synthesis (gene expression in Table 1). Fig. 4 Lower shows the probability density for the switch-delay times. The narrowest distribution corresponds to response to a noisy signal and the two others correspond to the lower dispersion limit when all rate constants can be chosen freely but signal noise is insignificant (Eq. A8). The quasi-stationary distributions of the noisy signal were NB, but the same effect is observed in all cases that give rise to SF (Figs. 2 and 3).

Table 1.

Macro- and mesoscopic fluxes and their stationary distributions (Eq. A3)

	Standard	Michaelis–Menten elimination	Auto-catalysis	Standard modification	Zero-order modification	Gene expression
J+[s]	k′s	k′s	k′s + k[s]	ks(C − [s])	k′s	k′sρ/(1 − ρ)
J−[s]	kd[s]		kd[s]	kd[s]	k′d	kd[s]
J+(n)	ks	ks	ks + kn	ks(N − n)	ks	ks (burst)
J−(n)	kdn		kdn	kdn	kd	kdn
Distribution	Poisson	NB	NB	Binomial	Trunc. Geo.	NB

Primed and unprimed constants are related as k_s = vk_s′ and the reaction volume v goes to infinity in the macroscopic limit but is time constant. Standard, autocatalysis, standard modification, and gene expression are linear and the rate equation for the average number of molecules take the same form as the macroscopic equation. For Michaelis–Menten elimination and zero-order modification the average behaves in a more complicated way. 

Though signal noise also can increase the uncertainty in the switch delay, the effects in Fig. 4 Lower are in no way restricted to the specific assumptions of the given example. Similar effects can, for instance, be observed if synthesis of a monomer is shut off at time t = 0 so that the number of dimers (signal molecules) fluctuates around a decreasing average.

Discussion

Regulatory reliability is a double-edged concept. To operate in a broad range of conditions, a regulatory mechanism must be robust (21) to many biochemical changes but must at the same time respond hypersensitively to specific changes for precise control (10). The present work inspects how sensitivity is affected by signal noise.

Biological Impact: Evolutionary Exploitation of Noise.

Biochemistry on the level of single molecules has received much attention in the last years (22). It is also becoming increasingly appreciated that the probabilistic nature of chemical reactions can invoke large random variation in regulatory responses and that this noise could be exploited for nongenetic variation (6, 11). Accordingly, gene regulation has been called a noisy business (13). Because it is also a nonlinear business, the sources and effects of the noise must be carefully analyzed. For instance, the validity of macroscopic approaches to describe averages cannot be taken for granted because the average of a nonlinear function is generally not the same as the function of the average. This was demonstrated for bimolecular reactions in 1953 (32). However, the most interesting aspect is not related to the modeling tools but to the fact that noise affects the qualitative nature of kinetic mechanisms. Here we show that as a direct consequence of this principle, standard nonlinear control in fact allows signal noise that arises naturally from biochemical reactions to reduce the random variation in regulated processes. The resolution of this paradox lies in the fundamental connection between noise and sensitivity amplification, two aspects of intracellular regulation that generally are treated separately.

Regulatory mechanisms' capacity for sensitivity amplification greatly affects the random variation in regulated processes and realistic mechanisms have internal restrictions that invoke an uncertainty also in the response to noise-free signals. However, signal noise can render an intrinsically insensitive kinetic mechanism a great capacity for sensitivity amplification through SF. This may apply to any rate that depends nonlinearly on a noisy concentration, e.g. bimolecular reactions, and was here demonstrated for hyperbolic inhibition. It is thus not necessary to combine threshold-dominated control with limited signal molecule fluctuations to obtain precise regulation. Organisms may acquire the same effect by exploiting fluctuations to turn insensitive and simple biochemical mechanisms into thresholds, i.e., by letting one alleged problem solve the other. It may seem like cells have insufficient information when making regulatory decisions based on noisy signals. However, selection acts to link a certain state of the cell to a certain response, not to make it possible to determine this state from a sample of the signal concentration.

SF and Multistep Control.

A first step toward understanding how signal noise can attenuate response noise is to strip terms like signal and noise from their anthropocentric baggage. Significant internal noise only means that a system's multivariate nature cannot be summarized by a scalar. It has long been appreciated that high sensitivity can be achieved when a signal regulates multiple subsequent transitions (23, 24). In a similar way, the probability that the number of signal molecules randomly moves from the average to extreme values depends on the underlying kinetic parameters at every transition. As a consequence, the probability mass in the tails of distributions generally responds very sensitively to changes in the average. Because nonlinear kinetic mechanisms may receive a disproportional contribution from the tails, SF can be formulated as a multistep kinetic mechanism that exploits the internal degrees of freedom that comes with signal noise. In macroscopic descriptions internal states are lumped together and only averages are considered.

SF and Stochastic Resonance (SR).

Quoting Moss and Pei (25): “The property of certain nonlinear systems whereby a random process—the noise—can optimally enhance the detection of a weak signal is called stochastic resonance (SR).” SF and SR thus show conceptual resemblance. However, SR is related to how threshold systems can use fluctuations to respond to subthreshold signals (26, 27), and SF describes how fluctuations can turn a gradual mechanism into a threshold. There is also a difference in both signal and noise concepts. SR signals are generally periodic, though aperiodic SR has been demonstrated (28), and the noise is typically external and explicitly added to a noise-free system. To our knowledge, all SR reports where noise is modeled as an effect of the internal degrees of freedom interpret the noise differently.

It is shown that neurophysiological sensory systems have evolved to take advantage of SR (29). For SF, fluctuations arise from underlying chemical pathways that are affected by single point mutations. Consequently, not only can a regulatory mechanism evolve to exploit signal noise, the properties of the noise can evolve to accommodate the regulatory mechanism.

Conclusion.

Deterministic intracellular behavior does not necessarily rely on large numbers of signal molecules. These processes operate far from equilibrium, with large fluctuations in concentrations and are regulated through nonlinear kinetics. Surprisingly, these properties can produce cellular determinism through the principle of SF.

Abbreviations

SF

stochastic focusing

NB

negative binomial

SR

stochastic resonance

Appendix

Hyperbolic Control.

Hyperbolic control arises from a multitude of schemes, for instance:

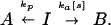This can be derived from the master equations:

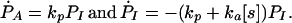A1

P̄_A, the probability of ending up in state A, corresponds to hyperbolic inhibition (q in Eq. 1) and P̄_B to hyperbolic activation as in the Michaelis–Menten equation:

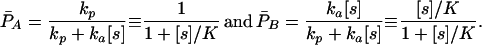A2

Signal Noise.

The distributions (with averages) used are:

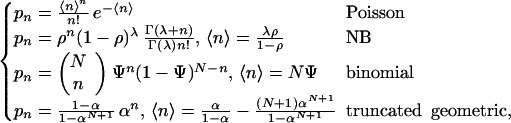A3

where Γ is the gamma function.

Changes in a concentration s is determined by the in and out fluxes J₊[s] and J₋[s], respectively:

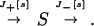With J₊(n) and J₋(n) as mesoscopic birth and death intensities when there are n molecules, the general rate and master equations (for one-step processes) are:

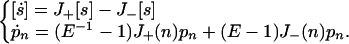A4

E is a “step operator” (16) defined by E^jf(n) = f(n + j). A number of kinetic mechanisms is given in Table 1.

Standard.

Individual formation and elimination events are independent (15, 16).

Michaelis–Menten elimination.

K′ is the Michaelis constant and a stationary distribution exists when k_d < k_s.

Autocatalysis.

As was shown in an analysis of maser amplification (16, 18), a stationary distribution exists and is NB when k < k_d. Because a/(1 + [s] + b[s]/(1 + [s]) ≈ a + b[s] for small [s], this kind of autocatalysis also may approximate positive hyperbolic control that increases the synthesis rate from a to b.

Standard modification.

The number of signal molecules n is determined by independent individual modification-demodification reactions of a constant total number of molecules in the system, N = Cv, where C is the total concentration.

Zero-order modification.

As above but with constant modification-demodification rates (extreme zero-order ultrasensitivity; ref. 19). The rate of modification drops to zero when there are zero unmodified molecules and vice versa. When α < 1, n follows a geometric distribution truncated at n = N and vice versa for N − n when α > 1.

Gene expression.

Macroscopically identical to standard, but every synthesis event now adds a geometrically distributed number, b, of molecules, g_b = ρ^b(1 − ρ). The master equation is more complicated than Eq. A4 and includes probability flows between all states, but it is still easily solved by using moment generating functions. Closely related mechanisms have received much attention in studies of stochastic gene expression (7–9, 12, 30). The value ρ = 10/11 used in the figures corresponds to an average burst size of 10 molecules.

Effective Reaction Probabilities.

When fluctuations are so rapid that the number of signal molecules changes significantly during an individual response reaction, Eq. 2 must be replaced by a more complicated integral formulation that depends on the exact reaction dynamics. For the branching reaction in scheme 3, 〈q〉 can be calculated from the probability ϕ_j(t) of still being in state I at time t, given that state I is reached at time t = 0 and that there were j signal molecules at that time, governed by:

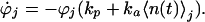A5

〈n(t)〉_j is the signal average at time t, given that there were j molecules at t = 0. This gives:

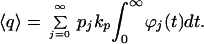A6

When the inhibitor fluctuates exceptionally rapidly, so that k_d ≫ k_p and 〈n〉_j = 〈n〉, Eq. A6 simplifies to 〈q〉 = q(〈n〉).

Switching Delays.

Assume that the signal synthesis rate declines exponentially in normalized time:

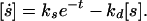A7

The general solution follows from direct integration. If k_d is high so that [s] rapidly equilibrates to the current steady state, then [s] ≈ [s]₀ e^−t where [s]₀ is the initial steady state.

The switch intensity is kq(t) where k is the uninhibited transcription intensity. The probability density for the switching delay is thus f(t) = kq(t)T₀(t) where T₀(t) is the probability of no transcriptions up to time t, governed by the master equation Ṫ₀ = −kq(t)T₀. With q from Eq. 1 and [s] = [s]₀ e^−t, the general f(t) is easily calculated analytically. The lowest dispersion possible corresponds to the limit when both k and [s]₀/K tend to infinity, so that hyperbolic inhibition works with maximal sensitivity, and corresponds to:

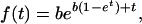A8

where b = kK/[s]₀ is the initial intensity.

When signal fluctuations are significant, the intensity kq(t) fluctuates randomly. f(t) then can be found by sampling the switch time by using Monte Carlo simulations (20). The data in Fig. 4 Lower represent fluctuations so rapid that outcomes of subsequent transcription attempts can be approximated as independent. A more precise f(t) then is found by numerically integrating Ṫ₀ = −kq(t)T₀ with q(t) = 〈q(t)〉 where p_n in Eq. 2 change with time. In Fig. 4 we used the NB distribution (Eq. A3) with λ(t) = λ₀e^−t. All choices of underlying random process that give rise to a stationary NB (Table 1) give identical results.