Resolving intermediates in biological proton-coupled electron transfer: A tyrosyl radical prior to proton movement

Abstract

The coupling of proton chemistry with redox reactions is important in many enzymes and is central to energy transduction in biology. However, the mechanistic details are poorly understood. Here, we have studied tyrosine oxidation, a reaction in which the removal of one electron from the amino acid is linked to the release of its phenolic proton. Using the unique photochemical properties of photosystem II, it was possible to oxidize the tyrosine at 1.8 K, a temperature at which proton and protein motions are limited. The state formed was detected by high magnetic field EPR as a high-energy radical intermediate trapped in an unprecedentedly electropositive environment. Warming of the protein allows this state to convert to a relaxed, stable form of the radical. The relaxation event occurs at 77 K and seems to involve proton migration and only a very limited movement of the protein. These reactions represent a stabilization process that prevents the back-reaction and determines the reactivity of the radical.

Redox active tyrosines in enzymes exhibit a diverse range of chemical properties, with radical lifetimes ranging from microseconds to days (1). Tyrosine oxidation results in a pK_a shift of >12 units so it is expected that the loss of the electron is accompanied by deprotonation (1). The protein controls the reactivity of the tyrosine and its radical through modulation of the proton transfer reactions that are coupled with electron transfer (1-3).

One of the most intriguing examples of the influence of the protein on the properties of tyrosyl radicals is found in the water-oxidizing enzyme of photosynthesis, photosystem II (PSII; refs. 2 and 3). This enzyme contains two symmetrically positioned redox active tyrosyl residues, Tyr_D and Tyr_Z, one on each subunit of the heterodimeric core of the photosynthetic reaction center (2-6), a system that seems to have evolved from a homodimeric protein ancestor in which both redox active tyrosines had identical properties (7).

The function and chemical properties of the two tyrosyl radicals are quite distinct. 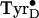exhibits high stability (days in the intact enzyme) and has a relatively low redox potential (2, 3). Although Tyr_D is not essential for enzyme activity (5, 6), its redox poises the Mn cluster (8) and may electrostatically tune the adjacent chlorophyll cation radical (9). The other PSII tyrosyl radical, 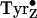, is short-lived (tens of microseconds to a few milliseconds) in the functional enzyme, is kinetically competent in water oxidation, and has a redox potential estimated to be from 0.95 to 1.1 V (2, 3). In addition, 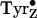is close to the Mn cluster, and in some models 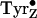chemistry is seen as being directly involved in water oxidation (10).

The tyrosyl radicals of PSII are especially attractive as an experimental system, not only because of the interest in comparing 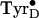and 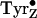, but also (because of the unique properties of the photochemical reaction center) because it is possible to study radical formation with rapid kinetics (2, 3, 11) and, for Tyr_D at least, at cryogenic temperatures (12). Thus, 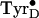formation is potentially a rare, possibly unique, case in which proton-coupled electron transfer can be studied at cryogenic temperatures, conditions under which protein and proton motions are greatly restricted, thus allowing the trapping of unstable intermediate radical states before the occurrence of temperature-dependent relaxation processes.

Here, we have looked for such intermediate states by using the highest resolution possible with high-frequency high magnetic-field EPR (HFEPR). EPR spectra of tyrosyl radicals obtained with 9-GHz microwaves are dominated by proton hyperfine couplings that are determined by the magnetic interaction between the unpaired electron spin and nearby proton nuclei. By contrast, when 285-GHz microwaves are used, the EPR spectra of tyrosyl radicals are dominated by the resolved anisotropy in the g-tensor (13–15). The three components of the g-tensor define the interaction energy of the unpaired electron spin of the radical with the applied magnetic field and is very similar to the chemical shift in NMR (Fig. 1). We have previously demonstrated that the g-tensor component along the phenolic bond, g_x, of tyrosyl radicals (16) is a particularly effective measure of their electrostatic environment (13, 14).

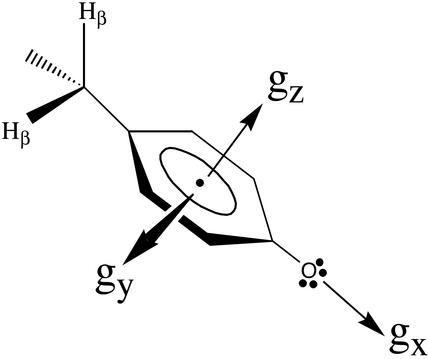
Fig. 1.

The orientation of g-tensor with respect to the molecular frame of a tyrosyl radical: the g_x is directed along phenolic bond, g_z perpendicular to the phenyl ring plane, and g_y mutually perpendicular to the other two components. When the magnetic field is applied along the bond (g_x) direction, a peak at the magnetic field corresponding to the g_x value is observed in the high-field EPR spectrum and likewise for g_y and g_z.

Materials and Methods

The PSII-enriched membranes from spinach were prepared essentially by the method of Berthold, Babcock, and Yocum (17). Mn was depleted from PSII by treating with NH₂OH as reported (11) but maintained in darkness. Darkness was maintained for all subsequent sample manipulations. Before use, the pH of the PSII samples was adjusted by resuspension of the sample in Tricine/NaOH (pH 8.7) buffer (40 mM). The final Chl concentration for EPR measurements was 4 mg of Chl per ml.

Tyr_D is known to be hydrogen-bonded to a nearby histidine (His-189 of the D2 subunit in Synechocystis 6803). The structures and energies of such a tyrosine-histidine hydrogen-bonded pair were determined from geometry optimization of a p-cresol-imidazole supramolecular complex by using the program gaussian-94 (18) using the BLY3P (19-21) method and 6+31(d,p) and 6+311(2d,p) basis sets. Similar calculations have been reported on the phenol-imidazole complex (22). The structures and hydrogen-bonding energies of the initial and final states were from global optimizations. For the intermediate states formed immediately after electron transfer but before relaxation, the structure and hydrogen-bonding energies were calculated by restricting the position of the pair to the geometry before tyrosine oxidation. In all cases, the calculation showed that the ring planes remained coplanar.

The 9-GHz EPR spectra were recorded with a Bruker (Rheinstetten, Germany) ESP 300 spectrometer equipped with an Oxford Instruments (Oxon, U.K.) cryostat cooled with liquid helium. Illumination at 5–15 K was carried out in the EPR cavity by using an 800-W tungsten lamp filtered through 5 cm water and three infrared cut-off filters. The high-field EPR spectrometer has been described (23). Illumination at 1.8–15 K was done by using a 20-W quartz halogen lamp directed at the microwave output waveguide window. The light was carried via the microwave waveguide to the sample in the cryostat.

Results

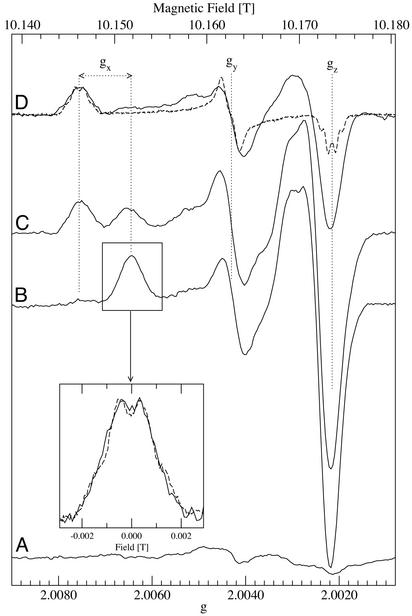
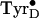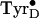Fig. 2 B–D shows that the HFEPR spectra of the radical photo-generated at liquid helium and physiological temperatures are strikingly different from each other, even though the conventional 9-GHz EPR spectra are indistinguishable (Fig. 3; ref. 12). The most obvious difference in the high-field spectra is that the g_x feature in the low-temperature spectrum is at a higher field position (Fig. 2B) compared with that of the 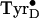generated at physiological temperature (Fig. 2D).

Fig. 2.

High-field 285-GHz EPR spectra of the 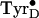generated in Mn-depleted PSII at low temperatures. (A) Baseline spectrum before illumination. (B) After illumination at 1.8 K. (C) Same sample warmed to 77 K for 10 min. (D) Solid line, same sample warmed to 200 K for 1 min; dashed line, similar sample (24) with the radical obtained at physiological temperatures. Spectra were obtained at 285 GHz at 4.2 K and were normalized averages of 8–16 scans obtained with a field modulation of 20 G. The dotted black lines from right to left are positioned at g-values of 2.00215, 2.00430, 2.00645, and 2.00756. (Inset) Comparison of the g_x region of radical obtained after 1.8-K illumination (10 G modulation, solid-line) and radical obtained at physiological temperatures (3 G modulation, dashed line, also shown in its entirety in D).

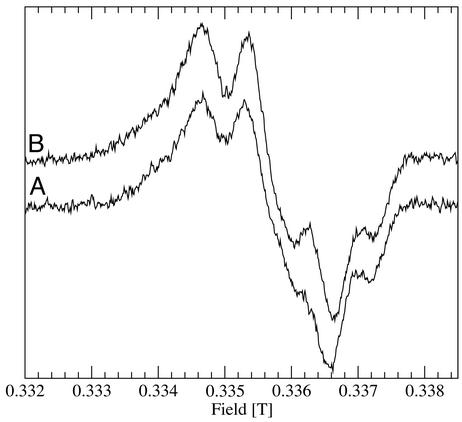
Fig. 3.

Nine-gigahertz EPR spectra of 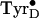photo-generated in Mn-depleted PSII at 4 K (A) and after warming to 200 K (B). Both spectra were obtained at 4 K.

When the liquid helium temperature-illuminated sample was incubated for 10 min at 77 K in darkness, the g_x feature in the high-field EPR spectrum decreased in amplitude, the g_y (and less clearly the g_z) feature did not change amplitude, and an additional signal appeared with the g-values corresponding to that of the normal 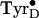as generated at physiological temperatures (Fig. 2C). Clearly a partial conversion from the low-temperature spectrum to the physiological temperature spectrum occurred. Further incubation in darkness at 200 K for 1 min resulted in the disappearance of the low-temperature 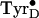signal, with the ambient temperature-type spectrum left in its place (Fig. 2D).

By varying the 77-K incubation time, it was possible to trap different proportions of the low temperature and physiological-type 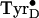signals. The half-conversion time was estimated to be ≈7 min at 77 K. No broadening occurred in any of the spectral features of the two forms of the signals nor were signals observed with intermediate g-values. These observations indicate that warming results in the conversion of one well-defined tyrosyl radical species into another.

The partially resolved fine-structure seen in both the 9-GHz spectra (Fig. 3) and the high-field spectra of the g_x region recorded under high-resolution conditions (Fig. 2 Inset) arises from magnetic interactions between nearby protons and the unpaired electron. The largest of these hyperfine couplings is due to a β-methylene proton (Fig. 1) and is determined by the relative orientation of this proton with respect to the tyrosyl ring (≈48°; ref. 24). The fact that the hyperfine structure is identical whether the radical was generated at 1.8 K or at physiological temperatures indicates that the angular orientation of the tyrosyl ring relative to the methylene protons is the same in both cases. Again, the data indicate two well-defined states and a step-wise change from one to the other.

The g-values of the tyrosyl radicals were determined by computer simulation. The g_x-value for the cryogenically generated radical was 2.00643 compared with 2.00756 for tyrosyl radical generated at physiological temperatures (25). The difference in g_x values reflects differences in the electrostatic environment of the two radicals. In the literature, the g_x-values for tyrosyl radicals range from 2.0065, due a strong hydrogen-bond (16), to 2.0094, in a nonpolar environment (15). Thus, the g_x-value of the low-temperature 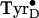reported here is the lowest reported for a tyrosyl radical, indicating the most electropositive environment yet encountered (13–15, 23)

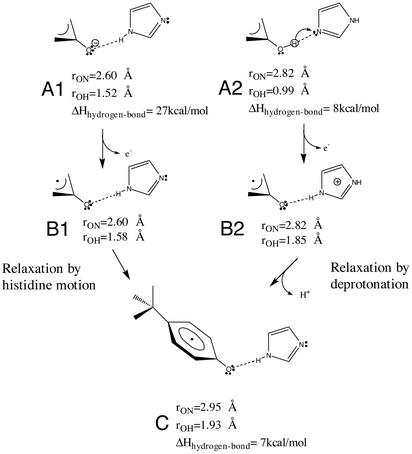
We carried out hybrid density-functional Hartree–Fock calculations on the p-cresol-imidazole molecular complex to obtain insights into the structure of the intermediate states and the relaxation events associated with two different models for the reactions detected here. The models and the results are illustrated in Fig. 4, and they are described in detail in Discussion.

Fig. 4.

Structural model for the stable tyrosyl radical in PSII and two possible reaction pathways for its formation via strained intermediate states. The scheme shows structures for the reduced state (structures A1 and A2), the intermediate state (B1 and B2), and the final relaxed state (C). The pathway on the right is the proton-coupled electron transfer model, and it starts and ends with a neutral pair: Tyr_D-His (A2) and 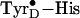(C), respectively, with the latter having lost both an electron and a proton. The high-energy intermediate state (B2) results from the close proximity of the cationic histidine residue to the neutral radical. Relaxation of this state (B2) is dominated by the deprotonation of the imidazole ring, leading to a neutral state with hydrogen-bonding that is energetically favorable (C). The pure electron transfer is shown on the left; the starting point is the Tyr_D-His pair, which has a very short 1.52-Å hydrogen-bonding distance due to negative charge on the tyrosine residue (A1). Oxidation at liquid helium temperature results in a neutral tyrosyl radical with a very short hydrogen bond (1.58 Å), resulting in an energetically highly strained state (B1). The relaxation in this case is attributed to a separation of the neutral 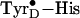pair (O to N distance changing from 2.60 to 2.95 Å), allowing for the lengthening of the compressed hydrogen bond to form the final stable state (C).

It should be noted that the HFEPR spectra also contained contributions from a narrow radical centered just above the free electron g-value (g_e = 2.00232). This radical arose from a fraction of centers in which β-carotene is oxidized instead of Tyr_D (12, 26, 27). When the sample temperature was raised, a chlorophyll cation radical replaced the β-carotene due to a temperature-dependent electron transfer reaction (26) and was responsible for small changes around the free electron region (27). We have shown earlier that a brief intense illumination results in a high yield of 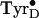whereas longer illumination results in carotene radical formation (12). The 9-GHz spectra were obtained by using illumination conditions to avoid β-carotene radical formation. Because of geometric limitations, formation of carotene radical in a fraction of the centers could not be avoided in the HFEPR experiment.

Discussion

An intermediate state in 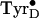oxidation has been trapped by generating the radical at liquid helium temperatures by using the unique photochemical properties of the PSII reaction center. This state is characterized by a very electropositive environment and can be considered as a high-energy transition state. On warming to 77 K, this electropositive environment changes and becomes indistinguishable from that seen when 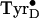is formed at physiological temperatures. The relaxation process seems to involve a single-step phenomenon between two discrete states. In what follows, we discuss the nature of the relaxation event, taking into account insights gained from molecular orbital calculations.

From considerations of (i) the amino acid sequence and the protein folding model based on the structure of the purple bacterial reaction center, (ii) site-directed mutagenesis, and (iii) spectroscopic studies, it seems very likely that 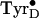is hydrogen-bonded by His-189 of the same protein subunit (D2; refs. 2 and 3). Thus, discussion of electron transfer and the associated protonation changes in this system minimally involves both the Tyr_D itself and His-189, its hydrogen-bonding partner.

In previous work, we have invoked two specific models to describe the unexpected submicrosecond kinetics and low-temperature chemistry of Tyr_D (11, 12): (i) proton-coupled electron transfer (Fig. 4, right branch) and (ii) pure electron transfer (Fig. 4, left branch). The evidence described here for a discrete intermediate state formed immediately after electron transfer can be incorporated into these models.

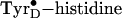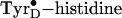The hybrid density-functional Hartree–Fock calculations on the p-cresol-imidazole molecular complex showed that, for the pure electron transfer model, the neutral intermediate has an extremely short hydrogen-bonding distance (Fig. 4B1), arising from a very strong hydrogen-bond interaction between the anionic tyrosine and neutral histidine (Fig. 4A1). The relaxation of the strained neutral intermediate requires an increase in distance of 0.35 Å and a rotation of 5° in the hydrogen-bonding geometry.

In contrast, the proton-coupled electron transfer pathway starting from the reduced neutral state (Fig. 4A2) involves a small proton motion (0.9 Å) from the tyrosine to the histidine resulting in an intermediate that consists of the 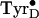that is hydrogen-bonded by a histidinyl cation (Fig. 4B2). The relaxation of this state requires deprotonation of the histidinyl cation and only a small 0.13-Å separation and a 16° rotation of the Tyr-His pair. The bulk of the stabilization comes from the loss of the positive charge on the histidine residue. The small shift and modest rotation in hydrogen-bonding geometry represents only a small (1 kcal/mol) gain in stabilization relative to hydrogen-bonding geometry of the strained oxidized state. Hence, the hydrogen-bonding energies and geometries of the initial (reduced, Fig. 4A2) and final (oxidized, Fig. 4C) states are more closely matched than in the pure electron transfer case. This finding indicates that, in the proton-coupled electron transfer oxidation pathway, only proton motion is likely to be necessary.

The proton-coupled electron transfer model presupposes that the deprotonation of the histidinyl cation is blocked at liquid helium temperature but can occur at 77 K. Presumably, this deprotonation would occur by proton transfer to another proton acceptor. The identity of this species is unknown. Clearly, the temperature dependence of this proton transfer event reflects a thermally activated process that could in itself involve protein motion. Given the lack of information on this secondary aspect of this model, more detailed discussion of this process seems premature.

The g_x-value of the low-temperature-generated 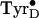intermediate did not allow us to distinguish between the two models because the electrostatic influence of a strong hydrogen bond from a neutral donor was estimated to be equivalent to that of a modest hydrogen bond from a cationic donor. However, we tend to favor the proton-coupled electron transfer model for the following reasons: (i) the deprotonation of the reduced tyrosine requires quite a large pK_a shift from the expected pH 10 to the measured pH 7.7; (ii) the relaxation step in the proton-coupled electron transfer model involves mainly proton transfer (at least at the level of the Tyr-His pair), whereas the relaxation step in the pure electron transfer model requires more significant protein motion; and (iii) the step-wise nature of the relaxation, involving no motion of the tyrosyl ring, argues for a process dominated by proton movement rather than protein movement. Because none of these arguments is particularly strong, we still entertain the pure electron transfer model as a serious option.

The strained low-temperature state represents an unexpected intermediate that is likely to be transiently formed at physiological temperature. Because the intermediate is in an unusually electropositive environment, it is predicted to be a highly oxidizing species. We have observed (unpublished results) that this intermediate state is unstable at low temperature, undergoing a charge recombination reaction at 40 K with the electron from the semiquinone 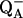(the reduced electron acceptor) presumably via the chlorophyll cation P⁺ (the oxidant of Tyr_D). At physiological temperature, there may be a competition between this back reaction from the unstable intermediate and the relaxation reaction. The previously unexplained observation that a fraction of flash-induced 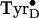decays on the first few flashes (figure 1C in ref. 11) may represent this competition reaction. The relaxation process represents a local stabilization step that prevents this wasteful back reaction. Such local stabilization reactions could play crucial roles elsewhere in biology, not only in tyrosine redox chemistry, with the most obviously relevant case being Tyr_Z, the sister tyrosine on the other half of the reaction center, but also in other major processes in bioenergetics, particularly where related quinone chemistry is also linked to proton movements (28, 29).