Abstract
The electron density and electrostatic potential in an aldose reductase holoenzyme complex have been studied by density functional theory (DFT) and diffraction methods. Aldose reductase is involved in the reduction of glucose in the polyol pathway by using NADPH as a cofactor. The ultra-high resolution of the diffraction data and the low thermal-displacement parameters of the structure allow accurate atomic positions and an experimental charge density analysis. Based on the x-ray structural data, order-N DFT calculations have been performed on subsets of up to 711 atoms in the active site of the molecule. The charge density refinement of the protein was performed with the program mopro by using the transferability principle and our database of charge density parameters built from crystallographic analyses of peptides and amino acids. Electrostatic potentials calculated from the charge density database, the preliminary experimental electron density analysis, DFT computations, and atomic charges taken from the amber software dictionary are compared. The electrostatic complementarity between the cofactor NADP+ and the active site shows up clearly. The anchoring of the inhibitor is due mainly to hydrophobic forces and to only two polar interaction sites within the enzyme cavity. The potentials calculated by x-ray and DFT techniques agree reasonably well. At the present stage of the refinement, the potentials obtained directly from the database are in excellent agreement with the experimental ones. In addition, these results demonstrate the significant contribution of electron lone pairs and of atomic polarization effects to the host and guest mechanism.
We recently showed that accurate electron density analyses may be carried out on proteins if ultra-high-resolution data are available (1). Experimental charge density methods (2–4) give an analytical representation of the valence electron density (5) from the refinement of nonspherical atomic scattering factors (program mopro, which was developed by us for this work and is available from C.J., B.G., or C.L.) (6). Electron density multipoles taken from our oligopeptide charge density database (7) are the necessary starting parameters to perform a protein charge density analysis. Therefore, any property depending on the static charge density may be computed (8): one of the properties of greatest importance for drug design and biochemistry in general is the electrostatic potential, which provides information about reactivity (9). Correspondingly, order-N density functional theory (DFT) methods may be used for estimating precisely the valence charge density and the related properties of proteins and large molecules (10, 11).
Podjarny and collaborators (12, 13) have recently collected accurate diffraction intensities to ultra-high resolution (0.66 Å) on an enzymatic complex: aldose reductase (AR) plus NADP+ plus inhibitor IDD594 (Fig. 1). This system gives a unique opportunity to test the accuracy of theoretical methods for calculating the electrostatic potential in protein complexes compared with experiment and vice versa. Therefore, we report on the crystallographic and DFT electrostatic properties of the AR complex, a 315-aa protein involved in diabetic complications, studied largely for the purpose of inhibitor development.
Fig. 1.
Ribbon view of the AR-NADP+ inhibitor complex (Left) and chemical formula of the inhibitor IDD594 (Right).
AR is involved in the reduction of glucose to sorbitol using NADPH as a cofactor. When there is an abnormal glucose excess in tissues, the accumulation of sorbitol leads to biochemical alterations that can result in lesions (14). This study contributes to the search for inhibitors for the pharmacotherapy of diabetic complications through the analysis of electrostatic forces in the cofactor and inhibitor binding. For the first time, the host–guest mechanism is analyzed at a detailed level that goes beyond usual structural and steric features. The contribution of atomic polarization effects on the electrostatic complementarity of the protein active site with its ligands will be demonstrated by ultra-high-resolution crystallography and order-N DFT methods.
Materials and Methods
The crystallization of human AR was described by Podjarny and colleagues (12). The crystals are monoclinic, space group P21 (a = 49.43, b = 66.79, c = 47.40 Å, β = 92.40°, one molecule per asymmetric unit). The 0.66-Å resolution diffraction data of the AR–NADP+–IDD594 complex (Fig. 1) were collected at 100 K on the ID19 beamline at the Advanced Photon Source (Argonne, IL) (13). A total of 2,262,072 reflections have been measured from two crystals and were merged with program scalepack (15) to 511,265 unique reflections [Rint(I) = 2.9% and 2.7% for crystals 1 and 2]. Eighty percent of the merged reflections have their intensities >3σ. The completeness of the data is 89% (0.66 < d < 20 Å). The structure was first determined by Cachau et al. (13) using the shelxl-97 program (16). The hydrogen atoms in the active site area were all visible in the electron density maps. The refined protein structure model includes all of the protein-ligand hydrogen atoms and 629 water molecules.
The charge density refinement strategy with mopro (6) was as follows. The starting position and thermal parameters were those of Cachau et al. (13), and the initial charge density parameters were those of neutral spherical atoms. Because the thermal motion in some parts of the protein (especially in the N- and C-terminal parts) does not allow a charge density analysis, a subset of the structure was selected, based on atomic equivalent thermal B factors <8 Å2 (see Fig. 2). This charge-density-refinement substructure included all main-chain atoms, except the three N-terminal and three C-terminal amino acids and the Trp-219–Ser-226, Glu-229–Asp-230, and Phe-276–Val-297 residue ranges.
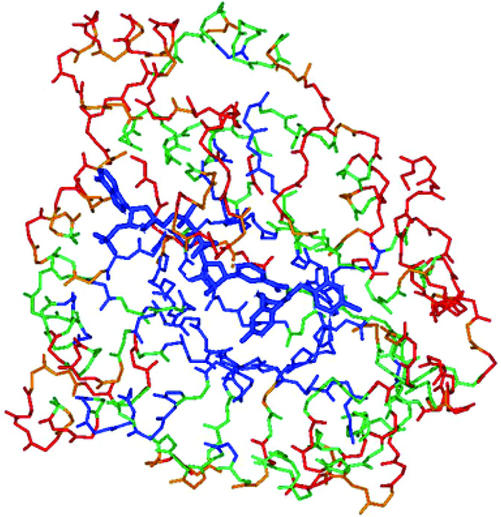
Fig. 2.
View of AR backbone structure with NADP+ and inhibitor represented in the same orientation as Fig. 1. Amino acids are colored according to their average equivalent temperature factor. Blue, Beq < 4Å2; green, 4 < Beq < 6 Å2; orange, 6 < Beq < 8 Å2; red, Beq > 8 Å2.
At first, a high-order spherical atom refinement was performed with mopro (6) on the nonhydrogen atoms of the substructure, to start the electron density refinement with the least biased positional and thermal parameters. This refinement was performed against high-resolution shells of decreasing size. The three successive resolution ranges used were 0.5–0.76 Å–1 (327,546 reflections), 0.6–0.76 Å–1 (216,984), and 0.65–0.76 Å–1 (152,454). A zero intensity over sigma cutoff, which corresponds to a completeness of 68% for the highest resolution shell (0.7–0.76 Å–1), was applied. The high-order refinement strategy consisted of alternate refinement of positional and anisotropic thermal motion parameters, without any stereo-chemical or dynamical restraints, until total convergence, for each of the three resolution ranges. In each case, significant improvements in the agreement factors R(F) and Rfree(F) were observed. For example, in the 0.6–0.76 Å–1 range, the R(F) [Rfree(F)] factor dropped from 12.68% (13.42%) to 12.23% (13.31%).
In the second stage of refinement, the starting electron density parameters were transferred from our nonspherical atoms multipole database (7) describing all of the chemical groups present in proteins. All atoms of the protein were assigned nonspherical scattering factors; water molecules were modeled as free oxygen atoms. The starting parameters for NADP+ were from the charge density analysis of NAD+ (11), and spherical atom scattering factors were used for the IDD594 inhibitor compound. All hydrogen atoms were displaced along the X—H bonds to standard bond distances obtained by neutron diffraction studies (17) and were subsequently kept fixed.
The transfer procedure led to an immediate improvement of statistical agreement indices, with the R(F) factor dropping from 11.45% to 11.05% and Rfree(F) from 12.07% to 11.77% for 467,214 reflections with I/σI > 0 and 0 < s < 0.76 Å–1. This decrease of the crystallographic R-factors, and the improvement of the resulting residual density, fully justify the multipolar parameters transfer procedure.
The electron density refinement was performed with mopro for the main-chain atoms (including hydrogen atoms) of the substructure described above, against the 456,477 reflections in the 0.15- to 0.76-Å–1 resolution range. For the atoms of the protein side chains, of the ligands and of the water molecules, only positions and thermal parameters were refined. This charge density analysis included the refinement of the multipolar parameters and the valence populations. Electron density constraints were applied, taking advantage of the chemical equivalence of the peptide units. Local symmetry constraints were also applied, because only the nonzero multipole parameters of the databank were allowed to vary.
The low-resolution truncation makes some allowance for the problem of the disordered solvent, because an exponential scaling model turned out not to be helpful at this stage of our study. One of the next improvements of the procedure will be to perform the bulk solvent correction using the flat solvent model (18).
This preliminary charge density refinement led to a description of the average electron density and atomic charges along the main chain, which was subsequently used for a computation of the electrostatic potential obtained from multipolar refinement (MUL) (6). The resulting set of valence population parameters (Pv) for the protein main-chain atoms are as follows: Cα, 4.04 (7); O, 6.32 (8); N, 5.12 (7); C, 4.09 (7); Hα, 0.86 (9); HN, 0.81 (8) [R(F) factor drops from 10.21% to 10.10% and Rfree(F) from 11.04% to 10.68% in the 0.15- to 0.76-Å–1 resolution range]. The experimental charge density refinement of the AR complex is still being completed and will be reported in detail in a forthcoming paper.
DFT Calculations. All calculations were performed at the experimental geometry with the DFT program siesta (19, 20). This software allows calculations that scale linearly with, rather than with the cube of, the number of atoms in the system. This allowed the study of large parts of the AR complex. Some of the approximations made are described in this article, and a detailed description can be found in refs. 19–21.
Exchange and correlation of the Kohn–Sham theory (22) are treated with the generalized gradient approximation functional proposed by Perdew et al. (23). Core electrons were replaced by scalar-relativistic norm-conserving pseudopotentials generated using the Troullier–Martins scheme (24) in their fully nonlocal formulation (25). A uniform mesh with a plane-wave cutoff of 75 Ry was used to represent the Hartree and exchange-correlation potentials and the local part of the pseudopotential.
Valence electrons were described using a basis set of finite-range numerical atomic orbitals. Radial parts of these orbitals are based on the scheme of pseudoatomic orbitals of Sankey and Niklewski (26), who proposed a scheme to build single-ζ bases. In siesta, the bases are generalized to arbitrarily complete bases up to double-ζ with polarization orbitals (21). The orbital confinement energies used were defined in an earlier report (10), in which the final set of cutoff values was selected so the electronic density would be comparable to the experimental density in the database. Use of these finite-range orbitals, which give rise to sparse overlap and Hamiltonian matrices, and of pseudo potentials in the Kleinman–Bylander factorized form, allows the Kohn–Sham Hamiltonian to be built with order-N operations. More details on these techniques are given in refs. 19–21.
The DFT quantum chemical modeling included (i) a substructure consisting of 64 amino acid residues that surround the active site: 18–22, 42–49, 76–81, 109–116, 121–123, 129–131, 158–161, 182–184, 208–215, 297–312, and HOH464 (603 atoms); (ii) a substructure consisting of the 64 active-site residues plus the NADP+ cofactor (676 atoms); and (iii) a substructure including the same residues, plus the NADP+ cofactor and the IDD594 inhibitor (711 atoms).
For these calculations, the atomic positions were held fixed at the crystallographic geometry. The 64 aa in the DFT-calculation substructure completely surround the cofactor NADP+ nicotinamide moiety and the inhibitor.
Electrostatic Potential. The experimental electrostatic potentials were computed from the electron density at the refined geometry with electros (27) in two ways: first [electrostatic potential obtained directly from multipolar data base (TRF) (7)], using directly the charge density parameters transferred from the multipolar atoms database (7, 28); and, second (MUL), using the parameters obtained from the preliminary multipole refinement of the protein main-chain atoms. The experimental potential of NADP+ was derived from the NAD+ charge density analysis reported previously (11).
The theoretical DFT potential was obtained from the siesta calculations. For the analysis of the binding interactions, the electrostatic potential of the cofactor NADP+, of the inhibitor, and of the enzyme active site were computed separately in vacuo without any interaction and compared with the electrostatic potential generated by the complex.
For the sake of comparison, the electrostatic potential obtained from the amber dictionary (AMB) generated by the protein without the cofactor was computed by using the point charges force field of the amber dictionary (29).
The electrostatic potential generated by the protein was computed in all cases using the 64-aa substructure surrounding the active site (603 atoms).
Results
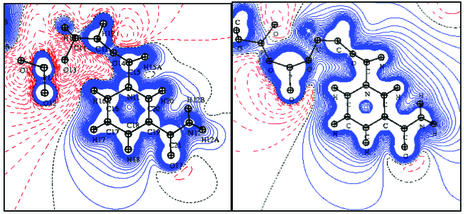
Quality of the TRF. The electrostatic potential generated by the NADP+ cofactor is shown in Fig. 3. The DFT and TRF compare well around the nicotinamide moiety, whereas the negative potential around the pyrophosphate group of NADP+ appears significantly stronger in the TRF map than in the theoretical one.
Fig. 3.
Electrostatic potential generated by the NADP+ cofactor in the plane of the nicotinamide ring. (Left) Experimental. (Right) Theoretical. Contour levels are ±0.05 e/Å. Blue, positive; red, negative; black dotted line, zero level.
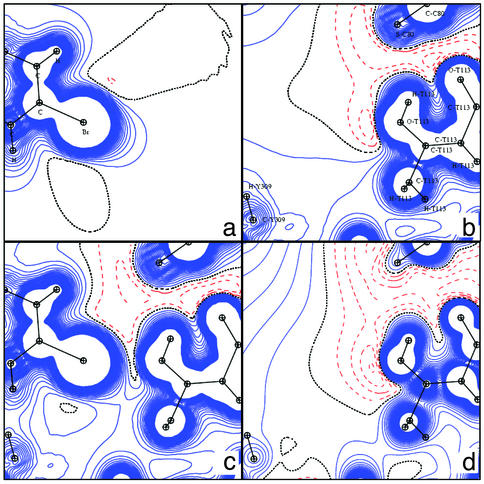
The potential in the protein active site obtained by DFT is compared with the transferred experimental TRF obtained directly from the charge density database in Figs. 4 a and b, 5 b and c, and 6 b and d. The agreement between the DFT and TRF maps is generally good: the positive and negative potential regions are similar, but the TRF negative potential wells are generally deeper.
Fig. 4.
Electrostatic potential generated by the apoenzyme in the active site. The projection plane is the same as in Fig. 3. (a) DFT. (b) TRF. (c) MUL. (d) Point charges (amber).
Fig. 5.
Electrostatic potentials in the C6H4Br plane. (a) DFT (inhibitor alone). (b) DFT (apoenzyme). (c) TRF (apoenzyme). (d) MUL (apoenzyme).
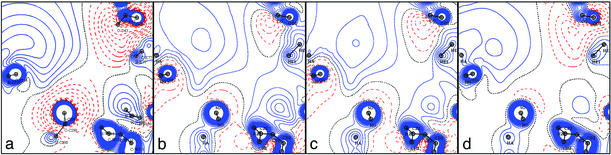
Fig. 6.
Electrostatic potentials in the Br... OG1-HG1 region. All projection planes contain the Br and OG1-HG1 atoms. (a) DFT (inhibitor alone). (b) DFT (apoenzyme). (c) DFT (AR complex). (d) TRF (apoenzyme).
This good agreement demonstrates that a TRF calculated (at small computing cost) using the database of charge and multipole parameters (7) and high-resolution (d < 1.5 Å) crystallographic atomic positions (including hydrogen atoms) is very reliable, and can be obtained routinely as soon as a high-resolution structure with hydrogen atoms is available.
Electrostatic Complementarity of Ligand–Protein Interactions. NADP+ is naturally bound by AR to enable sugar hydroxyl reduction. Although, in the crystal studied, the ligand is not a sugar but an inhibitor, it is likely that NADP+ interacts in a very similar way with the protein. The cofactor is made of five functional groups, namely, nicotinamide, ribose, pyrophosphate, ribose, and adenine. In the studied complex, the first three groups are buried within the active site, whereas the last two are partly outside of the protein, solvated by water molecules.
The NADP+ cofactor alone displays a large negative potential around the pyrophosphate group (DFT, –0.28 e/Å; TRF, –0.40 e/Å) near the pyrophosphate oxygen atoms, and a positive potential around the nicotinamide ring due to the global positive charge of the protonated base (Fig. 3). The oxygen of the NADP+ amide group generates a small negative potential (DFT, –0.04 e/Å; TRF, –0.04 e/Å3). The zero-level contour is very similar for the two methods. Fig. 4 shows the electrostatic potential in the nicotinamide ring plane generated by the apoenzyme alone calculated by the DFT, TRF, and MUL methods and from the amber point charges (AMB). As discussed previously, MUL and TRF are in excellent agreement.
In comparison with Fig. 3, DFT, MUL, and TRF apoenzyme electrostatic potentials clearly display genuine complementarity with the NADP+ potential. To each negative potential region around the cofactor (pyrophosphate group and amide oxygen atom) corresponds a positive potential region in the active site: the enzyme positive regions are located near Pro-211 and Ser-210 (Fig. 4) (DFT, +0.34; TRF, +0.18; MUL, +0.14; AMB, +0.14 e/Å) and near Asn-160-NH2 and His-110 Nε2–Hε2 (DFT, +0.20; TRF, +0.26; MUL, +0.12; AMB, +0.06 e/Å).
Fig. 4 also reveals two negative potential wells: one close to Cys-298 Sγ (DFT, –0.18 e/Å; TRF, –0.06 e/Å; MUL, –0.08 e/Å; AMB, –0.04 e/Å) and the second one near Asp-43-Oδ1 (DFT, –0.28 e/Å; TRF, –0.14 e/Å; MUL, –0.14 e/Å; AMB, –0.18 e/Å). In the enzyme–cofactor interaction, these two negative potential regions complement the strong positive potential of NADP+. The second of the two negative potential wells is created by a special configuration of at least 10 protein atoms: one sulfur atom (Cys-298 Sγ) and nine oxygen atoms (Cys-298 O, Tyr-209 OH, Gln-183 Oε1 and O, Asp-43 Oδ1, Oδ2 and O, and Thr-19 O and Oγ1), of which all are nearly located in a plane almost perpendicular to the nicotinamide ring. An important point is that most of these atoms do not interact directly with NADP+. Only three of them form hydrogen bonds with NADP+: Cys-298 Sγ, Asp-43 Oδ1, and Gln-183 O (Fig. 2 and Table 1). It is clear that all other atoms contribute through long-range electrostatic attraction to the binding of the cofactor. These results demonstrate that considering only the short-range H bonds involved in the ligand binding clearly underestimates the interaction strength.
Table 1. Distances and angles of the hydrogen bonds involving NADP+ or the inhibitor.
| Acc... Donor | AD, Å | DHA, o |
|---|---|---|
| IDD594-IDD594 | ||
| O34... N17 | 2.984 (9) | 174 |
| IDD594-protein | ||
| O33... OH_Y48 | 2.731 (6) | 174 |
| O33... Nδ2_H110 | 2.667 (6) | 159 |
| O34... Nε1_W111 | 3.068 (8) | 154 |
| NADP+-protein | ||
| O15... N_T19 | 3.248 (6) | 152 |
| All others | ||
| O16... N_W20 | 2.906 (6) | 137 |
| O11... Nζ_K21 | 2.827 (7) | 150 |
| O17... Nδ2_N160 | 2.887 (7) | 165 |
| O12... Oγ_S210 | 2.803 (7) | 167 |
| O29... Oγ_S263 | 2.669 (9) | 159 |
| O27... Nζ_K262 | 2.751 (9) | 171 |
| O22... N_K262 | 2.861 (7) | 173 |
| O29... NH1_R268 | 3.028 (9) | 162 |
| N25... Nδ2_N272 | 3.030 (11) | 173 |
| O_W584... O25 | 2.680 (12) | 165 |
| Oδ2_D43... O15 | 2.682 (6) | 147 |
| Oγ_S159... N12 | 2.847 (7) | 140 |
| Oε1_Q183... N12 | 2.904 (5) | 165 |
| Oε1_Q183... C20 | 3.038 (7) | 136 |
| Oε2_E271... N24 | 2.940 (15) | 156 |
| Oδ1_N272... N24 | 2.860 (14) | 148 |
The standard deviation between non-H atoms is given in parentheses.
Although there is a qualitative agreement among the four techniques of potential computation, some differences remain. A significant one is that the amber charges yield a weaker negative potential near Cys-298 Sγ. Also, all of the positive AMB potentials seem to be lower than the DFT, TRF, and MUL values. The similarity of DFT, TRF, and MUL indicates that they are more precise than point-charge point potentials, apparently because they take into account a certain degree of atomic polarization. Further crystallographic refinement of the side chains, including Cys-298 Sγ, will further clarify this point.
Inhibitor–Active Site Interactions. The chemical structure of the IDD594 inhibitor (Fig. 1) differs significantly from that of glucose, but the inhibitor carboxylate group should bind in a similar region of the enzyme active site as the reacting hydroxyl group of glucose (13, 14). Because no high-resolution data exist for the glucose complex, the discussion will focus on inhibitor interactions. The charge density refinement of the inhibitor was done ab initio, because of the lack of multipole values in the database for the specific chemical groups. Therefore, the IDD594 electrostatic potentials displayed in the present study are derived from the DFT calculations only. Fig. 5 gives the DFT potential generated by the inhibitor. Except for the carboxylate group, the potential is slightly positive without any large extension, reflecting the hydrophobic nature of the compound. An orthogonal view (not shown) gives similar information, except a slightly negative well (DFT value, –0.02 e/Å) in the vicinity of the Br-bearing aromatic ring leading to a π–π interaction with Trp-111. This contrasts with the binding of NADP+, which is strongly electrostatic. Fig. 5 also shows that the corresponding cavity of the apoenzyme displays an overall low positive potential, with two negative wells created by Cys-80 Sγ and the Thr-113 hydroxyl group (DFT, –0.1 e/Å; TRF, –0.2 e/Å; MUL, –0.25 e/Å). The experimental MUL and TRF maps give a negative potential around Tyr-309 (TRF and MUL, –0.10 e/Å), whereas the theoretical value is slightly positive (DFT, +0.02 e/Å).
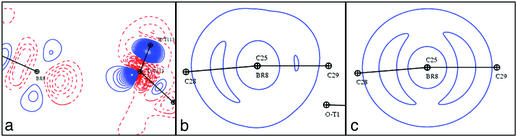
The bromine atom of the inhibitor forms an exceptionally short contact with the Oγ1 oxygen atom of Thr-113 (distance, 3.0 Å). As pointed out by Podjarny and colleagues (30), this is the shortest Br.. .O contact observed so far according to the Cambridge Structural Database (31). Fig. 6 shows the potential around the bromine atom, within the protein complex, for the ligand alone, and for the active site. The hydroxyl hydrogen atom of the Thr-113 is not directed toward the bromine atom, as might have been expected, but is involved instead in a hydrogen bond with the Thr-113 main-chain carbonyl (30). The negative potential due to the lone pairs of Oγ1 of Thr-113 can be directly superposed with the positive potential developed by the bromine atom of the inhibitor; this renders this short interaction essentially electrostatic. The theoretical deformation density maps also reveal effects of the interaction on the bromine with oxygen atom nonbonding electron density (Fig. 7a, shown in the same plane as Fig. 6). The orthogonal views of the torus-shaped deformation density around the Br atom (Fig. 7 b and c), for the ligand alone and in the complex, reveal the effects of the interaction on the bromine atom. Through the interaction with the Oγ1 of Thr-113, the bromine atom is polarized and loses its cylindrical symmetry.
Fig. 7.
Theoretical deformation density maps of the Br... OG1-Thr-113 region in the complex and alone. (a) Map in the Br... O—H plane. Also shown are maps displaying the bromine deformation density of toric shape in the plane perpendicular to the C—Br bond in the complex (b) and for the inhibitor alone (c).
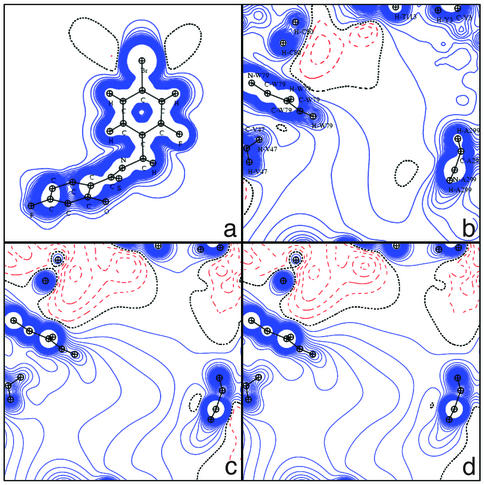
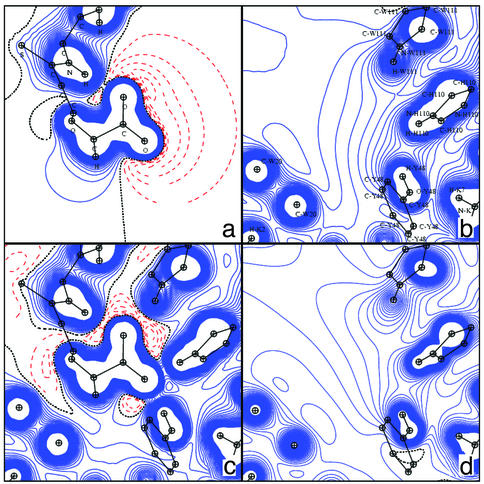
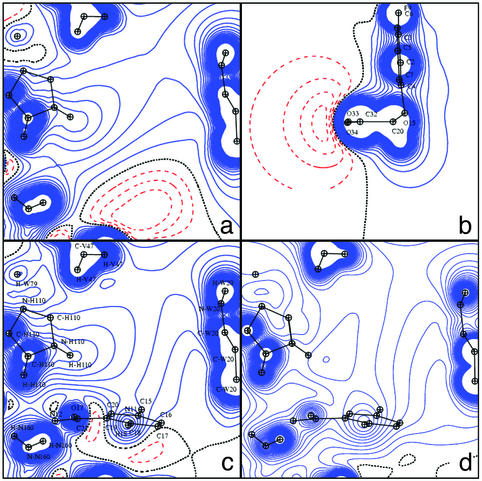
The second polar interaction site of the ligand is located on the other side of the molecule (Fig. 1). Fig. 8 displays the DFT potential generated in the carboxylate plane by the ligand alone (a), by the apoenzyme active site (b), and by the complex (c). Fig. 8d shows the TRF generated by the apoenzyme. The carboxylate group of the inhibitor interacts with the enzyme by means of three hydrogen bonds; it also accepts an intramolecular hydrogen bond (Table 1). For both oxygen atoms O34 and O33, the electron lone pairs are approximately located on the direction between acceptor and donor atoms. Such directional effects on hydrogen bonding around the oxygen atoms are better described by a multipolar atom model than by atomic point charges.
Fig. 8.
Electrostatic potentials shown in the inhibitor carboxylate plane. (a) DFT (inhibitor alone). (b) DFT (apoenzyme). (c) DFT (AR complex). (d) TRF (apoenzyme).
The DFT electrostatic potentials in the plane perpendicular to the inhibitor carboxylate are represented around the ligand alone (Fig. 9b), in the active site of the protein alone (Fig. 9a) and in the active site of the protein–NADP+ complex (Fig. 9c); the corresponding TRF is given Fig. 9d. Both Figs. 8 and 9 show the good agreement between experimental and theoretical active site potentials, which confirms the feasibility of interaction analyses using the database and high-resolution x-ray refinement only. There is a local complementarity between the potentials; in addition, several electrostatic potential saddle points, characteristic of H-bonds, can be observed. The potential in the plane perpendicular to the inhibitor carboxylate (Fig. 9) shows that the attraction of the ligand carboxylate requires the presence of the NADP+ cofactor. The positively charged nicotinamide group contributes to the electrostatic complementarity and therefore to the anchoring of the inhibitor carboxylate (Fig. 9 c and d). Indeed, without the cofactor (Fig. 9a), the protein active site displays a large negative potential that would hinder the binding of COO– (Fig. 9b).
Fig. 9.
Electrostatic potentials shown in the plane perpendicular to the inhibitor carboxylate. (a) DFT (protein alone). (b) DFT (inhibitor alone). (c) DFT (protein plus NADP+). (d) TRF (protein plus NADP+).
Discussion and Conclusion
Obtaining accurate electrostatic properties to understand interactions among proteins, ligands, and cofactors is very challenging and has many potential applications in life sciences, as shown by the increasing number of publications devoted to this topic. First, this research needs atomic resolution diffraction data to be able to locate and refine the hydrogen atoms of the active site. The use of dipolar scattering factors for hydrogen atoms, as defined in our database, is necessary. Recent developments of diffraction techniques at third-generation synchrotrons (32) and progress in cryocrystallography (33) and protein crystallization promise more high-resolution data, which will require nonspherical atom models to yield more accurate atomic coordinates and thermal-displacement parameters. This will also permit more precise location of molecules and ions with important roles in bioelectrostatics in the protein solvation shell. Given a well refined high-resolution structure, electrostatic properties may be calculated in different ways: directly by multipolar analysis or using DFT (this work) and/or QM/MM methods (34–36) or by using fragments experimentally (TRF; ref. 27 and this work) or theoretically calculated (37–41), or by point charge models such as amber (29), charmm (42), or grasp (43).
This paper has demonstrated that DFT quality potentials can be obtained quickly and almost routinely from high-resolution diffraction data (TRF). Such a calculation can be routinely performed, at very low cost, with any protein structure at atomic resolution. An application of these methods to allosteric insulin hexamers is under way (R. H. Blessing, G. D. Smith, E. Ciszak, W. A. Pangborn, B.G., and C.L., unpublished data). A direct determination from an accurate experimental charge distribution transfer plus refinement is also possible, as shown in this paper (MUL). But this latter possibility still needs further testing and development tests to define the best refinement strategies (even though the refinement program mopro is available) to ensure that the resulting potential is more accurate than the database-transferred one. This issue will be discussed in a forthcoming publication.
Concerning the complex AR–NADP+ inhibitor, and enzymology more generally, this work reports, for the first time to our best knowledge, an experimental and theoretical analysis of the protein host–guest interaction at the electrostatic level, i.e., beyond geometrical or putative hydrogen bonding considerations. The roles of coulombic long-range interactions and of atomic polarizability have been clearly evidenced in the AR–cofactor complex. The results show remarkable electrostatic apoenzyme–cofactor complementarity within the active site, and good hydrophilic/hydrophobic complementarity between the enzyme and the inhibitor. The carboxylate group of the inhibitor is the source of the main polar interaction with the enzyme, and the electrostatic complementarity is with the positive potential produced by the NADP+ cofactor. In addition, the polarizable bromine atom of the inhibitor forms a short polar contact with an hydroxyl oxygen atom.
Further work is planned with AR to develop optimal charge density refinement and potential mapping strategies, and to evaluate apoenzyme–cofactor–ligand electrostatic interaction energies.
Acknowledgments
We gratefully acknowledge A. Mitschler, A. Joachimiak, R. Sanishvili, B. Chevrier, and A. Podjarny for providing us with the crystallographic structure factors and preliminary anisotropic refinements results on the AR-IDD594 complex; E. Artacho and M. V. Fernandez-Serra for help on the siesta program; and M. M. Rohmer and M. Bénard for helpful discussions. Our colleague, V. Pichon-Pesme, is greatly acknowledged for the many discussions about the database. N.M. was supported by a grant from the Association pour la Recherche sur le Cancer, and B.G. was supported by a fellowship from the French Minister of Research and Technology.
Abbreviations: DFT, density functional theory; AR, aldose reductase; MUL, electrostatic potential obtained from multipolar refinement; TRF, electrostatic potential obtained directly from multipolar data base; AMB, electrostatic potential obtained from the amber dictionary.
References
- 1.Jelsch, C., Teeter, M. M., Lamzin, V., Pichon-Pesme, V., Blessing, R. H. & Lecomte, C. (2000) Proc. Natl. Acad. Sci. USA 97, 3171–3176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lecomte, C. (1995) Adv. Mol. Struct. Res. 1, 261–302. [Google Scholar]
- 3.Coppens, P. (1998) Acta Crystallogr. A 54, 779–788. [Google Scholar]
- 4.Coppens, P. (1997) X-Ray Charge Densities and Chemical Bonding (Oxford Univ. Press, Oxford).
- 5.Hansen, N. K. & Coppens, P. (1978) Acta Crystallogr. A 34, 909–921. [Google Scholar]
- 6.Guillot, B., Viry, L., Guillot, R., Lecomte, C. & Jelsch, C. (2001) J. Appl. Crystallogr. 34, 214–223. [Google Scholar]
- 7.Pichon-Pesme, V., Lecomte, C. & Lachekar, H. (1995) J. Phys. Chem. 99, 6242–6250. [Google Scholar]
- 8.Stewart, R. F. (1976) Acta Crystallogr. A 32, 565–574. [Google Scholar]
- 9.Politzer, P. & Murray, J. S. (1993) Trans. Am. Crystallogr. Assoc. 26, 23–40. [Google Scholar]
- 10.Fernandez-Serra, M. V., Junquera, J., Jelsch, C., Lecomte, C. & Artacho, E. (2000) Solid State Commun. 116, 395–400. [Google Scholar]
- 11.Guillot, B., Muzet, N., Jelsch, C., Artacho, E. & Lecomte, C. (2003) J. Phys. Chem., in press.
- 12.Lamour, V., Barth, P., Rogniaux, H., Poterszman, A., Howard, E., Mitschler, A., Van Dorsselaer, A., Podjarny, A. & Moras, D. (1999) Acta Crystallogr. D 55, 721–723. [DOI] [PubMed] [Google Scholar]
- 13.Cachau, R., Howard, E., Barth, P., Mitschler, A., Chevrier, B., Lamour, V., Joachimiak, A., Sanishvili, R., Van Zandt, M., Sibley, E., et al. (2000) J. Phys. [French] IV 10, 3–13. [Google Scholar]
- 14.Yabe-Nishimura, C. (1998) Pharmacol. Rev. 50, 21–32. [PubMed] [Google Scholar]
- 15.Otwinowski, Z. & Minor, W. (1997) Methods Enzymol. 276, 307–326. [DOI] [PubMed] [Google Scholar]
- 16.Sheldrick, G. M. (1997) shelxl-97, Program for the Refinement of Crystal Structures (Univ. of Göttingen, Göttingen, Germany).
- 17.Allen, F. (1986) Acta Crystallogr. B 42, 515–522. [Google Scholar]
- 18.Jiang, J.-S. & Brünger, A. T. (1994) J. Mol. Biol. 243, 100–115. [DOI] [PubMed] [Google Scholar]
- 19.Sanchez-Portal, D., Ordejon, P., Artacho, E. & Soler, J. M. (1997) Int. J. Quantum Chem. 65, 453–461. [Google Scholar]
- 20.Soler, J. M., Artacho, E., Gale, J. D., Garcia, A., Junquera, J., Ordejon, P. & Sanchez-Portal, D. (2002) J. Phys. Condens. Matter 14, 2745–2779. [DOI] [PubMed] [Google Scholar]
- 21.Artacho, E., Sanchez-Portal, D., Ordejon, P., Garcia, E. & Soler, J. M. (1999) Phys. Stat. Sol. B 215, 809–817. [Google Scholar]
- 22.Kohn, W. & Sham, L. J. (1965) Phys. Rev. A At. Mol. Opt. Phys. 140, 1133–1136. [Google Scholar]
- 23.Perdew, J. P., Burke, K. & Ernzerhof, M. (1996) Phys. Rev. Lett. 77, 3865–3868. [DOI] [PubMed] [Google Scholar]
- 24.Troullier, N. & Martins, J.-L. (1991) Phys. Rev. B Solid State 43, 1993–2006. [DOI] [PubMed] [Google Scholar]
- 25.Kleinman, L. & Bylander, D. M. (1982) Phys. Rev. Lett. 48, 1425–1428. [Google Scholar]
- 26.Sankey, O. F. & Niklewski, D. J. (1989) Phys. Rev. B Solid State 40, 3979–3995. [DOI] [PubMed] [Google Scholar]
- 27.Bouhmaida, N., Ghermani, N.-E., Lecomte, C. & Thallal, A. (1999) Acta Crystallogr. A 55, 729–738. [DOI] [PubMed] [Google Scholar]
- 28.Jelsch, C., Pichon-Pesme, V., Lecomte, C. & Aubry, A. (1998) Acta Crystallogr. D 54, 1306–1318. [DOI] [PubMed] [Google Scholar]
- 29.Bayly, C. I., Cieplak, P., Cornell, W. D. & Kollman, P. A. (1993) J. Phys. Chem. 97, 10269–10280. [Google Scholar]
- 30.Howard, E. I., Sanishvili, R., Cachau, R. E., Mitschler, A., Chevrier, B., Barth, P., Lamour, V., Van Zandt, M., Sibley, E., Bon, C., et al. (2003) Proteins, in press. [DOI] [PubMed]
- 31.Allen, F. H. & Kennard, O. (1983) Chem. Design Automation News 8, 31–37. [Google Scholar]
- 32.Longhi, S., Czjzek, M. & Cambillau, C. (1998) Curr. Opin. Struct. Biol. 8, 730–737. [DOI] [PubMed] [Google Scholar]
- 33.Samygina, V. R., Antonyuk, S. V., Lamzin, V. S. & Popov, A. N. (2000) Acta Crystallogr. D 56, 595–603. [DOI] [PubMed] [Google Scholar]
- 34.Eurenius, K. P., Chatfield, D. C., Brooks, B. R. & Hodoscek, M. (1996) Int. J. Quantum Chem. 60, 1189–2000. [Google Scholar]
- 35.Gao, J. (1996) Acc. Chem. Res. 29, 298–305. [Google Scholar]
- 36.Leach, A. R. (1996) in Molecular Modelling: Principles and Applications (Longman, Essex, U.K.).
- 37.Karle, J., Huang, L. & Massa, L. (1998) Pure Appl. Chem. 70, 319–324. [Google Scholar]
- 38.Walker, P. D. & Mezey, P. G. (1994) J. Am. Chem. Soc. 116, 12022–12032. [Google Scholar]
- 39.Bader, R. W. F. (1990) Atoms in Molecules: A Quantum Theory (Oxford Science, Oxford).
- 40.Koritsanszky, T., Volkov, A. & Coppens, P. (2002) Acta Crystallogr. A 58, 464–472. [DOI] [PubMed] [Google Scholar]
- 41.Dittrich, B., Koritsánszky, T., Grosche, M., Scherer, W., Flaig, R., Wagner, A., Krane, H. G., Kessler, H., Riemer, C., Schreurs, A. M. M. & Luger, P. (2002) Acta Crystallogr. B 58, 721–727. [DOI] [PubMed] [Google Scholar]
- 42.Brooks, B. R., Bruccoleri, R. E., Olafson, B. D., States, D. J., Swaminathan, S. & Karplus, M. (1983) J. Comput. Chem. 4, 187–217. [Google Scholar]
- 43.Honig, B. & Nicholls, A. (1995) Science 268, 1144–1149. [DOI] [PubMed] [Google Scholar]