Skip to main content
NCBI home page
The Journal of Physiology logoLink to The Journal of Physiology
. 2004 Sep 16;561(Pt 1):123–131. doi: 10.1113/jphysiol.2004.066639

Chronometric readout from a memory trace: gamma-frequency field stimulation recruits timed recurrent activity in the rat CA3 network

Shigeyoshi Fujisawa 1, Norio Matsuki 1, Yuji Ikegaya 1
PMCID: PMC1665348  PMID: 15375190

Abstract

Synchronous population activity is prevalent in neurones of the central nervous system and experimentally captured as oscillatory electric fields, the frequency of which can represent the state of the neural circuit, e.g. theta (∼5 Hz) and gamma (∼40 Hz). Such field oscillations, however, are not merely a result of coherent neuronal activity. They may also play active roles in information processing in the brain. In this study, we observed that, in cultured hippocampal slices, CA3 pyramidal cells responded to single-pulse stimuli with monosynaptic and polysynaptic potentials and firing spikes which occurred after variable latencies. The variability of the spike latencies was greatly reduced in the presence of weak electric field oscillations, especially the oscillation in the gamma-band frequency range, that per se induced only small fluctuations in the subthreshold membrane potential, and this effect was inhibited by blockade of NMDA receptor activity. Furthermore, the latency of the firing spikes changed if the stimulus was applied at a different phase of the imposed gamma oscillations. These results may suggest that the background field oscillations serve as an extracellular time reference and assure accurate and stable decoding of a memory trace present in cortical feedback networks.

Neural information is represented by a spatial and temporal pattern of spikes generated by individual neurones embedded in the network. Persistent activity is a characteristic spike pattern that is widely observed in cortical and subcortical brain regions (Goldman-Rakic, 1996) and is believed to rely on positive feedback operations of recurrent ‘reverberating’ excitation through synaptic connections (Amit & Brunel, 1997; Lisman et al. 1998; Durstewitz et al. 2000b), although the evidence is still controversial (Marder et al. 1996; Egorov et al. 2002). One of the brain regions that are involved in the densest recurrent connectivity is the hippocampal CA3 area, in which single pyramidal cells extend their longitudinal axons and synapse with approximately 10 000 other CA3 pyramidal cells, forming an autoassociative network (Amaral & Witter, 1989). Indeed, CA3 pyramidal cells display persistent reverberatory activities through the positive feedback loops of recurrent collaterals (Miles & Wong, 1983).

Previous studies have mainly focused on the mechanisms underlying the induction and maintenance of the persistent activities, and little is known about readout from these activities. Buonomano (2003) has recently shown that in cultured neocortical slices, a memory trace present in the cortical circuit can be retrieved as a late suprathreshold response even after tens or hundreds of milliseconds. In his study, however, spike output timing was extensively jittered from trial to trial (standard deviation (s.d.) was up to ∼100 ms), indicating that the cortex seems unable to process information with temporal precision. The biophysical law of synaptic plasticity requires millisecond precision (Markram et al. 1997; Bi & Poo, 1998). We thus think that there might be a certain cellular mechanism that enhances temporal fidelity of the readout process to a point that meets the requirement of the physiological constraints.

One of the characteristic behaviours of hippocampal neurones is synchronous population activity (Harris et al. 2003), which causes periodic oscillations in extracellular electric fields. According to frequency, the oscillatory activity is categorized into distinct states, e.g., theta (∼5 Hz) and gamma (∼40 Hz). Artificially applied weak electric fields have been shown to be capable of modulating cortical activity both in vivo and in vitro (for review, see Jefferys, 1995), so we hypothesize that these electroencephalographic oscillations may enhance spike precision. By recording intracellular responses of CA3 pyramidal cells in hippocampal slice cultures, we examined the effect of field oscillations on the readout process. The results may be relevant to the possible mechanisms of persistent activity during short-term memory and shed light on the mechanisms by which network activity influences neuronal processing.

Methods

Culture of hippocampal slices

Hippocampal slices prepared from postnatal day 7 Wistar/ST rats (SLC, Shizuoka, Japan) were cultured as previously described (Ikegaya, 1999). Briefly, rat pups were chilled, and the brains were aseptically removed, according to the National Institutes of Health guidelines for laboratory animal care and safety. The caudal half of the whole brain was horizontally cut into 300-μm-thick slices using a DTK-1500 vibratome (Dosaka, Kyoto, Japan) in aerated, ice-cold Gey's balanced salt solution (Invitrogen, Garthersburg, MD, USA) supplemented with 25 mm glucose. The entorhino-hippocampi were dissected out under stereomicroscopic controls and cultivated using the membrane interface technique, in which they were placed on sterile 30-mm-diameter membranes (Millicell-CM, Millipore, Bedford, MA, USA). Cultures were fed with 1 ml of 50% minimal essential medium (Invitrogen, Gaithersburg, MD, USA), 25% horse serum (Cell Culture Laboratory, Cleveland, OH, USA) and 25% Hanks' balanced salt solution (Garthersburg) and were maintained in a humidified incubator at 37°C in 5% CO2. The medium was changed every 3.5 days. Electrophysiological experiments were performed at days 9–20 in vitro.

Electrophysiological recordings

Whole-cell recording was performed as described elsewhere (Fujisawa et al. 2004). A cultured slice was transferred to a recording chamber and continuously perfused with oxygenated artificial cerebrospinal fluid consisting of (mm): 124 NaCl, 25 NaHCO3, 3 KCl, 1.24 KH2PO4, 1.4 MgSO4, 2.2 CaCl2 and 10 glucose (25°C). Micropipettes (4–7 MΩ) were filled with internal solutions consisting of (mm): 136.5 KMeSO4, 17.5 KCl, 9 NaCl, 1 MgCl2, 10 HEPES, 4 MgATP, and 0.2 EGTA (pH 7.2). Tight-seal whole-cell recordings were obtained from CA3 pyramidal neurones under IR-DIC microscopy. Recordings were carried out with an Axopatch 200B amplifier (Axon Instruments, Union City, CA, USA). Signals were low-pass filtered at 1 kHz, digitalized at 10 kHz and analysed with pCLAMP 8.0 software (Axon Instruments) and custom Igor Pro (WaveMetrics, Inc., Lake Oswego, OR, USA)/MATLAB (The Mathworks, Inc., Natick, MA, USA) routines. Bipolar tungsten electrodes were placed in the CA3 stratum pyramidale, and a single pulse (50 μs, 5–10 μA) was applied every 15 s in the presence of 20 μm picrotoxin to stimulate pyramidal neurones. In order to apply small electric fields, parallel tungsten electrodes (300 μm interval) were set, about 20 μm above CA3 stratum pyramidale, parallel to the cell layer axis (i.e. vertical to the direction of the apical dendrites of CA3 pyramids). Sinusoidal field stimulation was incessantly applied as background oscillations, the frequency ranging from 5 to 100 Hz (typically 40 Hz). The intensity was adjusted to produce field oscillations comparable to carbachol-induced gamma oscillations in terms of the fluctuation amplitude of electric fields (∼5 mV mm−1). The amplitude of the imposed field oscillations was decreased as the distance from the parallel electrodes increases; the amplitude was reduced roughly by 70% every 200 μm.

We report the mean ± standard deviation (s.d.) in all measurements.

Results

Recurrent activity in CA3 autoassociative networks

Visually identified CA3 pyramidal neurones were held in current clamp, and a stimulating electrode was placed in the CA3 pyramidal cell layer about 500 μm from the recording patch-clamp electrode. We found that single-pulse stimuli evoked complex intracellular responses that consisted of multiple EPSPs and occasional action potentials (Fig. 1A). The initial EPSP, presumably monosynaptic, was observed at 4.0 ± 0.8 ms of latency (mean ± s.d., n = 23). The peak amplitude was only 11.7 ± 5.5 mV, which did not reach the spike threshold. The initial response was followed by consecutive EPSPs, which accumulated over time, and eventually led to the firing of action potentials. These late responses are suggestive of recurrent excitation and may represent a memory trace that is involved in production of suprathreshold outputs, i.e. action potentials, with a delay.

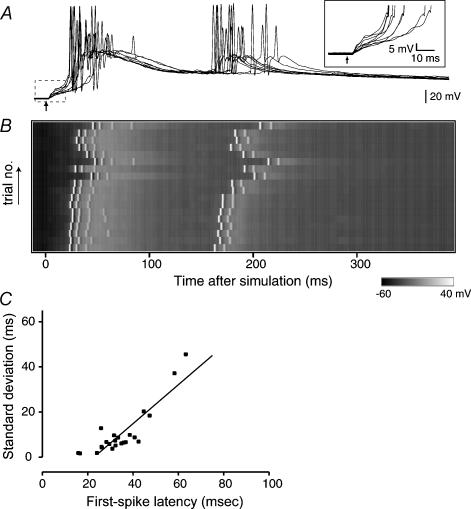
Figure 1. Spike jitters increase linearly with their latencies in the CA3 recurrent circuit.

Figure 1

Open in a new tab

A, intracellular responses of a CA3 pyramidal cell following a single-pulse stimulus (arrow) applied to the CA3 stratum pyramidale. The traces of the boxed region are magnified in the inset. B, voltage map of intracellular responses. Horizontal sweeps represent 20 successive trials, out of which the odd 10 traces are shown in panel A. A stimulus was given every 15 s at time 0. C, linear correlations between the mean latency of the first spikes and its standard deviation. Each point represents each neurone and the line is the best fit with linear regression (r = 0.89, d.f. = 27, P < 0.0001).

We observed that the onset of the initial EPSP was relatively consistent across trials (Fig. 1A inset) although their slopes slightly varied from trial to trial because of the near-threshold intensity of stimulation (Buonomano, 2003). As compared with the EPSP onsets or slopes, the timing of subsequent spikes varied greatly from trial to trial and from cell to cell. For example, in the cell shown in Fig. 1A and B, the latency of the first spike ranged from 25.2 to 49.0 ms, the mean being 33.6 ± 8.5 ms (s.d. of 20 trials). Figure 1C is a plot of the mean and s.d. of the first spike latency of 28 cells tested. There was a positive correlation between these two parameters (r = 0.89, P < 0.0001), indicating that the variance (spike jitter) increased as the interval increased. This led us to the idea that the accuracy of response decreases linearly as the number of synapse steps increases, which is supported by a previous study using neocortical preparations (Buonomano, 2003).

Chronometric spiking behaviours generated by an external oscillator

One of the typical population activities of hippocampal neurones in vivo is gamma rhythmic synchronization (Bragin et al. 1995; Csicsvari et al. 2003). In slice preparations, such periodic activity is usually absent, but it can reliably be induced by carbachol, a muscarinic agonist (Fisahn et al. 1998; Fellous & Sejnowski, 2000). We recorded extracellular field potentials from the slices of the CA3 region, and applied carbachol. We observed no gamma activities before application of carbachol, but the gamma oscillations emerged as a peak in the fast Fourier transform (FFT) power spectrum after application of 20 μm carbachol (Fig. 2A).

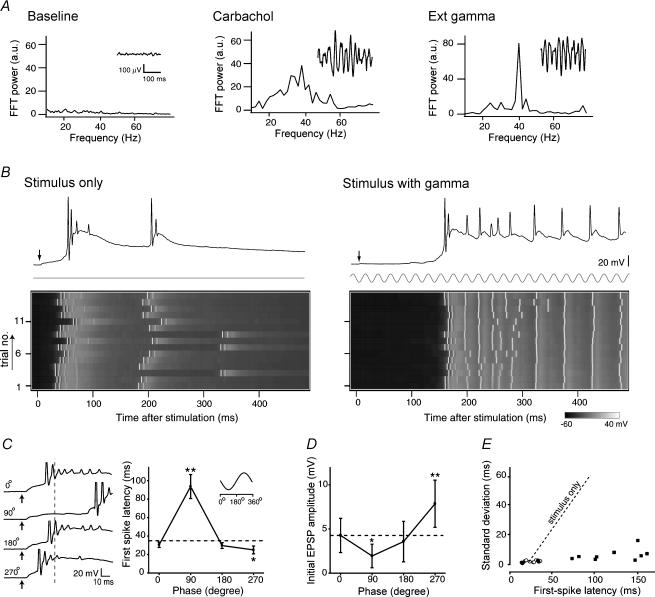
Figure 2. External field oscillators ensure stable propagation of activity and chronometric spike output.

Figure 2

Open in a new tab

A, representative field waveforms and their FFT power spectra obtained from the CA3 region in the presence of 20 μm carbachol (Carbachol) or oscillating electric fields at sinusoidal 40 Hz (Ext gamma). B, representative voltage maps in the absence (Stimulus only) and presence of extracellular 40-Hz oscillations (Stimulus with gamma). Each trace in the inset shows a representative intracellular recording in each case. Stimulation was applied at phase 90 deg of gamma. C, stimulus phase-dependent spike timing. The ordinate indicates the mean latency of the first spike evoked by a single-pulse stimulus that was applied at either 0, 90, 180, or 270 deg in gamma cycle. Left traces show representative late responses (spikes truncated). In the both panels, the broken lines indicate the mean latency of the first spike in the absence of gamma oscillations, referred to here as ‘stimulus only’. *P < 0.05, **P < 0.01 versus stimulus only; Fisher's protected least significant difference following one-way ANOVA (n = 5 cells). D, stimulus phase-dependent initial EPSP responses. The ordinate indicates the amplitude of the initial EPSPs evoked by a single-pulse stimulus. The dashed line indicates the mean amplitude of monosynaptic response in the absence of gamma oscillations. *P < 0.05, **P < 0.01 versus stimulus only; Fisher's protected least significant difference following one-way ANOVA (n = 5 cells). E, signal propagation with small spike jitters. The mean latency and standard deviation of the first spike latency were independent of each other. The filled circles represent the data of phase 270 deg, the filled squares 90 deg, and the open circles 0 and 180 deg. The dashed line indicates a correlation of stimulus only (derived from Fig. 1C).

To simulate the intrinsic gamma field oscillations, parallel electrodes were positioned above the CA3 pyramidal cell layer to apply oscillatory electric field stimulation at a gamma-band frequency (40 Hz). As shown in Fig. 2A, the waveform and amplitude of imposed gamma oscillations were similar to those of carbachol-induced ‘intrinsic’ gamma activity, but the width of a peak in FTT was narrower in imposed oscillations than that of carbachol-induced gamma activity; the full-width half-maximum (FWHM) was 1.4 Hz for the imposed oscillator and 16.2 Hz for carbachol. This external gamma oscillator allowed us to customize the frequency and phase of oscillations and also examine the pure effect of field oscillations without interference from other coherent activities and side-effects induced by carbachol. Carbachol not only induces various frequencies of oscillations other than gamma but may also elicit unexpected cellular responses by activating diverse signalling cascades, such as the diacylglycerol, phosphatidylinositol-3,4,5-trisphosphate and cyclic AMP signalling pathway, via muscarinic receptors (Lucas-Meunier et al. 2003).

To determine whether background gamma oscillations modulate the recurrent firing activities, we applied single-pulse stimuli in the absence or presence of the external oscillator. In the neurone shown in Fig. 2B, single-pulse stimuli evoked typical late responses in the absence of background gamma oscillations (the control) with the first spike latency being 38.7 ± 9.7 ms. In the presence of background gamma oscillations, the same stimuli, which were applied at the phase of 90 deg of the gamma cycle, significantly delayed the occurrence of the first spike to 157.9 ± 7.0 ms (P < 0.001, Student's t test). When the imposed gamma oscillations were terminated, the latency of the first spikes returned to the control level, 26.4 ± 4.1 ms. That may indicate that field oscillations reversibly modify the readout process of a circuit memory.

We next sought to determine whether the latency of the first spikes is related to the gamma phase at which the stimulus is applied. Interestingly, the latency of the first spikes changed greatly with the phase of the gamma oscillations at which the single-pulse stimuli were applied (Fig. 2C). Contrary to the case of stimuli at 90 deg, the first spike was advanced when the stimulation was applied at the phase of 270 deg compared with the control, but no change was observed for the stimulation at 0 or 180 deg. It seemed that the latency of the spike output from the activated circuit might be predicted from the timing stimuli at the phase of gamma oscillation. The latencies of the initial EPSPs did not show much variance among stimulations at different phases, which were 4.20 ± 0.19, 4.30 ± 0.19, 4.44 ± 0.19, 4.25 ± 0.19 and 4.22 ± 0.19 ms in the control and 0, 90, 180 and 270 deg phases, respectively (see also Fig. 2C traces), but the amplitudes varied depending on the phase at which the stimuli were applied (Fig. 2D). The amplitudes of the initial EPSPs were smallest at the phase of 90 deg and largest at the phase of 270 deg, and they seemed to be responsible for the variation of the first spike latency among stimulations at different phases. The plot of the mean and s.d. of the first spike latencies revealed that in the presence of the imposed gamma oscillations, the s.d. was kept low, regardless of the latencies, indicating that the spike precision was maintained during the signal propagation over hundreds of milliseconds (Fig. 2E). With field oscillations, the circuit is likely to operate with high reliability as if it works as a ‘timer’.

We also examined whether the time when the spike occurs is related to the phase of the gamma oscillations. The times of the first spike occurrence did not seem to be related to the phase of the gamma oscillations (Fig. 1A of the on-line Supplementary Material accompanying this paper). The interspike intervals (ISIs) and the spike numbers were plotted for evaluation of the times of successive spikes following the first spike (Supplementary Fig. 1B). The ISIs were not always locked to a multiple of the gamma cycle (25 ms), but they were sometimes locked to some particular intervals, depending on the case, indicating that the individual timings of discharging spikes after the first spike is not strongly affected by the imposed gamma oscillations but may probably be related to the intrinsic properties of the individual neurones.

Gamma-specific enhancement of recurrent excitation

We next examined the dynamics of the subthreshold membrane potentials to find some mechanism for how the background gamma oscillations affect the recurrent activity. The subthreshold responses were monitored through QX314-loaded patch-clamp electrodes to block action potentials. We found that the gamma field oscillations per se induced small, virtually negligible fluctuations in membrane potential (Fig. 3A, Gamma only), and single-pulse stimuli elicited successive polysynaptic EPSPs following the initial monosynaptic EPSP (Fig. 3A, Stimulus only), but when the background gamma oscillations were applied, the polysynaptic EPSPs occurred more frequently, and their occurrence seemed to be in synchrony with the gamma cycles (Fig. 3A, Stimulus with gamma). The onset times of the individual EPSPs and the phase of the gamma oscillations were plotted for the evaluation of the synchronization (Fig. 3B). The onset times of the recurrent EPSPs were found to be predominantly locked at the phases of 310–360 deg of the gamma oscillations, probably indicating that the synaptic inputs are regulated by the imposed gamma oscillations.

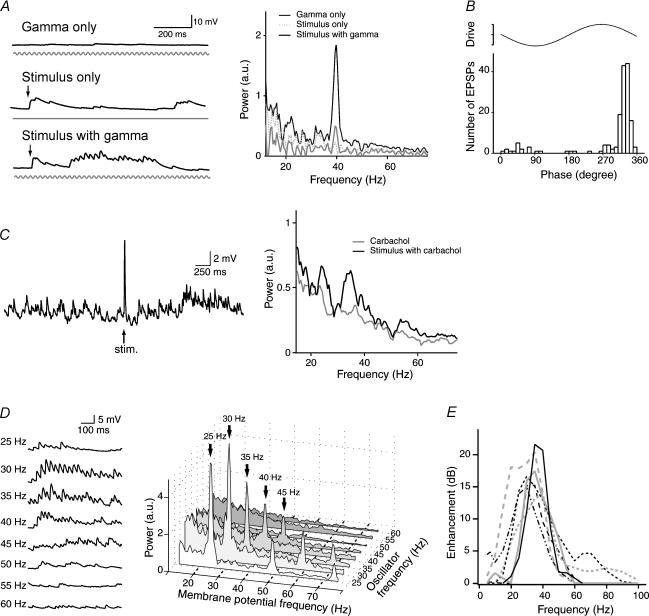
Figure 3. Gamma frequency-specific amplification of subthreshold membrane potential.

Figure 3

Open in a new tab

A, subthreshold responses and their FFT power spectra of a QX314-loaded CA3 pyramidal neurone to extracellular gamma oscillations (Gamma only), a single-pulse stimulus (Stimulus only), and a combination of both (Stimulus with gamma). Stimulation was applied at phase 90 deg of gamma. The salient 40-Hz peak in the FFT spectrum indicates a supralinear enhancement of gamma field oscillations. B, onset timings of EPSP occurrence relative to the gamma phase. Data were obtained from Fig. 3A (Stimulus with gamma). Recurrent synaptic inputs were phase-locked. C, carbachol induces gamma-frequency recurrent inputs. The responses (insets) evoked by a single stimulus applied in the presence of 20 μm carbachol were FFT-transformed. D, frequency-dependent enhancement of field oscillations. Typical stimulus-evoked responses (left) and their FFT power spectra (right) to an external oscillator with its frequency ranging form 25 to 60 Hz. E, summary of the frequency preference in the oscillation enhancement. The degrees of amplification are expressed in decibels. Each line shows each cell (n = 7).

We did Fourier transformation of the subthreshold voltage responses to evaluate the overall frequency distribution of EPSPs (Fig. 3A). Single-pulse stimuli only did not show any peaks in the FFT spectrum of the voltage responses, and gamma oscillations only displayed a small peak at 40 Hz, but when the single-pulse stimulus was applied in the gamma background, the peak at 40 Hz was greatly increased, indicating that the background gamma oscillations can be amplified by the recurrent activity evoked by single-pulse stimuli. Then, we did the same experiment applying 20 μm carbachol. Carbachol, without single-pulse stimuli, increased the number of spontaneous EPSPs, and the FFT analysis revealed the wide frequency components mostly in the gamma range (Fig. 3C, Carbachol). Interestingly, when a single-pulse stimulus was applied, the components in the gamma range were greatly enhanced (Fig. 3C, Stimulus with carbachol). We were unable to examine the phase effect of stimulation for carbachol-induced oscillations because the oscillation involved a wide-range continuum of gamma-band fluctuations and hence we could not precisely predict the phase at which a stimulus should be given online.

We next applied background gamma oscillations with different frequencies trying to find the frequency preference in the gamma enhancement. These results and their FFT power spectra are shown in Fig. 3D. Different frequencies of the background gamma oscillations displayed different degrees of synchronization with the polysynaptic EPSPs, which can be more clearly seemed by the peak amplitudes in the FFT power spectra. In the cell shown in Fig. 3D, the highest peak was at 30 Hz, but it varied from cell to cell. By changing the oscillation frequency in the range from 5 to 100 Hz, we did a broad scan frequency preference in the background frequency enhancement (Fig. 3E). The maximal peaks ranged from 28.4 to 36.9 Hz (mean 33.5 ± 3.5 Hz, n = 7 cells), and the width at half-height ranged from 8.0 to 15.8 Hz (mean 12.5 ± 2.6 Hz). Therefore, the enhancement of the background oscillations seemed to show a preference for the gamma-band frequency.

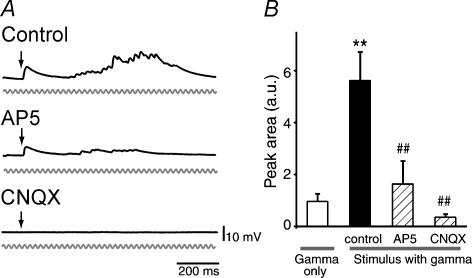
Correlated network operation has been considered to be through NMDA receptors (Lisman et al. 1998; Wang, 1999). Considering this, we applied d,l-AP5, an NMDA receptor antagonist, and found that the later polysynaptic EPSPs, which evoke gamma enhancement, were blocked, but the initial EPSPs were spared (Fig. 4). Both the initial and late responses were abolished by CNQX, a non-NMDA receptor antagonist (Fig. 4). These results suggested that the gamma enhancement is network-based, and depends on NMDA receptor activity.

Figure 4. Gamma-rhythmic recurrent inputs are network driven, NMDA receptor dependent.

Figure 4

Open in a new tab

A, representative subthreshold responses of a CA3 pyramidal neurone to a single-pulse stimulus with 40-Hz field oscillations in the absence (Control) and presence of 50 μm d,l-AP5 or 20 μm CNQX. B, NMDA and non-NMDA receptor antagonists block the enhancement of gamma oscillations. The areas under the curve of the 40-Hz peak (37–43 Hz range) were measured in the FFT power spectra. **P < 0.01 versus gamma only, ##P < 0.01 versus control: Tukey's multiple range test after one-way ANOVA (n = 8–23 cells).

Discussion

Synchronous activity generated by a subset of neurones is common in the CNS and is understood to play a part in temporal processing of neural information. Such coherent neuronal activity evokes field oscillations in the electroencephalogram. Naturally, these field oscillations have long been regarded as a consequence of neuronal population activity. However, field oscillations per se can contribute actively to spike processing; that is, we have shown here that even in the absence of intrinsic oscillations, externally imposed field oscillations modulate spike timing. Although we cannot ruled out the possibility that our external oscillator recruited internal oscillation machinery, thereby indirectly regulating spiking activity, it is still undoubted that field oscillations alone are sufficient to trigger such temporal modulations. Because the amplitude and frequency of the field oscillations we applied were physiologically plausible, our findings imply that synchronous activity can exert its remote influence on nearby neurones that do not originally participate in the synchronization; that is, if a subset of neurones present in the network generates synchronized activity, this neurone group inevitably produces electric field oscillations in its surrounding environments, and the resultant field oscillations would in turn influence the spiking behaviours of neurones outside the synchronized group. Therefore, this work proposes a novel form of non-synaptic communications between neurones (Kruglikov & Schiff, 2003). A theoretical study has indicated that in the olfactory bulb circuit, such global oscillations can work as a ‘common’ drive to stabilize odour representations and ensure precise odour discrimination (Brody & Hopfield, 2003).

Following an input stimulus, the CA3 circuit displayed a suprathreshold output with a delay that far exceeded a monosynaptic interval. To do this, the circuit has to ‘remember’ a previous transitory stimulus; activity must be present in the circuit until the first spike emerged in a recorded neurone. In this sense, the late spike output represents readout from a memory trace registered in the circuit. Subthreshold membrane potential during the ‘memory’ emerged as accumulating polysynaptic responses. The memory trace is hence likely to depend on local circuit reverberation (Wang, 2001) or attractor dynamics (Durstewitz et al. 2000a), both of which have been theorized to exist in a feedback network such as the CA3 circuit. Consistent with this, blockade of NMDA receptors interfered with evoked polysynaptic responses (Lisman et al. 1998; Wang, 1999).

Under naive conditions, the CA3 memory trace appears unreliable in temporal precision, however. Spike jitter easily expanded as the latency increased, and this nature might limit the cortical function. However, field oscillations are capable of reducing this indeterminacy, stabilizing activity propagation. In addition, the circuit output was precisely timed by input timings relative to the oscillatory phases. Oscillations may ensure accurate decoding of cortical networks by offering an external clock reference. The cellular mechanisms by which spike output was modulated by input phases cannot be deduced from this study alone. Our computational simulation using a layered recurrent network with an inner oscillator and noise replicates similar phase-dependent dynamics of spike modulations (see Supplementary Fig. 2); the result that the modulation range is narrower than that of the real network is probably due to much fewer layers of neurones, but we consider it noteworthy that the phase-dependent dynamics can be mimicked even in the neural networks consisting of only three layers. In this model, synchronization of synaptic transmission was essential for the phase modulation, so it is possible that similar paradigms are implemented in realistic neural networks because our empirical data showed that polysynaptic EPSPs were entrained to the forcing oscillations.

The effect of field oscillations was specific for the gamma-band frequency range. This is intriguing because gamma rhythmic activity is involved in sensory binding (Gray, 1994; Singer, 1999), memory encoding (Fell et al. 2001), attention (Fries et al. 2001), and conscious experience (Varela et al. 2001; Ward, 2003). The CA3 network responses may inherently be optimized to resonate with electric field oscillations only for frequencies in the gamma range. Gamma field oscillations, which alone induced minimal changes in membrane potential of CA3 neurones, facilitated recurrent excitation when an input stimulus was given together. How can gamma field oscillations modulate neural processing only when the circuit is activated? A single-pulse stimulus induced a persistent depolarization shift of membrane potential (a so-called UP state). During the period of a UP state, the neurones are more sensitive to small inputs (Shu et al. 2003; Destexhe et al. 2003). The enhancement of neuronal responsiveness to field oscillations may induce spike synchronization, increasing the temporal reliability (Diesmann et al. 1999). Another, but not exclusive, possibility is synchronization of membrane potential at synapses. The synapses are small structures, and their surface-to-volume ratios are quite high. It is possible therefore that synapses are more susceptible to the surrounding electric field than the soma so that their membrane potential may be subject to synchrony with field oscillations; note that such local oscillations, if any, cannot be detected by whole-cell recordings due to the problem of incomplete ‘space clamp’ (Rall & Segev, 1985; Koch, 1998). If presynaptic membrane potential oscillations are synchronized across synapses, synaptic transmission would also be correlated in time. This is consistent with our observations that polysynaptic EPSPs were synchronized with field oscillatory cycles.

In conclusion, the present study has addressed the effect of field oscillations on temporal processing of the CA3 recurrent circuit and suggests the presence of a novel mode of interneuronal communications mediated by local electric fields, that is, neural synchronization is capable of affecting the spiking behaviours of other neurones. Depending on input timings relative to the gamma cycle, the output latency was coordinated with high reliability, and the shift range (> 100 ms) was several oscillation cycles long, being far longer than the delay of a single-synapse step, which suggests that the input phase alters the trajectory of information flow in the microcircuit. Thus, field oscillations rapidly settle functional cortical architectures into a preferred memory trace in a state-specific manner.

Supplementary Material

Supplemental Data
jphysiol_2004.066639_index.html (873B, html)

Acknowledgments

We are grateful to Dr Jiayi Zhou and Mr Neil A. Gray for their critical reviews of this manuscript.

Supplementary material

The online version of this paper can be accessed at:DOI: http://jp.physoc.org/cgi/content/full/jphysiol.2004.066639/DC1 and contains supplementary material entitled ‘Network modelling’ and two figures:

Supplementary Figure 1. Spike timing relative to ongoing gamma oscillations during persistent depolarization shift

Supplementary Figure 2. Computational confirmation of oscillation-induced modulations of the first spike latency in the layered recurrent neural network

This material can also be found at:http://www.blackwellpublishing.com/products/journals/suppmat/tjp/tjp544/tjp544sm.htm

References

  1. Amaral DG, Witter MP. The 3-dimensional organization of the hippocampal-formation – a review of anatomical data. Neuroscience. 1989;31:571–591. doi: 10.1016/0306-4522(89)90424-7. [DOI] [PubMed] [Google Scholar]
  2. Amit DJ, Brunel N. Dynamics of a recurrent network of spiking neurons before and following learning. Network. 1997;8:373–404. [Google Scholar]
  3. Bi GQ, Poo MM. Synaptic modifications in cultured hippocampal neurons: Dependence on spike timing, synaptic strength, and postsynaptic cell type. J Neurosci. 1998;18:10464–10472. doi: 10.1523/JNEUROSCI.18-24-10464.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bragin A, Jando G, Nadasdy Z, Hetke J, Wise K, Buzsaki G. Gamma (40–100-Hz) oscillation in the hippocampus of the behaving rat. J Neurosci. 1995;15:47–60. doi: 10.1523/JNEUROSCI.15-01-00047.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Brody CD, Hopfield JJ. Simple networks for spike-timing-based computation, with application to olfactory processing. Neuron. 2003;37:843–852. doi: 10.1016/s0896-6273(03)00120-x. [DOI] [PubMed] [Google Scholar]
  6. Buonomano DV. Timing of neural responses in cortical organotypic slices. Proc Natl Acad Sci U S A. 2003;100:4897–4902. doi: 10.1073/pnas.0736909100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Csicsvari J, Jamieson B, Wise KD, Buzsaki G. Mechanisms of gamma oscillations in the hippocampus of the behaving rat. Neuron. 2003;37:311–322. doi: 10.1016/s0896-6273(02)01169-8. [DOI] [PubMed] [Google Scholar]
  8. Destexhe A, Rudolph M, Pare D. The high conductance state of neocortical neurons in vivo. Nat Rev Neurosci. 2003;4:739–751. doi: 10.1038/nrn1198. [DOI] [PubMed] [Google Scholar]
  9. Diesmann M, Gewaltig MO, Aertsen A. Stable propagation of synchronous spiking in cortical neural networks. Nature. 1999;402:529–533. doi: 10.1038/990101. [DOI] [PubMed] [Google Scholar]
  10. Durstewitz D, Seamans JK, Sejnowski TJ. Neurocomputational models of working memory. Nat Neurosci. 2000a;3:1184–1191. doi: 10.1038/81460. [DOI] [PubMed] [Google Scholar]
  11. Durstewitz D, Seamans JK, Sejnowski TJ. Dopamine-mediated stabilization of delay-period activity in a network model of prefrontal cortex. J Neurophysiol. 2000b;83:1733–1750. doi: 10.1152/jn.2000.83.3.1733. [DOI] [PubMed] [Google Scholar]
  12. Egorov AV, Hamam BN, Fransen E, Hasselmo ME, Alonso AA. Graded persistent activity in entorhinal cortex neurons. Nature. 2002;420:173–178. doi: 10.1038/nature01171. [DOI] [PubMed] [Google Scholar]
  13. Fell J, Klaver P, Lehnertz K, Grunwald T, Schaller C, Elger CE, Fernandez G. Human memory formation is accompanied by rhinal-hippocampal coupling and decoupling. Nat Neurosci. 2001;4:1259–1264. doi: 10.1038/nn759. [DOI] [PubMed] [Google Scholar]
  14. Fellous JM, Sejnowski TJ. Cholinergic induction of oscillations in the hippocampal slice in the slow (0.5–2 Hz), theta (5–12 Hz), and gamma (35–70 Hz) bands. Hippocampus. 2000;10:187–197. doi: 10.1002/(SICI)1098-1063(2000)10:2<187::AID-HIPO8>3.0.CO;2-M. [DOI] [PubMed] [Google Scholar]
  15. Fisahn A, Pike FG, Buhl EH, Paulsen O. Cholinergic induction of network oscillations at 40 Hz in the hippocampus in vitro. Nature. 1998;394:186–189. doi: 10.1038/28179. [DOI] [PubMed] [Google Scholar]
  16. Fries P, Reynolds JH, Rorie AE, Desimone R. Modulation of oscillatory neuronal synchronization by selective visual attention. Science. 2001;291:1560–1563. doi: 10.1126/science.1055465. [DOI] [PubMed] [Google Scholar]
  17. Fujisawa S, Yamada MK, Nishiyama N, Matsuki N, Ikegaya Y. Neurotrophins boost spike fidelity in chaotic neural oscillations. Biophys J. 2004;86:1820–1828. doi: 10.1016/S0006-3495(04)74249-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Goldman-Rakic PS. Memory: Recording experience in cells and circuits: Diversity in memory research. Proc Natl Acad Sci U S A. 1996;93:13435–13437. doi: 10.1073/pnas.93.24.13435. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Gray CM. Synchronous oscillations in neuronal systems: mechanisms and functions. J Comput Neurosci. 1994;1:11–38. doi: 10.1007/BF00962716. [DOI] [PubMed] [Google Scholar]
  20. Harris KD, Csicsvari J, Hirase H, Dragoi G, Buzsaki G. Organization of cell assemblies in the hippocampus. Nature. 2003;424:552–556. doi: 10.1038/nature01834. [DOI] [PubMed] [Google Scholar]
  21. Ikegaya Y. Abnormal targeting of developing hippocampal mossy fibers after epileptiform activities via L-type Ca2+ channel activation in vitro. J Neurosci. 1999;19:802–812. doi: 10.1523/JNEUROSCI.19-02-00802.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Jefferys JGR. Nonsynaptic modulation of neuronal activity in the brain: electric currents and extracellular ions. Physiol Rev. 1995;75:689–723. doi: 10.1152/physrev.1995.75.4.689. [DOI] [PubMed] [Google Scholar]
  23. Koch C. Biophysics of Computation. New York: Oxford University Press; 1998. [Google Scholar]
  24. Kruglikov SY, Schiff SJ. Interplay of electroencephalogram phase and auditory-evoked neural activity. J Neurosci. 2003;23:10122–10127. doi: 10.1523/JNEUROSCI.23-31-10122.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Lisman JE, Fellous JM, Wang XJ. A role for NMDA-receptor channels in working memory. Nat Neurosci. 1998;1:273–275. doi: 10.1038/1086. [DOI] [PubMed] [Google Scholar]
  26. Lucas-Meunier E, Fossier P, Baux G, Amar M. Cholinergic modulation of the cortical neuronal network. Pflugers Arch. 294;1:11–38. doi: 10.1007/s00424-002-0999-2. [DOI] [PubMed] [Google Scholar]
  27. Harris KD, Abbott LF, Turrigiano GG, Liu Z, Golowasch J. Memory from the dynamics of intrinsic membrane currents. Proc Natl Acad Sci U S A. 1996;93:13481–13486. doi: 10.1073/pnas.93.24.13481. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Markram H, Lubke J, Frotscher M, Sakmann B. Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science. 1997;275:213–215. doi: 10.1126/science.275.5297.213. [DOI] [PubMed] [Google Scholar]
  29. Miles R, Wong RK. Single neurones can initiate synchronized population discharge in the hippocampus. Nature. 1983;306:371–373. doi: 10.1038/306371a0. [DOI] [PubMed] [Google Scholar]
  30. Rall W, Segev I. Space clamp problems when voltage clamping branched neuron with intracellular microelectrodes. In: Smith TG, Lecar H, Redman SJ, Gage PW, editors. Voltage and Patch Clamping with Microelectrodes. New York: Oxford University Press; 1985. pp. 191–215. [Google Scholar]
  31. Shu Y, Hasenstaub A, Badoual M, Bal T, McCormick DA. Barrages of synaptic activity control the gain and sensitivity of cortical neurons. J Neurosci. 2003;23:10388–10401. doi: 10.1523/JNEUROSCI.23-32-10388.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Singer W. Neuronal synchrony: a versatile code for the definition of relations. Neuron. 1999;24:49–65. doi: 10.1016/s0896-6273(00)80821-1. [DOI] [PubMed] [Google Scholar]
  33. Varela F, Lachaux JP, Rodriguez E, Martinerie J. The brainweb: phase synchronization and large-scale integration. Nat Rev Neurosci. 2001;2:229–239. doi: 10.1038/35067550. [DOI] [PubMed] [Google Scholar]
  34. Wang XJ. Synaptic basis of cortical persistent activity: the importance of NMDA receptors to working memory. J Neurosci. 1999;19:9587–9603. doi: 10.1523/JNEUROSCI.19-21-09587.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Wang XJ. Synaptic reverberation underlying mnemonic persistent activity. Trends Neurosci. 2001;24:455–463. doi: 10.1016/s0166-2236(00)01868-3. [DOI] [PubMed] [Google Scholar]
  36. Ward LM. Synchronous neural oscillations and cognitive processes. Trends Cogn Sci. 2003;7:553–559. doi: 10.1016/j.tics.2003.10.012. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental Data
jphysiol_2004.066639_index.html (873B, html)
jphysiol_2004.066639_TJP544_SupMat.doc (831KB, doc)

Articles from The Journal of Physiology are provided here courtesy of The Physiological Society

RESOURCES