A neuronal network model of macaque primary visual cortex (V1): Orientation selectivity and dynamics in the input layer 4Cα

Abstract

In this paper, we offer an explanation for how selectivity for orientation could be produced by a model with circuitry that is based on the anatomy of V1 cortex. It is a network model of layer 4Cα in macaque primary visual cortex (area V1). The model consists of a large number of integrate-and-fire conductance-based point neurons, both excitatory and inhibitory, which represent dynamics in a small patch of 4Cα—1 mm² in lateral area—which contains four orientation hypercolumns. The physiological properties and coupling architectures of the model are derived from experimental data for layer 4Cα of macaque. Convergent feed-forward input from many neurons of the lateral geniculate nucleus sets up an orientation preference, in a pinwheel pattern with an orientation preference singularity in the center of the pattern. Recurrent cortical connections cause the network to sharpen its selectivity. The pattern of local lateral connections is taken as isotropic, with the spatial range of monosynaptic excitation exceeding that of inhibition. The model (i) obtains sharpening, diversity in selectivity, and dynamics of orientation selectivity, each in qualitative agreement with experiment; and (ii) predicts more sharpening near orientation preference singularities.

The mammalian primary visual cortex (area V1) marks the first site along the “visual pathway” [Retina → Lateral geniculate nucleus (LGN) → V1 → And beyond], where selective response is observed to elementary features of visual scenes, such as orientation and spatial frequency. Despite 40 years of intense research effort, a detailed account of the neural basis for this selectivity in V1 remains elusive. In this paper we focus on orientation selectivity, the selective response of a single neuron to some orientations of a bar or grating, and not to others. This property of single cortical cells was discovered by Hubel and Wiesel (1) in 1962; it is probably important for tasks such as edge detection and contour completion (2). A basic question is still unanswered: to what degree, and by what mechanisms, does cortical processing contribute to orientation selectivity?

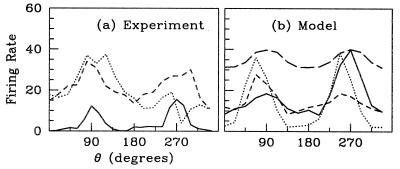
V1 is a layered structure, with different layers having different tuning properties and functional architectures. Here, we focus on layer 4Cα because it is an input layer for stimulus from the LGN (magnocellular pathway). Data illustrating examples of orientation selectivity in an input layer in V1, 4Cα, are shown in Fig. 1 (D. Ringach, M. Hawken, and R.S., unpublished work). Fig. 1a shows sample tuning curves for three simple cells in layer 4Cα, in response to a drifting grating oriented at angle θ (angles separated by 180° designate gratings of the same orientation drifting in opposite directions). These are tuning curves of the steady-state firing rate averaged over many repeated periods of drift. These curves hint at the great diversity observed in the selectivity of 4Cα neurons. Two neurons show peaks at their “preferred angles,” with one weakly and the other more strongly selective, whereas the third neuron is weakly selective for orientation but is directionally selective. Such diversity is found in all layers, although on average neurons in the input layers, 4Cα and 4Cβ, are somewhat less selective for orientation than cells in other layers (3).

Figure 1.

Sample orientation tuning curves from drifting grating stimuli: (a) Experiment (three 4Cα simple cells). The response is measured as time-averaged firing rate and is plotted in units of impulses per sec. Stimuli were at optimal temporal frequency for each neuron, 2−10 Hz). (b) Model (excitatory neurons, 8 Hz). The model results also include the orientation selectivity obtained by an uncoupled neuron (long-dash line, the “feed-forward response”), normalized for comparison to a peak response of 40 spikes per sec. As shown, some of the model's neurons may be directionally selective (dashes), as are some 4Cα cells.

Originally it was proposed that the primary origin of the orientation selectivity of a neuron in V1 is a “feed-forward” convergence of several LGN neurons onto a given cortical neuron (1). The cortical-cooling experiments of Ferster et al. (4) were interpreted as providing evidence for such a feed-forward mechanism. However, note that, for drifting grating stimuli, there is no orientation selectivity in the time-averaged steady-state LGN input to a cortical neuron (2, 5). For such stimuli the average firing rate of an individual LGN cell is not selective for orientation, and so the sum of activities of many, averaged over time, is also not selective, whatever their geometry (even very elongated). The mechanisms in cortex underlying the observed orientation selectivity remain unknown at present, and are the subject of extensive investigation and debate (see refs. 2 and 6). Cortical models have been used to show how steady-state orientation selectivity could be produced in cortex, based on “center–surround” interactions in the orientation domain in the cortical network (7–9). However, these theories did not attempt to use realistic cortical circuitry.

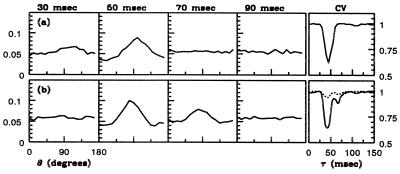
Another kind of experiment on orientation selectivity is a challenge for any theory of visual cortex. Through reverse time correlation (RTC) experiments, Ringach et al. (3) obtained information about the dynamical behavior of orientation selectivity. A sample RTC measurement of the dynamics of orientation selectivity for a 4Cα neuron is shown in Fig. 2a. As in the steady-state experiments, broad diversity is found in RTC orientation selectivity and dynamics (3). The stimulus used in the RTC experiments kept most of the measured cortical cells in a persistently excited state. This is unlike the situation in the drifting grating experiment, in which spike firing rate could be zero at nonpreferred orientations. And so, a second major test of a neuronal network model is to see how well it matches the cortex's dynamics of orientation selectivity measured in the RTC experiments.

Figure 2.

P(θ, τ) from RTC at several times τ, showing the dynamics and sharpening of orientation selectivity. A time series for the stimulus is constructed by choosing a fixed-wavelength sinusoidal standing grating (parametrized by orientation and a spatial phase) randomly from a stimulus set. Stimuli are shown successively, each for 17 msec. The spike train of a visually responsive neuron is recorded and is correlated against the stimulus time series. The normalized correlation, P(θ, τ), is the probability that τ msec before a spike was produced, an image with angle θ was presented. The graph's left vertical scale is probability, whereas the vertical scale on the right, for the rightmost boxes only, is in units of circular variance. (a) Experiment (4Cα simple cell, 18 angles). (b) Model (16 angles). The rightmost boxes show circular variance CV[P(⋅, τ)] (see Eq. 4). The dashed CV[P] curve in b is that for an uncoupled model neuron, and it shows that feed-forward input by itself produces only a small reduction in CV in the RTC experiment.

In this paper, we address these issues of orientation selectivity through a network model of 4Cα that uses a more realistic cortical architecture than has been previously studied. The model consists of a small area (≃1 mm²) of input layer 4Cα, containing four “orientation hypercolumns” of excitatory and inhibitory neurons. Convergent feed-forward input from many LGN neurons sets up an orientation preference, laid out as pinwheel patterns, each with an orientation preference singularity at its center. The intracortical connectivity across the layer is isotropic, with axonal length scales for excitation exceeding those of inhibition. Through large-scale simulation, we find that our model can achieve good orientation selectivity for both steady-state (drifting grating) and dynamical (RTC) stimuli, even though these two types of stimulation place the cortex at very different “operating points.” Two consequences of the cortical architecture are: First, in the neighborhood of pinwheel centers, inhibition can be global in orientation coordinates, yielding greater selectivity, despite being shorter-range in cortical coordinates. Second, this correlation of selectivity with proximity to pinwheel centers contributes to the observed diversity in our model and suggests new physiological experiments.

Materials and Methods

A Neural Model.

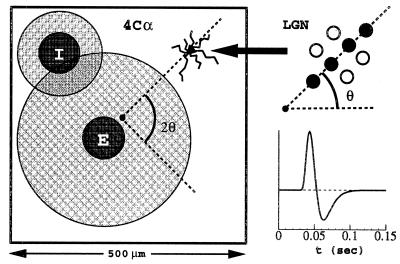
Our model, shown schematically in Fig. 3, is a two-dimensional layer of coupled excitatory (E) and inhibitory (I) integrate-and-fire (I&F) neurons. In the model, 75% of the neurons are excitatory, and 25% are inhibitory, in rough agreement with anatomical data (10). A neuron's membrane potential, v_{E(or I)}^j, is the fundamental variable. The superscript j = (j₁, j₂) indexes the spatial location of the neuron within the cortical layer. Membrane potential changes are induced by conductance changes. We specify several cellular biophysical parameters, using commonly accepted values (11): the capacitance C = 10⁻⁶ F⋅cm⁻², the leakage conductance g_R = 50 × 10⁻⁶ Ω⁻¹⋅cm⁻², the leakage reversal potential V_R = −70 mV, the excitatory reversal potential V_E = 0 mV, and the inhibitory reversal potential V_I = −80 mV.

Figure 3.

Schematic of a model layer 4Cα hypercolumn (Left), with axonal (gray circle) and dendritic (dark circle) arbor widths indicated for excitatory (E) and inhibitory (I) cells. The neuron along the ray at angle 2θ (emanating from the pinwheel center) in the cortex inherits its orientation preference on the basis of convergent input from a distribution of ON/OFF cells (Upper Right). The distribution's orientation at angle θ in the visual field sets the orientation preference. In this inset, the OFF cells are indicated by filled circles. The Lower Right graph shows the LGN temporal kernel G.

The spike-generation mechanism for an integrate-and-fire neuron is as follows: The voltage across the cell membrane is driven up and down by ionic currents. When the cell's voltage becomes more positive than the threshold v̄ = −55 mV, that time is recorded (the “spike time”), and the cell voltage is reset to v̂ = V_R (rest and reset potentials are taken as equal). Conductance changes are then induced in other neurons, relative to this spike time. Neurons' voltages evolve by the coupled system of differential equations which, after normalization in which only time t retains dimension, takes the form:

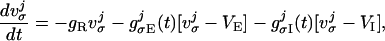1

where σ = E or I indexes excitatory or inhibitory neurons. In this equation, −2/3 ≤ v_E^j, v_I^j ≤ 1. (This normalization sets the spiking threshold v̄ to unity, the reset voltage v̂ to zero, V_E = 14/3, and V_I = −2/3.)

Conductances.

The time-dependent conductances (excitatory g_E/I,E^j(t) and inhibitory g_E/I,I^j(t) arise from the LGN input, from noise to the layer, as well as from the cortical network activity of the excitatory and inhibitory populations. They have the form:

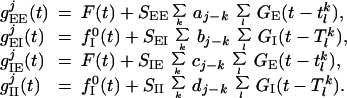2

Here t_l^k (T_l^k) denotes the time of the lth spike of the kth excitatory (inhibitory) neuron. The input conductances are F(t) = g_lgn(t; θ, k, φ) + f_E⁰(t), for excitation, and f_I⁰(t) for inhibition (described below). We describe next the visual stimuli we have studied, and the spatial and temporal pattern of LGN input to the cortex in the model.

Visual Stimuli.

The visual stimulus is a sinusoidal grating with intensity pattern I(x⃗, t) = I₀[1 + ɛ sin[k⃗⋅x⃗ − ωt + φ]]. Here k⃗ = k(cos θ, sin θ), with θ ∈ [−π, π) the orientation of the grating, φ ∈ [0, 2π) its phase, ω its drifting frequency, I₀ its intensity, and ɛ its contrast. We use two types of stimuli: (i) a drifting grating (ω > 0); and (ii) flashed, randomly oriented gratings, as used in the RTC experiments of Ringach et al. (3), for which ω = 0 and θ ∈ [0, π). Refreshed every 17 msec, each pattern is taken randomly and independently from a collection of patterns with N values of the orientation {θ = kπ/N, k = 1, ⋅⋅⋅, N} and M values of the phase {φ = k2π/M, k = 1, ⋅⋅⋅, M}.

LGN Response to Visual Stimuli.

In response to visual stimuli, LGN neurons produce spikes that impinge on 4C. Visual properties of macaque LGN neurons in the magnocellular layers are estimated from experimental studies (12, 13) as follows: LGN neurons have (i) no orientational selectivity; (ii) a center–surround receptive field; and (iii) a temporal impulse response of the center mechanism that increases to peak at approximately 40 msec, followed by a delayed undershoot that bottoms at approximately 60 msec; and (iv) this LGN temporal impulse response has zero integral.

Consistent with these experimental observations, our model represents the firing rate of the nth LGN neuron, caused by a stimulus I(x⃗, t), as

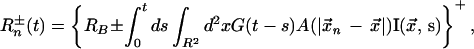3

where {R}⁺ = R, R > 0; {R}⁺ = 0, R ≤ 0. Here R_n⁺ represents an “on-center” and R_n⁻, an “off-center,” x⃗_n denotes the center of the receptive field of this neuron, and x⃗ is the coordinate of the visual plane. To mimic the findings i and ii above, A(x⃗) is taken as a difference of Gaussians with parameters like those used in other recent models (5, 9). To mimic findings iii and iv for the magnocellular input to 4Cα, the response function G(t) approximates measured zero-integral LGN cell kernels (12, 13).

Convergence of LGN Output into 4C.

Consider a single neuron in the input layer 4Cα and a set of LGN neurons (call it C) whose output converges to this cortical neuron. A typical spatial distribution of such ON/OFF centers is shown in Fig. 3 (14). If X⃗ denotes the center of the receptive field of this cortical neuron, the centers of the receptive fields of the LGN neurons convergent to it are all located near X⃗. Experimental evidence suggests that the total number of convergent LGN neurons in C should be approximately 20, and in the model we use 17 (14). The orientation (and spatial phase) preference of each cortical neuron is encoded in the model through the locations and layouts of the assembly of LGN inputs. The summed LGN input to a cortical cell is thus:

Our model does not currently incorporate in the LGN input any mean drift in receptive field center nor any diversity in the arrangement of ON/OFF subregions. To mimic spatial phase shifts associated with varying ON/OFF subregion arrangements and receptive field location, we choose X⃗ randomly, and independently, for each cortical neuron.

Note that, for drifting gratings, there is no orientation selectivity of the LGN input to each cortical neuron, if time-averaged input rate is the measured response variable (2, 5). Nevertheless, as discussed below in Results, the temporal modulation of the LGN input is tuned, and this is what confers the orientation preference on the cortical cells in the model.

Pinwheel Centers and the Orientation Map.

Optical imaging measurements (15–18) show in superficial layers 2/3, “pinwheel” patterns of orientational preference on the cortex; neurons of like-orientation preference reside along the same radial spoke of a pinwheel, with the preferred angle sweeping through 180° as center of the pinwheel is encircled. These pinwheels tile the cortical layer, with their centers located (statistically) near the centers of ocular dominance columns, separated from each other by approximately 500 μm (approximately the width of the ocular dominance columns).

While imaging shows these pinwheel patterns in the outer layers, we assume that there is a correlated structure in the LGN input to layer 4C, and we build a pinwheel structure into the model by tying the preferred orientation angle of a given 4C neuron to its location in the layer with respect to the pinwheel pattern. In the model, we tile the layer periodically with pinwheels. Four pinwheels, chosen with alternating “handedness,” are placed upon a square, and then extended periodically. This periodic configuration permits rapid evaluation of cortical interactions through fast Fourier transforms.

Random Inputs.

The terms f_E⁰(t) and f_I⁰(t) in Eq. 2 are random inputs, excitatory and inhibitory, respectively, that represent input to layer 4C neurons from layer 6 neurons and other sources of excitation or inhibition. These stochastic terms were chosen so that the spike firing statistics of neurons in the model would resemble those seen in V1 neurons (19).

Cortico–Cortical Coupling.

The kernels (a, b, c, d)_j–k, in Eq. 2 represent the strength of spatial coupling between neurons. Their length scales are based on neuroanatomy. While there is evidence that long-range connections (>1000 μm) can be anisotropic and orientation selective, the local dense connections (<500 μm) appear spatially isotropic (20). Here we assume this local isotropy, taking the density of these local connections as Gaussians:

where h denotes a spatial discretization. We use anatomical data to estimate the coupling lengths L_σσ_′. This includes population stainings (orthograde and retrograde) (21), and individual neuron stainings (21–27). These anatomical measurements classify distinct types of neurons and measure the spatial extent (both local and long-range) of their axonal and dendritic arbors. From these measurements we estimate the mean 4Cα local coupling lengths: r_{E and I}^D ≃ 50 μm, r_E^A ≃ 200 μm, r_I^A ≃ 100 μm, where r_{E(or I)}^D, r_{E(or I)}^A denotes the mean radii of the excitatory (or inhibitory) dendritic and axonal arbors. The interaction radii are then given naturally by L_σσ′ = , or L_EE ≃ L_IE ≃ 200 μm, L_EI ≃ L_II ≃ 100 μm. Thus, the longest space scales arise from the axonal arbors of the excitatory (not inhibitory) neurons.

The temporal kernels G_σ(t) model the time course of synaptic conductance changes in response to arriving spikes from the other neurons. The cortical temporal kernels are of the form

where H(t) is a unit step function. The time constants are based on experimental observations (ref. 11, and A. Reyes, personal communication). The time to peak for excitation (3 msec) is shorter than that for inhibition (5 msec). In addition, based on recent experimental findings (B. Connors, personal communication), we add a second, longer, time-course of inhibition (≈30 msec in duration).

Synaptic Weights.

In Eq. 2 all cortical kernels have been normalized to have unit integral; hence, the parameters S_EE, S_EI, S_IE, and S_II label the strength of interaction and represent synaptic strengths. They are treated as adjustable parameters in the model. In the model reported here, the strength vector (S_EE, S_EI, S_IE, S_II) was set to be (0.8, 7.6, 1.5, 7.6). The effect of this choice of synaptic weights can be estimated most directly by observing the synaptic conductances of model neurons and comparing them to the leakage conductance (set to 50 sec⁻¹), plus the (random) background conductances, with peak values of 200 sec⁻¹. In these units, the peak LGN conductance during stimulation reaches values of 180 sec⁻¹; the peak cortico–cortical excitatory conductance reaches 60 sec⁻¹; and the peak inhibitory conductance reaches values of 650 sec⁻¹. This choice of synaptic strengths made the model stable and filled with orientation-tuned simple cells. It also led to high membrane conductances during stimulation.

Results

Orientation Selectivity.

Fig. 1b shows orientation tuning curves for sample neurons from the model, in response to a grating stimulus drifting at 8 Hz. Also shown is the feed-forward tuning curve of an uncoupled neuron, obtained by shutting off all cortical interactions. These tuning curves from the model should be compared with those from experiment, shown in Fig. 1a.

The response of a neuron uncoupled from the network (also shown in Fig. 1b) is very weakly selective for orientation. We term this the feed-forward case because the visual driven input to the cortical cell is only from the LGN. While the time-averaged input from a sum of LGN cells is untuned for orientation (2, 5), the observed feed-forward selectivity arises from the cortical cell's leaky integration of the input's broadly tuned temporal modulation, background noise, and spike thresholding. This only weakly sharpens the cortical response (see also ref. 28).

In the present model there is no diversity in feed-forward responses. While orientation preference changes from neuron to neuron, forming the pinwheel spatial patterns, the selectivity in the absence of cortical coupling is identical for every neuron.

In the presence of cortical coupling, the tuning curves in Fig. 1b show that significant sharpening and diversity occur in the model. This takes place with recurrent connections whose spatial arbor sizes are consistent with anatomical observations (21–27, 29, 30)—with the axons of excitatory neurons possessing the largest local arbors.

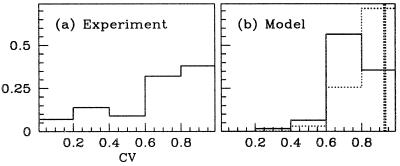
The diversity in orientation selectivity emerges from the cortico–cortical interactions, and its presence is consistent with experimental data. This diversity is quantified in Fig. 4. There, the degree of selectivity is measured through the CV of the (time-averaged) firing rate m_j(θ) of the jth neuron, as in ref. 28:

4

Sharply tuned neurons have CVs near 0, whereas broadly tuned neurons have CVs near 1. Fig. 4 shows these data for the model (b) and for a population of 42 neurons in 4Cα available from experiment (a). In the model, the CV of neurons in the absence of cortical coupling is 0.9 (thick dashed line in b). Thus, due solely to cortical interactions, the distribution of CVs over the population shows considerable diversity. The model's distribution of CV is not as diverse as in experiment, but we found that adding variability in the pattern of spatial convergence of the LGN input could produce more broadening of the CV histogram. The histogram for the inhibitory population shows also that the model's inhibitory neurons are on average more broadly tuned than the excitatory.

Figure 4.

Histogram (fraction of total population) of tuning curve CVs. (a) Experiment, 42 4Cα neurons (presumably excitatory). (b) Model, showing both excitatory (solid) and inhibitory (dotted) neurons. (Neurons with low peak firing rates are discarded.) Also shown is the CV of the feed-forward response (thick dashed vertical line).

Spatial Distribution of Selectivity.

The model shows intriguing spatial distributions of firing and selectivity, relative to the location of the neurons within the pinwheel pattern. Fig. 5 shows a color-coded two-dimensional representation of average firing rate in response to a drifting grating, and the CV[m_j] of excitatory neurons. The firing rate distribution shows higher activity near the pinwheel centers. The spatial distribution of CV shows typically higher orientation selectivity near the pinwheel centers. While this accounts for a large part of the observed diversity, there are other well-tuned neurons scattered across the cortex. Similar observations hold for the inhibitory neuron population.

Figure 5.

Spatial distribution of response properties across the model's four hypercolumns. (The upper left quadrant is that hypercolumn depicted in Fig. 3.) The left two hypercolumns show the time-averaged firing rate of the excitatory population in response to a grating drifting at angle θ = 45° (averaged over 50 cycles). The lines emanating from pinwheel centers label orientation columns at 0° (green), 45° (red), 90° (yellow), and 135° (blue). The right two hypercolumns show the spatial distribution of circular variance, CV[m_j]. The scale on the left is in spiltes per second, and on the right is the range [0, 1] of the CV.

RTCs.

Fig. 2b shows RTC data for a model neuron. The figure shows P(θ, τ), the probability that τ time units before a spike is fired, visual stimulation at angle θ occurred. The parameters used in these RTC simulations are identical to those in the drifting grating simulations described above. There is qualitative agreement between the model and experiment—in particular, a simple response with a single maximum at a preferred angle θ_p, which grows and then relaxes. Also shown is the CV[P], which captures the temporal course of selectivity—a latency, followed by sharpening, then relaxation. Again experiment and model are roughly consistent, although this particular model neuron shows a second, lesser, peak in CV (sometimes observed in experiment). Minimum CVs for RTC experiments in the 0.6 range are observed in the model as in the cortex.

Included in Fig. 2b is CV[P] for an uncoupled model neuron, which shows the weak dynamical selectivity of feed-forward response (cf. ref. 28). The CV for this neuron is near 1, meaning it is unselective for orientation. This implies that the orientation selectivity seen in the RTC simulations is a consequence of cortico–cortical interactions.

Discussion

This paper describes the performance of a neuronal network model of the input layer 4Cα of macaque V1. This model differs from others in the literature in several ways. (i) It is designed largely from data for the anatomy and physiology of layer 4Cα of macaque (i.e., length scales and patterning of connectivity, and pinwheel centers). (ii) It uses cortical coordinates rather than idealized coordinates as in “ring models” (7, 8, 28) or “near-ring models” (9), whose coordinate labels are angles of orientation preference, rather than cortical locations within the layer. (iii) It has only short-range local inhibition, which is consistent with anatomical data, rather than an inhibition which is explicitly long-range in orientation preference, as is standard for many models (7–9, 31). (iv) It uses membrane potential, driven by synaptic conductances, as the fundamental variables, rather than activities or mean firing rates (7, 8, 32), or a probabilistic “population-density” representation (31, 33, 34). (v) Its local coupling architecture is not long-range, anisotropic, or “orientation specific” (35)—it is local and isotropic. (vi) As a large-scale network model, it necessarily consists of point neurons rather than multicompartmental models (36–38). The model most similar to ours, in attempting to account for orientation selectivity with a realistic cortical network, is that of Troyer et al. (5). The main difference between their model and ours lies in the spatial pattern of cortico–cortical connectivity. Theirs is phase and orientation specific, whereas ours is isotropic.

Our neuronal network model obtains agreement with physiological experiments with regard to (i) sharpening of orientation selectivity, (ii) diversity in orientation selectivity, and (iii) dynamical characteristics of orientation selectivity. Requiring that the model account for physiological experiments, while also following the neuroanatomy and neurophysiology of cortical cells, places demanding performance criteria on the model. For instance, requiring sharpening of orientation selectivity with short-range monosynaptic inhibition, and agreement with RTC experiments, severely constrains the values of the free parameters in the model. In most models of orientation selectivity, sharpening is achieved by a direct long-range monosynaptic inhibition, usually in an effective angle coordinate. In macaque 4Cα, a long-range inhibition in cortical coordinates is not supported by anatomical evidence, although, as our model suggests, a long-range inhibition in angle may arise near pinwheel centers.

Orientation Selectivity, Diversity, and Pinwheels.

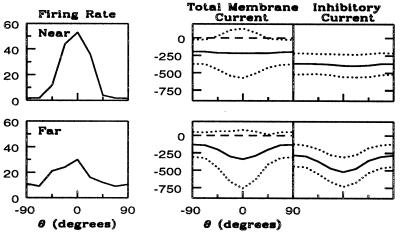
An intriguing prediction of the model is the spatial distribution of CVs in the steady-state experiments (with drifting gratings as stimuli). The model shows CVs near pinwheel centers smaller than those away (Fig. 5). Analyzing this characteristic reveals how the model achieves its selectivity and part of its diversity. Fig. 6 shows the orientation tuning curves firing rates and for intracellular currents for two representative excitatory neurons, one near and one far from the pinwheel center. The far neuron's tuning curve has a high CV because of the relatively high response at angles orthogonal to its preferred orientation. The near neuron's orientation tuning curve has a lower CV because its response drops to near zero at angles orthogonal to preferred, and its peak response is higher. In the model, the orientation selectivity is initiated by the temporal modulation of the LGN current about its mean, and the differences in selectivity between these two neurons is accounted for by the differences in the mean inhibition as a function of orientation.

Figure 6.

Differences underlying selectivity for an excitatory neuron near (Upper) and another far (Lower) from a pinwheel center. (Left) Average firing rate as a function of θ. (Center) Time-averaged current at threshold (center curve), plus and minus 1.5 standard deviations (dotted curves), as a function of θ. (Right) Time-averaged inhibitory network contributions, plus and minus 1.5 standard deviations, to this current.

First, consider the tuning curve for total current. The mean current (solid line), and the mean ± 1.5 standard deviations (the two dotted lines), are plotted vs. orientation θ. The near, more selective, neuron's mean + 1.5 standard deviation exceeds the threshold for spike firing (long-dash line) over a much narrower range of angles than does the far neuron's. This is the underlying cause of the sharper selectivity. But why is the total current of the near neuron more tuned? As is observed from the separation of the standard deviations in the two graphs (near and far neurons), the modulation of the total current (from LGN and cortico–cortical interactions) is approximately the same for the two neurons. Therefore, the differences in selectivity must come from differences in tuning of the mean current.

The different patterns of mean inhibitory input across θ is the primary reason for differences in orientation selectivity and sharpening for the near and far neurons. This is seen in Fig. 6 Right. The near neuron receives mean inhibition that is essentially independent of θ, whereas the far neuron receives inhibition that depends on θ and is maximal at its preferred orientation. The reason underlying this difference is that inhibitory inputs arrive solely from other cortical neurons. For the neuron near the pinwheel center, the interaction length for inhibition (L_II and L_EI) extends over all orientations; thus, its sharpening is achieved by a global inhibition in orientation. This is not true for the far neuron. Its inhibitory inputs are from cortical neurons whose orientation preference is nearly the same as its own. In this case inhibition is not global in orientation, and thus is less effective in sharpening the excitation's broad selectivity.

The experiments of Maldonado et al. (18) suggest that the degree of selectivity is not strongly correlated to distance from a pinwheel center. However, their data from cat cortex are not correlated directly with the laminar structure. This makes it difficult to compare their experimental results with the model's predictions. Future experiments on the spatial distribution of CV in macaque V1 would provide a strong test of our model.

High Conductances.

In our model, cortico–cortical interactions are dominated by inhibition, and the membrane conductances are high during stimulation, mainly because of the inhibition. This high-conductance regime follows from two constraints the model must satisfy if it is to simulate the biological cortex adequately—both (i) orientation selectivity and (ii) peak firing rates must agree with physiological observations. From the results of a series of numerical experiments, we have observed that these two constraints are met as follows: To obtain adequate orientation selectivity, a significant level of inhibition is required. To obtain adequate firing rates, the excitatory conductance must overcome both this inhibition and the leakage conductance. In addition, the excitatory and inhibitory currents must be roughly balanced, for the voltage not to be driven above threshold all of the time, or to dwell near rest all of the time. Such a balance of currents seems consistent with experimental data (39). This balance of currents immediately implies that the inhibitory conductance must be higher than the excitatory (g_EV_E ≃ g_I|V_I| ⇒ g_I ≃ (V_E/|V_I|)g_E = 7g_E). The high (inhibitory) conductance regime at which the model operates is also supported by recent experiments: large inhibitory conductances, evoked by visual stimuli, have been observed experimentally in visual cortical cells (40, 41).

Dynamics.

In the RTC simulations, orientation selectivity is observed and is qualitatively consistent with that measured in 4Cα cells (3). By design, the RTC experiments (3) caused most cortical cells to be persistently excited above threshold. A selectivity mechanism based on the sharpening of broad feed-forward inputs by a fixed threshold would likely give much poorer selectivity in the RTC experiments than in the steady-state experiments (as seen in the responses of the uncoupled model neuron; see Figs. 1b and 2b). But this is not what is observed, either in experiment or in the model network. In the model network, the orientation selectivity occurs through a dynamical thresholding that is set through an interplay between LGN excitation, cortico–cortical excitation, and cortico–cortical inhibition. Also, in the RTC simulations the model gives a correlation between the degree of selectivity and the proximity to pinwheel centers—similar to that seen in the steady-state simulations. This is another prediction of the model that could be tested experimentally.

Abbreviations

LGN

lateral geniculate nucleus

RTC

reverse time correlation

CV

circular variance