CELL SIGNALLING DYNAMICS IN TIME AND SPACE

PREFACE

The specificity of cellular responses to receptor stimulation is encoded by the spatial and temporal dynamics of downstream signalling networks. Computational models provide insights into the intricate relationships between stimuli and responses and reveal mechanisms that enable networks to amplify signals, reduce noise and generate discontinuous bistable dynamics or oscillations. These temporal dynamics are coupled to precipitous spatial gradients of signalling activities, which guide pivotal intracellular processes, but also necessitate mechanisms to facilitate signal propagation across a cell.

INTRODUCTION

Cells respond to a multitude of external cues using a limited number of signalling pathways activated by plasma membrane receptors, such as G protein-coupled receptors (GPCRs) and receptor tyrosine kinases (RTKs). These pathways do not simply transmit, but process, encode and integrate internal and external signals. In recent years, it has become apparent that distinct spatio-temporal activation profiles of the same repertoire of signalling proteins result in different gene activation patterns and diverse physiological responses^1-3. Thus, pivotal cellular decisions, such as cytoskeletal reorganization, cell cycle checkpoints and apoptosis (active cell death), depend on the precise temporal control and relative spatial distribution of activated signal-transducers.

Signalling by RTKs has long been in the limelight of scientific interest owing to its central role in the regulation of embryogenesis, cell survival, motility, proliferation, differentiation, glucose metabolism, and apoptosis^4-6. Malfunction of RTK signalling is a leading cause of major human diseases that range from developmental defects to cancer, chronic inflammatory syndromes and diabetes^6-8. Upon stimulation, RTKs undergo dimerization (for example, the epidermal growth factor (EGF) receptor) or allosteric transitions (insulin receptor) that results in activation of the intrinsic tyrosine kinase^4,9. Subsequent phosphorylation of multiple tyrosine residues transmits a biochemical message to a number of cytoplasmic proteins, triggering their mobilization to the cell surface^4,10. The resulting cellular responses occur through complex biochemical circuits of protein interactions and covalent-modification cascades.

An emerging picture of interconnected networks has replaced the earlier view of discrete linear pathways that relate extracellular signals to specific genes, raising questions about the specificity of signal-response events. In fact, the protein complement that mediates signal transduction is similar for all RTK pathways¹¹. Both GPCRs and RTKs activate kinase/phosphatase cascades, such as mitogen-activated protein kinase (MAPK) cascades, that turn on nuclear transcription factors. For any individual receptor pathway, there is no single protein or gene responsible for signalling specificity. Rather, specificity is determined by the temporal and spatial dynamics of downstream signalling components. The classical example is the distinct biological outcome of PC12 cell stimulation with EGF and nerve growth factor (NGF). EGF-induced transient MAPK activation results in proliferation, whereas a sustained MAPK activation by NGF changes the cell fate and induces differentiation^1,2. However, the factors controlling the kinetics of MAPK cascades are intricate. MAPK cascades can generate bistable dynamics (where two stable “On” and “Off” steady states coexist), abrupt switches, and oscillations^12-14, and their responses depend dramatically on subcellular localization or recruitment to scaffolds^15,16.

The purpose of this review is to survey dynamic and spatial aspects of intracellular communication. Wherever possible, I outline general principles by which chemical transformations and Brownian motion of myriad signalling molecules create coordinated behaviour in time and space and generate stimulus-specific responses. I explain how the timing, amplitude and duration of signalling responses are elucidated by exploiting mechanistic systems-level models that help unravel crucial interactions and kinetic factors. Extremely complex dynamic behaviours are shown to arise from simple basic modules, adding to the repertoire of specific signalling outcomes. A number of excellent reviews have focused on computational functions of signalling networks, offering an intriguing glimpse into the parallels between biological and human-made control systems^17-20. However, there are important distinctions between electronic and living cell circuitry, which are illustrated by examining the spatial dynamics of intracellular communication. This analysis has lead to unexpected predictions, including intracellular gradients of signalling activities^21,22 and the recognition that diffusion alone cannot account for effective propagation of phosphorylation signals terminated by phosphatases^23,24. The transfer of information over intracellular distances of more than a few micrometers requires facilitated transport mechanisms, including movement of phosphorylated kinases/signalling complexes on scaffolds and endosomes driven by molecular motors and travelling waves of phosphoproteins^23,25-28.

TEMPORAL DYNAMICS OF SIGNALLING NETWORKS

Mechanistic models can reveal crucial regulations

Since the 1990s, modelling has emerged as a novel tool to handle the rapidly growing information on the molecular parts list and the overwhelmingly complex interaction circuitry of signalling networks^29-41. These mechanistic models aspired to create in silico replicas of cellular networks with the initial purpose of understanding the temporal dynamics of signalling responses. General principles of model building are illustrated exploiting models of the EGF receptor (EGFR) network (BOX 1). Importantly, EGFR is not only the best studied RTK, but together with other members of the ErbB family plays a pivotal role in carcinogenesis^7,8,42,43. Phosphorylation of a number of tyrosine residues on EGFR and binding and activation of EGFR adapter and target proteins (Supplementary Table S1) initiates signal propagation through multiple interacting branches including the phospholipase C-γ (PLCγ), phosphatidylinositol 3-kinase (PI3K)/Akt and extracellular-signal-regulated kinase (ERK)/MAPK pathways (see EGF network diagrams in reference⁴⁴ and at: http://www.grt.kyushu-u.ac.jp/spad/pathway/egf.html, http://www.biocarta.com/pathfiles/egfPathway.asp). Merely qualitative arguments fall short of providing insights into the complex temporal responses of a variety of downstream EGFR targets, and reliable and testable computational models are required to predict signalling dynamics^45-47.

BOX 1. Mechanistic models: keeping track of molecular processes.

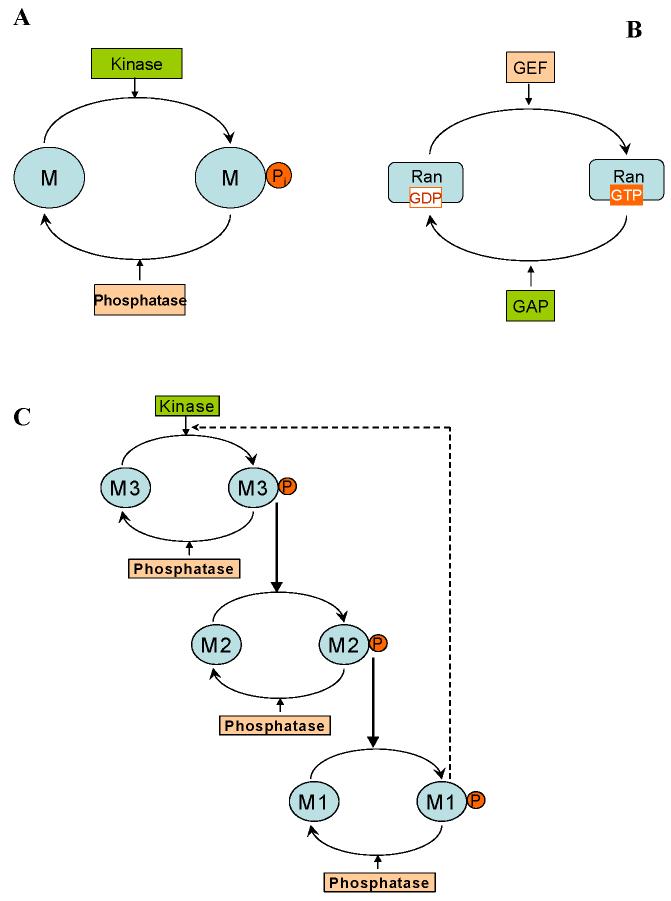
The temporal dynamics of signalling networks is described by ordinary differential equations, which are known as chemical kinetics equations¹⁰³ and are derived similarly to the Michaelis-Menten equation, familiar to any biologist. The derivation begins with listing all chemical transformations thereby providing a kinetic scheme of a pathway. Figure, part A shows a simplified scheme of the signalling routes emanating from the epidermal growth factor receptor (EGFR), including the Shc, Grb2-SOS, GAP and phospholipase C-γ (PLCγ) signalling branches, and the RasGDP/RasGTP circuit (phosphorylated proteins are indicated by added “P” after protein name, R is EGFR, molecules within complexes are abbreviated, and the designations are given in Supplementary Table S2). The scheme is translated into differential equations, one for each time-dependent molecular species. The rate of the concentration change is the sum of the reaction rates producing a given species minus the sum of consuming rates. Numerical integration (simulations) gives the time-course of the concentrations (see figure, parts B and C where EGF-induced responses were simulated using the scheme shown in part A^49,104).

Comparison of simulations with data helps generate novel hypotheses and often instigates an overhaul of a model. Data obtained from isolated hepatocytes (black squares and red triangles, see figure, parts B and C) demonstrate that despite the constant level of EGF (10nM), phosphorylation of EGFR and PLCγ is markedly transient (with the peaks reached within the first 15 seconds and the low pseudo-stationary levels within few minutes), whereas phosphorylation of Shc increased almost monotonically^30,105. The mechanistic model elucidates that the transient time-course of EGFR phosphorylation arises from the protection of phosphotyrosine residues against phosphatases, whilst these residues are occupied by an adaptor/target protein. Transient patterns of tyrosine phosphorylation of PLCγ are explained by the slow dissociation of the PLCγ-phosphatase complex^30,104. In fact, the existence of such complexes was reported¹⁰⁶. Hypotheses generated by computational models have a certainty and precision, furthering our understanding of signalling dynamics. A variety of software tools can assist in quantitative modelling^{56,58,107-109}, and several databases of biological models have been developed, offering an interesting environment to generate and test novel hypotheses by using a computer keyboard^110-112.

The first mechanistic model of the EGFR network was published in 1999 and explained the temporal dynamics of signalling responses in liver cells stimulated with EGF³⁰. Interrogation of this model generated a number of hypotheses and counterintuitive predictions (BOX 1). A particularly surprising prediction was that EGFR-mediated phosphorylation of the Src homology and collagen domain protein (Shc) would decrease its binding affinity and facilitate Shc dissociation from the receptor. EGFR phosphorylates Shc on Tyr317 located within the central collagen-homology linker region, distant from the N- and C-terminal domains that mediate binding to EGFR. The modular structure underlying protein interactions¹⁰ might imply that phosphorylation of residues outside the Shc binding domains should not influence the affinity. However, molecular dynamics simulations revealed that Tyr317 phosphorylation significantly affects collective motions of Shc domains, increases structural rigidity of the linker region and decreases the flexibility of the binding domains, significantly reducing their capacity to interact with EGFR⁴⁸. These findings corroborated the prediction of the kinetic model³⁰ and favoured a broader view that the affinities of many RTK-binding partners (for example, the p85-subunit of PI3K) might decrease following RTK-mediated phosphorylation. In recent years, a number of EGFR pathway models with predictive and explanatory power have been developed. These models addressed various aspects of EGFR-mediated signalling, including (1) transient versus sustained responses of the MAPK cascade “gatekeepers” (small GTPases Ras and Rap1) to various growth factors^32,41,49, (2) the non-linear dependences of the amplitude of MAPK activation on the EGFR numbers³⁴, (3) autocrine positive-feedback loops⁵⁰, (4) cross-talk between the MAPK and Akt pathways³⁷, and (5) integration of EGFR signalling from the plasma membrane and the endosomes⁵¹.

Challenges in mechanistic modelling

Perhaps, the most significant challenges that face mechanistic modelling are (i) the lack of quantitative kinetic data and (ii) the combinatorial increase in the number of emerging distinct species and states of the protein network being simulated^38,52. The first challenge is beginning to be addressed by nascent quantitative proteomics of posttranslational modification^53,54.The second challenge arises because RTKs and many signalling proteins possess multiple docking sites, serving as scaffolds that generate a variety of heterogeneous multi-protein complexes, each involved in multiple parallel reactions. Even initial steps in signal transduction can generate hundreds of thousands of distinct states³⁸, referred to as “micro-states” of a network⁵⁵. Because of the exceedingly high numbers of micro-states, previous models merely ignored this combinatorial variety and simulated only a small part of feasible states and reactions. Several methods of handling this problem have been proposed, all based on specifying rules that automatically generate species and reactions. Programs implementing these methods include StochSim⁵², BioNetGen^56,57, and Moleculizer⁵⁸. The entire micro-state network can either be generated in advance for deterministic simulations^56,57, or the species and reactions can be generated as needed during a stochastic simulation^52,57,58.

An alternative “domain-oriented” approach rigorously simplifies or approximates a mechanistic micro-state picture in terms of “macro-states”, such as the phosphorylation levels and the fractions occupied by binding partners^55,59. A necessary prerequisite is the presence of domains/sites that do not allosterically influence each other. This domain-oriented framework drastically reduces the number of states and differential equations to be solved and, therefore, the computational cost of both deterministic and stochastic simulations.

Cycle and cascade motifs

A universal motif found in cellular networks is the cycle formed by two or more interconvertible forms of a signalling protein, which is modified by two opposing enzymes, such as a kinase and phosphatase for phosphoproteins, or a guanine nucleotide exchange factor (GEF) and GTPase–activating protein (GAP) for small G-proteins (FIG.1). Cascades of such cycles form the backbone of most signalling pathways that propagate external stimuli from the membrane to the nucleus or other distant targets. The well-known property of these cycles is “ultrasensitivity” to input signals, which occurs when the converting enzymes operate near saturation⁶⁰. Depending on the degree of saturation, the response of either interconvertible form ranges from a merely hyperbolic to an extremely steep sigmoidal curve. Sequestration of a signalling protein by converting enzymes significantly decreases sigmoidicity of responses. Likewise, ultrasensitivity can disappear if converting enzymes are inhibited or saturated by their products⁶¹. By contrast, multi-site phosphorylation (following a distributive, multi-collision mechanism⁶²) was shown to increase output-input sensitivity dramatically, resisting the sequestration effect and leading to switch-like responses^62-65. Multi-site protein modification as a variation of the basic cycle motif is repeatedly used in nature, and this has pivotal ramifications for signalling dynamics^62-65.

FIG. 1.

Universal motifs of cellular signalling networks. A. One-site phosphorylation cycle. The protein M is phosphorylated by a kinase to yield the phosphorylated form M_p, which is dephosphorylated by an opposing phosphatase. B. A cycle of a small GTPase (Ran). A guanine nucleotide exchange factor (GEF) catalyzes the transformation of an inactive guanosine diphosphate (GDP)-bound form (Ran-GDP) into an active guanosine triphosphate (GTP)-bound form (Ran-GTP). A GTPase–activating protein (GAP) is the opposing enzyme that catalyzes the reverse transformation. C. A cascade of cycles. Negative feedback provides robustness to noise, increasing resistance to disturbances inside the feedback loop, but brings about oscillations if it is too strong and the cascade is ultrasensitive¹²,²⁰. Positive feedback greatly increases the sensitivity of the target to the signal and may also lead to bistability and relaxation oscillations¹²,¹⁸,⁴⁶,⁷².

Feedback loops induce complex dynamics

An increase in the number of interconnecting cycles in a cascade^66,67 or positive feedback further increases the sensitivity of the target to the input signal. The notion of feedback is one of the most fundamental concepts in biological control. Positive feedback amplifies the signal, whereas negative feedback attenuates it. However, feedback loops not only change steady-state responses, but also favour the occurrence of instabilities. When a steady state becomes unstable, a system can jump to another stable state, start to oscillate or exhibit chaotic behaviour. Positive feedback can cause bistability¹⁴, but also either alone or in combination with negative feedback, it can trigger oscillations, for example, the Ca²⁺ oscillations arising from Ca²⁺-induced Ca²⁺ release⁴⁶ and the cell cycle oscillations^68,69. Such positive-feedback oscillations generally do not have sinusoidal shapes and are referred to as relaxation oscillations, operating in a pulsatory manner: a part of a dynamic system is bistable, and there is a slow process that periodically forces the system to jump between “Off” and “On” states, generating oscillations (BOX 2).

BOX 2. Complex temporal dynamics in a nutshell.

Exotic dynamics emerges from simple, basic signalling motifs. Known examples include bistability arising from multi-site phosphorylation in a single protein cycle or from positive or double-negative feedback in a two-cycle cascade, and negative-feedback oscillations in a cascade with at least three cycles^12,18,65. Here I show two additional basic signalling modules that bring about bistable and oscillatory dynamics. A single-site phosphorylation cycle generates only ultrasensitive, but not discontinuous switches. Yet, positive feedback from the phosphorylated form (M_p) to its kinase can render this cycle into a bistable switch. Assuming the kinase (v_kin) and phosphatase (v_phos) rates follow Michaelis-Menten kinetics (including the activation term), this system is described by a remarkably simple equation,

$$\begin{array}{c}\frac{{\mathit{dM}}_p}{\mathit{dt}}=v_{\mathit{kin}}-v_{\mathit{phos}}=\frac{k_{\mathit{kin}}^{\mathit{cat}}{E}_{\mathit{kin}}M}{(K_{m1}+M)}\cdot \frac{(1+{\mathit{AM}}_p∕K_a)}{(1+M_p∕K_a)}-\frac{k_{\mathit{phos}}^{\mathit{cat}}{E}_{\mathit{phos}}{M}_p}{(K_{m2}+M_p)},\\ M=M^{\mathit{tot}}-M_p\end{array}$$ (1)

Here, the products of the catalytic constants and enzyme concentrations $k_{\mathit{kin}}^{\mathit{cat}}{E}_{\mathit{kin}}$ and $k_{\mathit{phos}}^{\mathit{cat}}{E}_{\mathit{phos}}$ are the maximal rates of the kinase and phosphatase, K_m1, K_m2, K_a and A are kinetic constants, M^tot is the protein abundance. In a wide parameter range, there are three distinct solutions to the steady-state relationship v_kin = v_phos . The low and high M_p concentrations correspond to stable “Off” and “On” states, whereas the intermediate state is unstable. The steady-state M_p dependence on the input kinase (phosphatase) activity (known as one-dimensional bifurcation diagram) displays hysteresis, the hallmark of bistability (figure, part A). Likewise, phosphatase rate inhibition by M_p , phosphatase rate activation or kinase rate inhibition by M can produce a similar bistable switch (Supplementary Table S3).

If, in addition, the phosphorylated form M_p inhibits transcription/translation of the kinase protein or promotes its degradation (Supplementary Eqs.S2-S3 and Table S3), thereby creating negative feedback, the universal cycle becomes a relaxation oscillator (figure, part B),

$$\frac{{\mathit{dE}}_{\mathit{kin}}}{\mathit{dt}}=v_{\mathit{kin}}^{\mathit{synth}}-v_{\mathit{kin}}^{\mathrm{deg}}=V_{\mathit{kin}}^0\frac{(1+M_p∕K_I)}{(1+I\cdot M_p∕K_I)}-k_{\mathit{kin}}^{\mathrm{deg}}{E}_{\mathit{kin}},I>1\cdot$$ (2)

Likewise, alternative negative feedback design where M_p activates the phosphatase protein transcription/translation (or inhibits its degradation) also generates relaxation oscillations (figure, part C),

$$\begin{array}{c}\frac{{\mathit{dE}}_{\mathit{phos}}}{\mathit{dt}}=v_{\mathit{phos}}^{\mathit{synth}}-v_{\mathit{phos}}^{\mathrm{deg}}=V_{\mathit{phos}}^0\frac{(1+A_{\mathit{dp}}{M}_p∕K_d)}{(1+M_p∕K_d)}-k_{\mathit{phos}}^{\mathrm{deg}}{E}_{\mathit{phos}},\\ A_{\mathit{dp}}>1\end{array}$$ (3)

This negative feedback might result from changes in mRNA or protein turnover, immediate-early gene expression, or de novo synthesis of transcription factors regulating protein levels. Different scenarios will correspond to different time scales and affect the period and shape of oscillations.

While positive feedback endows signalling cascades with the potential for bistability and relaxation oscillations, negative feedback can bring about adaptation and robustness to parameter variations within the feedback loop (for instance, caused by genetic variability)^20,70. Although negative feedback can stabilize the cascade output when demand fluctuates, above certain threshold strength, this feedback induces damped or sustained oscillations. These oscillations are caused by the time delay within the negative feedback loop and require some degree of ultrasensitivity of individual cascade cycles¹². Notably, relaxation oscillations and negative-only feedback oscillations differ in their robustness to noise⁷¹ and generally exhibit different shapes and control of the amplitude and period.

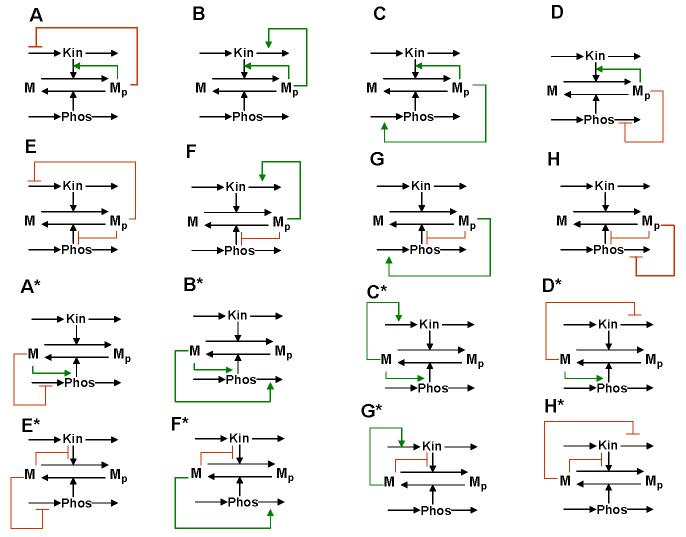
Intricate dynamic properties have been traditionally associated with cascades of cycles^69,72, yet even single cycles can exhibit complex dynamics, such as bistability and relaxation oscillations (BOX 2). For instance, multi-site protein modification not only increases ultrasensitivity, but potentially leads to bistability⁶⁵. The reported kinetic data allow us to suggest that a single MAPK cascade level, e.g., the dual phosphorylation ERK cycle, can exhibit bistability and hysteresis within a certain parameter range⁶⁵; this prediction is awaiting experimental verification. A simple one-site modification cycle can turn into a bistable switch by four different regulatory mechanisms, in which one of the protein forms stimulates its own production or inhibits its consumption, thereby creating a destabilizing control loop (BOX2 and Supplementary Table S3). An extra (stabilizing) feedback loop that affects the rate of synthesis or degradation of a converting enzyme can render this bistable switch into a relaxation oscillator (the resulting 32 distinct feedback designs that can give rise to oscillations are shown in FIG.2 and Supplementary FIG.S1).

FIG. 2.

Feedback designs that can turn a universal signalling cycle into a bistable switch and relaxation oscillator. Simple cycle can turn bistable in four distinct ways; either M_p or M stimulates its own production (positive feedback) by product activation or substrate inhibition of the kinase or phosphatase reactions. Each of the four rows of feedback designs correspond to a different bistable switch, provided that the kinase and phosphatase abundances are assumed constant and only single feedback (within the M cycle) is present. Sixteen relaxation oscillation designs are generated by extra negative feedback brought about by negative or positive regulation of the synthesis or degradation rates of the kinase protein or phosphatase protein by M_p or M. Designs A*-H* are mirror images of designs A-H. Although synthesis and degradation reactions are shown for both the kinase and phosphatase proteins, the protein concentration that is not controlled by feedback from the M cycle is considered constant, resulting in only two differential equations for each diagram. All feedback regulations are described by simple Michaelis-Menten type expressions (BOX 2 and Supplementary Table S3). The remaining sixteen relaxation oscillation designs are shown in Supplementary FIG.S1 and can require some degree of cooperativity within feedback loops.

Cascade dynamics govern cellular functions

Following stimulation, signalling proteins become involved in collective dynamic behaviour that none of the individual molecules can exhibit in isolation. Inherently complex dynamics of universal signalling motifs allows a cascade of these motifs to generate even large spectrum of temporal patterns that contribute to the signal-response specificity. A multitude of negative and positive feedback loops enables cascades to generate gradual and ultrasensitive responses, multi-stability and oscillations^{12,18,20,46,47,72-74}. For instance, the same basic architecture allows MAPK cascades to operate as negative feedback amplifiers that reduce noise, as ultrasensitive or discontinuous switches, or flexible integration modules; these theoretical predictions were verified experimentally^13,16,72.

The signalling dynamics can become multi-stable, when two or more bistable cycles form a cascade, such as MAPK cascade⁶⁵. The biological outcome of multi-stability is the ability to control multiple irreversible transitions, for instance, sequential transitions in the cell cycle. Central components of the cell cycle machinery are cyclin-dependent kinases (such as, CDK1/Cdc2), which sequential activation/inactivation governs cell-cycle transitions. CDK1/Cdc2 activity is low (OFF) in G1-phase (resting state) and has to be high (ON) for entry into mitosis (M-phase). Recently, hysteresis and bistability were shown to occur in the activation/inactivation of CDK1/Cdc2, confirming a theoretical prediction made by Novak and Tyson a decade ago⁷⁵. Bistability in the CDK1/Cdc2 cycle arises from positive and double-negative feedback loops in the reactions, where CDK1/Cdc2 activates its activator (the phosphatase Cdc25) and inactivates its inhibitor (the kinases Wee1 and Myt1). Negative feedback from the anaphase promoting complex (APC) renders the CDK1/Cdc2 bistable switch into a relaxation oscillator that drives the cell cycle^68,69. Intriguingly, Cdc25 and Wee1 themselves can be phosphorylated on multiple sites and therefore can potentially exhibit bistability, implying that the entire CDK/cyclin system can display multiple steady states⁶⁵ (this prediction is awaiting experimental verification). Sequential bifurcations of multiple steady states provide more flexibility in the control of the cell fate and allow for a number of check points in the cell cycle.

SPATIAL DIMENSION OF SIGNALLING NETWORKS

Activation of cell-surface receptors and their downstream targets leads to the spatial relocation of multiple proteins within the cell. During evolution, cells have developed not only means to control the temporal dynamics of signalling networks, but also mechanisms for precise spatial sensing of the relative localization of signalling proteins. The regulation of signalling within the cellular space is pivotal for a number of physiological processes, such as cell division, motility and migration. Here I show how basic principles of the control of reaction rates, diffusive movement and directed transport underlie sophisticated mechanisms to activate signalling routes by the membrane recruitment of binding partners, to provide spatial cues that guide the mitotic-spindle assembly and to transmit signals to distant cellular targets.

Regulation of signalling by membrane recruitment

Receptor stimulation triggers the mobilization of cytosolic adaptor proteins and enzymes to cellular membranes. Subsequent phosphorylation results in the assembly of signalling complexes on receptors, scaffolds and cytoskeletal elements⁷⁶. These spatial relocations are effective control mechanisms of switching-on signalling pathways⁷⁷. The classical example is the control of the Ras/MAPK cascade by membrane recruitment of SOS and RasGAP (GEF and GAP for the small GTPase Ras, respectively), mediated by RTKs (for example, by EGFR) and membrane-bound scaffolds. It has been previously proposed that the role of this recruitment is to increase diffusion-limited (first-encounter) rates, but it was recently shown that the function of membrane localization is to amplify the number of complexes that are formed between the signalling partners^76-78. SOS and RasGAP bound to EGFR are confined to a small volume near the membrane that results in a 10² – 10³-fold increase in the apparent affinity of these catalysts for Ras. Simulations corroborate the theory, demonstrating that in the absence of the membrane recruitment, the cytoplasmic concentrations of SOS and RasGAP would have to increase 10² – 10³-fold to account for the observed rates of Ras activation/deactivation⁴⁹. We conclude that the spatial organization of the Ras circuit is crucial for the effective control of Ras activity.

Location determines signalling outputs

The localization of signalling proteins to distinct subcellular regions, such as internal membranes and membrane microenvironments (including lipid rafts) modulates signalling outputs^76,79. Specific anchoring subunits direct catalytic subunits of kinases and phosphatases, such as cAMP-dependent protein kinase, protein kinase C and serine/threonine protein phosphatases PP1, PP2A and PP2B to different cellular regions⁸⁰. The general mechanism is to orient broad-specificity enzymes towards specific targets and physically separate them from undesirable substrates. Discrete subcellular distribution enhances the specificity and fidelity of phosphorylation and dephosphorylation catalyzed by these kinases and phosphatases.

Qualitatively different patterns of signalling are generated by receptors and downstream effectors associated with endosomes or the plasma membrane⁸¹. Likewise, the same protein cascades operate in surprisingly dissimilar ways when localized to different cellular compartments. The input-output sensitivity of MAPK cascade is different for signalling from the plasma membrane, the Golgi apparatus and endosomes^16,82. Computational models have yet to take into full account the ramifications of subcellular localization on signalling outcomes.

Spatial gradients of signalling activities

In the late 1990s, the novel concept of protein activity gradients within a cell was proposed ^21,83-85. This concept has matured in recent years, when fluorescence resonance energy transfer-based biosensors enabled discoveries of intracellular gradients of the active form of the small GTPase Ran⁸⁶ and the phosphorylated form of stathmin-oncoprotein 18 (Op18/stathmin) that regulates the microtubule polymerization⁸⁷. Spatial gradients of protein activities organize signalling around cellular structures, such as membranes, chromosomes and scaffolds, and provide positional cues for key processes, including cell division. During mitosis, the microtubule network changes from the radial architecture emanating from the centrosome to a bipolar spindle. How this remarkable rearrangement occurs is not completely understood. Spatial gradients of several molecules that influence microtubule dynamics, including Op18/stathmin and RanGTP, which interacts with the nuclear-transport receptor importin-β, were recently suggested to guide microtubule-kinetochore positioning during the mitotic-spindle assembly^88-91.

The basic prerequisite for signalling gradients is the spatial segregation of opposing reactions (for instance, kinase and phosphatase) in a universal protein-modification cycle (FIG.3). For a protein phosphorylated by a membrane-bound kinase and dephosphorylated by a cytosolic phosphatase, Brown & Kholodenko predicted that there can be a gradient of the phosphorylated protein (BOX 3) -high concentration close to the membrane and low concentration within the cell²¹. Given measured values of protein diffusivity and kinase and phosphatase activities, it was estimated that phosphoprotein gradients might be large within the intracellular space (Fig. 3C). Even in small bacterial cells, spatial gradients of this kind were recently suggested for chemotaxis proteins^22,92. Interestingly, the existence of intracellular cAMP-gradients generated by the membrane-associated adenylate cyclase and cytosolic phosphodiesterase was conjectured theoretically in 1980⁹³.

FIG. 3.

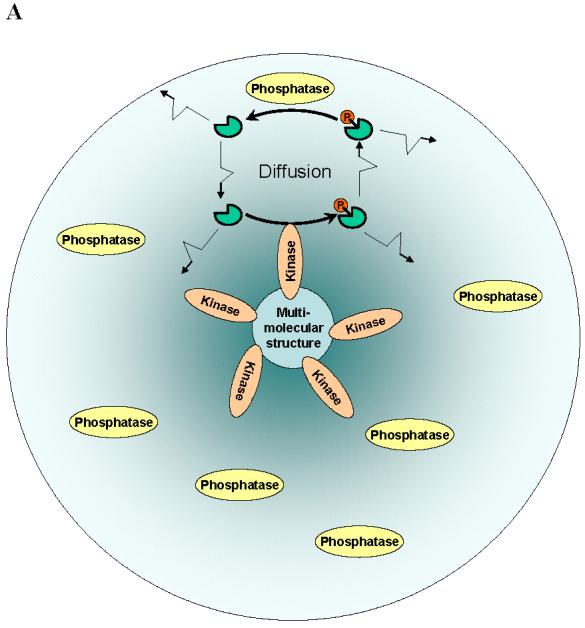
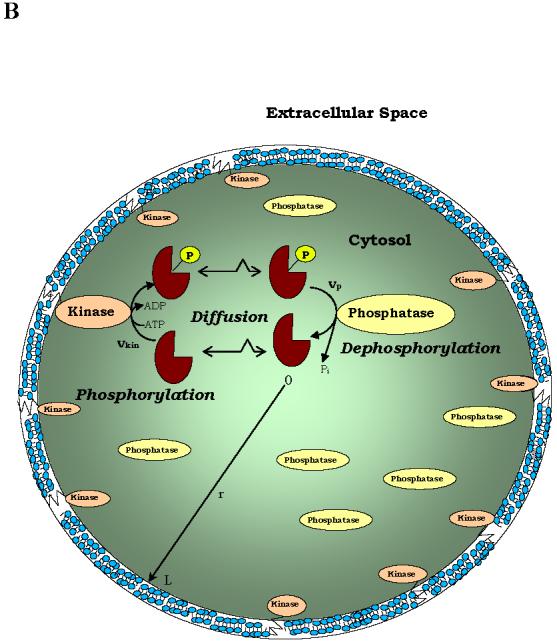
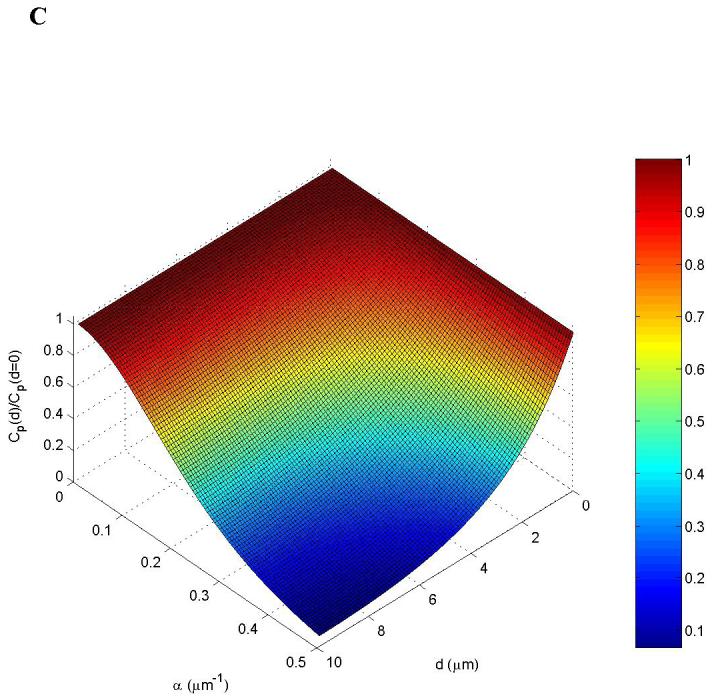
Spatial segregation of two opposing enzymes in a protein-modification cycle generates intracellular gradients. Kinases localize to (A) supra-molecular structures (sphere) or (B) the cell membrane, whereas phosphatases are homogeneously distributed in the cytoplasm. The concentration gradients are shown by colour intensity. C. Stationary phosphorylation levels c_p decline with the distance d from the cell membrane toward the centre[Brown, 1999 #61 (see panel B). The steepness of the gradient (reciprocal of the characteristic length) is determined by the parameter α(α² = k_p/D is the ratio of the phosphatase activity k_p and the protein diffusivity D, BOX 3).

BOX 3. When do the spatial activity gradients occur?

Here I show how intracellular signalling gradients arise from chemical transformation and diffusion. For a spatially-confined kinase and homogeneously-distributed phosphatase (or a similar enzyme pair, GEF and GAP), the spatio-temporal dynamics of the phosphorylated form c_p of the interconvertible protein is governed by the reaction-diffusion equation,

$$\frac{\partial c_p}{\partial t}=D\Delta c_p-v_p\left(c_p\right)$$ (1).

When the diffusivities D are equal for the phosphorylated c_p and unphosphorylated c_u forms, their total concentration is constant across the cell, c_p + c_u = C_tot (which is untrue for different diffusivities⁸³).

The simplest one-dimensional geometry corresponds to a cylindrical (for instance, bacterial) cell of the length L with the kinase localized to one pole (surface-reaction with rate $v_{\mathit{kin}}^{\mathit{mem}}$ at x = 0 ) and the cytoplasmic phosphatase (rate v_p). The steady-state spatial profile c_p (x) is determined by letting the time-derivative in Eq.1 equal zero and imposing the following boundary conditions (the diffusive flux equals $v_{\mathit{kin}}^{\mathit{mem}}$ at the kinase pole and zero at the opposite pole),

$$D\frac{d^2{c}_p}{\partial x^2}-v_p=0,-D\frac{{\mathit{dc}}_p}{\mathit{dx}}{\mid }_{x=0}=v_{\mathit{kin}}^{\mathit{mem}},\frac{{\mathit{dc}}_p}{\mathit{dx}}{\mid }_{x=L}=0$$ (2)

When the phosphatase is far from saturation, v_p = k_pc_p (k_p = V_max/K_m is the observed first-order rate constant), the analytical solution to Eq.2 reads,

$$c_p\left(x\right)=c_p\left(0\right)\left(\frac{e^{\alpha x}+e^{2L\alpha }{e}^{-\alpha x}}{1+e^{2\alpha L}}\right),{\alpha }^2=\frac{k_p}{D}$$ (3)

When $\alpha L\ll 1$, the phospho-protein concentration decreases almost linearly, and when αL ≥ 1, it decreases nearly exponentially c_p (x)/c_p (0) ≈ e^−αx with distance x from the membrane. This provides a simple, but powerful criterion⁸³ that large phospho-protein gradients exist when the dephosphorylation time 1/k_p is smaller than the diffusion time L²/D. The kinase activity only influences the concentration c_p (0) near the membrane^21,83.

Spherical symmetry simplifies analysis of signalling in three dimensions. For a cell of the radius L with a kinase located on the cell surface and phosphatase in the cytoplasm (FIG.3A), the steady-state phospho-protein concentration decreases from the membrane towards the cell centre nearly exponentially if αL ≥ 1, FIG. 3C²¹.

A similar exponential decrease in the phosphorylation signal c_p (r) may occur when a kinase is bound to a supra-molecular structure (of radius s) and a phosphatase resides in the surrounding area (of the radius L, FIG.3B). Assuming spherical symmetry, the steady-state concentration c_p(r) is determined by (Supplementary FIG.S2),

$$\begin{array}{c}\frac{D}{r^2}\frac{d}{\mathit{dr}}\left(r^2\frac{{\mathit{dc}}_p}{\mathit{dr}}\right)-k_p{c}_p=0,\\ -D\frac{{\mathit{dc}}_p}{\mathit{dr}}{\mid }_{r=s}=v_{\mathit{kin}}^{\mathit{mem}},\frac{{\mathit{dc}}_p}{\mathit{dr}}{\mid }_{r=L}=0\\ c_p\left(r\right)=c_p\left(s\right)\frac{{\mathit{se}}^{-\alpha r}}{{\mathit{re}}^{-\alpha s}}\left(\frac{e^{2\alpha r}(\alpha L+1)+e^{2\alpha L}(\alpha L-1)}{e^{2\alpha s}(\alpha L+1)+e^{2\alpha L}(\alpha L-1)}\right),{\alpha }^2=\frac{k_p}{D}\end{array}$$ (4)

Considering how c_p (r) decreases for different values of αL , we conclude that signalling gradients cannot be built merely by diffusion, but require the spatial segregation of opposing enzymes.

For a simple cycle of two opposing enzymes, one confined to a cellular structure and the other in the cytoplasm, the characteristic size of the gradient is determined predominantly by the protein diffusivity and the activity of the cytoplasmic enzyme (BOX 3). If the enzyme in the cytoplasm is saturated, the gradient length also depends on the activity of the enzyme confined to the structure²³. Cells employ additional means to control the shape and the extent of spatial gradients. For instance, if the input activity changes gradually in space, ultrasensitive responses would generate precipitous, short-length gradients, whereas linear responses can generate shallow output gradients. Kinase and GTPase cascades can expand gradients over large spatial regions (BOX 4). How far gradients of the active form reach into the cytoplasm can also be controlled by the association with an adaptor protein that protects against the deactivating enzyme. In fact, the complex of RanGTP with importin-β generates more extended gradients than RanGTP alone because the GTP hydrolysis by RanGAP is prevented during the life-time of the RanGTP-importin-β complex ⁹¹. Alternatively, binding an adaptor that enhances the deactivation rate will decrease the length of the gradient.

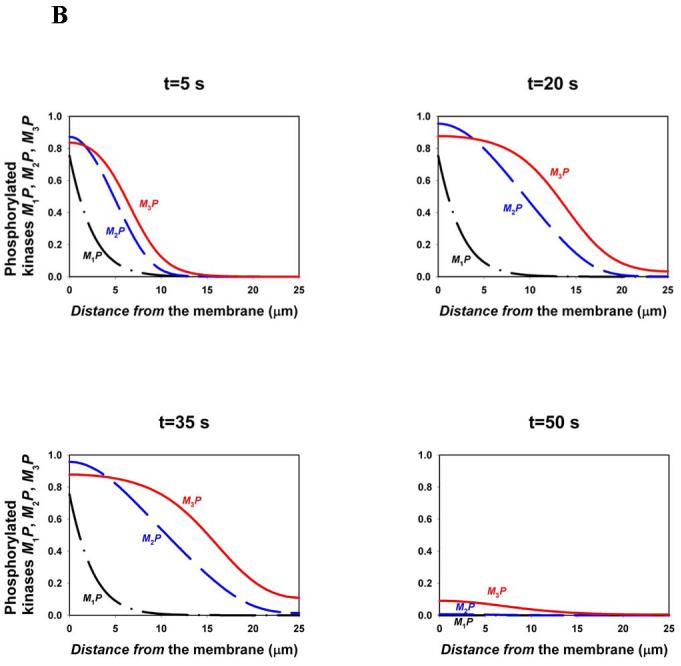
BOX 4. Facilitated communication through kinase cascades.

For a cascade where a kinase (M_i) at each level activates a kinase (M_i+1) at the subsequent downstream level, the gradients of the phosphorylated forms become shallower down the cascade²¹. For a spherical cell, where a membrane-bound kinase phosphorylates M₁ (rate $v_{\mathit{kin}}^{\mathit{mem}}$) and all other kinases and phosphatases diffuse in the cytoplasm, the spatio-temporal dynamics of a three-level cascade (Fig. 1C) is described by the following equations,

$$\begin{array}{c}\frac{\partial M_{1}P}{\partial t}=\frac{D}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial M_{1}P}{\partial r}\right)-v_p^1\left(M_{i}P\right),\hfill \\ \frac{\partial M_{i}P}{\partial t}=\frac{D}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial M_{i}P}{\partial r}\right)+M_{i-1}P\cdot w_{\mathit{kin}}^i\left(M_{i}P\right)-v_p^i\left(M_{i}P\right),i=2,3\hfill \\ D\frac{\partial M_{1}P}{\partial r}{\mid }_{x=L}=v_{\mathit{kin}}^{\mathit{mem}},\hfill \\ \frac{\partial M_{i}P}{\partial r}{\mid }_{x=0}=0,i=1,2,3,M_i+M_{i}P=M_i^{\mathit{Tot}}=\mathit{const}\hfill \end{array}$$ (1)

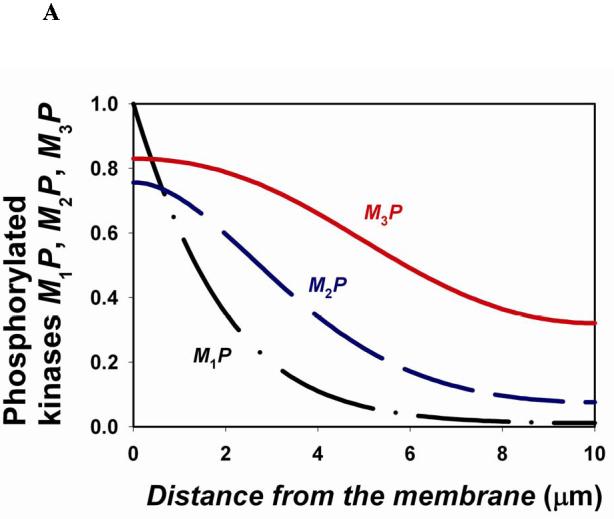
Here $M_{i-1}P\cdot w_{\mathit{kin}}^i\left(M_{i}P\right)$ is the rate of phosphorylation of M_i (proportional to the concentration M_i-1P of the active kinase upstream) and $v_p^i\left(M_{i}P\right)$ is the rate of the i-th phosphatases (Supplementary Table S4). The calculated steady-state spatial profiles (figure, part A) show that descending down the cascade, phosphorylated kinases reach further into the cell.

Although the existence of more levels in a cascade facilitates signal transfer over several micrometers, signalling over longer distances (for instance, from the plasma membrane to the nucleus in large cells, such as Xenopus eggs) requires additional means, such as vesicular or non-vesicular transport of phosphorylated kinases along microtubules and travelling waves of protein phosphorylation. Such waves propagating through bistable protein modification cascades (Supplementary FIG.S3) were recently predicted²⁶. In fact, travelling waves in bistable systems are well-known in physics, chemistry and biology²⁷. Bistability intrinsic to the multisite activation/deactivation cycles in the cytoplasm⁶⁵ (such as the MAPKK or MAPK cycles) gives rise to travelling waves that propagate binary phosphorylation signals to distant targets. Figure, part B shows the travelling phosphorylation wave that propagates through a three-level cascade following a 30-second pulse of activity of the input membrane-bound kinase ($V_{\mathit{kin}}^{\mathit{mem}}$, Supplementary Table S5). Additional positive feedback in the cytoplasm may enable phosphorylation waves to propagate with high velocity over exceedingly long distances, possibly solving a long-standing enigma of survival signalling in neurons.

Temporal signalling dynamics can induce spatial gradients

The time-course of signalling responses and the formation of spatial gradients of signalling activities are directly related. The spatial segregation of opposing enzymes is often initiated by specific signals. For instance, the cyclin-dependent kinase CDK1/Cdc2 phosphorylates the nuclear localization signal (NLS) of RCC1, which is a GEF for Ran⁹⁴. In the G1-phase CDK1/Cdc2 activity is low and, therefore, the NLS phosphorylation level is low. CDK1/Cdc2 becomes active to drive cells into mitosis. Owing to NLS phosphorylation by CDK1/Cdc2, RCC1 binds to the chromosomes and catalyzes the conversion of inactive RanGDP into active RanGTP. Since the opposing RanGAP activity is predominantly cytoplasmic, spatial gradients of active Ran emerge with high RanGTP concentration near mitotic chromosomes and low in the surrounding area. Therefore, the RanGTP-related gradients that guide the mitotic-spindle self-organization⁹¹ are driven by the temporal dynamics of CDK1/Cdc2.

FACILITATED COMMUNICATION WITHIN CELLS

Phosphoprotein gradients in MAPK cascades

Phosphoprotein gradients are hallmarks of kinase/phosphatase cascades, including MAPK cascades. MAPK cascades contain three interconnected cycles of MAPK, MAPK kinase (MAPKK) and MAPKK kinase (MAPKKK). In the MAPK/ERK cascade (the most well-characterized biochemically), these kinases are ERK, MEK and Raf. Upon RTK stimulation and Ras activation, the cytosolic Raf is recruited to the cell membrane, where it binds to and phosphorylates MEK on two serine residues. Phosphorylated MEK drifts into the cell interior, where it phosphorylates ERK on threonine and tyrosine residues. Because MEK is dephosphorylated in the cytoplasm, spatial gradients of phosphorylated MEK, and subsequently phosphorylated ERK might occur. Calculations show that these gradients can be precipitous^23,24, decreasing the strength of the phosphorylation signal to the nucleus. Instructively, the phosphorylation signal reaches further into the cell if the cascade has more levels, and this might be one of the reasons that cascades exist (BOX 4). The cascades found in eukaryotes tend to have more levels than the cascades in prokaryotes; this can be related to larger distances of signal propagation in eukaryotes.

Endocytosis and signalling: a marriage of convenience

Many cytosolic proteins that are phosphorylated at the plasma membrane travel into the cell interior to interact with the targets, which are confined to mitochondria, cytoskeleton, the Golgi, and the nucleus. The membrane confinement of kinase activity and the cytosolic localization of phosphatases can result in unfavorable gradients of phosphorylated signal-transducers provided they spread solely by diffusion; this would impede information transfer^21,23. In view of this problem, alternative mechanisms to relay stimuli from the surface to distant targets were proposed including trafficking of phosphorylated kinases with endosomes (“signalling endosome”) or non-vesicular signalling complexes driven by molecular motors^{23,26,28,95,96}. Motor-mediated movement of the endosomes and kinase complexes along microtubules is remarkably distinct from chaotic diffusive motion and is able to prevent the formation of precipitous reaction-diffusion gradients^23,26. Although in the past, endocytosis was thought to be a mechanism to attenuate signalling, a dual role of endocytosis is now emerging: a robust, immediate signal transducer on a short time-scale and a downregulator of receptor signalling on longer times^23,95. Distinct endocytic compartments, including clathrin, caveolae, and Rab domains, can deliver differential sets of proteins to diverse cellular targets, generating specific signalling outputs^95,97.

Retrograde transport and phosphoprotein waves

An interesting puzzle in neurobiology concerns the mechanisms used by neurons to transfer signals over long distances. The survival of developing neurons depends on neurotrophins, such as the nerve growth factor (NGF) and its receptor, TrkA. NGF is produced by peripheral tissues and binds to TrkA on distal axons that are located as far as one meter away from the neuronal soma. How do survival signals reach the cell body in a physiologically relevant span of time? Diffusion is ruled out as a mechanism of long-range signalling, because it would be prohibitively slow. In fact, we have seen that diffusion may be insufficient even for spreading signals across the cytoplasm of large cells, such as Xenopus eggs^23,26.

Retrograde transport of endosomes containing the NGF-TrkA complexes is critical for neuronal survival^96,98. Yet, recent evidence indicates that survival signals can also be transmitted by NGF-independent mechanisms⁹⁹. These might include lateral waves of receptor activation propagating along the axon membrane^25-27 and movement of a signalling complex of phosphorylated ERK with intermediate filament vimentin and importin, driven by the molecular motor dynein²⁸. However, lateral propagation of TrkA activation can be excluded, as nearly complete inhibition of TrkA in the cell bodies/proximal axons did not affect survival, whereas TrkA inhibition at distal axons induced apoptosis¹⁰⁰. Although transport of phosphorylated kinases driven by molecular motors is a robust mechanism of retrograde signalling, it cannot account for the initial burst of tyrosine phosphorylation, which reaches neuron bodies as early as several minutes after NGF stimulation¹⁰⁰. This initial rapid signal cannot be carried out by molecular motors that move at 1 to 10 μm/sec^96,101. It is feasible that the first survival signals are transmitted by waves of protein phosphorylation emerging from kinase/phosphatase cascades, such as MAPK or PI3K cascades, or GEF/GAP cascades of G-protein activation (BOX 4).

Outlook/Future directions

Quantitative models that generate novel experimentally testable hypotheses will have an increasingly important role in postgenomic biology. Future models will integrate data on the distinct spatio-temporal dynamics of signalling from different cellular compartments and provide new insight into the connection between external stimuli and the signalling outcome in terms of gene expression responses. Challenges of the combinatorial complexity of signalling networks and experimental uncertainty in parameter values will be addressed by modular approaches, stochastic and pattern-oriented modelling. The goal of the pattern-oriented approach is to predict and explain dynamic patterns of cellular responses to a multitude of external cues and perturbations. An exceedingly large number of quantitative and also qualitative data patterns will facilitate the verification of the proposed molecular mechanisms and exclude models that are too simplistic and uncertain¹⁰². These systems-level, data-driven models will generate new knowledge and provide strategies for the regulation of the cellular machinery. Understanding mechanisms underlying signalling network function will provide breakthroughs in the identification of critical controlling factors that will be targets for pharmacological interventions in the treatment of major human diseases.

Figure Box 1. Parts A, B and C.

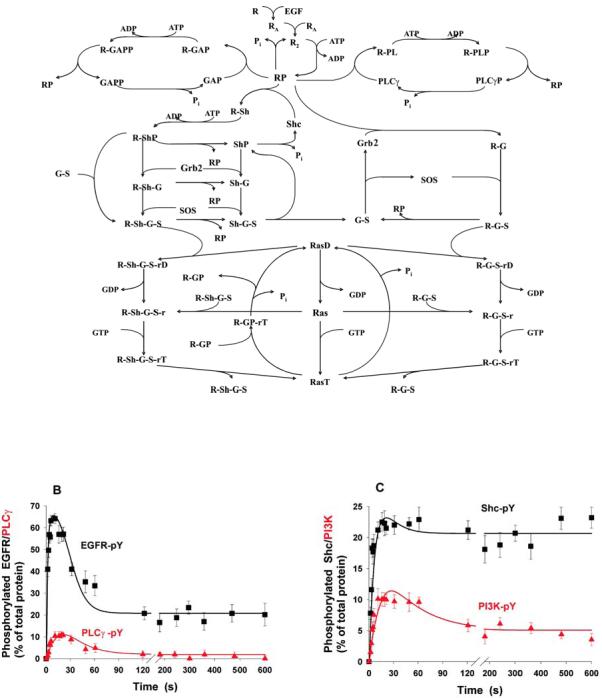
Figure Box 2. Parts A, B and C.

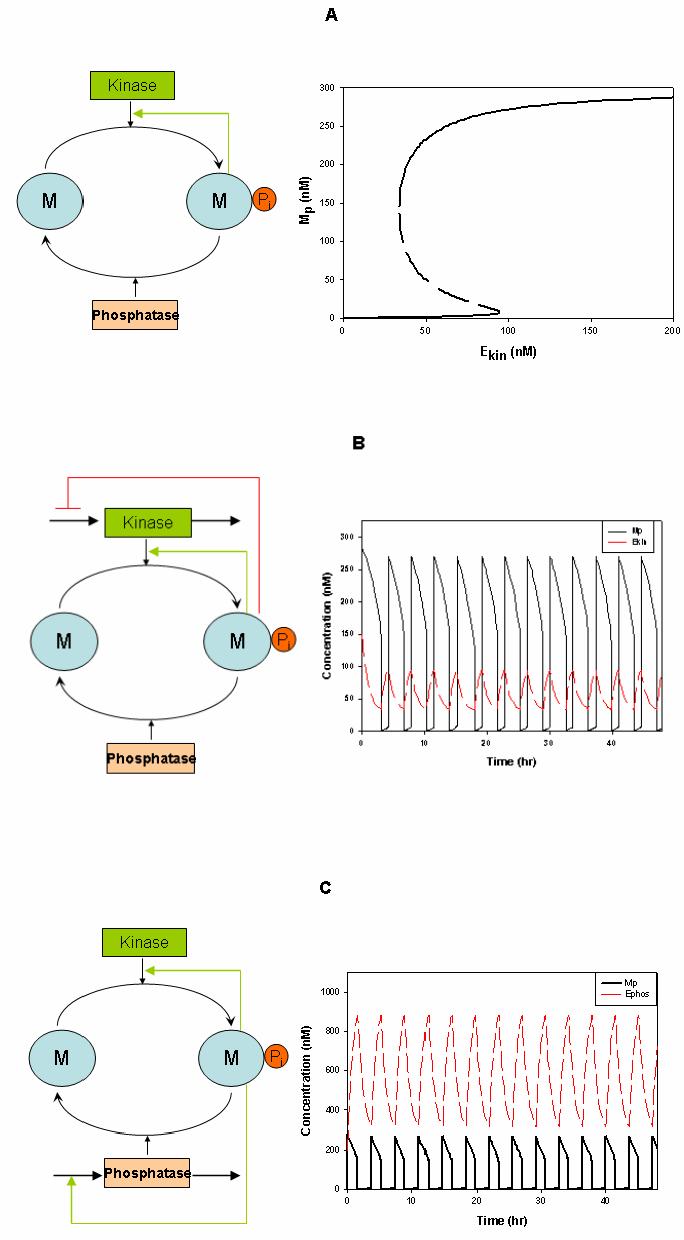
Figure Box 4, Part A, Part B.