Abstract
Transcription regulation has been responsible for organismal complexity and diversity in the course of biological evolution and adaptation, and it is determined largely by the context-dependent behavior of cis-regulatory elements (CREs). Therefore, understanding principles underlying CRE behavior in regulating transcription constitutes a fundamental objective of quantitative biology, yet these remain poorly understood. Here we present a deterministic mathematical strategy, the motif expression decomposition (MED) method, for deriving principles of transcription regulation at the single-gene resolution level. MED operates on all genes in a genome without requiring any a priori knowledge of gene cluster membership, or manual tuning of parameters. Applying MED to Saccharomyces cerevisiae transcriptional networks, we identified four functions describing four different ways that CREs can quantitatively affect gene expression levels. These functions, three of which have extrema in different positions in the gene promoter (short-, mid-, and long-range) whereas the other depends on the motif orientation, are validated by expression data. We illustrate how nature could use these principles as an additional dimension to amplify the combinatorial power of a small set of CREs in regulating transcription.
Keywords: computational method, matrix factorization, MED, principles of transcription regulation, transcriptional regulatory networks, yeast
Introduction
Transcription is the first step in the universal pipeline of the biological information flow from genome to proteome. Accordingly, the regulation of transcription is critical for the development, complexity, and homeostasis of all living organisms (Davidson, 2001; Levine and Tjian, 2003). Although transcription can be regulated at different levels (e.g., chromatin structure level), one fundamental level, first discovered by Jacob and Monod (Jacob and Monod, 1961), is that the production of transcripts of a given gene is governed by a complex combinatorial interplay of cis-regulatory elements (CREs) (henceforth referred to as motifs) present in the gene's promoter region, and associated transcription factors (henceforth referred to as regulators) present in the cellular environment. Because regulators are gene products, their productions in principle are also controlled by motifs. Therefore, transcription of a gene is fundamentally regulated by the motif set present in such gene's promoter, acting as the gene's condition-independent signal receivers, and the set of functions describing the dependency of motif strength—the quantitative level of motif's influence on gene expression–on promoter context constitutes the set of principles of transcription regulation.
Major efforts have been made in identifying motifs in different species using a variety of approaches (McGuire and Church, 2000; McGuire et al, 2000; Guhathakurta et al, 2002a, 2002b; Siggia, 2005; Tompa et al, 2005; Xie et al, 2005). Of those organisms, the yeast Saccharomyces cerevisiae has gained the most attention owing to the availability of multiple yeast genomes and high-quality mRNA. In fact, many methods developed for finding motifs and determining condition-dependent motif (or associated transcription factor) activity have used yeast as the model organism (Roth et al, 1998; Tavazoie et al, 1999; Bussemaker et al, 2000, 2001; Hughes et al, 2000; Wang et al, 2002; Conlon et al, 2003; Liao et al, 2003; Segal et al, 2003; Gao et al, 2004; Pritsker et al, 2004; Tompa et al, 2005) (also see Siggia, 2005 for a more complete list of references). However, less attention has been paid to the effects of motifs on gene expression as a function of their promoter context, and such effects remain poorly understood. Works by Pilpel et al (2001) and Sudarsanam et al (2002) studied the effect of motif cooccurrence on gene expression by measuring the degree of coexpression within the set of genes containing motif combinations of interest. Although their work could infer the combinatorial effects of motif–motif interactions on gene expression, it did not address how such effect is influenced by other factors that determine the properties of the promoter context such as geometric constraints. A recent study by Beer and Tavazoie (2004) began to take geometric features into account by way of a Bayesian network model of yeast expression profiles in order to learn the effect of motif position and orientation on gene expression. Although this later approach works quite well, it does not consider the individual expression patterns of each single gene, but instead analyzes the expression profiles of gene clusters, a process that can potentially cause loss of information and may not be suitable for modeling genes in the genome that do not belong to any well-defined cluster. Because the common assumption underlying these works is that coexpression implies coregulation, these approaches are limited by the need to detect motif influence from statistically aggregated expression data rather than from individual genes, and this typically restricts their application to subsets of genes with large gene expression signals, or those in predefined clusters, or with specific promoter properties. Furthermore, although metrics for measuring the degree of gene coexpression using expression coherence (Pilpel et al, 2001; Sudarsanam et al, 2002) or average of pairwise correlation (Beer and Tavazoie, 2004) employed in these works can infer the effects of motifs on gene expression well, such metrics do not provide a direct quantitative measure of motif influence on gene expression.
In this article, we present a deterministic mathematical strategy, the motif expression decomposition (MED) formalism, whose framework provides just such a quantitative measure—motif strength. MED operates on all genes in the genome of a particular organism under consideration, and assigns a strength to each motif in the promoter of each individual gene, without depending on averaging or clustering of gene expression profiles. Motif strength as a function of promoter context can then be derived using the concept of gene ensemble and gene ensemble instance illustrated in Figure 1 and discussed below. To demonstrate the method, we applied MED to the yeast S. cerevisiae transcriptional networks. We identified four functions describing four different ways that motifs can quantitatively affect gene expression levels, and validated these predicted functions by expression data. We will show examples where the computed measure of motif strength can be used to dissect the appearance of motif synergy in the yeast S. cerevisiae transcriptional networks.
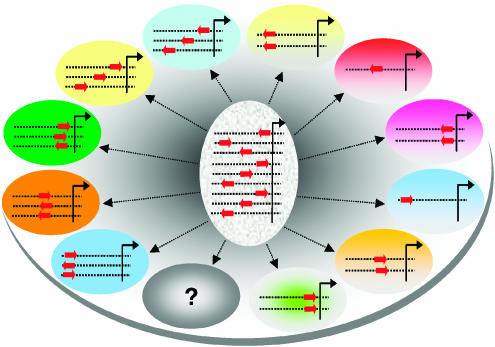
Figure 1.
An illustration of the concept of the gene ensemble (vertical oval) and the gene ensemble instance (horizontal oval), representing the essence of the MED method for deriving principles of transcription regulation. A gene ensemble is defined as a collection of genes containing a motif set of interest, whereas one of its instances comprises a subset of this collection containing the motif set with specified constraints such as motif geometry. Other constraints can also encompass motif exact sequence (a specific instance motif consensus sequence), multiplicity, cooccurrence with other motif sets, or any combination. Each horizontal oval object's color represents a gene expression pattern pertaining to such gene ensemble instance.
Results and discussion
The MED computational framework for deriving principles of transcription regulation
From the physical standpoint, the effect of a given motif on gene expression—motif strength—must depend on its context such as its exact sequence, geometry (i.e. location or orientation), and cooccurrence with other motifs, simply because these parameters underlie the physical nature of the complex combinatorial interactions between motifs and regulators at the atomistic level for regulating transcription. Similar to the concept of the potential of mean force in statistical mechanics (McCammon and Harvey, 1987), each of these attributes of the motif context can be considered as a reaction coordinate along which the observed motif strength—a multivariable function—can be projected on. To this end, we propose the concept of gene ensemble and gene ensemble instance (Figure 1) as a way of describing quantitatively the relationship between motif strength and its context. A gene ensemble is defined as a collection of genes containing a specific motif set of interest, whereas one of its instances comprises the subset of genes in such collection containing the motif set that fits a specific promoter context, which can be motif's geometry, sequence, multiplicity, cooccurrence with other motif set, etc., or combination of these. Within this conceptual framework, a function representing the dependency of motif strength on its context in the promoter can then be readily established from the average motif strength of each gene ensemble instance a posteriori from the motif strength derivation process. To calculate the strength of each motif in each individual gene promoter, we determine the extent to which each motif contributes to the expression level of each gene it regulates using equation (1), which reflects Jacob and Monod's fundamental transcriptional model, without assuming motif context a priori, and the by means of a matrix decomposition technique. These two steps together constitute the framework of the MED formalism. The detailed description of the MED method is presented in the Materials and methods section.
Transcriptional regulatory principles derived from S. cerevisiae transcriptional networks
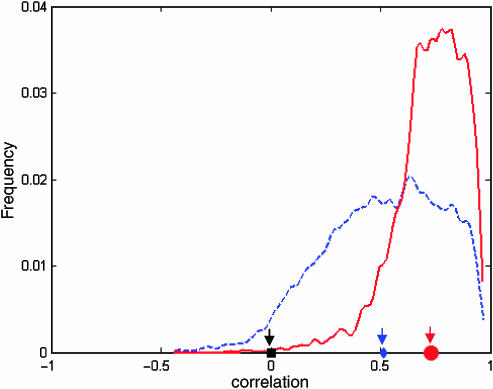
We applied MED to yeast S. cerevisiae transcriptional networks with a combined gene expression data set covering 255 conditions involving different environmental stresses (Gasch et al, 2000) and multiple stages of the cell cycle (Spellman et al, 1998). We used crossvalidation (see Materials and methods) as an unbiased way to measure MED's ability to fit the biological data contained in the data set. We obtained an average correlation coefficient of 0.52 (Figure 2 , blue diamond) between predicted and actual expression for all 5719 genes (Figure 2, blue curve). To put this number into perspective, a previous study using a Bayesian network analysis on the same expression data set reported an average correlation coefficient of 0.51 on a subset of 2587 genes in 49 expression clusters (Beer and Tavazoie, 2004). On this same gene subset, MED achieves an average correlation coefficient of 0.72 (Figure 2, red curve and red circle). However, direct comparison is complicated by the fact that, unlike MED, Beer and Tavazoie do not reconstruct individual gene expression patterns, but rather consider only the profiles of 49 gene clusters, and then assess the correlations between genes' actual cluster profiles and the cluster profiles predicted by their Bayesian network. Nevertheless, this latter result clearly shows that the more fine-grained MED approach does achieve a good fit to the expression data without overfitting (see Materials and methods section). Furthermore, we also compared MED to the multiple regression method (Bussemaker et al, 2001; Beer and Tavazoie, 2004) in a similar manner as above. We obtained the corresponding average correlation of 0.14 for all 5719 genes and 0.22 for 2587 genes. MED's better performance in the latter comparison is expected, as our model introduces variables (which, when solved, correspond to our motif strengths) where the multiple regression method uses constants (i.e. number of motif instances), and thus MED should generate better fit against gene expression profiles.
Figure 2.
The distribution of correlation coefficients between actual and MED-predicted gene expression derived from crossvalidation (see Materials and methods section). The blue curve, whose average is 0.52 presented as the blue diamond, is the distribution for all 5719 genes in the S. cerevisiae genome, whereas the red curve, whose average is 0.72 presented as the red circle, is the distribution for about 2600 genes earlier work (Beer and Tavazoie, 2004) used for comparison purpose. the black square represents the average of 10 average correlation coefficients derived from 10 crossvalidation runs with the input expression data whose rows were permuted. The superiority of MED lies in its ability not only to produce good prediction, but also to reduce bad prediction (i.e. genes with little or even negative correlation). It is worth noting that these ∼2600 genes used by early work (Beer and Tavazoie, 2004) stand out automatically as an outcome of MED without the need for heuristically selecting them out in the first place.
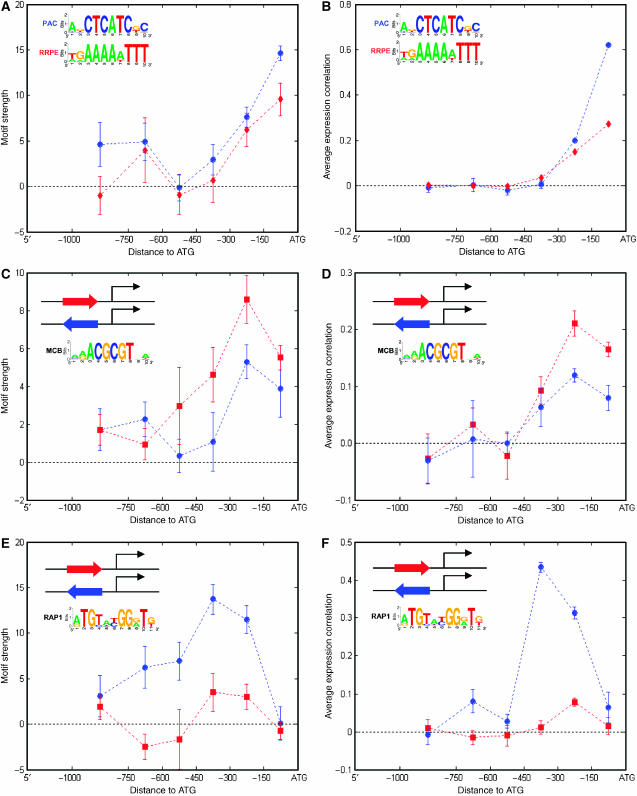
To demonstrate the proof-of-concept that MED is capable of deriving principles of transcription regulation, in this study we chose to focus primarily on motif position and orientation with respect to the start codon, two geometric constraints known to play a role in gene coexpression (Beer and Tavazoie, 2004). We found that motifs do not always have the same level of influence on the gene expression simply owing to their presence in the gene promoter, nor exert the largest influence on the gene expression when they are near the start codon in yeast, but rather follow a function of a complex shape. Here we illustrate existence of four functions of motif strength (Figure 3 ), distinguishing themselves by their extrema with respect to motif position and orientation, and describing four different ways that motifs can affect gene expression levels given their geometric context. The first function describing the dependency of motif strength on motif position has the maximum when the motif is within 150 bp from the start codon (Figure 3A and B), henceforth referred to as the so-called short-range type. The second (Figure 3C and D) and third (Figure 3E and F) functions, also describing the dependency of motif strength on motif position, have the maximum when the motif is spaced at an intermediate (150–300 bp) or longer (300–450 bp) distance from the start codon, and henceforth referred to as the so-called mid-range and long-range types, respectively. Unlike the first three functions, the fourth function (Figure 3E and F) describes the dependency of motif strength on motif's relative orientation with respect to the start codon rather than the position, henceforth referred to as the so-called orientation-dependent type. In order to derive this kind of function, one needs to establish the functions of motif strength for a given motif's both orientations.
Figure 3.
Four classes of transcriptional regulatory principles in S. cerevisiae. These graphs illustrate the dependency of motif strength on motif geometric constraints for the PAC (A, blue curve), RRPE (A, red curve), MCB (C), and the RAP1 (E) motifs. The position of the start codon is indicated by ‘ATG'. To form instances of a gene ensemble containing each of these motifs (see Materials and methods section), the motif distance relative to ATG is binned with a bin size of 150 bp, except the last bin with a bin size of 250 bp. The average motif strength of each of these motif-containing gene ensemble instances (see Supplementary information 3 for the distribution of correlation coefficients) is plotted in the middle of each bin, with the error bar indicating the standard error of the average. Panels (B), (D), and (F) show the degree of gene coexpression, as measured by the average pairwise expression correlation, for the corresponding motif-containing gene ensemble instances for panels (A), (C), and (E). For MCB and RAP1 motifs, their orientational effects (5′ represented in red, 3′ represented in blue) on gene expression are also presented in addition to their geometric constraint.
The PAC and RRPE motifs (Tavazoie et al, 1999; Hughes et al, 2000), which are found in promoters of genes encoding ribosomal proteins, are examples of the short-range motifs (Figure 3A). Both of these motifs exhibit significantly higher average motif strength within 150 bp of the start codon than would be expected from randomized expression data (P Shuffling≪0.01), and significantly higher than at positions further upstream (P Wilcoxon<10−16 for PAC, <1.83 × 10−5 for RRPE) (see Materials and methods section for definitions of P Shuffling and P Wilcoxon). To validate this form of regulatory principle, we computed the corresponding function describing the dependency of the degree of gene coexpression, as measured by the average pairwise expression correlation (Beer and Tavazoie, 2004) (e.g., average of expression correlation coefficients of all gene pairs in a given gene set), on motif position for the same set of gene ensemble instances (Figure 3B) using the expression data. The comparison between these two functions shows that MED's prediction of regulatory principles for these short-range motifs agrees very well with the experimental data, despite some discrepancy while PAC is far from the start codon. As shown in Figure 3A and B, the PAC motif retains its strength at such a far distance, whereas the degree of gene coexpression of such PAC-containing ensemble instances becomes insignificant. However, our further analysis shows that the loss of correlation in such PAC-containing gene ensemble instances arises because the genes split into clusters with anti-correlated expression profiles, whose average correlation is therefore close to zero (see Supplementary information 1). This illustrates how MED's analysis of motif strength reveals different information about gene expression than can be obtained from average correlations.
The MCB motif (Koch et al, 1993), which plays a role in DNA synthesis and replication during the S1 phase of the cell cycle, is an example of the mid-range motif (Figure 3C). Unlike the PAC and RRPE motifs, this motif achieves the greatest strength when it is further upstream, spaced between 150 and 300 bp (P Wilcoxon<1.15 × 10−4; P Shuffling≪0.01). Furthermore, the MCB motif also exhibits a small degree of orientational effect around the position of its maximum strength; hence, it may also weakly belong to the orientation-dependent motif type (P Wilcoxon<0.1). These predicted forms of regulatory principles are validated by expression data (Figure 3D) in the similar manner as being carried out for the PAC/RRPE motifs. Note that although the core of the MCB motif (ACGCGT) is invariant and palindromic, its full sequence we used in this work is not, as there is a slight non-palindromic signature in its flanking bases (see Figure 3C for sequence logo), and individual instances of this motif often deviate from the palindrome. For example, MCB exact sequences like AGACGCGTAA, CAACGCGTAA, and CGACGCGTAA, which have the top ScanACE scores (16.17, 15.93, and 15.82, respectively), are clearly not palindromic. Therefore, MED's ability to distinguish MCB orientation-dependent behavior is entirely due to the non-palindromic signature induced by flanking bases, so that any orientation effect detected by MED suggests a possible role for these flanking bases in motif function.
Finally, the RAP1 motif (Lascaris et al, 1999), which controls the production of ribosomal proteins, is an example of the long-range and orientation-dependent motif (Figure 3E). Unlike the MCB motif, RAP1 acquires the largest strength when it is even further upstream, spaced between 300 and 450 bp (P Wilcoxon<7.90 × 10−7; P Shuffling≪0.01). In addition, it has a clear preferential orientation for regulating gene expression almost over the entire promoter length (P Wilcoxon<4.84 × 10−8). As with the PAC, RRPE, and MCB motifs, these predicted forms of regulatory principles by RAP1 are also validated by expression data (Figure 3F).
Biological relevance
To cope with both a myriad of environmental conditions and the internal complexity of cellular functions, eukaryotes are known to employ combinatorial strategies to generate a variety of expression patterns from a relatively small set of regulatory motifs (Kellis et al, 2003; Levine and Tjian, 2003). The combinatorial potential has been understood primarily in terms of motif cooccurrence and synergy. However, the transcriptional regulatory principles described here suggest several avenues of research into how nature may also exploit motif geometry as another dimension of combinatorial power for regulating transcription. For instance, given the observation that PAC motif strength varies along the length of the promoter, we foresee an experiment that explores the effect of PAC motif location on a reporter gene in relation to the hypothesis that reporter expression level should vary as indicated in Figure 3A in conditions for which the PAC-binding protein is predicted to be active. It would also be of great interest to look for evidence that shifts of PAC motif location have actually been selected over the course of evolution. While one possibility is to look for PAC location shifts in gene promoters in related yeast strains, this is complicated by the difficulty of assessing the functional significance of any observed shifts, as individual genes may have different requirements for control by PAC that themselves changed over evolutionary history, while the PAC transcriptional regulatory principle of Figure 3A may have changed as well. Therefore, a clearer initial (if indirect) path towards exploring the possible evolutionary significance of motif location might be to perform a high-throughput competitive growth experiment (Winzeler et al, 1999; Giaever et al, 2002) looking for differential fitness effects of large numbers of engineered mutations in PAC location across many PAC-containing genes. Finally, it would be of great interest to elucidate genetic and biochemical mechanisms by which motif geometry controls transcription, for instance, by identifying protein domains or cofactors that might be responsible for establishing the distance at which a motif has maximal effect. In some cases, however, including PAC, this may need to await identification of the proteins that bind these motifs.
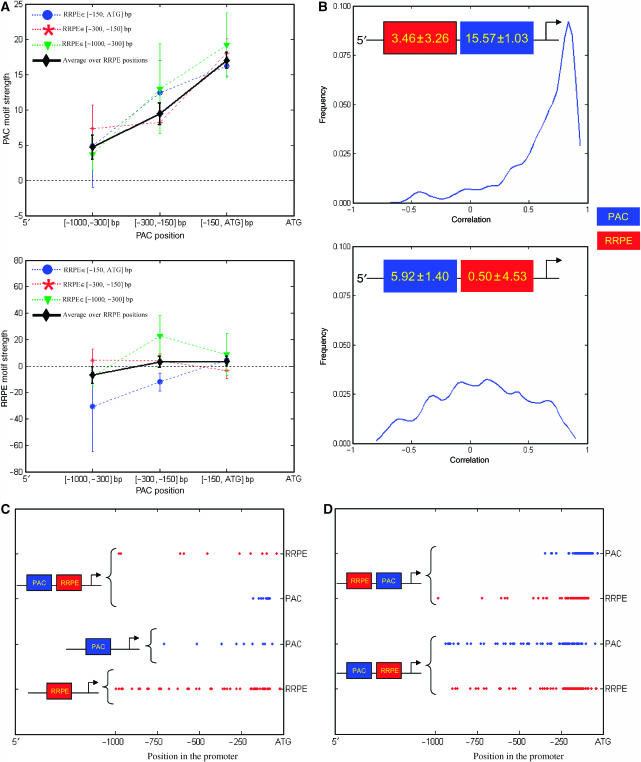
To further illustrate the potential use of motif geometry by nature for regulating transcription, we use MED to dissect the appearance of synergism between the PAC and RRPE motifs (Pilpel et al, 2001; Sudarsanam et al, 2002; Beer and Tavazoie, 2004). This notion of synergism was based on the higher coherence of gene expression in the gene ensemble containing both, compared to the PAC-only and RRPE-only ensembles (Supplementary information 2). However, MED analysis, as shown in Figure 4A , shows a surprising fact that in the PAC/RRPE-containing gene ensemble, whereas the strength of PAC decreases with distance from the start codon, the strength of RRPE is close to zero at every distance. Analysis of variance (ANOVA) (see Materials and methods) of PAC motif strengths obtained from PAC/RRPE-containing gene ensemble supports these observations, finding a significant main effect of PAC position on PAC motif strength (P ANOVA-PAC=2.6 × 10−5), no effect from RRPE position (P ANOVA-RRPE=0.96), and no interaction (P ANOVA-PAC--RRPE=0.52). A similar analysis of RRPE strengths finds insignificant or marginal effects (P ANOVA-PAC=0.19, P ANOVA-RRPE=0.1, and P ANOVA-PAC–RRPE=0.18). These findings indicate that there is no actual synergistic effect between the two motifs, an analysis consistent with the reported inability by Das et al (2004) to detect PAC–RRPE interaction in a cell cycle data set also used in this work. Instead, the appearance of synergism in expression level is sufficiently explained by the proximity of the PAC motif to the start codon (Figure 4 and Table 1) in the PAC/RRPE-containing gene ensemble, and does not require invoking any functional interaction. Similarly, proximity of the PAC motif to the start codon also explains an apparent synergy in the order of the two motifs (Figure 4B and D). Even for the motif arrangement that favors the closeness of PAC to the start codon (an arrangement associated with a high degree of gene coexpression), MED analysis shows that RRPE possesses no significant strength (Figure 4B). As for why the RRPE motif behaves almost the same way as PAC in terms of contributing its influence to the gene expression in general (Figure 3A) but does not have a significant role on the expression of PAC–RRPE-containing gene ensemble, recent work by Tanay et al (2005) observes that the PAC motif is relatively younger than the RRPE motif and also provides evidence for mechanisms by which one motif can replace another by passing through an intermediate stage in which both are present in gene promoters. We hypothesize that the PAC motif may have been evolved to be better suitable for S. cerevisiae than the RRPE motif, and to smoothly assume RRPE's functional role in genes containing both of them in this way. These two examples clearly show that nature could use motif geometry as an additional dimension to regulate transcription.
Figure 4.
The analysis of the gene ensemble that contains both the PAC and RRPE motifs. (A) Relative distance of PAC and RRPE to ATG is binned into three bins: [−150,ATG], [−300,−150], and [−1000,−300] bp, forming a total of nine PAC/RRPE-containing gene ensemble instances for nine combinations of promoter structures. Average motif strength is plotted against the position of PAC (along the x-axis) and RRPE (different curves). The black diamond curve represents motif strength averaged over all genes in three ensemble instances corresponding to three binned positions of RRPE (see Supplementary information 2 for motif strength averaged over all genes in three ensemble instances corresponding to three binned positions of PAC). In (B), predicted PAC and RRPE motif strengths are shown as a function of their relative order with respect to ATG (5′-RRPE-PAC-ATG and 5′-PAC-RRPE-ATG). For the 5′-RRPE-PAC-ATG ensemble instance, the magnitude of the PAC motif strength is about three times higher than the instance that contains these motifs in the reverse order, consistent with the corresponding degree of gene coexpression. Nevertheless, the motif strength of RRPE motif is insignificant regardless of motif order. In (C) and (D), the positions of PAC and RRPE motifs relative to ATG of gene promoters that contain them are presented. In (C), the location of each motif in RRPE-only (red), PAC-only (blue), and PAC/RRPE-only containing gene ensembles is represented by a filled circle of appropriate color located at a position it occurs in gene promoter relative to ATG. The choice of these ‘only' ensembles is discussed in Supplementary information 2. Likewise, in (D), the positions of PAC and RRPE are plotted for PAC/RRPE gene ensemble with two different motif order arrangements. Data in (A) and (B) clearly indicate that there is no actual synergism between PAC and RRPE. This finding appears to contradict the appearance of PAC and RRPE synergic behaviors suggested in Supplementary information 2 and earlier work (Beer and Tavazoie, 2004). However, data shown in (C) and (D) and average pairwise expression correlation coefficient date in Table 1 not only confirm MED's prediction but also illustrate nature's use of geometry as another dimension for regulating transcription.
Table 1.
Average expression correlations for various instances of PAC/RRPE-containing gene ensemble
| PAC ∈[ATG,−150] bp | PAC ∈[−150,−300] bp | PAC ∈[−300,−1000] bp | |
|---|---|---|---|
| RRPE ∈[ATG,−150] bp | 0.72 | 0.36 | 0.12 |
| RRPE ∈[−150,−300] bp | 0.70 | 0.27 | 0.03 |
| RRPE ∈[−300,−1000] bp | 0.64 | 0.34 | −0.02 |
Degree of gene coexpression measured for different PAC and RRPE geometric configurations in the PAC/RRPE-containing gene ensemble. Average gene expression correlation coefficients derived from expression data for nine different instances of the PAC/RRPE-containing gene ensemble are shown. This is the same set of ensemble instances used to calculate both PAC and RRPE motif strengths shown in Figure 4A. As shown, the degree of coexpression of the PAC/RRPE-containing gene ensemble depends primarily on the position of the PAC motif with respect to ATG, and is not affected significantly by the position of RRPE.
Conclusion
We have demonstrated a novel mathematical strategy for deciphering principles of transcription regulation using S. cerevisiae as a model system. We identify four regulatory principles that motifs obey in order to regulate transcription. These principles reveal the complexity of how a motif can exert its influence on gene expression beyond its mere presence, absence, or closeness to the start codon. In addition, we have also illustrated an example showing how nature could exploit geometry as another means for regulating transcription, hence increasing the combinatorial power of a relatively small set of motifs. With the emergence of new research paradigms in modern biology, where the process of biological research begins with a system-level theoretical prediction followed by experimental validation (Gilbert, 1991), we believe that MED can play an important role in fostering the development of biological theory necessary for explaining how regulatory motifs can control transcription. Furthermore, with the technology recently available to allow the high-throughput synthesis of oligomers (Tian et al, 2004), we foresee a new research direction aiming at engineering new and improved biological systems with desired properties. To this end, we believe that MED can be a valuable tool for such bioengineering process by providing necessary knowledge and parameters regarding motif's behaviors.
Materials and methods
The MED method
MED is composed of two main steps. In the first step, each individual gene is analyzed for the strength of each motif in its promoter without taking into account any information about motif's context. The way in which such motif strength is derived in MED is based on the Jacob and Monod's model of transcription (Jacob and Monod, 1961), whereby the log ratio expression level of a gene is a function of a motif set present in its promoter and regulators' activities in the cellular environment (see equation (1)). The outcome of this step consists of two matrices: a matrix of motif strength, where each element represents the condition-independent strength of each motif in each gene promoter; and a matrix of regulator activity, where each element represents the global proxy activity of each regulator under a particular environmental condition. In the second step (the regulatory rule deduction step), regulatory principles are derived from the matrix of motif strength using the gene ensemble concept as illustrated in Figure 1.
Step 1: Derivation of motif strength
For a given gene g, let Ω g be a set of motifs occurring in its promoter; then its log ratio expression level E gc in a specific environmental condition c can be approximated using the following :

where M gj represents strength of motif jth on the expression level of gene g and A jc represents a global proxy for the regulator activity associated with motif jth under condition c. Unlike previous works (Bussemaker et al, 2001; Gao et al, 2004), where the matrix element M gj is a known constant and equal to the number of instances that motif jth occurs in the promoter of gene g or ChIP log ratio for transcription factor jth binding to the promoter of gene g, MED optimizes both M gj and A jc to best fit the expression data. Therefore, for all genes and conditions, equation (1) becomes
![]()
where E is an m genes by n conditions expression matrix, M is an m genes by k motifs matrix of condition-independent motif strengths, and A is a k regulators by n conditions matrix of condition-dependent global proxy activity of regulators for k motifs. Note that if a particular motif jth does not exist in the promoter of gene ith, then the matrix element M ij of the above matrix M is zero and remains so. The problem posed in equation (2) becomes a matrix decomposition problem. This portion of the MED algorithm consists of the procedure for decomposing the data matrix E into a product of matrices M and A uniquely using the motif–gene relationship as constraints (see proof in Supplementary information 4). The procedure we employed here is based on the factor analysis (Anderson, 1984; Gifi, 1990; Paatero et al, 2002; Liao et al, 2003) with Tikhonov regularization (Tikhonov and Arsenin, 1977) imposed on the matrix M to ensure uniqueness. To compute matrices M and A:
Initialize the non-zero elements of the motif matrix M using a weighted sum of the number of motif instances if motifs are represented in the position-specific weight matrix form, or simply the number of motif occurrence in each gene promoter (see Supplementary information 5 for details).
Given E, M, and let E be the product M·A, use least squares (see Supplementary information 6 for exact formula) to find the matrix A, the current global proxy activity of regulators for all motifs with current estimate of matrix M that minimizes
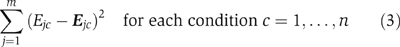
Normalize the matrix A in such a way that each row has unit norm.
Given E and A computed in (c), find the optimal strength M gj for each motif jth in the promoter of each gene g that minimizes
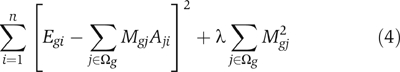 for each gene g=1, …, m. Alternatively, note if a predefined target M
gi
* for the strength of motif jth in the promoter of gene g is known a priori, one may wish to use the following instead:
for each gene g=1, …, m. Alternatively, note if a predefined target M
gi
* for the strength of motif jth in the promoter of gene g is known a priori, one may wish to use the following instead:
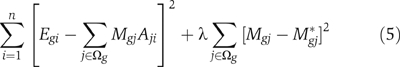
Repeat step (b) with the newly computed matrix M until convergence condition is met.
In the above algorithm, steps (b) to (d) are sufficient to ensure a unique solution M and A from the expression matrix E (see proof in Supplementary information 4). In equations (4) and (5), the second term is critical for producing a unique matrix M regardless of the linear dependency or near linear dependency of the rows of matrix A (see proof in Supplementary information 4). It can also be used to constrain the strength of motif jth in the promoter of gene g to a predefined value M gi * if such value is known a priori. Although the parameter λ can be chosen using more sophisticated methods (Shock, 1984; Engl and Neubauer, 1985; Guacaneme, 1988; Wahba, 1990), in this work it is chosen in such a way that it does not noticeably affect the test error computed from crossvalidation (Supplementary information 7). We used equation (4) to compute the motif strength and λ was set to a scalar value of 10−4, although it can be a vector quantity in general for weighting motifs in different gene promoters differently. The convergence criterion used in this work is the total variance of the residual matrix defined in Supplementary information 7. Note that, as each motif has its own binding strength to regulators and hence having its own scale of influence on gene expression, only relative motif strengths of the same motif across different instances of gene ensemble are meaningful for comparison purposes. Finally, equation (1) can be extended to include the nonlinear term accounting for the motif–motif interactions (Supplementary information 8) and the MED formalism shown above can still be applied transparently.
Step 2: Deduction of regulatory principles
We construct the gene ensemble containing a specific motif set of interest, partition this ensemble into instances based on the specific promoter properties of interest, and calculate the average motif strength and standard error across these instances (Figure 1) using motif strength data obtained from the previous step. Regulatory principles can then be derived from the relationship between motif strength and its context in the promoters (or constraints). Apart from the geometric constraints illustrated in this work, other constraints could include motif multiplicity (number of motif instances in a promoter), spacing, exact motif sequence, motif–motif cooccurrence, or any combination of these. Note that as the space between transcription start site and translation start site is usually fixed in yeast S. cerevisiae (Hurowitz and Brown, 2003), it is equally good to choose either one of them as the origin for geometric constraints. For convenience, we chose the latter. As for the discretization of the promoter length into bins for projecting motif strength in deriving distance-based regulatory principles, the choice of bin size (i.e. how many base pairs in each bin) is a non-trivial task. A large bin size will effectively bury all important signals, whereas a small bin size will allow noise to be manifest. Therefore, the goal in choosing a good bin size should be to choose the one that maximizes extractable signals contained in the data set as possible whereas minimizing noise. In this work, we used a bin size of 150 bp, which seems to be an optimal one, for deriving data presented in Figure 3 and the P Wilcoxon values confirm our choice of the bin size.
Data
We used a combined gene expression data set obtained from environmental stresses (Gasch et al, 2000) and cell cycle (Spellman et al, 1998) with a total of 255 conditions. Ideally, we want to use motifs that are derived directly from the ChIP-chip data without depending on the clustering in the gene expression space (Harbison et al, 2004); however at the time of this work, such data were not available. Therefore, we used 62 DNA regulatory motifs, represented as position-specific weight matrices, that were generated using literature (37 motifs) and the multiple sequence alignment program AlignACE (Roth et al, 1998) (25 motifs) as described previously (Roth et al, 1998; Hughes et al, 2000; Pilpel et al, 2001). We used ScanACE (Roth et al, 1998; Hughes et al, 2000; Pilpel et al, 2001) to find motif occurrences in promoter regions up to 1000 bp upstream. The expression data matrix E was centralized to remove column and row means.
Crossvalidation
To analyze the performance of MED, we used crossvalidation, in which we partitioned the expression data matrix into 100 blocks, each of which consists of 20% of random genes and 5% of random conditions (of these genes). For each run, we left out one of these blocks and trained the model on the remaining data. This allowed us to use gene expression data on all 255 conditions (but only across 80% of the genes) in order to compute matrix A in step (b) of the MED algorithm, and likewise, to use information on all the genes (but only across 95% of the conditions) to compute the motif matrix M in step (d) of the MED algorithm. Upon convergence, we then used the resulting matrices M and A to predict gene expression of the block of 20% genes and 5% condition the model has not been trained on. This process was repeated for each of the 100 blocks, each time predicting expression on the block of data that was left out, in order to obtain a complete expression matrix, each element was predicted by this crossvalidation scheme. The result presented in Figure 2 was computed by plotting the histogram of correlation coefficients between predicted and actual expression. Although we have a large number of parameters (i.e. the total number of non-zero elements in matrices M and A), we still have roughly 40 times more data points in our data set, and at each step of the algorithm we only fit a small number of parameters. In addition, crossvalidation ensures that the model performance is always tested on data that were not used to train the model. We also repeated the whole crossvalidation procedure as outlined above 10 times. Each time, all the rows of the input data matrix E were randomly permuted. We obtained the average and standard deviation (s.d.) of these 10 average correlation coefficients of 0.0014 and 0.0057 for all 5719 genes, respectively, making the average correlation coefficient derived from real data about 91 s.d. away. For the subset of 2587 genes early work used (Beer and Tavazoie, 2004), we obtained the corresponding average and s.d. of −0.0012 and 0.0101, respectively, making the corresponding average correlation coefficient derived from real data about 71 s.d. away. These results are shown as the black square in Figure 2. Therefore, the results obtained from crossvalidation to measure MED's predictive power are without the risk of overfitting to the training data.
Statistical tests
To further ensure that the type of each motif presented in this work is statistically significant in addition to the degree of gene coexpression, we performed two additional statistical tests: one is the Wilcoxon rank sum test (Wilcoxon, 1945; Lehmann, 1975) and the other is from the 100 random shuffling of complete gene expression profiles. In the Wilcoxon test, we determined if the motif strength at the position of extremum is statistically different from the motif strengths elsewhere. For the MCB and RAP1 motifs, we also determined if the strength of a motif oriented along one direction is statistically different compared to that of reversed direction. The level of statistical significance in the Wilcoxon rank sum test is measured by the Wilcoxon P-value (P Wilcoxon). In the random shuffling test, we permuted all elements of the expression matrix E 100 times, generating 100 expression matrices E i , i=1, …, 100, for computing the strengths of each motif presented in this work. In this test, we determined if the strength of a motif at a particular promoter position obtained from the actual expression data is statistically more significant than the corresponding one derived from the random shuffling of expression data. The level of statistical significance in this test is measured by the P-value (P shuffling): the fraction of motif strengths obtained from the random shuffling of expression data larger than the corresponding one obtained from the actual expression data. Note that, as there are 100 random shuffling runs, the smallest P-value, P shuffling, attainable in this test is 0.01 if no assumption is made about the distribution of motif strengths derived from the randomly shuffling of expression data. However, as shown in Supplementary information 10 and Supplementary Figure SF6a–c, the P-values for these observed motif strengths can be much smaller than 0.01 owing to the Chebyshev's inequality (P Chebyshev) (Abramowitz and Stegun, 1972), as the computed motif strengths of the PAC, RRPE, MCB, and RAP1 motifs at the promoter location of their extremum derived from the actual data are far away from the mean of the distribution of the corresponding ones derived from the random shuffling of expression data (by at least 28 s.d.).
We also performed two-way ANOVA on PAC and RRPE motif strengths derived from the PAC/RRPE-containing gene ensemble using the MatLab's anovan command (MatLab) using the model=‘full' and default ss-type parameters. Two factors were specified, PAC distance from start codon, whose P-value is denoted as P ANOVA-PAC, and RRPE distance from start codon, whose P-value is denoted as P ANOVA-RRPE, where each consisted of three levels corresponding to the distance bins in Figure 4. The P-value for the interaction between these two factors is denoted as P ANOVA-PAC--RRPE.
Competing interest statement
The authors declare that they have no competing financial interests.
Supplementary Material
Supplementary Material
Supplementary Material
Acknowledgments
We thank Nikos Reppas, Zhou Zhu, Xiaoxia Lin, Dana Pe'er, Saeed Tavazoie, Eric Siggia, and Joel Bader for critical reading of the manuscript. We thank John Aach for critical reading of the manuscript and useful suggestions on statistical tests. We are indebted to George M Church for his guidance and support of this work. Dat H Nguyen acknowledges support from the Alfred P Sloan and US Department of Energy Postdoctoral Fellowship in Computational Molecular Biology and Bioinformatics, and travel fellowships provided by the National Science Foundation Institute for Pure and Applied Mathematics at UCLA. George M Church was supported by US Department of Energy GTL Grant No. DE-FG02 02ER63461. PD was supported by PhRMA/Harvard CEIGI grant, and is currently supported by an LDRD grant at Lawrence Livermore National Laboratory.
References
- Abramowitz M, Stegun IA (1972) Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover [Google Scholar]
- Anderson TW (1984) An Introduction to Multivariate Statistical Analysis. Chichester, New York: Wiley [Google Scholar]
- Beer MA, Tavazoie S (2004) Predicting gene expression from sequence. Cell 117: 185–198 [DOI] [PubMed] [Google Scholar]
- Bussemaker HJ, Li H, Siggia ED (2000) Regulatory element detection using a probabilistic segmentation model. Proc Int Conf Intell Syst Mol Biol 8: 67–74 [PubMed] [Google Scholar]
- Bussemaker HJ, Li H, Siggia ED (2001) Regulatory element detection using correlation with expression. Nat Genet 27: 167–171 [DOI] [PubMed] [Google Scholar]
- Conlon EM, Liu XS, Lieb JD, Liu JS (2003) Integrating regulatory motif discovery and genome-wide expression analysis. Proc Natl Acad Sci USA 100: 3339–3344 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das D, Banerjee N, Zhang MQ (2004) Interacting models of cooperative gene regulation. Proc Natl Acad Sci USA 101: 16234–16239 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davidson EH (2001) Genomic Regulatory Systems: Development and Evolution. San Diego: Academic Press [Google Scholar]
- Engl H, Neubauer A (1985) Optimal discrepancy principles for the Tikholov regularization of integral equations of the first kind. In Constructive Methods for the Practical Treatment of Integral Equations, Hoffmann Ha (ed) Vol. 73, pp 120–141. Basel, Boston: Birkhäuser Verlag [Google Scholar]
- Gao F, Foat BC, Bussemaker HJ (2004) Defining transcriptional networks through integrative modeling of mRNA expression and transcription factor binding data. BMC Bioinform 5: 31 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gasch AP, Spellman PT, Kao CM, Carmel-Harel O, Eisen MB, Storz G, Botstein D, Brown PO (2000) Genomic expression programs in the response of yeast cells to environmental changes. Mol Biol Cell 11: 4241–4257 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giaever G, Chu AM, Ni L, Connelly C, Riles L, Veronneau S, Dow S, Lucau-Danila A, Anderson K, Andre B, Arkin AP, Astromoff A, El-Bakkoury M, Bangham R, Benito R, Brachat S, Campanaro S, Curtiss M, Davis K, Deutschbauer A, Entian KD, Flaherty P, Foury F, Garfinkel DJ, Gerstein M, Gotte D, Guldener U, Hegemann JH, Hempel S, Herman Z, Jaramillo DF, Kelly DE, Kelly SL, Kotter P, LaBonte D, Lamb DC, Lan N, Liang H, Liao H, Liu L, Luo C, Lussier M, Mao R, Menard P, Ooi SL, Revuelta JL, Roberts CJ, Rose M, Ross-Macdonald P, Scherens B, Schimmack G, Shafer B, Shoemaker DD, Sookhai-Mahadeo S, Storms RK, Strathern JN, Valle G, Voet M, Volckaert G, Wang CY, Ward TR, Wilhelmy J, Winzeler EA, Yang Y, Yen G, Youngman E, Yu K, Bussey H, Boeke JD, Snyder M, Philippsen P, Davis RW, Johnston M (2002) Functional profiling of the Saccharomyces cerevisiae genome. Nature 418: 387–391 [DOI] [PubMed] [Google Scholar]
- Gifi A (1990) Nonlinear Multivariate Analysis. Chichester, New York: Wiley [Google Scholar]
- Gilbert W (1991) Towards a paradigm shift in biology. Nature 349: 99 [DOI] [PubMed] [Google Scholar]
- Guacaneme JE (1988) An optimal parameter choice for regularized ill-posed problems. Integr Equat Oper Theory 11: 610–613 [Google Scholar]
- Guhathakurta D, Palomar L, Stormo GD, Tedesco P, Johnson TE, Walker DW, Lithgow G, Kim S, Link CD (2002a) Identification of a novel cis-regulatory element involved in the heat shock response in Caenorhabditis elegans using microarray gene expression and computational methods. Genome Res 12: 701–712 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guhathakurta D, Schriefer LA, Hresko MC, Waterston RH, Stormo GD (2002b) Identifying muscle regulatory elements and genes in the nematode Caenorhabditis elegans . Pac Symp Biocomput 425–436 [DOI] [PubMed] [Google Scholar]
- Harbison CT, Gordon DB, Lee TI, Rinaldi NJ, Macisaac KD, Danford TW, Hannett NM, Tagne JB, Reynolds DB, Yoo J, Jennings EG, Zeitlinger J, Pokholok DK, Kellis M, Rolfe PA, Takusagawa KT, Lander ES, Gifford DK, Fraenkel E, Young RA (2004) Transcriptional regulatory code of a eukaryotic genome. Nature 431: 99–104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hughes JD, Estep PW, Tavazoie S, Church GM (2000) Computational identification of cis-regulatory elements associated with groups of functionally related genes in Saccharomyces cerevisiae . J Mol Biol 296: 1205–1214 [DOI] [PubMed] [Google Scholar]
- Hurowitz EH, Brown PO (2003) Genome-wide analysis of mRNA lengths in Saccharomyces cerevisiae . Genome Biol 5: R2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacob F, Monod J (1961) Genetic regulatory mechanisms in the synthesis of proteins. J Mol Biol 3: 318–356 [DOI] [PubMed] [Google Scholar]
- Kellis M, Patterson N, Endrizzi M, Birren B, Lander ES (2003) Sequencing and comparison of yeast species to identify genes and regulatory elements. Nature 423: 241–254 [DOI] [PubMed] [Google Scholar]
- Koch C, Moll T, Neuberg M, Ahorn H, Nasmyth K (1993) A role for the transcription factors Mbp1 and Swi4 in progression from G1 to S phase. Science 261: 1551–1557 [DOI] [PubMed] [Google Scholar]
- Lascaris RF, Mager WH, Planta RJ (1999) DNA-binding requirements of the yeast protein Rap1p as selected in silico from ribosomal protein gene promoter sequences. Bioinformatics 15: 267–277 [DOI] [PubMed] [Google Scholar]
- Lehmann EL (1975) Nonparametric Statistical Methods Based on Ranks. New York: McGraw-Hill [Google Scholar]
- Levine M, Tjian R (2003) Transcription regulation and animal diversity. Nature 424: 147–151 [DOI] [PubMed] [Google Scholar]
- Liao JC, Boscolo R, Yang YL, Tran LM, Sabatti C, Roychowdhury VP (2003) Network component analysis: reconstruction of regulatory signals in biological systems. Proc Natl Acad Sci USA 100: 15522–15527 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matlab. Waltham: The MathWorks Inc [Google Scholar]
- McCammon JA, Harvey SC (1987) Dynamics of Proteins and Nucleic Acids. Cambridge: Cambridge University Press [Google Scholar]
- McGuire AM, Church GM (2000) Predicting regulons and their cis-regulatory motifs by comparative genomics. Nucleic Acids Res 15: 4523–4530 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGuire AM, Hughes JD, Church GM (2000) Conservation of DNA regulatory motifs and discovery of new motifs in microbial genomes. Genome Res 10: 744–757 [DOI] [PubMed] [Google Scholar]
- Paatero P, Hopke PK, Song X, Ramadan Z (2002) Understanding and controlling rotations in factor analytic models. Chemometr Intell Lab Syst 60: 253–264 [Google Scholar]
- Pilpel Y, Sudarsanam P, Church GM (2001) Identifying regulatory networks by combinatorial analysis of promoter elements. Nat Genet 29: 153–159 [DOI] [PubMed] [Google Scholar]
- Pritsker M, Liu YC, Beer MA, Tavazoie S (2004) Whole-genome discovery of transcription factor binding sites by network-level conservation. Genome Res 14: 99–108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roth FP, Hughes JD, Estep PW, Church GM (1998) Finding DNA regulatory motifs within unaligned noncoding sequences clustered by whole-genome mRNA quantitation. Nat Biotechnol 16: 939–945 [DOI] [PubMed] [Google Scholar]
- Segal E, Shapira M, Regev A, Pe'er D, Botstein D, Koller D, Friedman N (2003) Module networks: identifying regulatory modules and their condition-specific regulators from gene expression data. Nat Genet 34: 166–176 [DOI] [PubMed] [Google Scholar]
- Shock E (1984) Parameter choice by discrepancy principles for the approximated solution of ill-posed problems. Integr Equat Oper Theory 7: 895–898 [Google Scholar]
- Siggia ED (2005) Computational methods for transcriptional regulation. Curr Opin Genet Dev 15: 214–221 [DOI] [PubMed] [Google Scholar]
- Spellman PT, Sherlock G, Zhang MQ, Iyer VR, Anders K, Eisen MB, Brown PO, Botstein D, Futcher B (1998) Comprehensive identification of cell cycle-regulated genes of the yeast Saccharomyces cerevisiae by microarray hybridization. Mol Biol Cell 9: 3273–3297 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stormo GD (2000) DNA binding sites: representation and discovery. Bioinformatics 16: 16–23 [DOI] [PubMed] [Google Scholar]
- Sudarsanam P, Pilpel Y, Church GM (2002) Genome-wide co-occurrence of promoter elements reveals a cis-regulatory cassette of rRNA transcription motifs in Saccharomyces cerevisiae . Genome Res 12: 1723–1731 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanay A, Regev A, Shamir R (2005) Conservation and evolvability in regulatory networks: the evolution of ribosomal regulation in yeast. Proc Natl Acad Sci USA 102: 7203–7208 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tavazoie S, Hughes JD, Campbell MJ, Cho RJ, Church GM (1999) Systematic determination of genetic network architecture. Nat Genet 22: 281–285 [DOI] [PubMed] [Google Scholar]
- Tian J, Gong H, Sheng N, Zhou X, Gulari E, Gao X, Church G (2004) Accurate multiplex gene synthesis from programmable DNA microchips. Nature 432: 1050–1054 [DOI] [PubMed] [Google Scholar]
- Tikhonov AN, Arsenin VA (1977) Solutions of Ill-Posed Problems. New York: Wiley [Google Scholar]
- Tompa M, Li N, Bailey TL, Church GM, De Moor B, Eskin E, Favorov AV, Frith MC, Fu Y, Kent WJ, Makeev VJ, Mironov AA, Noble WS, Pavesi G, Pesole G, Regnier M, Simonis N, Sinha S, Thijs G, van Helden J, Vandenbogaert M, Weng Z, Workman C, Ye C, Zhu Z (2005) Assessing computational tools for the discovery of transcription factor binding sites. Nat Biotechnol 23: 137–144 [DOI] [PubMed] [Google Scholar]
- Wahba G (1990) Spline Models for Observational Data (CBMS-NSF Regional Conference Series in Applied Mathematics). Philadelphia: SIAM [Google Scholar]
- Wang W, Cherry JM, Botstein D, Li H (2002) A systematic approach to reconstructing transcription networks in Saccharomyces cerevisiae . Proc Natl Acad Sci USA 99: 16893–16898 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilcoxon F (1945) Individual comparisons by ranking methods. Biometrics 1: 80–83 [Google Scholar]
- Winzeler EA, Shoemaker DD, Astromoff A, Liang H, Anderson K, Andre B, Bangham R, Benito R, Boeke JD, Bussey H, Chu AM, Connelly C, Davis K, Dietrich F, Dow SW, El Bakkoury M, Foury F, Friend SH, Gentalen E, Giaever G, Hegemann JH, Jones T, Laub M, Liao H, Liebundguth N, Lockhart DJ, Lucau-Danila A, Lussier M, M'Rabet N, Menard P, Mittmann M, Pai C, Rebischung C, Revuelta JL, Riles L, Roberts CJ, Ross-MacDonald P, Scherens B, Snyder M, Sookhai-Mahadeo S, Storms RK, Veronneau S, Voet M, Volckaert G, Ward TR, Wysocki R, Yen GS, Yu K, Zimmermann K, Philippsen P, Johnston M, Davis RW (1999) Functional characterization of the S. cerevisiae genome by gene deletion and parallel analysis. Science 285: 901–906 [DOI] [PubMed] [Google Scholar]
- Xie X, Lu J, Kulbokas EJ, Golub TR, Mootha V, Lindblad-Toh K, Lander ES, Kellis M (2005) Systematic discovery of regulatory motifs in human promoters and 3′ UTRs by comparison of several mammals. Nature 434: 338–345 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Material
Supplementary Material