Noise resistance in the spindle assembly checkpoint

Abstract

Genetically identical cells vary in the amount of expressed proteins even when growing under the same conditions. It is not yet clear how cellular information processing copes with such stochastic fluctuations in protein levels. Here we examine the capacity of the spindle assembly checkpoint to buffer temporal fluctuations in the expression of Cdc20, a critical checkpoint target whose activity is inhibited to prevent premature cell cycle progression. Using mathematical modeling, we demonstrate that the checkpoint can buffer significant fluctuations in Cdc20 production rate. Critical to this buffering capacity is the use of sequestering-based mechanism for inhibiting Cdc20, as apposed to inhibition by enhancing protein degradation. We propose that the design of biological networks is limited by the need to overcome noise in gene expression.

Introduction

The spindle assembly checkpoint is an evolutionary conserved mechanism that ensures proper chromosome segregation during mitosis (Musacchio and Hardwick, 2002; Cleveland et al, 2003; Lew and Burke, 2003) (Figure 1A). A principle target of the checkpoint is Cdc20, a protein required for cell-cycle progression (Hwang et al, 1998). In wild-type cells, Cdc20 is held inactive until all chromosomes are properly attached to the mitotic spindles. Once attachment is completed, Cdc20 is rapidly activated (Shaw et al, 1998; Shonn et al, 2000), and initiates the anaphase by activating the anaphase-promoting complex, APC (Peters, 2002). Under conditions that compromise Cdc20 inhibition, chromosomes segregate prematurely. The consequences of such a premature segregation are cell death, aneuploidy and possibly cancer (Rajagopalan and Lengauer, 2004).

Figure 1.

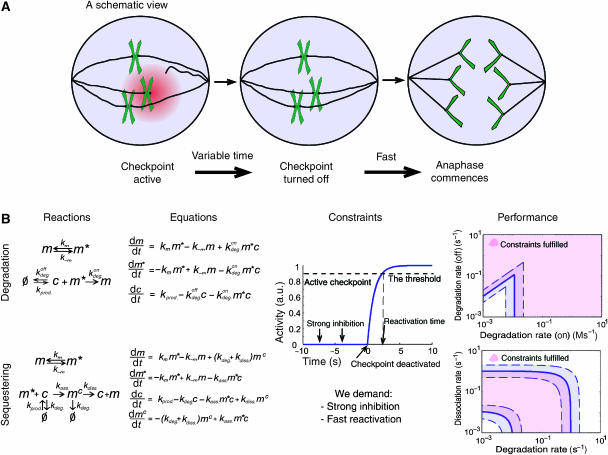
‘The spindle assembly checkpoint'. (A) A scheme of the checkpoint: as long as even a single kinetochore is not properly attached to the mitotic spindles, anaphase does not commence. The ‘stop-anaphase' signal is generated at the unattached kinetochores. Once all kinetochores are attached, anaphase initiation is rapid. (B) Two models for Cdc20 inhibition: Cdc20 can be inhibited either by enhanced degradation or by sequestering. Cdc20 and the inactive and active complexes are denoted as ‘c', ‘m' and ‘m*' respectively. The models were solved and analyzed with respect to their ability to tightly inhibit Cdc20 (quantified by the ‘amplification' ratio), and to activate rapidly the system once the last kinetochore is attached (reactivation). Both models were found to fulfill the requirements for a broad range of parameters (right most panel). Solid lines represent the borders for a solution where the amplification (ρ) is 100 and the reactivation time (τ) is 200 s. Dashed lines represent an increase or decrease of these restraints by a factor of 2. Parameter used: m_total=10 and k_ass.=k_deg.^on=10 M s⁻¹.

The checkpoint signal is generated at the kinetochore, a protein complex localized to the chromosome. The kinetochore serves as the microtubule docking site, allowing for the sensing of microtubule attachment (Cleveland et al, 2003; McAinsh et al, 2003). Importantly, even a single unattached kinetochore is sufficient to withhold cell cycle progression (Rieder et al, 1995). It is likely that the checkpoint signal diffuses away from the kinetochore to inhibit Cdc20 throughout the nucleus (Murray, 2004; Doncic et al, 2005). Notably, this tight inhibition of Cdc20 activity prior to chromosomal attachment does not compromise its rapid re-activation once attachment is complete.

Multiple mechanisms were implicated in Cdc20 inhibition. First, Cdc20 may be sequestered by some protein generated at the kinetochore, thus preventing it from binding APC and signaling cell-cycle progression. Indeed, the MCC complex, which is composed of key checkpoint proteins, is known to bind Cdc20 through its Mad2 and Mad3 subunits (Brady and Hardwick, 2000; Hardwick et al, 2000; Sudakin et al, 2001). Second, Cdc20 becomes phosphorylated when the checkpoint is active by Bub1, which further inhibit its activity (Chung and Chen, 2003; Tang et al, 2004). Finally, it was recently shown that Cdc20 degradation is upregulated in a checkpoint-dependent manner (Prinz et al, 1998; Pan and Chen, 2004), leading to the suggestion that enhanced degradation may also contribute to the reduction in Cdc20 activity by reducing its abundance.

Tight monitoring of Cdc20 activity at all times is critical for preventing premature segregation. Still, evidence suggests that Cdc20 is continuously produced even at the time when its activity is inhibited by the checkpoint. Given the considerable noise in protein expression characterized in several recent papers (Elowitz et al, 2002; Blake et al, 2003; Paulsson, 2004; Raser and O'Shea, 2004; Golding et al, 2005; Kaern et al, 2005; Pedraza and van Oudenaarden, 2005; Bar-Even et al, 2006; Cai et al, 2006), this continuous production is likely to impart to temporal fluctuations in Cdc20 levels.

Using mathematical modeling, we examined the capacity of the mitotic spindle checkpoint to buffer temporal fluctuations in Cdc20 production rate. Our results suggest that inhibiting Cdc20 through a sequestering mechanism allows for a significant buffering of protein production noise.

Results

Parameter region supporting checkpoint function under constant conditions

In a recent study (Doncic et al, 2005), we formulated two requirements on checkpoint function. First, prior to the attachment of microtubule to kinetochore (checkpoint ‘on'), Cdc20 needs to be tightly inhibited. We denote the inhibition ratio, defined as the ratio between active Cdc20 in the absence or presence of checkpoint function by ρ=c^off/c^on, with c^off and c^on being the Cdc20 levels when the checkpoint is active and inactive, respectively. Second, once the last kinetochore is attached, Cdc20 is rapidly reactivated. Experimental evidences in budding yeast suggest that the reactivation time, denoted by τ, is of the order of several minutes (Shonn et al, 2000). In a recent study (Doncic et al, 2005), we have analyzed several mechanisms with respect to their capacity to provide both requirements when realistic diffusion constants are considered. We found that the two properties exhibit interplay, such that rapid activation comes at the expense of tight inhibition. At least in the yeast Saccharomyces cerevisiae, where nucleus size is relatively small, inhibition that is confined to the kinetochore itself is not sufficient to ensure both tight inhibition and rapid activation. Thus, the inhibitory signal generated at the kinetochore (e.g. activated complex) should be allowed to diffuse and inhibit Cdc20 throughout the nucleus in order to be consistent with both properties.

Our previous analysis focused on the generation of the signal, but was not specific about the means by which Cdc20 is inhibited. Here we extend the model by considering two broad classes of mechanisms by which Cdc20 can be inhibited (Figure 1B). First, inhibition can be accomplished by enhancing Cdc20 degradation. Second, sequestering Cdc20 from binding the APC can be maintained, for example, by binding to some complex or through phosphorylation. To examine for possible difference between the two mechanisms, we studied each of them separately. Notably, combining both mechanisms increases inhibition in a linear manner, but does not produce synergistic effects (see Supplementary information).

The mathematical equations formulating the two classes of the inhibitory mechanisms are given in Figure 1B (see also Materials and methods for the assumptions used). Analysis of the two models shows that both can support reliable checkpoint function over a broad parameter ranges (Figure 1B). Importantly, the limitations on the parameter ranges required for supporting proper checkpoint behavior can be readily understood analytically (Table I, and Materials and Methods/Supplementary information).

Table 1.

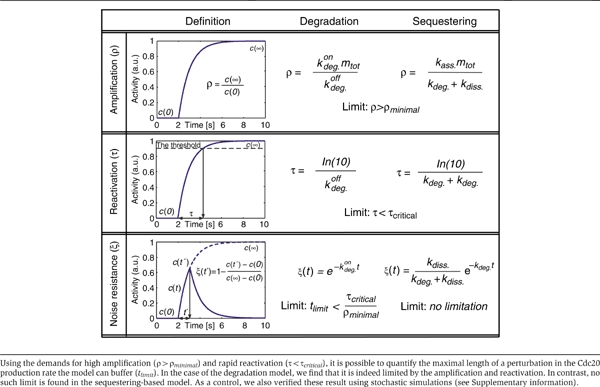
Definitions of ρ, τ and ξ, and their solutions for the two models

Inhibition by sequestering provides efficient noise filtering

We examined the sensitivity of the two mechanisms to noise in the rate by which Cdc20 is produced. To properly compare the response of the degradation-based versus the sequestering-based models, we considered parameters resulting in the same inhibition ratio, and the same re-activation time. We let the two systems relax to their (inhibited) steady state, and then subjected them to a pulse-like change in the rate of Cdc20 production.

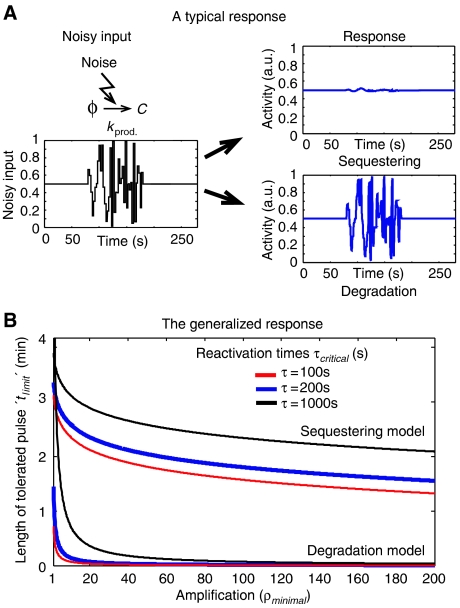
Interestingly, although the two mechanisms seem to perform equally well in inhibiting and reactivating Cdc20 under constant conditions, the effect of noise in the rate of Cdc20 synthesis was significantly more pronounced in the case of degradation-based inhibition. In fact, in the degradation-based model, the temporal levels of active Cdc20 followed the instantaneous changes in Cdc20 production rate, whereas only a marginal increase in Cdc20 was seen in the case of the sequestering-based model (Figure 2A).

Figure 2.

Noise resistance. (A) A typical response to noise: The two models were exposed to the identical noisy input shown, and their dynamics was followed. We note that the sequestering-based model is much more resistant to noise than the degradation-based model. A frequency–response analysis of this system was also performed, which confirmed these results (see Supplementary information). Parameters used: Degradation model: k_prod.=1 M s⁻¹, k_deg.^on=0.1 M s⁻¹ and k_deg.^on=1 s⁻¹. Sequestering model: k_prod.=0.01 M s⁻¹, k_deg.=0.01 s⁻¹, k_ass.∼0.01 M s⁻¹ and k_diss.∼0.1 M s⁻¹. Both models: m_tot.=10, k_m=1 s⁻¹and k_−m=100 s⁻¹. (B) In order to compare the two models, we defined a noise resistance threshold corresponding to the time, ‘t_limit', it takes for either model to reach a fraction of 1−e⁻¹ of the difference between its initial and final value. The larger t_limit, the longer time it takes for the system to reach its final steady-state value. t_limit is thus a measure of how long perturbations the system can handle. In the figure, we see how the critical time varies with the amplification and reactivation time. The fact that the sequestering-based model is able to buffer longer perturbations is clearly seen. Worth noting is also that the vertical location of the sequestering curve depends on the free parameter k_deg., the current value was thus chosen as an example rather than as an absolute value. Parameter used: degradation model — k_prod.=1 M s⁻¹, k_deg.^on=0.1 M s⁻¹ and k_deg.^on=1 s⁻¹; storage model — k_prod.=0.01 M s⁻¹, k_deg.=0.05 s⁻¹ and k_ass.∼0.1 M s⁻¹; both models—m_tot.=10, k_m=1 s⁻¹and k_−m=100 s⁻¹.

To examine the generality of this result, we defined a noise-resistance parameter: ξ(t). This parameter quantifies the dynamic response of the system to a pulse-like change in Cdc20 production, with ‘t' being the length of the pulse. ξ(t) is defined as the maximal change in Cdc20 following the pulse, relative to the maximal possible response (level of new steady state). Note that the levels of ξ(t) range from zero (poor noise resistance) to one (good noise resistance). Using simple algebraic equations, this parameter can easily be calculated for both inhibition models (Table I and Supplementary information).

For the degradation-based inhibition model, we find that the noise resistance is given by

where k_deg.^on is the (rapid) rate of Cdc20 degradation when the checkpoint is active. Note that this noise resistance is simply the extent by which the system decays to its (new) steady state during the time of the pulse. Thus, the checkpoint can filter perturbations whose typical correlation time is t_limit<1/k_deg.^on, but will be sensitive to longer perturbations. Notably, k_deg.^on (and thus also t_limit) is limited by the need to provide high amplification and rapid reactivation, with

where ‘τ_critical' is the maximal reaction time allowed and ‘ρ_minimal' is the minimal amplification needed for adequate inhibition. Thus, for an amplification ratio of one-hundred, a system that allows a rapid reactivation time of about 2 min will only be able to filter out only high-frequency noise with a correlation time of less than 2 s. Since subsequent activations of a Cdc20, even for short time interval, may initiate the anaphase, such an effect may be detrimental for the cell.

In contrast, in the case of sequestering-based inhibition, the noise resistance is given by

where k_diss. denotes the rate of dissociation of Cdc20 from the complex, while k_deg. denotes the basal (fixed) level of Cdc20 degradation. Notably, in this case, amplification ratio is only limited by the association rate of Cdc20 to the complex k_ass., which does not appear in this equation, whereas the reactivation time is defined by a combined function of both k_diss. and k_deg. (Table I). Hence, the decay to the new steady state is only determined by the dissociation and degradation rates.

Noise in the Cdc20 production is thus buffered by its tethering to the activated complexes. It has therefore no impact on the demands for high amplification and rapid reactivation.

Consequently, parameters can easily be chosen to provide efficient buffering of even slowly varying noise with a correlation time scale of several minutes (Figure 2B).

Taken together, we conclude that the degradation-based model provides poor noise filtering since the response to the noise is defined by the rapid time scale ensuring strong inhibition when the checkpoint is ‘on'. Contrastingly, response to noise in the sequestering-based model is defined by the relatively slow time scale associated with checkpoint reactivation, thus providing an efficient noise filtering.

Discussion

Biological systems are challenged by the need to ensure reliable function in the presence of highly noisy surrounding. It had been argued that the design of biological circuits had evolved to buffer such stochasticity; however, a connection between network design and robustness was established only for a small number of cases (Eldar et al, 2002; Kollmann et al, 2005).

Here we examined the capacity of the spindle assembly checkpoint to buffer fluctuations in protein production rate. A critical aspect of the checkpoint activity is to inhibit efficiently Cdc20 activity, since any fraction of active Cdc20 might plunge the cell into anaphase prematurely. Fluctuations in the level of active Cdc20 might thus be detrimental, making noise resistance a good criterion for distinguishing between different checkpoint mechanisms. Indeed, we have shown theoretically that inhibiting Cdc20 through a sequestering mechanism greatly enhances the capacity to buffer production noise, in particular when compared to inhibition through Cdc20 degradation. This conclusion will hold also for other systems, which need to maintain tight protein inhibition in the presence of some signal, while allowing for rapid activation when the signal is released. It could be tested experimentally by following simultaneously, and in individual cells, the protein production rate (using reporter gene expression) and the network output (e.g. by following cohesion degradation). Manipulating the connectivity by genetic means could in principle distinguish experimentally the potential advantage of the chosen design.

The spindle assembly checkpoint is governed by a complex network of molecular interactions. Here we focused on only the key aspect of its function. Future studies will be required to address the role of additional network attributes and define their contribution to network function and robustness.

Materials and methods

Model of the spindle assembly checkpoint

To formulate a model of the spindle assembly checkpoint, we consider a simplified sphere-like nucleus of radius R. A single unattached kinetochore positioned at the center generates a signal to inhibit Cdc20. Assuming that the inhibitory signal and Cdc20 is widely diffusible, and that Cdc20 is produced at the boundary of the nucleus with some rate ‘k_prod.', we found that the length scale was large enough for the inhibitory signal and Cdc20 to be distributed uniformly throughout the nucleus (see also the Supplementary information).

Cdc20 is denoted ‘c' in the model, the emitted inactive signal ‘m', and its active form as ‘m^*'.

Hence, the two different classes of inhibition were modeled with systems of ordinary differential equations (Figure 1B). Both systems were solved numerically using a standard Runge–Kutta algorithm and analytically (see the Supplementary information for the complete analytical solution).

To analyze the solutions, three measurable quantities were defined: amplification, reactivation time and noise resistance. The amplification is defined as the ratio between the amounts of Cdc20 when the checkpoint is active and inactive, thus giving an estimate of the inhibiting capability of the checkpoint. The reactivation time is the time it takes after the inactivation of the checkpoint to reach a certain fraction of its inactive steady-state value (90% was used consistently). The noise resistance was defined as the increase of Cdc20 after a perturbation lasting ‘t' seconds divided with the would-be steady-state level of the same perturbation (see Table I and the Supplementary information for details).

Model assumptions

The following assumptions are used:

1. The total amount of emitted complex ‘m_tot' is considered to be constant. This reflects the fact that mRNA of all the constituents of the MCC complex appear not to vary during the cell cycle (Spellman et al, 1998).

2. For simplicity, we assume that the production of active inhibitory complex (m ↔ m^*) is fast.

3. We also assume that both models are capable of inhibiting the Cdc20 in an efficient way. This implies that we either have a large m_tot (for physical tethering) or a high association/active degradation rate (for phosphorylation).

Rigorous mathematical formulation of these assumptions is given in the Supplementary information.

Supplementary Material

Supplementary Information