Markov propagation of allosteric effects in biomolecular systems: application to GroEL–GroES

Abstract

We introduce a novel approach for elucidating the potential pathways of allosteric communication in biomolecular systems. The methodology, based on Markov propagation of ‘information' across the structure, permits us to partition the network of interactions into soft clusters distinguished by their coherent stochastics. Probabilistic participation of residues in these clusters defines the communication patterns inherent to the network architecture. Application to bacterial chaperonin complex GroEL–GroES, an allostery-driven structure, identifies residues engaged in intra- and inter-subunit communication, including those acting as hubs and messengers. A number of residues are distinguished by their high potentials to transmit allosteric signals, including Pro33 and Thr90 at the nucleotide-binding site and Glu461 and Arg197 mediating inter- and intra-ring communication, respectively. We propose two most likely pathways of signal transmission, between nucleotide- and GroES-binding sites across the cis and trans rings, which involve several conserved residues. A striking observation is the opposite direction of information flow within cis and trans rings, consistent with negative inter-ring cooperativity. Comparison with collective modes deduced from normal mode analysis reveals the propensity of global hinge regions to act as messengers in the transmission of allosteric signals.

Introduction

A central goal in structural biology is to understand the mechanism of allosteric communication in supramolecular systems. Allostery is the cooperative process by which local effects propagate across the structure, often to regions spatially distant from initiation sites. A prime example of allostery is the transition of hemoglobin from low-affinity (T; tense) to high-affinity (R; relaxed) state upon oxygen binding. Two classical models have been proposed to describe allosteric transitions in such multimeric proteins: the Monod–Wyman–Changeux (MWC) (Monod et al, 1965) and Koshland–Nemethy–Filter (KNF) (Koshland et al, 1966) models. The former assumes a concerted, all-or-none change in all subunits, whereas the latter allows for the sequential transition of individual subunits. Although these models, and more complicated ones, are still being debated, the emerging view from experimental and computational studies is that many regulatory multimeric proteins, and in particular allosteric enzymes, possess the intrinsic ability to undergo MWC-like changes in structure, conferred by their three-dimensional (3-d) network of inter-residue interactions (in the absence of ligands). Such cooperative effects, enhanced by structural symmetry in the case of oligomers (Changeux and Edelstein, 2005), are usually triggered or stabilized upon ligand binding at particular susceptible sites (Tobi and Bahar, 2005). Recent computational studies also lend support to the intrinsic role of inter-residue contact topology in defining functional dynamics (Bahar and Rader, 2005; Ma, 2005). Yet, the pathways of signal transduction favored by the network of inter-residue contacts in supramolecular structures remain to be established.

The allostery-driven system we explore here is the bacterial chaperonin system GroEL–GroES, a widely studied molecular chaperone that assists folding of a subset of Escherichia coli proteins (Thirumalai and Lorimer, 2001; Saibil and Ranson, 2002; Horovitz and Willison, 2005). GroEL has a cylindrical structure, 150 Å long and 140 Å wide, consisting of 14 identical chains/subunits organized in two back-to-back stacked rings of seven subunits each (Xu et al, 1997) (Figure 1). Each chain is composed of three domains, equatorial (E1 and E2), intermediate (I1 and I2) and apical (A), sequentially ordered as E1-I1-A-I2-E2. During the allosteric cycle that mediates protein folding, the rings alternate between open (cis) and closed (trans) forms in an ATP-regulated manner, providing access to, or release from, the central cavity where the folding of encapsulated (partially folded or misfolded) protein/peptide is assisted.

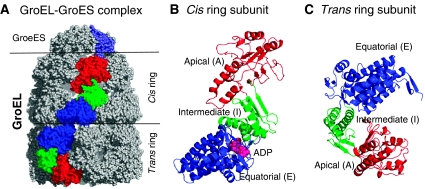
Figure 1.

Structure of the GroEL–GroES complex. (A) Space-filling model from the crystal structure determined by Xu et al (1997) (Protein Data Bank (PDB): 1AON). GroEL has a cylindrical structure, composed of two rings, termed the cis and trans rings, depending on the position of the GroES cap. Each ring in GroEL is composed of seven subunits. One subunit in each ring is shown in color (red, green and blue) in (A), along with one of the chains of the heptameric co-chaperonin (shown in gray/slate). The colored subunits on the GroES cap and the GroEL cis and trans rings correspond to three representative chains (identified as chains R, D and K in the PDB file (Berman et al, 2000)) whose communication dynamics will be examined below (see Figure 3C). (B) and (C) display ribbon diagrams of these two subunits belonging to the cis and trans rings, respectively. Each subunit consists of three domains, A, I and E, which refer to the apical, intermediate and equatorial domains, respectively. The corresponding residue ranges are: [A] Met193–Gly375; [I] Cys138–Gly192 (I1) and Val376–Gly410 (I2); and [E] Met1–Pro137 (E1) and Val411–Pro525 (E2). ADP molecule bound to the equatorial domain of the cis ring subunit is displayed in pink in panel B.

Chaperonin function requires an efficient communication between distant locations on the complex. For example, ATP binding to E-domains is accompanied by a cooperative conformational change (T → R) that facilitates the binding of co-chaperonin GroES at the A-domains in the same (cis) ring, whereas substrate binding and ATP binding to opposite (trans) ring triggers the release of GroES, substrate protein and ADP from the cis ring. Although several studies have been undertaken to unravel the mechanism of allostery in GroEL–GroES (Xu et al, 1997; Ma and Karplus, 1998; Sigler et al, 1998; de Groot et al, 1999; Ma et al, 2000; Thirumalai and Lorimer, 2001; Kass and Horovitz, 2002; Keskin et al, 2002; Horovitz and Willison, 2005), the underlying pathways of allosteric communication remain to be elucidated, as well as the key interactions that mediate the intra-ring (positive) and inter-ring (negative) cooperativity.

In this paper, we introduce a novel approach for unraveling potential pathways of signal transduction in large structures. Motivated by the recent success of network-based approaches in exploring structural motifs/mechanisms for allosteric communication (Keskin et al, 2002; Xu et al, 2003), we model structures as networks of residues (Bahar et al, 1997; Haliloglu et al, 1997; Hinsen, 1998; Doruker et al, 2000; Atilgan et al, 2001) and study the Markov propagation of ‘information' across these networks. We rely on the premise that signaling/communication ability is an intrinsic property of the 3-d structure and that naturally selected structures are those predisposed to optimally meet these functional requirements. We show how a Markovian network formalism based on information theory (Kullback, 1959; McLachlan and Basford, 1988; Chennubhotla and Jepson, 2005) and spectral graph methods (Chung, 1997) helps understand the pathways of communication between spatially distant sites and significantly reduces the complexity of the problem. In particular, we analyze how information diffuses between ATP-binding and GroES-binding sites in GroEL–GroES.

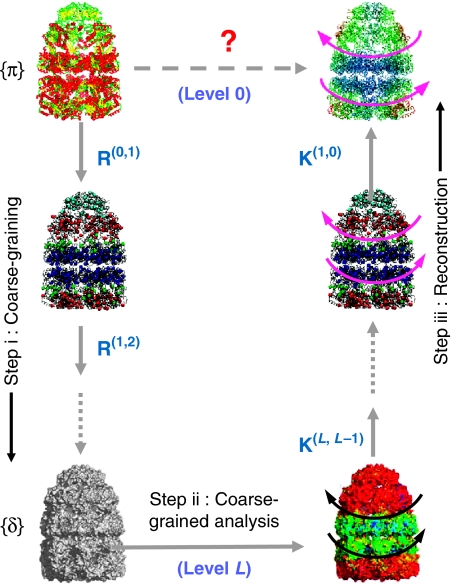
Our approach is structure-based, rather than sequence-based (Lock-less and Ranganathan, 1999; Kass and Horovitz, 2002; Stan et al, 2003; Suel et al, 2003), in that it maps a full-atom representation into a hierarchy of networks of decreasing resolution, performs the analysis of dominant patterns in reduced space(s) and reconstructs the detailed models with a minimal loss of information (Figure 2). Such dimensionality reduction algorithms based on Markov propagation stochastics expressed in terms of Fokker–Planck operator have been shown to convey useful information on the diffusion processes in complex systems (Bahar et al, 1994; Coifman et al, 2005; Nadler et al, 2006). The communication properties at different levels of the hierarchy allow for partitioning the complex structure into soft clusters. The probabilistic distribution of amino acids in these clusters, or the so-called ownership of residues by the clusters, permits us to evaluate the communication entropies of individual residues. Residues distinguished by high entropies possess a high potential to transmit allosteric signals, hence their identification as sites of large allosteric potential (Ming and Wall, 2005).

Figure 2.

Hierarchical network decomposition overview. Step i: mapping of the structure to its optimal reduced level representation (coarse-graining); step ii: structural/dynamic analysis—for example, GNM analysis of collective dynamics (Bahar et al, 1997; Haliloglu et al, 1997)—in the reduced space; and step iii: reconstruction of the detailed structure dynamics. The communication/couplings of residues at a given level are assumed to obey a Markov propagation process consistent with the distribution of atom–atom contacts in the original structure. Steps i and iii are achieved by two sets of operators, R for model reduction and K for model reconstruction (Chennubhotla and Jepson, 2005) explained in Materials and methods. Several models of intermediate complexity (not shown) are usually generated between the highest and lowest levels. R and K at each level ensure that similar stochastic characteristics (signal propagation probabilities and stationary distribution of communication) are retained between successive levels of the hierarchy. In particular, the reduction operator R^(l,l+1) propagates residue information from level l to l+1. Successive multiplication of such transformation matrices, as in R^(0,L)=∏_l=0^L−1 R^(l,l+1), ensures the passage of information from the original, or the highest, resolution representation (level 0) to the most reduced level (level L) of the hierarchy. The arrows on the right illustrate the most cooperative motion (counter-rotation of the two rings) predicted by elastic network model analysis of GroEL–GroES(ADP)₇ (Keskin et al, 2002).

Notably, our analysis provides evidence for the critical role played by the GroES mobile loops Glu18–Ala33 in establishing the communication with GroEL cis ring. Also, we identify the residues that establish positive intra-ring cooperativity. Negative cooperativity between the two rings is suggested by the tendency of the two rings to engage in intra-ring communication of opposite rotational direction. The cis ring E-domains exhibit stronger intra-ring coupling than their trans ring counterparts in the presently examined ADP-bound complex, and they unambiguously emerge as centers with the highest propensity for ‘broadcasting' perturbations to the entire structure. Finally, we identify residues acting as hubs and/or messengers for collecting and passing information across the network and we determine maximum likelihood communication pathways from nucleotide-binding site to co-chaperonin mobile loop across the rings. A significant property that emerges from the comparison of the present results with those from normal mode analysis of GroEL–GroES collective dynamics is the propensity of the global hinge sites identified with the Gaussian network model (GNM) (Bahar et al, 1997; Haliloglu et al, 1997; Bahar and Rader, 2005) to play the critical role of messengers in the transmission of allosteric signals, as will be demonstrated below.

Markov process of network communication

A discrete-time, discrete-state Markov process is defined by setting the communication probability between residue pairs to be a function of their interaction strength, also called affinity. In particular, the {ij}th element of the affinity matrix A={a_ij} is defined as

where N_ij is the total number of atom–atom contacts made between residues v_i and v_j based on a cutoff distance of r_c=4.5 Å and (N_i, N_j) are the total numbers of heavy atoms in the individual residues (v_i, v_j). The network may be alternatively viewed as a mass-spring system where pairs of (interacting) residues are connected by elastic springs with force constant a_ij=a_ji. The self-contact a_ii is similarly defined, but all bonded pairs are excluded. This representation captures to a first approximation the strong (weak) interactions expected to take place between residue pairs with large (small) numbers of atom–atom contacts, and removes biases due to size effects.

Using a measure of the local interaction density at each residue, given by d_j=∑_i=1ⁿ a_ij=∑_j=1ⁿ a_ji (where n is total number of residues in the network), which in matrix form is D=diag{d_j}, we define m_ij=d_j⁻¹ a_ij as the conditional probability of transmitting information to residue v_i in one time step given that the signal is initially positioned at residue v_j. Note, d_j serves as a normalizing factor to ensure ∑_i=1ⁿ m_ij=1. The conditional probability matrix M={m_ij}, also called the Markov transition matrix, given by

fully defines the stochastics of signal diffusion over the network of residues.

Suppose the probability of initiating the Markov propagation process at node j is p_j⁰. Then, the probability of reaching residue v_i in one time step is m_ijp_j⁰. In matrix notation, the probability of ending up on any of the residues v=[v₁, v₂,…,v_n] after one time step is given by the distribution p¹=Mp⁰, where p^k [p₁^k,…,p_n^k]. Clearly, this process can be iterated, so that after β steps we have

Assume there is a path connecting every pair of residues in the network. Then, as β → ∞, the Markov chain p^β approaches a unique stationary distribution π, the elements of which are given by π_i=d_i/∑_k=1ⁿ d_k. Whereas the evolution of the diffusion process is a function of the starting distribution, the stationary distribution is invariant to the details of initiation (Norris, 1997).

Hierarchical model reduction based on Markov stochastics

For a clear understanding of the most probable mechanisms of signal propagation across the structure, we mapped the original structure onto successively lower resolution network models, while maintaining its stochastic characteristics (Figure 2). To build a hierarchy of intermediate resolution networks, we devise two sets of new operators: R for model reduction and K for model expansion/reconstruction (see Materials and methods). The {ij}th element R_ij^(0,L) describes the probabilistic participation of residue v_i in cluster j at hierarchical level L. Alternatively, R_ij^(0,L) may be viewed as a measure of the ownership of residue v_i by cluster j generated at level L. The maximal ownership of a given residue v_i is defined as

for 1⩽k⩽c(L), where c(L) is the total number of clusters at level L. R_i,max^(0,L) provides a measure of the involvement of residue v_i in the cluster that maximally owns it. In particular, this property reflects the potential of a residue for serving as a hub in any cluster derived at level L.

We also define the entropy S_i^(0,L) of residue v_i as

where the summation is performed over all clusters. S_i^(0,L) provides a measure of the communication ability of residue v_i between clusters at level L. High entropy values refer to residues more or less uniformly shared by multiple clusters, thus playing the key role of a messenger in transmitting signals/perturbations. These are also referred to as sites having a high allosteric potential.

Soft partitioning of structure into stochastically coherent clusters

The GroEL–GroES(ADP)₇ structure (Xu et al, 1997) of n=8015 residues/nodes was mapped into a series of hierarchically reduced representations, comprised of c(L)=1316, 483, 133, 35 and 21 nodes for L=1–5, using the Markov chain propagation theory described in Materials and methods.

Each node at a given reduced level is a coherent cluster that provides a soft partitioning of the original structure, with regard to its communication stochastics, over increasingly large distance ranges. Thus, in contrast to the deterministic assignment of one-node-per-residue in the original network (level ‘0'), each cluster probabilistically contains a subset of residues, quantitatively expressed by its ownership distribution.

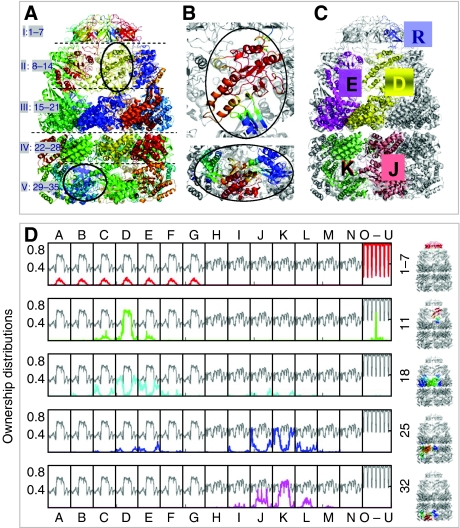
We focus on reduced level 4 (c=35) as the highest level that provides new insights into Markov propagation stochastics (level 5 practically partitions the complex into its 21 monomeric chains). Five sets (I–V) of seven symmetrically related clusters (Figure 3A) are obtained, centered near the GroES chains (clusters 1–7), the domains A–I (8–14) and E (15–21) of the cis ring and the domains E–I1 (22–28) and A–I2 (29–35) of the trans ring. Interestingly, the GroEL subunits are each partitioned into two clusters, although they comprise three structural domains E, I and A. Domain-I residues play a pivotal role, being integrated into E- or A-centered clusters, and their type and strength of participation in these clusters differ in the cis and trans rings. Panel B in Figure 3 illustrates the probabilistic participation of residues in two example clusters (encircled in panel A). The color code from red to blue indicates the gradually decreasing strength/probability of being owned by the particular clusters. A more quantitative analysis of these ownerships and comparison with experimental data are presented next.

Figure 3.

Soft partitioning of the chaperonin complex into stochastically coherent clusters. A total of 35 clusters are identified at reduced level 4, each shown by a different color in (A). Owing to the seven-fold cylindrical symmetry, five distinct types of clusters are observed: clusters (I) 1–7 centered on the GroES monomers, (II) 8–14 centered on A–I domains of the cis ring subunits, (III) 15–21 around the E-domain of cis ring subunits, (IV) 22–28 near the E–I domains of trans ring subunits and (V) 29–35 near A–I domains of trans ring subunits. (B) displays The soft participation of residues in two example clusters encircled in panel A, clusters 11 (top) and 32 (bottom) respectively, by ribbon diagrams, color-coded red–orange–yellow–green–cyan in the order of decreasing probabilistic participation. Results are valid for all cylindrically related seven subunits along the heptameric rings, but for illustration we focus on chains D (yellow) and E (magenta) on cis ring, J (pink) and K (green) on trans ring and R (blue) on GroES, in (C). (D) shows ownership distributions (curves in color) for representative clusters of different types, numbered 1–7, 11, 18, 25 and 32, with the associated clusters shown in color on the ribbon diagrams to the right. The labels on the abscissa indicate the chain identities: A–G on cis ring, H–N on trans ring and O–U on GroES cap. The gray curve in each panel shows the maximal responsibility curve deduced from the maxima of all ownership curves. The portions of the ownership curves, which overlap with the maximal responsibility curve, define the hard clusters displayed in panel A.

Intra- and inter-subunit couplings and biological implications

Five ownership distributions (labeled 1–7, 11, 18, 25 and 32 in Figure 3D; colored curves) are displayed, representative of each respective type (I–V) of clusters (Table I). The chain identifiers (A–G for cis subunits, H–N for trans subunits and O–U for GroES chains) adopted in the PDB (Berman et al, 2000) are shown along the abscissa. We focus on the subunits that are predominantly owned by the five representative clusters, that is, chains D, E, K, J and R, the locations of which on the 3-d structure are shown in Figure 3C. The results are valid for all seven symmetrically related clusters/subunits. The gray curve in each panel depicts the maximal responsibility R_i,max^(0,L) (equation (4)), assumed by residue v_i in the overall communication stochastics of the network.

Table 1.

Distribution of residues in representative clusters

	Cap	Cis		Trans
	Clusters 1–7	Cluster 11	Cluster 18	Cluster 25	Cluster 32
Chain R	ALL except E18–A33	E18–A33
Chain C			E1: A2–V6 E2: D523–P525
Chain D		A: ALL I1: ALL except  *S139–D140 I2: ALL except  A384–V387,  A406–G410	E1: ALL except  A2–V6,  V38–I49 E2: ALL except  D523–P525 I1: S139–D140 I2: A406–G410
Chain E			E1: V38–I49 I2: A384–V387
Chain K				E1: ALL except R36–K51 E2: ALL I1: C138—E164 I2: K393—G410	A: ALL I1: A165–E178,  Q184–G192 I2: V376-K380
Chain J				E1: R36–K51	I1: D179–L183 I2: V381–K392 A: V268–K272

See Figure 4 for the position of the clusters (in panel A) and GroEL-GroES chains (in panel D).

The ownerships of individual clusters reveal several functional features. Below is a summary of results and relevant experimental data by various groups (see also Table I and Supplementary Table S1 (Supplementary information)).

Key role played by GroES residues Glu18–Ala33 in achieving the communication between the cis ring and the co-chaperonin

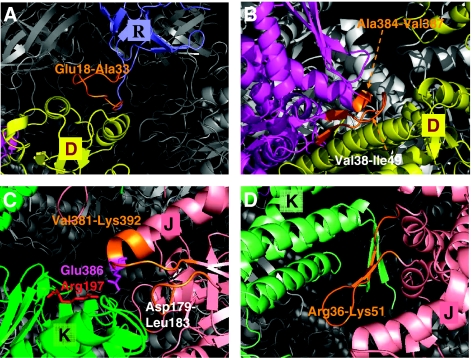
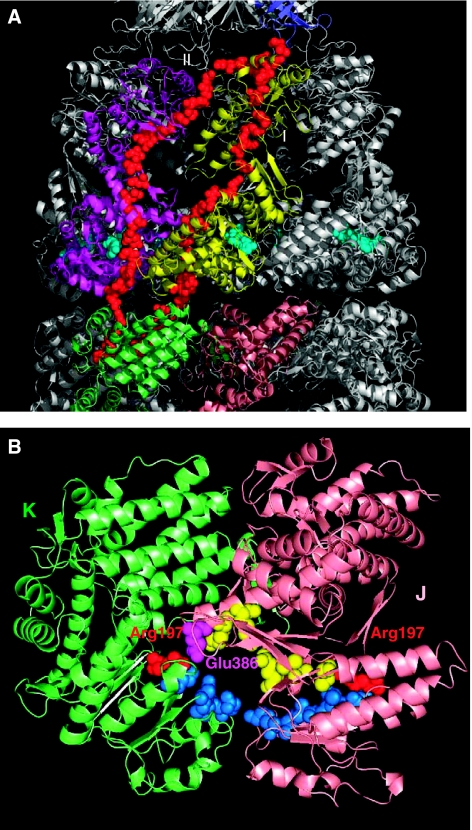
This segment coincides with the exceptionally long ‘mobile loop' that has been pointed out to serve as an allosteric modulator of the GroEL/substrate affinity (Landry et al, 1993) and chaperonin cycle speed (Shewmaker et al, 2001). It undergoes a transition from disordered to ordered (β-hairpin) form concomitant with binding to the A-domain of GroEL subunits (Shewmaker et al, 2004). Site-directed mutagenesis experiments also support its key role in chaperone function (Landry et al, 1993; Hohfeld and Hartl, 1994; Kovalenko et al, 1994; Richardson and Georgopoulos, 1999; Richardson et al, 1999, 2001). Our analysis demonstrates that this GroES loop is anchored into the apical domains of the adjoining cis ring subunits. This feature follows from the examination of the ownership curve for cluster 11 in Figure 3D. This cluster owns the entire A- and I-domains of chain D, except for a few residues in its I-domain (Ser139–Asp140, Ala384–Val387 and Ala406–Gly410). Remarkably, this cluster embodies the loop residues Glu18–Ala33 (peak at the O–U portion of the curve) that (chemically) belong to the neighboring co-chaperonin chain R. Figure 4A illustrates the mediating role of this loop (colored orange) between the apical domain of chain D (yellow) and the R chain of the cap (blue).

Positive intra-ring cooperativity imparted by crosstalks between the equatorial domains of adjacent subunits

Let us first examine cluster 18. The corresponding ownership curve in Figure 3D shows that this cluster is centered around the E-domain of subunit D. It embodies the entire E-domain except for the N- and C-termini (Ala2–Val6 and Asp523–Pro525) and the E1 residues Val38–Ile49. We note that Val38–Ile49 form two anti-parallel β-strands connected by a loop that extends toward the neighboring subunit C and indeed belong to the adjoining cluster centered at subunit C, whereas the same stretch of residues on subunit E is integrated into the cluster 18 centered on subunit D (Figure 4B). Thus, viewed from the cap, all seven clusters of type III recruit this particular segment from their clockwise neighbor into their own cluster. Figure 4B shows this subunit E segment (orange) at the interface between subunits D (yellow) and E (magenta).

In the case of trans ring, on the other hand, a close examination of cluster 25 ownership reveals that inter-subunit coupling is achieved by the segment Arg36–Lys51 on the equatorial domain. Figure 4D illustrates how this particular segment of subunit J establishes the bridge between subunits J (pink) and K (green). This type of insertion of segments of 10–15 residues into neighboring stochastically coherent clusters suggests a functional mechanism for ensuring inter-subunit, intra-ring communication. The repetition of the same type of coupling across all the seven subunits is consistent with the known positive intra-ring cooperativity.

Intra-ring couplings exhibit opposite rotational directions in the cis and trans rings

Clusters 25 and 32 on the trans ring are comparable to the respective clusters 18 and 11 on the cis ring, in that they are dominated by the respective domains E and A of their subunits. The counterpart of chain D becomes chain K (green in Figure 3C), and its most closely communicating neighbor is chain J (pink), which replaces E. The counterpart of Figure 4B becomes Figure 4D. Comparing these two panels, an immediate observation is that the trans ring clusters recruit segments (colored orange) from their counterclockwise neighbors when viewed from the cap, as opposed to the engagement of clockwise neighbors by cis ring subunits. We note that the two rings exhibit comparable contact topology and communication stochastics, when examined in isolation. However, their particular back-to-back arrangement within the quaternary structure results in opposite angular directions of communication around the cylindrical axis of symmetry. This anti-correlation in the communication directions of the two rings is suggestive of an intrinsic, structure-induced tendency to convey signals in opposite directions, which seems consistent with the well-known negative cooperativity between the two rings (Yifrach and Horovitz, 1995).

Figure 4.

A closer view of intra- and inter-subunit couplings at the interface of the clusters. Results are shown for the representative chains D (yellow) and E (magenta) on cis ring, J (pink) and K (green) on trans ring and R (blue) on GroES. The chain segments that establish the communication between clusters are colored orange. (A) Residues Glu18–Ala33 in the mobile loop (orange) of GroES chain R integrated into the cluster centered at the A-domain of chain D establish the communication between cis ring and co-chaperonin. (B) Positive intra-ring cooperativity imparted by the coupling of chain E residues, Val38–Ile49 and Ala384-Val387 shown in orange, into cluster 18 dominated by chain D. (C) Inter-subunit couplings at trans ring A-domains. Cluster 32 embodies the A-domain of chain K, but also captures a few residues (Val381–Lys392, Asp179–Leu183; shown in orange) from chain J. (D) Cluster 25 is centered on the E-domain of chain K on trans ring. Note that this cluster engages E1 residues Arg36–Lys51 from chain J. Negative cooperativity between the two rings can be compared by comparing panels B and D, both corresponding to the E-domains of the respective cis and trans rings. The residues serving as messengers (orange) between the subunits belong to either clockwise (panel B) or counterclockwise (panel D) neighbors, as viewed from the cap, that is, the two rings have opposite rotational direction of inter-subunit couplings. The distribution of different chain residues in the examined representative clusters is listed in Table I.

Coherence of trans ring assisted by inter-subunit communication between apical domains

Clusters 32 and 11 are both centered on the A-domains of the respective chains K and D. A striking difference between them is, however, the close involvement of an intra-ring neighbor J in the former, whereas the latter is confined to the single chain D. In other words, a coupling between adjacent subunits on trans ring is ensured by the apical-domain-centered clusters, whereas their counterparts in the cis ring do not entail any intra-ring communication, but rather a coupling to the cap chain R. Two segments from I-domains of chain J are recruited by chain K: Asp179–Leu183 and Val381–Lys392 (Figure 4C).

This type of I–A domain inter-subunit coupling operating exclusively in trans ring may fulfill a functional requirement, in that the trans ring, when compared to cis, lacks the stabilizing effect of a bound co-chaperonin cap. Among the two stretches of residues that achieve this stabilizing effect, we note, in particular, that Glu386 on chain J forms a salt bridge with Arg197 on chain K (Figure 4C). This interaction has been pointed out to be crucially important for interlocking the seven subunits in their ‘closed' form assumed in the trans ring; in the ‘open' form of the subunits (i.e. cis ring), on the other hand, these salt bridges are broken in concert with the conformational changes that accommodate the binding of ATP and co-chaperonin GroES (Braig et al, 1994; Yifrach and Horovitz, 1998; Ma et al, 2000).

Key structural elements mediating allosteric interactions

The present analysis permits us to identify two classes of key residues: those serving as hubs in the individual clusters at a reduced level representation, and those mediating the communication between these clusters.

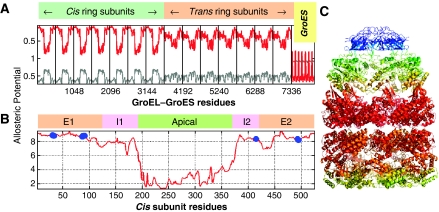
Hubs are distinguished by peaks in the maximal responsibility R_i^max distributions, shown by the (identical) gray curves in Figure 3D, also reproduced in Figure 5A. The hubs identified on the cis ring are Ile333–Asp334, Lys321–Val323, Glu214–Ser217. Interestingly, the hubs coincide with β-strands termini or β-hairpins, or helices, suggesting a role for secondary structures in mediating allosteric communication. Val323 was also identified as an important site for allosteric communication in the study of Kass and Horovitz (2002). We note that no hub center is located on the intermediate domains. The I-domains indeed serve as regions for communication (messengers), rather than collection (hubs), of signals. As to the trans ring, Arg350–Glu355 in the apical domains and Val128–Glu129 serve as hub centers. Finally, we note that the GroES chains yield very high peaks in the R_i^max distributions (Figure 3D). The corresponding hubs are found to be Glu50–Glu53.

Figure 5.

Regions of high broadcasting ability. (A) Residues acting as hubs lie on the peaks of maximal responsibility curve shown in gray, whereas residues shared by multiple clusters take on the job of messengers. They have high entropy values (red curve). (B) A detailed representation of the entropy curve for subunit D in the cis ring. Blue circles represent residues making at least two atom–atom contacts with the ADPs in the GroEL–GroES(ADP)₇ complex. All amino acids in/near the nucleotide-binding pocket are located in this high entropy region. (C) Entropy values as a color-coded ribbon diagram. Code: red–orange–yellow–green–blue, in the order of decreasing entropy. Equatorial domains of the cis ring subunits possess the highest entropy values, whereas the cap residues are distinguished by their low entropies.

The residues in the second class are shared by multiple clusters, and take on the job of messengers between these clusters. They are distinguished by their high allosteric potential, that is, their high ‘entropy' values, S_i^(0,L), deduced from their stochastic participation in different clusters (equation (5)). Both the red curve in Figure 5A and B and the color-coded ribbon diagram in panel C (colored from red-to-blue with decreasing entropy) reveal that the E-domains on the cis ring possess the highest entropies in the GroEL–GroES complex. The caps are distinguished by their low entropies.

In terms of the ability to communicate information, the predicted entropies point to the propensity of the cis ring E-domains to ‘broadcast' information to all other structural parts, and in particular to transmit allosteric signals across the ring–ring interface. The highest entropy residues presently identified (peaks in Figure 5B) are Glu461–Val464, and Thr30–Lys34 in both cis and trans rings. Strikingly, the mutant E461K has been shown in a recent study by Saibil and co-workers (Sewell et al, 2004) to cause defective folding. This behavior has been explained by the fact that the signal induced by ATP binding to the trans ring could not be transmitted across the ring–ring interface, and consequently the cis ring could not release its bound GroES. This observation lends support to the role of these highest entropy residues in ensuring the communication between the two rings. Finally, we note that ATP-binding residues generally exhibit high entropies, consistent with the requirement to propagate signals to distal regions. The filled circles in Figure 5B refer to the amino acids Pro33, Thr90, Gly88, Ile493, Leu31, Gly32, Thr91, Asp495, Gly415 and Asp87 that coordinate ADPs in the examined structure.

Proposed path(s) of communication between nucleotide- and co-chaperonin-binding sites

Among the residues located in the nucleotide-binding site, two highly conserved residues are distinguished by their large number (⩾15) of atom–atom contacts with ADPs: Thr90 and Pro33. We focused on these two residues as initiation loci for signal transmission, and examined how the allosteric communication with the co-chaperonin-binding site is established. The GroES residues Ile25 and Gly24, reported in previous work to be conserved (Stan et al, 2003), were found here to act as communication cores (highest R_i^max) within the loop residues. So we explored the maximum likelihood pathways originating from Thr90/Pro33 in the trans ring and ending at GroES-Ile25/Gly24, by using an algorithm similar to the shortest-path algorithm of Dijkstra's (Cormen et al, 1990). In particular, we define the distance between two residues v_i and v_j in the network as −log(m_ij); so the higher the communication probability, the lower the distance between nodes, and these distances in turn are taken into consideration in evaluating the maximum-likelihood path.

Figure 6A displays the resulting two maximum likelihood pathways. The first, labeled (I), runs between Thr90 (subunit K) and Ile25 (subunit R) following the scheme T90 → V94 → N97 → T101 → K105 → A109 on subunit K, succeeded by K105 → E102 → I99 → A508 → Q505 → R501 → E409 → E408 → R404 → V174 → A370 → K371 → M193 → I332 → I220 → F219 → V240 → A241 on subunit D and ending at I25 → G24 on the cap chain R. The shortest path originating from Pro33 (labeled (II) in Figure 6A), on the other hand, is P33 → G32 → I454 → R452 → on chain K succeeded by E461 → E460 → C458 → K34 → P33 → N153 → S154 → D155 → V158 → L161 → L187 → V189 → V190 → Q194 → F195 → R197 → G198 → Y199 → P202 → Y203 on chain E and I305 → G306 → K311 → E310 → M233 → L234 on chain D, and finally ending at G23 → G24 on the cap chain R. Interestingly, these two paths, both originating from the same ATP-binding region on subunit K in the trans ring evolve through different subunits (D and E) on the cis ring to merge at the same target site on the co-chaperonin mobile loop.

Figure 6.

Inter- and intra-ring communication pathways. (A) Two maximum likelihood pathways (red spheres), labeled I and II, originating from residues Thr90 and Pro33 respectively, on subunit K near the nucleotide-binding site, and ending in residue Gly24 on the GroES mobile loop. The ADP molecule near subunit D is shown in cyan. (B) Maximum likelihood pathway originating from Arg197 (red) on subunit K and ending in Arg197 (red) on subunit J. The pathway is shown in yellow, achieved readily through the salt bridge Arg197–Glu386. Residue Glu386 on subunit J is shown in magenta. Also shown in blue is the pathway computed for the mutant R197A. The latter involves four additional residues in subunit K.

Several residues on these pathways exhibit interesting features: the boldfaced ones are conserved within the Hsp60/GroEL family (Fenton et al, 1994; Stan et al, 2003); and those written in italic are distinguished by their high communication entropies. We note that the intra-subunit interaction between residues E409 and R501 has been pointed to be implicated in the allosteric mechanism of GroEL (Aharoni and Horovitz, 1997). We also note that D155 has been pointed out to disrupt the intra-ring cooperativity of the ATP-bound ring (Danziger et al, 2003; Horovitz and Willison, 2005). Inter-ring cooperativity was observed by Aharoni and Horovitz (1996) to be disrupted in the GroEL double mutant (R13G, A126V), while the double mutant was functional both in vivo and in vitro (Fenton et al, 1994). These residues could not be observed in the presently examined maximum likelihood pathways.

The on-pathway residues at the interface between the cis and trans rings (A109, K105, R452, E461) should be expected to play a key role in assisting the communication between the two rings. We note among them Glu461 in cis subunit E that is receiving signal from R452 on trans subunit K. Note that Glu461 is the residue whose substitution by lysine has been shown in a recent work by Saibil and co-workers (Sewell et al, 2004) to impede the release of the co-chaperonin (bound to the cis ring). This long-range effect has been shown to be owing to the disruption of the inter-ring transmission of the signal from ATP-binding site on the trans ring, caused by the of the originally out-of-register alignment of subunits across the rings (K, D and E in the present case) into in-register alignment (Sewell et al, 2004). The present analysis demonstrates that Glu461 (on cis subunit E) is indeed on the most probable pathway, and significantly, it forms an intermolecular salt bridge (with R452 on trans subunit K) at the interface between the two rings.

Additionally, the above analysis focuses on inter-ring communication. Of interest is to assess pathways of intra-ring communication as well (Figure 6). We focus in particular on R197, a conserved residue whose mutation to alanine has been pointed out in previous work to elicit allosteric changes (White et al, 1997). As pointed out above, Arg197 participates in the small set of residues (see Table I and Supplementary Table S1 (Supplementary information)) that establish the inter-subunit communication in the trans ring, by way of forming a salt bridge with Glu386. In order to assess the role of Arg197 in ensuring/facilitating the intra-ring communication, we explored the maximum likelihood pathways originating from Arg197 on trans ring and ending, again, on Arg197 in neighboring subunit in the same ring (an effect that propagates across all seven subunits in the ring). In Figure 6B, residue R197 is shown in red on subunits K and J. Calculations were performed both for the wild-type protein and the R197A mutant generated in silico. We obtained the path

for the mutant, as opposed to the path

for the original structure. Here the subscripts refer to the subunits involved, and conserved residues (Fenton et al, 1994) are shown in boldface. Clearly, the wild-type sequence samples a much shorter pathway. The passage across the two subunits is readily achieved through the salt bridge R197–E386 at the initiation step. In Figure 6B, residue Glu386 is shown in magenta on subunit J. A cascade of charge–charge interactions is implicated in this pathway, suggesting an effective signal transfer mechanism. The most probable path undertaken by the mutant R197A, on the other hand, involves four additional residues in subunit K, before reaching the neighboring subunit J. In particular, the interaction with the conserved residue K277 seems to favor this longer pathway.

Correlation with collective dynamics: physical role of hubs and messengers

Significant progress has been made in recent years in improving our understanding of the collective dynamics of biomolecular systems in relation to their biological functions and interactions, using normal mode analyses with coarse-grained models (Bahar and Rader, 2005; Ma, 2005). The GNM (Bahar et al, 1997; Haliloglu et al, 1997) is such a model widely resorted to in recent years. Based on statistical mechanical theory of macromolecular networks (Flory, 1976), the GNM provides a rapid assessment of the key mechanical sites (e.g., hinges) that coordinate global (domain) motions (see e.g. Yang and Bahar (2005) for a systematic analysis of enzyme dynamics). The application of the GNM and its extensions to GroEL–GroES (Keskin et al, 2002) has shown that concerted counter-rotations of the cis and trans rings are the most probable collective motions intrinsically favored by the overall architecture, in accord with the motions deduced from the comparison of X-ray or cryo-EM structures determined in different states.

The approach taken by the GNM analysis is to deduce the spectrum of normal modes from the eigenvalue decomposition of the Kirchhoff matrix of inter-residue contacts, Γ, specific to the examined structure/network topology. A bridge between signal propagation dynamics presented here (based on information theory, graph theoretic methods and Markovian stochastics) and the GNM dynamics (based on fundamental concepts of solid state physics and macromolecular statistical mechanics) is the relationship

Equation (6) identically holds provided that the nonzero off-diagonal elements of A and Γ are defined as a_ij=Γ_ij=1 in line with the original GNM, or as

after the presently defined affinity matrix (equation (1)). The latter provides a more detailed description of inter-residue interactions than the original GNM, as it incorporates information on the density of atom–atom contacts in addition to the information on network connectivity. Γ is also referred to as the combinatorial Laplacian in graph theory (Chung, 1997).

The equilibrium dynamics of the network is fully defined by Γ; in particular the mean-square fluctuations of residues are readily computed from the relation

where [Γ⁻¹]_ii designates the ith diagonal element of the inverse of Γ, k_B is the Boltzmann factor, T is the temperature and γ is the spring constant that uniformly scales the amplitudes of fluctuations, without affecting their residue distributions (for a review see Chennubhotla et al, 2005).

We used the presently introduced Markov chain-based hierarchy to build reduced Kirchhoff matrices,

at increasingly lower levels of resolution, ranging from c=8015 nodes at the full-residue representation to c=21 nodes at level L=5, congruent with the à matrices derived at various hierarchical levels. We repeated the GNM analysis at successive levels to explore how well the original (L=0) fluctuation behavior is preserved upon mapping the structure to its lower resolution counterparts, performing the GNM analysis in the reduced spaces and reconstructing the fluctuation dynamics at the original level (see the scheme in Figure 2). We call this new approach the hierarchical GNM (see Chennubhotla and Bahar, 2006 and Supplementary information for more details). In addition to this ‘fidelity' test, we also explored how the correlation between theoretically predicted mean-square fluctuations of residues and experimental data, X-ray crystallographic B-factors in this case, varies by adopting various levels of coarse-graining.

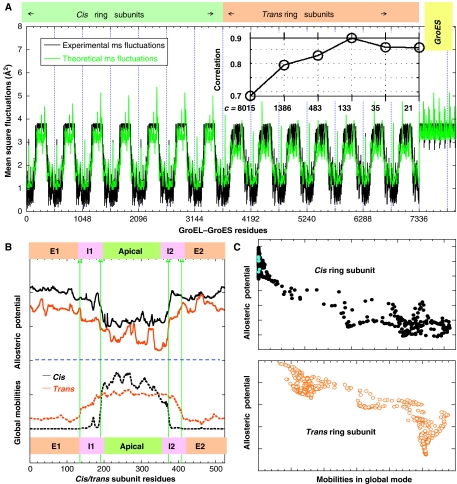
Figure 7A displays the comparison of the fluctuations of residues, 〈Δr_i^T Δr_i〉, obtained at various levels of Markov hierarchy with those indicated by the X-ray crystallographic B-factors (black curve) B_i=(8π²/3)〈Δr_i^T Δr_i〉 reported in the PDB (Xu et al, 1997). The theoretical fluctuations computed at various levels are hardly distinguishable and are all represented by the red curve. As shown in the inset, a correlation coefficient of 0.86 is achieved between experimental and theoretical fluctuation distributions after mapping the structure of 8015 residues into a network of 21 soft clusters. Thus, the fluctuation profile of residues is accurately predicted despite a drastic reduction in the complexity of the examined network. Interestingly, a maximum correlation coefficient of 0.89 is obtained at an intermediate level of resolution, c=133, which may be attributed to an optimal elimination of noise in the data.

Figure 7.

Collective dynamics and comparison with communication entropies. (A) Comparison of the experimental (black) and theoretical (green) distributions of mean-square fluctuations of residues. The theoretical curve is reconstructed from level 3 of the hierarchy. The inset shows the correlation coefficient between the theoretical B-factors derived from each level of the hierarchy (from full residue representation (c=8015) to the coarsest scale (c=21) and the experiment. Interestingly, the full residue representation (with 8015 residues) yields a correlation coefficient of 0.68 that is lower than coarse-grained representation. In particular, at level 3 (c=133), the correlation coefficient is 0.89. (B) Comparison of the communication potentials (entropies) of residues (upper panel) with their mobilities in the global mode (lower panel) for trans (orange) and cis (black) ring subunits. The communication entropies are computed using equation (5), at level L=4. Mobilities (normalized square displacements) are found from the lowest frequency GNM mode, almost identically reproduced at all levels of the hierarchy. (C) (Anti-)correlation between communication entropies and global mobilities, shown for the cis (top) and trans (bottom) ring subunits. The two sets of data yield respective correlation coefficients of 0.94 and 0.89, revealing a dual role, both mechanical stability and efficient signal propagation for a subset of residues distinguished by their restricted mobility. Also shown in panel C as blue dots are the locations of ATP-binding residues Leu31–Pro33, Asp87–Thr91, Gly415 and Asp495, exhibiting high entropies and low mobilities.

Next, we examine the role of hubs and messengers in the context of the collective dynamics of GroEL/GroES. It is also of interest to elucidate the type of involvement of residues distinguished here by their high allosteric potentials (maxima in entropy curve (red) in Figure 5A) in the most cooperative (global) modes of motion of the entire complex. A comparison of the entropy profiles of residues in the cis and trans ring subunits with their mobilities in the global mode of the chaperonin is presented in Figure 7B. The mobility profiles represent the distributions of square displacements in the lowest frequency mode, determined by eigenvalue decomposition of

for the entire complex. We note that the global modes are also verified to be maintained with a correlation coefficient of 0.99 at all levels 0⩽L⩽5 of the hierarchy. The high mobility of the apical domain delimited at the A–I interfaces is revealed in Figure 7B, while the equatorial domains are rather stable. An immediate observation is the anti-correlation between the two sets of profiles in the top and bottom panels of Figure 7B. This property is more evident in panel C, where a decrease in allosteric potential is accompanied by an increase in mobility, in general. Thus, the minima in the global mode profiles, which have been shown in numerous applications to play a critical role (acting as hinges or anchors) in coordinating the functional dynamics of biomolecules (Bahar and Rader, 2005; Ma, 2005), act as messengers in the transmission of allosteric signals. Also shown in Figure 7C as blue dots are the locations of ATP-binding residues Leu31–Pro33, Asp87–Thr91, Gly415 and Asp495, exhibiting high entropies and low mobilities.

Conclusions

In the present study, we introduced a new methodology for elucidating the pathways of allosteric communication in large biomolecular systems. The approach is based on Markov propagation of information/perturbation over the network of interactions that stabilize a given structure. The approach permits us to simplify the original complex structure as a collection of ‘soft clusters' at different levels of resolution. Each cluster probabilistically ‘owns' groups of residues obeying coherent signal propagation stochastics. Those residues more or less equally ‘shared' by adjoining clusters are instrumental in transmitting information across clusters and serve as messengers, whereas those almost completely owned by a given cluster serve as hubs. This description greatly simplifies our understanding of the dominant mechanisms and key elements that mediate the communication across distant regions in complex structures.

Using this new framework, we identified two pathways that are most likely to mediate the communication between the ATP- and co-chaperonin-binding sites (Figure 5D), comprising many conserved residues as well as those serving as hubs or detected in previous studies to be critical for chaperonin machinery. Two alternative mechanisms seem viable inasmuch as this coupling between E- and distal A-domains is crucial for function. We note that in a recent φ-value analysis, Horovitz et al (2002) presented evidence for the existence of parallel pathways for the allosteric transition of the rings.

Our analysis highlights the pivotal role played by the I-domain in establishing intra-ring and inter-subunit communication. We observed inter-subunit I–A domain couplings that operate exclusively at trans ring. This may be a functional requirement, to ensure the coherence of the trans ring that lacks, compared to the cis ring, the stabilizing effect of the bound co-chaperonin cap. Among the residues that achieve this stabilizing effect, we note, in particular, Glu386, which forms an inter-subunit salt bridge with Arg197, confirming previous results (see Table I and Supplementary Table S1 (Supplementary information)). We also studied the effect of the mutation R197A on intra-ring communication. R197 on the trans ring E-domain exhibits a strong preference to communicate with its salt-bridge-forming partner E386 on the nearest cis ring subunit in the wild-type structure, whereas the mutant R197A generated in silico preferentially interacts with K277 and D253 on the same (trans) ring, and reaches the cis ring via a substantially longer pathway.

A most striking observation is that inter-subunit couplings occur in opposite directions in cis and trans rings. Intriguingly, the information flows presently identified within the cis and trans rings have well-defined preferences for opposite rotations (clockwise versus counterclockwise, when viewed from the cap). For example, subunit D engages E in the cis ring, whereas K engages J in the trans ring (see Figure 4B and D). It should be noted, however, that this cooperativity is different in character than the one observed within rings. The intra-ring cooperativity is inherently ensured by the association of neighboring clusters via residues that are being shared, repeated across all seven subunits, consistent with a classical MWC cooperativity (Monod et al, 1965; Horovitz and Willison, 2005). Such an integration of neighboring clusters is not observed across the interface between the two rings. The lack of a close cluster association at the interface, in contrast to that occurring within the rings, suggests that the stochastics of intra- and inter-ring couplings differ in their character and timescale, reminiscent of MWC type (intra-ring) interactions nested in KNF-like (Koshland et al, 1966) inter-ring interactions (Horovitz and Willison, 2005).

The present analysis takes account of residue specificities in an approximate way (through the numbers of atom–atom contacts for each residue pair) and does not distinguish between strong or weak interactions. No electrostatic and solvent effects are included either. Despite the neglect of these physical features, the method offers a plausible model for information propagation between distinct functionally relevant sites of GroEL–GroES. The property rigorously taken into consideration here is the intricate topology of inter-residue contacts and local packing/interaction densities in the native state. The present analysis thus lends support to the dominant role of inter-residue contact topology in defining cooperative interaction mechanisms/pathways on a global scale, in accord with recent computational studies based on coarse-grained models (Bahar and Rader, 2005).

Identification of hubs and messengers raises implications for protein design. In the network communication paradigm, the equatorial domains of the cis ring emerge unambiguously as the regions with the highest propensity for ‘broadcasting' the perturbations occurring in their domain. In particular, the E-domain residues Ser463 and Glu461 emerge as the amino acids with the highest allosteric potential (see equation (5); Figure 5). The critical role of Glu461 in establishing the negative inter-ring cooperativity is now established by the recent work of Saibil and co-workers (Sewell et al, 2004), whereas that of Ser463 remains to be experimentally confirmed. The high broadcasting ability does not necessarily imply efficient transmission to a given target because the signal can be dissipated in many directions. Yet, the observed involvement of messengers in maximum likelihood pathways may have other functional implications, for example, inducing other co-operative effects such as processing the substrate protein. We also examined the role of hubs and messengers in the context of collective dynamics of GroEL/GroES deduced from normal mode analysis. A significant property that emerges is that the minima in global mode profiles, which have been shown to play a critical role in coordinating functional dynamics of biomolecules, act as messengers in the transmission of allosteric signals. Automated identification of such residues serving as hubs and messengers in a given architecture, as proposed and illustrated here for GroEL–GroES, may help in efficient design and modification of protein structure and function.

Materials and methods

Deriving stationary distribution in the reduced model

We begin by expressing the stationary distribution π=[π₁, π₂, …, π_n] as a probabilistic mixture of latent distributions,

where δ=[δ₁,δ₂,⋯,δ_c] is an unknown stationary distribution in a reduced (c-dimensional) representation of the structure, K={K_ij} is an n × c non-negative kernel matrix with elements K_ij and columns K_j being latent probability distributions that each sum to 1 and c≪n. The kernel matrix acts as an expansion operator, mapping the low-dimensional distribution δ to a high-dimensional distribution π (see Figure 2). The high-dimensional distributions are referred to as high- resolution, or low-level, descriptions, and the low-dimensional distributions, as low-resolution, or high-level, descriptions.

We derive a maximum likelihood approximation for δ using an EM type algorithm (McLachlan and Basford, 1988). To this aim, we minimize the Kullback–Liebler distance measure (Kullback, 1959) between the two probability distributions π and Kδ, given by

A maximum likelihood estimate is obtained by minimizing

subject to the constraint ∑_j=1^c δ_j=1, ensured by the Lagrange multiplier λ. Setting the derivative of E with respect to δ_j to be zero, we obtain

The contribution made by kernel j to a node i (or to its stationary probability π_i) is given by K_ij (or by the product K_ijδ_j), and hence we can define an ownership of node i in the high-resolution representation by a node j in the low resolution as

We note that the mapping between the two resolutions is not deterministic, but probabilistic in the sense that ∑_j=1^c R_ij=1.

Using this relation, and the equalities ∑_j=1^c δ_j=1 and ∑_i=1ⁿ π_i=1, summing over j in equation (10) gives λ=1. This further leads to the stationary distribution δ at the coarse scale

Following Bayes theorem, K_ij can be related to the updated δ values as

In summary, the operators K and R and stationary distribution δ are computed using the following EM type procedure: (1) select an initial estimate for K and δ (see Supplementary information for details); (2) E-step: compute ownership maps R using equation (11); (3) M-step: estimate δ and update K using equations (12) and (13) respectively; and finally, (4) repeat E- and M-steps until convergence.

Transition and affinity matrices at reduced levels

The Markov chain propagation at the reduced representation obeys the equation q^k+1=M̃q^k, where q^k is the coarse scale m-dimensional probability distribution after k steps of the random walk. We expand q^k into the fine scale using p^k=Kq^k, and reduce p^k back to the coarse scale by using the ownership value R_i,j as in q_j^k+1=∑_i=1ⁿ p_i^k R_i,j. Substituting equation (11) for ownerships, followed by the expression for p^k, in the equation for q_j^k+1, we get

Using the definition of M̃, and the corresponding stationary distribution δ, we generate a symmetric affinity matrix à that describes the node–node interaction strength in the low-resolution network

To summarize, we use the stationary distribution π and Markov transition matrix M at the fine scale to derive a transition matrix M̃, and its stationary distribution δ, at the coarse scale. It is obvious that this procedure can be repeated recursively to build a hierarchy of lower resolution network models.

Application to GroEL–GroES: interactions/affinities at different hierarchical levels

We examined the Markov process of inter-residue communication in the structure GroEL–GroES(ADP)₇, crystallographically characterized by Sigler and co-workers (Xu et al, 1997), also known as the R′′ state of the bacterial chaperonin (Thirumalai and Lorimer, 2001). First, the inter-residue affinity matrix A based on all atom–atom contacts (a total of ≈10⁶ interactions, based on an interaction range of 4.5 Å between all non-bonded heavy atoms) is constructed, which is then used in equation (2) to derive the fine-scale Markov transition matrix M.

The kernel selection algorithm (Supplementary information) applied to M^β (β=4) yields 1316 (reduced level 1) kernels. Using these kernels as an initialization, a recursive application of the EM procedure derives stationary distributions δ (equation (12)), updated expansion matrices K (equation (13)), reduced level probability transition matrices M̃ (equation (14)) and the corresponding residue interaction matrices à (equation (15)). The respective dimensions of à turn out to be 483 (level 2) , 133 (level 3), 35 (level 4) and 21 (level 5). We note that the individual subunits of the GroEL–GroES are distinguished by their strong intra-subunit interactions, and a number of inter-subunit contacts are maintained at all levels, which presumably establish the communication across the protein at all levels. The dimension of the reduced model, c, is automatically defined during the kernel selection at each level of the hierarchy. The method thus avoids the arbitrary choices of sampling density and interaction cutoff distances at different hierarchical levels.

Supplementary Material

Supplementary Information