A driving and coupling “Pac-Man” mechanism for chromosome poleward translocation in anaphase A

Abstract

During mitosis, chromatid harnesses its kinetochore translocation at the depolymerizing microtubule ends for its poleward movement in anaphase A. The force generation mechanism for such movement remains unknown. Analysis of the current experimental results shows that the bending energy release from the bound tubulin subunits alone cannot provide sufficient driving force. Additional contribution from effective electrostatic attractions between the kinetochore and the microtubule is needed for kinetochore translocation. Interestingly, as the kinetochore moves to inside the microtubule, the microtubule tip is free to bend outward so that the instantaneous distance between the kinetochore and the microtubule tip is much closer than the rest of the microtubule. This close contact yields much larger electrostatic attraction than that from the rest of the microtubule under physiological ionic conditions. As a result, the effective electrostatic interaction hinders the further kinetochore poleward translocation until the microtubule tip dissociates. Thus, the kinetochore translocation is strongly coupled at the depolymerizing microtubule end. This driving-coupling mechanism indicates that the kinetochore velocity is largely controlled by the microtubule dissociation rate, which explains the insensitivity of kinetochore velocity to its viscous drag and the large redundancy in its stalling force.

During anaphase A, the kinetochore couples the chromosome to the plus end of microtubule spindle in an end-on manner (1–4). For budding yeast, the main kinetochore structure is a ring-like structure of many proteins (4–7). To achieve faithful chromosome segregation to its respective pole, the mitotic cell utilizes the combination of two major force-generation mechanisms that drive chromosome poleward translocation, both of which involve the kinetochore and the microtubule (8). One is the “microtubule flux” mechanism, where the dynein/dynactin-like motors drag the spindle microtubule poleward while the kinetochore microtubule undergoes treadmilling (8). The other is the “Pac-man” mechanism, where the driving force is generated by the kinetochore at the depolymerizing microtubule plus ends (1–4, 8). In the Pac-man mechanism, whereas the microtubule minus-end remains fixed at the pole, the kinetochore translocates at the depolymerizing microtubule plus end, as if it “chews” its way to the pole by itself. In this paper, we mainly focus on the Pac-man mechanism.

One fundamental question about the Pac-man mechanism (1, 3, 4) is: What is the origin of the driving force for the kinetochore movement? An important clue is that the stalling force for kinetochore poleward translocation is much larger than its apparent viscous drag force (9, 10). Conventional motor proteins would generate smaller forces for lower ATP level. However, during the stalling force measurements (10), the ATP level is normally abundant at ≈5 mM (11). Furthermore, it has been repeatedly shown that the kinetochore translocation could proceed normally even without ATP (3, 5, 7, 12–14), suggesting the existence of some generic driving force. Even more intriguing, it is found that the kinetochore poleward translocation speed is insensitive to its viscous drag force in low-Reynolds number limit (3, 15, 16). This observation strongly points to the possibility that it is the underlying spindle microtubule that governs the kinetochore translocation (3), instead of the kinetochore or chromosome itself. This finding suggests the further question: What is the coupling mechanism that firmly ensures kinetochore translocation at the depolymerizing microtubule end?

Many seminal experimental and theoretical studies (5–10, 12–20) are shedding light on these questions. It has been found that, as the tubulin subunits are incorporated into the microtubule, the chemical energy is converted into the bending strain. Upon microtubule depolymerization, the bending strain is released and provides a driving force for the kinetochore translocation (2, 12, 20). However, given the strong attachment of the kinetochore to microtubule of ≈12.5 k_BT (5, 14, 19), as our calculations in this paper suggest, a bending strain of ≈3 k_BT (2, 3, 20–23) is not sufficient. It has also been proposed that a ratchet-like biased one-dimensional diffusion model could account for the kinetochore translocation (17). Because of the diffusive nature of this model, it is predicted that there will be some considerable distance between the kinetochore and the microtubule tip (at least for certain period of time), although it appears this is not the case (5, 6). Furthermore, recent experiments (5, 6) identify another fundamental element in the kinetochore–microtubule system: the kinetochore ring complex interacts with microtubule through electrostatic attractions. How does this additional factor change kinetochore translocation dynamics?

Bearing the above facts in mind, we construct a minimal and unified theoretical model. Including all the identified energetic and dynamic factors, we investigate the basic principles of kinetochore translocation at the depolymerizing microtubule end. Our calculations suggest that the effective electrostatic attraction between the kinetochore and the microtubule could provide the additional driving force needed to overcome the kinetochore-binding potential and translocate it along the microtubule. More importantly, this effective electrostatic attraction quenches the ratchet-like diffusion by coupling the kinetochore translocation to the microtubule depolymerization. In this way, the microtubule dissociation rate essentially controls the kinetochore translocation velocity.

Theoretical Model

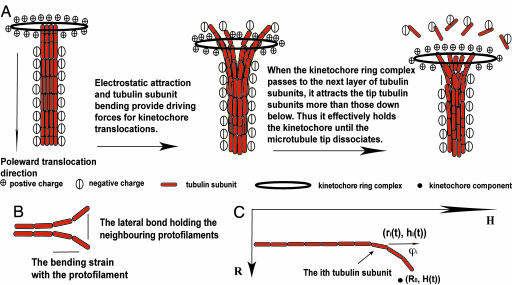
The central notion of the model is that the tip GDP–tubulin subunits flare out and push the kinetochore poleward, leading to a closer distance between the kinetochore and the tubulin subunits below the tip. This closeness enhances the effective poleward electrostatic attractions, which further drives the kinetochore translocation. Meanwhile, this poleward movement is opposed by the kinetochore binding potential at the tip, which constricts the curl-outs of the underlying tubulin subunits. As the kinetochore reaches the next tubulin subunit, the microtubule tip attracts it more than those down below, because the tip can now bend out much more and thus has a closer contact with the kinetochore. This asymmetry in the effective electrostatic attraction essentially prevents the further kinetochore poleward translocation until the tip dissociates. Thus, on one hand, the electrostatic attraction drives the kinetochore translocation; on the other hand, it couples the kinetochore translocation to the dissociating microtubule end.

Our model is schematically drawn in Fig. 1. The microtubule has a radius of 12.5 nm (5–7, 24). Its 13 protofilaments are assumed identical such that the microtubule configuration can be represented by one of the protofilaments. The protofilament is a series of N GDP–tubulin subunits connected end-to-end (N = 500 in the calculation corresponding to 4 μm length). Each subunit is modeled as a rigid rod of 8 nm long (l = 8 nm) (24), carrying a highly negative charge Q_MT ≈ 50 e per subunit (24, 25). The bound GDP–tubulin subunit has a preferred angle with respect to its neighbor ϕ⁽⁰⁾ = 0.4 rad (24). The bending strain ≈3 k_BT is thus stored in the subunits held in straight configuration (2, 3, 20–23), which is favored by lateral bonds ≈3 k_BT between the neighboring subunits in the adjacent protofilaments (19, 21, 22). In this paper, the kinetochore is represented as the Dam1 ring-like structure from budding yeast (5–7), which has a radius of 16 nm and consists of 16 identical components (5–7), each carrying at least six positive charges q_kt ≥ 6 under physiological conditions (5, 6). In an end-on manner, the kinetochore ring complex stays attached to the microtubule end via a harmonic binding potential ≈12.5 k_BT (5, 14, 19). The other end of the microtubule is fixed at the pole (denoted by zero height). The kinetochore ring complex also interacts with the rest of the microtubule through the electrostatic attraction, which is screened with a Debye length λ_D ≈ 1 nm. The total interaction energy V is

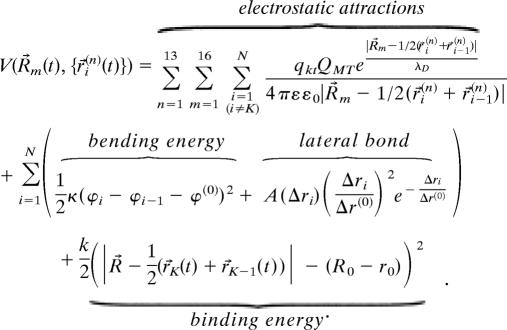In this paper, the electrostatic attraction refers to the interaction between the kinetochore and the microtubule subunits not directly bound to the kinetochore. The electrostatic interaction between the kinetochore and its bound tubulin subunits is absorbed into the binding potential. ε₀ = 8.85 × 10⁻¹² F/m and ε = 80 are used. R⃗_m(t) = (R₀, H(t)) is the position of the mth kinetochore component [radius R₀ = 16 nm and height H(t)]. Similarly, 1/2(r⃗_i + r⃗_i−1) is the mass center of the ith tubulin subunit along the nth protofilament (Fig. 1). The Kth subunit is the one that binds the kinetochore. h_i = h_i−1 + lcosϕ_i, ϕ_i = arcsin ((r_i − r_i−1)/l), Δr_i and Δr⁽⁰⁾ = 0.24 nm (20) are, respectively, the height, orientation angle, lateral bond length, and equilibrium lateral bond length of the ith subunit. The lateral bond strength corresponds to the maximum of A(Δr_i/Δr⁽⁰⁾)² e^{−Δri/Δr(0)} at Δr_i = 2Δr⁽⁰⁾, beyond which the lateral bond strength is zero. As the potential energy ΔE is stored in the tip, the effective microtubule dissociation rate is reduced k_off = k_off⁽⁰⁾e^−ΔE/kbT, and ΔE= 1/2κ(ϕ_tip − ϕ_next − ϕ⁽⁰⁾)² + A(Δr_tip)(Δr_tip/Δr⁽⁰⁾)² e^−Δr_tip/Δr⁽⁰⁾ + V_bind.

Fig. 1.

Schematic illustrations of the theoretical model on kinetochore-microtubule systems. (A) The central notion of the driving–coupling mechanism. (B) The interaction notions within the microtubule. (C) The kinetochore and the tubulin subunit's coordinate definitions.

Here, V_bind = k/2((r₀ − 1/2(r_tip(t) + r_next(t)))² + (H(t) − 1/2(h_tip(t) + h_next(t)))²) if the kinetochore binds to the tip; otherwise, V_bind is zero. k_off⁽⁰⁾ is the tubulin protofilament bare off-rate.

In the low-Reynolds number limit subject to thermal noise ξ_k1, the relaxation force from is balanced by the viscous drag: γ_MT dr/dt = −∂V/∂r_i and γ_kt dH/dt = −∂V/∂H + ξ_kt. As a leading order approximation, we absorb the chromatid effects into an effective drag coefficient for the kinetochore ring complex. Thus, in vivo, the kinetochore frictional drag coefficient is very large γ_kt ≈ 5–10 pN·s/μm (10, 26, 27); in vitro, with chromosome removed the kinetochore ring complex has a substantially reduced drag coefficient of γ_kt ≈ 0.1 pN·s/μm (6). It is estimated that a microtubule frictional drag coefficient of γ_MT ≈ 10–20 pN·sec/μm (see Supporting Text, which is published as supporting information on the PNAS web site). The Gaussian noise ξ_kt obeys 〈ξ_kt(t₁, r⃗₁)ξ_kt(t₂, r⃗₂)〉 ≈ γ_kt²D_kt/dt δ(t₁ − t₂)δ(r⃗₁ − r⃗₂), where the diffusion coefficient follows Einstein relations: D_kt = k_BT/γ_kt. The initial conditions are chosen such that the microtubule protofilaments are held up straight, and the kinetochore ring complex attaches to the center of the tip. The dynamics evolution is obtained by integrating the dynamic equations over time. (Further assumptions, the parameter estimates, and the simulation details are given in Supporting Text.)

Results

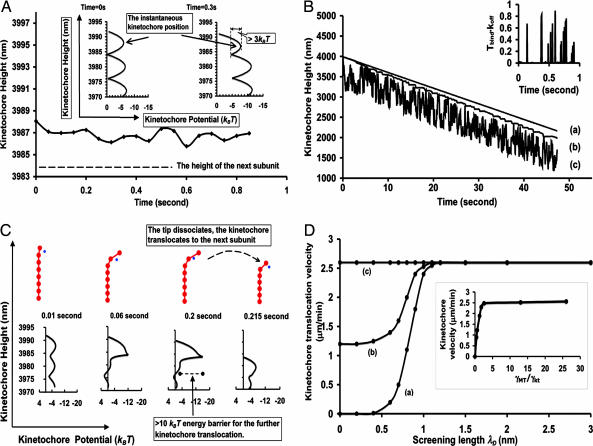
Fig. 2A shows that when the electrostatic attraction is zero, for the normal bending energy release per tubulin subunit (≈3 k_BT, refs. 21–23), the kinetochore can not pass to the next tubulin subunit before falling off together with the tip. As shown in Fig. 2A Inset, the kinetochore potential landscape becomes tilted towards the next subunit as the tip curls out. An energy barrier (≥3 k_BT), however, always remains due to the strong binding strength and lateral bonds. In vivo, given the small diffusion coefficient D_kt = k_BT/γ_kt ≈ 400–800 nm²/s, the kinetochore is thus trapped by this energy barrier. This trapping remains robust against the variations in binding energy, lateral bonds as well as bending energy under physiological conditions. Note that, for in vitro situations, with chromatid removed the kinetochore diffusion coefficient is ≈70 times larger (6), and the kinetochore cannot be trapped at all.

Fig. 2.

The kinetochore–microtubule dynamics. If not otherwise mentioned, the charge per kinetochore component q_kt = 6, the screening length λ_D = 1 nm, the binding energy is 12.5 k_BT, the bending energy is 3.0 k_BT, the lateral bond strength is 3.0 k_BT, k_off⁽⁰⁾ = 5 s⁻¹, and γ_kt = 5 pN·s/μm. The instantaneous kinetochore potential landscape is calculated from Eq. 1 (see Supporting Text). (A) Kinetochore translocation dynamics with zero electrostatic attraction q_kt = 0. (A Inset) The kinetochore potential landscape changes as the microtubule protofilaments flare out. An energy barrier (>3 k_BT) always remains, hindering the kinetochore translocation. (B) Kinetochore translocation dynamics with normal electrostatic attraction q_kt = 6. a, γ_kt = 5 pN·s/μm; b, γ_kt = 0.06 pN·s/μm; c, γ_kt = 0.03 pN·s/μm. (B Inset) k_offT_bind vs. time plot for B curve a. (C) The snapshots for the kinetochore–microtubule configuration and the corresponding kinetochore potential landscape during the kinetochore translocation in B curve a. Only the first a few tubulin subunits near the tip are shown for illustration purposes. (D) The kinetochore translocation dependence on the electrostatic attraction and the kinetochore diffusion. In a–c, γ_kt = 5, 2, and 0.15–0.02 pN·s/μm. (D Inset) The insensitivity of the kinetochore translocation velocity to the viscous drag.

When there is normal electrostatic attraction between the kinetochore and the microtubule, the kinetochore translocation at the depolymerizing end becomes sustained (Fig. 2B, curve a) and the energy barrier vanishes (Fig. 2C). The kinetochore is thus driven to the next layer of tubulin subunits by the downhill potential gradient. Because of the kinetochore constriction, the microtubule tip can not fully flare out (Fig. 2C). Thus, the stored strain energy as well as the binding potential significantly reduces the effective microtubule dissociation rate. The kinetochore residency time at the tip T_bind < 1/k_off (Fig. 2B Inset). This finding means, at the mean-field level, the kinetochore always has enough time to reach the next subunit before the tip dissociates. Fig. 2D shows that upon the driving force increase, the kinetochore velocity saturates at the microtubule bare off-rate. Conceptually, if the kinetochore reaches the next subunit before the tip dissociates, then the electrostatic attraction from the highly bent tip presents a large energy barrier >10 k_BT (Fig. 2C), preventing further kinetochore translocation until the tip dissociates. The peaks in Fig. 2B Inset correspond to the times when the kinetochore jumps back and forth between the tip and the next tubulin subunit. Thus, the kinetochore velocity is closely coupled and controlled by the microtubule dissociation rate, which is tightly regulated in cells (1–4, 28–32). This coupling mechanism explains the kinetochore velocity insensitivity on chromatid sizes (3, 15, 16), which directly correlate with its viscous drag. According to Fig. 2D Inset, if the kinetochore viscous drag coefficient is initially relative small compared with that of the microtubule, the kinetochore velocity could remain constant over 10-fold reduction in its viscous drag.

Fig. 2D also demonstrates the relative importance of the diffusion for sustained kinetochore translocations. When the electrostatic attraction decreases (λ_D ↓), there are three distinct cases. Curve a is the in vivo case. Given the small diffusion coefficient of the kinetochore, the energy barrier becomes insurmountable, and the kinetochore motion quickly gets stalled. For curve b, when the kinetochore diffusion is severalfold larger (smaller frictional drags), the kinetochore could translocate along the microtubule even without the electrostatic attraction; but the kinetochore translocation is slower than the microtubule bare shrinking rate. For curve c, when the kinetochore diffusion increases even further, it becomes so easy for the kinetochore to overcome the energy barrier and pass to the next tubulin subunit, such that the presence of the kinetochore does not reduce the effective microtubule tip dissociation rate much. Consequently, as the kinetochore undergoes the one-dimensional ratchet-like diffusion (17), its velocity is saturated at the bare microtubule shrinkage rate. As the electrostatic attraction increases (λ_D ↑), the kinetochore translocation velocity over large timescale (≈1 min) is limited at the bare microtubule shrinkage rate, independent of the diffusion. The kinetochore translocation behavior at the short time scale (<5 s), however, does depend on the kinetochore diffusion. As the kinetochore diffusion increases, it becomes more and more difficult for a fixed electrostatic attraction to couple the kinetochore translocation to the shrinking microtubule end, because the large diffusion could easily overcome energy barrier (>10 k_BT) imposed by the electrostatic attraction as the kinetochore passes to the next tubulin subunit (Fig. 2C). Thus, the kinetochore movement along the microtubule would change from the steady translocation at the shrinking tip (Fig. 2B, curve a) to the saltatory movement (Fig. 2B, curve b) (18), and to the complete ratchet-like diffusion with considerable distance between the kinetochore and the microtubule tip for some period of time (Fig. 2B, curve c).

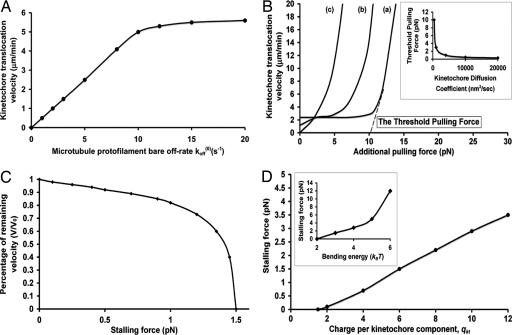
Fig. 3A shows the kinetochore velocity increases linearly with small k_off⁽⁰⁾. On the other hand, for large k_off⁽⁰⁾, the limiting factor for the kinetochore translocation velocity now becomes the kinetochore's first passage time to reach the next subunit, which is determined by the kinetochore driving force. In this case, the kinetochore velocity reaches the plateau ≈6 μm/min with increasing k_off⁽⁰⁾. As k_off⁽⁰⁾ > 20 s⁻¹, there will be high probability that the kinetochore falls off together with the tip. Such an upper speed limit for the stable kinetochore translocation could be increased by the driving force enhancement, such as the electrostatic attraction and the bending energy (data not shown). Thus, the coordination between k_off⁽⁰⁾ and the driving force for the kinetochore translocation is necessary to achieve faithful kinetochore translocations (1–4, 28–32). If we choose k_off⁽⁰⁾ ≈ 2–6 s⁻¹ (32), the kinetochore translocation speed is 1–3 μm/min, consistent with in vivo and in vitro measurements (3, 6, 12, 16).

Fig. 3.

Various factors affecting the kinetochore velocity. If not otherwise mentioned, q_kt = 6, λ_D = 1 nm, the binding energy is 12.5 k_BT, the bending energy is 3.0 k_BT, the lateral bond strength is 3.0 k_BT, k_off⁽⁰⁾ = 5 s⁻¹, and γ_kt = 5 pN·s/μm. (A) The dependence of kinetochore translocation velocity on the protofilament bare off-rate k_off⁽⁰⁾. (B) The kinetochore translocation dependence on the additional pulling force: a, q_kt = 6; b, q_kt = 3; c, q_kt = 0. (B Inset) The threshold pulling force depends on the kinetochore diffusion. (C) The velocity-load plot. (D) The stalling force dependence on the kinetochore charge q_kt. (D Inset) The dependence of the stalling force on the bending energy.

Fig. 3B shows the robustness of the kinetochore translocation coupled at the depolymerizing microtubule end with respect to additional pulling force. According to curve a, the kinetochore translocation coupling with the microtubule end remains unaffected for the additional pulling force <10 pN, which cannot overcome the large energy barrier imposed by the electrostatic attraction from the highly bent tip as the kinetochore passes to the next subunit (Fig. 2C). Consequently, the kinetochore translocation velocity is still under the tight control of microtubule dissociation. If the additional pulling force exceeds the threshold force of ≈10 pN, the energy barrier is overcome, and the kinetochore is driven along the microtubule at a much faster speed than is observed in anaphase A (3, 12, 16) or the in vitro experiments (6). Subsequently, the kinetochore translocation is completely decoupled from the microtubule shrinkage. As the effective electrostatic attraction decreases, the robustness of such coupling deceases (a → c). Fig. 3B Inset shows the threshold pulling force decreases with the increasing kinetochore motility. When the kinetochore diffusion coefficient is ≈10⁴ nm²/s, the threshold pulling force could decrease to ≈0.5 pN, which is reasonably consistent with the in vitro measurement (33). Therefore, on one hand, the effective electrostatic attraction provides the driving force for the kinetochore translocation; on the other hand, it robustly couples the kinetochore speed to the microtubule dissociation against the additional pulling force.

Fig. 3C shows the velocity-load curves. The stalling force is ≈1.5 pN, much larger than mean viscous drag for the corresponding kinetochore velocity γ_ktν̄_kt ≈ 0.2 pN. This difference is because of the coupling mechanism for the kinetochore translocation, whose speed is determined by the microtubule shrinkage rate, independent of viscous drag. No matter how fast the kinetochore could be driven to the next tubulin subunit, it is always hindered there until the tip falls off. Thus, the driving force does not necessarily correlate with the speed (and hence the mean viscous drag force), even in the low-Reynolds number limit. Shown in Fig. 3D and Inset, the kinetochore driving force, such as the electrostatic attraction and the bending energy release, controls the stalling force. Because the bound tubulin subunit extends its C terminus of 20 negative charges much closer to the kinetochore ring than 3.5 nm we used here (5–7, 21), the actual electrostatic attraction could be larger, which leads to a larger stalling force and the more robust coupling of the kinetochore translocation to the microtubule dissociation. In the model, the stalling force of ≈1.5 pN is the driving force capacity per microtubule, which corresponds to the situation in budding yeast. If one chromatid could accommodate multiple kinetochore-microtubules such as in human cells ≈35, the Pac-man mechanism would yield ≈1.5 pN × 35 = 52.5 pN. In some cells, the stalling force could reach hundreds of pN (10); we suspect that these cells could harness the “microtubule flux” mechanism as well (8). In this work, we only focus on the kinetochore-based translocation mechanism, and we will leave explorations in the microtubule flux mechanism for future work.

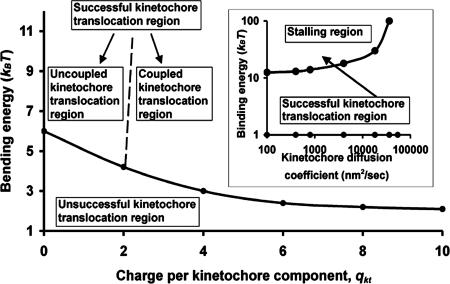
Fig. 4 is a quantitative phase diagram showing the sustained kinetochore translocation at the depolymerizing microtubule end requires both large bending energy and large electrostatic attraction indicating that, when the kinetochore is around the microtubule middle region, the electrostatic attraction from both directions cancel out. Accordingly, in comparison with its location at the tip (Fig. 2C), the kinetochore translocation is not governed by the microtubule dissociation rate any longer. If the diffusion is large, the kinetochore complex would diffuse along the microtubule, which is observed in (6). Fig. 4 Inset illustrates the optimal binding energy for kinetochore translocations. The binding strength needs to be strong (>1 k_BT) to prevent kinetochore detachment by diffusions, although it can not be too strong, because the strong binding increases the energy barrier and stalls the kinetochore movement. Meanwhile, strong binding increases the stored potential for the microtubule tip and reduces its off-rate. At a certain point, as new chemical equilibrium is established with solutions, the microtubule stops shrinking. This observation could explain the stallings of both the kinetochore movement and the microtubule shrinkage upon the two to three kinetochore rings accumulation along the microtubule (6), which enhances the binding strength (>25 k_BT) and decreases the diffusion (<2.0 × 10⁴ nm²/s).

Fig. 4.

Phase diagram for sustained kinetochore translocation (bending energy vs. q_kt). If not otherwise mentioned, q_kt = 6, λ_D = 1 nm, the lateral bond is 3.0 k_BT, the binding energy is 12.5 k_BT, the bending energy is 3 k_BT, k_off⁽⁰⁾ = 5 s⁻¹, and γ_kt = 5 pN·s/μm. (Inset) Phase diagram (binding energy vs. kinetochore diffusion). The arrow is the probable routine in which the kinetochore stalls after it collects one or two kinetochores during the translocation along the microtubule (6).

Fig. 4 also shows two subdomains within the successful kinetochore translocation region. In the “uncoupled kinetochore translocation region,” because the bending energy is much higher than the normal value, the energy barrier for the kinetochore translocation is negligible for kinetochore diffusion even without resorting to electrostatic attraction. In this case, without enough electrostatic attraction, the kinetochore translocation is no longer strictly coupled to the depolymerizing microtubule end; the kinetochore could diffuse far inside the microtubule while leaving the microtubule tip hundreds of nm (Fig. 2B, curve c). When the electrostatic attraction is sufficiently large, it quenches the diffusion and firmly couples the kinetochore translocation to the tip, and we denote this region as the “coupled kinetochore translocation region.”

Discussions and Conclusions

Here, we summarize our investigations into the roles of the diffusion, microtubule bending strain release, and the effective electrostatic attraction in kinetochore translocation. For in vivo situation, the effective kinetochore diffusion coefficient includes the large chromosome effect and thus it is very small ≈400–800 nm²/s. Because the microtubule bending strain is usually low (≈3 k_BT) [this value is supported by experimental measurement (23) and theoretical calculations (21, 22)], it alone could not drive the kinetochore to overcome local binding potential ≈12.5 k_BT (5, 14, 19). Thus, according to Fig. 2A, the kinetochore will become trapped by the energy barrier and cannot translocate along the microtubule. Our calculations suggest that the effective electrostatic attraction between the kinetochore and the microtubule provide sufficient additional driving force to overcome the energy barrier (Fig. 2 B and C). Recent experimental finding highlights the importance of electrostatic attraction: 1/4 of the negative charges per microtubule subunit remain unscreened (12 e) under physiological conditions (34). If we use Q_MT = 12 as unscreened charge per tubulin subunit in our model, the results remain essentially unchanged (data not shown). Even more importantly, the effective electrostatic attraction between the kinetochore and the microtubule provide a mechanism that couples the kinetochore translocation to the depolymerizing microtubule end. This coupling mechanism is very robust against the additional pulling force (Fig. 3B). For the in vitro situation (6), the kinetochore only consists of the ring complex, whose diffusion coefficient is very large ≈230 nm²/s (6). Also, the kinetochore could readily overcome the binding potential and diffuse freely (6), even without resorting to other driving forces. Now, the question is: How important is the effective electrostatic attractions in determining stable kinetochore translocation at the depolymerizing microtubule end? Our calculation suggests that although it may not be an important driving force in this case, the effective electrostatic attraction is essential in coupling the kinetochore translocation to the depolymerizing microtubule end. Such a conclusion could be corroborated by the in vitro experiments (6).

Within the observation interval ≈10 s in vitro experiment (6), the kinetochore ring complex should be able to diffuse over ≈730 nm along the microtubule. This finding means that, if the kinetochore ring complex translocates along the microtubule purely by diffusion, one should observe that it would position away from the depolymerizing tip far inside the microtubule, at least for some time. Furthermore, if the microtubule-bending strain release and the kinetochore diffusion are the only driving factors for kinetochore translocation, one would expect even more diffusive kinetochore motion near the microtubule depolymerizing end, because the curl-outs of the microtubule tip significantly lower the local energy barrier for kinetochore diffusion (Fig. 2A). However, it appears that the kinetochore always stays at the depolymerizing microtubule tip (6). Alternatively, one could attribute it to the fast microtubule depolymerization, which can catch up the kinetochore diffusive motion such that the kinetochore translocation and the dissociating end appear coupled, just like a ratchet (17). If this is true, then slow microtubule dissociation would decouple the kinetochore translocation and the microtubule end. In the in vitro experiment (6), the maximum microtubule dissociation rate from one end is ≈1.95 μm/min (32), thus the microtubule tip should shorten at most ≈325 nm for 10 s. Thus, at least for some period of time, this should lead to a separation of >400 nm between the microtubule tip and the kinetochore, which is not observed in ref. 6. Ultimately, experiments with higher temporal and spatial resolution can provide more confirmative results. Nonetheless, the current experiments strongly suggest the existence of some additional force that holds the kinetochore ring complex at the tip. As proposed here, the effective electrostatic attraction between the kinetochore and the microtubule could provide such a coupling mechanism, which strongly couples the kinetochore translocation to the depolymerizing microtubule end.

Note that this coupling mechanism is a generic mechanism that does not necessarily exclude other possibilities, such as motor proteins in vivo (8, 31). Moreover, the kinetochore structure in our model is specifically taken from the Dam1 ring complex in budding yeast (5–7). The kinetochore structure in other cells could be different from the ring-like geometry (35). In this aspect, this model could serve as a starting point for further investigations.

In conclusion, we have studied the Pac-man mechanism for the kinetochore translocation at microtubule depolymerizing end. In addition, the optimal coordination of the bending energy from the microtubule subunits, the lateral bonds as well as the binding energy, we have shown that the effective electrostatic attraction between the kinetochore and the microtubule is not only important in driving the kinetochore translocation, but also in coupling the translocation to the depolymerizing microtubule end. In this way, the kinetochore velocity is essentially controlled by the microtubule dissociation rate, which explains the insensitivity of the kinetochore poleward velocity to its viscous drag as well as the apparent discrepancy between the stalling force for the kinetochore translocations and its mean viscous drag. Our proposed mechanism here could be pertinent to the poleward chromatid movement in anaphase A in real cells.