Prediction of active nodes in the transcriptional network of neural tube patterning

Abstract

A transcriptional network governs patterning in the developing spinal cord. As the developmental program runs, the levels of sequence-specific DNA-binding transcription factors (SSTFs) in each progenitor cell type change to ultimately define a set of postmitotic populations with combinatorial codes of expressed SSTFs. A network description of the neural tube (NT) transcriptional patterning process will require definition of nodes (SSTFs and target enhancers) and edges (interactions between nodes). There are 1,600 SSTF nodes in a given mammalian genome. To limit the complexity of a network description, it will be useful to discriminate between active and passive SSTF nodes. We define active SSTF nodes as those that are differentially expressed within the system. Our system, the developing NT, was partitioned into two pools of genetically defined populations by using flow sorting. Microarray comparisons across the partition led to an estimate of 500–700 active SSTF nodes in the transcriptional network of the developing NT. These included most of the 66 known SSTFs assembled from review articles and recent reports on NT patterning. Empirical cutoffs based on the performance of knowns were used to identify 188 further active SSTFs nodes that performed similarly. The general utility and limitations of the population-partitioning paradigm are discussed.

Spinal cord development begins when the neural tube (NT) forms from a sheet of proliferative neuroepithelium. The proliferative ventricular zone around the lumen sheds postmitotic cells into a mantle layer from embryonic day (E)9.5 to E13.0 of mouse development. Many sequence-specific DNA-binding transcription factors (SSTFs) that mark discrete neuronal subpopulations during ontogeny have been identified (1–10). SSTFs also mark subdivisions in the motor neuron (MN) pool (11–15) and mark different types of ventral interneurons (16). Gene knockout experiments show that SSTFs specify neuronal types (17–21). Mutating them often leads to respecification of populations. The Lbx1 homeobox gene contributes to the specification of at least four spinal cell types. Loss of Lbx1 function leads to an organized respecification of transcription factor codes and projection patterns in Lbx1-marked populations (22, 23). It therefore is thought that a network of SSTFs can be used to describe patterning and specification in the NT.

The neuronal diversity generated by patterning mechanisms in the mouse NT between E9.0 to E13.0 is not greatly influenced by classic synaptic function. Voltage-dependent Na⁺ conductance first appears at E12 (24), periodic MN bursting begins at E12.5, and a full locomotor pattern generator is not observed until E16.5 (25). Electrical connectivity during the patterning phase of development appears to be limited to gap junctions (26). In addition, the primary afferent neurons begin to enter the dorsal horn only at the end of this phase, suggesting that there is little sensory contact with the external environment. The absence of neural circuitry and contact with the external environment suggests that neuronal diversification during this phase is driven primarily by developmental patterning mechanisms.

Patterning mechanisms in the dorsal NT give rise to six early (dI1–dI6) and two late (dI4L^A and dI4L^B) populations. They give rise to four interneuron (V0–V3) populations and the MN population in the ventral NT. Different types of MNs and glial cells are also specified and subdivisions in interneuron populations are emerging as more SSTF markers are examined. The combinatorial code of all SSTFs in each population is thought to set up the molecular specification by determining the gene expression pattern, or molecular predisposition, of a neuron just before the establishment of synaptic circuits. The current population definitions of neural populations will remain useful only if the expression patterns of most SSTFs respect population boundaries. Only SSTFs that are differentially expressed in NT populations have the potential to violate these boundaries.

A network is described as a set of nodes and edges (27). The nodes typically represent the molecules, and the edges represent their interactions. The most basic transcriptional network therefore will consist of two types of nodes, SSTFs and cis-acting regulatory elements on DNA. Protein–DNA and protein–protein interactions or genetic dependencies could be used to define functional interactions, or edges, between these nodes. A network description of any biological system must seek to limit the combinatorial space to the most salient elements in the process so that a computationally feasible and humanly understandable result emerges. In this work, we seek to measure and constrain the number of SSTF nodes required for a network model of our system, which is the transcriptional network that patterns the developing mouse spinal cord between E9.0 and E13. NT patterning is generally described in terms of altered SSTF expression levels (1–10), and we will proceed along this established paradigm. We will define active nodes as SSTFs that are differentially expressed within this system. Passive nodes are SSTFs that are uniformly expressed throughout this system. Passive nodes still could play a functional role in patterning by altering their activity rather than their level (i.e., phosphorylation, etc.). However, little has been reported regarding SSTF activity changes in the context of NT patterning, and the time scales of these processes tend to be much smaller than the developmental time scale (28). Constraining an initial network model to active nodes therefore should provide a useful simplification.

It is not known how many active nodes, differentially expressed SSTFs, exist in our system. We therefore have developed a generally applicable population partitioning method to obtain a minimum estimate of the number of active nodes in our system. If a developmental system is sorted along population boundaries, then SSTFs that are differentially expressed in any part of the system can be identified by comparing expression between the two population pools. Flow sorting was used to partition the neurons of E12.5 Lbx1^GFP/+ neural tubes along population boundaries. Microarray comparisons of RNA from the two population pools were used to estimate that at least 510 active SSTF nodes exist in the NT patterning. Remarkably, a large majority of 66 known markers of neuronal populations and their progenitor zones are in this group. Virtually all of the knowns with significant microarray signals showed >2-fold differences. We used this knowledge to create empirical cutoffs that allow us to identify 188 additional SSTFs that behave as the knowns. We predict that these will be active nodes in the transcriptional network of NT patterning and have confirmed 10% of the active nodes by quantitative real-time PCR (qRTPCR).

Results

Population Partitioning Model.

To estimate the number of active nodes in the NT transcriptional network, it was essential to determine the number of SSTFs, besides the 66 knowns discussed below, that are differentially expressed in the developing NT. Most expression patterns of SSTFs reported in the literature do not include appropriate cross-sections of the NT between E9 and E13. A high-throughput partitioning scheme that would identify differentially expressed genes was therefore devised. Assume that the system, the developing NT in this report, consists of p cell populations specified by SSTF combinatorial codes. Each population consists of N cells and expresses a given factor at concentration C. The total amount (A) of the factor in a given population p is therefore A_p = N_pC_p. The total amount of the factor in the system is given by:

Now suppose that the total set of populations in the system are partitioned into two population pools. The two population pools are green (G) and white (W) in this report. The population partitioning process must be based on the expression of a SSTF that helps define a combinatorial code. The partitioning is based on GFP expression in Lbx1^GFP/− embryos in this report. The total concentration of factor in each population pool would reflect the discrete set of populations it contains, the number of cells in each of those populations, and the concentration of the factor in each of the populations. For example, if pool G contains populations 1 and 2 and pool W contains populations 3–5, the concentration of factor in each pool is as follows:

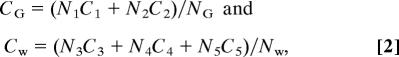where N_G and N_W are the total number of cells in each pool. The total concentration of the factor in each pool (C_G and C_W) can be readily compared in microarray or qRTPCR experiments. If a factor is ubiquitously expressed at a constant level throughout the NT, then all of the C terms would be equal, and C_W would equal C_G. However, if only one, or a subset, of populations in one pool expresses the factor at a different level, then C_W will differ from C_G. Only an exactly compensating change in the other pool could restore parity. The data below suggest that this is a rare event. In principle, different population partitions should produce the same list of differentially expressed factors, except for those with exact compensation. However, the largest fold changes between C_G and C_W will be observed for factors whose expression pattern is more closely correlated with the expression pattern of the gene that is used to make the partition. Thus, if Lbx1 was used to partition the populations of the system, then the largest fold changes would be expected for genes whose expression patterns correlate closely, either positively or negatively, with the Lbx1 expression pattern. Furthermore, in real experiments, measurement noise will obscure small fold changes, so that factors that are expressed only in small populations of the system or that come close to exact compensation will be not be identified. Thus, population partitioning measures only a minimum number of active nodes.

Estimation of Network Size.

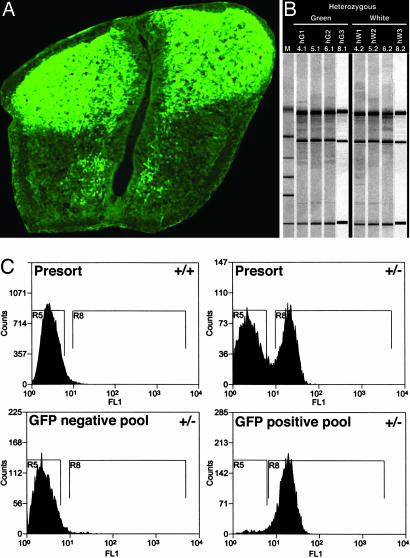
Lbx1^GFP knockin mice were used to test the partitioning model and to estimate the size of the transcriptional network that would describe NT patterning. These mice were developed initially for the analysis of limb muscle (29) and NT (23) development. EGFP is knocked in so that it is under the control of endogenous Lbx1 control elements and tightly reproduces the expression pattern observed with anti-Lbx1 antibodies. EGFP (Lbx1) is expressed in the vast majority of cells in the dorsal half of the spinal cord at E12.5 but is generally absent in the ventral half (Fig. 1). The EGFP⁺ green cell pool (G) contains the dI4–6, dI4L^A and dI4L^B populations. The EGFP⁻ cell pool (W) contains the 10 progenitor populations (p1–p10) and the postmitotic dI1–dI3, V0–V3, and several MN populations. Flow sorting was used to separate the two population pools (Fig. 1). Total RNA from 2 × 10⁶ green and nongreen neurons was obtained from E12.5 heterozygous NTs in a serum-free procedure that took 60 ± 5 min from dissociation to RNA extraction buffer. GFP⁺ cells constituted 41 ± 6% of the sorted events. The ratio of positive to negative cells accurately reflected the GFP expression observed in histology (Fig. 1).

Fig. 1.

Population sorting of dissociated neural tubes. (A) Cross-section of E12.5 neural tube of Lbx1^EGFP/+ embryo stained with anti-GFP antibody. Section was taken at the forelimb level. (B) Bioanalyser run of four sets of total RNA after DNase treatment. Three sets were used to generate microarray probes. (C) Sorting profiles of cells from dissociated E12.5 neural tubes from wild-type (Upper Left) and Lbx^EGFP/+ embryos (Upper Right). Aliquots of each pool were run after the sort was complete to determine sort purity. GFP-negative (Lower Left) and -positive (Lower Right) pools were always >95% pure.

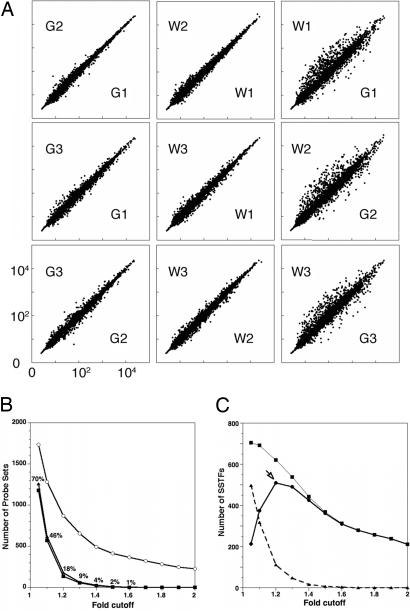
The concentration of RNAs encoding SSTFs was compared between G and W population pools by using Affymetrix mouse 430 arrays. The reproducibility of the microarray analysis in experimental repeats was assessed by comparing samples of the same or different kind (Fig. 2). Internal comparisons of G or W expression profiles showed relatively few changes from the unity line. In contrast, cross-comparisons between G and W showed many points off the unity line (Fig. 2A). The flow sorting and RNA preparation methods therefore gave stable, reproducible expression results.

Fig. 2.

False-positive rates and network size. (A) Single-array comparisons of 3,108 probe sets corresponding to 1,567 SSTFs. Six Affymetrix mouse 430 arrays were exposed to probes from independent RNA isolates. Three probes (G1, G2, and G3) were obtained from GFP⁺ cells, and three probes (W1, W2, and W3) were obtained from GFP⁻ cells. GCRMA normalized intensities for each SSTF probe set are plotted against each other for different pairings of arrays. (B) The number of probe sets with changes above each fold cutoff in three internal (filled) or in three cross-(open) comparisons. Internal comparisons were among W1–W3 arrays (triangles) or among G1–G3 arrays (squares). Cross-comparisons were between G and W arrays (circles). The plotted values are averages from all 84 permutations of three cross-comparisons. The number of differences in internal comparisons was divided by the number of differences in cross-comparisons to compute the false-positive rates (percentages shown at each fold cutoff). (C) The total number of SSTF genes with significant differences (95% confidence by t test) between the averaged green and averaged white signals is plotted at different fold cutoffs (squares). The false-positive rates from B were used to calculate how many these significant differences were expected to be correct (circles) or incorrect (triangles). The maximum number of correct differences was 510 at the 1.2-fold cutoff. This is the minimum network size.

The number of active nodes in the NT transcriptional network corresponds to the number of genes that show differential expression in the NT. In an ideal system, the number of nodes would correspond to the number of SSTFs off the unity line. However, measurement noise creates false positives. The number of false positives therefore was measured at different fold cutoffs by comparing sample replicates to each other (Fig. 2B; G vs. G or W vs. W). If the samples were identical, all genes should be expressed at identical levels and their data points should map to a line with a slope of 1. Points that deviate from that line therefore are false positives. The number of probe sets that were false positives in all three green–green (or white–white) comparisons was counted at fold cutoffs between 1.05 and 2. The number of false positives in these internal comparisons of green and white (squares) replicates was nearly identical at all fold cutoffs (triangles). In contrast, cross-comparisons between green and white samples produced far greater numbers of probe sets off the unity line at all fold cutoffs (circles). The rate of false positives was computed at each fold cutoff by dividing the number of false positives by the total number of positives in cross-comparisons.

The average and standard deviation of the three green and three white values also was determined for each probe set. Two-tailed t tests were performed to identify probe sets that differed significantly at a 95% confidence interval. The number of significantly changing SSTFs above each fold cutoff is shown in Fig. 2C (squares). This figure also shows the number of correct and incorrect calls calculated by using the false positive rates measured in Fig. 2B. Clearly, the number of correct calls reaches a maximum at the 1.2-fold cutoff. At lower fold cutoffs, measurement noise increased the number of false positives. At higher fold cutoffs, the number of calls was reduced because the real fold changes were not that large. Each correct call corresponds to a differentially expressed SSTF and, therefore, to an active node. The NT patterning network therefore contains at least 510 SSTFs (Fig. 3C, arrow) or approximately one-third of the available SSTFs.

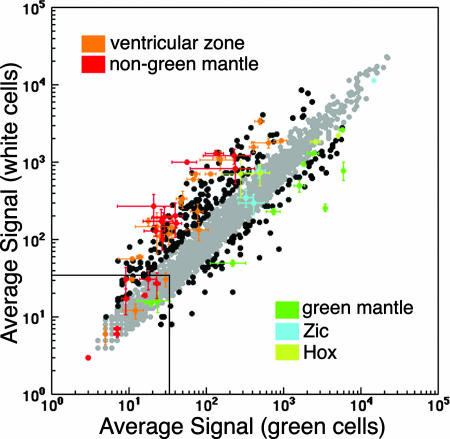
Fig. 3.

Identification of new active nodes by using properties of known SSTFs as constraints. The averages signal intensities of three microarrays were plotted against each other. Probe sets of known genes (SI Table 1) were color-coded by their known expression (orange, ventricular zone; red, mantle zone outside Lbx1-expressing populations; green, mantle zone in Lbx1-expressing populations; cyan, Zics 1, 2, 4, and 5; olive Hox genes b6, b8, c8, d9, and d10; see SI Table 1 for more details) and plotted with all other SSTF probe sets (black or gray). Error bars indicate the SD in the three replicates in each dimension and are only shown for knowns. Probe sets which exhibit a ≥2-fold change are indicated in black, whereas those that have fold changes below that threshold are indicated in gray. Two-fold change and >33 intensity thresholds accommodate the vast majority of known genes and can be used to identify SSTFs that change as much as the knowns. These are listed in SI Tables 2 and 3.

If the measurement of 621 significant changes is reduced by 111 expected false positives (18% at the 1.2-fold cutoff), then it could also be increased by the expected fraction of false negatives. The analysis described below indicates that only 71% of known positives are detected at the 1.2-fold threshold. Therefore, the estimate of 510 represents only 71% of active nodes. The total number of active nodes therefore would be estimated at 718, or approximately one-half of the available SSTFs.

Validation with Known Factors.

The relevance of the active nodes identified by the population partitioning scheme was tested by asking which SSTF genes that have known functions in NT patterning were identified. Review articles on NT development therefore were used to assemble an initial list of 51 genes relevant to NT patterning. Followup of literature on expression patterns, knockout analyses, and new publications in the field added 15 further genes to the list. These 66 genes were tracked by using literature citations in the Mouse Genome Informatics web site to find publications that describe their expression patterns in the NT [see supporting information (SI) Table 1 ]. All 66 were differentially expressed in the NT during the specified developmental interval. The population distribution listed in the table is a crude estimate for some of the genes because published information over the developmental time course and by coexpression analyses is irregular. The known list of 66 factors consisted of 46 homeodomain factors, 8 basic helix–loop–helix, 8 zinc-coordinated, and 2 winged-helix, and one β-scaffold factor(s). The fact that they are all SSTFs supports our working hypothesis that a network of SSTFs governs the patterning process. The fact that they are all differentially expressed suggests that differential expression within the NT is a good heuristic to identify functionally relevant SSTFs of the network.

The functional significance of this set of 66 SSTFs was assessed by tracking literature citations on knockout analyses for each gene. NT defects were reported for at least 47 of the genes. Many genes also had been analyzed by overexpression analyses in chick embryos (references not shown). The functional analyses typically involved tracking alterations in expression levels of SSTF target genes, again supporting the working hypothesis that a SSTF network governs the NT patterning process.

Only 3 of the 66 knowns were not represented on the microarray. The incidence of knowns that passed the 1.2-fold cutoff and the t test at the 95% confidence interval was 71% (45 of 63). This demonstrated a clear enrichment of knowns in the identified set, but also suggested that 29%, or 18, of the known factors were not being found. Four of the 18 passed at the 90% confidence interval. Eleven of the remaining 14 had no signal greater than 33 units in a dynamic range from 1 to 30,000 units, making them unreliable. The low signal intensity for Lmx1b, which is expressed broadly in the neural tube, was due to a dysfunctional probe set because qRTPCR demonstrates a robust 9-fold difference (data not shown). The low signal intensities for Phox2a, Evx2, En1, Lhx4, Isl2, Hlxb9, Etv4, Sim1, Lmx1a, Dbx2, Nkx6.2, Olig2, and Nkx2.9 were more likely due to the fact that these factors are expressed in very small populations and play a role earlier in NT development. If knowns with maximum signals > 33 are selected, then 87% (41 of 48) and 92% (44 of 48) pass the 1.2-fold threshold at 95% and 90% confidence thresholds, respectively. These results clearly demonstrate that population partitioning identifies active nodes of demonstrated function very efficiently. More biological replicates would increase the reliability of low signals and increase our ability to identify nodes that are active only in small populations of the system.

Identification of New Active Nodes.

To observe how the known genes perform in the population partitioning analysis, they were color coded and displayed in the context of all of the known changes (Fig. 3). Many of the known genes were represented by multiple probe sets on the array. To ensure that each known gene is represented by only one colored point, the probe set with largest absolute signal was selected for display. The probe sets that were omitted generally gave similar results (Table 1). The data clearly show that nearly all of the known genes change significantly. The known factors were not only significantly different, but were also among the SSTFs with the greatest fold changes.

This observation was exploited to assemble a list of the most salient SSTFs in the NT patterning network (SI Tables 2 and 3) that are not included in the known list (SI Table 1). The known genes were used to empirically set selection cutoffs for “interesting” SSTFs. With few exceptions, the known genes change 2-fold or more (Fig. 3). Those known genes that change <2-fold generally had signals <33 (see above). SSTFs that were above the 33 unit baseline and showed ≥2-fold changes therefore were selected as active nodes of the NT transcription network that are the most promising to focus on in an early network description. SI Table 2 shows predicted nodes that show higher expression in the Lbx1-expressing pool. These are SSTFs likely to play a role in dorsal postmitotic populations and essentially pool with the genes known to play a role in these populations (Fig. 3; below the unity line). SI Table 3 shows predicted nodes that show higher expression in the non-Lbx1 pool. These are SSTFs likely to play a role in ventral postmitotic populations and in progenitor populations of the ventricular zone. They also essentially pool with the genes known to play a role in these populations (Fig. 3; above the unity line). A total of 188 new SSTFs nodes were identified that behave like the 66 known SSTF nodes. This expands the working model network 4-fold to 254 SSTFs, half of the estimated total size.

Validation of Active Nodes by qRTPCR.

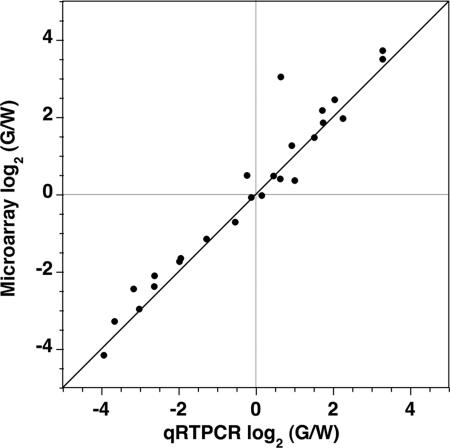
Microarray results were validated by qRTPCR. Twenty-nine SSTF genes, corresponding to 10 known, 16 predicted, and 3 nonpredicted active nodes, were selected. Known active nodes included those that were expressed at higher (Lbx1, Pax2, Lmx1b, and Zic1), lower (Isl1, Foxd3, and Olig3), or similar (Zic2, Zic4, and Zic5) levels in green pools. Newly predicted active nodes also included those that were measured at higher (Mafa, Sall4, Bcl11a, Bcl11b Gbx2, Pknox2, Satb2, Uncx4.1, Tsh2, and Pax8) or lower (Nr4a2, Sall1, Hmx2, Hmx3, Otp, and FoxP2) levels in green cells. Three nodes that were not predicted to be active also were included (Sall2, Sall3, and Zic3). Primers were designed by consulting an online primer bank (30), and the amplification of single bands were confirmed for all except Bcl11a. Standard curves were generated for each of the remaining 26 amplicons by using serial dilutions over four orders of magnitude of reverse-transcribed E12.5 neural tube total RNA. Five biological replicates were measured. Three technical replicates were performed for two of these biological replicates. The average fold change from the qRTPCR and microarray replicates were compared (Fig. 4). The fold changes observed by these two methods are qualitatively identical and quantitatively very similar, indicating that no false positives were detected in a screen of ≈10% of the predicted active nodes. This low error rate is consistent with the results of Fig. 2B, which predict <1% error at the 2-fold cutoff.

Fig. 4.

Validation of microarray measurements by qRTPCR. The average fold change observed between G and W population pools in three replicate microarrays is plotted against the average fold change measured by qRTPCR in five replicates. The expression of 25 different SSTF genes was compared. A strong correlation in fold change measured by the two methods was observed. No qualitative discrepancies in direction of change were observed. The outlier in the upper right quadrant corresponds to Mafa, which gave erroneous low values in qRTPCR because the crossing thresholds occurred after >30 cycles.

Discussion

The mouse NT is an attractive system to begin to understand how a network model can be used to describe mammalian developmental patterning events. It is a relatively large structure with well defined dorsal-ventral (D-V) and rostral-caudal (R-C) axes. Its tube shape allows many similar sections to be compared. This has allowed a large amount of gene expression information to be compared and assimilated into a population model. Different cell populations of the NT are defined by combinatorial expression of SSTFs. Loss or gain of many of these SSTF functions results in redirection of the patterning process. Our results identify 188 SSTFs that are differentially expressed to the same extent as a set of 66 “known” SSTFs that are extensively reviewed in articles on NT patterning. This represents a significant expansion in the number of nodes in the current working model. Our results also indicate that at least 510 active nodes would be required for a comprehensive NT patterning model. Genes that compensated across pools were missed. The current analysis also did not examine populations during the entire E9–E13 time frame. Thus, our estimate represents a lower bound on the complexity of the system.

A total of 3,108 probe sets representing 1,567 SSTFs were compared. If the network size is 510, then approximately one-third of the SSTFs in the genomes are active nodes in the NT patterning network. This is a large number if one considers that only 66 factors have been implicated and only 47 have demonstrated functional deficiencies (SI Table 1). On the other hand, the large number of changes is not surprising if one considers the number of populations being compared in the partitioned green and white pools. The current D-V patterning literature describes at least 10 progenitor and 15 postmitotic populations. Although the R-C patterning literature is less extensive, it indicates that the Hox genes create specifications along this axis (31, 32). The nested expression domains of these genes suggest that five to seven specifications exist along this axis below the hindbrain (more if the paralogs are not completely redundant). These must be multiplied by the postmitotic D-V populations because Hox genes appear to be off in the progenitor cells. This leads to a crude lower estimate of 85 specified populations (10 progenitor + (15 D-V × 5 R-C) postmitotic = 85). There is also some evidence that the progenitors layers produce successive rounds of differentially specified neurons and/or glial cells. This has been well documented in fly neurogenesis. If each progenitor layer produces four specified cell types in succession as fly neuroblasts do, then we would estimate 40 progenitor specifications (10 layers × 4 cycles) and their resultant 40 postmitotic specifications. This would lead to an estimate of 240 populations (40 progenitor + (40 D-V × 5 R-C) postmitotic = 240). These considerations place the estimate of NT populations between 85 and 240 and raise the following two questions. First, is it useful to define so many populations? Second, what is the most practical method to define populations and their specifications?

The utility of defining so many populations will depend on tracing each population into adulthood and establishing its function by using anatomical or electrophysiological methods. If two populations give rise to functionally equivalent neurons, the population distinction would not be useful. If, as many current working models suggest, each population becomes a different type of neuron, then the population model will provide an extremely useful organizing principle to study neuronal circuits in the adult spinal cord. It would allow a population of neurons that have a uniform, genetically defined predisposition to be tracked to see how individual neurons of this population adapt or diversify in response to environmentally induced nervous activity. Lineage-tracing mice that have CRE drivers knocked into the SSTF loci are being used to pioneer this approach. A full implementation requires that the populations be correctly defined.

As stated above, the populations are thought to be defined by a combination expressed SSTFs. How many and what type of factors are needed to define a population? The very limited expression patterns of some homeodomain SSTFs, such as Evx1, Lhx2, Lhx9, etc., held out the hope that populations can be coded by single factors if we search through the genome. The mammalian genome contains ≈250 homeodomain proteins. Our analysis used 361 probe sets to evaluate 222 of these. One hundred twenty-nine probe sets corresponding to 93 homeodomain SSTFs changed at the 95% confidence interval. All of these changes were >1.2-fold (only 116 above 1.3-fold), where we expect 18% false positives. Thus, 76 homeodomain SSTFs are among the expected 510 active nodes. Most of these are among the known list (SI Table 1) and are expressed in more than one population. Thus, homeodomain proteins are unlikely to provide single-factor population codes in the future. Similar arguments can be made for the Ets transcription factors that have also been postulated to form a simple code. It appears that specification by individual factors may be the exception rather than the rule.

Are certain types of SSTFs better at defining populations than others? The relative contribution of the four superclasses of SSTFs was measured. Helix–turn–helix factors contributed 42% of the active nodes (50% of class participate in network), zinc-coordinated factors contributed 34% of active nodes (31% of class), basic factors contributed 10% (34% of class), and β-scaffold and others contributed 7% each (31% and 28% of class). Helix–turn–helix SSTFs clearly contribute the most nodes to the network and have the highest superclass participation. However, the contributions of the other classes are substantial and well distributed and therefore cannot clearly be ignored. The specification of populations by combinatorial codes of SSTFs therefore is likely to involve SSTFs of all superclasses and many of their classes (see SI Tables 2 and 3).

The population model implies that groups of cells exist that have similar combinatorial expression profiles. Formally, a population is homogeneous if it can no longer be partitioned by SSTF expression. How much deviation of SSTF expression is allowed within a population before it become formally split into two populations? One expects a certain level of stochastic change within the cells of population as they respond to their microenvironments. It would not be useful to divide a population up on the basis of such changes. However, it is also apparent that the patterning process can specify very small groups of cells in an organized manner. If a large number of very small populations is specified (e.g., 240; see above), it will be necessary to monitor many SSTFs at once to define and compare combinatorial codes. Development of a formal network model will be useful in tracking the development of such codes.

Progressive application of the population partitioning paradigm could provide a systematic means of honing in on SSTF codes of rare populations. An initial partition, such as the one presented here, is used to identify SSTFs to be tested as population markers. An SSTF that marks a subpool of the initially marked pool (green) must be labeled with a different dye (red) and used to partition the initial green population into further population pools. One would expect that the number of identified SSTFs to decline as the structure that is partitioned contains less populations. Similarly, one would expect the fold changes of identified SSTFs to increase because there is less dilution by other populations in each pool. At the end of the analysis, one pool will contain only one population. None of the factors overexpressed in this terminal pool will systematically bifurcate the population.

Materials and Methods

Synchronous Lbx1^GFP/+ containing litters were removed at E12.5 and rapidly genotyped under a fluorescent microscope to identify heterozygotes. NTs between the caudal edge of the fourth ventricle and lumbar region were removed from the embryos and stored on ice until dissociation. NTs were dissociated 6 ± 1 min, sorted 30 min and were lysed at 1 h. Biotiylated probes for Affymetrix Mouse 430 arrays were generated by one cycle labeling of 3 μg of total RNA.

Data were normalized by using GCRMA on Genespring software. The TRANSFAC (Braunschweig) tree was used to guide a computer-assisted manual annotation effort that identified 3,108 probe sets for 1,567 genes encoding known DNA-binding domains. The RIKEN Genome Science Center recently has reported the nonredundant number of mouse transcription factors at 1,585 (33). However, this group includes general transcription factors and chromatin remodeling factors in their collection. Detailed methods are included as SI Materials and Methods.

Abbreviations

D-V

dorsal-ventral

En

embryonic day n

MN

motor neuron

NT

neural tube

qRTPCR

quantitative real-time PCR

R-C

rostral-caudal

SSTF

sequence-specific DNA-binding transcription factor.