Mechanistic home range models capture spatial patterns and dynamics of coyote territories in Yellowstone

Abstract

Patterns of space-use by individuals are fundamental to the ecology of animal populations influencing their social organization, mating systems, demography and the spatial distribution of prey and competitors. To date, the principal method used to analyse the underlying determinants of animal home range patterns has been resource selection analysis (RSA), a spatially implicit approach that examines the relative frequencies of animal relocations in relation to landscape attributes. In this analysis, we adopt an alternative approach, using a series of mechanistic home range models to analyse observed patterns of territorial space-use by coyote packs in the heterogeneous landscape of Yellowstone National Park. Unlike RSAs, mechanistic home range models are derived from underlying correlated random walk models of individual movement behaviour, and yield spatially explicit predictions for patterns of space-use by individuals. As we show here, mechanistic home range models can be used to determine the underlying determinants of animal home range patterns, incorporating both movement responses to underlying landscape heterogeneities and the effects of behavioural interactions between individuals. Our analysis indicates that the spatial arrangement of coyote territories in Yellowstone is determined by the spatial distribution of prey resources and an avoidance response to the presence of neighbouring packs. We then show how the fitted mechanistic home range model can be used to correctly predict observed shifts in the patterns of coyote space-use in response to perturbation.

1. Introduction

The advent of radio-telemetry in the late 1950s revolutionized animal ecology by allowing the routine, systematic measurement of animal locations (Siniff & Jesson 1969). Since its introduction, a variety of statistical models, including the minimum convex polygon (Odum & Kuenzler 1955), bivariate normal (Jennrich & Turner 1969), harmonic mean (Dixon & Chapman 1980), kernel (Worton 1989), and nearest-neighbour convex hull (Getz & Wilmers 2004) models, have been used to summarize home range patterns. While these statistical home range models provide useful summaries of relocation data, their descriptive nature means that they are unable to analyse the underlying determinants of observed patterns of space-use.

In the 1980s, resource selection analysis (RSA) emerged as a method for identifying the underlying determinants of animal space-use patterns (Johnson 1980). In contrast to traditional descriptive home range analysis, RSA uses a spatially implicit, frequentist approach to identify areas and habitats used disproportionately in relation to their occurrence on the landscape (Manly et al. 1993). RSA analyses can be conducted at a variety of spatial scales; however, here we limit our discussion to the RSA performed at a scale of individual home range—so-called ‘third-order’ selection (Thomas & Taylor 1990). As results from a number of studies have shown, RSA can be successfully used to identify associations between relative space-use by individuals and different forms of environmental heterogeneity, including habitat type, topography and resource availability (see Manly et al. 1993; Boyce & MacDonald 1999; Cooper & Millspaugh 2001; Erickson et al. 2001 for reviews).

In this study, we adopt a different approach, using a series of mechanistic home range models to analyse the observed patterns of space-use of coyotes (Canis latrans) in Yellowstone National Park, Wyoming. In contrast to RSA models, mechanistic home range models are spatially explicit, yielding predictions for the actual spatial patterns of space-use by individuals in the form of two-dimensional probability density functions that are formally derived from underlying correlated random walk descriptions of individual movement behaviour. In doing so, mechanistic home range models reflect the biological reality that animal home ranges are macroscopic spatial patterns, arising from the movements and decisions of individual organisms in response to each other and their environment (Moorcroft et al. 1999; Millspaugh & Marzluff 2001; Okubo & Levin 2001).

In a prior study, we showed how a mechanistic home range model incorporating behavioural avoidance responses to foreign scent-marks could be used to capture the influence of neighbouring home ranges on patterns of coyote space-use in a spatially uniform sagebrush landscape (Moorcroft et al. 1999). Here, we show how this model can be extended to gain biological insight into environmental heterogeneities affecting patterns of coyote space-use in the heterogeneous environment of Yellowstone National Park, and thus provide a new, spatially explicit alternative to RSA. This is possible because the underlying movement models of mechanistic home range models are, in essence, hypotheses for the underlying cause(s) of the observed patterns of space-use by individuals. As we show here, by deriving patterns of space-use that result from underlying movement models incorporating responses to different forms of spatial heterogeneity, it possible to test competing hypotheses for the underlying determinants of home range patterns against observed spatial distributions of relocations. We then show how fitted models can be used to correctly predict observed shifts in the spatial patterns of coyote space-use following a population perturbation.

2. Analysis

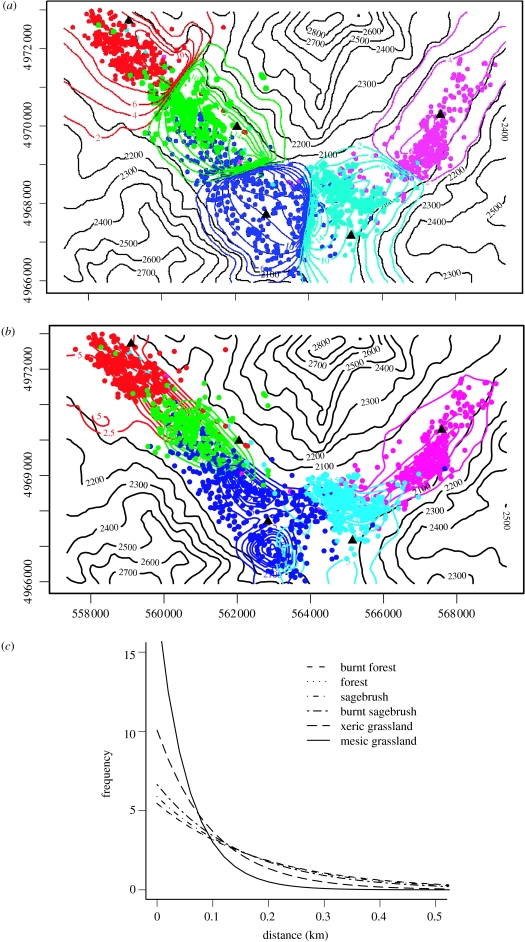
Figure 1a shows the spatial distribution of coyote home ranges in the Lamar Valley region of Yellowstone National Park during the period 1991–1993 (R. L. Crabtree et al. 1993, unpublished). During this period prior to the wolf re-introduction in 1995, the coyotes occupied distinct, relatively non-overlapping home ranges along the lower portions of the Lamar Valley (figure 1a).

Figure 1.

(a) Radio-tracking data for five contiguous packs in the Lamar Valley region of Yellowstone National Park (R. L. Crabtree et al. unpublished). Black contour lines show topographic relief in metres. Coloured points (filled circles) indicate relocations for individuals belonging to the Bison (red), Druid (green), Fossil Forest (blue), Norris (light-blue) and Soda Butte (pink) packs collected during the period 1990–1994 prior to wolf re-introduction. Filled triangles indicate the denning areas for each pack used in the model fitting as their home range centre. (b) Coloured contour lines showing fit of the CA home range model (equations (2.1) and (2.2)) to relocation data (filled circles) for the five groups in Lamar Valley. Black contour lines show topographic relief in metres. Coloured contour lines show the probability density function u⁽ⁱ⁾(x, y) for each pack (i=1, …, 5), in density units scaled so that both the domain area A and integral of u⁽ⁱ⁾(x, y) are unity. The home range centres for each pack are shown (filled triangles). Maximum-likelihood values, AIC scores and estimates for β and m are given in table 1. (c) Small mammal prey availability in the Lamar Valley region of Yellowstone National Park. Shading indicates small mammal biomass density in kg ha⁻¹ calculated using estimates of small mammal biomass density for different habitat types, and mapped onto the region using the Park Service Geographic Information System. Details on how small mammal biomass density was calculated can be found in appendix S3 of electronic supplementary material. Small mammal biomass densities in kg ha⁻¹ for the six different habitat types are: mesic grasslands 5.49, xeric grasslands 3.33, sagebrush 1.30, burned sagebrush 1.76, forest 1.02 and burned forest 1.01. Black contour lines show topographic relief in metres.

We first evaluated whether a proposed mechanistic home range model for carnivores based on conspecific avoidance (CA) responses to foreign scent-marks (Lewis & Murray 1993, see also White et al. 1996; Moorcroft et al. 1999) could account for the observed patterns of space-use seen in figure 1a. In this CA model, individuals (i) exhibit an avoidance response to foreign scent-marks (the scent-marks of individuals belonging to other packs), and (ii) increase their scent-marking rate following encounters with foreign scent-marks. Analysis shows that incorporating these two behavioural rules into a correlated random walk model for individual movement behaviour yields the following non-dimensionalized system of differential equations for the expected patterns of space-use and spatial distribution of scent-marks:

$$\underset{\text{random}\text{motion}}{\underbrace{{\nabla }^2{u}^{(i)}}}-\underset{\text{scent}‐\text{mark}\text{avoidance}}{\underbrace{\nabla \left[\beta {\mathit{x}}_i{u}^{(i)}\sum _{j\ne 1}^n{p}^{(j)}\right]}}=0,$$ 2.1

$$\frac{\text{d}p(i)}{\text{d}t}=\underset{\text{scent}‐\text{mark}\text{deposition}}{\underbrace{u^{(i)}\left[1+m\sum _{j\ne 1}^n{p}^{(j)}\right]}}-\underset{\text{scent}‐\text{mark}\text{decay}}{\underbrace{p^{(i)}}}=0,$$ 2.2

where u⁽ⁱ⁾(x, y) is a two-dimensional probability density function for the expected steady-state pattern of space-use by individuals belonging to pack i as a function of spatial position (x, y), x_i is a vector indicating the direction of the pack's home range centre (denning area) from position (x, y), and p⁽ⁱ⁾(x, y) is their expected spatial distribution of scent-marks (i=1, …, n) (see appendix S1 of electronic supplementary material). The model has just two non-dimensional parameters, β that reflects the strength of the scent-mark avoidance response of individuals, and m that reflects the strength of the over-marking response of individuals relative to their background rate of scent-marking.

Figure 1b shows the fit of equations (2.1) and (2.2) to the spatial distribution of coyote relocations in Lamar Valley shown in figure 1a. Details of the model fitting procedure can be found in appendix S2 of electronic supplementary material. As the figure shows, the foreign scent-mark avoidance behaviour underlying the CA model gives rise to distinct home ranges for the five packs in the study region; however, the predicted patterns of space-use give a poor fit to the observed spatial distribution of relocations, failing to capture the boundaries between home ranges and the confinement of the home ranges to the lower portions of the valley (figure 1b).

Two potential explanations for the poor fit of the CA model are that, in addition to avoiding foreign scent-marks, the coyotes are also responding to either the physical, abiotic heterogeneity of the landscape, avoiding steep, high-elevation terrain; or the biotic heterogeneity of the landscape, preferring areas of high prey availability. Figure 1c shows the spatial distribution of small mammal biomass in the Lamar Valley (details on how small mammal biomass density was calculated are given in appendix S3 of electronic supplementary material). As the figure shows, the patches of mesic grassland habitat found in low-elevation areas surrounding the Lamar River have considerably higher densities of small mammal biomass than higher-elevation areas. Distinguishing the effects of these two different sources of heterogeneity on patterns of space-use is thus inherently challenging because the spatial variability of prey availability and terrain within the study area are strongly correlated (figure 1c).

We tested the above two alternative hypotheses for the patterns of coyote space-use observed in Lamar Valley by incorporating additional rules into the underlying movement model. The effects of terrain were incorporated by specifying that individuals have a decreased likelihood of moving in directions of increasing terrain steepness. Adding this movement rule to the correlated random walk model yields the following equation for expected steady-state pattern of space-use:

$$0=\underset{\text{random}\text{motion}}{\underbrace{{\nabla }^{2}u(i)}}-\underset{\text{scent}‐\text{mark}\text{avoidance}}{\underbrace{\nabla \left[\beta {\mathit{x}}_i{u}^{(i)}\sum _{j\ne i}^n{p}^{(j)}\right]}}+\underset{\text{avoidance}\text{of}\text{steep}\text{terrain}}{\underbrace{\nabla \left[{\alpha }_z{u}^{(i)}\nabla z\right]}},$$ 2.3

where the parameter α_z reflects the strength of the steep terrain avoidance relative to the random component of motion (see appendix S1 of electronic supplementary material). The equation describing the spatial distribution of scent-marks (equation (2.2)) is unchanged. We label equations (2.2) and (2.3) the ‘steep terrain avoidance plus conspecific avoidance’ (STA+CA) home range model.

The effects of prey availability were incorporated by adding a simple foraging movement rule—reflecting empirical observations of coyote foraging behaviour—in which individuals reduce their movement speed and frequency of turning in response to resource availability, resulting in shorter distances between successive relocations in areas of high prey availability (Macdonald 1980; Laundre & Keller 1981). Incorporating this simple foraging movement rule into the underlying correlated random walk model in place of the steep terrain avoidance rule yields the following equation for the expected pattern of space-use:

$$0=\underset{\text{random}\text{motion}}{\underbrace{\nabla ·[e^{-{\alpha }_{r}h(\text{x})}\nabla u^{(i)}]}}-\underset{\text{scent}‐\text{mark}\text{avoidance}}{\underbrace{\nabla ·\left[e^{-{\alpha }_{r}h(\text{x})}{c}_P(\text{x}){\overrightarrow{\text{x}}}_i{u}^{(i)}\sum _{j\ne i}^{n_{\text{pack}}}{p}^{(j)}\right]}}\underset{\begin{array}{c}\text{directed}\text{movement}\text{toward}\text{areas}\text{of}\text{high}\text{resource}\text{density}\end{array}}{\underbrace{-\nabla ·[e^{-{\alpha }_{r}h(\text{x})}{u}^{(i)}\nabla h]}},$$ 2.4

where the parameter α_r reflects the coyote's sensitivity to local prey availability h (see appendix S1 of electronic supplementary material). As with the STA+CA model above, the equation describing the spatial distribution of scent-marks (equation (2.2)) is unchanged. We label equations (2.2) and (2.4) the ‘prey availability plus conspecific avoidance’ (PA+CA) model.

We then fit the STA+CA and PA+CA models to the spatial distribution of relocations using the maximum-likelihood fitting procedures described in appendix S2 of electronic supplementary material.

3. Results

The inclusion of either steep terrain avoidance response or a foraging response to prey availability substantially improves the characterization of home range patterns, resulting in home ranges that, like the observations, are restricted to the lower part of the Lamar Valley (figure 2a,b, ΔAIC=1683.4 and 2681.2, respectively, see table 1). However, comparing the goodness-of-fit obtained with the PA+CA model (figure 2b) to that obtained with the STA+CA model (figure 2a) shows that incorporating a foraging response to small mammal prey availability gives a greatly improved goodness-of-fit to the relocations compared to the steep terrain avoidance rule (ΔAIC=913.8, see table 1a).

Figure 2.

(a) Coloured contour lines showing fit of the STA+CA home range model (equations (2.2) and (2.3)) to relocation data (filled circles). The probability density function u⁽ⁱ⁾(x, y) for each of the five packs (i=1, …, 5), in density units scaled so that both the study area A and integral of u⁽ⁱ⁾(x, y) are unity. The home range centres for each pack are shown (filled traingles). Maximum-likelihood values and estimates for β, m and α_z are given in table 1. (b) Coloured contour lines showing fit of the PA+CA home range model (equations (2.2) and (2.4)) to the Lamar relocation data (filled circles). The home range centres for each pack are shown (filled triangles). Maximum-likelihood values, AIC scores and estimates for β, m and α_r are given in table 1. (c) Lines showing the expected distributions of movement distances for the different habitats within the Lamar Valley study area obtained from the fit of the PA+CA model (equations (2.2) and (2.4)) shown in (b). Distributions were calculated using the relationship between α_r, resource availability h(x, y) and the mean movement distance of individuals assuming that individuals are relocated every 10 min and that the distribution of distances between relocations in the absence of prey is exponential with a mean movement distance of 0.24 km.

Table 1.

(a) Details of the home range model fits (figures 1 and 2) to relocation data for five contiguous packs in Lamar Valley, Yellowstone National Park. (Parameter values, likelihood scores l(θ) and Akaike information criterion (AIC) scores are given for the fit of the conspecific avoidance (CA) home range model (equations (2.1) and (2.2)), the steep terrain avoidance plus conspecific avoidance (STA+CA) home range model (equations (2.2) and (2.3)), and the prey availability plus conspecific avoidance (PA+CA) model (equations (2.2) and (2.4)). The total number of data points used in the model fitting was 1955 relocations. Further details on the model fitting procedures can be found in appendix S2 of electronic supplementary material. In all three models, β indicates the ratio of directed movement per unit of scent-mark density encountered relative to the strength of non-directed movement, and m governs the sensitivity of an individual's marking rate to foreign scent-marks. The parameter α_z of the STA+CA model governs the magnitude of steep terrain avoidance relative to the strength of non-directed movement, and the parameter α_r of the PA+CA model governs the sensitivity of turning frequency to resource density. For more details on the interpretation of the model parameters, see appendix S1 of electronic supplementary material.). (b) Goodness-of-fit of the PA+CA model to the 1993 relocations before and after the removal of the Norris pack. (The total number of relocations in 1993 was 456. The significant improvement in fit of the model following the removal of the Norris pack indicates that the PA+CA model correctly predicts the changes in space-use that occurred after the Norris pack dissolved in January 1993.).

(a)
	CA	STA+CA	PA+CA
equations	(2.1) and (2.2)	(2.2) and (2.3)	(2.2) and (2.4)
parameters	2	3	3
β	2.86	3.31	3.35
m	0.047	0.34	0.0030
αz	—	30.8	—
αr	—	—	0.265
l(θ)	2453.5	3296.2	3753.1
AIC	−4903.0	−6586.4	−7500.2

(b)
	PA+CA model goodness-of-fit to the 1993 relocations
	before Norris removal	after Norris removal
l(θ)	747.4	767.2
AIC	−1488.8	−1528.4

Several factors contribute this improved goodness-of-fit. First, the home ranges of the Bison, Druid and Soda Butte (red, green and pink contour lines, respectively) packs are narrower, which gives a better fit to the spatial distributions of relocations for these packs (compare figure 2a,b). Second, the PA+CA model more accurately captures the partitioning of space between the Druid and Fossil Forest packs: while the STA+CA model predicts box-shaped home ranges for these two packs that are approximately equal in size, the PA+CA model captures the elongated shape of the Druid home range (green contour lines), and the larger size of the Fossil Forest home range (blue contour lines) (compare figure 2a,b). Third, the PA+CA model captures the clustering of the Norris pack relocations around the high-resource area located north of their home range centre (compare the light-blue contour lines in figure 2b,c to the spatial patterns of light-blue points in figure 1a). The substantial improvement in the goodness-of-fit of the PA+CA model over the STA+CA model seen in figure 2 implies that the spatial distribution of relocations in Lamar Valley is not arising from steep terrain avoidance, but rather is the result of foraging responses of the coyotes to spatial variation in prey availability.

The model fits yield predictions for how the fine-scale movement behaviour of individuals varies across the landscape. For example, figure 2c shows the distributions of movement distances between successive relocations of individuals in the different habitat types predicted by the PA+CA model fit. The higher prey availability in the mesic grasslands, and, to a lesser extent, in the xeric grasslands means that the distances successive between relocations are predicted to be substantially lower in these two habitats than in forested and sagebrush habitats (figure 2c).

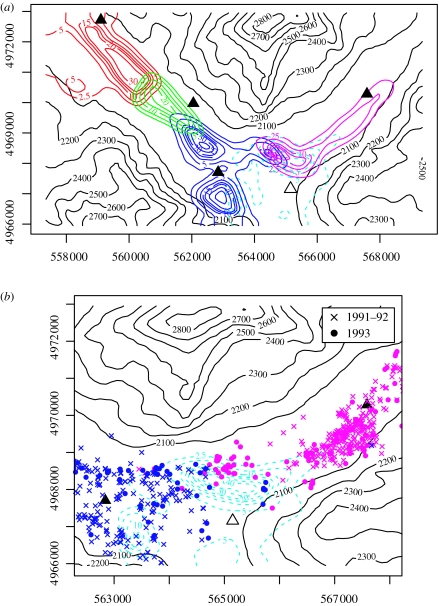
The mechanistic nature of the models used in the above analysis means that the model fits can also be used to predict how patterns of space-use will change in response to perturbation. For example, in January 1993 following the death of the alpha male, the Norris pack, whose home range is indicated by the light-blue contour lines in figure 2b, dissolved. Figure 3a shows the changes in home range configuration that the PA+CA model fit predicts will occur in response to this demographic perturbation. Individuals of neighbouring Soda Butte pack (pink contour lines) move into the former Norris home range, focusing their movements around the prey-rich mesic grassland situated north of the former Norris den site. The increased utilization of this high-resource area by the Soda Butte pack is accompanied by a contraction of their home range around the ribbon of mesic grassland habitat running along the valley floor, as the individuals focus their movements around these resource-rich areas (compare the pink contour lines in figures 2b and 3a). Individuals of the neighbouring Fossil Forest pack (blue contour lines) also move into the former Norris home range, again focusing their movements on the mesic grassland north of the former Norris den site. However, their shift in space-use is less marked than that of the Soda Butte pack (compare the blue contour lines in figures 2b and 3a).

Figure 3.

(a) Coloured contour lines show the spatial distribution of home ranges in Lamar Valley predicted by the PA+CA model following loss of the centrally located Norris pack in January 1993. Solid contour lines show the new configuration of home ranges in relation to the former home range of the Norris pack indicated by the dashed light-blue contour lines. Patterns of space-use of the prior to the removal are shown in figure 2b. Black contour lines show topographic relief in metres. The location of the former home range centre of the Norris pack (open triangle) and the locations of the home range centres of the remaining packs (filled triangles) are also shown. (b) Observed changes in space-use by the Soda Butte and Fossil Forest packs following the loss of the Norris pack in January 1993. As in (a), the dashed light-blue contour lines show the former home range of the Norris pack. Coloured points show the relocations of individuals in the neighbouring Soda Butte (pink) and Fossil Forest (blue) packs prior to (crosses) and following (filled circles) the loss of the Norris pack. As predicted by the model (a), the Soda Butte and Fossil Forest packs expand their territories into the former Norris home range following the loss of the Norris pack focusing their movements on the prey-rich mesic grassland north of the former Norris home range centre (open triangle).

These predicted changes in spatial configuration are consistent with the observed changes in patterns of space-use seen in 1993 following the loss of the Norris pack. Figure 3b shows the spatial pattern of relocations of the Soda Butte and Fossil Forest packs observed during 1991–1992 (crosses) and 1993 (filled circles). As predicted, the Soda Butte and Fossil Forest packs move into the areas occupied by the former Norris home range, focusing their movements on the high-resource mesic grassland area north of the former Norris den site, and, as predicted, the individuals of the Soda Butte pack also focus their movements around the mesic grassland habitat on the valley floor (compare figure 3a,b). Comparing the patterns of space-use predicted before (figure 2b) and after (figure 3a) the loss of the Norris pack to the spatial distribution of relocations observed in 1993 shows a significant improvement in the model's goodness-of-fit (ΔAIC=39.6), indicating that the model correctly predicts the changes in space-use that occurred following the loss of the Norris pack (see table 1b).

4. Discussion

Our analysis demonstrates how mechanistic home range models, derived from individual movement and interaction rules, can be used to determine the underlying ecological determinants of observed coyote home range patterns and predict changes in space-use in response to perturbation. Specifically, in this study, we evaluated terrain heterogeneity and prey availability as two potential hypotheses for the observed spatial distribution of coyote home ranges in Lamar Valley. By incorporating movement responses to these two sources of heterogeneity into correlated random walk models of individual movement behaviour, and then evaluating the resulting predictions for patterns of space-use against the observed spatial distribution of relocations, it was possible to show that heterogeneity in prey availability provides a better explanation for the observed patterns of coyote space-use than avoidance of steep terrain.

The predicted variation in the fine-scale movement behaviour of individuals in relation to food availability in different habitats (figure 2c) is consistent with independent behavioural observations of coyote foraging behaviour in Yellowstone. Reductions in the distance between successive relocations as food availability increases implies that individuals will spend more time in high-resource areas than in lower resource areas, a prediction consistent with field measurements of coyote activity budgets, which show that relative habitat use is linked to differences in foraging success (Gese et al. 1996a,b).

The mechanistic and spatially explicit nature of the home range models used in this analysis addresses three limitations of RSA-based approaches to analysing patterns of space-use. First, the mechanistic home range approach avoids the need to define, a priori, available habitat. This critical step in RSA often involves subjective judgment and frequently has a significant impact on its findings (Johnson 1980; Alldrege & Ratti 1986; Porter & Church 1987; Thomas & Taylor 1990; Aebischer et al. 1993; Arthur et al. 1996; Cooper & Millspaugh 2001; Matthiopoulos 2003). For example, in third-order RSA studies (analyses performed at the scale of an individual's home range), available habitat is often defined as the area encompassed by a minimum convex polygon, or another statistical home range model fit to the spatial pattern of relocations. This procedure is sensitive to the kind of statistical model used to define available habitat, and tends to exclude areas that have not been utilized from the definition of what is available to individuals, thereby underestimating the influence of landscape heterogeneity on patterns of space-use. In contrast, mechanistic home range analysis avoids the problematic issue of having to define a priori what areas are available to an individual, in effect, because the underlying model of individual movement behaviour determines the likelihood and feasibility of an individual moving in a particular direction and distance.

Second, the spatially explicit nature of mechanistic home range models means that they predict actual spatial patterns of space-use rather than simply relative rates of habitat utilization obtained from RSAs. This enables mechanistic home range models to account for the constraints that landscape geometry imposes on patterns of space-use by individuals, and thus make more complete use of the spatially explicit nature of telemetry data. For example, in RSA, all areas within the region defined as ‘available’ are assumed to be directly accessible to an individual, while on actual landscapes, the patchy spatial distribution of habitats—such as the patches of high small mammal biomass in Lamar Valley seen in figure 1c—means that individuals frequently traverse less favourable habitat in order to move between favourable areas. In RSA, the times individuals spend traversing unfavourable areas can register as a degree of selection, rather than as constraint imposed by the spatial geometry of the landscape. In contrast, by explicitly incorporating the process of individual-level movement, mechanistic home range models naturally incorporate the effects of geometric constraints on patterns of space-use.

Third, mechanistic home range models are able to incorporate the effects of behavioural factors affecting patterns of space-use by individuals. As we showed here, this is particularly important in analysing coyote home range patterns, where, as in other carnivores, den sites act as focal points for the movements of individuals, and individuals exhibit conspecific avoidance responses to the presence of neighbouring packs (figure 2b). As seen in figure 3, in addition to influencing current patterns of space-use by individuals, the spacial geometry of resources and the constraints imposed by the patterns of space-use of neighbouring packs significantly influence the way in which home range patterns shift in response to demographic perturbation.

The above benefits of mechanistic home range models come at a price, however. Compared to RSA, mechanistic home range analysis is challenging mathematically; the maximum-likelihood fitting procedure involves repeated numerical simulation of partial differential equations (such as equations (2.3) and (2.4)) in two-dimensional space for different parameter combinations. This high numerical cost of model fitting limits the numbers of different biotic and abiotic factors influencing movement that can be incorporated into a single mechanistic home range model. As shown here, the observed pattern of space-use in Yellowstone could be accounted for using a mechanistic home range model incorporating just two movement responses (prey availability and foreign scent-mark avoidance). In other situations, more complex models, incorporating responses to numerous different forms of landscape heterogeneity, may be required to account for observed home range patterns. In these situations, RSA is likely to be a useful tool for identifying key landscape heterogeneities influencing space-use. These factors can then be subsequently incorporated into mechanistic home range models to determine how they interact with landscape geometry and behavioural factors affecting movement to yield actual patterns of space-use, and to predict how home range patterns will shift in response to environmental or demographic perturbation.

The mechanistic home model formulations used in this analysis reflected the ecological and behavioural characteristics of coyote territoriality, including small mammal foraging, avoidance of foreign scent-marks, den sites acting as focal points for the movement of individuals, and over-marking responses to encounters with foreign scent-marks. These formulations could be readily applied to analyse space-use in other carnivore species that use relatively static prey resources, occupy distinct home ranges, and use scent-marks as indicators of territorial occupation. More generally, the approach used here for coyotes could also be used to analyse home range patterns in a variety of other animal groups, including primates (Waser 1985; Barret & Lowen 1988), ungulates (Jarman 1974; Clutton-Brock et al. 1982; Boyce et al. 2003), rodents (Ostfeld 1986), birds (Brown 1964) and lizards (Stamps 1977; Schoener & Schoener 1980; Roughgarden 1995). The resulting equations for predicted patterns of space-use would be comprised of different movement terms, reflecting the different underlying ecological and behavioural cues affecting movement in these different animal groups. For example, a mechanistic home range model for ungulates may include movement responses to forage quality, tree-cover and aggregative responses to conspecifics. If predators were also suspected to be a significant factor affecting space-use, predator avoidance terms would also need to be included, requiring information on the predator spatial distribution, either obtained from observations, or predicted from a coupled mechanistic home range model of the predator space-use.

Supplementary Material

Appendices S1–S3

Mechanistic home range model derivations, model fitting procedures and small mammal biomass estimation methods.