Rethinking the evolutionary theory of aging: Transfers, not births, shape senescence in social species

Abstract

The classic evolutionary theory of aging explains why mortality rises with age: as individuals grow older, less lifetime fertility remains, so continued survival contributes less to reproductive fitness. However, successful reproduction often involves intergenerational transfers as well as fertility. In the formal theory offered here, age-specific selective pressure on mortality depends on a weighted average of remaining fertility (the classic effect) and remaining intergenerational transfers to be made to others. For species at the optimal quantity–investment tradeoff for offspring, only the transfer effect shapes mortality, explaining postreproductive survival and why juvenile mortality declines with age. It also explains the evolution of lower fertility, longer life, and increased investments in offspring.

The classic evolutionary theory of aging, due to Medawar (1) and Williams (2) and formalized by Hamilton (3), seeks to explain why mortality rises with age as health and function decline. In this theory, as individuals age, their continued survival contributes less and less to reproductive fitness, because less of their lifetime fertility remains. Consequently, natural selection acts more weakly to reduce mortality at older ages. Although this theory has been extended and qualified, it is still the dominant paradigm for the evolution of aging (4, 5). However, the focus on fertility alone, by Hamilton and others (6–9), is limited. Reproduction involves conversion of foraged food into sexually mature offspring, a process requiring both fertility and investment per offspring (intergenerational transfers). An alternative theory considers both fertility and transfers, including parental care and help from others such as older siblings or grandparents. It is shown that selective pressure to reduce mortality also depends on the cumulated investment needed to produce a survivor to a given age, including costs wasted on offspring who died earlier. If the combination of numbers of offspring and investment per offspring is optimal (plausibly true for many species), then only the transfer effect matters for mortality selection. Unlike the classic theory, this one explains why juvenile mortality often declines with age (as cumulated investments rise) and why postreproductive survival occurs (investment in others continues). Quantitative predictions fit data on contemporary human hunter–gatherer mortality and transfers.

Strangely, transfers have not been incorporated in formal theories of aging, although their importance is widely appreciated (10). Fisher (11), after introducing his fertility-based concept of reproductive value, immediately noted that there would also be indirect effects on reproduction as when “a mother past bearing may greatly promote the reproduction of her children.” Medawar (1), Williams (2), Hamilton (3), and others (12) discuss, but do not develop, similar ideas. Less formal theories, such as the Grandmother Hypothesis (13, 14) and similar theories for nonhumans (15–18), explicitly link postreproductive survival to contributions by the elderly. However, it has not been recognized that the same arguments apply to selection on the mortality of reproductive-age parents, altering the classic theory, or that increasingly intense selection should conserve the growing value of cumulated investments in juveniles as they age. Drawing on theoretical work on transfers (19–21), I formally integrate selection due to transfers across the life course with the classical selection due to fertility. The theory and results apply more generally to life-history theory (22), which depends on perturbation analysis of population renewal (23) and on the concept of reproductive value (11).

Transfers and Selection

Informal examples will clarify the main ideas before turning to the formal analysis:

(i) In some species, postreproductive females make substantial contributions to their descendants, either through direct parental care or through grandparental care. Such contributions continue after birth in all mammals (most notably primates), all birds, many insects, and some fish (15). Postreproductive bottle-nose dolphins and pilot whales baby-sit, guard, and even breastfeed their grand-children (15). Selection against the mortality of postreproductive individuals in such species would be expected to continue. Sex differences in survival of anthropoid primates provide useful evidence: the sex that mainly provides care to offspring tends to have the higher life expectancy (18).

(ii) Turning to juvenile mortality when there is parental investment, contrast the death of a baby bird just after hatching with a death just before a baby fledges. The classic theory predicts equal selection against mortality at the two ages. However, the later death would be a total loss, whereas the early death would free up parental resources for greater investment in the surviving chicks, boosting their survival, size, and reproductive fitness, thus offsetting the direct effect and perhaps even increasing the survivors to maturity. More generally, if there is continuing parental investment, then the force of selection against mortality should rise with juvenile age, and mortality should fall.

(iii) Sometimes, breeding is cooperative and nonparental helpers contribute to rearing the young through transfers of resources (24). The average infant in an Efe hunter–gatherer group is cared for by 11 people in addition to its parents (25). Cooperative breeding occurs in some mammals, many insects, and ≈200 species of birds (26). In the theory developed here, the force of selection is proportional to the cumulative net transfers up to the age in question, including investments lost to earlier mortality. If a juvenile begins to make transfers to others, then these offset the transfers it received earlier, and the cumulative net transfer begins to decline and with it the force of selection. When these intergenerational transfers are included in a formal model, along with density dependence, the force of selection on mortality at a given age is found to be a weighted average of the classic effect, proportional to remaining fertility F(a), and another effect, proportional to remaining transfers to others T(a), or equivalently, to net transfers received up to age a. (The sum of transfers over the life cycle and population must be 0 on average, from which this equivalence follows.) If there are no postbirth investments, then transfers are always 0 and selection depends entirely on Hamilton's classic effect F(a).

Selection in other circumstances is more complex and depends on the relative importance for reproductive fitness of fertility versus investments per offspring, that is, the quantity–quality tradeoff, for a particular organism in a particular ecological setting. If higher fertility and less investment per offspring would improve fitness, then selection on mortality at a given age will be a weighted average of the classic and transfer effects, with positive weights on both. Lower mortality at younger ages would raise the growth rate, and lower mortality at younger and at older ages would economize on resources for investment, also raising the growth rate.

In the opposite case, where lower fertility and increased investments per birth would raise fitness, then lower juvenile mortality could actually reduce reproductive fitness by increasing competition for investments per surviving offspring. There would be strong selection for adult survival, but there might also be selection for increased juvenile mortality at early ages. In this case, the weight on the classic effect would be negative and greater than unity on the transfer effect. Most organisms that invest in the care of a reduced number of offspring must have passed through a long evolutionary period of this sort, where selection favors lower fertility but possibly also higher juvenile mortality as a wasteful second-best route to higher investments per survivor.

Most species that invest heavily per offspring, such as mammals, birds, and many insects, will have evolved an optimal allocation of resources between level of fertility and level of investment per offspring. In this case, small variations in fertility will have little or no effect on reproductive fitness. The classic Hamilton effect therefore gets a 0 weight in such cases, and the cumulative transfer effect is entirely responsible for the force of selection by age on mortality.

There is a growing literature on the evolution of life histories that explicitly models the optimal allocation of resources among growth, reproduction, and somatic repair (7–9 and 27). However, reproduction in these models is simply fertility, and because the resource constraints apply to individuals, parental investments and transfers are precluded. The same is true of other recent theoretical contributions (6). Although many smaller-scale models and theories take transfers into account, apparently no overarching theory has done so, although Kaplan and Robson (28, 29) come closest.

Population Equilibrium with Intergenerational Transfers

I will first develop a general model of population equilibrium that incorporates age distribution, density, and intergenerational transfers. The level of consumption, γ, is a key variable in what follows and is difficult to grasp. It is a device for abstracting from the infinite variety of possible changes by age in consumption, production, fertility, and mortality, and picking out a biologically relevant pattern of variation for each along a single dimension, indexed by γ. I will write individual consumption as a general function of age and γ, c(x, γ). Because I focus on steady states, I will not index on time. One specific example of such a function is c(x, γ) = γc(x), which says that consumption at all ages varies proportionately when γ varies. Another example is c(x, γ) = (γ/(x + k))c(x), in which case consumption increases or decreases more at younger ages and progressively less at older ones when food abundance varies. The theory developed below will hold for any function c(x, γ), so long as consumption at every age increases to some degree when γ increases [dc(x, γ)/dγ > 0 for all x].

Production (foraging success) at a given age depends in part on lifetime consumption, because it influences the individual's growth, size, and vigor, so the age-specific component is written y(x, γ). Production also depends on competition for resources in foraging, which increases with population size and density. This is expressed by π(E/N) where E is the resource base and N is the size of the population [a fuller treatment would include age-specificity in the denominator of E/N as well (30)]. Thus, production is given by π(E/N)y(x, γ).

Production minus consumption is the net transfer made to others at each age, τ(x, γ). It will typically be negative for young individuals and positive for older individuals. Greater parental investment per offspring (usually with increasing γ) may cause increased production of the offspring in maturity, depending on the specific forms of c, y, and γ.

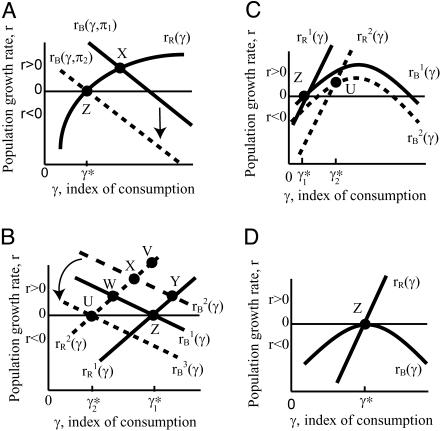
The level of consumption also influences reproduction. Fertility at age x, m(x, γ), rises when consumption is greater, whereas age-specific mortality, μ(x, γ), falls at each age. Because fertility rises with γ and mortality falls, evidently the steady-state (or stable or intrinsic) growth rate r rises with consumption. I will call the steady-state relationship between r and γ the renewal equation, and call the plot of r against γ the renewal curve (see Appendix). Stationary population equilibrium occurs when r = 0, corresponding to a unique level of consumption, γ^* (Fig. 1A).

Fig. 1.

(A) Equilibrium population size and age distribution, reflecting density and intergenerational transfers (see Population Equilibrium with Intergenerational Transfers for details). (B) The effect on r and γ of a mortality-reducing mutation when the balance curve is downward sloping (see Mutation and Selection Without Age). (C) Selection effects on the left of a hump, where the classical effects are reversed. Evolution moves toward the optimal equilibrium at the peak (see The Evolutionary Trajectory to the Optimal Equilibrium). (D) The optimal equilibrium is evolutionarily stable (see The Evolutionary Trajectory to the Optimal Equilibrium).

The share of the stable population age distribution at age x is proportional to e^-rxl(x), where r is the growth rate and l(x) is the proportion of births surviving to age x. More rapidly growing populations are younger, with more juveniles per adult. At a given growth rate r, populations with lower mortality (higher survival) will be older with fewer juveniles per adult.

For every minimal social unit that neither makes transfers to other units nor receives them, the sum of transfers across givers and receivers must be 0, assuming for simplicity that food is neither stored nor wasted [this assumption can be relaxed (20, 21)]. Such units might be individuals (if there are no transfers) or mother–offspring sets (if fathers do not contribute), parent–offspring sets, larger family groups, or cooperative breeders. Because every unit must be in transfer balance, the aggregation of units, which is the total population, must be so as well. It follows that in steady state, the sum of transfers over all ages, weighted by the stable population age distribution, must be 0. This is the “balance equation” for transfers that links together the level of consumption, population size, and population growth rate (Eq. 4 in Appendix). This balance equation (without density or γ) has been extensively analyzed (19–21), and it enters Kaplan–Robson's (28, 29) theory of human evolution. For any given population size, the balance equation implicitly defines a relationship between population growth r and consumption γ, which I call the balance curve. The balance curve is a key component of the theory.

General shapes of the renewal and balance curves might reflect broad features of taxa, such as primates or mammals, or ecological types, such as opportunistic or equilibrating species. In Fig. 1A, the solid line labeled r_R(γ) plots the renewal curve sloping up to the right. It also plots the balance curve as a solid line labeled r_B(γ) sloping down to the right, which is the simplest case. For a given population size, more rapid population growth (higher r) makes the population age distribution less favorable by reducing the ratio of adults to juveniles, and thereby reduces the consumption level γ. Hence, the downward slope.

An equilibrium (not necessarily stationary) requires that both the renewal equation and the balance equation be satisfied by the same r and γ, which occurs where the two lines intersect. If their intersection occurs where r is not 0, then it is a temporary equilibrium, not a true one. Fig. 1A illustrates a temporary equilibrium at X. Because r > 0, the population grows, raising density and reducing production at every age through the function π. With less production, unchanging consumption is possible only with a more favorable population age distribution, resulting from slower population growth. Therefore as population grows the balance curve shifts downward (lower r for every γ), until it intersects the renewal curve at zero population growth rate at Z, where the population is in true stationary equilibrium.

In the discussion of equilibrium and convergence that follows, processes are operating on four different time scales. The age distribution is assumed to converge to its steady state over the shortest time scale, and these steady states are described by the renewal equation and the balance equation for a given population size or density. Mutations occur on a longer time scale and are selected into or out of the population on the time scale of convergence to the density-dependent equilibrium, as will be discussed below in connection with Fig. 1. Finally, on the longest time scale, some species evolve toward the optimal equilibrium shown in Fig. 1D. I will not discuss true dynamics, but rather a succession of steady states. True dynamics could be studied by using simulations of deterministic dynamics together with stochastic mutations, which would require specific functional forms.

The formal analysis refers to a simplified single-sex case. With two sexes, the renewal curve refers only to one sex and the balance equation holds for the sum of the sexes. The balance for males or females separately can be nonzero. If only the mother provides care of offspring, then the no-wastage, no-storage assumption locks together the fertility schedule and the mother's transfer schedule in a way that could not actually hold as γ varies, given the rigid age schedules in the model. In nature, this rigidity would be relaxed through varying maternal body reserves, differential treatment by birth order, varying infant mortality by birth order, and so on. A fuller model would allow for individual variations in effort and consumption in response to changing circumstances and allow bodily reserves to be built up or depleted.

Mutation and Selection Without Age

Following Hamilton (3) and common practice, I take r (the stable growth rate) to measure fitness, with the force of selection on a mutation assumed to be proportional to its effect on r. Unlike Hamilton, however, I assess fitness at some particular density. To determine which of two competing subpopulations will dominate, we must ask which can continue to grow after the other is at its equilibrium density with r = 0. Mutations affecting fertility and mortality are assumed to occur relatively frequently, mostly with adverse effects on fitness, which selection constantly tends to remove. A mutation–selection balance will be reached at each age, with stronger selection leading to lower mortality (31).

Building on Fig. 1A, I will use a graphic analysis to show the direction of selection on mutations affecting fertility and mortality under differing circumstances. Later I will discuss the mathematical analysis. Suppose a mutation leads to lower mortality at some specific age a, with no effect on mortality at any other age. [The discussion mostly follows Hamilton in considering selection on favorable mutations, although probably most are adverse (31); my basic analysis is the same in either case.] A mutation reducing mortality at any age before the cessation of reproduction will shift the renewal curve upward, as shown in Fig. 1B, because the mutant line will have a higher growth rate for any given level of consumption. The size of this vertical shift (from Z to V) is the “force of selection” in Hamilton's theory. It depends on remaining fertility F(a) at the particular age affected by the mutation.

In the theory developed here there are additional effects. Lower mortality even at a postreproductive age reduces the ratio of juveniles to adults at any given growth rate, permitting higher consumption and therefore raising the balance curve for the mutant line from 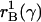to 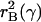. Additionally, the increased growth rate due to lower mortality makes the age distribution younger and less favorable, requiring lower consumption for the mutant line. The combined effect of all these influences is shown by the intersection of the new renewal and balance curves (long dashes), at point X. The vertical distance between Z and X is the actual force of selection on this mutation, smaller than the Hamilton effect Z to V.‡ If the mutation reduces mortality at a postreproductive age, then the renewal curve does not shift, and the Hamilton effect is 0. However, the balance curve still shifts upward (assuming postreproductive adults make transfers), intersecting the original renewal curve at a higher growth rate at Y, so this mutation is positively selected as well. If the mutation affects mortality only at age 0 (immediately after birth), then the renewal curve is strongly shifted but the balance curve is not shifted at all, and the temporary equilibrium is at W.

The mutant and original populations produce and consume separately, but they share the resource base. Production is reduced for both as total population (the sum of the original and mutant subpopulations) grows. At X, the mutant line grows whereas the original population is initially stationary at Z. As the total population grows, the mutant balance curve shifts down to 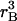(γ) (shorter dashes; change shown by curved arrow), intersecting the mutant renewal curve 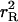(γ) at U, the new equilibrium, with lower consumption at 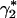. The balance curve for the original population shifts downward, and so the original population has r < 0 and therefore declines. Eventually the mutant line becomes 100% of the population. Note that the mutant stationary equilibrium has moved to the left. Lower mortality means that a larger, denser mutant population can reproduce itself at lower consumption. Similar density adjustments take place in the other cases considered, although not always to U.

A mutation that raises fertility has similar effects, except that initially only the renewal curve is shifted while the balance curve remains in its original position. As density eventually increases, the balance curve will be shifted down in this case as well.

For an organism evolving toward lower fertility with increased investment per offspring, the balance curve slopes upward rather than downward for several reasons (the formal expression for the slope of the balance curve is given in Eq. A2 in Mathematical Appendix, which is published as supporting information on the PNAS web site, www.pnas.org). (i) Higher consumption raises survival, particularly of juveniles, so wastage of resources is avoided, and the adult/juvenile ratio rises for a given population growth rate. (ii) Higher consumption raises productivity through larger body size and increased energy. (iii) Higher consumption may be associated with greater and longer investments in juveniles, which might have a high payoff for later production. In such a case, the balance curve is hump-shaped (inverted “U”) over some range of consumption, with a maximum at the optimal tradeoff between level of fertility and investment per offspring. The hump summarizes the outcome of allocational tradeoffs for the organism.

The Evolutionary Trajectory to the Optimal Equilibrium

On the right-hand side of any hump, the balance curve slopes down to the right as in Fig. 1B, which can therefore be used to analyze the dynamics when X and Z occur there. As we saw, selection moves the equilibrium to the left, toward the peak of the hump. Density-dependent adjustment of the balance curve drops it down until the peak of the hump touches the line r = 0 at a single point of tangency, which I call the “optimal equilibrium” (Fig. 1D).

Selection in the region to the left of the peak can be counterintuitive. Fig. 1C shows a hump-shaped balance curve with original equilibrium occurring at Z to the left of the peak with r = 0, γ = γ^*. First consider a decrease in mortality at age 0, which has exactly the same effect as an increase in fertility. This shifts the renewal curve upward, but has no effect on the balance curve. From inspection of Fig. 1C, the new intersection would occur to the left of the original equilibrium, at r < 0, and would be selected out of the population. An increase in mortality at age 0, or decrease in fertility, would be positively selected. The classic selection results are reversed here. The intuition is that higher mortality near age 0, for example at an early juvenile age, will thin out the number of surviving juveniles, permitting greater parental investment in each, which has a big payoff and raises the growth rate. Higher mortality is a poor substitute for lower fertility, and a more flexible model might instead imply situational infanticide as observed for birds in nature (32).

Next, consider a decrease in mortality at a postreproductive age. This would leave the renewal curve unchanged, but would shift the balance curve upward with an intersection at r > 0, and so would be positively selected, just as in Fig. 1B.

Finally, consider a mortality decrease at an intermediate age, between 0 and the cessation of fertility. Selection will be negative near age 0 and positive near the last age of fertility, with a crossover someplace between. Fig. 1C shows the case of a mutation that raises mortality at an intermediate age, shifting both the renewal curve and the balance curve downward. In the case shown, the net effect is to increase r, so higher mortality is selected. But, depending on the age affected, the opposite could also occur, depending on which curve shifted more, as will be discussed further later.

After any of these shifts, full adjustment toward the peak includes a downward shift in the balance curve as population size increases, as shown in Fig. 1C.

The end point of this process of directional evolution toward the optimal equilibrium at the peak of the hump is shown in Fig. 1D. It is evolutionarily stable, because mutation and selection steer the organism toward this point from either the right or the left, as we have just seen. If a mutation (higher fertility or lower mortality) shifts the renewal curve slightly upward, intersection with the balance curve moves slightly to the left, reducing consumption for the mutant line, although population density is unchanged. Consumption declines only because this mutation shifts the life history away from the optimal equilibrium and reduces reproductive efficiency at the given density level. Because the mutant r is slightly reduced, the mutant line goes extinct. This shows that the classic (Hamilton) selection effect vanishes at the optimal equilibrium, a consequence of the balance curve being flat at this point. Nonetheless, mutations shifting the balance curve upward by reducing mortality will still be positively selected. Therefore, at the optimal equilibrium, mortality selection is driven entirely by the transfer effects reflected in the balance curve.

As mutation and selection move the life history toward the peak from the left, consumption and density increase together. Selection leads to a more efficient life history, permitting the species to equilibrate at a higher density by investing more in each offspring (higher γ), and in this way crowds out the original population even though the original population can replace itself (r = 0) at a lower level of consumption. These strange and counterintuitive results to the left of a peak represent a positive feedback loop that selects for reduced fertility, higher consumption, greater investments in juveniles, and longer life. This describes the evolution of primates and other kinds of species with low fertility, heavy investment in offspring, and long adult life, a trajectory described elsewhere (16).

The Age-Specific Force of Selection

Fertility. To add age detail to this general picture, we examine the impact on the growth rate due to an age-specific perturbation in fertility, mortality, or transfers (23, 31). First we implicitly differentiate the full model with respect to a fertility perturbation, ε(a). The result (Appendix) after much simplification is the product of two factors. The first is identical to the Hamilton effect for fertility, proportional to the probability of surviving to that age (discounted by the population growth rate and divided by the mean age of fertility). The second factor depends on the slopes of the renewal curve and the balance curve, and it is this factor that determines the direction of evolution, which we discussed earlier using Fig. 1 B–D. This factor is always positive except on the left side of a hump, should there be one. Where it is positive, Hamilton's result for selection on age-specific fertility holds. However, to the left of a hump, the factor is negative, in line with earlier discussion. Thus, selection guides fertility toward its optimal level by reducing it when on the left of the hump and raising it on the right (Eq. 5 in Appendix).

Mortality. Next consider mortality, for which selection at age a is a weighted average of two components. The first component is the classic Hamilton effect for mortality, proportional to remaining fertility, F(a). The second component is the cumulative net investment (transfers) up to age a per birth (including mortality wastage), or equivalently, the remaining lifetime transfers made after age a per newborn, T(a). Intuitively, selection favors the survival of individuals that embody larger investments of resources by parents and others, or equivalently, that will themselves make larger investments in others in the future. (Equivalence follows from the balance equation, which must sum to 0, so the parts above and below any particular age must be equal, but of opposite sign.) (Eq. 6 in Appendix).

In the typical case with postbirth investment, cumulated net transfers received, T(a), will first rise after birth (or more correctly, after fertilization, because maternal investments before birth are relevant for prebirth survival of the egg, seed, or fetus) (33). At the age of economic maturity (when production equals or exceeds consumption), T(a) will be at its maximum, and will decline thereafter if the individual begins to contribute to others.

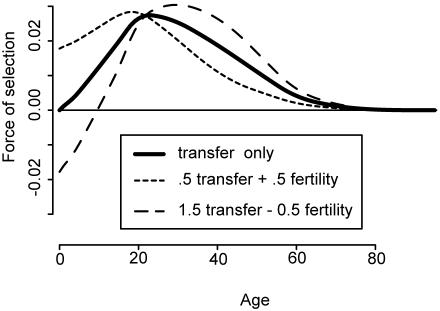
The full selection effect on mortality is the weighted average of the Hamilton effect and the transfer effect, with weights summing to unity (Eq. 6 in Appendix). Fig. 2 is based on data for the Ache, a well studied contemporary forager–horticulturist group in Paraguay, with transfers measured solely as the caloric value of food produced and consumed (35–37). The three lines represent the hypothetical force of selection if the species were evolutionarily located to the right (both weights positive) or left (fertility weight negative, transfer weight positive) of a hump, or at its peak (fertility 0, transfers unity). The actual location for humans and many other species is expected to be at the peak, or optimal equilibrium, where only transfers drive selection.

Fig. 2.

The force of selection on mortality is a weighted average of the fertility effect and the transfer effect (Eq. 6 in Appendix), illustrated for Ache forager–horticulturist data (35–37). Short dashes, selection to right of hump; long dashes, selection to left of hump; solid line, selection at peak of hump.

Production and Consumption. The force of selection on an increment to production, consumption, or net transfers can also be analyzed. If an organism evolves greater transfers to juveniles, permitting greater growth and development before they must begin production themselves, this investment should return higher net production at later ages. When the rate of return exceeds r for an increased investment in a juvenile of a given age, as would occur to the left of a hump, then a mutation raising such transfers will be selected, and conversely, as shown by Eq. 7 in Appendix, where the numerator is the cost of the investment plus the discounted and survival weighted benefit. When this sum is positive, the rate of return exceeds r.

Implications of the Theory

When an organism does not invest in offspring after birth, then T(a) = 0 and this theory collapses to the classic theory. However, it still applies prebirth, because the investment in the seed, egg, or fetus is itself relevant and should influence selection on mortality before birth. The greatest differences occur when there is significant parental or cooperative care.

This theory takes as given observable age profiles of fertility, mortality, and intergenerational transfers for a particular organism, and predicts relationships among them. Because these predictions are conditional on the observed age profiles, the theory generates strong testable predictions for single organisms. These could be extended to comparative predictions in obvious ways. The predictions apply to the component of mortality shaped by evolution, rather than to total mortality, but selection effects may be sufficiently powerful to dominate (Table 1).

Table 1. A summary of qualitative implications, according to whether the species in question makes transfers to offspring.

		Transfer theory
Qualitative prediction of theory	Classic (Hamilton)	If no transfers	If yes transfers
Adult mortality rises with age	Yes	Yes	Yes
Juvenile mortality declines with age	No	No	Yes
Postreproductive survival	Never	Never	Yes
Selection for lower fertility	Never	Never	Could
Selection for higher mortality	Never	Never	Could

For empirical work, measures of transfers would ideally include not just food but also such activities as warming, fanning, guarding, carrying, leading, and teaching, and would also reflect incremental mortality risks incurred in making these transfers. A recent field study of meerkats illustrates the feasibility of collecting field data on a number of these relevant transfers (34). Contributions by the elderly of knowledge and experience would be more difficult to quantify.

Application to Human Hunter–Gatherers

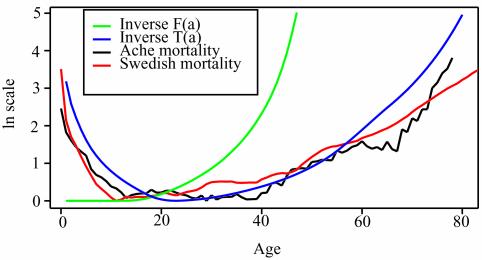
Fig. 3 is based on the Ache (35–37). Mortality should be inversely proportional to selection, so Fig. 3 compares the inverse of classic selection strength, 1/F(a), and transfer selection strength, 1/T(a), to age-specific death rates on a log scale. Mortality for the Ache and 18th-century Swedes accords well with the transfer effect but not the classic effect. The contrast is particularly strong for pre- and postreproductive age ranges. Transfers were measured based on production and consumption of food only. The recent important Kaplan–Robson theory (28, 29) addresses the coevolution of brain size and longevity in primates and humans. Their model incorporates a structure specific to the human case, unlike mine, and they explicitly model investment in somatic capital and the returns to such investment. This additional structure enables them to derive specific results about the evolution of humans and particularly the human brain. Like my theory, that of Kaplan and Robson stresses the role of intergenerational transfers and uses a population level constraint similar to my transfer balance equation to close their optimization problem. However, their theoretical setup is different from mine in important respects: (i) fertility is not included; (ii) productivity depends solely on human capital and is independent of natural resources, so there is no equilibrium population size or density; and (iii) the processes of mutation and selection are not modeled, and consequently mutation accumulation and antagonistic pleiotropy are not considered. Because of iii, Kaplan and Robson's theory does not predict biological aging and rising mortality unless a special assumption is added that productivity declines with age. This introduces an element of circularity, an issue they recognize as important. Because of points i and iii, their theory does not incorporate the insights of the classical theory of aging.

Fig. 3.

Comparison of actual mortality schedules with predicted mortality for classical theory and present theory. Mortality should be inversely proportional to force of selection, so logarithms of age-specific death rates, 1/F(a), and 1/T(a) are shown. Fertility, mortality, and transfers are for Ache (35–37). Also plotted is mortality for 18th-century Sweden (data from Human Mortality Database, University of California, Berkeley, and Max Planck Institute for Demographic Research, Rostock, Germany, and available at www.mortality.org or www.humanmortality.de). All curves are adjusted to have the same minimum at 0, because only shape is being compared. Actual juvenile and adult mortalities agree well with the transfer theory and poorly with classical theory.

Discussion

Among the various approaches to the evolutionary theory of aging, including the classic theory, the disposable-soma theory, formal life-history optimizations based on it, and other recent variations on these themes, none incorporates the flow of resources transferred to offspring. Reproduction is typically treated as a purely demographic matter: individuals at birth turn into sexually mature adults or die by the simple passage of time. For some organisms, this makes sense, because all of the parental effort goes into creating the seed or egg, which receives no further care or investment after “birth.” But for many others, continuing transfers to offspring are centrally important for survival, growth, and eventual reproductive success, and such organisms have evolved lower fertility, and plausibly optimize the quantity–quality tradeoff. The theory offered here shows how evolution shapes the life histories of such organisms for efficient use of parental and other resources and most strikingly shows that, in this case, only the transfer effect shapes mortality, explaining both postreproductive survival and why juvenile mortality declines with age.

The approach has implications for other areas of evolutionary theory and life-history analysis, because it implies a reformulation of the concept of reproductive value (11, 31) and a restatement of the sensitivity of growth rates to variations in life-history parameters (22, 23, 31), for example. There are also deep links to kin selection and inclusive fitness (38–40). The formulation here of population equilibrium to include age distribution, consumption, and transfer balance also has broader implications. From one point of view, fertility is most fundamental to evolution because it alone transmits genes to the next generation. From another point of view, however, the production of vast numbers of replicates of genetic material is cheap, whereas intergenerational transfers of food and care are costly and are often the binding constraint on successful reproduction.

Appendix

Derivation of selection effects is given in Mathematical Appendix. Variables are denoted as follows: a and x, age; ω, maximum age of survival; γ, index of consumption level; m(x, γ), birth rate at age x [dm(x, γ)/dγ > 0]; μ(x, γ), force of mortality at age x [dμ(x, γ)/dγ < 0]; l(x, γ), survival from birth to 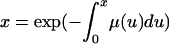; r, steady-state population growth rate (intrinsic growth rate); N, total population size; E, resource base; c(x, γ), consumption at age x [dc(x, γ)/dγ > 0]; π(E/N)y(x, γ), production; y(x, γ), age factor for production or foraging success at age x [dy(x, γ)/dγ > 0]; π(E/N), effect of density on production [dπ/dN < 0]; and τ(x, γ) = π(E/N)y(x, γ) - c(x,γ), transfers made to others at age x (received is negative). Remaining fertility at age a:

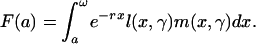[1]

Cumulative net transfers made above age a or, equivalently, received prior to age a:

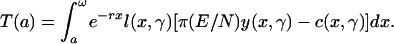[2]

Renewal equation:

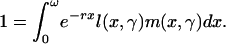[3]

Balance equation:

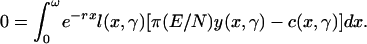[4]

Implicitly differentiate the renewal and balance equations with respect to a perturbation in fertility at age a, ε(a), or mortality, δ(a) (positive δ will mean reduction in μ, that is, lower mortality), holding N fixed in the balance equation, and equate the effects on γ in the two equations. Solve to find the following effects on r, noting the definitions given which lead to simplification (more details in Mathematical Appendix):

Fertility:

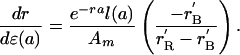[5]

Mortality:

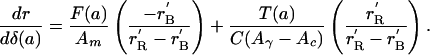[6]

Production or negative consumption:

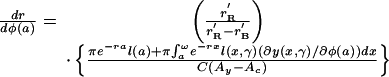[7]

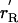and 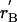are the slopes of the renewal and balance curves with respect to γ, holding π constant for 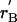(see Mathematical Appendix). C is the discounted sum of lifetime consumption. A_m is the average age of fertility in the stable population. A_y and A_c are the average ages of producing and consuming in the population. A_y - A_c > 0 when transfers on average flow downward from older to younger individuals, which is probably universal in nature. ε, δ, and φ are additive perturbations at age a in the functions describing fertility, mortality, and production.