Coupled two-way clustering analysis of gene microarray data

Abstract

We present a coupled two-way clustering approach to gene microarray data analysis. The main idea is to identify subsets of the genes and samples, such that when one of these is used to cluster the other, stable and significant partitions emerge. The search for such subsets is a computationally complex task. We present an algorithm, based on iterative clustering, that performs such a search. This analysis is especially suitable for gene microarray data, where the contributions of a variety of biological mechanisms to the gene expression levels are entangled in a large body of experimental data. The method was applied to two gene microarray data sets, on colon cancer and leukemia. By identifying relevant subsets of the data and focusing on them we were able to discover partitions and correlations that were masked and hidden when the full dataset was used in the analysis. Some of these partitions have clear biological interpretation; others can serve to identify possible directions for future research.

In a typical DNA microarray experiment, expression levels of thousands of genes are recorded over a few tens of different samples† (1, 3, 4). This new technology gave rise to a computational challenge: to interpret such massive expression data (5–7). The sizes of the datasets and their complexity call for multivariant clustering techniques (8, 9), which are essential for extracting correlated patterns and the natural classes present in a set of N objects, represented as points in the multidimensional space defined by D measured features.

Gene microarray data are fairly special in that it makes good sense to perform clustering analysis in two ways (1, 2, 8). The first views the n_s samples as the N = n_s objects to be clustered, with the n_g genes' levels of expression playing the role of the features, representing each sample as a point in a D = n_g-dimensional space. The different phases of a cellular process emerge from grouping samples with similar or related expression profiles. The other, not less natural, way looks for clusters of genes that act correlatively on the different samples. This view considers the N = n_g genes as the objects to be clustered, each represented by its expression profile, as measured over all of the samples, as a point in a D = n_s-dimensional space.

In previous work (1, 2, 10), samples and genes were clustered completely independently; here we introduce and perform a coupled two-way clustering (CTWC) analysis (8).‡

Our philosophy is to narrow down both the features that we use and the data points that are clustered. We believe that only a small subset of the genes participate in any cellular process of interest, which takes place only in a subset of the samples; by focusing on small subsets, we lower the noise induced by the other samples and genes. We look for pairs of a relatively small subset ℱ_i of features (either genes or samples) and of objects 𝒪_j, (samples or genes), such that when the objects in 𝒪_j are represented using only the features from ℱ_i, clustering yields stable and significant partitions. Finding such pairs of subsets, (𝒪_j, ℱ_i), is computationally hard; the CTWC method produces such pairs in an iterative clustering process.

CTWC can be performed with any clustering algorithm. We tested CTWC in conjunction with several clustering methods, but present here only results that were obtained by using the superparamagnetic clustering algorithm (SPC) (11, 12), which is especially suitable for gene microarray data analysis (13) because of its robustness against noise and its “natural” ability to identify stable clusters. By “stable” we mean those clusters that are statistically significant according to some criterion (see below).

CTWC was applied to two data sets, one from an experiment on colon cancer (1) and the other on leukemia (3). From both datasets we were able to “mine” partitions and correlations that have not been obtained in an unsupervised fashion by previously used methods. Some of these new partitions have clear well-understood biological interpretation. We do not report here discoveries of biologically relevant, previously unknown results. The main point of our message is twofold: (i) we were able to identify biologically relevant partitions in an unsupervised way, and (ii) other, not less natural, partitions were also found (http://www.weizmann.ac.il/physics/complex/compphys), which may contain new important information and for which one should seek biological interpretation.

CTWC

Motivation and Algorithm.

The results of every gene microarray experiment are organized in an expression level matrix 𝒜. A row of this matrix corresponds to a single gene, while each column represents a particular sample. In a typical experiment simultaneous expression levels of thousands of genes are measured. Gene expression is influenced by the cell type, cell phase, external signals, and more (14). The expression level matrix is therefore the result of all these processes mixed together. Our goal is to separate and identify these processes and to extract as much information as possible about them. The main difficulty is that each biological process on which we wish to focus may involve a relatively small subset of the genes; the large majority of those present on the microarray constitute a noisy background that may mask the effect of the small subset. The same may happen with respect to samples. A straightforward approach to finding pairs of subsets, (𝒪_j, ℱ_i), that lead to “meaningful” (see above) clusters, could be to take all possible submatrices of the original data and apply the standard (uncoupled) two-way clustering procedure to every one of them. By keeping track of all stable clusters that are formed in this process, and storing the identity of both genes and samples that define the particular submatrix, one is guaranteed to find every possible stable partition in the data. This approach is, of course, impossible to implement, because the number of such submatrices grows exponentially with the size of the problem. CTWC provides an efficient heuristic to generate such pairs of object and feature subsets by an iterative process that severely restricts the possible candidates for such subsets; we consider and test only those submatrices whose rows (columns) belong to genes (samples) that were identified (in a previous iteration!) as a stable cluster.

The iterative process is initialized with the full matrix—i.e., the sets of all genes (g⁰) and of all samples (s⁰) are used as (both) features and objects, to perform standard two-way clustering. Denote by g_i¹ and s_j¹ stable clusters of genes and samples found in this first step.

Every pair (g_iⁿ, s_j^m) (made of clusters obtained so far, n, m = 0, 1) defines a submatrix of the expression data; for every such submatrix we perform two-way clustering. The resulting stable gene (or sample) clusters are denoted by g_k² (or s_l²). Each cluster is stored in one of two “registers of stable clusters”; gene clusters in register 𝒢 and sample clusters in 𝒮. Together with each new cluster we also store pointers that identify the pair of “parent” clusters (g_iⁿ, s_j^m) that were used as the object and feature sets in the clustering process that generated it. These steps are iterated further, using pairs of all previously found clusters. We make sure that every pair is treated only once; the process is terminated when no new clusters that satisfy some criteria (such as stability, critical size, or the criterion used in ref. 8) are found (unpublished work).

Analyzing the Clusters Obtained by CTWC.

The output of CTWC has two important components. First, it provides a broad list of gene and sample clusters. Second, for each cluster (of samples, say) we know which subset (of samples) was clustered to find it, and which features (genes) were used to represent it. We also know for every cluster, say s, which other clusters can be identified by using s as the feature set. We present here some of the possible ways one can use this kind of information. Particular implementations are described in Applications.

Identifying genes that partition the samples according to a known classification.

This is a supervised test of clusters that were obtained in an unsupervised way. Denote by C a known classification of the samples, say into two classes, c₁ and c₂. CTWC provides an easy way to rank the clusters of genes in 𝒢 by their ability to separate the samples according to C.

First we evaluate for each cluster of samples s in 𝒢 two scores, purity and efficiency, which reflect the extent to which assignment of the samples to s corresponds to the classification C. These figures of merit are defined (for c₁, say) as

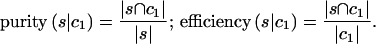Once a cluster s with high purity and efficiency has been found, we can use the saved pointers to read off the cluster (or clusters) of genes that were used as the feature set to yield s in our clustering procedure. Clustering, being unsupervised, as opposed to classification, discovers only those partitions of the data that are, in some sense, “natural.” Hence by this method we identify the most natural group of genes that can be used to induce a desired classification.

One can test a gene cluster g that was provided by CTWC also by more standard statistics, such as the t test (15) or the Jensen–Shannon distance (16). Both compare the expression levels of the genes of g on the two classes of samples, c₁ and c₂. Alternatively, one can also use the genes of g to train a classifier to separate the samples according to C (3) and use the success of the classifier to measure the relevance of the genes in g to the classification.

Discovering new partitions.

The members of every cluster s have been linked to each other and separated from the other samples on the basis of the expression levels of some coexpressed subset of genes. It is reasonable therefore to argue that the cluster s has been formed for some biological or experimental reason.

As a first step to understand the reason for the formation of a robust cluster s, one should try to relate it to some previously known classification (for example, in terms of purity and efficiency). Clusters that cannot be associated with any known classification have to be inspected more carefully. Useful hints for the meaning of such a cluster of samples may come from the identity of the cluster of genes that was used to find it. Similarly, sample clusters can be used to interpret clusters of genes that were not previously known to belong to the same process.

CTWC is a sensitive tool to identify subpartitions.

Sample clusters that emerged from clustering a subset s of the samples reflect a subpartition of s. When clustering the full sample set, this subpartition may be missed.

CTWC reveals conditional correlations among genes.

The CTWC method collects stable gene clusters in 𝒢. In many cases the same groups of genes may be added to 𝒢 more than once. This is caused by the fact that some genes are coregulated in all cells, and therefore are clustered together, no matter which subset of the samples is used as the feature set. For example, ribosomal proteins are expected to be assigned to the same cluster for any set of samples that is not unreasonably small.

Some gene clusters, however, are different; they are coregulated only in a specific subset of samples. We call this situation conditional correlation. The identity of the sample cluster that reveals the conditionally correlated gene cluster is clearly important to understand the biological process that makes these genes correlated.

All of the features listed above were tested on artificially generated expression data into which correlations, partitions, and subpartitions were incorporated and masked. CTWC successfully unraveled all of the hidden structure from these “toy data” (17).

Clustering Method, Statistical Significance, and Similarity Measures

Any reasonable clustering method can be used within the framework of CTWC. The optimal algorithm for analysis of gene expression data should have the following properties: the number of clusters should be determined by the algorithm itself and not externally prescribed [as is done when using self-organizing maps (SOMs) and K-means]; stability against noise; generating a hierarchy (dendrogram) and providing a mechanism to identify in it robust stable clusters; and ability to identify a dense set of points, which form a cloud of an irregular nonspherical shape, as a cluster. SPC, a hierarchical clustering method recently introduced by Blatt et al. (11), is the algorithm that best fits these requirements. The intuition that led to it is based on an analogy to the physics of inhomogeneous ferromagnets. Full details of the algorithm and the underlying philosophy are given in refs. 12 and 18.

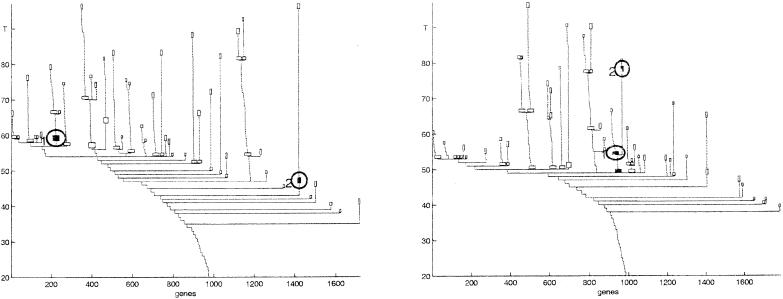
The input for SPC is a distance or similarity matrix d_ij between the objects 𝒪, calculated according to the feature set ℱ. A tunable parameter T (“temperature”) controls the resolution of the performed clustering. One starts at T = 0, with a single cluster that contains all the objects. As T increases, phase transitions take place, and this cluster breaks into several subclusters that reflect the structure of the data. Clusters keep breaking up as T is further increased, until at high enough values of T each object forms its own cluster. As opposed to most agglomerative algorithms, SPC has a natural measure for the relative stability of any particular cluster: the range of temperatures, ΔT, over which the cluster remains unchanged. The more stable a cluster is, the larger the range ΔT through which it is expected to “survive.” For a stable cluster s, the corresponding ΔT_s constitutes a significant fraction of T_max, the temperature at which the data break into single-point clusters. Inspection of the gene dendrograms of Fig. 3 reveals stable clusters and stable branches.

Figure 3.

Clustering genes of the colon cancer experiment, using all samples (Left) and using only tumor samples (Right) as the feature sets. Each node of this dendrogram represents a cluster; only clusters of size larger than 9 genes are shown. The last such clusters of each branch, as well as nonterminal clusters that were selected for presentation and analysis, are shown as boxes. In each dendrogram the genes are ordered according to the corresponding cluster analysis. The two circled clusters of the Left dendrogram are reproduced also in the Right, but there the two share a common “parent” in the tree. Note that the stability of a cluster is easily read off a dendrogram produced by the SPC algorithm.

In this work we chose the value of ΔT_c, above which a cluster is considered as stable, in the following way. We permuted at random elements of the expression matrix under investigation, and applied SPC to the randomized matrix. ΔT_c was selected so that for 500 different random permutations no clusters that survived for ΔT > ΔT_c were found. This gives a bound on the probability that clusters that we labeled as stable were in fact an artifact of noisy data.

Normalization of the Gene Expression Array.

The Pearson correlation is commonly used as the similarity measure between genes or samples (1, 2, 19). This measure conforms with the intuitive biological notion of what it means for two genes to be coexpressed; it captures similarity of the “shapes” of two expression profiles, and ignores differences between their magnitudes (2). The correlation coefficient is high between two genes that are affected by the same process, even if each has a different gain due to the process, over different background expression levels (caused by other processes). Note, however, that a positive correlation between two highly expressed genes is much more significant than the same value between two poorly expressed genes. By using correlations one ignores this dependence of the reliability on the absolute expression level.

As to samples, correlations do not always capture their similarity. Consider two samples, taken at different stages of some process, with the absolute expression levels of a family of genes much below average in one sample and much higher in the other. Even if the expression levels of the two samples over these genes are correlated, one would like to assign them to different clusters.

We therefore used the following normalization scheme. Denote by ℬ the matrix of the raw data. ℬ is an n_g × n_s matrix, where n_g is the number of genes and n_s is the number of samples.

We normalize ℬ in two steps. First, divide each column by its mean: ℬ′_ij = ℬ_ij/ℬ̄_j; ℬ̄_j = (1/n_g)Σ_i=1^n_g ℬ_ij, and then normalize each row, such that its mean vanishes and its norm is one:

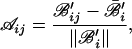where ℬ̄′_i = (1/n_s)Σ_j=1^n_sℬ′_ij and ∥ℬ′_i∥² = Σ_j=1^n_s (ℬ′_ij − ℬ̄′_i)².

For both genes and samples we used the Euclidean distance as the dissimilarity measure. For two genes (rows of 𝒜) the Euclidean distance is closely related to their Pearson correlation.

Applications

We applied CTWC to data from two experiments. Here we report only the results that were obtained by CTWC and could not be found by using a straightforward clustering analysis. We highlight a small subset of the partitions that we were able to extract from the data and for which satisfactory biological explanation was found. We do not report here new discoveries of biologically relevant, previously unknown results. Rather, we claim to have discovered a method that is capable to mine such information out of the available data. New, relevant information may be contained in the new partitions that were found, to which we were not yet able to assign biological meaning. Some new, uninterpreted results are also reviewed briefly; full lists of the corresponding clusters and their constituent samples or genes can be found at our website (http://www.weizmann.ac.il/physics/complex/compphys).

Analysis of Leukemia Samples.

Golub et al. (3) obtained data from 72 samples collected from acute leukemia patients at the time of diagnosis. Forty-seven cases were diagnosed as acute lymphoblastic leukemia (ALL) and the other 25, as acute myeloid leukemia (AML). RNA prepared from the bone marrow mononuclear cells was hybridized to high-density oligonucleotide microarrays, produced by Affymetrix (Santa Clara, CA), containing 6,817 human genes.

After rescaling the data in the manner described in ref. 3, we selected only those genes whose minimal expression over all samples is greater than 20. Only 1,753 genes survived this thresholding operation (http://www.weizmann.ac.il/physics/complex/compphys). The resulting array was then normalized as described above, to give a 1753 × 72 expression level matrix 𝒜 (see Fig. 1).

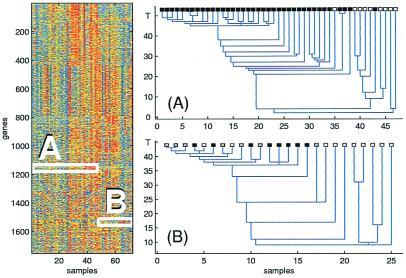
Figure 1.

The expression level matrix of the leukemia experiment is shown on the Left. Rows correspond to different genes, ordered by clustering them using all of the samples. The two boxes contain expression data from ALL patients (A) measured on one gene cluster and AML patients (B), on another gene cluster. On the Right, clustering the ALL samples, using the data in box A, yields good separation between T cell ALL (black) and B cell ALL (white). Clustering of AML samples, using the data in box B, yields a stable cluster, which contains all patients who were treated, with results known to be either success (black) or failure (gray). The vertical axis is the “temperature” parameter T, and on the horizontal axis the samples are ordered according to the dendrogram.

Two iterations of CTWC sufficed to converge to 49 stable gene clusters (LG1–49) and 35 stable sample clusters (http://www.weizmann.ac.il/physics/complex/compphys) (LS1–35). We highlight here four of our findings, which demonstrate the power of the method to solve problems listed above.

Identifying genes that partition the samples according to a known classification.

First we use the known ALL/AML classification of the samples to determine which gene clusters can distinguish between the two classes. We found a single cluster (LG1) of 60 genes that, when used as the feature set, induces a stable separation of the samples into AML/ALL clusters. (A cluster is identified with a certain class if both its purity and efficiency exceed 3/4.) This finding demonstrates the idea behind CTWC and its power. When SPC was applied, using the entire set of 1,753 genes, we did not find robust clusters that could be identified as AML or ALL tissues. Apparently, the two clouds of points in the 1,753-dimensional space, which contain the two groups of tissues, are displaced relative to each other, but they do have a region of overlap—the data in fact form a single cloud! In such a case SPC will not identify ALL and AML as separate clusters. Using only the genes of LG1 apparently eliminates this overlap of the points.

In such a situation, methods such as K-means and SOM may assign two centroids to the data, so that proximity to these centroids can be used to characterize the two different kinds of tissues. In such cases, however, it is important to preset the number of clusters into which one wishes to break the data. Indeed, Golub et al. (3) showed that two-cluster SOM analysis on a subset of the data did separate the AML and ALL tissues in a robust manner. They also identified two groups, of 25 genes each, whose expression levels differ between these two clusters. Of the 25 genes that had higher expression levels in the AML patients, only 12 survived our thresholding and were included in our set of 1,753. Of these 12 genes, 5 indeed reside in our separating cluster LG1.

Discovering new partitions.

Next, we search the stable sample clusters for unknown partitions of the samples. We focus our attention on sample clusters that were repeatedly found to be stable. One such cluster, denoted LS1, may be of interest; it includes 37 samples and was found to be stable when either a cluster of 27 genes (LG2) or another unrelated cluster of 36 genes (LG3) was used to provide the features. LG3 includes many genes that participate in the glycolysis pathway. Because of lack of additional information about the patients we cannot determine the biological origin of the formation of this sample cluster.

Identifying subpartitions.

Using a 28-gene cluster (LG4) as features, we tried to cluster only the samples that were identified as AML patients (leaving out ALL samples). A stable cluster, LS2, of 16 samples was found (see Fig. 1, box B); it contains most of the samples (14/15) that were taken from patients that underwent treatment (with known results—success or failure). For none of the other AML patients was any information about treatment available in the data. Some of the 16 genes of this cluster, LG4, are ribosomal proteins and some others are related to cell growth. Apparently these genes can partition the AML patients according to whether they did or did not undergo treatment.

This result demonstrates a possible diagnostic use of the CTWC approach; one can identify different responses to treatment, and the groups of genes to be used as the appropriate probe.

We repeated the same procedure, but discarding AML and keeping only the ALL samples. We discovered that when any one of five different gene clusters (LG4–8) are used to provide the features, the ALL samples break into two stable clusters; LS5, which consists mostly of T cell ALL patients and LS4, which contains mostly B cell ALL patients (see Fig. 1, box A). When all of the genes were used to cluster all samples, no such clear separation into T cell ALL vs. B cell ALL was observed. One of the gene clusters used, LG5, with T/B separating ability, contains 29 genes, many of which are T cell related. Another gene cluster, LG6, which also gave rise to T/B differentiation, contains many HLA histocompatibility genes.

It is important to understand the difference between our results and those of ref. 3, where Golub et al. applied the SOM algorithm to a subset of 38 mixed AML and ALL samples. The number of desired clusters K has to be used as an input to SOM. Setting K = 2, Golub et al. report finding AML/ALL separation; results for K = 3 were not reported; for K = 4 the clusters were identified as a single AML cluster, a T cell ALL cluster and two B cell ALL clusters. Our method, on the other hand, is completely unsupervised; it identified the T cell ALL/B cell ALL as a robust partition of the ALL samples, and also revealed that the genes that induce this partition are connected to the immune system.

These results demonstrate how CTWC can be used to characterize different types of cancer. Imagine that the nature of the subclassification of ALL had not been known. On the basis of our results we could predict that there are two distinct subclasses of ALL; moreover, by the fact that many genes that induce separation into these subclasses are either T-cell-related or HLA genes, one could suspect that these subclasses were immunology related.

As a different possible use of our results, note that some of the genes in the T-cell-related gene cluster LG5 have no determined function, and may be candidates for new T cell genes. This assumption is supported both by the fact that these genes were found to be correlated with other T cell genes and by the fact that they support the differentiation between T cell ALL and B cell ALL.

Analysis of Colon Cancer Data.

The data set we consider next contains 40 colon tumor samples and 22 normal colon samples, analyzed with an Affymetrix oligonucleotide array complementary to more than 6,500 human genes and expressed sequence tags (ESTs). Following Alon et al. (1), we chose to work only with the 2,000 genes of greatest minimal expression over the samples. We normalized the data to get a 2000 × 62 expression level matrix 𝒜.

CTWC was applied to this data set. Seventy-six stable sample clusters (CS1–76) and 97 stable gene clusters (CG1–97) were obtained (http://www.weizmann.ac.il/physics/complex/compphys) in two iterations. One of the latter was a cluster of ribosomal genes, similar to the one identified in ref. 1.

Identifying genes that partition the samples according to a known classification.

Again we search first for gene clusters that differentiate the samples according to the known normal/tumor classification. We found four gene clusters (CG1–4) that partition the samples this way (CG4 contains CG1). The genes of these clusters can be used if one wishes to construct a classifier for diagnosis purposes (see Fig. 2, box A). Alon et al. (1) calculated a muscle index, which can distinguish normal from tumor tissues. Of the 17 smooth muscle genes that contributed to their index, only 4 were included among the 2,000 that we used in our analysis. All of these were included in CG1 (and CG4).

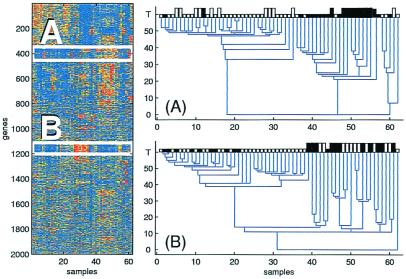
Figure 2.

The expression level matrix of the colon experiment is shown on the Left. Rows correspond to different genes, ordered by clustering them using all of the samples. The two boxes contain expression data of all samples for two gene clusters. On the Right, when the genes of the first cluster (A) are used, clear separation between tumor samples (white) and normal ones (black) is obtained. Another separation of the samples is obtained by using the second gene cluster (B). This separation is consistent with two distinct experimental protocols, denoted by short and long bars. The vertical axis is the “temperature” parameter T and on the horizontal axis the samples are ordered according to the dendrogram.

Discovering new partitions.

Five clusters of genes (CG2, CG4-CG7) generated very stable clusters of samples. Two of the five (CG2 and CG4) differentiated tumor and normal; two others were less interesting because the clusters they generated contained most of the samples. The gene cluster CG5, however, gave rise to a clear partition of the samples into two clusters, of 39 and 23 tissues (see Fig. 2, box B). Checking with the experimentalists (U. Alon, K. Gish, D. Mack, and A. Levine, personal communication), we discovered that this separation coincides almost precisely with a change of the experimental protocol; 22 RNA samples were extracted by using a poly(A) detector (“protocol A”), and the other 40 samples were prepared by extracting total RNA from the cells (“protocol B”). Cursory examination did not yield any obvious common features among the 29 genes of the cluster CG5 that gave rise to this separation of the tissues.

Identifying conditionally correlated genes and subpartitions.

Finally, we turn to identify conditionally correlated genes by comparing stable gene clusters formed when using different sample sets as features. We found that most gene clusters form irrespectively of the samples that are used. We did find, however, four special groups of genes (CG8–11) that formed clear and stable clusters when we used only the tumor samples as features, but were relatively uncorrelated—i.e., spread across the dendrogram of genes—when clustering was based on all of the samples or only the normal ones.

One of these four clusters (CG9), breaks up, at a higher resolution, into two subclusters, as shown in Fig. 3 Right. One of these subclusters (CG12), consists of 51 genes, all of which are related to cell growth (ribosomal proteins and elongation factors). The other subcluster (CG13), contains 17 genes, many of which are related to intestinal epithelial cells (e.g., mucin, cathepsin proteases). Interestingly, when the genes are clustered on the basis of either all samples or only the normal ones, both clusters (CG12 and CG13) appear as two uncorrelated distinct clusters, and their positions in the dendrogram are quite far from each other (Fig. 3).

The high correlation between growth genes and epithelial genes, observed in tumor tissue, suggests that it is the epithelial cells that are rapidly growing. In the normal samples there is smaller correlation, indicating that the expression of growth genes is not especially high in the normal epithelial cells. These results are consistent with the epithelial origin of colon tumor.

Two other groups of genes formed clusters only over the tumor cells. One (CG11, of 34 genes) is related to the immune system (HLA genes and immunoglobulin receptors). The second (CG10, of 62 genes) seems to be a concatenation of genes related to epithelial cells (endothelial growth factor and retinoic acid), and of muscle- and nerve-related genes. We could not find any common function for the genes in the fourth cluster (CG8).

Clustering the genes on the basis of their expression over only the normal samples revealed three gene clusters (CG14–16) that did not form when either the entire set of samples or the tumor tissues were used. Again, we could not find a clear common function for these genes. Each cluster contains genes that apparently take part in some process that takes place in normal cells, but is suppressed in tumor tissues.

Summary and Discussion

We proposed a new method for analysis of gene microarray data. The main underlying idea of our method is to zero in on small subsets of the massive expression patterns obtained from thousands of genes for a large number of samples. A cellular process of interest may involve a relatively small subset of the genes in the dataset, and the process may take place only in a small number of samples. Hence when the full data set is analyzed, the “signal” of this process may be completely overwhelmed by the “noise” generated by the vast majority of unrelated data.

We are looking for a relatively small group of genes, which can be used as the features used to cluster a subset of the samples. Alternatively, we try to identify a subset of the samples that can be used in a similar way to identify genes with correlated expression levels. Identifying pairs of subsets of genes and samples that produce significant stable clusters in this way is a computationally complex task. We demonstrated that the CTWC technique provides an efficient method to produce such subgroups.

The CTWC algorithm provides a broad list of stable gene and sample clusters, together with various connections among them. This information can be used to perform the most important tasks in microarray data analysis, such as identification of cellular processes and the conditions for their activation, establishing connection between gene groups and biological processes, and finding partitions of known classes of samples into subgroups. CTWC is applicable with any reasonable choice of clustering algorithm, as long as it is capable of identifying stable clusters. In this work we reported results obtained by using the SPC algorithm, which is especially suitable for gene microarray data analysis because of its robustness against noise, which is inherent in such experiments.

The power of the CTWC method was demonstrated on data obtained in two gene microarray experiments. In the first experiment the gene expression profile in bone marrow and peripheral blood cells of 72 leukemia patients was measured by using gene microarray technology. Our main results for these data were the following: (i) The connection between T-cell-related genes and the subclassification of the ALL samples, into T cell and B cell ALL, was revealed in an unsupervised fashion. (ii) We found a stable partition of the AML patients into two groups: those who were treated (with known results), and all others. This partition was revealed by a cluster of cell-growth-related genes. This observation may serve as a clue for a possible use of the CTWC method in understanding the effects of treatment.

The second experiment used gene microarray technology to probe the gene expression profile of 40 colon tumor samples and 22 normal colon tissues. Using CTWC, we find a different, less obvious, stable partition of the samples into two clusters. To find this partition, we had to use a subset of the genes. The new partition turned out to reflect two different experimental protocols. We deduce that the genes that gave rise to this partition of the samples are the ones that were sensitive to the change of protocol.

Another result that was obtained in an unsupervised manner by using CTWC is the connection between epithelial cells and the growth of cancer. When we looked at the expression profiles over only the tumor tissues, a cluster of cell growth genes was found to be highly correlated with epithelial genes. This correlation was absent when the normal tissues were used.

These features, discovered in data sets that were previously investigated by conventional clustering analysis, demonstrate the strength of CTWC. We find CTWC to be especially useful for gene microarray data analysis, but it may be a useful tool for investigating other kinds of data as well.

Abbreviations

CTWC

coupled two-way clustering

SPC

superparamagnetic clustering

SOM

self-organizing map

ALL

acute lymphoblastic leukemia

AML

acute myeloid leukemia