A statistical approach to close packing of elastic rods and to DNA packaging in viral capsids

Abstract

We propose a statistical approach for studying the close packing of elastic rods. This phenomenon belongs to the class of problems of confinement of low dimensional objects, such as DNA packaging in viral capsids. The method developed is based on Edwards' approach, which was successfully applied to polymer physics and to granular matter. We show that the confinement induces a configurational phase transition from a disordered (isotropic) phase to an ordered (nematic) phase. In each phase, we derive the pressure exerted by the rod (DNA) on the container (capsid) and the force necessary to inject (eject) the rod into (out of) the container. Finally, we discuss the relevance of the present results with respect to physical and biological problems. Regarding DNA packaging in viral capsids, these results establish the existence of ordered configurations, a hypothesis upon which previous calculations were built. They also show that such ordering can result from simple mechanical constraints.

Closely packed objects are ubiquitous in nature. Actual examples of such systems are the folding of leaves in buds (1), wing folding of insects in cocoons (2), crumpled paper (3–6), DNA packaging in capsids (7–11), or the confinement of chromatin in the nucleus of a cell (12). In all of these phenomena, the way the object is folded has a role in determining its function or in insuring its integrity during the unfolding process. Although these systems exist at different length scales, they share some common fundamental physical features, such as the symmetries of the folded structure and the dimensionality of the packed objects as well as those of the confining container.

Here, we study the packing of a one-dimensional object into a three-dimensional container, the size of which is very small compared to the length of the folded structure. This phenomenon arises in a number of scientific fields such as mechanics (6) and biology (7–12). Viral DNA packaging may be seen as an archetype of this phenomenon in biological systems. When packing a rod into a spherical container, the following questions naturally arise: which possible geometrical configurations does the rod adopt? What pressure does the container experience? What force is needed to inject (eject) the rod into (out of) the container? How do these mechanical properties depend on the configurations? Such questions stimulated a number of recent numerical and analytical studies on DNA packaging (13–19). However, a general theory that addresses these questions simultaneously is lacking. As a matter of fact, existing models of the DNA packaging problem (13, 15–17, 19) either assume a priori given conformations of the DNA inside the capsid or restrict these configurations to a very small class. This hypothesis of ordered configurations, although based on some experimental observations, does not take into account the possibility of topological changes in the conformations of the rod, whereas molecular dynamics simulations show that the conformations might change with the strength of the confinement (14). On the other hand, distinguishing the conformations of the DNA inside the capsid is very difficult experimentally, and noninvasive methods are almost impossible (7–9, 11). Therefore, one needs a theoretical model that gives the conformations as a function of the strength of the packing and the properties of the rod.

We introduce a statistical minimal model based on Edwards' theory to study the conformations of the rod. This approach proved its applicability in other fields such as granular materials (20) and polymer physics (21, 22). It led to important insights on the configurational and excluded volume constraints. This approach is suitable for the present problem because we are interested in close packing where thermal fluctuations are negligible, and where the system has accessibility to the entire phase space. In Edwards' thermodynamic approach, the steady state is characterized by a number of macroscopic quantities whose average is fixed and the steady state measure is the one obtained by maximizing the entropy over the configurations subject to these constraints. Therefore, one needs extensive manipulations such as tapping for equilibration.

This paper is organized as follows: we start by formulating the packing problem by considering an inextensible rod put inside a sphere of a given radius, and we write the reduced free energy of the system as a path integral over all possible configurations of the rod. The only interactions that are allowed are of elastic and self-avoiding nature. The addition of other interactions will be left for future investigations. Then, we proceed to the calculation of the free energy, by evaluating the path integral in a mean field approximation, and we show that a rod packed in a sphere undergoes a continuous transition from an isotropic phase to a nematic phase as the radius of the sphere is decreased below a critical length (put in other words, when the density of the rod on the sphere exceeds a critical value). This transition allows for a reduction in the pressure applied on the sphere as well as in the force needed to inject the rod into it. Let us emphasize here that the present system is different from those studied previously (21–23) because the transition is driven by the macroscopic length scale induced by the container. Finally, we discuss the relevance of our results with respect to physical and biological problems. Especially, the results show that no special intelligence is required on the side of the virus other than being dense enough in the capsid. Mechanical constraints take care of the rest.

Formulation of the Packing Problem

We consider an inextensible rod of length L put inside a sphere of radius ℓ and aim at a statistical study of its configurations. A configuration is parameterized by the position vector R(s) as a function of the curvilinear coordinate s along the rod. We assume that “cut-off” lengths such as the rod's typical thickness or the “monomer size” are very small compared to the geometrical lengths (L and ℓ), so that the rod can be treated as a material line. We also assume that the forces acting on the rod are only due to elastic stresses and self-repulsion. The energy has two contributions, one that penalizes bending of the rod and the other that penalizes self-intersections. To minimize bending and since the cut-off lengths have been set to zero, the rod will remain at the surface of the sphere. This condition is implemented as a constraint in the formulation. Moreover, we assume that the rod is long enough (L ≫ ℓ) so that a large number of energy minima are accessible and that states with the same energy are equiprobable. This is true for instance when the rod undergoes fluctuations either of thermal origin or coming from some form of tapping. Thus we write the reduced free energy Y as a path integral over all configurations R(s),

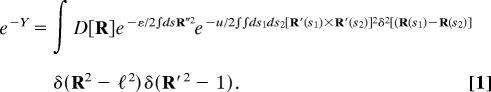The first term stands for the penalty for bending whose measure is the curvature |R″|, ε being a persistence length. The second term stands for the cost of self-intersections at (non zero) angles, with a strength u. Its form comes from Onsager's expression for the excluded volume between two thin rods (second virial approximation) (23), namely |R′(s₁) × R′(s₂)|. Here, we took the widely used squared form (21, 22) (which has the same essential properties: it is always nonnegative, has the same zeros, extrema,…) to make the calculations tractable. The two Dirac δ functions enforce the constraints, that of remaining on the sphere and that of inextensibility, on the rod configurations. For the sake of simplicity, the isotropic self-avoiding energy ∫ ∫ dsds′δ²[R(s) − R(s′)] is omitted. We checked that its inclusion amounts to a renormalization of ε and u. Note that Y can also be viewed as an effective volume function in the spirit of polymeric glasses (22). We call this model minimal since it does not consider other possible (and probably relevant) interactions such as internal twist of the rod or electrostatic forces.

It will prove useful in the following to introduce the orientation tensor defined as a function of the spatial coordinate r, and given by

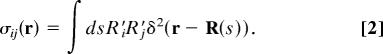The orientation tensor σ_ij(r), which is actually a collective coordinate, is a local measure of how the rod is oriented. At a given location, if there is no preferred orientation, R′ is a random unit vector so that σ_ij = δ_ij/d in d dimensions. In the present case, the rod is held on the sphere so that there will always be one direction (namely, the direction perpendicular to the surface of the sphere), which is excluded, and for which σ₃₃ = 0.

Evaluation

Now we proceed to the calculation of the reduced free energy defined in Eq. 1. Following refs. 21 and 22, the general approach is to reformulate the problem using the orientation tensor (Eq. 2), and then to evaluate the path integral in a mean field approximation. We begin with the introduction of conjugate fields to rewrite the δ functions as functional integrals. Then we use the mean field approximation, and finally determine the conjugate fields using the steepest descent method. We first rewrite the δ functions using the Fourier representation

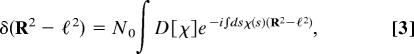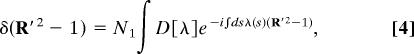where N₀ and N₁ are the normalization constants of the Fourier integrals. χ(s) and λ(s) appear as the conjugate fields associated with the position of the rod and its tangent vector respectively. Therefore, the one body term of Eq. 1 reads

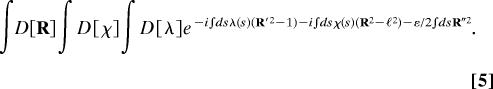Similarly, we rewrite the two-body term of Eq. 1 as

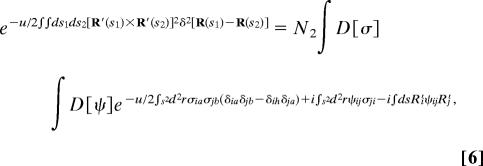where S² is the sphere of radius ℓ and we have used the identity

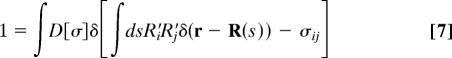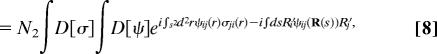to introduce the orientation tensor σ_ij, and its conjugate field ψ_ij.

Putting together all terms we find that the free energy is given by

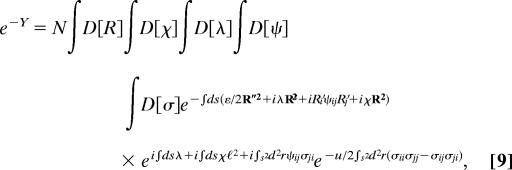where the three normalization constants have been absorbed into a single constant N. We compute the path integral (Eq. 9) using a mean field approximation such that χ and λ are treated as constants over the rod (i.e., independent of s), and σ_ij and ψ_ij are constant over the sphere (i.e., independent of r). This approximation corresponds to relaxing the local constraints (such as R² = ℓ²) to global ones (e.g. 〈R²〉 = ℓ²), i.e. local quantities can fluctuate but the average over the entire chain is fixed.

Before determining the conjugate fields, we consider a field-dependent free energy Ŷ in the form

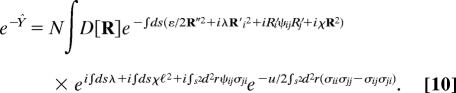As mentioned above, we assume that the rod length L as well as the radius of the confining sphere ℓ are much larger than “microscopic” length scales. Therefore, the path integral can be calculated by decomposing the trajectories R(s) in continuous Fourier (Rouse) modes

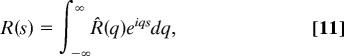and we obtain

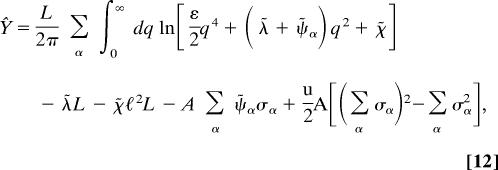where for convenience we use λ̃ = iλ, χ̃ = iχ and ψ̃_α = iψ_α. In addition σ_α and ψ_α are the eigenvalues of σ_ij and ψ_ij respectively, and A = 4πℓ² is the area of the sphere.

The conjugated fields (λ̃, χ̃, and ψ̃_α) and the orientation tensor (σ_α) are determined by the steepest descent method by setting the partial derivatives of Ŷ with respect to those fields to zero. Therefore, we get the following conditions

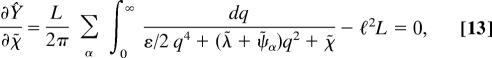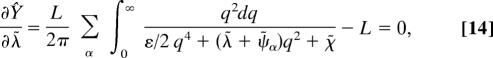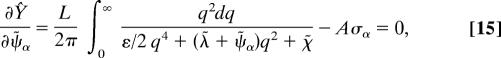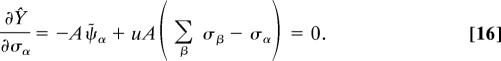After some algebraic manipulations (and omission of an irrelevant constant), we get the free energy as

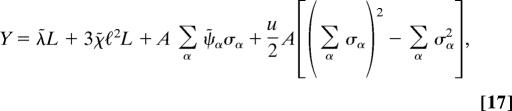where the conjugate fields and the principal values of the orientation tensor are determined by Eqs. 13–16.

Results

Solving for the conjugate fields and for the orientation tensor, we find two possible phases: an isotropic/disordered phase and an anisotropic/ordered phase. The transition between the two phases occurs at the critical sphere radius ℓ = t, defined by

This critical radius is proportional to the geometric mean of the rod length L and the persistence length ε and is an increasing function of the strength u of self-repulsion.

When the sphere is big, i.e., the radius is larger than the critical radius ℓ > t, the disordered phase is preferred. This phase is isotropic (on the sphere) because the local orientation tensor has two equal eigenvalues

and so using Eq. 17, the free energy in this phase is found to be

The reduced pressure exerted on the sphere is given by the gradient of the free energy with respect to the volume

and it has a strong dependence on the radius ℓ. The reduced force needed to inject more of the chain into the system is given by the gradient of the free energy with respect to the length of the rod L

Note that it has a linear dependence on L (through t² ≈ L).

When the sphere is small, i.e., when its radius is smaller than the critical radius ℓ < t, the ordered nematic phase is preferred. The local orientation tensor is anisotropic with two different eigenvalues

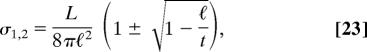and so using Eq. 17, the free energy in this phase is found to be

The pressure

is lower than that of the disordered phase, whereas the injection force

has only a square-root dependence on the length of the rod ($t\approx \sqrt{L}$).

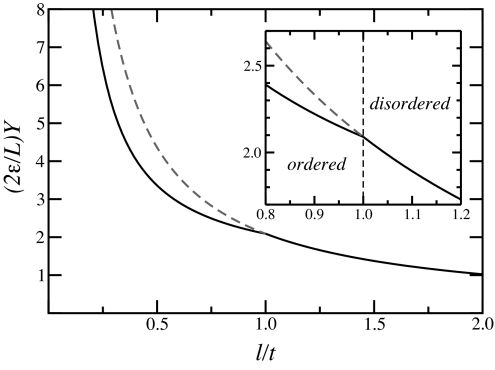
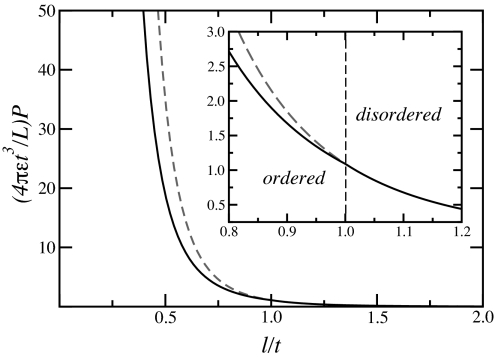
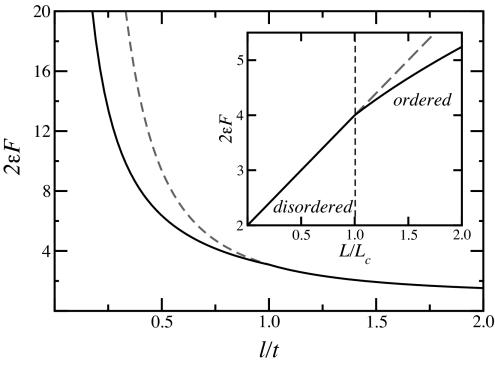
These results are presented graphically in Figs. 1–3. The transition to an ordered nematic phase appears to be continuous and allows for the reduction of the free energy as well as for a lower pressure and a smaller injection force compared to the case such that the system would remain isotropic.

Fig. 1.

The effective free energy Y (normalized by the rod length L and the persistence length ε) as a function of the sphere radius ℓ (in units of the critical radius t). The reduced persistence length is taken as ε/t = 0.3. (Inset) A close up near the transition point. The dashed lines correspond to the case such that the system would remain disordered.

Fig. 2.

The pressure P (normalized by the persistence length ε, the critical sphere radius t and the rod length L) as a function of the reduced sphere radius ℓ/t. The reduced persistence length is taken as ε/t = 0.3. (Inset) A close up near the transition point. The dashed lines correspond to the case such that the system would remain disordered.

Fig. 3.

The injection force F (normalized with the persistence length ε) as a function of the sphere radius ℓ (normalized by the critical radius t). The reduced persistence length is taken as ε/t = 0.3. (Inset) The force as function of the reduced rod length L/L_c, where the critical length L_c is related to the strength u of self-intersections by L_c = 8πℓ²/εu and the persistence length is taken as ε = ℓ. The dashed lines correspond to the case such that the system would remain disordered.

Discussion

We have shown that a rod packed on a sphere undergoes a continuous phase transition from an isotropic phase to a nematic phase as the radius of the sphere is decreased below some critical length t, which depends on the persistence length, on the rod length L, and on the cost of self-intersections u. This transition allows for a reduction in the pressure applied on the sphere as well as in the force needed to inject the rod inside. We stress that this transition is different from a bulk nematic transition because it is controlled by macroscopic length scales, i.e., the size of the container and the total length of the rod. However, the present calculation has two main limitations. The rod must be long enough, but its density on the sphere must be small enough so that it does not jump out of the surface and into the ball. These two conditions read (Lh²)^1/3 ≪ ℓ ≪ L, h being the radius of a cross-section of the rod.

We now turn to the estimate of the relevant quantities for DNA packaging in viral capsids. Our approach yields a good description of the first steps of packaging when there is one layer of DNA in contact with the capsid. We expect it to roughly hold at high density if we take half the radius of the capsid as an effective radius. We specialize to the bacteriophage φ29, for which the radius is ℓ ≃ 25 nm and the length of DNA is L ≃ 7 μm (10). Taking ε = 50 nm as the persistence length of free DNA (13, 15) and u ∼ 1 because it is dimensionless, we find t ≃ 100 nm > ℓ. This implies that the transition to nematic order occurs as soon as a few percents of the phage DNA are injected in the capsid. Using the thermal energy scale k_BT we find a pressure of the order of 1 atm and an injection force of the order of 1 pN. This force compares well with the measurements for the beginning of injection (see figure 3d in ref. 10). Two effects would increase these estimations: electrostatic forces and the effective radius of the capsid, which decreases at high packing density. The main limitation of this estimate is that it is not clear that the persistence length of DNA would not be changed in such compact configurations.

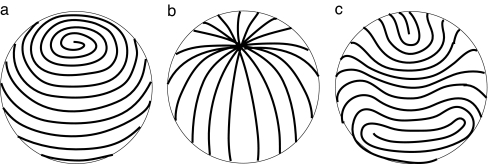
The present results establish the hypothesis of ordered configurations used in previous calculation regarding DNA packed in viral capsids (13, 15–17, 19). In addition, because we obtain a local nematic order on the sphere, we are led to propose three possible types of configurations for the rod, in the light of previous results on nematics living on a sphere (24, 25). In the first configuration (Fig. 4a), the rod spirals on the sphere from one pole to another, the nematic order having two singularities (+1 disclinations) at each pole; this is the so-called spool configuration observed in molecular dynamics simulations (13, 14). In the second one (Fig. 4b), the rod winds along meridians, still with two singularities (+1 disclinations) at the poles; we expect this striped configuration not to be observed because of the high cost of self-intersections at the poles. In the third one (Fig. 4c), the nematic field has four +1/2 disclinations at the vertices of a regular tetrahedron, and the rod winds around them; this tennis-ball-like configuration has not been observed so far; its existence should depend on the relative cost of the core of disclinations and the nematic energy of the disclinations themselves. A firm answer would require the computation of the elastic (Frank) constants of the nematic order. Moreover, it would not be too surprising to get many metastable states that would resemble those three pure configurations, just like in systems of polymeric glasses. Besides, the selection of the final configuration might be history-dependent.

Fig. 4.

Sketch of the possible configurations of the ordered phase. (a) Spool-like. (b) Striped. (c) Tennis ball-like.

Although this model is minimal with respect to the DNA packing problem, because it does not take into account other possible effects such as electric interactions or twist/torsion of the rod, it suggests that the transition from a disordered to an ordered structure is an intrinsic property of systems subjected to confining constraints. It also reproduces qualitatively the behaviors of the confining pressure and the injection force. A natural extension of the present study would be to include other relevant physical interactions. Finally, this theoretical study can be put in a larger perspective in the context of conformations and mechanical properties of confined low dimensional objects.