A robust measure of food web intervality

Abstract

Intervality of a food web is related to the number of trophic dimensions characterizing the niches in a community. We introduce here a mathematically robust measure for food web intervality. It has previously been noted that empirical food webs are not strictly interval; however, upon comparison to suitable null hypotheses, we conclude that empirical food webs actually do exhibit a strong bias toward contiguity of prey, that is, toward intervality. Further, our results strongly suggest that empirically observed species and their diets can be mapped onto a single dimension. This finding validates a critical assumption in the recently proposed static niche model and provides guidance for ongoing efforts to develop dynamic models of ecosystems.

Despite their complexity, the structure of natural food webs displays a number of remarkable regularities (1–9). The existence of these empirical regularities has prompted several researchers to develop simple models that aim to identify the mechanisms that underlie food webs. In particular, three recent “static” models, the niche model (2), the nested-hierarchy model (7), and the generalized cascade model (9) predict key statistical properties of food webs from a variety of environments, including deserts, rain forests, lakes, and estuaries.

Stouffer et al. (9) demonstrated that these three models share two fundamental mechanisms that account for the models' success in reproducing many of the empirical patterns. (i) Species form a totally ordered set in niche space, that is, species can be ordered along a single niche dimension. (ii) Each species has an exponentially decaying probability of preying on a given fraction of the species with equal or lower niche values (9). Despite these similarities, the models exhibit some differences; a crucial distinction concerns how species' prey are organized along the single dimension. In the niche model, species prey on a contiguous range of prey. In the nested-hierarchy and generalized cascade models, in contrast, the diets are not restricted to a contiguous range.

The differences in prey selection lead to drastic differences in the intervality of the food web graph^§ (Fig. 1 a and b). The significance of intervality in complex food webs was first noted by Cohen (10), who reported, as did subsequent studies (1, 11–13), that the vast majority of empirical food webs in the literature appeared to be interval graphs. Significantly, these studies also suggested that the probability that a food web is interval strongly depends on the number of species represented in the food web, decreasing from approximately one for very small food webs to close to zero for larger webs (1). The food webs that were analyzed in these studies typically comprised very few species, leaving open the question of whether, or to what degree, larger and more complex food webs are interval (1). More recent studies reported persistent nonintervality of highly resolved empirical food webs (2, 7).

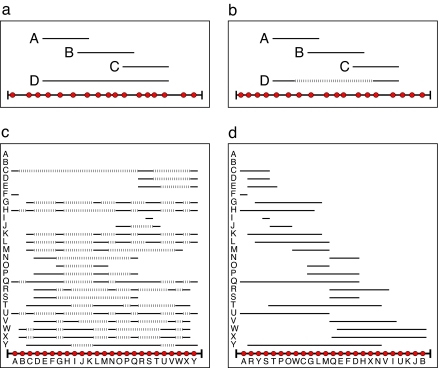
Fig. 1.

Illustration of interval and noninterval food webs. Species (red circles) are placed along a single dimension, which we denote the resource axis. For each predator (A–D) a line is placed above the prey (resources) it consumes. (a) A food web is interval if there exists a permutation of the species along the resource axis such that for each predator, the diet is contiguous. (b) A food web is noninterval if no permutation exists for which all diets can be represented as contiguous segments. (c) An unordered food web. The resource axis is shown along the bottom, and each red circle represents a species in the ecosystem. For each species in the vertical axis, we represent predation by a solid horizontal line (for example, C consumes A) and nonpredation by the dashed lines (for example, C does not consume B). The total number of gaps for this particular ordering is = 217. (d) An ordered food web. Our algorithm works by swapping the location of two nodes within the ordering in an attempt to minimize the value of 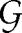. In this particular case, one can find an ordering with 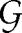= 0. It should be noted that this is one of potentially multiple permutations that can give rise to the same value Ĝ = G = 0.

Importantly, the degree of intervality of a food web is related to the number of trophic dimensions characterizing the possible niches in a community (11). More specifically, one may ask what is the minimum number of variables required to describe the factors that influence the trophic organization of the species in a community? Is this number the same or different for different communities (14–16)? If a food web is interval, then the species and their diets can be represented along a single dimension. It has been suggested that a single factor (species' mass) provides a suitable proxy for this dimension (6, 17–21). Any departure from intervality has been understood to imply additional complexity in the mechanisms responsible for the structure of the food web.

The number of higher-quality food web data sets has steadily increased, and these data have enabled researchers to uncover a number of solid empirical regularities (2–5, 7, 9). Thus, we believe that a more definitive answer to the question of food web intervality may be at hand.

In this article we address the question of how “noninterval” empirical food webs truly are. To this end, we define a measure of intervality that is more robust than those already in the literature. Notably, our results agree with previous studies that observed that empirical food webs are strictly noninterval; however, we demonstrate that their degree of “intervality” can be understood as a perturbation on an underlying interval structure. Our results provide support to the conjecture that species and their diets, that is, ecosystem niches, may be mapped onto a single dimension.

Food Web Intervality

In the studies of Cohen et al. (1), Cohen (10, 11), and Sugihara (12, 13), intervality was reported as a binary variable: a web either “is” or “is not” interval. Recently, two local estimates have been used to measure the “level of diet discontinuity” (7). The first measure, D_diet, is defined as the number of triplets of species with an “irreducible gap” divided by the number of possible triplets. An irreducible gap is a gap in a consumer's diet that cannot be made contiguous because of the constraints imposed by other consumers' diets (Fig. 1).

The second measure, Cy₄, is defined as the number of chordless cycles of length four in the consumer overlap graph. In the consumer overlap graph, two consumers are connected if they share at least one prey. That is, if species A and B share prey with species C and D, the consumer overlap graph would consist of links A ↔ C, A ↔ D, B ↔ C, and B ↔ D. This is a cycle because it is possible to travel from any one of the four species to any other in this graph. If species A and B do not share any prey and similarly species C and D do not share any prey either, this cycle is “chordless” and the four diets cannot be made contiguous simultaneously (11). The measure Cy₄ is related to Sugihara's (12) rigid circuit property, which states that in an interval food web every circuitous path of length l ≥ 4 in the consumer overlap graph is shortened by a chord.

Using these two measures, Cattin et al. (7) reported that the nonintervality of empirical food webs is a significant food web pattern. Caution, however, is required because both D_diet and Cy₄ yield only local estimates of intervality and cannot be directly extrapolated to an entire ecosystem.

Specifically, a cycle of length four in the consumer overlap graph with a chord may still contain irreducible gaps (1). Therefore, Cy₄ is, at best, a lower bound for what Cattin et al. (7) intended to measure. Likewise, when computing D_diet, the normalization factor used by Cattin et al. (7) accounts only for multiphagous consumers, not all species. By concentrating on species triplets, the resulting measure is an overestimation and not amenable to comparisons between food webs of different sizes and linkage densities. Moreover, as pointed out by Martinez et al. (22), Cattin et al. (7) also do not address what values of D_diet or Cy₄ would in fact be statistically significant or represent a large deviation from an interval food web.

In contrast to previous studies, we determine here the degree of intervality of an entire food web. To do this, we first find the order of species in the food web in such a way as to generate the “most interval” ordering of the food web. This process yields the best approximation to a food web where the species and their diets are organized along a single dimension.

We discuss our definition of most interval and its justification here in detail. In the idealized case of a fully interval food web, each consumer's diet is represented by a single contiguous range. If we consider a noninterval food web and attempt to reproduce the idealized web as closely as possible, we will want all prey of a given predator to “appear” as close together as possible on the resource axis (Fig. 1). For example, for a given consumer, a sequence of two adjacent prey, a gap of one species, and two more adjacent prey (i.e., … −PP−PP− …, where P represents a prey and − represents a nonprey) is preferable to the same sequence but with a gap of two species or larger (e.g., … −PP−PP− …). Indeed, the former situation would be far more likely given an interval web that experienced random omissions or changes, such as those possibly introduced by field sampling.

For a food web graph 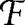with S species, there are S! possible species orderings O_k(S) = s₁^ks₂^k … s_S^k, with k = 1, … S!. Because of the large number of possible permutations, it is computationally unfeasible to determine the best ordering through enumeration. It is for this reason that we use simulated annealing, a heuristic technique that significantly reduces the computational effort required to find an optimal or close-to-optimal solution (see Methods and ref. 23 for details).

When attempting to find the most interval ordering, the objective is to minimize the discontinuity of all predators' prey (Fig. 1). We thus define a cost function 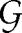(O_k), which is the sum of the gaps in all consumers' diets:

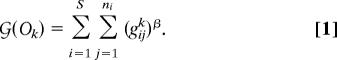Here n_i is the number of gaps in the diet of species i and g_ij^k is the number of species in the jth gap in the diet of species i for a given ordering O_k(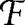). Here we report results for β = 1; however, the selection of other values, such as β = 2, yields similar orderings of the empirical data (Supporting Text and Fig. 3, which are published as supporting information on the PNAS web site). Simulated annealing yields an estimate Ĝ; for the total number of gaps G ≡ 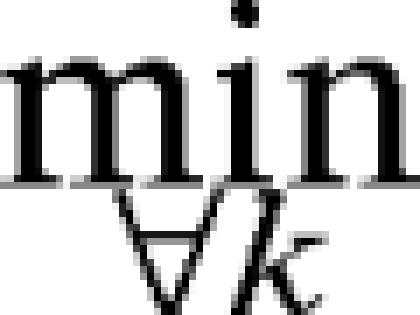{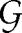(O_k)} of the food web^¶. The smaller Ĝ is the more interval the food web is.

Null Hypotheses for Food Web Intervality

As happens for other graph and combinatorial problems, the actual value of Ĝ is of little significance (24); rather, one needs to assess whether the measured value of Ĝ is significantly different from the expected value under suitable null hypotheses. To solve this problem, we have designed three complementary null hypotheses that place different restrictions on how consumers' diets may be organized within a food web.

Our first null hypothesis is the set of randomizations of the empirical food web. We perform this randomization by using the Markov-chain Monte Carlo switching algorithm (25, 26) and treat single, double, and cannibal links separately (see Methods for details). The randomized empirical food web stands as a food web graph with no constraints placed on consumers' diets. That is, in the randomization there is no correlation between the prey of a given species and their organization on the resource axis. We therefore expect that Ĝ for these randomized food webs will be maximal. Comparison to this null hypothesis thus provides verification of whether there are any structural regularities in the organization of species' diets within empirical food webs.

Our second null hypothesis is the set of food webs generated by the generalized cascade model (9). In the generalized cascade model, each of the S species i are assigned a niche value n_i drawn from a uniform distribution in the interval [0,1]. A predator j selects at random a fraction x of the species i with niche values n_i ≤ n_j as its prey, where x is drawn from a β-distribution p(x) = β(1 − x)^(β−1). Here β = (S²/2L) − 1 and L is the number of trophic links in the ecosystem.

The generalized cascade model food webs are generated with the same number of species S and linkage density L/S as the empirical food webs. Whereas randomization of the empirical food webs imposes no structural constraints on consumers' diets, the generalized cascade model does. Each predator may again select their prey at random, but instead of from the entire resource axis, their selections are restricted to only those species with niche values less than or equal to their own. This mechanism leads to a smaller number of gaps for species placed lower on the resource axis. Comparison of the empirical data to this null hypothesis will provide evidence as to whether empirically observed diets exhibit additional structural constraints.

Comparison to the two previous null hypotheses will provide an indication of whether empirical food webs have a larger number of gaps than would be expected for random structures with little or no bias toward contiguity of prey. To quantify any bias toward contiguity of prey in empirical food webs, we need to develop a third null hypothesis, which we base on a generalization of the niche model (2).

Let us first recall the definition of the niche model. Each of the 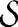species i are assigned a niche value n_i drawn from a uniform distribution in the interval [0,1]. A predator j in the niche model preys on a range r_j = n_jx of the resource axis, where x is drawn from a β-distribution just as in the generalized cascade model. The center of the range r_j is selected uniformly at random in the interval [r_j/2,n_j]. All species i whose niche values n_i fall within this range are considered prey of species j.

To allow for a tunable bias toward prey contiguity, we generalize the niche model in the following manner. First, we reduce the range r_j for a predator j to r′_j = cr_j = cn_jx, where c is a fixed parameter in the interval [0,1]. Because species are distributed uniformly at random on the resource axis, a predator j with range r_j has on average r_jS prey. The same applies to the reduced range r′_j, and therefore a predator has Δk = (r_j − r′_j)S = (1 − c)r_jS expected prey unaccounted for after the range reduction. Next, we select these Δk prey, rounded to the nearest integer value, randomly from the species i with niche value n_i ≤ n_j that are not already a prey of species j. If c = 0, we recover the generalized cascade model, whereas for c = 1, we recover the niche model.

Empirical Results

We study 15 empirical food webs from a variety of environments: three estuarine, Chesapeake Bay (27), St. Marks (28), and Ythan (29); five freshwater, Bridge Brook Lake (30), Canton Creek (31), Little Rock Lake (32), Skipwith Pond (33), and Stony Stream (31); three marine, Benguela (34), Caribbean Reef (35), and Northeast U.S. Shelf (36); and four terrestrial, Coachella Valley (37), Grassland (38), Scotch Broom (39), and St. Martin (40) (Table 3, which is published as supporting information on the PNAS web site).

For each empirical food web, we obtain Ĝ_e (Table 1). We find 1 ≤ Ĝ_e ≤ 700 for all food web, that is, none of the webs is interval. To compare these empirical values to our three null hypotheses, we perform the following steps. For each empirical food web, we generate a minimum of 100 model food webs corresponding to the respective null hypothesis and obtain Ĝ_model for each model food web.

Table 1.

Comparison of empirical data with the random model and the generalized cascade model

Food web	Ĝe	〈ĜR〉	zR	pR	〈ĜGC〉	zGC	pGC
Benguela	27	81	−10.31	<10−10	78	−3.59	<10−3
Bridge Brook Lake	1	51	−11.24	<10−10	48	−4.42	<10−5
Canton Creek	615	810	−7.65	<10−10	1,804	−9.38	<10−10
Caribbean Reef	298	498	−12.47	<10−10	340	−1.17	0.12
Chesapeake Bay	11	48	−5.86	<10−8	38	−3.08	<10−2
Coachella Valley	51	117	−10.74	<10−10	64	−1.04	0.15
Grassland	5	28	−5.08	<10−6	95	−5.76	<10−8
Little Rock Lake	427	1,347	−26.75	<10−10	1,641	−9.89	<10−10
Northeast U.S. Shelf	700	1,291	−17.76	<10−10	1,050	−5.84	<10−8
St. Marks	157	343	−14.12	<10−10	258	−2.95	<10−2
St. Martin	95	204	−12.18	<10−10	193	−4.06	<10−4
Scotch Broom	23	226	−15.67	<10−10	508	−8.94	<10−10
Skipwith Pond	26	36	−3.32	<10−3	42	−1.59	0.06
Stony Stream	645	915	−9.82	<10−10	2,225	−12.56	<10−10
Ythan	270	513	−11.69	<10−10	915	−8.52	<10−10

For each of the 15 food webs, we show Ĝ_e. For each of the two models, we show 〈Ĝ_model〉, z_model, and p_model. 〈Ĝ_model〉 is the average over at least 100 model-generated food webs. The z-score is defined as z_model = (Ĝ_e − 〈Ĝ_model〉)/σĜ_model. We use the Kolmogorov–Smirnov test (41) to examine each set of model-generated data and find that we cannot reject the hypothesis that the Ĝ_model values are drawn from a Gaussian distribution. We then use the fact that a Gaussian distribution describes the model data to directly calculate an estimate for the probability p_model of observing a value of Ĝ_model ≤ Ĝ_e. This probability is equivalent to the significance by which one may reject the underlying null hypotheses.

We then want to be able to estimate the probability that the value Ĝ_e appears given each null hypothesis. To do this, we examine not just the mean of Ĝ_model, but its probability distribution (Fig. 2). Using the Kolmogorov-Smirnov test (41), we determine that we cannot reject the hypothesis that the Ĝ_model values are drawn from a Gaussian distribution. We then use the fact that a Gaussian distribution describes the model data to directly calculate an estimate for the probability of observing a value of Ĝ_model ≤ Ĝ_e.

Fig. 2.

Estimated number of gaps for St. Marks and the null models discussed in the text. (a) Probability density of Ĝ for two of the null models: randomization of the empirical food web and the generalized cascade model. The generalized cascade model-generated food webs were specified to have the same number of species 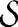and linkage density L/S as the empirical food web. Ĝ_e is shown by the spike. The probability of Ĝ_model ≤ Ĝ_e is <10⁻¹⁰ and <1.6 × 10⁻³ for the randomized empirical web and generalized cascade model, respectively. (b) Probability density of Ḡ for the generalized niche model and three different values of c. The generalized niche model-generated food webs were specified to have the same number of species S and linkage density L/S as the empirical food web. Ĝ_e is again shown by the spike. (c) Probability of observing Ĝ_GN(c) = Ĝ_e = 157 for the St. Marks food web. Values < 0.5 correspond to negative z-scores and thus represent the probability P_low of observing a value of Ĝ_GN ≤ Ĝ_e, whereas values > 0.5 represent the probability P_high of observing a value of Ĝ_GN ≥ Ĝ_e. The 95% confidence intervals on the value of c are given by the regions where both P_low ≥ 0.05 and P_high ≥ 0.05 are true (denoted by the dashed red lines). We find the 95% confidence interval to be c ∈ [0.625, 0.87] (shaded in gray). (d) Same as c but for the Chesapeake Bay food web with Ĝ = 11. We find the 95% confidence interval to be c ∈ [0.75, 0.92] (shaded in gray). The intervality values of I = 0.87 and I = 0.92 for St. Marks and Chesapeake Bay, respectively, imply that the empirical food webs are statistically indistinguishable from our generalized niche model only when there is a very strong bias toward contiguity of species' diets.

We first compare the set of empirical food webs {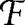} to the set of randomized food webs {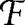_R} (Table 2). We find that, for every food web, Ĝ_e < 〈Ĝ_R〉. To estimate the significance of this difference for each of the individual food webs, we calculate the probability that the model exhibits a value Ĝ_R ≤ Ĝ_e. For 12 of the 15 food webs, p_R < 10⁻¹⁰. For the remaining three food webs, p_R < 10⁻³.

Table 2.

Empirical food web intervality

Food web	I
Benguela	0.96
Bridge Brook Lake	≈1.00
Canton Creek	0.95
Caribbean Reef	0.85
Chesapeake Bay	0.92
Coachella Valley	0.94
Grassland	≈1.00
Little Rock Lake	0.97
Northeast U.S. Shelf	0.93
St. Marks	0.87
St. Martin	0.93
Scotch Broom	≈1.00
Skipwith Pond	0.96
Stony Stream	0.96
Ythan	0.95

For each food web, we show the intervality I, the maximum value of c for which we cannot reject the hypothesis that the value of Ĝ_e could have been observed in the generalized niche model.

We now compare the set of empirical food webs to the set of generalized cascade model-generated food webs {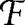_GC} (Table 1). We again find that for every empirical food web, Ĝ_e < 〈Ĝ_GC〉. We find that for 12 of the 15 food webs the probability that Ĝ_GC ≤ Ĝ_e is again quite small, p_GC < 10⁻². For the remaining three food webs, Skipwith Pond, Coachella Valley, and Caribbean Reef, we find larger probability values, 0.06, 0.12, and 0.15, respectively. Further analysis indicates that 〈Ĝ_GC〉 decreases with the directed connectance L/S² for a fixed number of species S.^‖ Thus the higher values of p_GC are likely caused by the higher connectance of these webs.

To conclusively reject the two random hypotheses, we apply a Bonferroni correction (42), which decreases the significance level for the two individual hypothesis for a particular food web to α = 0.05/2 = 0.025 to avoid spurious false positives. Upon considering each individual food web as compared with our two random hypothesis with this more conservative threshold, we can conclusively reject the two hypotheses for 12 of the 15 food webs; the exceptions are again Caribbean Reef, Coachella Valley, and Skipwith Pond.

To this point, our results provide an indication that the majority of empirical food webs are significantly more interval than would be expected for food webs with little or no bias toward prey contiguity. We now investigate our generalized niche model to determine how it compares with the empirical data for different values of c and therefore different levels of bias toward prey contiguity.

For each of the 15 remaining food webs, we compare the empirical food web Ĝ_e to the model 〈Ĝ_GN〉 for c ∈ [0.5,1.0]. We compare the model and empirical data as before, but focus particularly on the z-score, where

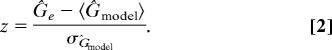Using the z-score, we can determine the upper bound of 95% confidence intervals on c for which the empirical Ĝ is likely to be observed in the generalized niche model (Fig. 2). We show the results of this comparison in Table 2.

For the 15 food webs we investigated, we find that the largest values of c that provide statistical agreement with the empirical data are remarkably close to one, 0.85 < c_max < 1.00.** This finding enables us to quantify in a statistically sound manner the intervality of a food web; specifically,

where {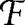_GN} is the ensemble of model food webs generated according to the generalized niche model with the same number of species and connectance of the real food web _i. For the 15 empirical food webs investigated, we find values of I very close to 1; in fact, 〈I〉 = 0.95. This result indicates that natural ecosystems are significantly interval, and consequently there is a strong bias toward contiguity in prey selection.

Discussion

The concept of “niche theory” or “niche space” is a fundamental concept in the study of ecosystems. Niche space was classically defined as an “n-dimensional hyperspace” with n given by the innumerable ecological and environmental characteristics (14, 15). Therefore, each species' niche is the “result” of all n factors acting on it and the niche represents the functional role and position of the organism in its community. The more recent “interpretation” of niche theory, however, relates to the niche providing species an ordering or hierarchy (15, 18, 20). This formulation provides a much simpler criterion than Hutchinson's (14) “n-dimensional hyperspace.” Studies have suggested that by using species' mass or size a food web can in fact be mapped to a single dimension (6, 18–21, 43). Furthermore, the placing of species onto a single dimension is a crucial ingredient in many models developed to describe food web structure (1, 2, 7, 9).

Recently, however, discussions as to how interval food webs truly are, were renewed by the contrast between the niche model, and its contiguous range of prey, and the generalized cascade and nested-hierarchy models, and their random predation (9). Our results allow us to conclusively demonstrate that natural ecosystems, while not fully interval, are significantly more interval than would be expected by chance alone. Indeed, we find the empirical food webs to be statistically indistinguishable from model food webs whose diets are between 85% and 100% contiguous. The idea that species and their diets can be so closely mapped onto a single dimension represents a significant insight that can guide us on how best to go about developing dynamic ecosystem models such as the recent integration of the niche model and nonlinear bioenergetic modeling proposed by Martinez et al. (44).

A number of future questions must be answered before the topic of food web intervality can come to a close. First and foremost is getting a better understanding of exactly what processes are behind the deviations from truly interval behavior. While some of the gaps within species diets may be caused by interactions not observed during field sampling, we find it unlikely that all gaps may be attributed to this factor. It was noted earlier, albeit on different food webs from those studied here, that ecosystems with multiple habitats, for example, an estuary, are less likely to be interval than single-habitat food webs (1, 10). Indeed, one would not expect food webs containing several habitats to be strictly interval because each habitat is likely to have its own separate resource axis.

It would likewise be very interesting to examine additional properties of the “most-interval” ordering or orderings, {O_k} (Supporting Data Set, which is published as supporting information on the PNAS web site). Studies that compared these orderings to those obtained when comparing species' masses, or related properties (6), would be particularly intriguing.

Methods

Simulated Annealing.

Simulated annealing is a stochastic optimization technique that enables one to find a “low-cost” configuration while still broadly exploring the space of possibilities (23). This is achieved by introducing a computational “temperature” T. When T is high, the system can explore configurations of high cost, whereas at low T the system can only explore low-cost regions. By starting at high T and slowly decreasing T, the system descends gradually toward deep minima.

For each iteration in the simulated annealing algorithm, we attempt to swap the position of two randomly selected species to go from the initial ordering O_i() to the proposed ordering O_f(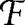). This updated ordering O_f(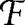) is then accepted with probability

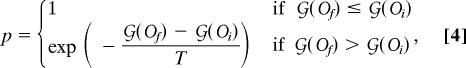where 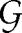(O_f) is the cost after the update and 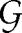(O_i) is the cost before the update. For each value of T, we attempt qS² random swaps with q ≥ 250. After the movements are evaluated at a certain T, the system is “cooled down” to T′ = cT, with c = 0.99.

Generating Randomized Networks.

To generate an ensemble of random networks, one must first define the constraints of the randomization (45, 46). In our analysis, we preserve the following attributes for each species during randomization of the food web: (i) number of prey, (ii) number of predators, (iii) number of single links, A → B, (iv) number of double links, A ↔ B, and (v) whether or not a species is a cannibal.

We use the Markov-chain Monte Carlo switching algorithm (26) and treat single, double, and cannibal links separately. For example, two single links A → B and C → D become A → D and C → B, provided both A → D and C → B do not already exist in the network and they do not form new double links. Similarly, two double links A ↔ B and C ↔ D become A ↔ D and C ↔ B, provided that both A, D and C, B are unconnected by a link in any direction.