Dynamic Origin of Spatially Discordant Alternans in Cardiac Tissue

Abstract

Alternans, a condition in which there is a beat-to-beat alternation in the electromechanical response of a periodically stimulated cardiac cell, has been linked to the genesis of life-threatening ventricular arrhythmias. Optical mapping of membrane voltage (V_m) and intracellular calcium (Ca_i) on the surface of animal hearts reveals complex spatial patterns of alternans. In particular, spatially discordant alternans has been observed in which regions with a large-small-large action potential duration (APD) alternate out-of-phase adjacent to regions of small-large-small APD. However, the underlying mechanisms that lead to the initiation of discordant alternans and govern its spatiotemporal properties are not well understood. Using mathematical modeling, we show that dynamic changes in the spatial distribution of discordant alternans can be used to pinpoint the underlying mechanisms. Optical mapping of V_m and Ca_i in paced rabbit hearts revealed that spatially discordant alternans induced by rapid pacing exhibits properties consistent with a purely dynamical mechanism as shown in theoretical studies. Our results support the viewpoint that spatially discordant alternans in the heart can be formed via a dynamical pattern formation process which does not require tissue heterogeneity.

INTRODUCTION

Spatiotemporal patterns are ubiquitous in biological systems and play important roles in biological function (1). In many cases the underlying mechanism that produces the observed spatiotemporal pattern is not clear. A fundamental question that arises is whether the observed pattern is due to preexisting heterogeneities of the substrate on which the pattern is formed or to dynamical properties of the system as a whole. This question is particularly relevant in biological systems where preexisting heterogeneities always coexist with dynamical factors.

In the heart, optical mapping and other techniques have revealed spatial gradients in the action potential duration (APD) and the intracellular Ca (Ca_i) transient. The presence of these gradients is important to the genesis of cardiac arrhythmias, since spatial heterogeneity can promote the occurrence of wavebreak and, subsequently, reentry (2–4). Electrophysiological gradients in cardiac tissue can be due to a variety of sources. For example, a base-to-apex gradient in APD and Ca_i has been observed and attributed to the nonuniform expression levels of ion channel/transporter proteins (5,6). Alternatively, spatial heterogeneities in tissue can also arise due to the complex beat-to-beat dynamics of V_m and Ca_i. Moreover, beat-to-beat alternating patterns in APD and the Ca_i transient can become spatially out of phase in different regions of tissue (2,3,7–10). That is, regions of cardiac tissue can alternate with a large-small-large APD or Ca_i transient adjacent to regions with small-large-small APD or Ca_i transient. Clinically, APD alternans is believed to be the mechanism underlying electrocardiographic T wave (repolarization) alternans, which has been shown to correlate with a high risk of sudden cardiac death (4).

The objective of this study is to determine, using computer simulations and experimental optical mapping techniques, how APD and Ca_i alternans at the cellular level becomes spatially discordant at the tissue level. At the single-cell level, APD and Ca_i transient alternans can be induced at high pacing rates due to instabilities of either membrane voltage (V_m), due to a steep APD restitution slope (11–13), or Ca_i-cycling dynamics (14,15). Moreover, when APD alternates, the Ca_i transient alternates secondarily because the size and duration of the APD regulates Ca_i release. Conversely, when the Ca_i transient alternates, APD alternates secondarily because Ca_i affects ionic currents (primarily the L-type Ca current and Na-Ca exchange) which regulate APD. Because of this bidirectional coupling between V_m and Ca_i, it has been difficult to determine experimentally if alternans is primarily due to the dynamical properties of V_m or Ca_i cycling.

Two mechanisms have been proposed to explain how APD and Ca_i alternans at the cellular level becomes spatially discordant at the tissue level. Pastore et al. (2,16) have hypothesized that this phenomenon resulted from the electrophysiological and anatomical heterogeneity inherent in cardiac tissue, such as base-to-apex and/or transmural gradients in APD (2) and Ca_i-cycling properties (5). Confirming the APD gradient conjecture, computer simulations in one-dimensional (1D) cables showed that sudden changes in pacing rate can induce spatially discordant APD alternans in heterogeneous tissue (17). However, computer simulation studies (17,18) also revealed that spatially discordant APD alternans can form in a perfectly homogeneous tissue via a purely dynamical mechanism. Specifically, spatially discordant alternans occurs when the conduction velocity (CV) of a propagating pulse has a sensitive dependence on the preceding DI, which we refer to as steep CV restitution.

The formation of discordant alternans due to steep CV restitution can be understood as follows. Consider a cable which is paced at a cycle length (CL) which induces APD alternans at the pacing site. The long APD beat will create a short DI for the next (short) APD beat, slowing its propagation. However the short APD beat will subsequently cause a long DI for the next (long) APD beat, so it will propagate more rapidly. The different speeds of alternate beats will lead to CL alternans along the cable as cells are stimulated at times which differ from the CL at the paced end. Hence, CV restitution will induce a spatial gradient of CL, which then induces a gradient in APD along the cable since cells are being paced with an alternating CL which varies in space. As shown in simulation studies (17,18), for sufficiently steep CV restitution, a discordant pattern of APD alternans can form in which an alternans phase reverses across a point distal to the pacing site, referred to as a node. This mechanism is purely dynamical and does not require a heterogeneous electrophysiological tissue substrate. Building on this result Echebarria and Karma (19) developed an elegant mathematical description of discordant alternans that showed that these patterns are governed by the bulk properties of cardiac tissue, such as the APD and CV restitution properties.

To date, to our knowledge, no experimental studies in real cardiac tissue have explicitly addressed the question of whether spatially discordant alternans is dynamically generated or is simply a consequence of the electrical and structural heterogeneities of APD and Ca_i-cycling properties normally present in heart tissue. The first goal of this work was to use computer simulations to develop criteria by which dynamically induced discordant alternans can be distinguished from heterogeneity-induced discordant alternans. This is not straightforward, since real cardiac tissue is both heterogeneous with respect to APD and Ca_i-cycling properties and also normally exhibits CV restitution at fast heart rates. Therefore, criteria for distinguishing between the different mechanisms must hold even though both factors are naturally present in real cardiac tissue. Moreover, although alternation in CV or CL during spatially discordant alternans is required for dynamically generated discordant alternans, it might also occur coincidentally during heterogeneity-generated alternans. We therefore focused on whether the behavior of nodal lines in response to pacing site and rate could distinguish between the two mechanisms, since previous studies have shown that dynamically generated discordant alternans due to CV restitution causes nodes to move toward the pacing site as the pacing rate increases (17,19). We used computer simulations to address the following novel questions: 1), Do dynamically generated nodes (or nodal lines) behave the same when the cellular mechanism of alternans is Ca_i-cycling dynamics, rather than steep APD restitution slope? 2), Do dynamically generated nodes (or nodal lines) due to CV restitution show the same behavior in response to pacing rate and site when the tissue is heterogeneous, rather than homogeneous (as in previous simulation studies)? And most critically, 3), do nodes/nodal lines formed due to tissue APD or Ca_i-cycling heterogeneity in the absence of CV restitution respond differently to pacing rate and site than dynamically generated nodes/nodal lines? Our simulations demonstrate that the answer to all three questions is affirmative, thereby establishing clear criteria to distinguish dynamically generated from heterogeneity-generated spatially discordant alternans. We then applied these criteria experimentally using optical mapping of V_m and Ca_i to track the movement and geometry of nodal lines in rabbit ventricles. Our main result is that nodal lines formed during rapid pacing move in a manner consistent with the steep CV restitution mechanism proposed theoretically and are difficult to explain based on static heterogeneities in APD or Ca_i cycling alone.

METHODS

Numerical simulations

We modeled a 1D cable and two-dimensional (2D) tissue using the reaction-diffusion equation

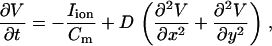(1)

where 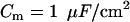is the transmembrane capacitance, 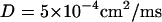is the effective diffusion coefficient of V_m in cardiac tissue, and 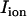is the total ionic current density. For the 1D cable, the computation was performed only along the x axis. The reaction-diffusion equation was integrated with an operator splitting method and adaptive time step method (20). The space step was 0.015 cm and the time step varied from 0.1 to 0.01 ms. The ionic current was modeled by integrating a model of Ca_i cycling of Shiferaw et al. (15), with the canine AP model of Fox et al. (21). Cellular alternans can be generated in this model either by a dynamical instability of V_m or by Ca_i dynamics (22). We simulated the case of electromechanically concordant alternans in which a long APD is associated with a large Ca_i transient, since this “positive coupling” scenario (22) agrees with the experimentally observed relationship in our rabbit ventricle preparation (see Results). The CV restitution curve was modified by adjusting the slow time constant of recovery (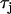) of the Na current (23). Details of the ionic model are given in the Appendix.

Tissue preparation

New Zealand White rabbits (female, 5–6 months old) weighing 3–5 kg were anesthetized with an intravenous injection of ketamine (10 mg) and xylazine (20 mg) containing 1000 units of heparin. After thoracotomy, the hearts were rapidly isolated and the ascending aorta was cannulated and secured for retrograde perfusion with warmed (36.5 ± 0.5°C), oxygenated Tyrode's solution at a rate of 30–40 mL/min. The Tyrode's solution contained (in mmol/L) NaCl 125, KCl 4.5, NaH₂PO4 1.8, NaHCO₃ 24, CaCl₂ 2.0, MgCl₂ 0.5, glucose 5.5, and albumin 50 mg/L in deionized water, pH 7.4 ± 0.05. Coronary perfusion pressure was maintained at 60 cm H₂O.

Dual optical mapping

To perform dual optical mapping of V_m and Ca_i, hearts were successively loaded with the calcium-sensitive dye Rhod-2 AM and the voltage-sensitive dye RH 237 (Molecular Probes, Eugene, OR). Rhod-2 AM (0.5 mg) was dissolved in 1 mL of dimethyl sulfoxide containing Pluronic F-127 (20% wt/vol). This solution was diluted in 300 mL of Tyrode's solution to achieve a final Rhod-2 concentration of 1.5 μmol/L and was infused into the heart over a 10-min period. Afterward, the heart was perfused with dye-free Tyrode's solution for 15 min for deesterification of Rhod-2 AM. The heart was then stained with the voltage-sensitive dye RH 237 (Molecular Probes) by direct injection into the perfusion system with 10–20 μL of the 1 mg/ml solution dissolved in dimethyl sulfoxide (24). The hearts were illuminated with a solid-state, frequency-doubled laser (Verdi, Coherent, Santa Clara, CA) at a wavelength of 532 nm. The emitted fluorescence was transmitted through a 585 ± 20-nm band-pass filter for the Rhod-2 signal and a 710-nm long-pass filter for the RH 237 signal and acquired with two charge-coupled device cameras (CA-D1-0128T, Dalsa, Waterloo, Canada) from 128 × 128 sites over a 20 × 20 mm² area of the epicardial ventricular surface at 4.0 ms/frame. Optical data were recorded to a personal computer using custom-designed software (LabVIEW, National Instruments, Austin, TX). We previously confirmed that there was no significant cross talk between the V_m and Ca_i signals (25). Cytochalasin D (Sigma, St. Louis, MO; 5 μM) was added to the perfusate to inhibit contraction (26).

Stimulation protocol

Stainless steel stimulating electrodes (tip diameter 0.20 mm) were paced on the ventricle. A 4-cm² stainless wire mesh situated on the posterior wall of the left ventricle served as the reference electrode. We applied two dynamic pacing protocols at various locations on the ventricle:

• Protocol 1. Twice diastolic threshold current pulses were applied with the pacing cycle lengths (PCLs) of 300, 250, and 200 ms, after which the PCL was shortened in 10-ms increments until capture was lost or VF was induced. At each PCL, pacing was applied for 10 s.

• Protocol 2. Twice diastolic threshold current pulses were applied at PCLs of 300, 250, and 200 ms. At each PCL, pacing was applied for 10 s. PCL was then decreased to 150, 145, 140, 135, and 130 ms every 10 beats and then by 2-ms decrements every 10 beats until ventricular fibrillation (VF) was induced.

DATA ANALYSIS

To determine the spatial distribution of Ca_i transient alternans across the mapped field, we computed the difference in the peak Ca_i transient from one beat to the next defined as

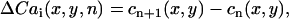(2)

where n denotes the beat number, and 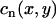is the peak of the Ca_i transient fluorescence measured at a pixel in position (x,y) in the 2D mapping field. The spatiotemporal evolution of Ca_i transient alternans was visualized by plotting 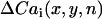, referred to as the amplitude of Ca_i transient alternans. The Ca_i nodal line was defined by tracking the contour where 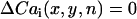in the mapping field.

Measurement of the spatial distribution of V_m alternans was more difficult. We found that given the temporal resolution of our optical mapping apparatus (4 ms/frame), measurements of APD were noisy despite clear beat-to-beat alternation in the AP morphology. To solve this problem we measured the beat-to-beat alternation in the area under the action potential waveform (API) instead of APD. We found that this measure robustly represented the alternans phase (see Appendix D for a more detailed discussion) and was significantly less noisy than the measurements of APD. API for the nth beat at position (x,y) in the tissue was defined as

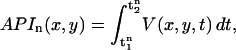(3)

where 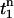is the first time when the voltage fluorescence 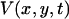crosses a threshold 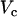during the upstroke of the nth beat, and 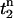is the time the same threshold is crossed during repolarization. The threshold 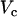was set to be slightly larger than the fluorescence during diastole at the resting membrane potential. Once this integral was computed for all pixels in the mapping field, we computed the beat-to-beat difference

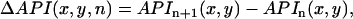(4)

and plotted this quantity in the 2D mapping field. The V_m nodal line was defined by tracking the contour where 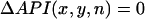. In Appendix D we demonstrate, in our numerical simulation model, that ΔAPI and ΔAPD nodes are similar and have the same dynamical behavior.

We have also measured the CV of propagating wavefronts as a function of the preceding DI, referred to as the CV restitution curve. This quantity was measured by computing the conduction time for a wavefront to travel a distance of 10 mm from the pacing site along the direction of propagation. We measured the CV restitution curve during protocol 2 by computing the CV for the last two propagating beats at each CL. We found it necessary to consider the last two beats, since alternans occurs at rapid rates and the CV for alternate beats will not be the same.

RESULTS

The dynamics of nodal lines: mathematical modeling predictions

Previous theoretical studies investigating spatially discordant alternans have considered only the case in which cellular APD alternans is caused by steep APD restitution slope. However, since recent experimental evidence indicates that Ca_i alternans may be more important in driving APD alternans (5,27), we developed two ionic models to simulate the electrophysiology of rabbit ventricular cells (see Appendix for model details):

1. V_m-driven model. Single-cell alternans is induced by adjusting the inactivation kinetics of the ion channels which control the slope of APD restitution. In this case, Ca_i transient alternans passively follows APD alternans.

2. Ca_i-driven model. Single-cell alternans is driven by a dynamic instability of Ca_i cycling, caused by a steep gain of Ca-induced Ca release (15). In this case, APD alternans passively follows Ca_i transient alternans.

Using these two models, we performed computer simulations of 1D and 2D tissue to investigate how the spatiotemporal properties of nodal lines formed during pacing-induced spatially discordant APD and Ca_i alternans depends on the following factors: 1), the dynamic instability at the cellular level causing alternans, i.e., whether alternans is due to V_m dynamics versus Ca_i-cycling dynamics; 2), CV restitution properties of the tissue; and 3) fixed electrophysiological heterogeneities in the tissue.

Properties of spatially discordant alternans generated dynamically by steep CV restitution

Previous theoretical studies (17,18,28) have shown that alternans due to steep APD restitution can become discordant when CV restitution is sufficiently steep. These studies also showed that for a given pacing rate nodes settled at a fixed distance from the pacing site. However, as the pacing rate was increased the nodes moved toward the pacing site. Here, we show that this is true even when APD or Ca_i-cycling characteristics of the tissue are heterogeneous and remains true when alternans is caused by Ca_i cycling rather than steep APD restitution.

V_m-driven alternans

Fig. 1 A shows the spatial distribution of APD and Ca_i transient alternans in a homogeneous 3-cm cable that was paced at the left end using a dynamic pacing protocol in which the PCL was decreased by 2 ms every 150 beats. In this model cellular alternans is due to steep APD restitution slope, and steep CV restitution causes the spatial discordance (see Appendix B for details). In Fig. 1 B we plot the node position as a function of the beat number. As shown in both graphs, the steady-state node position depends on the PCL and moves toward the pacing site as PCL is decremented. Note that the positions of the APD and Ca_i transient nodes are not exactly superimposed. This is because the precise location of the APD nodal line is strongly influenced by electrotonic effects of the APD in the surrounding tissue, whereas the local Ca_i transient is minimally influenced by the Ca_i transient of surrounding cells.

FIGURE 1.

Dynamic movement of nodal lines when alternans is V_m-driven and spatially discordant alternans is induced via steep CV restitution. (A) Spatial distribution of alternans on a 3-cm cable paced at the left end at a fixed PCL for 150 beats after which the PCL was decremented by 2 ms. The solid lines correspond to ΔAPD and dashed lines to ΔCa_i, measured after steady state has been reached. (B) Plot of nodal line position (x_node) versus beat number for the simulation in A. (C) Nodal lines in a simulated 2.25 × 2.25 cm² homogeneous tissue. The tissue is paced at the top left-hand corner using a dynamic pacing protocol where the PCL is decremented by 2 ms every 50 beats. The nodal lines are computed from ΔCa_i measured from the 49th and 50th beat. (D) Same dynamic pacing protocol applied to the bottom left-hand corner of a tissue with a fixed electrophysiological gradient in which the time constant of recovery (τ_f) of the L-type Ca_i channel increased linearly along the y axis.

Similar results are found in simulated 2D tissue. Fig. 1 C shows a 2.25 × 2.25 cm² tissue paced for 50 beats from the top left-hand corner at a given CL before decrementing the CL by 2 ms. Nodal lines corresponding to Ca_i alternans amplitude were computed using the difference of the Ca_i transient of the 50th and 49th beat at that CL. As shown, nodal lines emerged from the boundary of the tissue and moved toward the pacing site as pacing rate increased. As in the 1D simulations, APD nodes were close to but were not superimposed on Ca_i transient nodes (results not shown).

Since real cardiac tissue is heterogeneous and previous theoretical studies of spatially discordant alternans driven by steep APD restitution and CV restitution did not address how tissue heterogeneity affects the movement of dynamically generated nodal lines, we examined this issue. Based on the observation that APD alternans was larger in magnitude at the base than at the apex of the guinea pig heart (5), we increased the time constant of recovery of the L-type Ca current in the V_m-driven cell model along the y axis of the 2D tissue (see Appendix C for details) to gradually increase the amplitude of APD alternans along the y-direction. As shown in Fig. 1 D, although the electrophysiological gradient distorted the shape of the nodal lines, movement of the nodal line toward the pacing site as pacing rate increased was still observed. In this simulation we paced the tissue at the lower left-hand corner to illustrate that movement toward the pacing site is also independent of pacing site location.

Ca_i-driven alternans

We next examined whether equivalent results are obtained when spatially discordant alternans arises from a Ca_i-cycling instability, rather than steep APD restitution slope, which has not been previously studied to our knowledge. Accordingly, we adjusted the Ca-cycling features in our ionic model to induce alternans when the APD restitution slope was shallow so that alternans was independent of V_m dynamics (see Appendix B for details of the model). In Fig. 2, A and B, at steady state the node settles at a PCL-dependent distance from the pacing site, which decreases as PCL is decremented. Qualitatively similar results are found in 2D tissue (Fig. 2 C), where the nodal line moves toward the pacing site as the PCL is decreased. Thus, nodes behaved similarly whether the dynamic instability producing alternans was primarily caused by V_m or Ca_i dynamics. To test the robustness of this result, we show in Fig. 2 D the movement of the nodal line in the presence of a fixed base-to-apex gradient in Ca_i-cycling dynamics. Here, a spatial gradient of Ca_i cycling was induced by varying fractional Ca release from the SR in a given beat along the y axis of the tissue (see Appendix C for details). As shown, the nodal lines still marched toward the pacing site as the PCL decreased.

FIGURE 2.

Dynamic movement of nodal lines when alternans is Ca_i driven. Discordant alternans are induced via steep CV restitution. (A–C) Same simulations as Fig. 1, A–C, but the Ca_i-driven model was used. (D) Same simulation as C with a fixed gradient in Ca_i-cycling dynamics in which the slope of the sarcoplasmic reticulum (SR) Ca_i release versus SR Ca_i load increased linearly along the y axis of the tissue.

Properties of discordant alternans due to a heterogeneous substrate

Steep CV restitution is not the only mechanism which can induce spatially discordant alternans in cardiac tissue. As shown by Watanabe et al. (17) spatially discordant alternans can also be formed by an appropriately timed stimulus delivered after the formation of a heterogeneous spatial distribution of alternans. For example, if a heterogeneous tissue is paced at a CL PCL₁ at which the whole tissue is alternating in phase (…large-small-large…), a sudden change to a CL PCL₂ can cause a region of the tissue to change alternans phase (…small-large-small…), whereas other regions do not, inducing discordant alternans. To our knowledge, the evolution of nodal lines formed by this mechanism has not been previously characterized in detail, but is important if criteria are to be developed to distinguish dynamically generated from heterogeneity-generated discordant alternans. Here, we study the pacing rate-dependent properties of nodal lines induced via this mechanism for both V_m-driven and Ca_i-driven alternans.

V_m-driven alternans

We created two different types of electrophysiological heterogeneity in a 1D cable. In Fig. 3 A, we varied spatially the time constant of inactivation (τ_f) of the L-type Ca current along a 1D cable as shown to produce a gradient in APD restitution steepness. To induce spatially discordant alternans without engaging CV restitution, we paced the tissue at PCL₁ = 220 ms at which CV restitution is flat and made a sudden change to PCL₂ = 202 ms. A node formed at the new pacing rate but subsequently drifted away from the pacing site, so that after roughly 20 beats the node moved off the cable (Fig. 3 B) and alternans again became spatially concordant. We obtained similar results in 2D tissue.

FIGURE 3.

Numerical simulations of discordant V_m-driven alternans induced in heterogeneous tissue with flat CV restitution. (A) Spatial distribution of Ca_i transient alternans on a substrate with a nonuniform distribution of τ_f. The dashed line denotes the steady-state distribution of spatially concordant alternans at PCL₁ = 220 ms. An abrupt change in CL to PCL₂ = 202 ms yields spatially discordant alternans computed using the first two beats (thick black line). The thin black lines denote the subsequent evolution of ΔCa_i computed at every other beat. (B) Plot of node position (x_node) versus beat number at PCL₂ = 202 ms. (C) Beat-to-beat evolution of Ca_i transient nodal lines in 2D tissue. Spatially discordant alternans was created by first inducing spatially concordant alternans by pacing at PCL₁ = 300 ms and then abruptly decreasing the PCL to PCL₂ = 290 ms. The position of Ca_i nodal lines are shown after the 1st, 10th, 20th, and 40th beat at PCL₂.

To show that this result was not unique to the type of tissue heterogeneity we implemented, in Fig. 3 C, we created a gradient in APD in 2D tissue by varying the strength of the inward rectifier K⁺ (I_K1) current along the diagonal direction (which joins the top left with the bottom right corner of the tissue). The dashed line corresponds to the nodal line induced just after the change in CL to PCL₂, whereas the full black line denotes the nodal line after 40 beats. From the plot, we see that the nodal line drifted away from the pacing site as the tissue was paced at the new CL PCL₂. Hence, when CV restitution is not engaged, nodal lines do not achieve steady state, in sharp contrast to the discordant alternans pattern induced via steep CV restitution.

Ca_i-driven alternans

In Fig. 4 A, heterogeneous Ca_i cycling was created into a 1D cable by introducing a spatial gradient in the steepness, denoted by u, of the SR Ca_i release as a function of SR Ca_i content along the cable. In response to a sudden change in CL, the node transiently drifted away from the pacing site, after which it settled down in a fixed position. As shown in Fig. 4 B, the node position was nearly insensitive to the pacing rate as the PCL was further decremented by 2 ms every 100 beats. We obtained similar results in heterogeneous 2D tissue with a fixed gradient of Ca_i-cycling properties. In this case the variable u was increased linearly in the y-direction (see Appendix C for details). Fig. 4 C shows the nodal line 50 beats after the change in CL to 235 ms and also after decrementing the pacing rate by 2 ms every 50 beats. As in the cable, we found that the nodal line formed in a location determined by the underlying heterogeneities and remained close to that location despite further acceleration of the pacing rate.

FIGURE 4.

Same simulation as in Fig. 3 using the Ca_i-driven cell model and with a spatial distribution of the slope (u) of the SR Ca_i release versus SR Ca_i load. (A) The full dashed line denotes the spatial distribution of alternans at PCL₁, and the broken dashed line shows alternans distribution immediately after the change in CL to PCL₂. Thin black lines denote evolution of alternans plotted at the 10th, 30th, and 100th beat. The thick black line denotes the distribution of alternans after 500 beats. (B) Plot of node position versus beat number. PCL is subsequently decremented by 2 ms every 100 beats. (C) Plot of Ca_i transient nodal lines in 2D formed via an abrupt change in PCL. Plot of nodal line after 50 beats at PCL₂ = 235 ms, 233 ms, and 231 ms.

Summary of predictions from simulation results

Taken together, the simulation results indicate that

1. When spatially discordant alternans is induced dynamically by steep CV restitution, nodal lines move toward the pacing site as PCL decreases whether the cellular alternans arises from steep APD restitution or Ca_i-cycling dynamics. Moreover, this response is robust to the presence of fixed tissue heterogeneities in either APD or Ca_i-cycling properties.

2. When spatially discordant alternans is due to tissue heterogeneities in either APD or Ca_i cycling, nodal lines form at locations dictated by the underlying tissue heterogeneity. Once a nodal line forms it a), drifts away from the pacing site in a beat-to-beat manner when the alternans instability is due to steep APD restitution, or b), remains pinned near the position at which it originally formed even as the heart rate increases when the alternans instability is due to Ca_i cycling.

Thus, the clear differences in nodal line responses to pacing provide unequivocal criteria by which the mechanisms of spatially discordant alternans can be experimentally distinguished.

The dynamics of nodal lines in the rabbit heart: experimental findings

To determine which set of predictions on nodal line movement are obeyed in real cardiac tissue, we applied pacing protocols to intact rabbit hearts while mapping the distribution of nodal lines on a 2 × 2-cm section of the rabbit ventricle.

Demonstration of pacing-induced AP and Ca_i transient nodal line formation

In Fig. 5 A, the heart was paced from a site in the RV free wall near the top right corner of the mapped surface (green square). Fig. 5 B shows traces of V_m and Ca_i fluorescence at the three labeled sites a–c for the last few beats at a PCL of 110 ms. In these traces, alternans is electromechanically concordant, i.e., the large API (integral of the area under the voltage trace, used as a surrogate for APD) is associated with the large Ca_i transient. However, the alternans in API and Ca_i transient amplitudes at site a is out of phase with site c, whereas at the intermediate site b, alternans is minimal. Fig. 5, C and D, shows the spatial profiles of API and Ca_i alternans over the indicated mapping field obtained by plotting 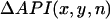and 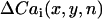, respectively (see Methods). Red and blue correspond to opposite phases of alternans, with the white lines indicating nodal lines. The API nodal line formed at a location that was close to, but did not overlap exactly with, the Ca_i transient nodal line, consistent with the simulations. Note also that two circular Ca_i nodal lines formed at the bottom of the mapping field, one of which was not present in the API alternans field. This is consistent with a Ca_i-driven mechanism for alternans, since Ca_i-cycling dynamics can cause the Ca_i transient amplitude to reverse the alternans phase even over subcellular distances (29–31), whereas the APD or API average can only reverse the phase over a much larger spatial scale due to electrotonic current flow. Similar findings were obtained in 11 pacing episodes in six different rabbit hearts.

FIGURE 5.

Experimental demonstration of spatially discordant action potential (AP) and Ca_i alternans. (A) Photograph of the Langendorff-perfused rabbit heart preparation. The green square indicates the optically mapped surface. The black square pulse indicates the pacing site at the top left corner of the RV. (B) Representative optical V_m and Ca_i traces at positions a–c indicated in A, acquired after 10 s of pacing at PCL = 110 ms using pacing protocol 1 (see Methods). The traces show that the AP and Ca_i transient at point a are alternating out-of-phase (LSLS) with point c (SLSL), and point b shows minimal alternans of either the AP and Ca_i. Note that the AP and Ca_i transient are electromechanically concordant, i.e., a large AP is always associated with a large Ca_i transient, and vice versa. C, D. Plots of the amplitudes of API (C) and Ca_i transient (D) alternans over the mapped surface, for the final two paced beats at PCL = 110 ms. Blue indicates a positive difference in API between the two beats, and red a negative difference, with white indicating no difference (nodal lines).

Effects of pacing rate and site on Ca_i nodal line formation

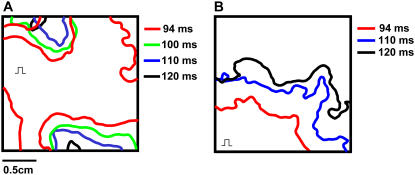
Fig. 6 shows the effects of pacing rate on the position of Ca_i nodal lines. During pacing at 140 ms for 10 s, a single-nodal line formed close to the apex (Fig. 6 A). When PCL was shortened to 130 ms, the nodal line moved closer to the pacing site and a second nodal line emerged above the pacing site (Fig. 6 B). Once a nodal lined formed at a given PCL, its position remained stable during steady-state pacing (Fig. 6 C). Thus, nodal lines formed stationary patterns whose location was dependent on the PCL. When the heart was paced at a shorter PCL, the nodal lines moved toward the pacing site. In addition, once formed, nodal lines did not drift. Similar findings were obtained in three pacing episodes in three different rabbit hearts. Fig. 7, A and B, illustrates the effects of the pacing site on the position of nodal lines. Whether the pacing site was located at the top left or bottom left, the nodal lines emerged far from the pacing site and moved toward the pacing site as the PCL was slowly decreased. Similar findings were obtained in two pacing episodes in two different rabbit hearts.

FIGURE 6.

The position of nodal lines remains stable during steady-state pacing and shifts toward the pacing site when pacing rate increases. (A, B) Map of Ca_i alternans amplitude after 10 s of pacing at PCL = 140 and 130 ms, respectively. Same color scale as in Fig. 3, with nodal lines shown in white. Pacing site is indicated by the square pulse. (C) Superimposed nodal lines for successive pairs of beats, computed from the last five paced at PCL of 140 and 130 ms, respectively. Only the area below the dashed line in B is shown.

FIGURE 7.

Nodal lines change position when the pacing site is changed. (A) Plot of Ca_i nodal lines computed using the last two beats at PCLs of 120 ms (black), 110 ms (blue), 100 ms (green), and 94 ms (red) when the heart was paced from the top left-hand corner of the LV (square pulse), using pacing protocol 2. (B) Same as A, but with the pacing site changed to the LV apex (square pulse).

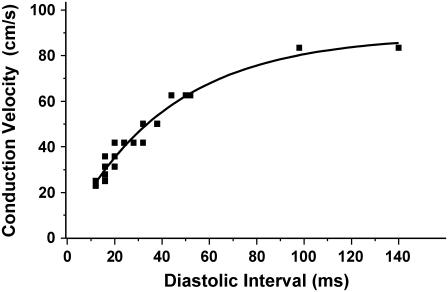
Restitution properties of rabbit ventricles

The above findings are more consistent with spatially discordant alternans in the rabbit ventricle arising dynamically from steep CV restitution rather than from intrinsic tissue heterogeneity. To confirm the presence of steep CV restitution in the rabbit ventricle, we measured the conduction times from the pacing site and a distance 10 mm away along the direction of propagation for the last two beats at each CL during protocol 2. These results are given in Fig. 8, which shows that CV varied by nearly a factor of 4 as DI decreased to its shortest value during the dynamic pacing protocol. This result is consistent with the above experimental findings on nodal line movement, indicating that steep CV restitution, rather than tissue heterogeneity, is the cause of spatially discordant alternans in the paced rabbit ventricle.

FIGURE 8.

Plot of CV versus DI during protocol 2. CV was estimated from the conduction time from the pacing site to a point 10 mm away along the fiber direction.

DISCUSSION

In this work we performed numerical simulations on the movement of nodal lines in response to pacing under a wide range of conditions. We then compared the predictions of the modeling to experimental results. Our experiments in the rabbit ventricles showed that during spatially discordant alternans, nodal lines evolved toward a steady-state pattern that depended on pacing rate. These patterns originated far from the pacing site and moved closer as pacing rate increased. We also paced the heart at different locations in the tissue and observed that the nodal lines moved toward the pacing site in each case. These experimental findings are consistent with computer simulations in which nodal line formation was dynamically generated by the combination of steep CV restitution with cellular alternans driven by either steep APD restitution or Ca_i dynamics. To confirm the presence of steep CV restitution in the rabbit experiments, we measured the CV restitution curve during the dynamic pacing protocol and found indeed that CV varied substantially with DI. In contrast, when nodal lines formed on a heterogeneous tissue substrate in the absence of CV restitution, they either moved away from the pacing site or remained pinned to the location where they formed, depending on whether the underlying cellular instability causing alternans was steep APD restitution or Ca_i dynamics. Thus, we conclude that spatially discordant alternans in this model is a dynamical entity which depends on the nonlinear properties of cardiac cells and wave propagation in tissue and cannot be accounted for solely by underlying tissue heterogeneity.

In contrast to the heterogeneity-based mechanism, when discordant alternans is dynamically generated by the steep CV restitution mechanism, APD alternans must be accompanied by both CL and CV alternans (17). Although detection of CL and CV alternans would have been the most direct test for distinguishing between these mechanisms, the predicted changes in CL (<2%) and CV (<10%) (17) during dynamically generated discordant alternans are very small and unfortunately below the threshold of detection of the optical mapping system. At a CL of 110 ms, the expected alternation of CL would be <2.2 ms, whereas the mapping data were acquired at 4 ms/frame. For these reasons, we were unable to confirm that CV or CL also alternate during spatially discordant alternans in the rabbit ventricle experiments. However, although the absence of CV and CL alternans excludes CV restitution as the cause of spatially discordant alternans, its presence does not prove this mechanism in heterogeneous tissue since the discordant alternans could be generated from the tissue heterogeneity with CV and CL alternans coincidental. We therefore developed more definitive criteria about nodal line behavior in response to pacing interventions and applied them experimentally to delineate the mechanism by which spatially discordant alternans forms in tissue.

An important question to address is whether the movement of nodal lines is robust to the presence of intrinsic heterogeneity expected to be present in real cardiac tissue. To assess this point, we performed numerical simulations of discordant alternans in the presence of a fixed gradient of L-type Ca current properties (Fig. 1 D) and also a fixed gradient of Ca-cycling properties (Fig. 2 D). In both cases we found that fixed heterogeneity changed the shape of the nodal line but did not affect the heart rate-dependent movement toward the pacing site. Hence, the direction of movement of nodal lines is robust to fixed tissue heterogeneity, although the quantitative degree of movement is dependent on the local electrophysiological properties of the tissue.

Another issue is whether short-term cardiac memory could have caused the observed nodal line movement. However, cardiac memory seems an unlikely explanation for the following reasons. First, in Fig. 6 C we showed that nodal line position for the last five beats after 10 s of pacing at 140 and 130 ms remained in a stable position, i.e., there was no discernible beat-to-beat drift toward the pacing site as long as the pacing rate was held fixed. Hence, it would be difficult to explain the suddenness of the ∼0.25 cm-shift in nodal line position based on a cardiac memory effect when the PCL was shortened modestly from 140 to 130 ms. Second, as shown in Fig. 7, A and B, nodal lines moved toward the pacing site regardless of location of the pacing site. This result is difficult to reconcile with a memory effect, since memory is a property of cardiac cells which should be independent of the direction of the wavefront. In other words, a drift of nodal lines due to changing restitution properties at fixed CL should be independent of the location of the pacing site. In contrast, the dynamical mechanism based on steep CV restitution requires that nodal lines are radially symmetric with respect to the pacing site, regardless of the location of pacing, as was observed experimentally. These arguments also make it unlikely that slow rate-dependent changes in cellular electrophysiology due to ion accumulation or pH changes could explain nodal line movement. The latter effects are equivalent to cardiac memory, broadly defined as pacing history-dependent effects on the APD and Ca_i transient.

Our findings also support the idea that Ca_i cycling may be more important than V_m dynamics in driving alternans in the rabbit ventricles during rapid pacing, consistent with the recent findings (5,27). We found that Ca_i nodal lines could develop in regions in which API alternans nodal lines were not present (Fig. 5). That is, Ca_i alternans could become locally spatially discordant in regions in which API alternans remained locally concordant. This is consistent with Ca_i-induced, but not V_m-induced, alternans for the following reasons. In V_m-driven alternans, the Ca_i transient amplitude in a cell passively follows the cell's APD in a graded fashion and is essentially unaffected by the Ca_i transient amplitude of adjacent cells (due to the slow diffusion of Ca_i between cells). In Ca_i-driven alternans, however, the Ca_i transient alternans can change phase over very short, even subcellular, distances (29,30) (again due to the slow diffusion of Ca_i), but the APD cannot follow suit due to the strong electrotonic influence of the nearby cells.

In our computer simulations, we have used a cell model partially based on the Fox canine ventricular model (21) coupled to our phenomenological model of Ca cycling based on rabbit ventricular data (15). We have used this mixed model, rather than a pure rabbit ventricular model, because, to our knowledge, no fully rabbit ventricular model is currently available which can generate cellular alternans at rapid pacing rates by either steep APD restitution slope or Ca_i-cycling dynamics. This feature is essential to allow us to probe the dynamics of nodal lines induced by either cellular mechanism. Despite this limitation, we expect that nodal movement consistent with the experimental findings can be reproduced by any detailed ionic model with a similar CV restitution curve. This assumption is strengthened by analytical studies (18,19) that are not based on a detailed ionic model, which show that spatially discordant alternans can be described in terms of restitution properties independent of detailed properties of the ionic model. However, it is clear that precise detailed models are necessary to predict quantitative aspects of nodal line movement. A further limitation of our computational study is that here we have studied spatially discordant alternans in only 1D and 2D. In three-dimensional tissue, nodal lines correspond to nodal surfaces which may have unique dynamical features not observed in lower dimensions. For example, in future studies it will be interesting to explore the role of transmural electrophysiological gradients on the properties of these nodal surfaces, which is critical for a complete characterization of spatially discordant alternans.

In our computer simulations, we studied only the case in which alternans was electromechanically concordant, i.e., a large APD or API was associated with a large Ca_i transient, and a small APD or API with a small Ca_i transient. We chose this case to match the experimental findings in the rabbit ventricle, indicating that alternans was electromechanically concordant (Fig. 5 B). However, alternans can also be electromechanically discordant (e.g., if the effect of Ca_i transient on Ca_i-induced inactivation of the L-type Ca_i current inactivation predominates over its effect on Na-Ca exchange). This case has been shown to lead to more complex dynamical behavior at the single-cell and tissue level (22,31,32). In this case, complex patterns of spatially discordant Ca_i and APD alternans emerge via a mechanism which is independent of CV restitution. A key feature of these patterns is that Ca_i transient nodes do not track APD alternans nodes, in sharp contrast to our experimental observations where Ca and APD nodal lines were similar. However, as shown by Rubenstein et al. (33) in cat ventricular myocytes, electromechanically concordant alternans can be converted to an electromechanically discordant alternans by simply reducing the temperature. This result raises the possibility that this regime might be explored in rabbit hearts by reducing the temperature or using various pharmacological interventions.

Spatially discordant alternans has been linked to the genesis of cardiac arrhythmias (2), and so preventing its occurrence is of therapeutic interest. Our study suggests that pharmacological interventions which seek to abolish discordant alternans can potentially be developed by targeting specific dynamical properties of cardiac cells. For instance, theoretical analysis predicts that by flattening CV restitution, e.g., by shortening the time constant of recovery of the Na current, it may be possible to abolish spatially discordant alternans. This therapeutic approach to eliminate spatially discordant alternans is fundamentally different from approaches that assume that static heterogeneities are responsible. Our experimental observations strengthen the dynamic viewpoint and should stimulate further exploration of therapeutic strategies based on dynamical properties.

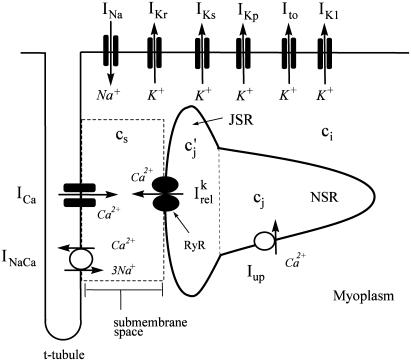
APPENDIX A: IONIC MODEL

The electrophysiology of an isolated cardiac myocyte was modeled using a recently developed model of Ca_i cycling by Shiferaw et al. (15) which was incorporated into the ionic model of Fox et al. (21). The ionic currents implemented, along with the relevant aspects of the Ca_i-cycling machinery, are illustrated in Fig. 9. The original Fox et al. (21) model included the ion currents 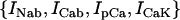, which we have omitted since these currents are small and have a negligible effect on the dynamical features of the model. Ca cycling in the rabbit myocyte was simulated using a model due to Shiferaw et al. (15). This model describes Ca released from the SR as a summation of local release fluxes distributed throughout the cell. The release flux from the SR, denoted 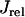, is modeled using the phenomenological equation

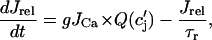(A1)

where 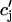is the average concentration within junctional SR (JSR) compartments, and is the average spark lifetime.

FIGURE 9.

Illustration of single-cell ion currents and Ca_i-cycling machinery.

APPENDIX B: DYNAMICAL PROPERTIES OF IONIC MODEL

Instability mechanisms

Ca_i transient alternans can occur due to Ca-cycling dynamics alone as shown in experiments with a single-cell paced with a periodic voltage clamp waveform (14). It has been argued both theoretically (15,34) and in recent experiments (35) that this period-doubling instability arises due to a steep dependence of SR Ca_i release on SR Ca_i load. The steepness of the SR release versus SR Ca_i load, at high loads, is determined by the parameter

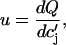(B1)

where the function 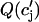denotes the JSR load dependence of local calcium release at the dyadic cleft. For a large enough value of u the model produces alternans that is due to a nonlinear dynamical instability of calcium cycling.

Alternans can also occur via instability in the voltage dynamics, independent of Ca_i cycling. In this scenario alternans can be induced by adjusting the kinetics of recovery of ion currents which regulate V_m. In the ionic model that we have used, this instability in the voltage dynamics is sensitive to the recovery from inactivation of the L-type Ca current

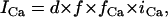(B2)

where 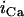is the single-channel current and d(f) is the fast (slow) voltage-dependent activation and inactivation gate, respectively. For the range of pacing rates investigated in this study, increasing the time constant of the f gate promotes alternans. The essential feature of this instability is that it is dictated by the gating kinetics of currents that regulate V_m rather than by the dynamics of Ca_i cycling.

The ionic model used in our simulation is adjusted so that at rapid rates, alternans can occur either due to purely V_m dynamics, whereas Ca_i cycling is stable, or vice versa. The former case, referred to as the V_m-driven model, is obtained by setting the time constant of recovery from inactivation of the L-type Ca_i channel to be large (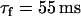), whereas the slope of the SR release versus SR load is kept small (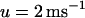). The latter case, referred to as the Ca_i-driven model, is obtained by inducing unstable Ca_i cycling by making the SR release versus SR-load large (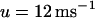), while keeping the time constant of recovery small ().

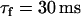CV restitution and discordant alternans

The dynamics of cardiac wave propagation is governed by the CV restitution curve, which relates the speed of a planar wave to the preceding diastolic interval (DI). The CV restitution curve is primarily dependent on the kinetics of the Na current, formulated as

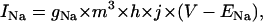(B3)

where m models the fast activation and h represents the fast inactivation of the sodium current. The slow recovery from inactivation is governed by the gate j, which is

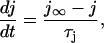(B4)

where 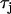governs the time constant of recovery.

To generate spatially discordant alternans via the mechanism proposed by Qu et al. (18) and Watanabe et al. (17), we found it necessary to control the shape of the CV restitution curve of the Fox et al. (21) ionic model. To accomplish this we have increased the time constant of the j gate by a factor of three (). In Fig. 10 A we plot the CV restitution curve for the parameters used by Fox et al. (21), along with the curve generated by increasing the slow time constant of recovery by a factor of three. As shown in the figure the steepness of the CV restitution curve is increased over a much broader range when 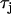is increased. Presence of a broad CV restitution curve in the rabbit heart was confirmed by our experimental measurements shown in Fig. 8. In Fig. 10 B we show the spatial distribution of Ca_i alternans on a 3.75-cm cable of V_m-driven cells paced at 240 ms at the left end of the cable. As shown, discordant alternans forms when 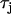is increased by a factor of 3. In Fig. 10 A we have drawn two vertical dashed lines to show the maximum alternation in DI along the cable. This shows that over the range of DI engaged along the cable, CV restitution is much steeper for the model with 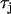increased by a factor of 3.

FIGURE 10.

CV restitution and discordant alternans on a 1D cable. (A) The black line is the CV restitution curve computed using 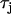from the Fox model. The dashed line is computed using 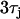. The thin vertical lines denote the maximum range of DI engaged during rapid pacing at 240 ms. (B) Spatial distribution of Ca_i alternans for steep (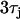) and shallow (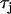) CV restitution. Alternans amplitudes are normalized to the leftmost cell.

APPENDIX C: MODELING HETEROGENEOUS TISSUE

Simulating fixed heterogeneity in tissue

We have also modeled heterogeneities in cardiac tissue. To model a base-to-apex gradient in the amplitude of APD alternans, which is implemented in Fig. 1 D, we let the voltage-dependent inactivation time constant of the L-type Ca current vary in space according to

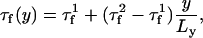(C1)

where 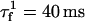, , 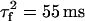and 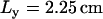. Heterogeneities of the Ca_i-cycling system are modeled in a similar way by varying spatially the slope of the release function 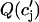, so that

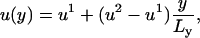(C2)

where 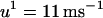and 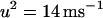. This form of Ca_i-cycling heterogeneity is implemented in Fig. 2 D.

Discordant alternans due to a heterogeneous substrate

Spatially discordant alternans can be formed in tissue with flat CV restitution via an appropriately timed change in PCL. The reason for this is that in heterogeneous tissue alternans amplitude varies spatially and it is always possible to time a pacing stimulus which reverses alternans phase in one part of the tissue and not in another. This mechanism for discordant alternans is applied numerically in 2D in Fig. 3 C and Fig. 4 C. In both cases CV heterogeneity is kept flat by using a value of 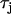given by Fox et al. (21), where the CV restitution curve is given by the black line in Fig. 9 A. In Fig. 3 C we model a heterogeneous V_m-driven cell model by simply varying the amplitude of the inward rectifier potassium current I_K1 along the diagonal direction of the tissue, so that above the diagonal line joining the top left-hand corner and the bottom right corner, the strength of I_K1 is 0.9 times the value given in Fox et al. (21), whereas below the diagonal it is 1.1 times this value. In this way we introduce a gradient in APD magnitude and APD restitution properties along the diagonal of the tissue. Subsequently, by pacing the cell to alternans at PCL₁ = 300 ms and then changing to PCL₂ = 290 ms after 40 beats, we induce spatially discordant alternans on the heterogeneous substrate. Fig. 4 C is formed using the same mechanism; only here the gradient is due to Ca_i-cycling heterogeneity, using the Ca_i-driven cell model, rather than APD heterogeneity. This is accomplished by first including the gradient given by Eq. C2, pacing at a PCL₁ of 270 ms, and then making a change in CL to 235 ms. In this way discordant alternans is formed on a heterogeneous substrate of Ca_i-cycling properties. In these simulations, the initiation of discordant alternans and the location of the nodal lines are sensitive to the gradients of heterogeneity in the tissue. However, the subsequent nodal line dynamics, i.e., whether the nodal lines moved away or remained pinned, is independent of the spatial distribution of heterogeneity.

APPENDIX D: COMPARISON OF ΔAPD AND ΔAPI ALTERNANS

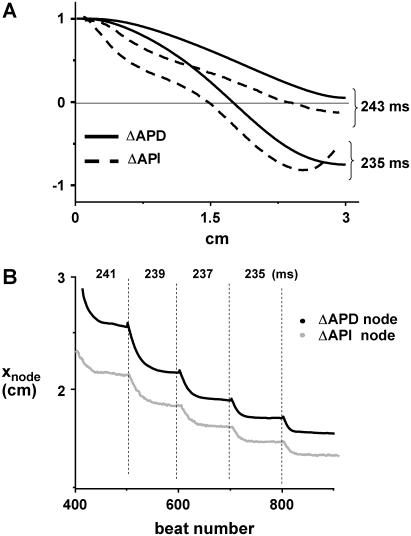
Here we demonstrate, using numerical simulation, that the spatial distribution of APD is similar to that of API. In Fig. 11 A we plot the ΔAPD and ΔAPI on 3-cm cable that is paced at the leftmost end. The ionic model is the same as that used in Fig. 1 A. The black lines denote the steady-state ΔAPD distribution at 243 ms and 235 ms, and the dashed lines correspond to the ΔAPI distribution. As shown, the spatial distribution and pacing rate dependence of ΔAPD and ΔAPI are similar, although the node position predicted by the ΔAPI is always closer to the pacing site. In Fig. 11 B we show the position of the node as a function of beat number during a dynamic pacing protocol (2-ms decrements every 100 beats). As expected, we find that both ΔAPD and ΔAPI settle to their steady-state values and obey the same rate-dependent behavior.

FIGURE 11.

Comparison of the spatial distribution of ΔAPA and ΔAPI alternans. (A) Steady-state spatial distribution of ΔAPA and ΔAPI alternans at 243 and 235 ms. The ionic model used is the same as that used for Fig. 1. (B) Nodal line position versus beat number during a dynamic pacing protocol where PCL is decremented by 2 ms every 100 beats.