A structural snapshot of an intermediate on the streptavidin–biotin dissociation pathway

Abstract

It is currently unclear whether small molecules dissociate from a protein binding site along a defined pathway or through a collection of dissociation pathways. We report herein a joint crystallographic, computational, and biophysical study that suggests the Asp-128 → Ala (D128A) streptavidin mutant closely mimics an intermediate on a well-defined dissociation pathway. Asp-128 is hydrogen bonded to a ureido nitrogen of biotin and also networks with the important aromatic binding contacts Trp-92 and Trp-108. The Asn-23 hydrogen bond to the ureido oxygen of biotin is lengthened to 3.8 Å in the D128A structure, and a water molecule has moved into the pocket to replace the missing carboxylate interaction. These alterations are accompanied by the coupled movement of biotin, the flexible binding loop containing Ser-45, and the loop containing the Ser-27 hydrogen bonding contact. This structure closely parallels a key intermediate observed in a potential of mean force-simulated dissociation pathway of native streptavidin, where the Asn-23 hydrogen bond breaks first, accompanied by the replacement of the Asp-128 hydrogen bond by an entering water molecule. Furthermore, both biotin and the flexible loop move in a concerted conformational change that closely approximates the D128A structural changes. The activation and thermodynamic parameters for the D128A mutant were measured and are consistent with an intermediate that has traversed the early portion of the dissociation reaction coordinate through endothermic bond breaking and concomitant gain in configurational entropy. These composite results suggest that the D128A mutant provides a structural “snapshot” of an early intermediate on a relatively well-defined dissociation pathway for biotin.

The dynamics of ligand entry and exit from protein binding sites are an important aspect of small-molecule recognition. Although the reaction coordinate model provides a useful context for understanding how enzymes manage activation barriers, there have been relatively few attempts to model ligand binding reaction coordinates in the same manner. On the association side, small molecule rates often fall near the diffusion limit, although the on-rate can be reaction controlled and involve dehydration and/or conformational rearrangement steps. Both theoretical and experimental studies have demonstrated that some proteins use electrostatic steering to enhance association rates, and thus specific side chains have been chosen to manage association–coordinate kinetic barriers (1–7). These models imply a relatively well defined and concerted sequence of conformational changes and bonding events and raise the question whether the exit pathway might be represented by a similar reaction coordinate.

An important related question is whether there even are well defined ligand exit pathways that can be described by a reaction–coordinate model. Do small molecules dissociate in a well-ordered sequence of bond breaking and protein conformational rearrangement events, or is it a stochastic process with a broad collection of pathways and barrier topologies (or something in between)? We have previously interpreted the streptavidin–biotin dissociation barrier in the context of an enzyme-like transition state model that implies a well-defined dissociation reaction coordinate (8). There is little experimental evidence, however, for defined exit pathways, and it is unclear whether specific side chains function on the dissociation coordinate to manage kinetic barriers apart from their role in generating binding free energy. The best characterized dissociation pathways involve the gaseous ligands of heme proteins such as myoglobin and hemoglobin (9, 10). Computational and experimental studies have investigated the role of specific side chains in managing dissociation barriers in a mechanistic context for ligands such as O₂ and CO and for gating of substrate–enzyme dynamics (11–16). Force microscopy techniques have provided another interesting opportunity to probe ligand dissociation energetics (8, 17). A detailed characterization of the energy landscape of streptavidin–biotin dissociation under force has been recently reported (18). Complementary computational studies of the force induced biotin exit pathway have suggested a concerted sequence of bond breaking and transient bond formation as biotin is sequentially pulled past the hydrogen bond donors and/or acceptors (19, 20).

In this study, we report the convergence of two separate lines of research into the dissociation pathway of biotin from streptavidin. First, site-directed mutagenesis, biophysical, and x-ray crystallographic approaches were used to determine the structural and thermodynamic effects of changing Asp-128 to Ala. The side-chain carboxylate of Asp-128 is hydrogen bonded to one of the ureido nitrogens of biotin. Independently, potential of mean force (PMF) molecular dynamics simulations were performed to investigate the exiting of biotin from native streptavidin. Unexpectedly, we have observed a concerted conformational alteration at the biotin binding site in the D128A mutant that closely mimics a key intermediate seen on the well-defined computed biotin dissociation pathway. Thus, with characterization of the activation thermodynamics of the mutant, these results suggest that the D128A mutant may represent a “trapped” mimic of an intermediate on the ligand exit pathway.

MATERIALS AND METHODS

Crystallography.

The D128A mutant was crystallized from a protein solution of 30 mg/ml in water and 50% 2-methyl-2,4-pentanediol in sitting-drop vapor diffusion experiments. The diffraction data were collected on a Siemens–Nicolet–Xentronics area detector system (Huber goniostat, Rigaku RU-200 rotating anode x-ray source). The data set was processed with the Siemens program package sadie/saint/sadabs for indexing, integration and empirical corrections. The data were merged with xprep. The overall R_merge was 0.03 (Table 1). For the crystals of the biotin complex of D128A, the protein solution at 30 mg/ml was incubated overnight with 2.5 molar excess of biotin. The data collection and processing was similar to that of the unliganded mutant. The overall R_merge was 0.05 (Table 1).

Table 1.

Crystallographic data

Protein	D128A	D128A/biotin
Space group	P21	P21212
Unit cell parameters	a = 48.0, b = 66.3, c = 82.3 Å; β = 97.3°	a = 55.7, b = 84.8, c = 50.0 Å
No. of tetramers per unit cell	2	2
Contents of the asymmetric unit	Tetramer	Dimer
Packing parameter VM, Å3/Da	2.9	2.5
Measured reflections, no.	56,045	39,212
Unique reflections, no.	31,972	14,716
Completeness
Overall, %	85.0	88.0
Outermost shell, %	46.0	43.0
Rmerge overall	0.03	0.05
Refinement
Nonhydrogen atoms, no.	3,416	1,783
Water molecules, no.	178	104
R factor*	0.167	0.156
Free R factor†	0.243	0.243
Average B factor,‡ Å2	32	31
Ramachandran quality§	0.91	0.89

^*For all data with F > 4σ(F), R = Σ_hkl ∥F_o| − |F_c∥/Σ_hkl |F_o|. 

^†For 10% of data with F > 4σ(F). 

^‡For all atoms. 

^§Fraction (except Gly and Pro) in most favored regions (30). 

The unliganded structure crystallized in one of the crystal forms that we had previously observed for wild-type streptavidin (21). The full-matrix, least-squares rigid-body refinement of the whole tetramer with the wild-type model (Protein Data Bank entry 1SWC, binding loop residues 45–52 and solvent deleted) with shelxl-97 (22) resulted in an R value of 0.31 (the R_free value) (23). All data from 10-Å to 2.0-Å resolution were included, after conjugate gradient least-squares refinements. Omit maps for residue 128 identified this residue as Ala. The final refined model included residues 16–44 and residues 48–132 (subunit 1), residues 16–132 (subunit 2), residues 16–46 and residues 51–132 (subunit 3), and residues 16–44 and residues 50–132 (subunit 4), as well as 178 water molecules.

The biotin-bound mutant structure was solved by using molecular replacement methods implemented in x-plor (24). One dimer of wild-type streptavidin (Protein Data Bank entry 1SWA without biotin binding loop residues and solvent) was used as the search model. After calculating the rotation and translation function for the model, the best solution had an R value of 0.508. Rigid-body refinement with shelxl-97 (22) lowered the R value [I > 2σ(I)] to 0.40 and R_free [I > 2σ(I)] to 0.43. After refinement of coordinates and B values, the |F_o| − |F_c| electron density showed convincing electron density for the two molecules of biotin in the asymmetric unit as well as the loop residues in the closed loop conformation. The final model included residues 16–133 (subunit 1) and residues 16–132 (subunit 2), as well as two molecules of biotin and 104 water molecules.

Both models were refined against the squares of the structure factor amplitudes by using conjugate gradient methods. All parameters (coordinates and isotropic displacement parameters) were refined simultaneously. Target values for 1,2- and 1,3-distance restraints were based on those tabulated by Engh and Huber (25). Similarity restraints were applied for isotropic displacement parameters. Planarity and chiral volume restraints were applied as were antibumping restraints if nonbonding atoms came closer than a target distance. Diffuse solvent regions were modeled with Babinet’s principle (26). Hydrogen atoms were geometrically idealized and refined by using a riding model. Sigma A-weighted |F_o| − |F_c| and 2|F_o| − |F_c| electron-density maps (27) were calculated with shelxpro. For graphical evaluation of the electron density and molecular model, xtalview was used (28). The structures were checked with whatif (29) and procheck (30). Water positions were found with shelxwat, a shelxl auxiliary program. All rms deviations for least-squares fits were calculated with x-plor using Cα atoms of 65 β-sheet residues. Details of the crystal structures will be published elsewhere (S.F., I.L.-T., P.S.S., and R.E.S., unpublished results).

Simulation Methods.

The details and full results of the PMF simulations will be presented in a separate publication (J.E.P. and T.P.L., unpublished results). The PMF calculations used a “virtual bond” between biotin and Ala-87 as the perturbation target. Test calculations where other residues were used for the virtual bond demonstrated that the results were independent of the specific assignment. As the length of this virtual bond was increased during the simulations, biotin was gradually pushed out of the binding pocket. Provided the perturbation is introduced slowly enough, the biotin molecule will follow the lowest energy pathway during the exit trajectory, yielding a detailed free energy profile for the dissociation reaction. All PMF calculations were performed with amber 4.1 (31), with an all-atom protein potential function (32) and the TIP3P water model. Partial atomic charges and other parameters for biotin were taken from the literature (33). The 2-Å resolution crystal structure for the biotin-streptavidin tetramer (21) was used as a starting point for all simulations. The system was hydrated either in a “droplet” centered on the biotin binding site or in a rectangular box with full minimal image periodic boundary conditions. The virtual bond was perturbed in 0.05-Å or 0.1-Å increments, with 2,000–10,000 equilibration and data sampling steps per discreet increment. A 1.0-fs time step was used in all simulations, with a 9-Å nonbonded cutoff. All covalent bonds were constrained at equilibrium values with the shake method (34) and the Berendsen coupling algorithm (35) was used for constant pressure (1 atm; 1 atm = 101.3 kPa) and temperature (298 K) control.

Gene Construction and Protein Expression.

The gene for the D128A mutant was constructed with cassette mutagenesis and subcloned into the PCR2.1 plasmid (Invitrogen). The D128A protein was produced in the pET-21a/BL21(DE3) expression system (Novagen) and refolded/purified as described (8).

Dissociation Kinetics.

The off-rate of biotin from D128A was determined by using a radiometric competition assay as described (36). Briefly, the protein was preloaded with a substoichiometric concentration of [8,9-³H]biotin (Amersham Pharmacia). The dissociation experiment was initiated by the addition of a large excess of nonradioactive biotin. The amount of unbound radioactive biotin was determined over time by separation through spin–ultrafiltration and quantitation in a scintillation counter. The k_off was determined by fitting of the expression for a first-order reaction. From the off-rates at each temperature, the transition-state enthalpy ΔH^‡ and entropy ΔS^‡ may be determined from a fit of the Eyring equation:

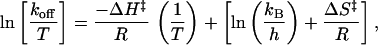1

where k_B is Boltzmann’s constant and h is Planck’s constant.

Equilibrium Thermodynamics.

The relative binding affinity of D128A versus wild-type streptavidin was determined at 37°C by using a radiometric competition assay that has been described (36). Briefly, in a mixture of [8,9-³H]biotin with histidine-tagged streptavidin (WT-HisTag) and D128A, partitioning of the [³H]biotin to D128A may be determined by removing WT-HisTag with Ni-NTA resin (where NTA is nitrilotriacetic acid; Qiagen, Chatsworth, CA) and centrifugation before quantitation in a scintillation counter. The binding enthalpies at 25°C and 37°C were determined with isothermal titration calorimetry on a CSC 4200 calorimeter (Calorimetry Sciences, Provo, UT). Streptavidin solutions (30–40 μM) were titrated with 15–20 injections of biotin (250–750 μM and 5–10 μl per injection). All experiments were performed at pH 7 in 50 mM Na₂HPO₄/100 mM NaCl. The enthalpy of binding was extracted from the isotherm by nonlinear least squares fitting to a model of independent binding sites by using dataworks and bindworks software from CSC (Chicago).

RESULTS AND DISCUSSION

The D128A mutant was constructed to investigate the equilibrium and activation energetic contributions of Asp-128 to the biotin binding reaction coordinate. Asp-128 is one of the key residues in the extensive hydrogen bonding network that forms when biotin binds to wild-type streptavidin (Fig. 1) (37, 38). One side-chain oxygen atom (OD2) is bound to a ureido nitrogen atom of biotin (Fig. 1B). In the second hydrogen bonding shell, this oxygen also networks with the side-chain nitrogen atoms of Trp-92 and Asn-23. The second carboxylate oxygen atom (OD1) forms hydrogen bonds with the side-chain nitrogen atoms of Trp-108 and Gln-24. This residue thus serves as a key direct link to biotin and as a connector between two of the important tryptophan binding contacts. It had been previously hypothesized that the Asp-128 carboxylate bridging of the Trp-92 and Trp-108 indole nitrogens might serve to lessen the configurational entropy costs of biotin binding by immobilizing the side chains in the unbound state. However, these residues appear to be fixed through packing interactions as the side chains are not altered in the D128A mutant structure versus wild type and also are similar in the bound and unbound states.

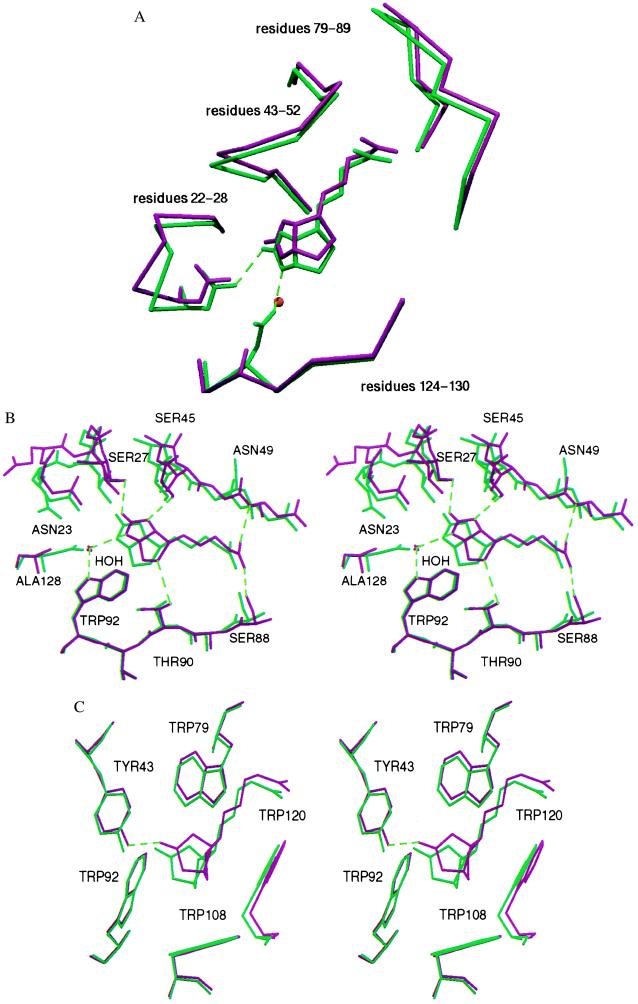
Figure 1.

Superposition of the wild-type (green) and D128A (red) biotin complexes in the region of the biotin binding site. (A) Only the Cα chain is depicted for clarity. Compared with wild-type streptavidin, three loops and biotin display a concerted shift away from the mutation site. For the hydrogen binding residues 23 and 128, the side chains are also depicted. A water molecule replaces an Asp-128 oxygen (OD2) in the mutant and interacts with biotin. (B) The hydrogen bonding network shows little deviations at residues Ser-88, Thr-90, and Trp-92, but there is no direct interaction of Ala-128 with biotin and the Asn-23–biotin hydrogen bond length is increased. (C) The tryptophan residues involved in hydrophobic interactions show only minor deviations.

There is a concerted shift of biotin out of the binding pocket in the Asp-128 mutant compared with the wild-type complex (Fig. 1). In both subunits of the asymmetric unit, a water molecule is positioned close to the site of the missing Asp-128 carboxylate OD2 atom. This water is hydrogen bonded to the ureido nitrogen of biotin and to Trp-92, just as the Asp-128 OD2 carboxylate oxygen is in the wild-type complex. The hydrogen bonds formed by the OD1 oxygen atom to Trp-108 and Gln-24 are not replaced by this water molecule. The superposition of the wild-type and mutant structures shows that biotin has partially shifted out of the pocket and away from the D128A mutation site. The binding site flexible loop is also shifted in the same direction so that Ser-45 and Asn-49 conserve their hydrogen bonding distances to biotin. Ser-27, which is located in another flexible loop region, has also shifted to maintain its side-chain-mediated hydrogen bond to biotin. The Asn-23 hydrogen bond, however, is lengthened from 2.8 Å to 3.5–3.8 Å in the D128A complex. There are only minor deviations in the positions of the tryptophans, which form important van der Waals contacts with biotin (Fig. 1). The biggest shift observed for any of the tryptophan contacts is that of Trp-79, which is the result of the concerted movement of biotin, the binding loop, and the neighboring loop of residues 79–87 away from the mutation site.

Before determining the crystal structure of the D128A mutant, PMF molecular dynamics calculations were performed on the native complex to provide computational insight into the dissociation pathway (J.E.P. and T.P.L., unpublished results). A variety of different initial starting conditions and simulation protocols were used to map the reaction coordinate in the PMF calculations. The early events along the dissociation pathway are very similar for 10 independent calculations performed to date, demonstrating that sampling in this crucial region of the reaction coordinate is thorough and adequate. A comparison of the biotin-bound D128A mutant crystal structure with the trajectories from PMF calculations of biotin dissociation revealed several remarkable structural similarities (Fig. 2). The first hydrogen bond to break in our simulations is the Asn-23 hydrogen bond to the ureido oxygen of biotin. As biotin was displaced from its bound state, the length of this hydrogen bond steadily increased from an average length of 2.7 Å to 3.4 Å. This hydrogen bond to biotin subsequently broke (exceeded 3.5 Å), whereas the other hydrogen bonds to the biotin ureido oxygen remained intact. The Asp-128 hydrogen bond to biotin was also lengthened during the early portion of the dissociation trajectories and became a water-mediated contact between Asp-128 and biotin when a water molecule entered from between streptavidin subunits 1 and 4. This water-mediated hydrogen bond was also observed in a molecular dynamics simulation of atomic force microscopy (AFM) experiments for a biotin–streptavidin monomer complex (19).

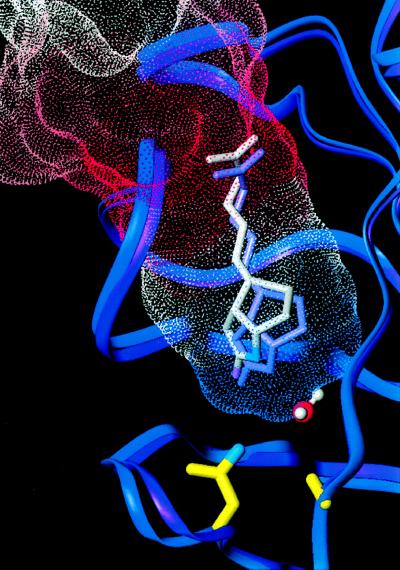
Figure 2.

A Connolly surface representing the PMF-calculated dissociation pathway of biotin from streptavidin, color-coded by energy (red highest), is overlaid on backbone ribbons representing the crystal structures of wild-type (purple) and D128A (blue) streptavidin. The D128A mutation causes the biotin to shift outward from the binding pocket allowing a water molecule to enter, mimicking features observed in the transition state of the PMF calculations.

It is interesting to note that the location of the first energy barrier in our simulations at 5 Å is consistent with the rupture length of 5 Å predicted for the biotin–streptavidin monomer complex (19) and a length of ∼4.5 Å predicted for biotin bound to the closely related avidin tetramer (20). These similarities to previous simulations are intriguing, given that our simulation protocol is radically different. Our system is a fully hydrated tetramer in a periodic box, and the biotin was gently pushed from the binding site (biotin was pulled from the binding site in the previous simulations with a relatively strong force to model the AFM experiments). In spite of these similarities with previous simulations, there are also dramatic differences. For example, our full tetrameric system includes the binding loop contributed by the neighboring subunit, and all the extensive hydrogen-bonding and van der Waals contacts this loop provides. Biotin dissociation in our simulated system requires a concerted motion of not only residues from the monomer binding pocket but also this binding loop (as in the real complex). None of these concerted motions and accompanying hydrogen-bonding and van der Waals disruptions can be observed in simulations of monomer complexes. Hydrogen bonds from Ser-27 to the ureido oxygen and Thr-90 to the biotin sulfur atom were broken as the ligand was displaced slightly further out of the binding pocket. The hydrogen bonds between Tyr-43 and the ureido oxygen and between Ser-45 and a ureido nitrogen were the last to be broken as biotin dissociated. This initial region of the dissociation reaction pathway includes the largest energy barrier, and we estimate dissociation binding free energy and enthalpy of ∼18 kcal/mol (1 cal = 4.184 J) and 24 kcal/mol, respectively, in good agreement with the experimental measurements.

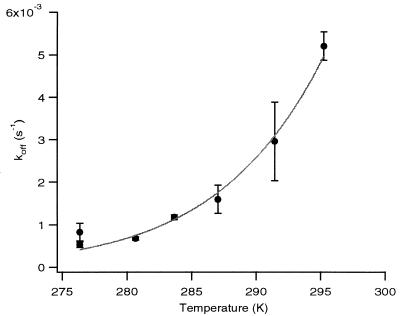
The D128A mutant displays a binding free energy decrease of 4.3 ± 0.1 kcal/mol relative to wild-type streptavidin (8, 36) at 37°C (Table 2). This ΔΔG° is enthalpically driven, with a large +7.9 kcal/mol loss of binding enthalpy at 37°C as determined by isothermal titration calorimetry. There is thus a significant reduction in the entropic costs of biotin association, with a calculated TΔΔS° of + 3.6 kcal/mol relative to wild-type streptavidin at 37°C. The dissociation rates were measured from 3 to 22°C, which allowed the determination of a ΔH^‡ of +20.7 ± 1.1 kcal/mol (mean ± SD) for D128A relative to +30.4 ± 0.2 for wild-type streptavidin (Fig. 3). The extrapolated ΔG^‡ was 20.4 ± 1.6 kcal/mol at 37°C versus 24.6 for wild-type streptavidin and the calculated TΔS^‡ was 0.3 ± 1.2 kcal/mol versus 5.8 kcal/mol for wild-type streptavidin. The activation and thermodynamic parameters for the D128A mutant are thus consistent with those predicted for a mimic of an intermediate that has traversed the early portion of the dissociation reaction coordinate through endothermic bond breaking and concomitant gain in configurational entropy. The equilibrium entropy term is also more favorable in the mutant, consistent with a “looser” bound state.

Table 2.

Thermodynamic parameters for D128A at 310 K

Parameter	Value
Kd ratio (D1238A/WT)	1,032  ±  74
ΔΔG°, kcal/mol	+4.3  ±  0.1
ΔΔH° kcal/mol	+7.9  ±  1.3
TΔΔS°, kcal/mol	+3.6  ±  1.3
koff, s−1	0.0281
ΔG‡, kcal/mol	20.4  ±  2.3
ΔH‡, kcal/mol	20.7  ±  1.1
TΔS‡, kcal/mol	0.3  ±  1.2

Figure 3.

Plot of k_off versus temperature. Solid line indicates weighted nonlinear least-squares fit used for calculation of transition-state parameters. Error bars denote one standard deviation.

CONCLUSION

The composite structural, computational, and biophysical results suggest that biotin dissociates along a relatively well-defined pathway. A striking property of the PMF calculations is the convergence of pathways in multiple dissociation simulations, where the same sequence of bond breaking and transient interactions is observed in nearly all simulations. Especially noteworthy is the early sequence where biotin slips out of the pocket as the Asn-23 bond is broken and a water molecule moves into the pocket to replace the lengthening Asp-128 carboxylate interaction with biotin. There is a nearly identical movement of biotin in the D128A crystal structure, along with the accompanying breakage of the Asn-23 hydrogen bond, and the presence of a water molecule that replaces the Asp-128 hydrogen bond to biotin. It is particularly interesting to compare these results with force microscopy measurements of the energy landscape encountered when pulling biotin out of the streptavidin pocket. A recent characterization of single biotin/streptavidin bonds under a wide range of loading rates suggested that the landscape consists of relatively sharp barriers, again consistent with a defined pathway. Thus, these results suggest that the biotin dissociation pathway in solution may be closely related to the pathway taken as biotin is pulled out of the pocket (18). This would perhaps be expected because the closest route of dissociation is along the direction where the carboxylate group of biotin exits the protein; i.e., the same point where biotin is tethered and pulled in the force microscopy experiments. It thus appears that a reaction coordinate model may be a useful representation of ligand dissociation from streptavidin, even with the complex set of molecular interactions that characterize the streptavidin–biotin interaction.

ABBREVIATION

PMF

potential of mean force