Epitope mapping using combinatorial phage-display libraries: a graph-based algorithm

Abstract

A phage-display library of random peptides is a combinatorial experimental technique that can be harnessed for studying antibody–antigen interactions. In this technique, a phage peptide library is scanned against an antibody molecule to obtain a set of peptides that are bound by the antibody with high affinity. This set of peptides is regarded as mimicking the genuine epitope of the antibody's interacting antigen and can be used to define it. Here we present PepSurf, an algorithm for mapping a set of affinity-selected peptides onto the solved structure of the antigen. The problem of epitope mapping is converted into the task of aligning a set of query peptides to a graph representing the surface of the antigen. The best match of each peptide is found by aligning it against virtually all possible paths in the graph. Following a clustering step, which combines the most significant matches, a predicted epitope is inferred. We show that PepSurf accurately predicts the epitope in four cases for which the epitope is known from a solved antibody–antigen co-crystal complex. We further examine the capabilities of PepSurf for predicting other types of protein–protein interfaces. The performance of PepSurf is compared to other available epitope mapping programs.

INTRODUCTION

The interaction between an antibody and its antigen is at the heart of the immune humoral response. The immune activity of an antibody is directed against a discrete site on its target antigen known as the epitope (1). Epitope identification is medically important in applications such as vaccine development. Vaccinating with the epitope only, rather than with the entire organism or the isolated antigen, could be much safer, and may be as effective (2). Epitope mapping has additional applications in the field of disease diagnosis and in immunointervention (3). Finally, epitope characterization is important in the context of drug design [reviewed in Ref. (4)]. Solved three-dimensional (3D) structures of antibody–antigen complexes provide a good starting point for the detailed functional characterization of epitopes, since they enable detecting those residues that comprise the interacting interfaces. Unfortunately, a solved 3D structure is unavailable for the vast majority of interacting antibody–antigen pairs. Therefore, one must resort to alternative approaches in order to characterize epitopes.

Phage-display peptide library is an established technology for displaying a large number (>10⁹) of random peptides. This technology is used to select from a large set of random peptides those with a high binding affinity to an antibody of interest (5). This selection process, termed biopanning, can be used to characterize the interacting interface of the antigen in the following manner. Let us assume that we are investigating an antibody and an antigen which are known to interact. A random peptide library is scanned against the antibody. The selected peptides are assumed to mimic the epitope in terms of physico-chemical properties and spatial organization. The algorithmic task is thus to utilize the information contained in the set of peptides, selected by the antibody, for correctly predicting the corresponding epitope on the surface of the antigen.

In the event that the panel of peptides has a common motif which corresponds well to a linear sequence within the antigen, mapping the epitope becomes self-evident. In such a case, the epitope can be inferred through standard sequence alignment approaches (6). Often, however, the isolated peptides have no obvious similarity to any linear fragment of the antigen. This reflects the fact that antibody–antigen interactions are mediated through their tertiary structures and, hence, the epitope is often composed of residues that are discontinuous in the linear sequence of the antigen. Therefore, a major computational challenge is to correctly correlate the peptides to the 3D interface they are taken to represent. Furthermore, some of the peptides may reflect noisy biological observations and should thus be filtered out by the algorithm.

Pizzi et al. (7) were the first to present an algorithm for mapping epitopes using affinity-selected peptides. In their approach, the surface of the antigen is represented by a ‘surface ensemble’ of short peptides. Short sequence motifs derived from the affinity selected peptides are searched against this ensemble. Following manual calibration, a resulting predicted epitope is assembled. Since then, several automated methods were suggested, in which the peptides are aligned to the antigen using various algorithms (8–11). In essence, the aim of all such methods is to align a set of linear sequences onto one common patch on the 3D structure of the antigen. However, none of the methods presented to date utilize a robust alignment procedure to fully scan the peptides versus the 3D structure of the antigen. The SiteLight algorithm (9) disregards the sequence order of the peptides. The algorithm of Enshell-Seijffers et al. (8) breaks the peptides to amino acid pairs and maps highly occurring pairs onto the antigen surface. The 3DEX method (11) searches for perfect matches; gaps may be allowed but are not penalized for. Finally, the MIMOP algorithm (10) first aligns the peptides to the antigen at the sequence level and only then incorporates information from the 3D structure.

Here, we present PepSurf, a novel algorithm for the prediction of epitopes using combinatorial phage-display libraries. PepSurf maps each of the affinity selected peptides onto the surface of the antigen. This is done by efficiently searching virtually all possible 3D paths for high similarities with the peptide sequences. We show that PepSurf successfully predicts the epitope of available test-case datasets, and compare its performance to all available epitope mapping programs. In addition, we study the use of PepSurf as a tool for the prediction of other types of protein–protein interfaces.

MATERIALS AND METHODS

Algorithm description

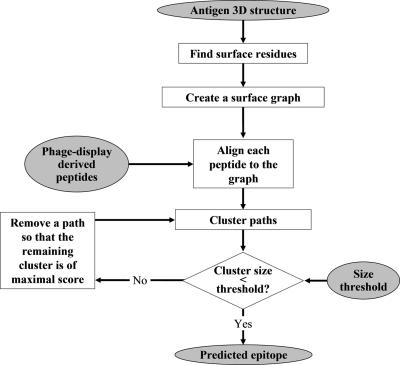
The input to PepSurf is a protein data bank [PDB; (12)] file of the antigen and a set of peptides selected by the antibody in a biopanning experiment. The output is one (or more) predicted patches of residues on the surface of the antigen that correspond to putative epitope sites. To tackle the problem of epitope mapping we translate it to the problem of finding high scoring paths in a graph. To this end, we represent the surface of the antigen as a graph (see below), and then search this graph for paths (i.e. a sequence of neighboring residues) that exhibit high similarity to each of the input peptides. This is, in fact, an alignment algorithm, in which a peptide may be aligned to antigen residues brought to proximity by folding. The resulting paths are then clustered and the epitope location is inferred. The main stages of the algorithm are shown in Figure 1.

Figure 1.

A schematic flowchart of the PepSurf algorithm.

Creation of a surface graph

As our algorithm aims at finding interacting interfaces, only solvent-exposed residues are considered. A residue is regarded as exposed if its solvent accessible surface area (ASA) in the 3D structure is >5% of its maximal ASA. The maximal ASA of a residue is calculated in an extended GXG tripeptide, where G denotes glycine and X denotes the residue in question (13). Solvent accessibility was determined using the Surface Racer program (14) with a probe sphere of radius 1.4 Å, corresponding to a water molecule.

We define a surface graph G = (V, E) as an undirected graph in which vertices represent surface residues. Vertices u and v are connected by an edge if the minimum Euclidian distance between any two heavy atoms of the residues corresponding to u and v is shorter than a default cutoff distance of 4 Å [as in Ref. (15,16)].

Mapping a peptide to the surface graph

Given a query peptide sequence, our aim is to find the path that yields the alignment with maximal weight (alignment score). Let Q = (q₁, … , q_k) be a query peptide of length k and P = (p₁, … , p_k) a simple path in G where p_i ∈ V. Let h(q_i, p_i) denote an amino acid similarity score between a query residue q_i and graph vertex p_i (see section ‘Scoring amino acid similarities’ below). The weight of the alignment between Q and P is the summation of the amino acid similarity scores between query residues and graph vertices

$$W(Q,P)={\displaystyle \sum _{i=1}^k}h(q_i,p_i).$$

An affinity-selected peptide, although linear, adopts a distinct 3D conformation. It is thus possible that not all residues in such a peptide correspond to residues on the antigen. Hence, residues of the peptide are allowed to be unmatched to graph vertices (i.e. gaps). Specifically, for each unmatched residue a gap penalty δ_D is added to the alignment score. In addition, we allow for cases in which only a subset of peptide residues are matched, i.e. no gap penalty is given to unmatched residues at either end of the peptide. Hence, the algorithm performs a local, rather than a global, alignment.

Ideally, all possible paths in G should be scanned and the path with the optimal alignment detected. However, the enumeration over all possible simple paths in G is computationally intractable for realistic-size problems. This intractability stems from the requirement that a path should not contain cycles, i.e. each graph vertex should appear at most once in the alignment. To address this constraint, we developed a dynamic programming based algorithm, which relies on the color-coding technique of Alon et al. (17). Color coding is an efficient technique for detecting simple paths in a graph. It proceeds by assigning every vertex v ∈ V a color c(v) drawn uniformly at random from the set C = {1, … , k}, where k is the length of the query peptide. Given such a colored graph, a dynamic programming scheme (detailed below) is used to find the highest scoring colorful path (spanning k distinct colors). However, since the coloring is random, there is no guarantee that the best alignment (the one that we globally aim to find regardless of the coloring) corresponds to a path of distinct colors. Thus, many random coloring trials are needed. In any given iteration, the probability that the optimal path is colorful is $k!/k^k$. Hence, the minimal number of trials needed in order to receive the best path with probability above p is $\left[\text{log}(1-p)/\text{log}(1-k!/k^k)\right]$. In all runs conducted here p was set to 0.95 to ensure that the best path is found with a high probability.

Given a colored graph, a dynamic algorithm is used to find the optimal aligned path of k distinct colors. Let W(i, j, S) denote the maximum weight of an alignment for the first i residues in the query that ends at vertex j ∈ V and visits a vertex of each color in S, where S is a subset of the colors. W(i, j, S) is computed recursively as follows:

$$\begin{array}{l}W(i,j,S)={\displaystyle \underset{m\in V}{\text{max}}}\{\begin{array}{l}W[i-1,m,S-c(j\left)\right]+h(q_i,j)(m,j)\in E\\ W(i-1,j,S)+{\delta }_D\\ 0\end{array}\\ W[1,j,c(j\left)\right]=\text{max}\left\{h(q_1,j),0\right\}\end{array}$$

The maximal weight of the alignment is ${\displaystyle \underset{j\in V,S\subseteq C}{max}}W(k,j,S)$. The corresponding alignment is obtained through standard dynamic programming backtracking. The running time of each coloring trial depends on the length of the peptide and the size of the surface graph, and is $O\left(2^k\left|E\right|\right).$ A similar dynamic programming scheme was used in (18) for querying pathways in a protein–protein interaction network.

The dynamic programming detailed above considers the whole space of different {i, j, S} values. Practically, the running time may be reduced considerably by applying a branch-and-bound technique. The full {i, j, S} matrix is first filled for small values of i. The dynamic algorithm proceeds only for entries that can theoretically result in higher scoring alignments than the best alignment produced in previous coloring trials. We have found that introducing this branch-and-bound addition results in ∼10-fold speed-up of the running time.

Assigning a P-value to a peptide-path alignment

The probability of obtaining a match with a specific score at random (P-value) is used in the proceeding clustering stage and is generated as follows. First, for each peptide an empirical background distribution of alignment scores is constructed by generating a set of m random sequences equal in length to that of the given peptide. The amino acids of each such sequence are drawn with probabilities derived from their frequencies in the surface of the antigen. Thus, this process approximates the generation of m random paths (in all runs conducted m = 10⁶). Each random sequence is then aligned to the given peptide. A P-value for each aligned path can be obtained from this empirical distribution. However, in order to construct an accurate distribution, an exceedingly large number of random sequences is needed. The distribution of local alignment scores is thus approximated using an extreme value distribution, whose parameters are fitted from the empirical distribution using the method of moments (19).

Clustering paths to predicted epitopes

Once each peptide is aligned to a highest scoring path, the question is how to combine these paths to obtain a predicted epitope. We define two paths to be connected if they share at least one residue. This defines clusters of connected paths. The score of each such cluster is the sum of −log (P-value) of the paths within it. We use this score rather than the sum of alignment scores since in some datasets not all peptides are equal in length and thus their alignment scores are not comparable.

The default clustering step views the peptides as a set of unique sequences. Obviously, different peptides bind the antibody with different affinities, which could be reflected by different frequencies of isolation for each peptide. This type of information can be integrated in the clustering step by multiplying the score of each path by the number of times its corresponding peptide was selected. We have found that including the number of times each peptide was selected (when this information was available) significantly improves the predictions (Supplementary Table S1).

We expect that an epitope would span a continuous region on the antigen surface. As the predicted cluster is composed of a set of paths, a residue that may not belong to any of the paths may still reside in the region encompassed by the cluster. Hence, we perform a cluster-fill-in step that augments the clusters with such missed residues. Specifically, a residue is added to the predicted cluster if 75% or more of its graph edges are connected to residues that are already in the predicted cluster.

In order to force the predicted epitope to be of a biologically realistic size, a maximal-size threshold for a cluster is given as an input for this clustering step. The size of a cluster is defined as the surface accessible area of all the residues within it. All clusters obtained are reduced in size until they conform to this threshold. This is achieved by iteratively removing a path until the remaining cluster does not exceed the size threshold. In each such iteration, the path to be removed is chosen so that the remaining cluster is of a maximal score. Finally, the cluster with the highest score is chosen as the predicted epitope. In all analyses conducted a size threshold of 2000 Ų was used. This value was chosen since it encompasses the size of 95% of all available epitopes in the PDB (Supplementary Data).

In the clustering algorithm detailed above no priority is given to a path that highly overlaps other paths. This suggests that residues supported by many paths should be prioritized over other residues. While the clustering algorithm detailed above considers whole paths only, a second clustering algorithm that groups individual residues was tested. Let p_i (i = 1, … , m) be the paths that include the residue r. The score S(r) for a residue r in the graph takes into account both the similarity score of the residue and the score of the path in which it participates:

$$S\left(r\right)={\displaystyle \sum _{i=1}^m}sim(r,p_i)+A(p_i)$$

where sim(r, p_i) is the similarity score of r in the alignment between p_i and the corresponding peptide, and A(p_i) is the alignment score of the path p divided by the length of the path. The algorithm then aims to find a connected component (i.e. a cluster) with a high score but yet with a restricted number of residues. Specifically, the patchFinder algorithm (16) is used to search the space of all possible patches and to find the cluster with the lowest probability to occur by chance. However, the results obtained with this ‘residue clustering’ algorithm were slightly inferior to the results obtained using the path clustering (Supplementary Table S5).

Scoring amino acid similarities

The alignment algorithm described above can be used with any log-odds substitution matrix to score amino acid similarities. Log-odds matrices were originally defined as the ratio between the observed and expected amino acid substitution frequencies derived from a large number of protein families (20). The substitution score thus depends on the frequency of each amino acid in the population of the protein families used to generate the matrix [e.g. the BLOSUM series; (21)].However, the expected amino acid frequencies of phage-display libraries are not necessarily the same as those of the original matrix. For example, in a library constructed using NNK oligonucleotides (where N stands for A, C, G or T and K stands for G or T) the expected frequency of tryptophan is 3.1%, compared to 1.3% in BLOSUM62. Thus, in order to derive the proper log-odds matrix for each set of peptides we modified the corresponding BLOSUM matrix by taking into account the amino acid frequencies employed when constructing the library. Specifically, the substitution score for amino acids i and j, h(i, j), is calculated as follows: $h(i,j)=q(i,j)/p\left(i\right)f\left(j\right)$ where q(i, j) is the observed probability of occurrence for each i, j pair in the original BLOSUM62 matrix [as described in Ref. (21)]; p(i) and f(j) are the probabilities of occurrence for i and j in the phage library and in the original BLOSUM62 matrix, respectively. We have found that accounting for the expected amino acid frequencies of each phage library generally resulted in more accurate predictions compared to the original BLOSUM62 matrix (Supplementary Table S3).

As an alternative to the BLOSUM substitution matrix, we have also considered using the Grantham similarity index (22). In this case, amino acid similarity is defined based on physico-chemical properties, including composition, polarity and molecular volume. Results obtained using the Grantham matrix were inferior to those obtained using the BLOSUM matrix (Supplementary Table S3). We thus present all subsequent analyses with the modified BLOSUM62 matrix for scoring amino acid similarities.

Program availability

The PepSurf epitope mapping algorithm described here is implemented in C++. The obligatory inputs to PepSurf are a set of peptides and a PDB file of the antigen. The program allows users to specify a number of optional parameters such as the gap penalty and the amino acid similarity matrix. The source code and binaries are freely available at http://www.tau.ac.il/~talp/PepSurf.html.

Comparison to extant methods

The predictions of PepSurf for all datasets were compared to three available epitope-mapping programs. Below we briefly describe how we used each of the programs and the necessary adjustments carried out in processing the results.

3DEX (11). The output of 3DEX is a mapping of each peptide onto the antigen surface. For each peptide, an unranked list of hits is given rather than a single predicted epitope. In order to compare a 3DEX prediction to the true epitope we first chose the longest hit of each peptide. We then applied the same clustering procedure used in PepSurf in order to obtain a single predicted epitope. In all runs, the frame size parameter of the program was manually adjusted to give a sufficient number of hits as recommended by the authors (M. Humbert; personal communication).

Enshell-Seijffers et al. (8). The algorithm requires random peptides as input and operates with two input parameters: the first parameter (ST) defines the statistical threshold of a pair to be regarded as statistically significant; the second parameter (D) defines the maximal distance between the carbon-α of two residues to be considered as neighbors on the 3D protein structure. We tested the algorithm's performance with nine different sets of parameters (ST = 2, 3 and 4; D = 8, 9 and 10). The results are presented with the set of parameters that gave the best predictions (ST = 3, D = 10).

MIMOP (10). The performance of MIMOP was evaluated using the recommended combined option of MIMALIGN and MIMCONS. In cases where the combined option failed to produce results, the MIMALIGN option was used instead. MIMOP outputs an unordered set of predicted epitope regions. The union of these regions was taken as the final prediction, as recommended by the authors (V. Moreau, personal communication).

Performance assessment

In order to assess the performance of PepSurf to accurately infer epitopes we applied it to publicly available phage-library datasets (Table 1) that fulfill the following requirements: (i) a set of affinity-selected peptides were derived by screening an antibody in a biopanning experiment and (ii) a 3D structure of the antibody–antigen complex is available. For each dataset, the prediction was compared to the ‘true’ epitope which was inferred using the ‘Contact Map Analysis’ server (23). All analyses were conducted with the BLOSUM62 as the substitution matrix (modified as described above) and a default gap penalty of −0.5.

Table 1.

Datasets with known binding sites used to assess the predictions accuracy

PDB ID	Antibodya	Antigena	Source	Library sizeb
Validation
1JRH	Ab A6	IFNgammaR	(25)	60 × 5
				36 × 6
1BJ1c	VEGF	VEGF Ab	(26)	3 × 5
				2 × 4
Antibody–antigen
1g9M	mAb 17b	gp120	(8)	10 × 14
				1 × 12
1E6J	mAb 13b5	p24	(8)	14 × 14
				2 × 7
1N8Z	Herceptin Fab	Her-2	(34)	5 × 12
1IQD	mAb Bo2C11	Coagulation factor VIII	(35)	27 × 12
Protein–protein
1AVZ	Fyn SH3 domain	Nef	(27)	8 × 10
				10 × 12
1G83	Fyn SH3 domain	SH2	(27)	8 × 10
				10 × 12
1HX1	Bovine Hsc70	Bag chaperone regulator	(28)	8 × 15
Synthesized peptide
1HX1	Bovine Hsc70	Bag chaperone regulator	(28)	1 × 7

^aIn the case of protein–protein datasets, the antibody and the antigen correspond to the target and template proteins, respectively.

^bNumber of sequences × sequence length.

^cIn this experiment, the phage library was screened by VEGF and the mapping is onto the anti-VEGF mAb (see text for details).

The success of the various epitope-mapping methods is statistically assessed by testing if the number of residues correctly predicted is significantly higher than expectation by random. The random prediction is based on the hyper-geometric (HG) distribution and is calculated as follows. Suppose there are a total of S residues on the antigen surface; TE of them belong to the true epitope; PE is the number of residues in the predicted epitope. The probability of randomly obtaining TP (true positives) or more correctly inferred residues is the P-value of prediction:

$$P\text{-value}={\displaystyle \sum _{x=\text{TP}}^{\text{TE}}}\text{HG}(x,\text{PE,TE,}S).$$

We consider a prediction to be statistically significant if its P-value < 0.01. The HG distribution is only an approximation since the random-generated prediction is not required to be a connected component. A more thorough approach that requires randomization of the surface graph was not applied here since it requires a large number of iterations.

RESULTS

To exemplify the use of the PepSurf algorithm we first present a walkthrough of the algorithm using an example dataset. We then study the performance of PepSurf on several types of datasets. We start by analyzing two validation datasets that are expected to represent relatively easy cases for epitope mapping. We then demonstrate the ability of PepSurf to accurately map known epitopes in cases where the antibody–antigen 3D complex has been previously determined. We continue by demonstrating the ability of our algorithm to accurately map protein–protein interfaces outside the immunological context. Finally, we show that our algorithm outperforms all other available epitope mapping programs on this variety of data.

Algorithm flow

In order to illustrate the algorithmic flow of PepSurf we first present a detailed description of the mapping of the monoclonal antibody (mAb) 17b epitope on the surface of gp120, the envelope protein of HIV (dataset 1G9M in Table 1). This epitope has been previously determined by solving the 3D crystal structure of gp120 in complex with mAb 17b and CD4 [PDB identifier 1G9M; (24)]. By analyzing the solved antibody–antigen complex using the Contact Map Analysis server (23), 18 residues were identified as comprising the ‘true epitope’. 17b was used to screen a combinatorial phage-display library resulting in a set of 11 affinity-selected peptides (8).

A surface graph was derived from the 238 solvent-exposed residues of gp120 (chain G; PDB 1G9M). The PepSurf algorithm first mapped each of the 11 peptides to the graph. The most significant alignment was obtained for the peptide CEFFQQHMLRVPRC. The alignment is shown below; the upper row represents the peptide and the lower row represents the path (C296 denotes cysteine in position 296).

C

E

F

F

Q

Q

H

M

L

R

V

P

R

C

C296

—

F376

F382

K421

Q422

Y435

M434

—

—

V120

P118

K117

C205

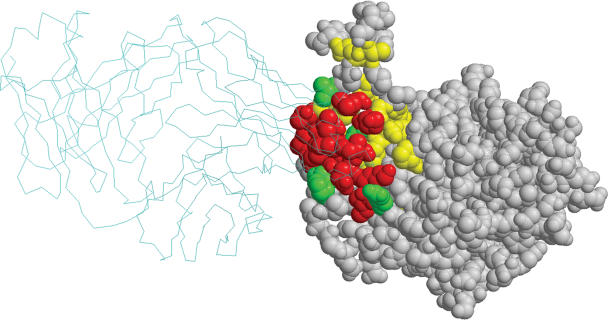
Clearly, the resulting path is not linear in sequence but is rather comprised by residues that are neighboring only on the 3D structure. The score of this alignment is 25.4. Based on the background empirical distribution (see Materials and Methods), the P-value of obtaining such a score is 5 × 10⁻⁷. Indeed, six residues of this path belong to the true epitope (underlined above). Interestingly, after aligning all 11 peptides to the graph, it was found that all corresponding paths contain at least one residue that overlaps the true epitope. These paths were then clustered to yield a 3D patch containing 72 residues that covers all 18 residues of the true epitope (P-value = 9 × 10⁻¹¹). This patch covers a total surface area of 4166 Ų and was then reduced in size until it conformed to the 2000 Ų size threshold (see Materials and Methods). In this process the least significant paths were excluded resulting in a patch that contains 36 residues (Figure 2). Fourteen of these residues are part of the true epitope while 22 are located around it and are regarded as false positives. The P-value of randomly obtaining such a prediction is 5 × 10⁻¹⁰, indicating a successful prediction.

Figure 2.

The prediction obtained by the PepSurf algorithm for the 17b–gp120 complex (PDB identifier 1G9M). The gp120 and 17b antibody are shown as a space-filling and backbone models, respectively. Residues successfully predicted are colored red, residues erroneously inferred to be part of the epitope are colored green, and genuine epitope residues not predicted are colored yellow.

Validation test cases

In order to validate the correctness of the PepSurf algorithm we first analyzed two datasets, for which the epitope mapping task is expected to be relatively easy. In the first dataset (labeled 1JRH in Table 1), short linear fragments of the interferon γ receptor (IFNγR) that are known to be important for interaction with mAb A6 were randomly mutated using a phage display library technique. As such, each phage particle contained the entire IFNγR protein with a short mutated fragment. The phage particles were then selected based on their ability to bind mAb A6 (25). Here, we test whether our algorithm is capable of mapping the selected mutated fragments back to the original fragment on the structure of IFNγR. In the second dataset (labeled 1BJ1 in Table 1) a similar experiment was conducted but here linear segments of the antibody were mutated and selected for binding to the antigen (26). In these two experiments the selected peptides are embedded in the whole protein and are thus subject to additional constraints of maintaining epitope structure. Thus, mapping the peptides back to the mutated region may seem easier than a ‘standard’ mapping problem and we regard them as validation test cases. Our results show that for both datasets the predictions of PepSurf indeed include almost the entire mutated regions (Table 2). For the 1JRH dataset all mutated residues were predicted except the two residues at the two extreme ends of the mutated region (P-value = 2 × 10⁻⁴). For the 1BJ1 dataset, the highest scoring cluster (which contains 30 residues) successfully predicted 11 out of 16 mutated residues (P-value = 2 × 10⁻⁹), while the second-ranked patch (containing eight residues) predicted the additional five mutated residues.

Table 2.

Comparative performance of epitope prediction programs

PDB ID	TEa	TPb/PEc P-valued
		PepSurf	Enshell-Seijffers et al.	MIMOP	3DEX
1JRH	12	10/28 2 × 10−4	9/59 0.52	0/9 1	8/35 0.06
1BJ1	16	11/30 2 × 10−9	7/167 0.82	0/0 1	0/35 1
1G9M	18	14/36 5 × 10−10	14/34 2 × 10−10	2/26 0.61	0/56 1
1E6J	15	14/23 6 × 10−14	7/11 2 × 10−6	11/19 9 × 10−10	0/20 1
1N8Z	23	8/11 2 × 10−9	9/27 1 × 10−6	4/21 0.035	0/8 1
1IQD	19	12/30 2 × 10−4	12/65 0.37	6/11 0.003	10/48 0.22
1AVZ	16	14/29 9 × 10-11	1/11 0.68	3/4 0.003	0/18 1
1G83	13	0/20 1	2/11 0.29	0/0 —	0/11 1
1HX1 (random)	22	12/27 0.003	4/16 0.54	8/27 0.62	0/13 1
1HX1 (synthesized)	22	5/7 0.007	Not applicable	6/10 0.009	4/6 0.02

^aNumber of residues in the true epitope.

^bNumber of true positives.

^cNumber of residues in the predicted epitope.

^dP-values of successful predictions are shown in bold type.

Epitope mapping for antibody–antigen datasets

There are four available cases in which an antibody was scanned with random peptides and a co-crystal of the antibody–antigen complex exists. In these cases each predicted epitope can be compared to the true epitope determined from the crystal structure. Peptides selected using the 17b, 13b5, Herceptin and Bo2C11 antibodies were mapped to the structure of their corresponding antigens, specified by the PDB identifiers 1G9M, 1E6J, 1N8Z and 1IQD, respectively (Table 1). For the present, these are the only publicly available antibody–antigen datasets for which such an assessment can be performed. As can be seen in Table 2, PepSurf successfully predicts all four epitopes (P-value < 10⁻⁴). The best prediction was obtained for the 1E6J dataset, which consists of a patch of 23 residues, 14 of which are true positives (P-value = 6 × 10⁻¹⁴).

The four antibody–antigen datasets tested here were constructed based on ‘cysteine-looped’ libraries. In these libraries each random peptide contains a pair of cysteine residues that form a disulfide bond, imposing a structural constraint on the resulting peptide. It is not clear whether these fixed cysteines should be treated as being part of the given peptide sequence. On the one hand, they may actively contribute to the binding. On the other hand, they were inserted as a means to impose structural constraints and are not truly random. Indeed, different epitope mapping programs deal differently with these cysteines: Enshell-Seijffers et al. (8) specifically integrates these fixed cysteines in the computation by treating the pairs they form as ‘semi random’. Moreau et al. on the other hand, recommend disregarding these cysteines since they might bias the output of the resulting alignments (V. Moreau, personal communication). The results presented in Table 2 were performed while including the flanking cysteines in the input peptide sequences. In order to check the possible influence of the flanking cysteines we also ran the four datasets with the cysteines removed. As seen in Table 3 removing the fixed cysteines resulted in decreased accuracy of predictions. This decrease might be explained by the existence of cysteines residues inside (1G9M, 1N8Z) and around (1E6J) the genuine epitopes. The 1IQD dataset does not contain any cysteines in the true epitope and including them in the peptides had a slight effect on the resulting prediction.

Table 3.

Results obtained with or without including fixed cysteines in the input peptides

PDB ID	Cysteines included	TEa	TPb/PEc P-valued
			PepSurf	Enshell-Seijffers et al.	MIMOP	3DEX
1G9M	+	18	14/36 5 × 10−10	14/34 2 × 10−10	2/26 0.61	0/56 1
	−	18	10/37 5 × 10−5	12/31 3 × 10−8	0/26 1	0/56 1
1E6J	+	15	14/23 6 × 10−14	7/11 2 × 10−6	11/19 9 × 10−10	0/20 1
	−	15	6/27 0.01	0/8 1	0/12 1	0/21 1
1N8Z	+	23	8/11 2 × 10−9	9/27 1 × 10−6	4/21 0.035	0/8 1
	−	23	0/10 1	9/27 1 × 10−6	3/12 0.02	0/10 1
1IQD	+	19	12/30 2 × 10−4	12/65 0.37	6/11 0.003	10/48 0.22
	−	19	12/32 5 × 10−4	13/65 0.2	10/23 0.005	9/52 0.53

^aNumber of residues in the true epitope.

^bNumber of true positives.

^cNumber of residues in the predicted epitope.

^dP-values of successful predictions are shown in bold type.

Using PepSurf for the prediction of protein–protein interfaces

Phage-display library is a general technique that can further be used for detecting interfaces of various types of interacting proteins. In this context, the phage library is scanned against a target protein. The affinity-selected peptides are then mapped onto the solved 3D structure of the target's interacting partner (termed the template protein). We have chosen two datasets as test cases of protein–protein interface detection. In the work of Rickles et al. (27), the Fyn-SH3 domain was used as a target to scan a semi-combinatorial random peptide library, resulting in 18 peptides. The co-crystals of Fyn-SH3 domain with two of its interacting proteins, Nef and Fyn-SH2 domain are available (PDB identifiers 1AVZ and 1G83, respectively; Table 1). We applied PepSurf to infer the interface of both Fyn-SH3 interacting proteins (Table 2). The predicted interface on the surface of Nef considerably overlaps the genuine interface, with 14 out of 16 residues of the true interface predicted. This prediction is highly significant (P-value < 9 × 10⁻¹¹). On the other hand, mapping the peptides onto Fyn-SH2 domain yielded only two small predicted clusters that do not overlap the genuine interface. Takenaka at al. (28) have screened a random phage library against the 70 kDa heat shock cognate (Hsc70) protein to obtain a set of peptides that bind Hsc70. We applied PepSurf to infer the interface between Hsc70 and the Bag chaperon regulator, for which a solved complex structure exists. The prediction of PepSurf successfully overlaps the genuine interface (P-value = 0.003).

Epitope mapping using synthesized peptides

The use of the PepSurf algorithm is not confined to mapping random peptides derived from a biopanning experiment, but is rather a general tool for aligning short sequences to a 3D structure. In the study of Takenaka at al. (28) mentioned above, a heptamer sequence was synthesized based on the peptides most frequently present in the enriched library. PepSurf was employed to align this heptamer to the surface of the Bag chaperon regulator. The resulting non-linear path (TILRKKK) on the 3D structure was found to be nearly identical to the synthesized heptamer (NIVRKKK). Five of the residues in this path belong to the true interface (P-value = 0.007).

Comparison to extant methods

The predictions of PepSurf for all datasets were compared to three available epitope-mapping programs (see Materials and Methods). The predictions of all programs are given in Table 2. For the two validation test cases, none of these three methods produced successful predictions, as opposed to PepSurf. The prediction of 3DEX for the 1JRH dataset overlaps the true epitope but does not attain statistical significance. For the 1BJ1 dataset only the second-ranked cluster of residues produced by 3DEX successfully overlaps with the true epitope. The MIMOP program produced a predicted region for only one of the two cases, which did not overlap with the true interface. This may stem from the algorithm's aim to produce a multiple sequence alignment of all peptides, while these peptides correspond to non overlapping regions of the antigen (25,26). Breaking the panel of peptides into three separate sets, corresponding to three separate libraries of affinity maturation-derived peptides, managed to produce a significant predictions for both datasets (P-value = 0.002 and 7 × 10⁻⁶ for the 1JRH and 1BJ1 datasets, respectively). The algorithm of Enshell-Seijffers et al. (8) produced very large predictions on both datasets, both statistically insignificant.

In the case of the four antibody–antigen datasets, the prediction of 3DEX overlapped the true epitope only for the 1IQD dataset (P-value = 0.22). However, when considering lower-ranked clusters, the second ranked cluster of the 1E6J dataset successfully overlapped the true epitope. The MIMOP program successfully identified three out of the four test cases, albeit with a marginally significant prediction for the 1N8Z dataset (P-value = 0.035). The algorithm of Enshell-Seijffers et al. (8) overlapped the true epitope in all four antibody–antigen datasets. For the 1IQD dataset, the predicted epitope size was very large, and hence was not statistically significant (P-value = 0.47).

The success of the three epitope mapping programs to predict protein–protein interfaces was lower compared to the antibody–antigen data (Table 2). The MIMOP algorithm succeeded in predicting the true interface for the 1AVZ dataset while the predictions of the two other programs did not. Using random peptides, none of the methods successfully predicted the 1HX1 dataset. However, using the synthesized peptide the predictions of both MIMOP and 3DEX overlapped the true interface in a statistically significant manner. The algorithm of Enshell-Seijffers et al. (8) could not be applied to synthesized peptides since it relies on random peptides and their comparison to expected amino acid frequencies of the phage library.

Tuning the parameters of the algorithm

The PepSurf algorithm depends on several parameters that may influence its resulting prediction. Such parameters include the gap penalty, the exact choice of the substitution matrix, the distance cutoff defining a graph edge, the maximal cluster size, the ‘fill-in’ cutoff and the P-value for obtaining the best path. The low availability of quality benchmark data severely limits our ability to properly learn PepSurf parameters, and test its performance using cross-validation techniques. We thus tested only a limited set of values for each parameter. In general, running the algorithm with a reasonable range for each parameter did not significantly influence the results. For example, the results obtained using a gap penalty in the range of −0.25 to −1.5 were quite similar, while not allowing for gaps at all generally resulted in inferior predictions. A detailed description of the effect of the various parameters on the accuracy of prediction is given in the supplementary material (Supplementary Tables S6–S9).

DISCUSSION

In this study we explored the ability to infer a protein interface by mapping a set of peptides, affinity selected by its binding partner. The PepSurf algorithm first maps each peptide onto the protein surface and then clusters the resulting hits, thus obtaining a predicted epitope. The novelty of the PepSurf algorithm is in its ability to perform a 1D to 3D alignment by locating the optimal threading of a sequence onto a 3D structure. The strength of our approach stems from the fact that it resides within the well-defined realms of alignment problems, and as such is statistically robust and can easily import features of general alignment problems such as gap penalties, different substitution matrices, profile versus sequence alignment, and so forth. Extending the alignment scheme out of its classic string-matching context can serve as an important tool in function-structure studies. While pairwise sequence alignment is the basis for homology searches, the alignment scheme developed here may similarly be used to ‘blast’ a structural motif against a set of proteins represented as graphs.

Our algorithm successfully predicts the epitopes of the four antibody–antigen test cases in a statistically significant manner. The reason for such a limited number of datasets available for validation stems from the fact that in most cases where a co-crystal of mAb–antigen exists there is no motivation for mapping the epitope using a phage-display experiment. Phage-display experiments are usually conducted when co-crystallization has failed, or to bypass costly co-crystallization of the antibody-antigen complex.

We have also demonstrated the potential of our approach for in silico inference of the interface of other types of interacting proteins outside the immunological context. This task, however, is more challenging since antibodies are known to bind their targets with high affinity compared to the average affinity of other types of protein–protein interactions as a result of affinity maturation to their target antigens. This implies higher likelihood of obtaining relevant peptides when scanning a phage library with an antibody. We can speculate that these reasons contribute to the overall reduced performance of all methods on the protein–protein datasets tested.

The PepSurf algorithm is basically divided into two steps: finding the optimal path for each peptide, and clustering these paths into a predicted epitope. The presented algorithm for clustering paths is a greedy heuristic approach for finding a connected subgraph (cluster) of maximal score subject to a size constraint. If the number of paths (corresponding to the number of peptides) is small, an exhaustive search is computationally feasible. Implementing this exhaustive search allowed us to test the efficacy of the heuristic search for datasets with no less than 20 peptides. On the six datasets tested we confirmed that the heuristic approach produces similar results compared to the exhaustive one (Supplementary Table S3). This approach, however, considers only the highest scoring hit for each peptide, while a query peptide potentially gives rise to multiple matching paths. Although in the alignment algorithm alternative hits have lower scores, it is possible that choosing suboptimal hits would ultimately result in a higher scoring cluster. In addition, we can also exclude a certain peptide as being part of the resulting cluster. Using the exhaustive clustering approach we can choose for each peptide either its best scoring hit, its second best one, or remove the peptide from the analysis. Considering these alternatives improved the prediction for the 1N8Z dataset but worsened the prediction for the 1E6J dataset, with only the second-ranked cluster overlapping the true interface. The prediction for the 1G9M, 1AVZ, 1G83 and 1HX1 datasets did not change (Supplementary Table S4). Taken together, the heuristic clustering algorithm seems to equilibrate well between efficiency and efficacy.

Further improvements to the PepSurf algorithm are possible. The parameters of the algorithm can be tuned to specific types of interactions. For example, amino acid similarity scores can be adjusted for antibody–antigen interactions, taking into account the more frequent presence of aromatic residues in such interfaces (29). In addition, protein–protein interfaces are known to have typical characteristics (30,31). For example, they are known to be more evolutionary conserved compared to the other regions on the protein surface (32). This information can be combined with the information from the selected peptides to yield more accurate predictions.

Running time may be a concern in a PepSurf analysis. The rate limiting step is the scanning of possible paths to find the best alignment for a single peptide. The running time for the entire algorithm is thus approximately linearly dependant on the number of peptides. The running time of a single alignment step depends on the number of graph edges, the length of the peptides, and the desired P-value for obtaining the optimal path. For short peptides of up to 10 amino acids the running time is a few seconds long (using an Opteron processor of 2.4 GHz). However, in case of longer peptides (14 or 15 amino acids) the running time for one peptide is a few hours. When dozens of peptides are to be aligned, this may result in excessively long computations. This limitation may be resolved in several ways. One solution is to relax the requirement of obtaining the best path with a very high probability. Decreasing this probability from 0.95 to 0.5 produced identical results while the running time was considerably reduced (Supplementary Data). Another possible solution may be to partition long peptides to shorter overlapping segments, and then treat each one as an independent peptide.

PepSurf relies on having a solved 3D structure of the antigen. While the 3D structure of most proteins is still unknown, for soluble proteins the structural genomics initiatives provide predicted structures in various degrees of accuracy. This suggests an optional method for epitope mapping when only the linear sequence is known: first predict the structure, and then apply PepSurf on the resulting structure. When a few candidate structural predictions are available, one can choose the epitope resulting in the highest scoring cluster over all candidate structures.

Epitope mapping algorithms can assist in the challenging task of ab initio structural prediction. There are two variants for this approach. In the first, suggested by Mumey et al. (33), peptides are aligned to the linear sequence of the antigen. In contrast to classical sequence alignment methods, each peptide is allowed to be aligned to discontinuous regions of the antigen sequence. Thus, distant segments of linear sequence that are in close spatial proximity on the native form of the folded protein are revealed. The result is a network of structural constraints that can assist ab initio structure determination. In the second approach, a few candidate structures are predicted. The peptides can then be aligned to each structure (e.g. using PepSurf) and the structure on which the peptides best clustered is chosen. The applicability of this approach awaits further studies.

A challenging task is to use the epitope mapping algorithms in order to predict putative interacting partners of a given target protein. Assume, for example, a scenario in which two proteins (A and B) are suspected to interact with a given target protein. The target is scanned against a phage library. PepSurf can then be applied to infer the interaction interface on both suspected proteins, resulting in a high scoring prediction for protein A and a low scoring prediction for protein B. This result suggests that protein A is the true interactor. Extending this idea, the selected peptides can be scanned against a large dataset of proteins (such as the PDB). The highest scoring predictions will be considered as putative interactors. An immediate additional result would be the mapping of the putative interface region between the analyzed proteins.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.