Heavy Water Fractionation during Transpiration

MOTIVATION

A small proportion of water molecules contain the heavier isotopes of hydrogen and oxygen. There is a tendency for these heavier molecules of water to accumulate in leaves during transpiration. This has several interesting repercussions, including effects on the isotopic composition of organic matter, and of atmospheric water vapor, carbon dioxide, and oxygen. In turn, these effects aid temporal reconstruction of climate and spatial and temporal reconstruction of primary production in various ways. A recent, novel report by Miller et al. (2006) showed that tree-ring ¹⁸O measurements carried a record of hurricane activity.

The motivation for our laboratory to study water isotopes was to enhance studies of transpiration efficiency (TE; the leaf contribution to water-use efficiency at the plant, crop, or ecosystem level). The instantaneous TE is A/[g_wν], where A is the rate of photosynthetic uptake of CO₂, g_w is the conductance to diffusion of water vapor to the atmosphere from the sites of evaporation within the leaf (made up of the stomatal conductance, g_s, and boundary layer conductance, g_b, in series), and ν is the leaf-to-air water vapor concentration difference. Carbon isotope composition of leaves can be measured to determine the carbon isotopic discrimination, Δ¹³C, during photosynthesis. In turn, Δ¹³C relates to A/g_t, the ratio of CO₂ assimilation rate to the total conductance to diffusion of CO₂ from the atmosphere to the sites of carboxylation. The two measures are obviously related, and it was suggested that the oxygen isotope composition (δ¹⁸O) of leaf material could be used to pick up differences in ν (Farquhar et al., 1994).

Further, because g_w affects δ¹⁸O and A does not, it was hoped that measurements of Δ¹³C and δ¹⁸O in organic matter could be combined to separate photosynthetic capacity effects on TE from g_w effects (Yakir and Israeli, 1995; Saurer et al., 1997; Farquhar et al., 1998). The heavy isotopes of water, expressed in organic matter, have promise as a means of identifying genetic variation in g_w. In an ecological and population biology context, the carbon, hydrogen, and oxygen isotope measurements could provide a practical surrogate for measures of the marginal water cost of carbon gain, ∂E/∂A, with E the rate of transpiration (Cowan and Farquhar, 1977), as one might expect different stomatal and photosynthesis strategies to be associated with environments with differing rainfall statistics (Cowan, 1982).

In this Update on heavy water fractionation, we focus on how transpiration “leads” to enrichment and ask whether enrichment is a measure of transpiration. We then sketch some applications.

THE BASICS OF WHY LEAVES BECOME ENRICHED

On earth, roughly 0.204% of oxygen is ¹⁸O and 0.037% is ¹⁷O; 0.015% of hydrogen is ²H. There are usually more of these heavy isotopes in leaf water than in the soil/xylem water because (1) the vapor pressure of heavy water is less than that of the most common isotopolog, ¹H₂¹⁶O, and (2) the binary diffusivity with air of heavy water vapor is less than that of light water. So, when water evaporates from the leaf, heavier molecules tend to be left behind. This process continues until the leaf water becomes sufficiently enriched that the exit of heavy and light molecules through the stomata matches that of the supply of water from the xylem.

The theoretical basis for leaf water enrichment, derived by Craig and Gordon (1965), Dongmann et al. (1974), Farquhar et al. (1989), and Flanagan et al. (1991), is as follows. The transpiration rate, strictly that of the light water, is given by:

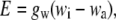(1)

where w_i and w_a are the mole fractions of water vapor in air inside the leaf and in the ambient air (the vapor pressures divided by the total atmospheric pressure), respectively.

The rate of transpiration of heavy water is given by:

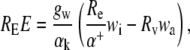(2)

where R_E is the molar isotope ratio (heavy/light) of the transpired water (e.g. ¹⁸E/¹⁶E), R_e the isotope ratio of liquid water at the sites of evaporation and R_v that of the ambient water vapor, α_k (>1) is the kinetic isotope effect associated with the difference in diffusivities, and α⁺ (>1) is the equilibrium isotope effect associated with the differences in vapor pressure.

Dividing the second equation by the first, we obtain an expression for R_E:

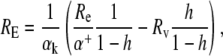(3)

where h is the relative humidity.

Rearranging, we obtain the isotope ratio at the sites of evaporation relative to that of the transpired water (as applied by Harwood et al. [1998]):

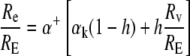(4)

We note that, in steady state, R_E must be close to the isotope ratio of source (soil) water, R_s.

It is convenient to express the enrichment, Δ_e (=R_e/R_s − 1), in terms of the liquid-vapor equilibrium fractionation ɛ⁺ (=α⁺ − 1), kinetic fractionation ɛ_k (=α_k − 1), and vapor enrichment Δ_v (=R_v/R_s − 1), so that, in steady state:

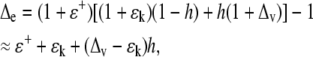(5)

where the approximation follows since the values for ɛ⁺ and ɛ_k are small (0.08 and 0.03 for deuterium) and are particularly good for oxygen (0.009 and 0.03). Equation 5, often called the Craig-Gordon equation with the enrichment denoted Δ_e = Δ_C, was originally derived to explain the isotopic enrichment of a lake, analogous to our leaf, undergoing steady-state evaporation. Normally, the right-hand side of the equation is greater than unity, which means that transpiration causes heavy water (deuterium or ¹⁸O) enrichment in leaves. Indeed, in moist field conditions, for example, after rain, Δ_v is often approximately equal to −ɛ⁺. In such conditions:

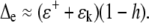(6)

Thus, from Equations 5 and 6, the maximum isotope effect is the sum of the equilibrium and kinetic fractionation terms and is realized when atmospheric humidity is very low. The isotope effect is generally small when atmospheric humidity approaches 100%.

AS E INCREASES, ISOTOPIC ENRICHMENT SHOULD ALSO INCREASE. TRUE OR FALSE?

Heavy water enrichment increases with increase in E. This was the recent conclusion of Sheshshayee et al. (2005) in a paper titled “Oxygen isotope enrichment (Δ¹⁸O) as a measure of time averaged transpiration rate.” The authors report a relationship that holds regardless of whether the variation in E is caused by variation in g_w or variation in evaporative demand, ν. Does this make sense?

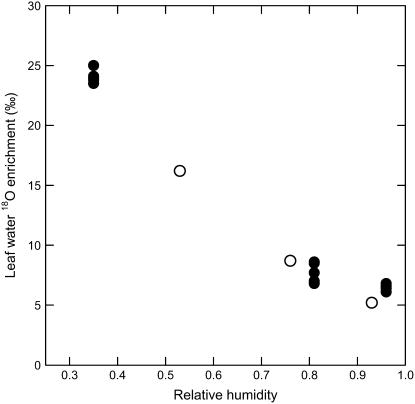
If the source of variation is evaporative demand, it does, as can be seen by reducing relative humidity h in the equations above. Supporting evidence comes from many sources, and a nice example is from Helliker and Ehleringer (2002a, 2002b; Fig. 1).

Figure 1.

Enrichment of leaf water versus relative humidity in five C₃ grass species. All grasses were grown in chambers where the isotope ratio of source water was held constant, leaf boundary layer development was minimized by high wind speeds, and only relative humidity varied across treatments. Note that relative humidity was calculated based on leaf temperature as opposed to ambient temperature similar to the convention of Equation 5, where h = w_a/w_i. Black and white circles are data from Helliker and Ehleringer (2002a) and Helliker and Ehleringer (2002b), respectively.

If the source of variation is stomatal, we need to examine the changes in the various parameters. First, the kinetic fractionation is affected. For ¹⁸O, kinetic fractionation is given by:

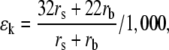(7)

where r_s and r_b are the stomatal and boundary layer resistances to diffusion of water vapor, respectively (Farquhar et al., 1989). The value for fractionation during diffusion, 32/1,000, is normally written as 32‰, where the symbol means per mil, or parts per thousand. It is a recent experimental measurement by Cappa et al. (2003) and is significantly greater than the value previously used (Merlivat, 1978). The fractionation factor in the boundary layer, 1.022, derives from 1.032^2/3 and is less than that in the stomatal pore. This means that as stomatal resistance increases, its fractionation tends to dominate and ɛ_k increases. That is, the leaf water should become more enriched as stomata close and as E is reduced. Second, stomatal closure and reduced transpiration cause heating of the leaf, so that w_i increases, and h decreases. This should also cause an increase in enrichment. The change in leaf temperature will have a small effect on ɛ⁺ in the opposite direction, but too small to matter in this context.

So as far as stomatal-induced changes in transpiration rate are concerned, we have two effects that should lead to a negative relationship between E and isotopic enrichment, these being of opposite sign to the positive effect of evaporative demand on both E and Δ_e. There is a third effect that reinforces these. The enrichment of water in the leaf, Δ_L, will usually be less than that at the sites of evaporation, Δ_e, because mass flow from the xylem of unenriched water will oppose the diffusion of enriched water from the sites of evaporation back toward the xylem. Farquhar and Lloyd (1993) called this the Péclet effect, after a French mathematician, and formalized it as follows: Enrichment falls off from the value at the sites of evaporation, as exp(−P), where P is the dimensionless number vl/D, with v = velocity, l = distance from sites, and D the diffusivity of heavy water in water. Velocity is proportional to transpiration rate. Average enrichment, Δ_L, in a simple system would be given by ([1 − exp(−P)]/P) Δ_e. The Péclet number P is proportional to E, and so, as E increases, average leaf enrichment, Δ_L, becomes increasingly depleted compared with Δ_e. It represents another reason for Δ_L to decrease as g_w increases. The Péclet effect should also apply when E is increasing because of a reduction in h, but the calculated negative effect on average leaf water enrichment is less than the direct effect of increasing Δ_e.

What is the experimental support for these mathematical ideas about a negative relationship between E and Δ_L, when the source of variation is g_w? At present, the data on direct effects of stomatal conductance on Δ_L are fairly thin, and particularly so for the so-called Péclet effect. It is a common, but not universal, observation that leaf water is less enriched than would be predicted from the modified Craig-Gordon equation. However, the evidence that the Péclet effect explains the shortfall is as yet largely indirect. Barbour et al. (2004) reanalyzed the data of Roden and Ehleringer (1999b) and found that the predictions of leaf water enrichment were improved by including the Péclet effect. Cernusak et al. (2002, 2005) included the effect in simulating their field observations of Δ_L, and it also improved the fit greatly compared to the simple use of the Craig-Gordon model. This was so for both hydrogen and oxygen isotopes. However, this improvement is largely one of making Δ_L less than Δ_e, and the dependence on changes in g_w tended to be lost in the variation caused by changes in Δ_e. There are few direct measurements in the laboratory of the effect of changes in g_w on Δ_L. The main difficulty of such measurements is their intrinsically destructive nature, meaning one leaf per datum, together with what appears to be variable Péclet lengths, l, between individual leaves. If aquaporins play a role in determining the effective length (Barbour and Farquhar, 2004) and if they are dynamic (Flexas et al., 2006), this might explain some of the variability. One cannot subsample leaves and hope to obtain representative values of average leaf water enrichment, as enrichment is often heterogeneous (Yakir et al., 1989; Bariac et al., 1994).

OXYGEN ISOTOPE ENRICHMENT OF PLANT ORGANIC MATTER

Although the direct evidence that an increase in g_w should reduce leaf water enrichment is lacking, there is indirect evidence via the effects on isotopic composition of organic matter. The factors controlling oxygen isotopic composition of organic matter are better understood than those controlling the hydrogen isotope composition, and for the former the major step appears to be the exchange of oxygen atoms between water and carbonyl oxygens in triose phosphates via a gem-diol intermediate. The analogous equilibration between acetone and water was studied by Sternberg and DeNiro (1983), who found that the oxygen in the organic matter ended up enriched by about 28‰ compared to the water. In the formation of Suc, the water undergoing exchange will be both that in the chloroplasts, probably close to Δ_e (Farquhar et al., 1993), and that in the cytosol, which is presumably less enriched. Barbour et al. (2000b) examined the oxygen isotopic composition of Suc bled from the petioles of castor bean (Ricinus communis) leaves undergoing gas-exchange measurements. The technique has the advantage that repeated measurements can be made of the same leaf under differing conditions. The results were consistent with a fractionation of 27‰, and, by subtracting that value from the enrichment of the Suc, they were able to obtain the composition of the effective substrate water. The latter was less enriched than Δ_e, and the difference increased with increasing E as would be expected from theory. Cernusak et al. (2003b) compared destructive measurements of Δ_L with the enrichment of phloem Suc and also obtained a fractionation of 27‰. However, the underlying processes, including their spatial distribution, are complex and may involve processes other than carbonyl exchange (Schmidt et al., 2001) Thus, at this stage it is unknown how reliable, or constant, is the fractionation taken here as 27‰. Suc molecules are broken down to Glc and rejoined to make cellulose. This exposes some carbonyl oxygens again to water, and, since that water is often less enriched than in source leaf cells, the enrichment in cellulose is likely to be less than that in the feeding Suc. The proportion exposed is at minimum 20%, but more if there is futile recycling of hexose phosphates through triose phosphates. The net proportion appears to be around 40% (Cernusak et al., 2005). Despite these complexities, clear leaf water signals can be discerned in the oxygen isotope composition of cellulose and, indeed, of general organic matter.

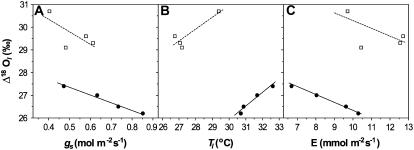
An example of g_w affecting cellulose enrichment was provided by cotton (Gossypium hirsutum) plants fed various concentrations of abscisic acid (ABA; Barbour and Farquhar, 2000). See Figure 2. As concentration increased, stomata closed (diminishing the stomatal conductance, g_s, as well as g_w) and the cellulose became more enriched. That is, a reduction of transpiration was associated with an increase in oxygen isotopic composition. Reassuringly, the reverse association was seen in plants where E was reduced by higher humidity. So increasing E via effects on evaporative demand were consistent with increased heavy water accumulation in the photosynthesizing leaves, while increasing E via effects on g_w were consistent with decreased accumulation. Nevertheless, contrary to this, Sheshshayee et al. (2005) observed a positive relationship between g_w and oxygen isotopic composition in plants fed ABA. However, recently Thompson et al. (A. Thompson, J. Andrews, B.J. Mulholland, J.M.T. McKee, W. Howard, H.W. Hilton, J.S. Horridge, G.D. Farquhar, and I.B. Taylor, unpublished data) examined two tomato (Lycopersicon esculentum) lines, sp12 and sp5, that overexpress a gene encoding 9-cis-epoxycarotenoid dioxygenase and are involved in abscisic synthesis. The increases in ABA content were associated with a decrease in g_w and with an increase in organic δ¹⁸O, thus conforming to theoretical expectations. Further, unpublished data of J. Masle and G. Farquhar show that plants growing in compacted soils have lower g_w and are enriched in δ¹⁸O compared to plants growing in loose soil.

Figure 2.

The relationships of cotton leaf organic matter oxygen isotopic enrichment with stomatal conductance, g_s (A); leaf temperature T_l (B); and E for plants grown at 43% relative humidity (white squares) and 76% relative humidity (black circles; C). The source of variation was the concentration of the hormone, ABA (from left to right within each section, 0, 10⁻⁵, 10⁻⁴, and 10⁻³ m), sprayed on the developing leaves. Data and figure are redrawn from Barbour and Farquhar (2000).

The relevance of the Péclet effect to organic δ¹⁸O in trees is also supported by reanalysis of the cellulose data of Roden and Ehleringer (1999a, 2000) by Barbour et al. (2004). Cernusak et al. (2003a) showed that among Eucalyptus globulus trees at three adjacent field sites with differing soil water contents, variation in phloem sugar δ¹⁸O was negatively associated with variation in transpiration rates among the trees.

Thus, apart from the puzzling and, therefore, interesting results of Sheshshayee et al. (2005), the conclusion is that increasing E can be associated with either increasing enrichment of heavy water, Δ_L, when the source of variation is evaporative demand, or decreasing Δ_L, when the source of variation is g_w.

¹⁸O, STOMATAL CONDUCTANCE, AND BREEDING FOR IMPROVED GRAIN YIELD IN IRRIGATED WHEAT

Carbon isotope discrimination has been used as a selection criterion in wheat (Triticum aestivum) breeding, and as a result water-use efficient wheat varieties have been released commercially (Condon et al., 2002; Rebetzke et al., 2002) for dryland agriculture. In well-watered conditions, yield potential is sought, and that appears to be associated with increases in both photosynthetic capacity and stomatal conductance and decrease in canopy temperature. CIMMYT grew eight short spring wheat species that they had released between 1962 and 1988 during three seasons in northwest Mexico. It was found that yield, A, and g_w all increased with year of release—the breeders had done their job well—and the canopy temperature and δ¹⁸O of the leaf cellulose decreased with year of release (Barbour et al., 2000a), again as theory would suggest.

It is often easier to collect leaves in the field for subsequent mass spectrometric analysis than to directly measure stomatal conductance with a porometer. And since g_w in the field is in any case a dynamic variable, δ¹⁸O of the leaf organic matter is an attractive measure when genetic differences in average conductance are sought. The measure is most effective when h is low, as was the case with the measurements in Mexico.

NON-STEADY STATE

At night time one would expect the leaf to lose its enrichment in heavy water because evaporative demand goes down. From what we have seen, it would be incorrect to think that enrichment should decline because closing stomata reduce E. In fact, night-time stomatal conductance is required for the leaf to lose its enrichment. The time constant for changes in isotopic composition of leaf water relates to the one-way flux out of the leaf (g_ww_i; Dongmann et al., 1974) and not to the net transpiration rate [g_w(w_i − w_a)]. This led Farquhar and Cernusak (2005) to observe that at relative humidities, h, greater than 50%, more water enters the leaf from the air (g_ww_a) than through the petiole [g_w(w_i − w_a)].

Farquhar and Cernusak (2005) extended the model of Dongmann et al. (1974) to include the Péclet effect. They also included changes in leaf water content as these are thought to be important sometimes (Yakir, 1998).

This led to the following non-steady state equations:

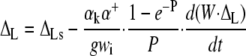(8)

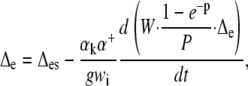(9)

where Δ_L is the actual leaf water enrichment, Δ_Ls is the steady value that would obtain in those conditions, and W (mol m⁻²) is the leaf water content. Δ_e and Δ_es are the actual and steady values of the enrichment at the sites of evaporation.

Cernusak et al. (2002, 2005) showed that inclusion of the Péclet effect was necessary for simulating the experimental results during the day, but less so at night when E was low. They found that the non-steady-state treatment was vital for reasonable simulation of observations at night, but less so during the day when open stomata allowed the leaf enrichment to follow changes in evaporative demand. The interest here in night-time stomatal opening is in whether it allows the leaf to lose enrichment in heavy water. This interest intersects with that in the isotopic exchange of oxygen between leaf water and CO₂ in the atmosphere. If the stomata are open at night, CO₂ can enter the leaf, exchange oxygen isotopically with leaf water, and diffuse back out to the atmosphere without any photosynthesis being involved (Cernusak et al., 2004).

SPATIAL HETEROGENEITY IN ENRICHMENT OF HEAVY WATER IN LEAVES

One of the frustrating features of heavy water enrichment, its variation within a single leaf, has turned out to be interesting and illuminating. Some of the variation is probably systematic with the ends of leaves being enriched compared to the bases. Some may be random and perhaps associated with dynamic stomatal heterogeneity (Peak et al., 2004). Yakir et al. (1989) proposed that there may be different metabolic pools of water within the leaf. This could conceivably come about because of hydraulic isolation of some parts of the tissue. One would think that internal vapor exchange would ensure that no part of the leaf is really isolated from the rest. Nevertheless, with the current interest in aquaporins and their possible dynamic nature, reversible isolation within cells could be imagined.

Progressive enrichment occurs along the leaf. It is seen in both monocots and dicots, but is easier to study in monocots. It occurs because when water first enters the leaf at the base, light water is preferentially transpired, leaving the heavy water behind. This heavy water tends to get swept further along the leaf. The process continues until a point is reached where the exchange no longer causes any enrichment. At this point the enrichment of the mesophyll will be maximal, Δ_M, and equal to the enrichment of the locally transpired water, Δ_E. We adapt this condition from the Craig-Gordon enrichment (Eq. 5):

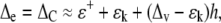and it then follows (Farquhar and Gan, 2003) that Δ_M ≈ Δ_C/h. So the greatest enrichment along a leaf is the normal Craig-Gordon value divided by the relative humidity. Of course, the base of the leaf must be depleted so that the whole leaf average enrichment at the sites of evaporation is still given by the Craig-Gordon average. The origin of these concepts was a string-of-lakes model of Gat and Bowser (1991), which Yakir (1992) suggested could be applied to a line of evaporating cells. This was done by Helliker and Ehleringer (2000) and applied to observations on monocot leaves. They used a finite number of “lakes,” and the concept was extended to an infinite number of elements by Farquhar and Gan (2003) and later applied to maize (Zea mays) leaves by Gan et al. (2003).

The detailed theory requires several elements. One needs to consider both mesophyll and veins (Allison et al., 1985), as well as the Péclet effect discussed already. The latter is essentially a radial effect, from xylem to stomata. But there is a longitudinal Péclet effect also, and here the value of P will be large, as the advection along a vein will be great compared to back diffusion. The full theory is complex and depends on the pattern of transpiration and on any taper of the leaf and of xylem elements (Farquhar and Gan, 2003; Barnes et al., 2004; Ogée et al., 2007). Recently Ogée et al. (2007) have used an iterative model to extend progressive enrichment into non-steady-state conditions. The detailed experimental testing of these models requires multiple measurements in space and time. So far the uncertainty has mostly related to why the leaf tip is less enriched than Δ_M. The modeling of this aspect is sensitive to the nature of leaf tapering.

APPLICATIONS

Thus far we have considered the application in terms of interpretation of the isotopic composition of organic matter. Ecophysiological applications include resource utilization by mistletoes (Amyema miquelii, Amyema preisii; Cernusak et al., 2004) and interpretation of effects of pollution (Saurer et al., 2001). Recently, Helliker and Griffiths (2007) modeled and validated the changes in δ¹⁸O of Tillandsia usneoides (Spanish moss, a rootless epiphytic crassulacean acid metabolism plant) that occur after rain falls as the plant dries out. They emphasize the importance of the one-way fluxes between the plant and the atmosphere and show how herbarium material of this species may be used as a proxy for δ¹⁸O of water vapor.

There are effects on atmospheric isotopic composition also. Atmospheric CO₂ undergoes oxygen isotopic exchange with leaf water and soil water, and changes in the δ¹⁸O of CO₂ can be used to study spatial and temporal variation in the net exchange of CO₂ in terrestrial ecosystems, and its underlying causes, dominated by photosynthesis and respiration (Farquhar et al., 1993; Cuntz et al., 2003). It had earlier been thought that CO₂ respired from leaves would be in isotopic equilibrium with leaf water, minus a diffusional fractionation factor of about 8‰ (Yakir et al., 1994). However, as with water vapor fluxes into and out of the leaf, it is the one-way fluxes that must be considered, and it is now recognized that invasion of CO₂ from the atmosphere, followed by exchange with leaf water, can enrich the isotopic signature of respired CO₂ (Cernusak et al., 2004), although just what part of the leaf water exchanges, and to what degree, is not fully understood.

O₂ is released by the plant during photosynthesis. The isotopic composition of evolved oxygen is identical (within an experimental error of <0.01‰) to that of the substrate water in the chloroplast thylakoids (Guy et al., 1993), and so an understanding is required as to where the chloroplasts sit in the catena of isotopic enrichment from soil water to the sites of evaporation within leaves. Changes in the oxygen isotope ratios of atmospheric O₂ are revealed on long time scales in the Dole effect (Dole et al., 1954), where atmospheric oxygen is currently enriched in ¹⁸O by 23.5‰ compared with mean ocean water. Recorded changes in the Dole effect are applied in the study of variations in the balance of terrestrial and marine productivity (Bender et al., 1985; Bender et al., 1994). As well as oxygenesis, the Dole effect depends on fractionation during respiration and weakly on stratospheric phenomena.

The processes leading to enrichment of water isotopes in leaves fractionate O₂ isotopes and the oxygen isotopes of CO₂ in a mass-dependent way, as does respiration. That is, the enrichment in ¹⁷O over ¹⁶O is about half of the enrichment of ¹⁸O over ¹⁶O. In contrast, photochemical reactions among O₃, O₂, and CO₂ in the stratosphere fractionate oxygen isotopes in a non-mass-dependent way and with about equal lowering of δ¹⁷O and δ¹⁸O in atmospheric O₂, and, similarly, about equal enhancement of δ¹⁷O and δ¹⁸O in atmospheric CO₂ (Thiemens et al., 1995; Luz et al., 1999; Luz and Barkan, 2000; Hoag et al., 2005). This causes a ¹⁷O anomaly in O₂ that depends on the relative rates of photosynthetic O₂ production and stratospheric photochemical reactions. If the latter rates are known, the overall global rate of photosynthetic oxygenesis can be estimated from the magnitude of the ¹⁷O anomaly in O₂ (Bender et al., 1994). This approach was applied by Luz et al. (1999) and Blunier et al. (2002), using air trapped in polar ice cores, to estimate the global rate during the last glacial period. It relies, of course, on assumptions concerning constancy or otherwise of the stratospheric reaction rates. The most recent contribution to plant physiology in this field describes fractionation of the three stable oxygen isotopes by photosynthesizing organisms (Helman et al., 2005).

Leaf transpiration contributes water vapor to the atmosphere, with an oxygen isotope composition equal to that of soil water. Similarly, the evaporation of rain intercepted by leaves involves no fractionation when all the water has been evaporated. However, soil evaporation and sublimation (snow) involve hydrogen and oxygen isotope fractionation of water molecules (Moser and Stichler, 1975; Gibson, 2001), and water at the mouth of rivers with a notable evaporative component is enriched in the heavy isotopes, compared with catchment precipitation. In hydrology it is important to be able to distinguish transpiration from soil evaporation. The evaporation component in the evapotranspiration (ET) flux can be estimated using isotope mass balance equations, such as those proposed by Gat and Bowser (1991), Gat and Matsui (1991), and Gibson et al. (1993, 1996). Recently, this was done for the Mississippi watershed by Lee and Veizer (2003), who used their results to predict net primary productivity for the region. Their calculations incorporated “water-use efficiencies” derived from the data of Shantz and Piemeisel (1927) for C₃ and C₄ species; however, modern studies with measurements of vapor pressure deficits and carbon isotope composition (Farquhar and Richards, 1984) would have been of great benefit in their approach.

Measurements of the isotopic composition of water vapor have been used to estimate transpiration fluxes in rice (Oryza sativa) crops (Brunel et al., 1992). Such estimates were shown to be in good agreement with one-dimensional aerodynamic energy budget calculations, although the technique is restricted to stable conditions when vertical gradients of isotopic composition near the ground are relatively high.

At an ecosystem scale, ET may also be partitioned by making Keeling plots of isotopic composition of water vapor versus water vapor partial pressure over a period of a few hours (Yepez et al., 2003). The intercept at infinite partial pressure is taken as the average composition of ET and then compared with soil water (representing the composition of transpired water) and the composition of evaporated water (using a calculated value based on the Craig-Gordon equation applied to soils; Williams et al., 2004). The assumptions underlying the above applications need to be tested against our understanding of leaf water isotopic composition, although they involve different timescales from those discussed earlier. For example, initially, intercepted water evaporated from a leaf surface after rain will be depleted (Farquhar and Cernusak, 2005), while remaining enriched water will also be evaporated over the following hours, so that, on a daily time scale, this particular form of evaporation can be regarded as not discriminating. Similarly, transpiration from a leaf itself at this time scale can be considered as not discriminating (Harwood et al., 1999).

The isotopic composition of water vapor plays a direct role in nearly all topics discussed above since it is a key component in the calculation of leaf water isotopic enrichment (Lee et al., 2006). It is likely that detailed general circulation models of the water cycle will increasingly involve isotopic considerations, and leaf processes are relevant here also (see IPILPS program at http://ipilps.ansto.gov.au).

It is now accepted that plants play an important role in the world's climate, affecting it as well as being affected by it. These plant-atmosphere interactions will be better understood as we probe them using models and measurement of the heavy isotopes of water.