Penetrating arterioles are a bottleneck in the perfusion of neocortex

Abstract

Penetrating arterioles bridge the mesh of communicating arterioles on the surface of cortex with the subsurface microvascular bed that feeds the underlying neural tissue. We tested the conjecture that penetrating arterioles, which are positioned to regulate the delivery of blood, are loci of severe ischemia in the event of occlusion. Focal photothrombosis was used to occlude single penetrating arterioles in rat parietal cortex, and the resultant changes in flow of red blood cells were measured with two-photon laser-scanning microscopy in individual subsurface microvessels that surround the occlusion. We observed that the average flow of red blood cells nearly stalls adjacent to the occlusion and remains within 30% of its baseline value in vessels as far as 10 branch points downstream from the occlusion. Preservation of average flow emerges 350 μm away; this length scale is consistent with the spatial distribution of penetrating arterioles. We conclude that penetrating arterioles are a bottleneck in the supply of blood to neocortex, at least to superficial layers.

The mammalian brain has developed specialized vascular architecture to maintain and regulate the distribution of blood. The large cerebral arteries supply blood to the cortex through a highly redundant grid of surface arterioles. Flow in this grid may be considered as a robust compliant source of blood (1, 2). In contrast to the 2D architecture of this surface network, the subsurface microvascular bed consists of a tortuous plexus of small vessels that course in three dimensions, in which much of the exchange of gas, metabolites, and heat occurs. The surface and subsurface networks are bridged by penetrating arterioles, which branch from the surface arterioles and dive radially into the brain tissue (3). However, it is not known whether the penetrating arterioles associate with spatially segregated territories of microvasculature, as opposed to territories that are interdigitated (4, 5).

Past work has shown that the location of a clot within the anatomical subregions of the microvascular network strongly determines the extent of the resulting ischemia. For example, a clot in a surface arteriole, which constitutes one branch of the surface network with its extensive anastomoses, leads to a relatively weak reduction in flow in downstream surface vessels (2). A clot in deep-lying microvessels, where the vasculature is relatively less interconnected (6, 7), results in a significant decrement in blood flow (8). In contrast to the substantial interconnections within the surface and subsurface networks, the penetrating arterioles that bridge these networks appear to be largely devoid of anastomoses (4, 9). This architecture casts the penetrating arterioles as a singular element for the regulation of blood flow to columnar-sized regions of cortex (10–12). Yet this very same feature is likely to cause pronounced ischemia if the penetrating arterioles are occluded. In support of this hypothesis, the microstrokes observed in human patients are often centered around penetrating arteries and arterioles with obstructed lumens (13, 14). Further, the occlusion of penetrating arterioles in animal models by the intraarterial injection of occluding particles, such as microemboli or microbeads, can result in infarcts (15–18).

In this work, we examine the hypothesis that penetrating arterioles are bottlenecks in the supply of blood to the cortex. We ask: (i) What is the magnitude and extent, both in terms of topology and space, of the reduction of blood flow after the occlusion of a single penetrating arteriole? (ii) Is there a relationship between the size of the territory with flow reductions and the spacing between an occluded arteriole and neighboring patent penetrating arterioles?

Results

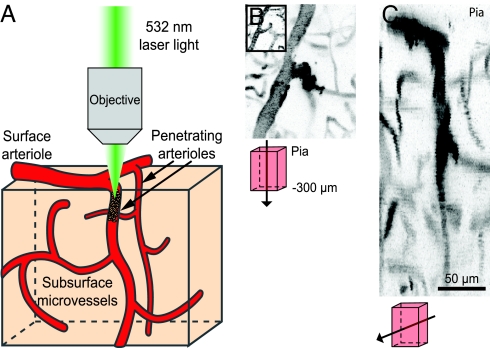
Large-scale maps of the brain vasculature of rat in the field of a craniotomy, obtained with in vivo two-photon laser-scanning microscopy (TPLSM) (19) and labeling of the blood plasma with fluorescein/dextran, reveal branches of the surface communicating arteriole network as well as penetrating arterioles. Candidate vessels for photothrombotic clotting are identified from the maps and traced back to a readily identifiable artery or vein on the pial surface; we targeted only arterioles that had branches in the upper 400 μm of cortex (Fig. 1A). High-resolution planar images were used to measure the diameter of the penetrating arteriole and to map vessels that lie up- and downstream from the target. Line-scans along the axis of a vessel were used to measure red blood cell (RBC) velocity (2, 20–24). After baseline velocities were determined, the photosensitizer rose bengal was injected, and green laser light was focused at high-numerical aperture into the target penetrating arteriole to form a clot (2) (Fig. 1A).

Fig. 1.

Induction of clots in penetrating arterioles by photothrombosis. (A) Schematic of experimental set-up. Green laser light is focused into a penetrating arteriole by a microscope objective concurrent with TPLSM of the vasculature. (B and C) Maximal projections in the tangential (B) and sagittal (C) directions of image stacks through a penetrating vessel clot; schematics indicate the directions and volumes of projection. The clot is visualized as a dark mass in the target vessel that is often surrounded by bright areas of stalled, labeled plasma. The images are inverted for clarity. B Inset shows tangential view before irradiation.

Our photothrombotic clots occluded the most proximal portion of the target vessel (Fig. 1 B and C), so that there was no flow in the section from the last surface branch to at least the first vessel that branches laterally below the pial surface. Only one penetrating arteriole per animal was occluded. Before occlusion, the mean speed of RBCs in the targeted vessels was 9.2 ± 4.8 mm per s (mean ± SD; n = 16), and the average diameter was 10.5 ± 3.4 μm. Blood flow in the surrounded vasculature was quantified before and after occlusion of a penetrating arteriole.

Topological Dependence of Impacted Flow.

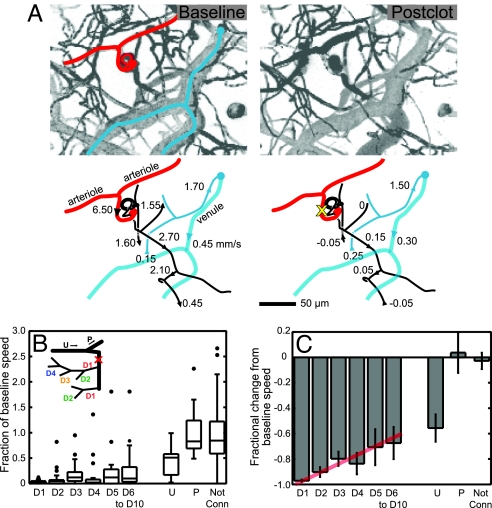
We categorized the flow in microvessels by their connectivity to the target penetrating arteriole (Fig. 2B Inset). The measured vessels included those that lie both upstream and parallel to the target vessel, and subsurface microvessels down to ≈400 μm below the pia. Vessels that branched laterally off the penetrating arteriole were denoted as downstream (D) and were categorized by the number of branches between the measured vessel and the penetrating vessel. Thus, D1 vessels were directly connected to the penetrating arteriole, whereas D2 vessels were two branch points away, etc. In a few cases, the penetrating vessel did not maintain a trunk that stayed larger than capillary diameter, i.e., ≈5 μm, and in these cases, the penetrating vessel was categorized as a D1 vessel after its size diminished to capillary diameter. Vessel segments from surface arterioles that fed the penetrating vessel were categorized as upstream (U), and arterioles that shared the same source as the penetrating vessels were categorized as parallel vessels (P).

Fig. 2.

Blood-flow changes categorized by topology. (A) Projections of image stacks in the vicinity of the occluded arteriole and schematics of RBC velocity before (Upper) and after (Lower) clot generation in a penetrating arteriole. The target vessel is marked by a yellow X and spirals into the parenchyma. Negative numbers indicate flow direction has reversed in direction after clot relative to baseline. (B) The fraction of baseline speed after the clot across all measurements. Each box contains the middle two quartiles of the data, middle-line segment indicates median, whiskers indicate acceptable range of data, and dots indicate outliers that are outside the range of the middle two quartiles ± 1.5 times the interquartile distance. Downstream branches are grouped by number of branches from target penetrating vessel (D1–D10), as indicated in schematic on the left. Upstream (U), parallel (P), and vessels that had no connection to the target vessel visible in TPLSM stacks are grouped separately. (C) Fractional change from baseline speed vs. connectivity. We show the mean values and the SEM. The red line is a guide to highlight the trend in the data.

An example data set (Fig. 2A) demonstrates both increases and decreases in blood speed after the occlusion, as well as reversal in the direction of flow (8), and is suggestive of a high variability in the observed changes in the speed of RBCs. As indicated by the values in each branch order (105 vessels total across 16 animals), the speed of RBCs in vessels downstream from the occluded penetrating vessel was severely reduced and did not recover to baseline values even as far as 10 branches distal to the target vessel (Fig. 2 B and C). In the first branch downstream from the penetrating arteriole (D1), RBCs are almost stalled as median speeds dropped to 0.03-times their baseline values after penetrating arteriole occlusion (D1; Fig. 2B). Branches further downstream showed smaller decreases in speed, but median speeds only approached 0.1-times their baseline speed even as far as 10 branches downstream (D3–D10; Fig. 2B). If we consider the mean values of speed, which highlights trends in the data, we see that the speed tends toward its baseline level from a value of 0.03 ± 0.01 (mean ± SEM) −times baseline for D1 vessels to 0.33 ± 0.13 −times baseline for D6–D10 vessels (Fig. 2C).

Spatial Dependence of Flow Change.

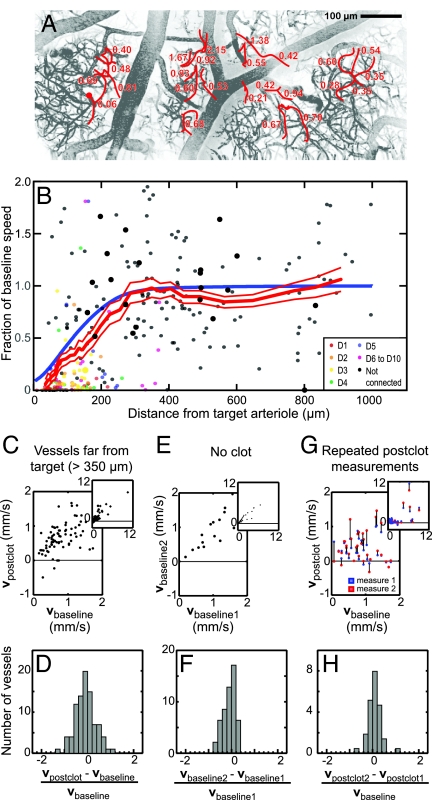
The decrement in RBC flow in response to occlusion of a penetrating arteriole extended far downstream, so much so that our ability to maintain accurate count of the branch order was limited by the penetration depth of TPLSM imaging. We thus analyzed changes in RBC speed in deep microvessels with respect to the lateral distance from the occluded arteriole and without respect to connectivity. As in the analysis according to branch order (Fig. 2), we found a broad range of changes in blood flow after occlusion of the penetrating arteriole (295 vessels across 16 animals) (Fig. 3A). These changes include both increases and decreases in RBC speed in vessels that lie hundreds of micrometers away from the target vessel. A compendium of all data, pooled across the 50- to 400-μm depth of the measurements, shows a trend in the mean RBC speed relative to baseline that increases from near zero at the target penetrating arteriole and returns to baseline by 350 μm away (Fig. 3B; the branch order of the measured vessels is color-coded), with half of the baseline speed obtained by 165 ± 25 μm (red line is running mean of 50 data points ± SEM). Last, the change in RBC speed showed no dependence on depth below the pia (data not shown) within the range of our measurements.

Fig. 3.

Distance dependences of changes in blood flow after an occlusion. (A) Maximal projection of vessels across the cortex, with the fraction of baseline RBC speed after photothrombotic clot indicated. The clotted penetrating arteriole is indicated by the red circle. (B) Fraction of baseline RBC speed after the occlusion vs. distance from the occluded arteriole. The connectivity of the measured vessels is color-coded, as indicated. The thick red line through the data is the smoothed response averaged over a window that included 50 points, with ±1 SEM limits indicated by the thin red lines, and the blue line is the prediction of the change in RBC speed from a model with an exponential spatial distribution for the flow away from a blocked penetrating arteriole (Fig. 6). Large dots are from the case illustrated in Fig. 5. (C and D) Data graphs (C) and histogram (D) of changes in RBC speed induced by a clot >350 μm away from the measured vessels. Two outliers, with relative speeds of 2.6 and −2.8, were excluded from analysis in D. (E and F) The inherent variability in two measurements separated by 30–60 min, with no clot present. (G and H) The inherent variability in two measurements separated by 30–60 min, with both measurements taken after a clot in the targeted arteriole was formed. The first and second measurements after induction of the clot are shown in blue and red, respectively, with black lines linking measurements on the same vessel. Insets show the full range of the data.

The mean RBC speed remained at baseline values for distances ≈350–900 μm from the target arteriole, yet these postclot speeds appeared to show increased variability (Fig. 3B). This spread in values is most apparent from a graph of the postclot velocity, denoted v_postclot, vs. the baseline velocity, denoted v_baseline (Fig. 3C). We quantified the spread about a linear dependence between v_postclot and v_baseline in terms of the ratio (v_postclot − v_baseline)/v_baseline (Fig. 3D), which has a root-mean-square (rms) width of σ ≈ 0.45. To establish that the spread was dominated by variability in the value of RBC velocities that is induced by the clot, as opposed to intrinsic variability in RBC speed (21) and/or biases in our measurement process, we performed two control experiments. In the first set, we sought to estimate the inherent variability in RBC flow through microvessels. We used animals with no clots in penetrating arterioles and measured the baseline speed of RBCs at two different times, 30–60 min apart, in deep microvessels (Fig. 3E). The data set consisted of vessels of similar depth and caliber as those measured in experiments with occluded vessels (Fig. 3 A and B), and the spread in measurements was quantified in terms of the analogous ratio (v_baseline2 − v_baseline1)/v_baseline1 (Fig. 3F). The distribution for this control data had a rms width of σ ≈ 0.30, less than that for the postclot data. In a second set of control experiments, we sought to establish whether the flow in vessels after an occlusion evolves over the timescale of our measurements. A penetrating arteriole was blocked and RBC velocities were measured at two different times, again 30–60 min apart, after the formation of the clot (Fig. 3G). The mean speeds for the two sampling times were statistically indistinguishable, i.e., v_postclot1 = 0.85 ± 0.28 mm/s (mean ± SEM) vs. v_postclot2 = 0.90 ± 0.35 mm/s, whereas the spread in value between the two measures, quantified in terms of the ratio (v_postclot2 − v_postclot1)/v_baseline (Fig. 3H), also had a rms width of σ ≈ 0.30. There is no statistical difference between the distributions of velocities for the two control groups (P < 0.75 as compared with the Fisher–Snedecor f distribution). Critically, the normalized distribution of the change in velocities among distant vessels after vs. before a clot was statistically broader than the distributions for the control groups (P < 0.0002) (compare Fig. 3 D vs. F and H). Thus the variability in blood flow through microvessels is increased after occlusion of even a distant penetrating arteriole.

Validation of a Localized Occlusion.

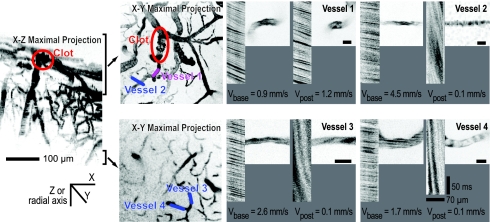
Several aspects of the blood flow measurements made within ≈200 μm of the targeted penetrating arteriole indicated that the observed ischemia does not reflect nonlocalized effects of photothrombosis. First, we monitored blood flow in upstream and parallel vessels on the surface. Flow in upstream vessels, at one branch point away from occluded vessel, showed a decrease to about half the baseline speed after an occlusion, as expected for an increase in resistance distal to the upstream source (Fig. 2 B and C). Flow in parallel vessels showed almost no change on average (Fig. 2 B and C). These results for the surface vessels suggest that the effects of photothrombosis are localized only to the targeted penetrating arteriole. Second, we measured RBC flow in deep vessels that were present in the same field of view as the vessels downstream of the target but had no obvious connection to the occluded penetrating arteriole. In the case illustrated in Fig. 2A, examples of unconnected vessels, indicated in blue, were connected to a radially draining venule and showed little effect from the laser. On average, blood flow in nonconnected vessels within 200 μm of the target vessel slowed to only 0.88 ± 0.15 (mean ± SEM) of the initial RBC speed after penetrating vessel occlusion, whereas flow in vessels within the same spatial range that were observed to be connected to the target slowed to 0.16 ± 0.03 of the initial speed (Fig. 2 B and C). In vivo image stacks also showed that the majority of vessels in the vicinity of the target vessels appeared normal. In the case illustrated by Fig. 4A and B, we consider two microvessels that lie close to the clot. Flow in one vessel is essentially stopped after the clot (vessel 2), whereas flow in the other continues largely unchanged (vessel 1). Two deeper vessels are observed to have substantially reduced flow (vessels 3 and 4); additional details are in supporting information (SI) Fig. 8. In general, RBC flow in vessels in the vicinity of the occluded arteriole indicates that the majority of vessels in the neighborhood of the target were neither clotted nor structurally affected by the laser light.

Fig. 4.

Blood flow in vessels in the immediate neighborhood of the clot. Side projection in the coronal (x-z) plane of image stacks around a penetrating arteriole clot (yellow ellipse). The depth of the projections in the tangential (x-y) plane is noted and the line segments indicate specific microvessels whose velocity, and spatial profile was measured before and after the occlusion. High-magnification images and line-scan data for indicated vessels are shown before and after induction of a clot. For the latter data, the nonfluorescent RBCs appear as dark streaks on a bright background; the sign and magnitude of the slope of the streaks reflects the direction and speed, respectively, of RBC motion.

Histological effects of a penetrating arteriole occlusion were assessed in qualitative assays of brain pathology. We identified the territory in which the clotted vessel resided by the fluorescence of groups of vessels that retained fluorescein/dextran dye. This effect is likely to be a consequence of laser irradiation but is independent of measured blood flow changes (2) (Fig. 5A2′). These fluorescent regions were found to be selectively marked by tissue hypoxia, as inferred from immunocytochemical identification of cellular uptake of pimonidazole hydrochloride (HypoxyProbe, Chemicon, Temecula, CA) (Fig. 5 A2 and A2 Inset) and from the absence of similar concentrations at levels 0.5 mm both medial and lateral (Fig. 5 A1 and A3). The clot territory was also marked by vascular immunoreactivity to IgG, a sign of abnormal vessel leakiness (25) (Fig. 5 B2 and B1′–B3′). Immunostaining for IgG also extended more weakly to tissue sections located 1.1 mm medial and lateral from the clot territory (Fig. 5 B1 and B3). This spatially extensive vascular immunoreactivity for IgG is consistent with the observation of increased variability in blood flow, in which some vessels show substantial decreases after clot formation in a distant penetrating arteriole (Fig. 3 C and D).

Fig. 5.

Tissue reactions in region of occluded penetrating arteriole. Sagittal section series taken across a 2.2-mm span centered on the fluorescent vessels that demarcate the core territory of the clotted arteriole (A2′, inverted image). These sections relate to the experiment that gave rise to the large dots in Fig. 3B. (A) Sections stained to localize tissue hypoxia demonstrate a confined high-density of staining at the level of the center of this series. The location of the clot is confirmed by trapped fluorescein/dextran (A2′). (B) Sections stained for immunoreactivity to IgG illustrate that vessel leakiness (B1′, B2′, and B3′) is concentrated at the center of this series (B2) yet extends up to 1.1 mm in medial and lateral directions.

Spatial Distribution of Penetrating Arterioles.

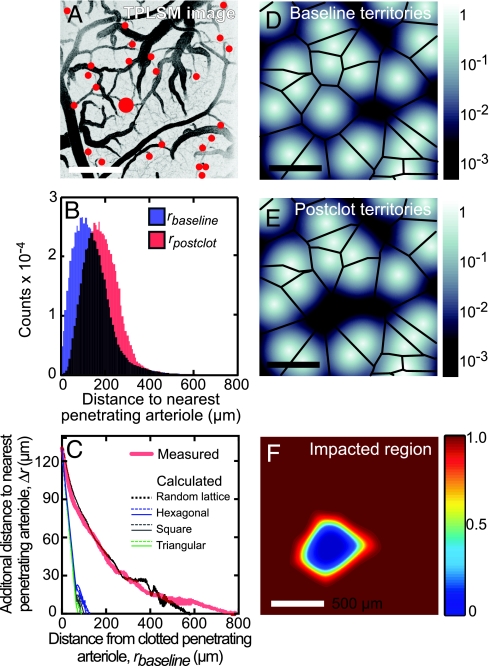
We measured the distribution of penetrating arterioles to analyze how their statistics might affect the area impacted by occlusion of a single penetrating arteriole. The locations of all arterioles were identified from large-area images of the cortical vasculature (Fig. 6A). The mean distance between nearest-neighbor pairs of penetrating arterioles was 130 ± 60 μm (mean ± SD) with an irregular distribution (n = 125 arterioles across four animals). A measure relevant to the flow of blood is the radial distance from every pixel across the cortical surface to the nearest arteriole, denoted r_baseline (see SI Text and SI Fig. 9). We numerically calculated the distribution of r_baseline (n = 71 after arterioles at the edge of the imaging field are excluded), and observed a mean distance of <r_baseline> = 145 μm (blue histogram; Fig. 6B). The effect of an occlusion of a penetrating arteriole was estimated by deleting an arteriole and calculating the radial distance from pixels within the territory of the deleted vessel to the nearest remaining arteriole, denoted r_postclot. The distribution of r_postclot was calculated across all arterioles, and the mean value was <r_postclot> = 205 μm (red histogram; Fig. 6B). Finally, the effect of the clot on flow at a given location across cortex may be related to the increased distance to unclotted arterioles relative to the distance to the original but now clotted arteriole. We denote this change in distance by Δr r_postclot − r_baseline. Near the clotted arteriole, Δr = 130 μm, which equals the mean distance between nearest neighboring arterioles, as expected. The value of Δr decreases to an asymptotic value Δr → 0 far from the vessel, where the average distance to the clotted penetrating arteriole equals to the distance to an unperturbed arteriole (red trace; Fig. 6C). The distance to achieve half of this decrement is 135 μm, which is also close to the value of the mean spacing between arterioles.

Fig. 6.

Spatial analysis of vascular territories. (A) Image of the surface vasculature with penetrating arterioles marked with red dots; largest for the occluded arteriole. (B) Histograms of distances from pixels in the images to the nearest penetrating arteriole (r_baseline, blue) and the second-nearest arteriole (r_baseline, red). (C) The difference in radial distance from the first- and second-nearest penetrating arteriole, Δr, as a function of distance from the nearest arteriole, r_baseline (red curve). The calculation was performed for penetrating arteriole locations that were randomly assigned while maintaining a mean density of arterioles equal to the measured value (black curve) and for arterioles arranged in regular patterns, i.e., hexagonal (blue curve), square (gray curve), and triangular (green curve) lattices; see SI Text. (D–F) Model of blood flow from penetrating arterioles, in which the contribution of flow in the tissue was described by an exponential decay, i.e., e^−r/λ′, where r is the radial distance from the arteriole, and λ′ = 40 μm. The calculated sum of the flow from all penetrating arterioles, located as in A, is shown in D. The calculated sum of the flow with an occluded arteriole, modeled by the removal of the arteriole marked in red in A, is shown in E. Black lines in D and E demarcate the pixels that are equidistant from more than one arteriole. The calculated ratio of blood flow that remains after occlusion of a penetrating arteriole (A) is shown in F.

As a means to gain insight between the functional form of Δr and the spatial arrangement of the penetrating arterioles, we numerically calculated the form of Δr for different spatial arrangement of arterioles. We used a distribution of randomly located penetrating vessels that maintained the same average density of penetrating arterioles as the experimental measurement, i.e., 13 ± 3 vessels/mm² (mean ± SEM; four animals) and found that the dependence of Δr on r_baseline was similar to the experimental data (compare black and red traces in Fig. 6C). For comparison, we calculated Δr for simulated distributions of arterioles arranged in triangular, square and hexagon lattices (SI Text and SI Fig. 10). The edge length of each lattice was set equal to the measured mean distance between pairs of nearest neighbor arterioles to force Δr for the simulations to equal the experimental value at r_baseline = 0. These simulations with regular lattices show a much more rapid decrease in Δr with distance from the occluded arteriole than the actual data. In an alternative calculation, the density of penetrating arterioles in each lattice was set equal to the experimentally observed value, with a concomitant increase in nearest neighbor distance from the measured mean value of 130 μm, to values of 277 μm for square, 290 μm for triangular, and 243 μm for hexagonal lattices. In all three regular lattices, Δr decreases to zero at r_baseline < 300 μm. We conclude the observed distribution of increased distance to a patent penetrating arteriole after a clot is consistent with a random spatial distribution of arterioles (Fig. 6C).

A Model for Blood-Flow Reduction.

The parsimonious interpretation of our data is that collateral flow from other penetrating arterioles makes a limited contribution to the territories about each diving arteriole. We attempted to quantify this notion by relating the dependence of the decrement in RBC speed on distance (Fig. 3B) to the spatial distribution of penetrating arterioles (Fig. 6 D–F). A 2D continuum model of the contribution of one penetrating arteriole to the perfusion of local tissue was constructed by using the measured locations of penetrating arterioles, as above. We represented the parenchymal flow from each arteriole by a monotonically decreasing function with cylindrical symmetry about the arteriole and assumed that the blood flow at any point in the tissue was the sum of the contributions from every penetrating arteriole (SI Text and Fig. 11). We then calculated the expected decrement in flow as a function of the distance from the occlusion for different radial functions. An exponential decay with length constant of 40 μm, which corresponds to the nominal distance between branch points of microvessels (26), together with the observed random distribution of arteriole spacing (Fig. 6C), yields a good fit to the average flow changes as a function of distance (blue and red lines in Fig. 3B). The predicted flow within the territory that surrounds each penetrating arteriole is relatively uniform except near some boundaries between neighboring territories (Fig. 6D). The occlusion of a single penetrating arteriole yields a well localized region of decremented flow (Fig. 6 E and F). Thus our model accounts for the major effect of an occlusion.

Discussion

Our measurements of the changes in blood flow induced by an occlusion suggest that a single penetrating arteriole contributes significantly to blood flow over a cortical area that extends up to 350 μm in radius (Figs. 3 and 6). Detailed flow measurements on a branch-by-branch basis highlight the severe decrement in flow close to the occluded arteriole (Figs. 2 and 4). These measurements support the idea that the microvascular bed contains distinct territories that are supplied by a single penetrating arteriole. However, there is also significant variability in the speed of RBC well beyond the territory of an occluded vessel (Fig. 3 C and D). We interpret this variability as evidence that different territories are also interconnected at the microvascular level, albeit with insufficient capacity to maintain normal levels of flow.

The measured distribution of distances between penetrating vessels is consistent with random spacing (Fig. 6C). Further, the density is sparse compared with lattices of penetrating arterioles whose spacing is set equal to the mean distance between nearest neighboring arterioles. In lattices, the territory of each arteriole is smaller than the experimentally measured spatial configurations (Fig. 6C). A model of blood flow that incorporates the measured distribution suggests that removal of a penetrating vessel can have a long-range effect based on purely the geometric distribution (Fig. 6E), as observed (compare data and model in Figs. 3B and 6C). The result of this analysis suggests that the changes observed in blood flow after penetrating vessel occlusion are passive properties of the vascular geometry. Thus, variation in nearest-neighbor arteriole distances may play a role in modulating the severity and area of ischemia after occlusion.

Flow Within the Cerebrovascular Hierarchy.

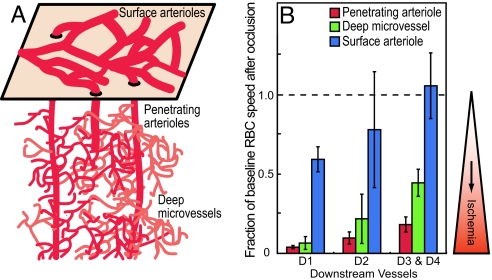
A comparison of the sensitivity to changes in blood flow after a clot among three different levels in the cerebral vascular hierarchy suggests that ischemia is most severe when a clot is located in a penetrating vessel (Fig. 7). Previous work has shown that a clot in the surface network of arterioles generates only a mild decrease in blood flow, even as close as the first branch downstream (2). This is consistent with the richly interconnected 2D nature of this network. In contrast, a clot in a deep microvessel leads to a severe drop in the speed of RBCs in the first downstream branch (8), similar to the drop observed after the occlusion of a penetrating arteriole. However, the flow returns to 0.5-times baseline values within three branches from the blockage, consistent with collateral flow through microvessels that originates from the same penetrating arteriole. In contrast to the case for surface arterioles and deep microvessels, occlusion of a penetrating arteriole has a devastating effect on the flow through downstream microvessels, as collateral flow from neighboring penetrating arterioles is limited. Thus, the penetrating vessels are bottlenecks in the link between surface arterioles and the tortuous network of microvessels that supplies blood throughout the depth of cortex (Fig. 7).

Fig. 7.

Summary of flow changes from occlusions at different levels of cortical angioarchitecture. (A) Schematic of the highly interconnected surface network of arterioles and tortuous network of microvessels below the surface. (B) Bars show the mean and SEM of fraction of baseline RBC speed after occlusion of either penetrating arterioles (this work), deep microvessels (8), or surface communicating arterioles (2) for vessels at different downstream branches relative to the occluded vessel.

Relation to Human Microstroke.

The dramatic decrease in blood flow after the photothrombotic occlusion of penetrating arterioles is consistent with observations of pathology in human patients. Our results support the clinically based hypothesis that penetrating arterioles and arteries may be of central importance in small strokes (13, 14). For example, subcortical regions are particularity vulnerable to ischemia that results in lacunar lesions, because the blood flow in these regions comes from relatively long penetrating arteries (27). The extent of ischemia we measured in rat around an occluded penetrating arteriole (Fig. 3) suggests that lesions to the penetrating arteries are an important mechanism in cerebrovascular disease in humans. Recent work indicates that microstrokes that are completely or largely confined to the gray matter (28–30), along with small pial infarcts after certain strokes (31), have clinical consequences. We suggest that progress in treatment of small strokes will benefit from animal models of small stroke that target penetrating arterioles.

Methods

Our subjects were 16 male Sprague–Dawley rats, 100–350 g in mass, that were anesthetized by interperitoneal injection of urethane (150 mg per 100 g of rat) and maintained and surgically prepared for in vivo TPLSM imaging of parietal cortex as described (2). Image stacks of surface vasculature that were taken with a 0.28-N.A., ×4 air objective (Olympus, Melville, NY) and a 0.30-N.A. ×10 dipping objective. High-resolution imaging, line-scan measurements, and photoexcitation of the photosensitizer dye made use of a 0.8-N.A. ×40 dipping objective. The care and experimental manipulation of our animals have been reviewed and approved by the Institutional Animal Care and Use Committee at University of California at San Diego.

Occlusion of Penetrating Arterioles.

Penetrating arterioles were defined as vessels that branched off of a surface arteriole, penetrated into the brain parenchyma, and served as the sources for capillaries. All occluded penetrating arterioles selected for study had at least a short segment in which the flow was confined to the brain surface. This segment was used to measure the RBC velocity before the occlusion.

Photothrombotic occlusions made use of injections of rose bengal, as described (2). Green laser light, 0.1–5 mW, was focused in a diffraction-limited spot coplanar with the imaging beam to permit near real-time monitoring of clot progression. The spot was aimed into the lumen of the target vessel in locations that ranged from just distal from its upstream source on the brain surface to above the first branch to the capillary bed, but no deeper than 50 μm below the pia. The vessel was irradiated in bouts that lasted 2–5 s with the spot scanned to ensure a complete clot.

Immunohistochemistry.

In seven cases, animals were injected with the ischemia marker pimonidazole hydrochloride (HypoxyProbe-1) (90201; Chemicon) 1 h before death. After anesthesia overdose, the animals were perfused transcardially with 100 ml of phosphate-buffered saline (PBS), followed by 100 ml of 4% (wt/vol) paraformaldehyde in PBS. Fiducial marks were made at known locations relative to the target vessel by passing −20 μA through a single tungsten electrode that was translated at 2 mm/s through the tissue. The brain was removed and cryoprotected with 50% (wt/vol) sucrose in PBS, and 50-μm-thick sections were cut in a sagittal plane on a freezing-sliding microtome. Sections near the location of the clots were selected based on the location of the targeted vessels relative to the fiducial marks.

Reduced pimonidazole was visualized in tissue sections by incubation for 48 h in primary antibody (anti-HypoxyProbe) (90204; Chemicon), diluted 1:1,000 in PBS with 10% (vol/vol) goat serum and 2% (vol/vol) Triton X-100, followed by biotinylated rat-adsorbed anti-mouse IgG antibody (BA2001, Vector Laboratories, Burlingame, CA), avidin-biotinylated peroxidase complex (PK4000; Vector Laboratories), and finally a diaminobenzidine reporter (SK4100; Vector Laboratories). Immunoreactivity to IgG was performed by overnight incubation of sections in biotinylated antiuniversal IgG antibody (PK6200; Vector Laboratories) at 1:1,000 dilution in the PBS-based diluent followed by the previous sequential incubation steps.

Abbreviations

TPLSM

two-photon laser-scanning microscopy

D

downstream

U

upstream

P

parallel.